56 Резонанс напряжения и резонанс тока - услуги электромонтажа, строительства и ремонта

Из формулы (74) следует, что, изменяя емкость C или индуктивность L, мы можем изменить частоту ω₀ электричества и тока в цепи, т.е. можно настроить нужную частоту.

Содержание

§56 Резонанс напряжения и резонанс тока

Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, в котором происходит процесс колебания электрической энергии, переходящей от индуктивности к емкости и обратно. В идеальном колебательном контуре колебания не затухают.

Когда колебательный контур подключен к источнику переменного тока, угловая частота ω источника может стать равной угловой частоте ω₀с которой колеблется электрическая энергия в цепи. В этом случае возникает явление резонанса, т.е. частота свободных колебаний ω₀Резонанс в электрической цепи может быть получен тремя способами: изменением угловой частоты ω источника переменного тока, индуктивности L или емкости C.

Резонанс в электрической цепи может быть получен тремя способами: изменением угловой частоты ω источника переменного тока, индуктивности L или емкости C. Различают резонанс, когда L и C соединены последовательно -. резонанс напряжения а если они соединены параллельно – резонанс токов. Угловая частота ω₀при котором происходит резонанс, называется резонансная частота или собственная частота резонансного контура.

Резонанс напряжения.

В резонансе напряжений (рис. 196, а) индуктивность X_L равно емкостному сопротивлению X_с и полное сопротивление Z становится равным активному сопротивлению R:

В этом случае напряжение на индуктивности U_L и емкость U_c равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R мало, то ток в цепи быстро увеличивается, так как реактивное сопротивление цепи X = X_L-X_с становится равным нулю. В этом случае ток I находится в фазе с напряжением U и I=U/R. Быстрое увеличение тока в цепи во время резонанса напряжения вызывает аналогичное увеличение напряжения U_L и U_cЭти напряжения могут быть во много раз выше, чем напряжение U источника, питающего цепь.

Угловая частота ω0, при которой возникают условия резонанса, определяется уравнением ω_oL = 1/(ω₀С).

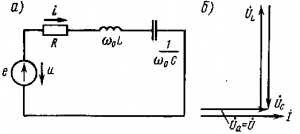
Рисунок 196: Схема (a) и векторная диаграмма (b) электрической цепи, содержащей R, L и C в резонансе напряжений

Если угловая частота ω источника плавно изменяется, то импеданс Z начинает уменьшаться и достигает своего наименьшего значения в резонансе напряжений (при ω_o), а затем увеличивается (рис. 197, а). Следовательно, ток I в цепи сначала увеличивается, достигает своего максимального значения при резонансе, а затем уменьшается.

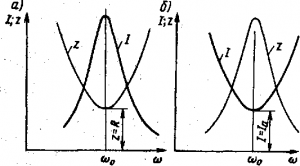
Рисунок 197. Зависимость тока I и импеданса Z от ω для последовательной (a) и параллельной (b) цепи переменного тока

Резонанс токов.

Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, a). В идеальном случае, когда в параллельных проводниках нет активного сопротивления (R₁=R₂ = 0), условием резонанса токов является равенство реактивностей ветвей, содержащих индуктивности и емкости, т.е. ω_oL = 1/(ω_oC).

alt=”Рисунок 198. Электрическая схема (a) и векторные диаграммы (b и c) для резонансных токов” width=”300″ height=”98″ />.Рисунок 198: Электрическая схема (a) и векторные диаграммы (b и c) для резонансных токов

Поскольку в этом случае активная проводимость G = 0, ток в неразветвленной части контура при резонансе I=U √(G 2 + (B_L-B_C) 2 )= 0. Значения токов ветвей I₁ и я₂ будут равны (рис. 198,b), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности задерживается относительно напряжения U на 90°, а ток в емкости I c задерживается относительно напряжения U на 90°).

Следовательно, такой резонансный контур является бесконечным сопротивлением току I, и в контур не поступает электрическая энергия от источника. В то же время, токи I_L и я_сЭто означает, что в цепи происходит непрерывный обмен энергией. Эта энергия передается от индуктивности к емкости и наоборот.

Из формулы (74) следует, что при изменении емкости C или индуктивности L частота ω₀ электричества и тока в цепи, т.е. настройка цепи на нужную частоту.

Если бы в ветвях, в которых находятся индуктивность и емкость, не было активного сопротивления, то этот процесс колебания энергии продолжался бы бесконечно, т.е. энергия и токи I_L и я_с.

Однако реальные индукторы и конденсаторы всегда поглощают электрическую энергию (из-за наличия активного сопротивления проводов в индукторах и наличия реактивных токов, нагревающих диэлектрик в конденсаторах), поэтому реальный контур в резонансном токе получает некоторую электрическую энергию от источника и некоторый ток I протекает через неразветвленную часть контура.

Условие резонанса в реальном резонансном контуре, содержащем активные сопротивления R₁ и Р₂уравнение реактивной проводимости B_L = B_C ветви, в которые включены индуктивность и емкость.

Из рис. 198, в следует, что ток I в неразветвленной части цепи находится в фазе с напряжением U, так как реактивные токи 1_L и я_с равны, но противоположны по фазе, так что их векторная сумма равна нулю.

Если частота ω_о При подаче переменного тока импеданс цепи начинает увеличиваться, достигает своего максимального значения при резонансе, а затем уменьшается (см. рис. 197b). Следовательно, ток I начинает уменьшаться, достигая наименьшего значения I_min = I_a при резонансе, а затем увеличивается.

В реальных колебательных контурах, содержащих активный резистор, каждое колебание тока сопровождается потерей энергии. В результате энергия, поступающая в цепь, расходуется довольно быстро, а колебательный ток постепенно уменьшается. Для получения затухающих колебаний необходимо постоянно восполнять потери энергии в активном резисторе, что означает, что цепь должна питаться от источника переменного тока достаточной частоты ω₀.

Явления резонанса напряжения и тока и колебательные контуры очень широко используются в радиотехнике и высокочастотных приложениях. С помощью колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах.

Колебательный контур – самый важный компонент любого радиоприемника. Это обеспечивает его избирательность, т.е. способность отделять сигналы конкретной радиостанции от радиосигналов разной длины волны (т.е. разных частот), передаваемых разными радиостанциями.

Общая сумма энергии в индуктивности и емкости (магнитном и электрическом полях) постоянна. Это происходит потому, что между этими полями происходит колебательный обмен энергией. Общее количество энергии неизменно в любой момент времени. Однако обмена энергией между ее источником E и цепью не происходит. Вместо этого происходит непрерывное преобразование одной формы энергии в другую.

Применение резонанса напряжения

Явление колебательного резонанса широко используется в радиоэлектронике. В частности, входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, которая изменяется путем регулировки емкости конденсатора, совпадает с частотой принимаемого сигнала радиостанции.

В электроэнергетике возникновение резонанса напряжения из-за связанных с ним перенапряжений чревато нежелательными последствиями. Например, если длинную кабельную линию (которая представляет собой колебательный контур с распределенными емкостью и индуктивностью) подключить к генератору или промежуточному трансформатору без подключения приемной стороны к нагрузке (это называется холостым ходом), то вся цепь может стать резонансной. В этой ситуации напряжения, генерируемые в некоторых частях цепи, могут быть выше расчетных напряжений. Это может привести к повреждению изоляции кабеля и его разрушению. Эта ситуация предотвращается путем использования вспомогательной нагрузки.

Резонанс – это явление, при котором частота колебательной системы увеличивается под воздействием внешней силы.

Резонанс напряжения

Когда активный элемент $r$, емкостной элемент $C$ и индуктивный элемент $L$ последовательно соединены в цепи переменного тока, может возникнуть физическое явление, называемое резонансом напряжения. Тогда частота колебаний источника напряжения будет равна частоте колебаний контура. Это явление, как известно, может быть как полезным (например, в радиотехнике), так и вредным (в мощных электроустановках), например, внезапный скачок напряжения в системах может привести к поломке или даже пожару.

Резонанс напряжения обычно достигается тремя способами:

Путем подбора индуктивности катушки;
Путем подбора емкости конденсатора;
Регулируя угловую частоту $w_0$.

Все значения емкости, частоты и индуктивности определяются по формулам:

Предполагается, что частота $w_0$ является резонансной. Если и напряжение, и сопротивление $r$ в цепи неизменны, то ток при резонансе напряжений в цепи будет максимальным и одинаковым:

При этом предполагается, что ток совершенно не зависит от реактивного сопротивления цепи. В ситуации, когда пассивное сопротивление $XC = XL$ больше активного сопротивления $r$, на клеммах катушки и конденсатора будет напряжение, значительно превышающее напряжение на клеммах цепи.

Кратность превышения напряжения на зажимах емкостного и индуктивного элемента по отношению к питающей сети дается выражением:

Величина $Q$ характеризует резонансные свойства контура и называется коэффициентом качества контура. Резонансные свойства также характеризуются значением $frac<1>.$, что является затуханием цепи.

) и его эквивалентная схема (
б
) Для него условием резонанса является то, что его реактивная проводимость равна нулю:
ImY =
0
. Это равенство означает, что мы должны иметь мнимую часть комплексного выражения Y
быть равным нулю. Определите комплексную проводимость цепи. Это равно сумме проводимостей комплексных ветвей:

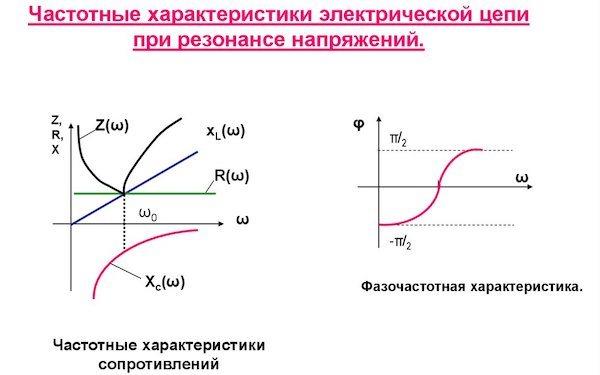
Резонансные характеристики

Все параметры, содержащиеся в схеме и присутствующие в полученном уравнении, так или иначе влияют на показатели, характеризующие резонансные явления. В зависимости от параметров, входящих в уравнение, решение может иметь несколько различных вариантов. При этом все решения будут соответствовать своим собственным вариантам, а затем приобретут физический смысл.

В различных типах электрических цепей явление резонанса обычно рассматривается в анализе для нескольких вариантов. В этих же случаях может быть проведен синтез схемы, в которой параметры резонанса заранее определены.

Электрические цепи, имеющие большое количество соединений и реактивных элементов, представляют собой серьезную проблему при анализе. Они никогда не используются в синтезе с заранее заданными свойствами, потому что не всегда можно получить желаемый результат. Поэтому на практике изучаются биполярные устройства простейших конструкций, а на основе полученных данных создаются более сложные схемы с заранее заданными параметрами.

Выразим резонансную частоту

Резонансные токи

Резонансные токи возникают в цепи с резистором и конденсатором, соединенными параллельно.

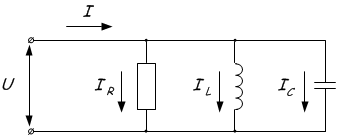
Условием резонанса токов является то, что резонансная частота источника равна резонансной частоте w=w_рпоэтому проводимость B_L=B_C. Это означает, что при резонансе токов емкостная и индуктивная проводимости равны.

Чтобы проиллюстрировать график, давайте на мгновение отвлечемся от проводимости и перейдем к сопротивлению. С увеличением частоты общее сопротивление цепи увеличивается, а ток уменьшается. Когда частота равна резонансной частоте, сопротивление Z максимально, поэтому ток в цепи принимает наименьшее значение и равен активной составляющей.

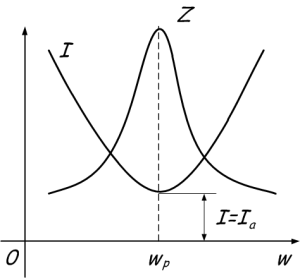
Выразим резонансную частоту

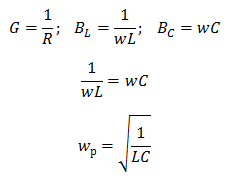Как видно из этого выражения, резонансная частота определяется так же, как и для резонанса напряжения.

Явление резонанса может быть как положительным, так и отрицательным. Радиоприемник, например, основан на колебательном контуре, который настраивается на нужную радиоволну путем изменения индуктивности или емкости. С другой стороны, явление резонанса может вызвать скачок напряжения или тока в цепи, что, в свою очередь, приводит к аварии.

Здесь cos φ₀ – это коэффициент мощности. Как безразмерная физическая величина, она характеризует приемник переменного тока с точки зрения реактивной составляющей в нагрузке и показывает, насколько сильно переменный ток, протекающий через нагрузку, сдвинут по фазе относительно приложенного к нему напряжения.

Чтобы получить доступ к этому и другим видеоурокам из набора, вам необходимо добавить его в свой личный кабинет через покупку в каталоге.

Получите удивительные возможности

Конспект урока “Резонанс в цепи переменного тока”.

Вспомните, что при выводе закона Ома для цепи переменного тока, содержащей резистор, индуктор, конденсатор и источник переменного напряжения, нам помогла векторная диаграмма амплитуд напряжений на резисторе, конденсаторе и индукторе.

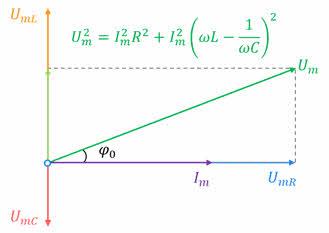
Мы показали, что амплитуда приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол между амплитудами приложенного напряжения и тока определяет разность фаз между током и напряжением. Тангенс этого угла, как показано на рисунке, равен отношению разности между амплитудами напряжений на индукторе и конденсаторе и амплитудой напряжения на активном резисторе:

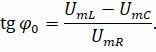
Используя закон Ома для данного участка цепи, легко показать, что тот же угол определяется соотношением реактивного и активного сопротивлений:

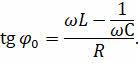
А средняя мощность, имеющаяся в цепи на активном сопротивлении, будет определяться выражением, показанным на экране:

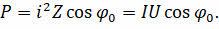
Здесь cos φ₀ – это коэффициент мощности. Как безразмерная физическая величина, она характеризует нагрузку переменного тока с точки зрения реактивной составляющей в нагрузке и показывает, насколько сильно переменный ток, протекающий через нагрузку, сдвинут по фазе относительно приложенного к ней напряжения.

Из последних двух формул следует, что если реактивное сопротивление цепи равно нулю, то уравнение мощности примет известный вид:

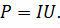
В этом случае в цепи выделяется максимальная мощность – возникает явление резонанса.

Резонанс в электрическом колебательном контуре – это явление быстрого увеличения амплитуды вынужденных колебаний тока или напряжения, когда частота внешнего переменного напряжения совпадает с частотой собственных колебаний контура:

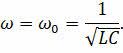
Давайте рассмотрим этот феномен подробнее. Для начала представим, что мы раскачиваем маятник, воздействуя на него периодически изменяющейся силой. В этом случае маятник будет колебаться не самостоятельно, не свободно, а под действием периодической внешней силы. Эти колебания маятника, как мы помним, называются вынужденные колебания.

В электрических колебательных контурах также могут возникать вынужденные электромагнитные колебания. Если в колебательном контуре, состоящем из индукционной катушки и конденсатора, все время работает генератор переменного тока, то ЭДС генератора будет индуцировать в этом контуре переменный электрический ток, частота которого будет равна частоте колебаний ЭДС генератора.

Частота этого вынужденного колебания обычно не совпадает с собственной частотой контура:

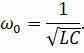
Когда собственная частота колебательного контура далека от частоты ЭДС, действующей в цепи, полное сопротивление цепи велико и ток в цепи пренебрежимо мал. Однако если емкость конденсатора и индуктивность катушки в такой цепи выбраны так, что их сопротивления равны, то разность фаз между колебаниями тока и напряжения будет равна нулю, т.е. изменения тока и напряжения будут синфазными:

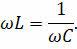
Таким образом, условием резонанса в колебательном контуре является то, что частота внешнего напряжения, приложенного к контуру, равна частоте собственных колебаний контура:

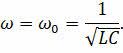
Эта частота называется резонансная частота.

В этом состоянии полное сопротивление цепи становится наименьшим и равным активному сопротивлению, а амплитуда тока при заданном напряжении принимает наибольшее значение. В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к цепи (U_0r = U₀), а напряжения на индукторе и конденсаторе равны по модулю и противоположны по фазе:

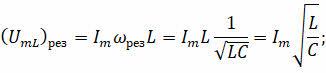
Обратите внимание, что амплитудные значения резонансных напряжений на индукторе и конденсаторе равны друг другу и могут быть намного больше амплитуды приложенного напряжения:

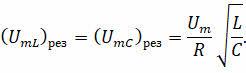
Это явление называется резонанс напряжения. В этом случае, чем меньше сопротивление цепи, тем сильнее ток в цепи и тем круче резонансная кривая. Это то, что известно как резкий резонанс.

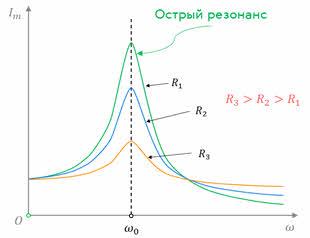
Контур с резким резонансом очень чувствителен к колебаниям резонансной частоты. Это широко используется в радио- и электротехнике для усиления колебаний напряжения определенной частоты.

Так, например, радиоволны от разных передающих станций возбуждают в радиоантенне переменные токи разных частот, поскольку каждая передающая станция работает на своей частоте. К антенне индуктивно подключен колебательный контур, в катушке которого возникают вынужденные колебания тока и напряжения. Однако только при наступлении резонанса контур выбирает из различных частот, генерируемых в антенне, только те колебания, частота которых равна его собственной частоте. Настройка схемы на нужную частоту обычно осуществляется путем изменения емкости конденсатора.

Теперь рассмотрим участок цепи переменного тока, содержащий конденсатор и индуктор в параллель.

Предположим, что активное сопротивление цепи настолько мало, что им можно пренебречь. Предположим, что к цепи приложено переменное напряжение, изменяющееся синусоидально:

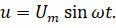
Тогда ток, протекающий в ветви с емкостным сопротивлением, будет обгонять по фазе приложенное напряжение на π/2. А ток, протекающий в ветви с индуктивным сопротивлением, будет задержан по фазе на π/2 от приложенного напряжения:

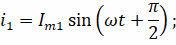
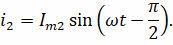
Таким образом, разность фаз токов в двух ветвях составляет πт.е. колебательные токи в ветвях находятся в противоположных фазах. Амплитуда тока во внешней цепи равна модулю разности амплитуд токов в двух ветвях:

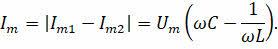
Если частота колебаний в контуре равна резонансной частоте, то амплитуды токов в ветвях будут равны, а амплитуда тока во внешнем контуре будет равна нулю.

Очевидно, что при наличии активного сопротивления разность фаз не будет πни значение амплитуды тока во внешней цепи не будет равно нулю. Но он будет принимать минимально возможное значение. В этом случае амплитуды токов ветвей могут быть намного больше амплитуды внешнего тока.

Явление быстрого уменьшения амплитуды тока во внешней цепи, питающей параллельно конденсатор и индуктор, по мере приближения частоты приложенного напряжения к резонансной частоте, называется резонансным током (или параллельным резонансом).

Это явление используется в резонансных усилителях для выделения одного конкретного колебания из сигнала сложной формы, а также в индукционных печах для того, чтобы сделать ток в питающих проводах намного меньше тока в катушке.

Чтобы закрепить новый материал, давайте вместе с вами решим следующую задачу. Цепь, состоящая из конденсатора емкостью 507 мкФ, катушки индуктивностью 20 мГн и резистора сопротивлением 100 Ом, последовательно подключена к сети переменного тока частотой 50 Гц и напряжением 220 В. Определите ток в цепи, сдвиг фаз между напряжением и током и резонансную частоту цепи.

Читайте далее: