Что это такое: Алгебра логики - услуги электромонтажа, строительства и ремонта

Любое сложное выражение, полученное из простых высказываний с помощью основных логических операций, называется формулой алгебры логики.

Содержание

Алгебра логики

Алгебра логики – это Раздел математической логики, занимающийся изучением высказываний с точки зрения их логических значений (истинных или ложных) и логических операций над ними.
В алгебре логики мы обычно связываем истинность высказывания с цифрой 1, а его ложность – с цифрой 0 (A = 1 и C = 0 означает, что A истинно, а C ложно).

Так что же такое алгебра логики?

Зачем нам нужна булева алгебра?

Что такое алгебра логики?

Булева алгебра (булева алгебра) – это раздел математики, возникший в 19 веке в результате работы английского математика Дж. Буля. Первоначально булева алгебра не имела практического значения. Однако уже в 20 веке его обозначения нашли применение в описании работы и проектировании различных электронных схем. Законы и аппарат булевой алгебры стали использоваться при проектировании различных частей компьютеров (память, процессор). Однако это не единственная сфера применения данной науки.

Что такое алгебра логики?

Во-первых, она изучает методы определения истинности или ложности сложных логических утверждений с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое предложение описывается функцией, результат которой может быть

является либо истинным, либо ложным (1 или 0). Аргументы функции (простые выражения) также могут иметь только два

значения: 0 или 1.

Что такое простой

логическое выражение? Это такие фразы, как “два больше одного”, “5,8 – целое число”. В первом случае мы имеем дело с истинным, а во втором – с ложным. Алгебра логики не затрагивает сути этих утверждений. Если кто-то решит, что утверждение “Земля квадратная” истинно, то булева алгебра примет это как факт. Дело в том, что булева алгебра занимается вычислением результата сложных логических высказываний на основе ранее известных значений простых высказываний.

Логические операции. Сцепление, соединение и отрицание

Как же простые логические утверждения объединяются в сложные утверждения? В естественном языке мы используем различные союзы и другие части речи. Например: “и”, “или”, “либо”, “не”, “если”, “то”, “тогда”. Пример сложного предложения: “Он обладает знанием

и навыки”, “она приедет во вторник,

или Среда”, “Я буду играть

затем“когда я делаю домашнее задание”, “5.

не равняется 6″. Как мы можем определить, правду нам сказали или нет? Каким-то логическим образом, даже бессознательно, основываясь на предыдущем жизненном опыте, мы понимаем, что истина в связке “и” возникает, когда оба простых утверждения истинны. Как только один из них становится ложным, все высказывание становится ложным. С другой стороны, в случае с связкой “или”, только одно простое утверждение должно быть истинным, и тогда все утверждение становится истинным.

Булева алгебра перенесла этот жизненный опыт в аппарат математики, формализовала его и ввела строгие правила для получения однозначного результата. Отношения здесь стали называться логическими операторами.

Алгебра логики предоставляет множество логических операций. Однако три из них заслуживают особого внимания, поскольку их можно использовать для описания всех остальных, и, следовательно, при построении схемы можно использовать меньшее количество различных устройств. Эти операции представлены следующим образом

подключение (И),

дизъюнкция (OR) и

отрицание (НЕ). Соединение часто называют

&а дизъюнкция – это

||а отрицание – тире над переменной, обозначающей утверждение.

В сочетании истинность сложного выражения возникает только в том случае, если все простые выражения, входящие в состав сложного выражения, истинны. Во всех остальных случаях составное выражение будет ложным.

При дизъюнкции составное выражение становится истинным, если в нем истинно хотя бы одно простое выражение или два одновременно. Иногда составное выражение состоит более чем из двух простых выражений. В этом случае достаточно, чтобы одно простое выражение было истинным, и тогда все высказывание будет истинным.

Отрицание – это унарная операция, поскольку она выполняется по отношению к одному простому выражению или по отношению к результату составного выражения. Результатом отрицания является новое утверждение, противоположное исходному.

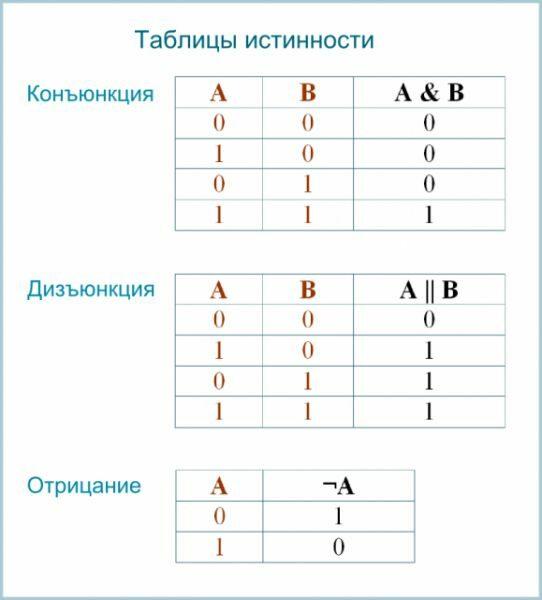
Таблицы истинности

Логические операции удобно описывать с помощью так называемых таблиц истинности.

Таблицы истинностиA и B), которые отражают результаты вычисления сложных утверждений при различных значениях исходных простых утверждений. Простые утверждения обозначаются переменными (например, A и B).

Логические основы информатики

Компьютеры используют различные устройства, работа которых хорошо описывается алгеброй логики. Эти устройства включают группы переключателей, триггеров и сумматоров.

Кроме того, связь между булевой алгеброй и компьютерами заключается также в системе счисления, используемой в компьютерах. Известно, что он является бинарным. Поэтому в компьютерных устройствах можно хранить и преобразовывать как числа, так и значения логических переменных.

Коммутационные схемы

В компьютерах используются электрические цепи, состоящие из ряда переключателей. Выключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае ток течет, а во втором – нет. Очень удобно описывать работу таких схем с помощью булевой алгебры. В зависимости от положения переключателей можно принимать или не принимать сигналы на выходах.

Клапаны, триггеры и сумматоры

Вентиль – это логический элемент, который принимает одни двоичные значения и выдает другие, в зависимости от его реализации. Например, существуют вентили, реализующие логическое умножение (конъюнкция), сложение (дизъюнкция) и отрицание.

Триггеры и сумматоры представляют собой относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггеры могут хранить одну двоичную цифру, поскольку могут находиться в двух стабильных состояниях. Триггеры чаще всего используются в регистрах процессора.

Сумматоры широко используются в арифметическом логическом блоке (ALU) процессора и выполняют суммирование двоичных цифр.

А теперь немного о жизни.

Зачем нам нужна булева алгебра?

А теперь немного жизни.

В математической логике дается точное определение алгоритма и вычислимости. Вопрос о существовании алгоритмов имеет большое значение в математике (например, алгоритм существования решений системы уравнений). Разрешимые алгоритмы были получены для многих теорий, например, элементарной геометрии, упорядоченного поля вещественных чисел, булевой атомной алгебры и т.д. Неразрешимые теории (т.е. не существует единого алгоритма для решения всех задач) элементарной арифметики, анализа, класса всех конечных симметричных групп (т.е. групп перестановок), аксиоматических систем теории множеств.
В последние годы большое внимание уделяется теории сложности алгоритмов и вычислений. Оказалось, что одного лишь существования алгоритма, решающего заданную массовую проблему, далеко не достаточно для практики. После уточнения понятия вычислительной сложности стали изучаться такие вопросы, как внутренняя сложность вычислительной функции и ее криптографическая стойкость, что стало особенно важным с развитием коммуникационных сетей, компьютерных технологий и систем автоматического управления.

Зачем изучать историю и философию? Чтобы ваш мозг научился анализировать ситуацию вокруг вас!!!!
Почему вы изучаете исчисление и геометрию? Возможно, писать полезные программы для решения практических задач!
Метод резолюций, например, лежит в основе логического программирования (которое, в свою очередь, является основой для развития искусственного интеллекта и экспертных систем).
Формулы булевой алгебры используются в РКС, на которых построен любой компьютер.
Они также могут быть использованы для решения различных логических задач, где есть много условий, и все они должны быть проанализированы, собраны вместе и сделать правильный вывод.

Конечно, есть темы чисто теоретические. но без них тоже не обойтись. аксиоматика является основой любой научной теории. если теория не может быть подкреплена системой аксиом и правил дедукции, то по самой своей природе она не может считаться научной!

Если вам нужны знания только для механической работы с компьютерами, сетями и прочими вещами, то вам следовало бы пойти на технические специальности, они не так глубоко погружаются в теоретическую науку!

Герсеванов, Николай Михайлович – советский ученый в области механики грунтов, член-корреспондент Академии наук СССР
В 1923 году он попытался применить булеву алгебру к техническим расчетам. За разработку и внедрение новых методов строительства на макропористых (лессовых) грунтах Г. получил Сталинскую премию (1948).

Методы структурного синтеза пневматических систем, основанные на булевой алгебре, широко используются в инженерной практике, так как значительно облегчают проектирование.

БУЛЕВА АЛГЕБРА – Часть математической логики, занимающаяся изучением утверждений, рассматриваемых с точки зрения их логических значений (истинности или ложности) и логических операций над ними. A. Л. появилась в середине 19 века в трудах Дж. Рейнольдса. В 19 веке в работах Дж. Буля (см. [1], [2]) и далее в работах С. Т. Энциклопедия математики.

Булева алгебра

БУЛЕВА АЛГЕБРА – Система алгебраических методов решения логических задач, а также множество задач, решаемых этими методами. А. л. в узком смысле является алгебраическим. (табличная, матричная) конструкция классической логики теорем, в которой проблемы… Философская энциклопедия

алгебра логики – АЛГЕБРА ЛОГИКИ Исторически первая форма математической (символической) логики, разработанная в последней трети 19 в. Ее возникновение связано с аналогией между решением алгебраических уравнений и выведением следствий из теорем, а также с тем, что… Энциклопедия эпистемологии и философии науки

алгебра логики – Булева алгебра – [L. Г. Суменко. Англо-русский словарь по информационным технологиям. М.: ГП “ЦНИИС”, 2003] Тематика информационных технологий в целом Синонимы Булева алгебра EN Булева алгебра … Справочник технического переводчика

БУЛЕВА АЛГЕБРА – Алгебраическая система решения логических задач и набор таких задач; в узком смысле – табличная, матричная конструкция логики утверждений, задающая логические операции над ними,… Большой энциклопедический словарь

БУЛЕВА АЛГЕБРА – Ветвь математической логики, изучающая структуру сложных логических теорем и способы определения их истинности алгебраическими методами. В формулах A. L. переменные являются логическими или бинарными, т.е. принимают только два… …. Большая политехническая энциклопедия

Алгебра логики – Не путать с булевой алгеброй. Булева алгебра (алгебра высказываний) – это раздел математической логики, занимающийся изучением логических операций над высказываниями[1]. Чаще всего предполагается (известная как двоичная или бинарная логика, в … … Википедия

алгебра логики – Система алгебраических методов решения логических задач и набор таких задач. * * * * * * ЛОГИЧЕСКАЯ АЛГЕБРА ЛОГИЧЕСКАЯ АЛГЕБРА, система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле – массив, матрица … … Энциклопедический словарь

Булева алгебра – logikos algebra statusas T sritis automika atitikmenys: angl. algebra logiki vok. Algebra der Logik, f; logische Algebra, f рус. алгебра логики, f pranc. algèbre logique, f … Автоматический терминал žodynas

БУЛЕВА АЛГЕБРА – Ветвь математической логики, занимающаяся изучением высказываний, рассматриваемых с точки зрения их логических значений (истинных или ложных) и их логических операций. A. Л. появился в середине 19 века в трудах Дж. Рейнольдса. Она была разработана в 19 веке в работах Дж. Буля (см. [1], [2]) и получила дальнейшее развитие в работах К…. Энциклопедия математики

АЛГЕБРА ЛОГИКИ – Ветвь математической логики, занимающаяся изучением утверждений, рассматриваемых с точки зрения их логических значений (истинности или ложности) и их логических операций. В А. Л. принято отождествлять истинность высказывания с числом 1, а его ложность с числом О (А = 1 и С … Большой энциклопедический словарь Лодзинского технического университета

Важным аспектом формализации, принятой в алгебраической логике, является то, что знаки этих операций (т.е. их значения, соответствующие коннекторы) могут быть использованы для соединения любых утверждений без ограничений, включая те, которые сами по себе являются сложными. В этом случае можно точно и строго описать класс всех рассматриваемых выражений булевой алгебры. В данном случае он состоит из констант И и Лпеременные A, B… и все те выражения, которые получаются из них путем конечного числа соединений с “×”, “⋁”, “→” и “

Булева алгебра

Булева алгебра – является одной из фундаментальных отраслей … символическая логикакоторая основана на применении алгебраических методов к логика (см. “Логика”). Булева алгебра является исторически первой формой символической логики (см. Символическая логика), которая появилась в середине 19 века в работах Дж. Буля. Он был разработан в результате аналогия между решением алгебраических уравнений и дедукцией последствия z предположениеи что алгебраические уравнения применимы для решения задач в различных областях знаний. Первоначально предметом алгебраической логики были классы (как объемы понятий), отношения между классами с точки зрения их объема и связанных с ними операции на них. Позднее, в связи с появлением в 19 веке теория множествкоторый взял на себя часть этих проблем, предмет алгебры логики значительно изменился. Его основной темой стали заявления (суждения, предложения), рассматриваемые с точки зрения их логических значений (истинно, ложно, бессмыслица и др.) и логических операций над ними.

Попытки свести логику к алгебре предпринимались на протяжении веков. К тем, кто реорганизовал логику на основе алгебры, относятся Г.В. Лейбниц и особенно Ж.Г. Ламберт, который первым использовал термины “алгебра логики”, “логическая алгебра”. В то время основным предметом алгебры было решение уравнений, и Ламберт пытался представить логические связи с помощью уравнений, а логические выводы – с помощью решений соответствующих уравнений. Таким образом он пытался сохранить в “алгебраической логике”, которую он называл искусством знаков, все операции обычной алгебры.

В 19 веке продолжался поиск способов решения логических задач алгебраическими методами. Были введены четкие понятия операций над логическими объектами, что стало возможным, прежде всего, благодаря трактовке понятий в зависимости от их объема. Более того, концепция Вселенная – Подклассы Universe были введены в качестве объектов, над которыми были определены операции, суждения были представлены в форме равенства.

Фундаментальный прорыв в алгебраизации логики был сделан А. де Морганом и Дж. де Морганом. Буля; “Формальная логика” де Моргана и “Математический анализ логики” Буля были опубликованы в 1847 году. Построения обоих ученых содержали основы того, что мы сейчас называем “булевой алгеброй”. Де Морган также исторически разработал первую систему реляционной алгебры. Система Буля, названная “алгеброй логики”. (и иногда “алгебра классов”), была более широко известна, чем конструкции де Моргана. В работах У.С. Джевонса, И.И. Жегалкина, Э. Шредера, К.С. Пирса, П.С. Методы булевой алгебры были усовершенствованы Порецким и другими.

Сердцем обычной, так называемой классической алгебры логики является абстракция предложения как величина, имеющая одно (и только одно) из двух значений: “правда” или “false” (короче: И, Л), или он может принимать оба значения (но не одновременно). В первом из этих случаев мы имеем индивидуальное заявление (заявление в узком, наиболее принятом смысле этого слова), во втором, a заявление-функция .. Примерами таких заявлений являются: “2 × 2 = 4”, “0 ≤ 0”, “Сократ – мужчина”, “0 = 1”, “2 × 2 = 5”, “x 2 = y», «z – человек”, “если x = yзатем y = 0“, “если x = 2затем x 2 = 4», «x равно y или x не равна y“. Первые три утверждения таковы И (т.е. они истинны), и Л (т.е. ложь), , , – функциональные выражения (если, например, значения литеральных переменных x и y могут быть целыми числами, а переменная z – живые существа), и имеют значение И (для всех возможных значений переменных x и y). Последние три из этих утверждений являются сложными, в отличие от предшествующих им простых утверждений.

Абстракция в алгебре логики идет дальше. Все истинные высказывания отождествляются друг с другом, поскольку истинное высказывание не отличается от другого истинного высказывания по смыслу (другие стороны высказываний абстрагируются в алгебре логики). Ложные утверждения также отождествляются друг с другом. Когда мы рассматриваем теорема-функции в алгебре логики, мы обычно абстрагируемся от рассмотрения их зависимости от других переменных, кроме тех, которые имеют значения и как теоремы, и вводим в их рассмотрение буквенные переменные, называемые теоремами переменных. Таковы письма A, B, C, … Α₁, A₂, A₃, … и так далее (при этом выбор букв является вопросом не факта, а конвенции), при условии, что они выступают в качестве переменных, значениями которых могут быть все возможные унитарные высказывания, то есть в силу абстракций, упомянутых “констант” И и Л.

Кроме простых утверждений, обозначаемых одиночными буквами A, B… или И, ЛСложные высказывания также рассматриваются как результат объединения высказываний с союзами или их отрицанием (соответствующим частице “не”). Сложные высказывания рассматриваются как функции содержащихся в них литеральных переменных A, B, C и так далее. Это приводит к понятию функций булевой алгебры, т.е. функций на аргументах, которые являются операторами переменных, т.е. принимают значения И, Лкоторая (функция) может принимать только эти значения.

Вводятся алгебраические операции над высказываниями: конъюнкция A × B (читать “A и B“, другие обозначения: AB, A & B, A ⋀ B; другие названия: логическое умножение, булево умножение), дизъюнкция A ⋁ B (“читать A или B“; другое обозначение: A + B; другие названия: логическое сложение, булево сложение), импликация A → B (читай: “Если Aтогда B” или “A связывается с B” или “A подразумевает B“, или “С тех пор как A следует B“; другое обозначение: A ⊃ B; другое название: логическое следствие), эквивалентно А

В (читать: “A эквивалентный B” или “A эквивалент B“, или “Aесли и только если B“: другие обозначения: A ≡ B, A ↔ B; другие обозначения: эквивалентность, эквивалентность, эквивалентность), отрицание A (читай: “не A“, или “A ложный”, или “ложный, который A“, или “отрицание A“; другие обозначения: ¬. A,

A, A´(другое название: инверсия), а иногда и другие операции.

Важным аспектом формализации, принятой в алгебре логики, является то, что знаки этих операций (то есть, по смыслу, соответствующие связки) могут соединять любые теоремы без ограничений, включая те, которые сами по себе являются сложными. В этом случае можно точно и строго описать класс всех рассматриваемых выражений булевой алгебры. В данном случае он состоит из констант И и Лпеременные A, B… и все те выражения, которые получаются из них с помощью конечного числа соединений с “×”, “⋁”, “→” и “

” и отрицания. Это следует из требования, что операции должны быть определены таблично как функции, и что значение сложного утверждения зависит только от значения простых утверждений.

Суть булевой алгебры как системы методов заключается в применении преобразований высказываний на основе алгебраических законов, которые имеют место для операций над высказываниями. Эти законы обычно принимают форму тождеств (см. Тождества), т.е. уравнений, которые верны для всех значений переменных.

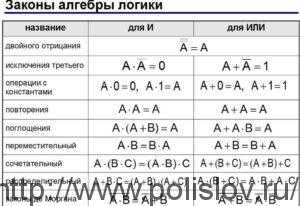
Следующие личности играют важную роль:

I. AB = AB, A ⋁ B = B ⋁ A (законы коммутативности);
II. (AB) C = A (БК), (A ⋁ B ⋁ C = A ⋁ (B ⋁ C) (законы об ассоциациях);
III. Α (Α ⋁ Β) = A, A ⋁ AB = A (законы поглощения);
IV. A (B ⋁ C) = AB ⋁ AC (закон делимости);
V. A ¬ A = Л (закон противоречия);
VI. A ⋁ ¬ A = И (закон исключенной третьей стороны).

Эти идентификаторы, установленные, например, с помощью массивов, позволяют вывести другие идентификаторы. Тождества I-VI достаточны для того, чтобы вывести из них любое (очевидно истинное) тождество методом преобразования тождеств, левая и правая части которого являются выражениями булевой алгебры, состоящими из переменных A, Bконстанты И, Л и символы ‘×’, ‘ν’ ‘-‘ (не обязательно все). Добавление идентичности VII A → B = ¬ A ⋁ B, A

B = AB ⋁ ¬ A ¬ B позволяет вывести любые тождества, содержащие также символы “→”, “

Тождества V, VI, VII показывают, что константы И и ЛИмпликация и эквивалентность, рассматривая их как функции, могут быть выражены конъюнкцией, дизъюнкцией и отрицанием. Существует теорема, что каждая функция в алгебре логики может быть представлена этими тремя операциями, то есть записана в виде выражения, содержащего только знаки этих операций и литеральные переменные. Точнее говоря, каждая функция Φ (A₁, A₂, … A_n) можно записать как дизъюнкцию всех выражений вида:

Л – на А_iи стирание “коэффициентов” Φ (a₁, a₂, … a_n“) равно И (согласно закону о И × A = A) и отбрасывая члены с “коэффициентами”, равными Л (в соответствии с законом (Л × A = Л, Л ⋁ A = A), мы получим (если функция не постоянна) выражение, упомянутое в теореме.

Дизъюнктивная нормальная форма (ДНФ) – это выражение, которое представляет собой букву И или Л или имеет вид A₁ ⋁ A₂ ⋁ … ⋁ A_sгде каждый член A_iявляется либо литеральной переменной, либо ее отрицанием, либо их связкой, где s не должно отличаться от 1, т.е. символы “⋁” могут не существовать. ДНФ называется совершенной, если она И или Л или каждый термин содержит ровно один раз все буквы (переменные) в нем, и ни один термин не является одинаковым. Каждое выражение булевой алгебры может быть сведено к ДНФ. Каждая ДНФ может быть сведена к совершенной ДНФ путем “умножения” членов на недостающие буквы (по закону A = AB ⋁ A ¬ B) и устранением повторений букв в терминах (согласно закону AA = A, A ¬ A = Л, Л × A = Л, Л ⋁ A = A) и повторение членов (в соответствии с законом A ⋁ A = A).

Редукция к совершенной ДНФ позволяет для любых двух заданных выражений A и B решает, выражают ли они одну и ту же функцию, т.е. является ли тождество A = B.

Важную роль играет так называемый уменьшенный DNF. Последняя может быть определена как ДНФ, в которой 1) ни одна буква не повторяется ни в одном термине; 2) не существует таких пар терминов А_i, и A_jчто каждый коэффициент умножения А_iтакже в А_jи 3) для любых двух таких терминов, один из которых содержит в качестве фактора некоторую букву, а другой – отрицание той же буквы (при условии, что в этой паре терминов нет другой буквы, для которой это происходит), существует (в той же ДНФ) термин, равный объединению других факторов этих двух терминов.

В дополнение к ДНФ также используются конъюнктивные нормальные формы (КНФ). Это выражения, которые можно получить из ДНФ путем замены ‘⋁’ на ‘×’ и ‘×’ на ‘⋁’.

Преобразование двойственности – это такое преобразование выражения булевой алгебры, при котором знаки всех операций заменяются знаками двойственных операций в этом выражении и константами: И на Л, Л на И; и действие (или функция) Φ называется двойным для операции Ψ, если массив, определяющий Φполучается из таблицы, определяющей Ψ, путем подстановки везде в нее И на сайте Л, а Л на И (что означает одновременную подстановку значений функции и ее аргументов). Если Φ дуален к Ψ и Ψ дуален к Xтогда Φ = X. Например, конъюнкция и дизъюнкция дуальны друг другу, отрицание дуально самому себе, константа И (как функция) двойственна константе Л. Функция Φ(A₁, A₂, … A_n) двойственна функции Ψ (A₁, A₂, A_n) тогда и только тогда, когда верно следующее тождество: ¬. Φ(A₁, A₂, … A_n) = Ψ (¬ A₁, ¬ A₂, … ¬ A_n).

Совершенный и сокращенный КВЧ и сокращенный КВЧ можно определить как такой КВЧ, что их двойственные выражения являются, соответственно, совершенной ДНФ и сокращенной ДНФ. Идеальная и сокращенная ДНФ и сокращенная ДНФ могут быть использованы для решения задачи рассмотрения всех гипотез и всех следствий данного выражения алгебры логики. Более того, в предположении, что выражение A булевой алгебры естественно понимать такое выражение Bчто B → A тождественно истинно, и следствие из выражения A – это такое выражение Bтакой, что A → B тождественно истинна.

Другая степень абстракции, часто используемая в алгебре логики, заключается в определении И с цифрой 1 и Л – с числом 0. Вводится операция. A + Bприведены в таблице: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0. Это называется сложением (точнее, сложением по модулю 2; другое название: дизъюнкция дизъюнкции; читайте: “A плюс B“, или A не эквивалентна B“, или “либо Aили B»).

Любая алгебраическая логическая функция может быть представлена умножением (т.е. конъюнкция), сложение и константа 1 (теорема Зегальского). В частности, верны следующие тождества:

Обратные представления имеют вид:

X. A + B = A ¬ B ⋁ ¬ AB, 1 = A ⋁ ¬ A.

Тождества VIII позволяют нам “переводить” выражения на “языке” соединения, дизъюнкции и отрицания (KDO) на “язык” умножения, сложения и единства (UCE), а тождества X позволяют нам делать обратный “перевод”.

Преобразования идентичности также могут быть сделаны на “языке” UCE. Они основаны на следующих законах:

XI. AB = BA, A + B = B + A (закон коммутативности);
XII. (AB) C = A (БК), (A + B) + C = A + (B + C) (закон спаривания);
XIII. A (B + C) = AB + AC (закон делимости);
XIV. AA = A, A + (B + B) = A;
XV. Α × 1 = A.

Этих тождеств достаточно для вывода любого (правильного) тождества, две части которого являются выражениями “языка” UCE. Добавляя тождества VIII, мы можем вывести все тождества “языкового” CCE.

Выражение “языка” UCE называется сокращенным многочленом, если оно равно 1 + 1 (т.е. нулю) или имеет вид A₁ + A₂ + … + А_s где каждый член Aлибо 1, либо буквенная переменная, либо произведение последних, причем ни одна буква не повторяется ни в одном термине, ни в двух одинаковых терминах (в том же смысле, что и выше), и S не должно быть больше 1 (т.е. не может быть знаков “+”). Любое выражение алгебры логики можно свести к данному многочлену (теорема Жегалкина).

Кроме “языков” BDE и UCE, существуют и другие “языки”, обладающие тем свойством, что любая функция алгебры логики может быть представлена операциями (и константами) этих “языков”. Такие системы называются (функционально) полными системами. Примерами полных систем являются:

Сплоченность и отрицание;
Дизъюнкция и отрицание;
Импликация и отрицание;
Импликация и 0;
Умножение, эквивалентность и 0;
тире Шеффера A|B;
медиана (A, B, C), [определение: (A, B, C) = AB ⋁ AC ⋁ БК];
отрицание и 1;
медиана, эквивалентность и сложение.

Иногда делается еще один важный шаг абстрагирования. Они уходят от табличного задания операций и от того факта, что значения литеральных переменных являются декларациями. Вместо этого допускаются различные интерпретации рассматриваемого “языка”, состоящего из некоторого набора объектов (служащих значениями литеральных переменных) и системы операций над объектами этого набора, удовлетворяющих тождествам из полной системы тождеств этого “языка”. “Язык” KDO в результате этого шага абстракции превращается в “язык” так называемой булевой алгебры, “язык” UCE – в “язык” так называемого булева кольца (с единицей), “язык” конъюнкции и дизъюнкции – в “язык” так называемой дистрибутивной структуры.

Важным примером булевой алгебры является алгебра классов, в которой роль элементов играют подмножества (классы) некоторого фиксированного множества (так называемой вселенной) Uроль 0 играет пустое множество 0, роль 1 играет пустое множество 1. Uроль AB, A ⋁ B и ¬ Α – соответственно, операции пересечения, объединения и сложения в теории множеств. Связь между алгеброй классов, алгеброй предикатов и алгеброй теорем, этими тремя наиболее важными интерпретациями абстрактной алгебры логики как “языка” булевой алгебры, такова: первая преобразуется во вторую путем замены множеств (классов) их так называемыми характеристическими предикатами (т.е. множествами A – предикатом x ∈ Aговоря: “x принадлежит множеству A“), если операции и константы 0 и 1 также преобразуются соответствующим образом, а второе преобразуется в третье путем подстановки некоторого постоянного значения предикатов вместо их аргументов во всех предикатах. Более точно, этот переход от алгебры классов к алгебре предикатов приводит к алгебре сингулярных предикатов. Другим важным случаем является алгебра бинарных предикатов, чаще называемых отношениями. С ней тесно связана алгебра отношений, которая отличается от нее только тем, что в последней, помимо трех операций булевой алгебры, есть еще две операции.

Любая булева алгебра может быть “преобразована” в булево кольцо путем определения операций A + B в соответствии с законом X (и отбрасывая операцию A ⋁ B). Например, в случае алгебры множеств роль A + B это так называемая симметричная разность множеств A и B (состоящий из всех тех элементов вселенной, которые принадлежат одному и только одному из множеств A или B). И наоборот, любое булево кольцо (с единицей) может быть “преобразовано” в булеву алгебру. Понятия булевой алгебры и булевых колец связаны с Дж. Булем. Однако концепции (не говоря уже о терминах) сформировались гораздо позже. Первые работы по алгебре логики были посвящены проблемам

выражение логических отношений между количествами понятий (соответственно утверждений) в виде уравнений (equation);
Целью данной работы является разработка алгоритмов решения булевых уравнений и систем уравнений для автоматизации способов извлечения информации (того или иного вида) из заданных предположений (неявных).

В настоящее время булева алгебра развивается в основном под влиянием проблем в области ее приложений. Она широко используется в инженерии и, наоборот, развивается под влиянием технических и программных проблем. Вопросы, касающиеся понятий самой булевой алгебры, приводят к проникновению неалгебраических методов (таких как табличные, топологические, описательные методы) в булеву алгебру и, соответственно, к постепенному выделению из булевой алгебры отдельной области – теории алгебраических булевых функций (или, другими словами, теории булевых функций). Другие направления возможного дальнейшего развития булевой алгебры связаны с успехами теории алгоритмов и попытками ее алгебраизации, т.е. построения алгебраической теории алгоритмов.

Теория булевых функций как отдельная область, выделенная из алгебры логики, находит все большее применение. В результате, концепция функциональной системы (P_n, C), где P_n это множество всех функций n-логика четности (или множество всех функций логики четности) P_ω) с определенной на нем операцией суперпозиции CP_n обычно рассматривается как обобщение множества всех булевых функций P₂. Известно разумное понятие функциональной системы (P_n, C) является его частным случаем), которая основана на рассмотрении таких пар (Ρ, Ω), где Ρ это множество отображений, реализуемых системами управления определенного класса, а Ω – операция построения новых систем управления на основе данных. В свою очередь (P₂, Q эквивалентна алгебре логики. Таким образом, от алгебры формул, изучаемой в алгебре логики, он перешел к алгебре функций. И хотя это алгебра логики, т.е. классический логика высказываний (см. логика утверждений) является основой для проектирования интегральных схем в современной цифровой электронике, включая компьютеры, аналогичная работа ведется также на основе многозначная логика (см. Многозначная логика).

Другим направлением развития современной алгебраической логики является алгебраическая логика. Она интересна тем, что ставит и частично решает проблему построения алгебр o неклассические логики. (См. неклассические логики), т.е. такие варианты булевой алгебры, которые соответствуют неклассическому исчислению предложений. В этой области основополагающим вопросом является построение алгебраическая семантика, под которым мы понимаем класс всех моделей некоторой алгебры, соответствующей логике Lпоскольку с помощью алгебраической семантики такие метрологические проблемы, как полнота L (в отношении общей достоверности в классе всех моделей), разрешимость L и другие. Наконец, мы приходим к общему вопросу о том, какие логики являются алгебраически представимыми, т.е. какие логики имеют алгебраическую семантику, а какие нет. Ответ на этот вопрос можно найти в работе Блока и Пигоцци (1989).

Важным моментом является то, что современное развитие алгебраической логики представляет собой систематическое применение методов и, самое главное, аппарата универсальной алгебры к символическая логика. Сегодня мы уже говорим об алгебраическом изложении всей символической логики, и результаты здесь весьма важны. Например, если Alg (L) обозначает класс алгебр, соответствующий некоторой логике L (если L является классической пропозициональной логикой, тогда Alg (L) является классом булевых алгебр), можно сформулировать теорему о том, что L обладает определенным логическим свойством тогда и только тогда, когда Alg (L) обладает определенным алгебраическим свойством. Это позволяет алгебраически характеризовать такие логические свойства, как полнота, наличие дедуктивной теоремы, компактность, разрешимость, интерполируемость Крейга, истинность формул в модели и так далее. Таким образом, первые два свойства имеют следующий вид: L имеет строго полную гильбертовскую аксиоматизацию (Γ ⊦ A если и только если Γ ⊨ A) тогда и только тогда, когда Alg (L) является конечно аксиоматизируемой квазиманифестацией; L допускает теорему дедукции тогда и только тогда, когда Alg (L) имеет определяемые уравнениями главные конгруэнции.

Устройство, способное запоминать, хранить и считывать информацию – это триггер. Он был изобретен в начале 20-го века Бонч-Бруевичем.

Выводы.

Подводя итоги работы, можно сформулировать следующие выводы:

Образованный гражданин современного общества должен уметь получать, обрабатывать и эффективно использовать информацию, и информационные технологии могут помочь ему в этом. Обработка информации в компьютере заключается в выполнении различных арифметических и логических операций. Все вычисления в компьютере выполняются с помощью логических элементов, которые представляют собой электронные схемы, выполняющие логические операции. Основными логическими элементами являются вентили, сумматоры, полусумматоры и триггеры. Выполняя определенную работу над информацией, логические элементы компьютера преобразуют напряжение электрического тока. Логические элементы и схемы основаны на законах и правилах алгебры логики. Алгебра логики оперирует логическими высказываниями. Заявление – это любое утверждение, относительно которого есть основания утверждать, что оно истинно или ложно. Считается, что высказывание удовлетворяет закону исключенных третей, т.е. каждое высказывание либо истинно, либо ложно и не может быть одновременно истинным и ложным.

В алгебре логики существует множество логических операций. Однако три из них заслуживают особого внимания, поскольку их можно использовать для описания всех остальных, а значит, при построении схем можно использовать меньшее разнообразие устройств. Эти операции представлены следующим образом подключение (И), дизъюнкция (OR) и отрицание (НЕ).

Анализируя мою работу, следует отметить, что, к сожалению, этих знаний слишком мало для окончательной победы в технической битве, но их достаточно, чтобы знать основные принципы работы компьютера и отвести угрозу от машины. Это означает, что я достиг своей цели и решил все задачи. В будущем я хотел бы продолжить свои исследования и изучить эту тему более подробно, а может быть, даже изобрести собственное инновационное техническое устройство, согласованное с помощью логических устройств. Также я надеюсь, что смогу сдать ЕГЭ по информатике.

Читайте далее: