Что такое электрическое сопротивление; Школа для электриков: электротехника и электроника - услуги электромонтажа, строительства и ремонта

Практически, в описаниях синусоидальных цепей переменного тока в терминах импеданса можно встретить такие термины, как “активно-индуктивный характер нагрузки” или “активно-емкостная нагрузка” или “чисто активная нагрузка”. Речь идет о следующих вопросах:

Содержание

Что такое электрическое сопротивление

В цепях постоянного тока важную роль играет активное сопротивление R. Для цепей синусоидально переменного тока одно лишь сопротивление не справится с задачей. Если в цепях постоянного тока емкости и индуктивности заметны только во время переходных процессов, то в цепях переменного тока они проявляются в гораздо большей степени.

Термин “электрическое сопротивление” – Z или комплексное (полное) сопротивление двухполюсника на гармонический сигнал – поэтому вводится для соответствующего расчета цепей переменного тока. Иногда говорят просто “импеданс”, опуская слово “электрический”.

Понятие импеданса позволяет применить закон Ома к участкам цепей синусоидально переменного тока. Проявление индуктивной составляющей в биполярной цепи (нагрузке) приводит к задержке тока по отношению к напряжению на заданной частоте, а проявление емкостной составляющей приводит к задержке напряжения по отношению к току. Активный компонент, с другой стороны, не вызывает задержки между током и напряжением, ведя себя по существу так же, как в цепи постоянного тока.

Компонент импеданса, содержащий емкостную и индуктивную составляющие, называется реактивной составляющей X. Графически активная составляющая R импеданса может быть построена вдоль оси x, а реактивная – вдоль оси y, так что импеданс в целом представляется как комплексное число, где j – мнимая единица (мнимая единица в квадрате равна минус 1).

В этом случае ясно, что реактивная составляющая X может быть разложена на емкостную и индуктивную составляющие, которые имеют противоположные направления, т.е. оказывают противоположное влияние на фазу тока: если преобладает индуктивная составляющая, импеданс цепи будет в целом положительным, т.е. цепь будет задерживаться относительно напряжения, но если преобладает емкостная составляющая, напряжение будет задерживаться относительно тока.

Схематически эта биполярная цепь выглядит следующим образом:

В принципе, любую схему биполярной линейной цепи можно свести к аналогичной форме. Здесь мы можем определить активную составляющую R, которая не зависит от частоты тока, и реактивную составляющую X, которая содержит емкостную и индуктивную составляющие.

Из графической модели, где сопротивления представлены векторами, следует, что модуль импеданса для синусоидального тока на заданной частоте рассчитывается как длина вектора, который является суммой векторов X и R. Импеданс измеряется в омах.

Практически, при описании синусоидальных цепей переменного тока с точки зрения импеданса можно встретить такие термины, как “активно-индуктивная нагрузка”, “активно-емкостная нагрузка” или “чисто активная нагрузка”. Речь идет о следующих вопросах:

Если в цепи преобладает влияние индуктивности L, реактивная составляющая X положительна, а активная составляющая R мала – это индуктивная нагрузка. Примером индуктивной нагрузки является индукционная катушка.

Если в цепи преобладает влияние емкости C, реактивная составляющая X отрицательна, а активная составляющая R мала – это емкостная нагрузка. Примером емкостной нагрузки является конденсатор.

Если в цепи преобладает активное сопротивление R, а реактивная составляющая X мала, то это активная нагрузка. Примером активной нагрузки является лампа накаливания.

Если активная составляющая R в цепи значительна, но индуктивная составляющая перевешивает емкостную, т.е. реактивная составляющая X положительна, то нагрузка называется активно-индуктивной. Примером активно-индуктивной нагрузки является асинхронный двигатель.

Если в цепи имеется значительная активная составляющая R, но емкостная составляющая перевешивает индуктивную составляющую, т.е. реактивная составляющая X отрицательна, то нагрузка называется активно-емкостной. Примером активно-емкостной нагрузки является источник питания для люминесцентных ламп.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Для получения подробного графика необходимо специализированное программное обеспечение и измерительная станция. Но чтобы узнать значение активного сопротивления (в самом низкочастотном диапазоне), достаточно иметь бюджетный мультиметр, стоимостью от 200 рублей.

Внутриканальные наушники

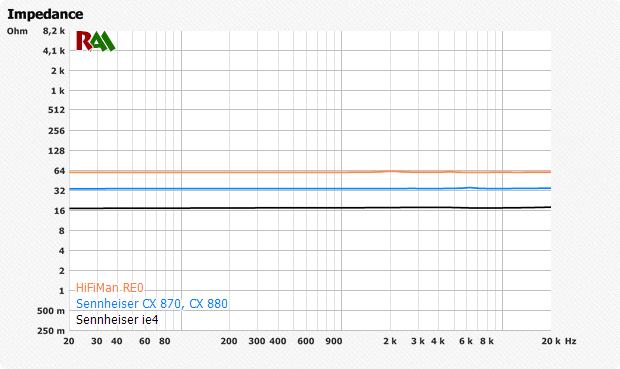
Большинство динамические внутриканальные наушники имеют плоскую кривую импеданса, а значение 16, 24 или 32 Ом показывает отсутствие изменений для частот от 20 до 20 кГц.

На графике горизонтально отображаются частоты от 20 Гц до 20 кГц. Вертикальная линия указывает импеданс (в логарифмическом масштабе).

Полноразмерные динамические наушники

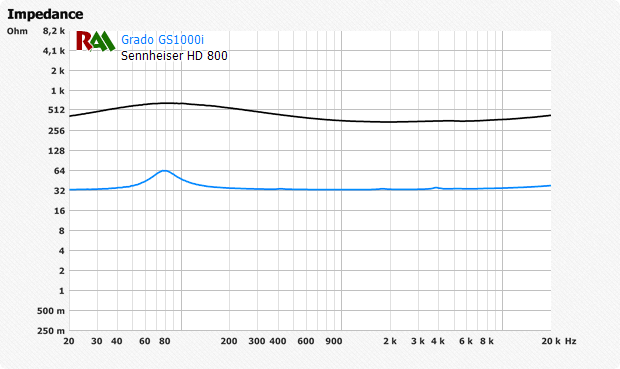
У полноразмерные динамические наушники Часто можно заметить характерную неравномерную кривую импеданса, с небольшим перепадом в низкочастотном диапазоне и небольшим перепадом в высокочастотном диапазоне.

Сопротивление может быть 32 Ом без реактивной части (условно это 0 Гц, измеряется любым универсальным мультиметром), но на практике оно может быть вдвое больше на определенных частотах.

Неравномерность (подъем) может указывать как на резонанс, так и на конструктивные особенности динамика в корпусе наушников. Например, при измерении импеданса частота и величина подъема может значительно отличаться в зависимости от того, лежат ли наушники свободно на столе или помещены на манекен, в этом случае внутренняя часть наушников демпфируется.

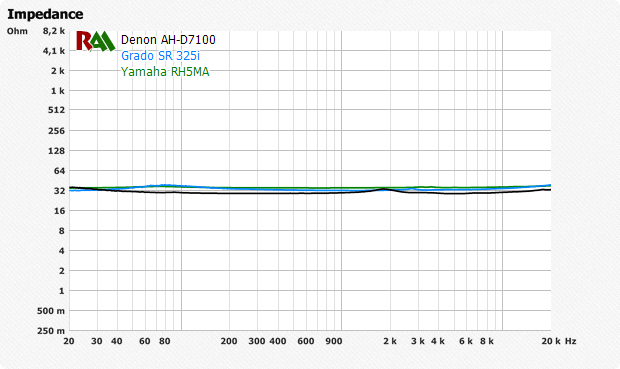
У некоторых динамических наушников нет заметного резонанса или уклона. Такая линия условно идеальна, но выбирать наушники таким образом не рекомендуется. В стремлении улучшить одну характеристику приходится жертвовать другой.
Среди наушников высокого класса можно найти кривые импеданса как с минимальными отклонениями, так и со значительными. Если наушники демонстрируют узкополосное усиление (Grado GS1000 на схеме выше), выберите усилитель с низким выходным сопротивлением для лучшего контроля басов (как, кстати, Grado RA1).

Изодинамические (ортодинамические) наушники

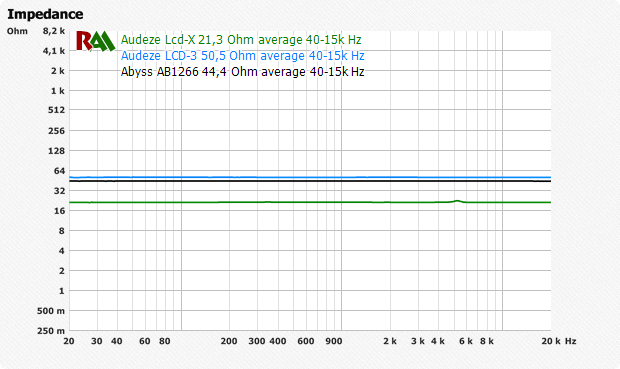
В дополнение к динамическим водителям в настоящее время все большее распространение получает изодинамический тип. Изодинамический тип водителя (и аналогичный тип, ортодинамический) в настоящее время получает все более широкое распространение. Эти наушники всегда имеют прямую линию импеданса. Изодинамические наушники сегодня производят компании Abyss, Audez’e, HiFiMan, Oppo, Fostex. В советское время такими наушниками были ТДС-5/м, ТДС-7, ТДС-15, ТДС-16 и ТДС-25. Сегодня моддинг больше распространен среди моделей ТДС-7 и ТДС-15.

Технически, это идеальная нагрузка для усилителя, но в диапазоне сверхвысоких частот (мегагерцы и гигагерцы) некоторые модели имеют пониженное сопротивление и стремятся к нулю. Это коварство не видно на стандартном графике и может привести к плохой работе с некоторыми усилителями.

Внутриканальные арматурные наушники

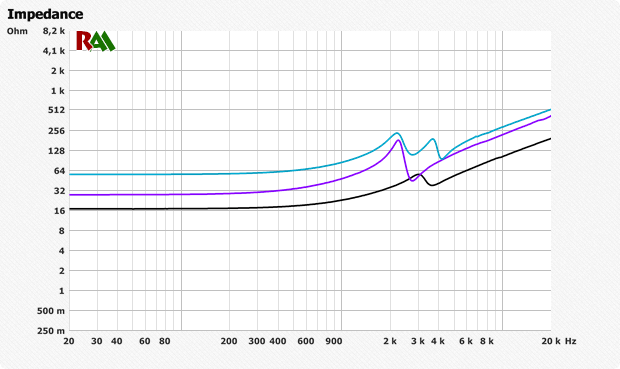
Импеданс едва предсказуем Внутриканальные наушники с арматурными динамиками. Общей особенностью моделей с одним динамиком является то, что всегда присутствует локальное усиление в верхних средних (около 1-3 кГц) и самых высоких частотах. Из-за усиления высоких частот большинство моделей арматурных динамиков с одним динамиком “звучат чисто” в высокочастотном диапазоне, поскольку усилитель производит меньше искажений в этом диапазоне частот.

В низкочастотном диапазоне типичный импеданс обычно составляет 8, 16, 24 или 32 Ом. Выше 500 Гц начинается усиление.
Если импеданс указан как 100 Ом при 1 кГц – это не значит, что наушники имеют высокий импеданс, их импеданс может быть даже 16 Ом, согласно показаниям мультиметра (в низкочастотном диапазоне).

Гибридные и многополосные наушники

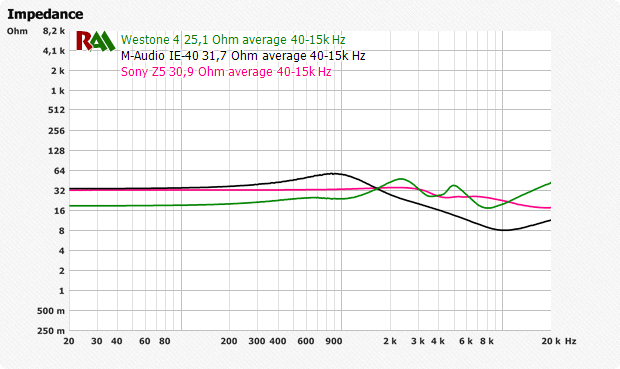
Невозможно предсказать кривую импеданса для мультидрайвер и Кривая импеданса многодрайверных или гибридных внутриканальных наушников не может быть предсказана.. Кривая импеданса может быть любой выше 500 Гц. Затухание сопротивления может достигать 4 Ом при заявленных 100 Ом на частоте 1 кГц.

Общие выводы

Сопротивление в реальности будет такой же, как на коробкеесли наушники: Динамика в канале или изодинамический
Сопротивление в реальности будет соответствовать коробке и будет иметь неизвестный ростесли наушники: Динамические накладные расходы i nполный размер
Импеданс в реальности НЕ будет на коробкеесли наушники: монтаж или Гибрид

Если вы хотите узнать фактический импеданс арматурных или гибридных наушников, вы можете попробовать поискать результаты измерений в Интернете. Методы измерения импеданса обычно дают одинаковый результат и не зависят от программного обеспечения испытательного стенда или измерительной установки.

Модуль электрического сопротивления или импеданс микрофона – это значение сопротивления на его выходных клеммах.

Значение слова “импеданс”

1. физ. комплексное сопротивление (электрическое, акустическое или механическое) Импеданс в последовательной цепи – это сумма импедансы его элементов.

Фразеологические выражения и устойчивые сочетания

Создавайте лучшие карты слов вместе

/> Меня зовут Lampbot, и я компьютерная программа, которая помогает мне создавать карты Word. Я отлично разбираюсь в математике, но пока не очень хорошо понимаю, как устроен ваш мир. Пожалуйста, помогите мне разобраться!

Спасибо! Я стал немного лучше понимать мир эмоций.

Вопрос: – Является ли он нейтральным, положительным или отрицательным?

Синонимы к слову “импеданс

Предложения со словом “импеданс&raquo

Благодаря своему опыту в электронике он знал, что идеальная электрическая цепь – это цепь с наименьшим сопротивлением, или, точнее, с наименьшим сопротивлением. импеданспотому что именно так электроэнергия может быть использована наиболее эффективно.

Концепции со словом “импеданс”

Опубликовать комментарий

Читать далее

Предложения со словом импеданс

Благодаря своему образованию в области электроники он знал, что идеальная электрическая цепь – это та, которая имеет наименьшее сопротивление, или, точнее говоря. импеданспотому что именно так электроэнергия может быть использована наиболее эффективно.

Модуль электрического сопротивления или импеданс микрофона является величина сопротивления на его выходных клеммах.

Сопротивление жировой ткани прохождению сигнала называется биоэлектрическим сопротивлением. импеданс.

где S – площадь динамика.

IMPEDANCE

IMPEDANCE (Импеданс – это физическая величина, которая описывает сопротивление среды колебаниям различного происхождения.

В зависимости от типа вибрации различают электрический импеданс, механический импеданс и акустический импеданс.

Электрическое сопротивление – это полное (комплексное) сопротивление среды. это полное (комплексное) сопротивление электрической цепи переменному току. В общем, электрическое сопротивление – это полное (комплексное) сопротивление электрической цепи для переменного тока. Электрический (Z) является геометрической суммой активного сопротивления (R) и реактивного сопротивления (X) цепи:

Активное сопротивление B является обратной величиной электропроводности ткани и слабо зависит от частоты переменного тока. Реактивная X составляющая комплексного сопротивления Z для различных проводящих биол. субстратов in vivo и in vitro зависит от частоты электрического тока. В Международной системе единиц в качестве единицы измерения электрического тока I принят ом (Ω, ohm).

Измерение электрической величины I используется для характеристики электрических свойств тканей, органов, отдельных клеток (см. Электропроводность биологических систем). Электропроводность биологических тканей уменьшается с увеличением частоты приложенного электрического поля, что связано с наличием емкостной составляющей электропроводности, обусловленной в основном явлением поляризации (см.)

И. Циркуляция крови (наполнение кровью кровеносных сосудов) особенно влияет на ткани организма. Поэтому измерение I в определенных частях тела, особенно в конечностях, является основой для изучения периферического кровообращения – так называемой реографии (см.). В реографии мы используем переменный ток частотой 20-30 кГц.

Электрическая И. биол. тканей изменяется в зависимости от их функционального состояния. Поэтому наблюдаемые изменения в конкретных условиях могут быть связаны со структурными и ионными преобразованиями в ткани. Исследование электрических И. компонентов клеточных суспензий позволяет определить электрические параметры как самих клеток, так и их поверхностных мембран, оценить изменения их проницаемости (см.).

Измерение импеданса на высоких частотах (выше 1 МГц) позволяет оценить общую концентрацию свободных электролитов в клетках и тканях (см. главу “Электрический импеданс”). Кондуктометрия). Измерение электрической И. также позволяет регистрировать изменения в физической и химической структуре живых тканей в нормальных и патологических условиях. Поэтому данный метод может быть использован для изучения динамики изменений, происходящих при различных заболеваниях и травмах, а также для оценки эффективности их лечения.

Акустический импеданс – Мера импеданса, введенная для характеристики сопротивления любой акустической системы распространению звуковых колебаний.

Рассмотрение акустического импеданса важно при изучении распространения звука, акустических свойств как физических систем (трубы переменного сечения, рупоры, излучатели и приемники звука, их мембраны, диффузоры и т.д.), так и биологических систем (органы слуха, речь и т.д.), а также при разработке устройств для коррекции слуха и речи.

I. Акустика, как и электричество, имеет активные и реактивные компоненты. Активный компонент связан с потерями энергии при прохождении звука через акустическую систему и с потерями на трение. Реактивная составляющая (реактанс) описывает инерционные и упругие силы, действующие на систему. Поэтому реактивное сопротивление также называют инерционным сопротивлением или упругим сопротивлением.

Акустический импеданс измеряется в ньютон-секундах на метр до пятой силы (Н-с/м-5) в системе СИ и в дин-секундах на сантиметр до пятой силы (дин-сек/см-5) в системе СГС. Последнюю единицу иногда называют акустическим омом.

Механический импеданс описывает сопротивление среды распространению различных вибраций (звук, ультразвук и т.д.). Измерение механического импеданса используется в медицинских и биологических исследованиях для изучения вибраций и их воздействия на организм в промышленных условиях.

Механическая единица СИ – ньютон-секунда на метр (Н-с/м). И. акустический (Za) и механический (Zm) связаны соотношением:

где S – площадь акустической системы.

Библиография: Биофизика, под ред. Б.Н. Тарусова и О.Р. Коллиера, М., 1968, библиография; С кучи к Е. Основы акустики, перевод с английского, т. 1-2, Москва, 1976.

В следующей таблице приведено значение терминов, используемых при описании импеданса цепи.

Термин: Импеданс

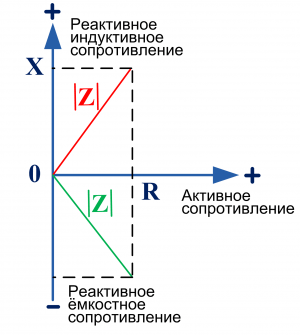
Электрический импеданс (комплексный импеданс, импеданс) – комплексное сопротивление двухполюсника для гармонического сигнала. Импеданс аналогичен понятию сопротивления для постоянного тока в применении к синусоидальному току. Эта концепция позволяет применить закон Ома к участку цепи для синусоидальных токов. Если двухполюсник имеет индуктивную составляющую на данной частоте, то синусоидальный ток будет задержан относительно напряжения на клеммах двухполюсника, а если он имеет емкостную составляющую, то напряжение будет задержано относительно тока. Если двухполюсник активен, то задержки между током и напряжением не будет. Если мы придадим реактивной составляющей импеданса X соответствующий знак на оси Y, а активной составляющей R на оси X, мы получим графическую интерпретацию импеданса как комплексное число

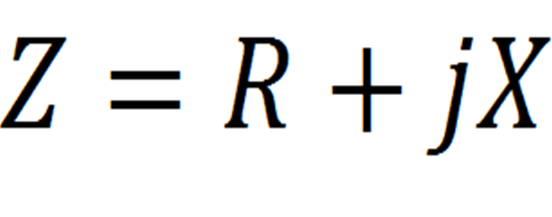
для которого j – мнимое единичное число в представлении комплексного числа (j 2 =-1), а реактивная составляющая X может быть теоретически представлена выражением

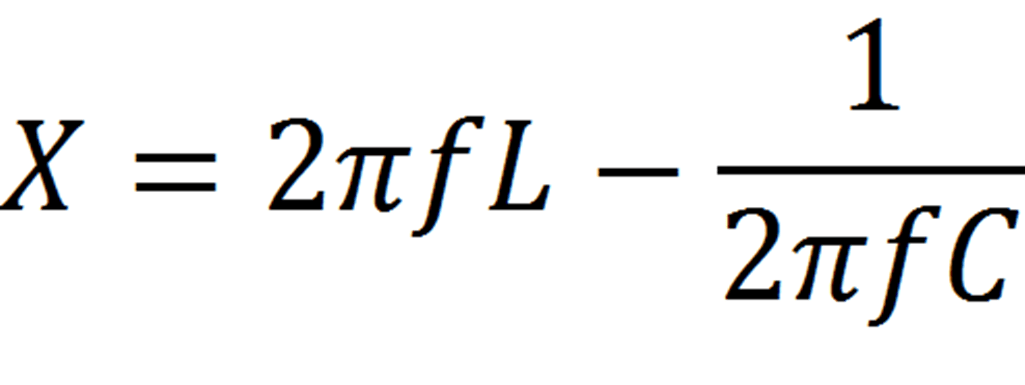
где f [Герц] – синусоидальная частота; L [Генри] выражает влияние индуктивной составляющей импеданса, а 1/C [Фарад -1 ] – влияние емкостной составляющей. Как видно из формулы, при доминировании индуктивной составляющей в сопротивлении X > 0 и доминировании емкостной составляющей X < 0.

Эта теоретическая модель импеданса Z соответствует следующему физическому двухполюснику:

Эта модель импеданса может быть сведена к модели любого линейного двухполюсника, для которого можно определить его активную составляющую R, зависящую от частоты, и реактивную составляющую X, зависящую от частоты.

Модуль импеданса |Z| (измеряется в омах), как видно из диаграммы, определяется как длина вектора суммы векторов R и X:

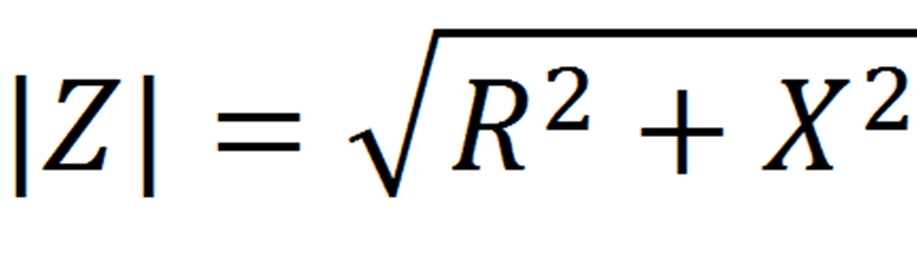
Опять же, значение комплексного импеданса Z = R + jX и его модуль |Z| определены только для данной частоты синусоидального тока в цепи.

В следующей таблице объясняется значение терминов, используемых для описания импеданса цепи.

Характеристика импеданса Z=R+jX	Активный компонент R	Реактивный компонент X
Индуктивный	Маленький	Позитив
Активно-индуктивный	Значительный	Позитив
Активный	Значительный	Маленький
Активно-емкостные	Значительный	Негатив
Емкостной	Маленький	Негатив

Если токи в цепи не являются синусоидальными, понятие импеданса применяется отдельно к каждой гармонической составляющей тока на данной частоте (если в решаемой задаче имеет смысл рассматривать импеданс для каждой такой составляющей). В этом смысле Импеданс можно интерпретировать как полное сопротивление цепи по отношению к рассматриваемой частотной составляющей переменного тока в этой цепи..

Понятие импеданса и анализ цепи для синусоидального тока см. в Бессонов, Л. А. Теплофизика, глава 3.

где E_t, Н _t – тангенциальные компоненты напряженности электрического и магнитного полей, п – единица, нормальная к S, Его направление обычно выбирается таким образом, чтобы проекция на него усредненного по времени потока энергии (вектор Поенинга P=(с/8p)Rе [EH*] является положительным. I.в (2) в общем случае является тензором, компоненты которого зависят от поляризации поля. В случаях, когда Е_t и Н_t взаимно перпендикулярны, мы вводим скалярное поле Z. В гауссовых единицах поле IM безразмерно, а в СИ – это размерность сопротивления. Иногда для ИМ используется выражение в гауссовых единицах, и в этом случае оно имеет размерность сопротивления. моды) характеризуются различными полями ИМ, определяемыми волновыми фронтами. Таким образом, для поперечной плоской волны (типа ТЕМ), распространяющейся в направлении п направление в изотропной среде или в волноводе, (m, e – относительные магнитная и диэлектрическая проницаемости среды, e₀, m₀ – проницаемость вакуума, в гауссовых единицах e₀=m₀=1). В вакууме Ома эта размерная константа называется характеристическим сопротивлением вакуума (в системе единиц Гаусса). Для таких волн, как ТМ и TE соответствующие значения I следующие:

IMPEDANCE

(Импеданс (комплексное сопротивление) является аналогом электрического сопротивления для гармонических процессов. Различают импеданс элемента цепи переменного тока (импеданс двухполюсной цепи) и импеданс к.-системы. Понятие поля I было введено в электродинамику О. Хевисайдом (О. Lodge) и С. Щелкуновым (С. Schelkunoff, 1938). Хевисайда и Лоджа, а также S. Шелкунов в 1938 году ввел понятие импедансных характеристик поля. Характеристики импеданса используются не только в электродинамике, но и для описания линии электропередач Они также могут использоваться в электродинамике для описания линий передачи волновых возмущений любой природы (см., например, акустический импеданс). Акустический импеданс).
Биполярный импеданс. В теории электрических цепей любая часть цепи, состоящая из пассивных линейных элементов (таких как сопротивления r, индуктивности L,емкость С, трансформаторы) и имеющие две точки (полюса), соединенные с остальной частью цепи (рис. 1), могут, в случае квазистационарных гармонических процессов с зависящими от времени

exp(iwt) можно рассматривать как пассивный двухполюсник, все внешние свойства которого описываются одной комплексной величиной Z, Это так называемый биполярный ИП и он равен комплексной величине Z. Комплексная величина Z называется I для биполярности и равна

Z (w) = V/I =R(w) + iX(w).

Рис. 1. Электрическая цепь, содержащая пассивные линейные элементы и имеющая два полюса: a – принципиальная схема; b – эквивалентный двухполюсник с импедансом Z(w).

Здесь V – комплексная амплитуда напряжения между полюсами 1 и 2, I – комплексная амплитуда тока в направлении от полюса 1 к полюсу 2; R – компонент импеданса (активного сопротивления), X – мнимая часть импеданса (реактивности, реактивного сопротивления). Модуль сопротивления |Z|=(R 2 +X 2 )1/2 называется полным сопротивлением двухполюсника. В системе СИ он измеряется в омах, в Система единиц Гаусса. Его размер обратно пропорционален скорости. Иногда наряду с Z используется обратная величина s=Z-1, называемая адмиттансом. P (среднее значение за период колебаний Т=2п/б P=R|I| 2 /2. Реактивность описывает энергию, пульсирующую с частотой 2w (и, следовательно, усредненную за период, равный нулю), которая накапливается в двухполюснике и отдается обратно источнику. Знак реактивности определяется зависимостью от времени: в инженерной и прикладной физике (и в этой статье) это предполагается теоретически. В случае чисто индуктивного двухполюсника ( индуктивное сопротивление) X=X _L=wL (в единицах СИ; в гауссовых единицах X_L=c -2 wL), и для чисто емкостных (емкость) X=Xc=-.(wC) -1 . Разница в знаках обусловлена двойной асимметрией Уравнения Максвелла (E “H, H “-E ) и отражает связь между фазами напряжений и токов: ток через идеальную катушку самоиндукции равен p/2 после приложенного напряжения, а ток через идеальный конденсатор равен p/2 до напряжения, приложенного к его обмоткам. Принципы последовательного и параллельного сложения такие же, как и для обычных омических сопротивлений: при последовательном соединении двухполюсников добавляются индуктивности. Z, а в случае параллельного соединения – адмиттансы Z -l . Например, для двухполюсника, показанного на рис. la, имеем:

Z -1 = (r+ iwL) -1 +iwC.

Импедансная матрица. Шарнирная схема с более чем двумя точками соединения называется многополюсной [если число пар точек соединения (входов) составляет N, схема называется 2N -полюс]. Входы мультиполяризатора должны иметь заданное опорное направление для напряжений и токов (рис. 2). Если многополюсник содержит только линейные, пассивные и взаимно обратные элементы, то для квазистационарных гармонических процессов все его внешние свойства описываются матрицей импеданса ||Z_ab||, которая связывает комплексные амплитуды напряжений и токов на входах в произвольной комбинации с когерентными источниками:

Например, для тетраэдра, изображенного на рис. 3, а, элементы матрицы I. равны: Z₁₁=Z₁+Z₃,Z₂₂=Z₂+Z₃, Z₁₂=Z₂₁=Z₃. Под принцип взаимности матрица |Z_ab| является симметричным, т.е. Z_ab=Z_ba
Входной импеданс. Свойства мультиполей также могут быть описаны так называемыми входными импедансами. входы.

Рисунок 2: Мультиполь, все внешние свойства которого определяются матрицей импеданса ||Z|||.

Рисунок 3. Квадруполь: a – эквивалентная схема; b – схема для определения входного импеданса.

В этом случае, по отношению к выбранному входу, многополюсник рассматривается как биполярный, а все остальные входы рассматриваются как произвольно нагруженные I _н_b. Поэтому входной I зависит не только от частоты, но и от нагрузки I. Таким образом, для квадратуры, показанной на рис. 3:

Для соответствия любой нагрузке Z _н к источнику, который имеет внутреннюю I. Z _wиспользуется нерассеивающий четырехугольник (без демпферов), получая условие Z _w(Z _н)=Z* _w (* означает комплексное соединение). Таким образом, достигается максимальная передача энергии от источника к нагрузке (КПД составляет 50%, остальная энергия поглощается внутри источника). Если требуется высокая эффективность передачи, четырехполюсный терминатор должен быть выбран таким образом, чтобы выполнялись следующие условия: R _w(Z _н )eR _w, X _w(Z _н)=-Х _{На стр.}.
Волновое сопротивление. Вход четырехполюсника I, удовлетворяющий условию Z _w(Z _н=Z _в)=Z _н= Z _вМы называем волновое сопротивление волновым сопротивлением, потому что в бесконечной цепи одинаковых четырехугольников волны (в общем случае экспоненциально затухающие) с постоянным отношением напряжения к току будут распространяться без отражения. В пределе непрерывной однородной линии передачи это отношение в каждом нормальном сечении постоянно и при отсутствии потерь равно Z _в = (L _п/C _п) 1/2 , где L _п, С _п– линейная (на единицу длины) индуктивность и емкость линии.Z _в, коэффициент отражения (отношение комплексных амплитуд отраженной и падающей волн) – это

На Z _н=0 и Z _н “:, что соответствует короткозамкнутой и разомкнутой линиям, происходит полное отражение (G=71). Длинные линии не являются квазистационарными системами, поэтому термин напряжения является условным. Обычно он применяется только к точкам, лежащим на одном участке нормальной линии S_n, и путь интегрирования g₁₂ выбирается так, чтобы лежать в том же сечении.

Поверхностный (полевой) импеданс вводится для монохроматических электромагнитных полей Е(r)exp(iwt), H(r)exp(iwt) на любой условной поверхности S следующим образом:

где E_t, Н _t – тангенциальные компоненты напряженности электрического и магнитного полей, п – единица, нормальная к S, Его направление обычно выбирается таким образом, чтобы проекция на него усредненного по времени потока энергии (вектор Поенинга P=(с/8p)Rе [EH*] является положительным. I.в (2) в общем случае является тензором, компоненты которого зависят от поляризации поля. В случаях, когда Е_t и Н_t взаимно перпендикулярны, мы вводим скалярное поле Z. В гауссовых единицах поле IM безразмерно, а в СИ – это размерность сопротивления. Иногда для ИМ используется выражение в гауссовых единицах, и в этом случае оно имеет размерность сопротивления. моды) характеризуются различными полями ИМ, определяемыми на волновых фронтах. Таким образом, для поперечной плоской волны (типа ТЕМ), распространяющейся в направлении п направление в изотропной среде или в волноводе, (m, e – относительные магнитная и диэлектрическая проницаемости среды, e₀, m₀ – проницаемость вакуума, в гауссовых единицах e₀=m₀=1). В вакууме Ома эта размерная константа называется характеристическим сопротивлением вакуума (в системе единиц Гаусса). Для таких волн, как ТМ и TE соответствующие значения I следующие:

где k – волновое число, k_|| – продольная составляющая волнового вектора. Для критических частот (k_|| “0) Z_ТМ “0, Z_TE “:, а для сверхкритических – когда волна превращается в экспоненциально убывающую по модулю:

то есть Если нет потерь, то импеданс поля для распространяющихся волн является правильным значением; иногда его называют волновым импедансом, но импеданс поля для распространяющихся волн является истинным значением; если нет потерь, то импеданс поля для распространяющихся волн является истинным значением. Волновое сопротивление среды. Поскольку он обладает многими свойствами волнового сопротивления линии или цепочки четырехугольников, его называют волновым сопротивлением среды. В частности, когда плоская волна падает из среды 1 на плоскость раздела со средой 2, коэффициент отражения (в терминах амплитуды поля) аналогично (1) выражается как

Это выражение Формула Френеля, записанный И. (поляризация p соответствует режиму ТМ,(s-поляризация соответствует ТМ-моде; s-поляризация соответствует ТЕ-моде TE,(k_||/k) (1,2) =cosq ( l, 2) , q ( l) и q ( 2) – углы падения и преломления). При исследовании отражения от плоских неоднородных сред уравнения поля часто преобразуются в уравнения поля и порядок уравнений уменьшается. Важны так называемые импедансные поверхности, т.е. уравнения поля не являются фиксированными. На самом деле, фиксация происходит (в большинстве случаев приблизительно), когда структура поля “под поверхностью” инвариантна и определяется определенными свойствами среды или полеобразующих устройств. Таким образом, когда волна ударяет в хорошо поглощающую среду, она распространяется внутри среды почти вдоль нормали, независимо от угла падения, поэтому “входной” FD можно считать постоянным и равным Z (2) _TEM (граничное условие Леонтовича). Импедансные поверхности используются для моделирования границ направляющих устройств в антеннах, системах задержки и т.д. Лит: Основы теории цепей, 4-е издание, М., 1975; Ландау Л.Д., Лифшиц Е.М., Электродинамика сплошных сред, 2-е издание, М., 1982; Buduris J., Chenevier P., Ultrahigh Frequency Circuits, перевод с французского, М., 1979. В. Пермитин, М.А. Миллер.

Энциклопедия физики. В 5 томах. – Москва: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Читайте далее: