Плотность тока, наряду с другими факторами, характеризует движение зарядов. Формула для плотности тока описывает электрический заряд, переносимый за 1 секунду через определенное сечение проводника, направленное перпендикулярно этому току.
Таким образом, с физической точки зрения, плотность тока – это заряды в определенном количестве, протекающие через данную единицу площади за единицу времени. Это векторная величина, представляющая собой отношение силы тока и площади поперечного сечения проводника, по которому течет ток. Модульное значение плотности тока будет: j = I/S. В этой формуле j – модуль вектора, I – сила тока, а S – площадь поперечного сечения.
Какова плотность тока
Электрические провода под напряжением постоянно подвергаются определенной нагрузке. Поэтому очень часто задается вопрос о том, что такое плотность тока и как она влияет на качество поставляемой электроэнергии. Фактически, это значение характеризует степень электрической нагрузки на кабели. Это позволяет избежать ненужных потерь при прокладке кабельных линий. При использовании высокочастотного оборудования необходимо учитывать дополнительные электродинамические эффекты.
Электрический ток характеризуется следующими особенностями текущий I (рис. 4.1).
4.1 Сила тока и плотность тока в проводнике
В проводнике некоторые валентные электроны не связаны с конкретными атомами и могут свободно перемещаться по всему объему проводника. В отсутствие электрического поля, приложенного к проводнику, эти свободные электроны, электроны проводимости, хаотично перемещаются, часто сталкиваясь с ионами и атомами, изменяя при этом свою энергию и направление. Через любое поперечное сечение проводника в одном направлении проходит столько же электронов, сколько и в противоположном направлении. Поэтому в таком сечении нет результирующего переноса электронов, и электрический ток равен нулю. Если к концам проводника приложить разность потенциалов, то свободные заряды в проводнике под действием электрического поля начинают перемещаться от большего потенциала к меньшему – возникает электрический ток. Исторически сложилось так, что направление тока принимается за направление положительных зарядов, что соответствует их движению от более высокого потенциала к более низкому.
Электрический ток характеризуется сила тока I (рис. 4.1).
Текущая сила скалярная величина, численно равная заряду, переносимому через поперечное сечение проводника в единицу времени
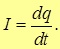
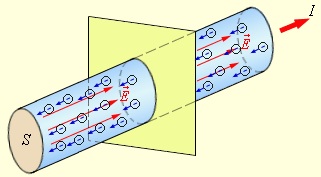
Рис. 4.1: Ток в проводнике
Согласно (4.1), ток в проводнике равен отношению заряда, протекающего через поперечное сечение проводника за время, к этому времени.
Примечание: В общем случае ток, протекающий через поверхность, равен потоку заряда через эту поверхность.
Если ток не изменяется во времени, т.е. через любой участок проводника через равные промежутки времени протекают одни и те же заряды, то ток называется неизменныйи затем заряд, который потек за это время. tможно найти как (рис. 4.2)
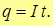
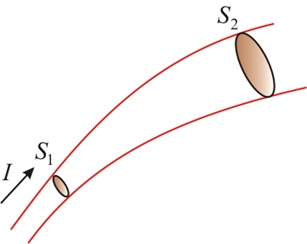
Рисунок 4.2: Постоянный ток, протекающий через различные сечения проводника
Значение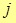 
Плотность тока, равная заряду на единицу площади поперечного сечения проводника в единицу времени, называется плотность тока.
Учитывая определение плотности тока, плотность тока в данном сечении может быть выражена в терминах тока, протекающего через это сечение
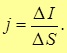
Если поток зарядов равномерно распределен по всему поперечному сечению проводника, то плотность тока составляет
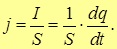
В системе СИ единицей тока является амперы (А). В системе СИ этой единицей измерения является основной.
Уравнение (4.1) применимо к единицам тока и заряда
Единицей измерения плотности тока в СИ является амперы на квадратный метр (А/м 2 ):
Это очень маленькое значение, поэтому на практике мы обычно имеем дело с более крупными единицами, например.
Плотность тока может быть выражена в терминах объемной плотности зарядов и их скоростей v (рис. 4.3).
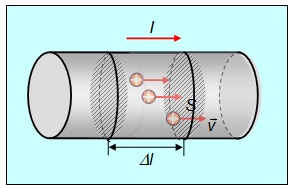
Рисунок 4.3: Зависимость плотности тока j от объемной плотности зарядов и скорости дрейфа v носителей заряда. В момент времени dt все заряды из объема dV = vdt S пройдут через площадку S
Общий заряд, протекающий в момент в момент времени dt через какую-то поверхность Sперпендикулярно вектору скорости vэто
С сайта dq/(Sdt) – модуль плотности тока jмы можем написать
Поскольку скорость v является векторной величиной, удобно также рассматривать плотность тока как векторную величину, следовательно
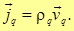
Здесь плотность заряда, скорость направленного движения носителей заряда.
Примечание: Для общности использован индекс, поскольку носителями заряда, которые могут участвовать в образовании тока проводимости, могут быть не только электроны, но и, например, протоны в пучке, полученном из ускорителя, или многозарядные ионы в плазме, или так называемые “дырки” в полупроводниках.р“, или, короче говоря, любые заряженные частицы, способные двигаться под воздействием внешних силовых полей.
Удобно также выразить плотность заряда через количество носителей заряда на единицу объема – (концентрацию носителей заряда). Результат
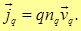
Следует отметить, что плотность тока, в отличие от силы тока, является дифференциальной векторной величиной. Зная плотность тока, мы знаем распределение потока заряда по проводнику. Силу тока всегда можно вычислить по его плотности. Отношение (4.4) может быть “перевернуто”: Если взять бесконечно малый элемент с площадью , то ток, протекающий через него, определяется как . Соответственно, ток, протекающий через любую поверхность S можно найти путем интегрирования
Что подразумевается под скоростью заряда vесли таких зарядов много и, очевидно, не все они движутся одинаково? В отсутствие внешнего электрического поля скорости теплового движения носителей тока распределяются хаотично в соответствии с общими законами статистической физики. Статистическое среднее является результатом изотропии распределения вдоль направлений теплового движения. При наложении поля возникает определенная скорость дрейфа – средняя скорость направленного движения носителей заряда:
которая будет отлична от нуля. Давайте воспользуемся аналогией. Когда вода вытекает из шланга и нам интересно, сколько ее попадает в русло в единицу времени, нам нужно знать скорость потока и поперечное сечение шланга. И нас совершенно не волнуют скорости отдельных частиц, хотя они очень велики, гораздо больше, чем скорость потока воды, как мы видели в предыдущей части курса.
Таким образом, скорость в выражении (4.7) – это скорость дрейфа носителей тока в присутствии внешнего электрического или иного силового поля, вызывающего направленное (упорядоченное) движение носителей заряда. Если в веществе могут двигаться носители зарядов разных знаков, то общая плотность тока определяется векторной суммой плотности потока зарядов каждого знака.
Как уже упоминалось, в отсутствие электрического поля движение носителей заряда хаотично и не приводит к возникновению результирующего тока. Если приложением электрического поля придать носителям заряда даже небольшую (по сравнению с их тепловой скоростью) дрейфовую скорость, то возникнет значительный ток из-за наличия в проводниках огромного количества свободных электронов.
Поскольку дрейфовая скорость носителей создается электрическим полем, логично предположить пропорциональность
поэтому плотность тока также будет пропорциональна вектору интенсивности (рис. 4.4)
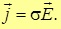
Более подробно это обсуждается в Приложении
Соотношение (4.9)
Коэффициент пропорциональности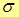 
называется проводимость вещества проводника.
Проводимость соотносит напряженность поля в данной точке с фиксированной скоростью “потока” носителей заряда. Поэтому она может зависеть от локальных свойств проводника вблизи этой точки (т.е. от структуры вещества), но не зависит от формы и размеров проводника в целом. Отношение (4.9) называется Закон Ома для плотности тока в проводнике (также называется Закон Ома в дифференциальной форме).
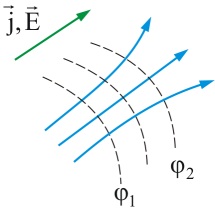
Рисунок 4.4: Линии электрического поля совпадают с линиями тока
Чтобы понять порядки величин, давайте оценим скорость дрейфа носителей заряда в одном из самых распространенных материалов – меди. Возьмем, к примеру, действующую силу I = 1 A и пусть площадь поперечного сечения провода будет
1 мм 2 = 10 -6 м 2 . Тогда плотность тока составляет j = 10 – 6 A/м 2 . Теперь воспользуемся соотношением (4.7)
Носителями заряда в меди являются электроны (е = 1.6-10 -19 K), и нам остается оценить их концентрацию. Медь относится к первой группе элементов в таблице Менделеева, имеет один валентный электрон, который может быть отдан в зону проводимости. Поэтому число свободных электронов приблизительно равно числу атомов. Плотность меди приведена из справочника r Cu=8,9-10 3 кг/м3. Молярная масса меди приведена в таблице Менделеева -. MCu = 63,5-10 -3 кг/моль. Соотношение
– число молей в 1 м 3 . Умножив на число Авогадро Na = 6,02-10 23 моль-1 , получим число атомов на единицу объема, т.е. концентрацию электронов
Теперь мы получаем требуемую оценку скорости дрейфа электрона
Для сравнения, скорость дрейфа электронов при 20°C в меди составляет 10 6 м/с, что на одиннадцать порядков выше.
Возьмем любую воображаемую замкнутую поверхность Sпересекаются зарядами, движущимися в разных направлениях. Мы видели, что полный ток, протекающий через поверхность, равен
где dq – заряд, который перемещается вдоль поверхности за время dt. Обозначим через q ‘ заряд внутри поверхности. Она может быть выражена как плотность заряда , интегрированная в объеме, ограниченном поверхностью
Из фундаментального закона природы закон сохранения заряда – следует, что заряд dqкоторый вовремя выбрался на поверхность dtуменьшит заряд q ‘ внутри поверхности на точно такую же величину, т.е. dq ‘ = –dq или
Подставляя вышеприведенные выражения для скорости изменения заряда внутри поверхности, получаем математическое соотношение, выраженное словами закон сохранения заряда в интегральной форме
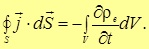
Напомним, что интегрирование производится по произвольным поверхностям S и ограниченный им объем V.
Сила тока I для тока, протекающего через некоторое сечение проводника S, эквивалентна производной от заряда q в момент времени t и определяет электрический ток.
Плотность тока. Зависимость плотности тока от заряда и силы тока
Определим небольшой объем d V произвольной формы в проводнике, в котором течет ток. Используя следующие обозначения υ, определим среднюю скорость носителей заряда в проводнике. Пусть n 0 обозначает концентрацию носителей заряда. На поверхности проводника выберем пренебрежимо малый квадрат d S , который ортогонален скорости υ (рис. 1).
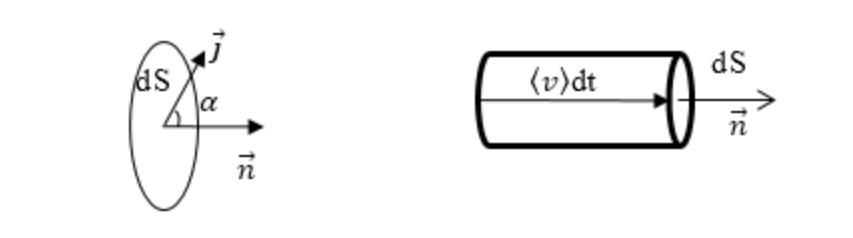
Представим на поверхности квадрата d S очень короткий прямой цилиндр высотой υ d t . Вся система частиц, находившаяся внутри такого цилиндра в момент времени d t, пересечет плоскость d S и перенесет через нее, в направлении скорости υ, заряд, выраженный следующим выражением
d q = n 0 q e υ d S d t ,
где q e = 1 , 6 – 10 – 19 K l – заряд электрона, другими словами, единичной частицы или носителя тока. Разделив приведенную выше формулу на d S d t, получим
где j – модуль плотности электрического тока.
где j – модуль плотности электрического тока в проводнике, где заряд переносится электронами. В случае, когда ток возникает при движении нескольких видов заряда, формула для плотности тока может быть определена в виде следующего выражения:
j = ∑ n i q i υ i ,
где i представляет носитель заряда. Плотность тока – это векторная величина. Снова обратимся к рисунку 1. Пусть n → обозначает единицу, перпендикулярную плоскости d S . Когда частицы, несущие заряд, положительны, заряд, переносимый ими в нормальном направлении, больше нуля. В общем случае элементарный заряд, переносимый в единицу времени, может быть записан в следующей форме:
d q d t = j → n → d S = j n d S .
Приведенная выше формула также справедлива, когда плоскость площадки d S неортогональна вектору плотности тока. По той причине, что составляющая вектора j → , направленная под прямым углом к нормали, не проводит ток через поперечное сечение d S . Исходя из вышеизложенных соображений, запишем плотность тока в проводнике по формуле j = n 0 q e υ в таком виде:
Поэтому плотность тока эквивалентна количеству электричества, другими словами, заряду, протекающему в секунду через единицу поперечного сечения проводника. В отношении однородного цилиндрического проводника можно записать, что:
где S играет роль площади поперечного сечения проводника. Плотность постоянного тока одинакова по всему поперечному сечению проводника. Для двух различных поперечных сечений проводника ( S 1 , S 2 ), в которых течет постоянный ток, справедливо следующее уравнение:
j 1 j 2 = S 2 S 1 .
На основе закона Ома можно записать следующее выражение для плотности тока:
где λ – коэффициент удельной проводимости. Определив плотность тока, мы можем выразить ток в следующей форме:
где интегрирование происходит по всей площади поверхности S любого сечения проводника. Единицей плотности тока является А м 2 .
Внимание! Минимальные площади поперечного сечения одинаковы для обоих типов проводников: 1 мм2 для меди и 2,5 мм2 для алюминия.
Какая плотность тока допустима для меди. Естественные науки
Плотность постоянного тока можно сравнить с плотностью газа, протекающего в трубе под давлением. Плотность тока – это отношение силы тока в амперах (A) к площади поперечного сечения проводника в квадратных миллиметрах (рис. 1). Он не зависит от материала проводника. Площадь поперечного сечения проводника берется по нормали (перпендикулярно) к его продольной оси.
Если, скажем, проволока имеет диаметр D = 1 мм, то площадь ее поперечного сечения составит S = 1/4(πD^2) = 3,1415/4 = 0,785 мм кв. Если по такому проводу течет ток I, равный 5 А, плотность тока j будет равна j = I/S = 5/0,785 = 6,37 А/кв. мм.
Хотя само значение плотности тока не зависит от материала проводника, в технике оно выбирается на основе его электрического сопротивления и длины провода. Дело в том, что высокая плотность тока вызывает нагрев проводника, его сопротивление увеличивается, и потери мощности в проводе или обмотке возрастают.
Однако если провода слишком толстые, вся установка будет слишком дорогой. По этой причине расчеты для бытовых кабельных сетей основаны на так называемой экономической плотности тока, при которой общие долгосрочные затраты на электрическую сеть минимальны.
Для не слишком длинных плоских кабелей может быть достигнута экономичная плотность тока 6 – 15 А на кв. мм, в зависимости от длины кабеля. Медный кабель диаметром 1,78 мм (2,5 кв. мм) в ПВХ-изоляции, проложенный под штукатуркой, может выдерживать ток до 30 или даже 50 ампер. Но при потребляемой мощности 5 кВт в квартире плотность тока составит (5000/220) = 23 А, а плотность тока в проводке – 9,2 А/кв. мм.
Экономическая плотность тока в линиях электропередачи гораздо ниже, в диапазоне 1-3,4 А/кв.мм. В электрических машинах и трансформаторах с промышленной частотой 50/60 Гц, от 1 до 10 А/кв.мм. В последнем случае он рассчитывается исходя из допустимого нагрева обмоток и величины электрических потерь.
Плотность тока на высоких частотах (например, телевизионные и радиосигналы) рассчитывается с учетом так называемого скин-эффекта. Суть его в том, что электромагнитное поле выталкивает ток на поверхность провода, поэтому для достижения нужной плотности диаметр провода должен быть больше, а не тратить лишнюю медь, чтобы сделать его полым, как трубку.
Эффект кожи важен не только для передачи высокой мощности. Если, например, для монтажа кабельного телевидения в квартире используется слишком тонкий коаксиальный кабель, потери в кабеле из-за скин-эффекта во внутреннем проводнике могут быть слишком высокими. Аналоговые каналы будут пульсировать, а цифровые – сминаться.
Глубина скин-эффекта зависит от частоты сигнала, а плотность тока плавно падает до нуля в центре провода. В инженерных целях, для упрощения расчетов, глубина поверхности кожи принимается там, где плотность тока падает в 2,72 раза по сравнению с поверхностным током (рис. 2). Значение 2,72 получено в инженерной электродинамике из соотношения электрической и магнитной постоянной, что упрощает расчет.
Ток смещения – довольно сложная электродинамическая концепция, но именно он заставляет переменный ток протекать через конденсатор и антенну излучать сигнал в эфир. Ток смещения также имеет плотность, но ее нелегко определить.
Чтобы найти плотность тока смещения, необходимо решить сложные уравнения электродинамики или провести компьютерное моделирование процесса. К счастью, во многих инженерных приложениях нет необходимости знать его значение.
и плотность тока
Электрический ток, сила тока и плотность тока
В электродинамике, отрасли науки об электричестве, которая занимается изучением явлений и процессов, вызванных движением электрических зарядов или макроскопических заряженных тел, наиболее важным понятием является понятие электрического тока.
Электрический ток это любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Ε положительные электрические заряды движутся в направлении поля, а отрицательные – в противоположном направлении. ток проводимости. Если упорядоченное движение электрических зарядов реализуется путем перемещения заряженного макроскопического тела в пространстве, возникает так называемый конвекционный ток. конвекционное течение.
Для возникновения и существования электрического тока необходимо, чтобы с одной стороны были свободные носители тока. перевозчики – Направление тока – это наличие электрического поля, энергия которого, так или иначе восполняемая, расходуется на упорядоченное движение заряженных частиц. Направление тока условно принимается за направление движения положительногоположительных зарядов.
Количественной мерой электрического тока является сила тока I – это скалярная физическая величина, которая определяется электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:
Ток, сила и направление которого не меняются с течением времени, называется инвариант. Для постоянного тока
где Q — это электрический заряд, протекающий в момент времени t через поперечное сечение проводника.
Единицей тока является амперы (А). Более подробно ток может быть охарактеризован вектором плотности тока j.
Плотность тока физическая величина, определяемая силой тока, протекающего через единицу площади поперечного сечения проводника перпендикулярно направлению тока:
Направление вектора j вектор совпадает с направлением упорядоченного движения положительных зарядов. Единицей плотности тока является ампер на квадратный метр (А/м 2 ).
Выразим ампер и плотность тока как функцию скорости v упорядоченное движение зарядов в проводнике. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то во времени dt в поперечном сечении S проводник несет заряд
/>,
и плотность тока
/>.
Ток, протекающий через любую поверхность S, определяется как поток вектора j, т.е.
/>,
где dS = n dS (n – единичный вектор нормали к поверхности dS, который связан с вектором j угол ).
Плотность тока в разных сечениях проводников S1 и S2 не одинакова:
Плотность тока
Величина, равная отношению силы тока к площади поперечного сечения проводника S, называется плотностью тока (символ δ ).
Плотность тока может быть определена следующим образом:
При этом предполагается, что ток равномерно распределен по сечению проводника. Плотность тока в проводниках обычно измеряется в а/мм 2 .
Плотность тока – это векторная величина. Вектор плотности тока в проводниках, соединяющих источники энергии и нагрузки, нормален к площади поперечного сечения проводника.
В неразветвленной электрической цепи плотность тока в различных сечениях проводника имеет одно и то же значение.
Если предположить, что величина постоянного тока в участках проводника S1 и S2 неодинакова (рис. 1), то заряды, протекающие через участки проводника S1 и S2 в единицу времени, будут разными. В результате в объеме проводника между этими секциями будет накапливаться положительный или отрицательный заряд. При постоянном токе происходило бы бесконечное накопление заряда, что невозможно при постоянном токе.
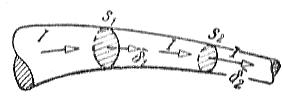
Рисунок 1: Электрический ток и плотность тока в различных сечениях неразветвленной электрической цепи.
Плотность тока в разных сечениях проводников S1 и S2 не одинакова:
δ1 = I / S1 , δ2 = I / S 2. В точке S1 > S2 получаем δ1 δ2
Если вам понравилась эта статья, пожалуйста, поделитесь ею в своих социальных сетях. Это очень поможет в развитии нашего сайта!
Читайте далее:- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Как работают атомы.
- Атомная структура.
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
- Электрический заряд и элементарные частицы. Закон сохранения заряда.
- Электричество. Сила электричества.
- Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.