Что такое векторные диаграммы и для чего они нужны; Школа для электриков: электротехника и электроника

Рисунок 1: Изображение вращающегося синусоидального вектора напряжения

Что такое векторные диаграммы и для чего они используются

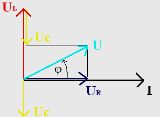Использование векторных диаграмм для расчета и испытания цепей переменного тока позволяет визуализировать происходящие процессы и упрощает электрические расчеты.

В цепях переменного тока часто требуется сложить (или вычесть) несколько однородных синусоидальных переменных одинаковой частоты, но с разными амплитудами и начальными фазами. Такая задача может быть решена аналитически с помощью тригонометрических преобразований или геометрически. Геометрический метод является более простым и описательным, чем аналитический.

Векторные диаграммы – это совокупность векторов, представляющих действующие синусоидальные ЭДС и токи или их амплитудные значения.

Гармонически переменное напряжение определяется выражением u = U_m sin ( ωt + ψ _и ).

Расположим под углом ψ i относительно положительной оси x вектор U _m длина которого в произвольном масштабе равна амплитуде представленной гармонической величины (рисунок 1). Положительные углы будут даны против часовой стрелки, а отрицательные – по часовой стрелке. Предположим, что вектор U _m начиная с момента времени t = 0, вращается против часовой стрелки вокруг начала координат с постоянной частотой вращения ω, равной угловой частоте представленного напряжения. В момент времени t вектор Um повернут на угол ωt и находится под углом ωt + ψ по отношению к оси абсцисс. Проекция этого вектора на ось ординат при заданном масштабе равна мгновенному значению отображаемого напряжения: u = U_m sin ( ωt + ψ _и ).

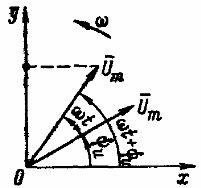
Рис. 1 Представление вращающегося вектора синусоидального напряжения

Поэтому величина, изменяющаяся гармонически во времени, может быть представлена вектором вращения . С начальной фазой, равной нулю, когда u = 0 , вектор U _m для t = 0 должна находиться на оси абсцисс.

График зависимости от времени любой переменной величины (включая гармонику) называется временной диаграммой. В случае гармонических переменных удобнее изображать на оси абсцисс не само время t, а пропорциональную ему величину ω_t . Временные диаграммы полностью определяют гармоническую функцию, поскольку дают представление о начальной фазе, амплитуде и периоде.

Обычно при расчете цепи нас интересуют только действующая ЭДС, напряжения и токи или амплитуды этих величин и их сдвиг фаз относительно друг друга. Поэтому постоянные векторы обычно рассматриваются для некоторого момента времени, который выбирается так, чтобы график был читаемым. Мы называем такую диаграмму векторной диаграммой. Фазовые углы строятся в направлении вращения векторов (против часовой стрелки), если они положительные, и в обратном направлении, если они отрицательные.

Например, если начальный фазовый угол напряжения ψ i больше, чем начальный фазовый угол ψi, то происходит сдвиг фаз φ = ψ _и – ψ_i и этот угол устанавливается в положительном направлении по отношению к вектору тока.

При расчете цепи переменного тока часто необходимо сложить ЭДС, токи или напряжения одинаковой частоты.

Это сложение может быть выполнено как аналитически, так и графически. Последний метод более очевиден и прост. Два дополнительных ЭМП e₁ и д₂ в некоторой степени представлены векторами E_{1 m} E _2m (рис. 2). Когда эти векторы вращаются с одинаковой частотой вращения, равной угловой частоте, взаимное положение вращающихся векторов остается неизменным.

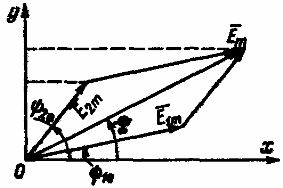
Рисунок 2. Графическое сложение двух синусоидальных ЭДС одинаковой частоты

Сумма проекций векторов вращения E_{1 m} и Е _2m на оси ординат равна проекции на ту же ось вектора E m, который является их геометрической суммой. Поэтому сумма двух синусоидальных ЭДС одинаковой частоты дает синусоидальную ЭДС, амплитуда которой представлена вектором E _mкоторая равна геометрической сумме векторов E_{1 m} и Е _2m: E _m = E_{1 m} + E _2m.

Векторы переменных ЭДС и токов – это графические представления ЭДС и токов в отличие от векторов физических величин, имеющих конкретный физический смысл: векторов силы, напряженности поля и других.

Приведенный метод может быть использован для сложения и вычитания любого количества ЭДС и токов одинаковой частоты. Вычитание двух синусоидальных величин можно понимать как сложение e₁– e₂ = e₁+ (- e₂), т.е. вычитаемое количество прибавляется к вычитаемому количеству, взятому с противоположным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для эффективных значений, пропорциональных амплитудным значениям, поскольку все расчеты цепи обычно выполняются для эффективных ЭДС и токов.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Затем в эти уравнения подставляется синусоидальный ток:

Оглавление

Векторные диаграммы можно рассматривать как вариант (и иллюстрацию) представления колебаний в виде комплексных чисел. В такой схеме ось Ox соответствует оси действительных чисел, а ось Oy – оси мнимых чисел (положительный единичный вектор, вдоль которого расположена мнимая единица).

Тогда вектор длины Aвращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ₀ записывается как комплексное число

UA в комплексном представлении

Для построения ВД можно также использовать математический аппарат, основанный на концепции комплексных чисел. Напомним, что комплексное число Z – это выражение: Z = a + b*i, где a и b – действительная и мнимая части комплексного числа, i – мнимая единица (i 2 = -1). Такая форма обозначения комплексного числа называется алгебраической.

В дополнение к алгебраической форме используются два других варианта обозначений: Z = |Z| * cos(φ)+ i * sin(φ) – тригонометрическая, Z = |Z| * e iφ – экспоненциальная.

Последняя называется формулой Эйлера в честь великого математика, который предложил и обосновал эту формулу в 18 веке. Комплексное представление гармонических колебаний позволяет упростить сложные тригонометрические вычисления за счет понятных и менее громоздких операций над экспоненциальными функциями. Рассмотренные ранее графические ВР можно рассматривать как аналог (вариант) представления гармонических колебаний с помощью комплексных чисел.

После вычисления всех координат линий, мы добавим их к нашему графику точек как новые линии с помощью инструмента из дополнительного меню: “WORKING WITH DIAGRAMS”-“CONSTRUCTOR”-“SELECT DATA” в окне “Select Data Source” используйте кнопку “Add”, чтобы добавить все 43 строки.

Подготовка данных для радарной диаграммы

Как упоминалось выше, в этом шаблоне будет возможность визуально выстроить отношения с 20 участниками (компаниями, филиалами, подрядчиками и т.д.). На вкладке “Книга” шаблона “Данные” есть таблица, в которую необходимо ввести значения входных данных. Например, заполним его для 14 участников рынка:

На том же листе создадим дополнительную таблицу, которая представляет собой матрицу отношений всех возможных участников, сгенерированную по формуле:

Мы закончили подготовку данных и теперь переходим к их обработке.

Как вычислить сумму векторов?

Векторы и матрицы в электронной таблице хранятся в виде массивов.

Мы знаем, что векторная сумма – это вектор, координаты которого равны суммам соответствующих координат выходных векторов:

Чтобы вычислить сумму векторов, выполните следующую последовательность действий:

– Введите значения числовых элементов каждого вектора в диапазоны ячеек одинаковой размерности.

– Выберите диапазон ячеек, для которых должен быть рассчитан результат с той же размерностью, что и исходные векторы.

– Введите формулу умножения диапазона в выбранном диапазоне

– = Вектор_адреса_1 + Вектор_адреса_2

– Нажмите комбинацию клавиш [Ctrl] + [Shift] +[Enter].

Даны два вектора:

Требуется вычислить сумму этих векторов.

Решение:

– Ячейки диапазона A2:A4 введите значения координат вектора a1, а в ячейках диапазона C2:C4 – координаты вектора a2.

– Выделите ячейки диапазона, в которых будет вычислен результирующий вектор C ( E2:E4 ) и введите формулу в выбранном диапазоне:

– Нажмите [Ctrl] + [Shift] + [Enter]. В ячейках диапазона E2:E4 будут вычислены соответствующие координаты результирующего вектора.

Таким образом, векторная диаграмма дает четкое представление о преимуществе или замедлении различных электрических величин.
Предположим, у нас есть ток, величина которого изменяется по определенному закону:

Что такое векторная диаграмма токов и напряжений? Как нарисовать векторную диаграмму

Использование векторных диаграмм при анализе, расчете цепей переменного тока позволяет проще и нагляднее рассматривать процессы, а в некоторых случаях значительно упростить расчеты.

Векторная диаграмма – это геометрическое представление синусоидальных (или косинусоидальных) направленных отрезков – векторов, представляющих параметры и среднеквадратичные значения синусоидальных токов, напряжений или их амплитуд.

Векторные диаграммы широко используются в электротехнике, теории колебаний, акустике, оптике и т.д.

Существует 2 типа векторных диаграмм:

• точно;
• качественный.

Смотрите ниже интересное видео о векторных диаграммах:

Точные получаются в результате численных расчетов при условии, что масштабы эффективных величин подходят. Нарисовав их, можно геометрически определить фазы и амплитудные значения искомых величин.

Они являются одним из основных инструментов для анализа электрических цепей, позволяя визуально изображать и качественно контролировать ход решения задачи и легко определять квадрант, в котором находится искомый вектор.

Для удобства при построении графиков постоянные векторы анализируются для определенного момента времени, который выбирается так, чтобы график имел понятный вид. Ось OX соответствует значениям действительных чисел, ось OY – мнимых чисел (мнимая единица). Синусоида представляет собой движение конца проекции по оси OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина представляет собой амплитудное значение текущей величины, угол равен фазе.

Векторы, представленные на такой диаграмме, имеют одинаковую угловую частоту ω. В результате их взаимное расположение не меняется во время вращения.

Еще одно полезное видео о векторных диаграммах:

Именно поэтому на векторных диаграммах один вектор может быть ориентирован в любом направлении (например, вдоль оси OX).

Остатки представлены по отношению к оригиналу под разными углами, равными фазовым углам соответственно.

Таким образом, векторная диаграмма дает четкое представление об опережении или замедлении различных электрических величин.
Предположим, у нас есть ток, величина которого изменяется по определенному закону:

i = Im sin (ω t + φ).

Из начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбрано так, что с положительным направлением оси OX вектор образует угол – соответствующий фазе φ.

В общем случае векторные диаграммы строятся для эффективных значений, а не для амплитудных. Векторы эффективных значений количественно отличаются от амплитудных значений – по масштабу, т.к:

I = Im /√2.

Основное преимущество векторных диаграмм заключается в том, что при расчете электрических цепей можно легко и быстро складывать и вычитать 2 параметра.

Проведите две взаимно перпендикулярные оси и из точки пересечения этих осей нарисуйте вектор I_mдлина которого в некотором масштабе M_i выражает амплитуду тока I_m:

Сложение и вычитание векторов

Основное преимущество векторов заключается в том, что две величины можно просто складывать и вычитать. Например: сложите два тока, заданных уравнением

Добавим два заданных тока i1 и i2 согласно известному принципу сложения векторов (рис. 12.12, а). Для этого мы представляем токи в виде векторов из общего начала 0. Результирующий вектор находится как диагональ параллелограмма, построенного на сложенных векторах:

Удобнее складывать векторы, особенно три и более, в следующем порядке порядок: один вектор остается на месте, остальные перемещаются параллельно
друг через друга так, чтобы начало следующего вектора совпадало с концом предыдущего.

Вектор I_mВектор, проведенный от начала первого вектора до конца последнего вектора, является суммой всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого производится путем сложения прямого вектора (уменьшающего вектора) и обратного вектора (вычитающего вектора) (рис. 12.13):

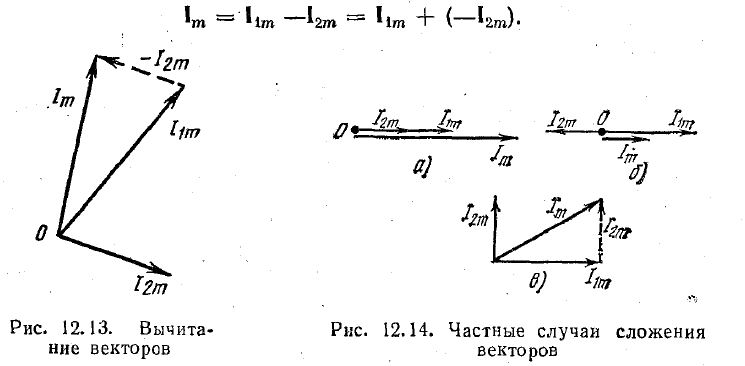
При сложении синусоидальных величин в некоторых случаях можно использовать аналитическое решение: как на рис. 12.12, а – по теореме косинусов; на рис. 12.14, а – сложение модулей векторов; б – вычитание модулей векторов; в – по теореме Пифагора.

Читайте далее:

• Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.
• Механические колебания и волны; FIZI4KA.
• Значение переменного тока (ЭДС, напряжения), соответствующее любому моменту времени, называется его мгновенным значением; Студопедия.
• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• Затухающие колебания – это. Что такое затухающие колебания?.
• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• Значение слова "амплитуда" в 11 словарях.