Эффективность источника тока; Студопедия - услуги электромонтажа, строительства и ремонта

излучаемый во внешней цепи, и мощность тепловых потерь излучаемого внутри текущего источника, т.е.

Содержание

Эффективность источника тока.

Рассмотрим физические свойства замкнутой электрической цепи, содержащей внешнее сопротивление, называемое полезной нагрузкой, и источник тока с электродвижущей силой 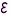При протекании тока тепло выделяется как на внешнем, так и на внутреннем сопротивлении. Общая тепловая мощность 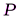генерируемая в цепи постоянного тока, представляет собой сумму полезная мощность

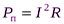, (6.17)

генерируемый во внешней цепи, и мощность тепловых потерь 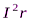генерируется внутри источника тока, т.е.

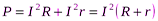. (6.18)

Полная развиваемая мощность является результатом действия внешних сил, которые распределяют заряды в источнике тока. Используя закон Ома для замкнутого контура [см. уравнение (6.13)], выражения для полезной и полной тепловой мощности можно записать как

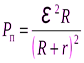(6.19)

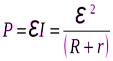. (6.20)

Коэффициент эффективности(КПД) электрической цепи определяется как отношение полезной мощности к 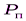до полной мощности:

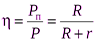. (6.21)

Поэтому эффективность зависит от соотношения внутреннего сопротивления и сопротивления нагрузки.

Каким должно быть сопротивление нагрузки, чтобы получить максимальную полезную мощность и максимальный КПД? Ответ на этот вопрос можно получить, графически и аналитически проанализировав выражения (6.19) и (6.21).

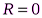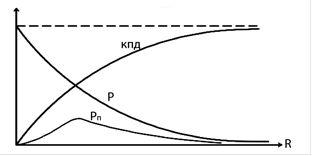
Полная мощность задается уравнением (12). Его максимум приходится на т.е. при коротком замыкании источника. Как следует из уравнений (11) и (13), в этом случае P_п и 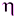(рис. 6.4).

На стороне 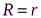кажущиеся мощность и ток составляют половину своих максимальных значений, КПД равен 0,5, а полезная мощность достигает своего максимального значения, равного половине полной мощности при данной нагрузке.

Чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность действительно максимальна, преобразуем правую часть выражения (6.19) следующим образом:

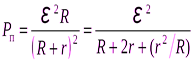. (6.22)

Полезная мощность максимальна, когда знаменатель выражения (6.22) минимален. Возьмем производную по R от этого знаменателя и приравняем ее к нулю. В результате получаем уравнение

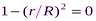, (6.23)

Из этого следует, что условием максимальной полезной мощности является равенство внешнего и внутреннего сопротивлений.

Сама максимальная полезная мощность определяется как

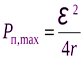, (6.24)

т.е. максимальная полезная мощность равна одной четверти мощности короткого замыкания:

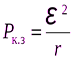. (6.25)

При неограниченном увеличении сопротивления нагрузки кажущаяся и полезная мощность стремятся к нулю, а КПД – к единице (рис. 6.4).

На рис. 6.4 видно, что требования к максимальному току цепи, максимальной полезной мощности и максимальному КПД противоречат друг другу. Для получения максимально возможного тока сопротивление нагрузки должно быть небольшим по сравнению с внутренним сопротивлением источника, но полезная мощность и КПД должны быть близки к нулю, поскольку почти вся работа, выполняемая источником тока, расходуется на выделение тепла от внутреннего сопротивления. r. Для того чтобы получить максимальную полезную мощность от данного источника тока, a согласованная нагрузкат.е. нагрузка с сопротивлением .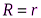

два источника питания для интегральной схемы
Днем у меня есть stm32, с одной стороны питающийся от автомобильной сети (скажем, через lm2576), с другой.

Максимальная мощность источника питания

При каких условиях источник питания (SB в моем случае – но это касается всех источников в целом) может выдать наибольшую мощность?
Я думал о коротком замыкании, т.е. Мощность равна p=U*I , ток максимален, но другие говорят, что напряжение равно нулю, но для меня оно равно нулю, потому что вольтметр имеет большое сопротивление, а амперметр – почти никакого, поэтому абсолютно весь ток проходит через амперметр и просто не достигает вольтметра, поэтому вольтметр не может его зарегистрировать, и теоретически он равен нулю, но в действительности это не так.

Помощь в написании экзаменов, курсовых и дипломных работ здесь.

Расчет схемы электропитания
Доброе утро. Мне нужна помощь в расчете схемы источника питания. Сразу же скажите, что в нем ничего нет.

Два источника питания для МК
Здравствуйте, есть stm32, одна сторона питается от автомобильной сети (допустим через lm2576), другая.

Как рассчитать активную мощность источника питания?
Даны U и R0 Как рассчитать активную мощность источника питания?

Используя принципиальную схему усилителя, определите мощность, потребляемую от источника питания
Используя принципиальную схему усилителя, определите мощность, потребляемую от источника питания.

Сопротивление шунта амперметра не равно нулю, поэтому на концах шунта будет существовать разность потенциалов, или Uf. Хотя он и небольшой, это все же Уф.
Ток известен (из показаний амперметра), следовательно, на шунте будет генерироваться мощность Psh=Ush*I. В лучшем случае шунт нагреется, в худшем – перегорит.

Максимальная мощность источника питания указана при номинальном напряжении и максимальном выходном токе. В чем смысл этого вопроса, неясно.

Сообщение от mzw

Например, возьмем обычное зарядное устройство для мобильного телефона – напряжение источника 5 В, максимальный выходной ток 1 А, соответственно, я могу предположить, что сопротивление источника 5 Ом,
Поэтому теоретически нагрузка также должна быть 5 Ом, соответственно, выходной ток по закону Ома равен 500мА=5В/10Ом, мощность 2,5Вт.

Ток короткого замыкания 1А, а мощность короткого замыкания (насколько я понимаю, тут могут быть разногласия) 5Вт.

Где я ошибаюсь?

Сообщение от Vytorryo

Ваше предположение неверно. Как рассчитать внутреннее сопротивление источника питания – я не знаю.

Если отбросить все защиты и т.д. в источнике питания и представить источник питания как своего рода трансформатор – тогда при уменьшении нагрузки ток будет увеличиваться, а напряжение уменьшаться. Взаимосвязь линейна, но выходит за рамки граничных условий.

Сообщение от Vytorryo Сообщение от китикот

китикот
Существует точный вариант определения сопротивления источника питания, например, те же 5В 1А, если добавить последовательно резистор, то ток будет U/Rp + Ri, где Rp – сопротивление резистора, который мы только что добавили, Ri – сопротивление источника,
Является ли это теоретически верным?

_pv
Ну, на данный момент моей целью является не использование блока питания по назначению, а проверка его максимальной выходной мощности,
А ребята говорят, что максимальная мощность источника питания не приводит к короткому замыканию и добавлению определенной (регулируемой) нагрузки, и это очень смущает в схеме проектирования, которой я занимаюсь.

Поэтому я хочу выяснить, как ее (максимальную мощность источника питания) найти/вычислить.

Ах, эти разработчики схем не знают, куда подключить закон Ома.

Первый принцип “сопротивление источника = сопротивление нагрузки” применим к идеальному источнику напряжения и некоторому внутреннему сопротивлению.
Импульсные источники – это идеальные источники напряжения с нулевым внутренним сопротивлением… т.е. напряжение не меняется при увеличении тока. Это относится только к рабочему диапазону выходного тока, а что происходит после этого, зависит от самого источника питания (стабилизация тока, отключение).

2 Нагрузка также различна. Они берут резистивную нагрузку в виде сферического коня и подсчитывают выделяемое им тепло. Но в реальной жизни существуют нагрузки, требующие минимального напряжения, ниже которого они просто не будут работать.

Сообщение от Vytorryo

_pv
Дело в том, что я хотел проверить максимальную мощность солнечной батареи, ребята на соседнем форуме сказали мне, что максимальную мощность источника нельзя найти в коротком замыкании, ее нужно найти с определенной нагрузкой, то есть при определенном сопротивлении есть максимум.

Я просто закорачиваю максимальную мощность солнечного элемента (SB), тестирую и ставлю нужную батарею.

Сообщение от Боттык

Нет, сначала к контроллеру заряда, а оттуда к батарее.

Если кому-то интересно, вот http://kazus.ru/forums/showpost.php?p=6 . stcount=20 ,
Я только разрабатываю схему, поэтому могу ошибаться, мне хотелось бы понять и решить подобные проблемы с питанием раз и навсегда, чтобы не совершать ошибок в будущем.

Сообщение от Vytorryo

Ну, все продумано и просчитано давным-давно.

Сообщение от sobokymk

Я не вижу на этом графике значений, которые я измерил сегодня,
При прямом солнечном свете панель 6×6 имеет напряжение 0,52 В и ток 0,5 А.

sobokymk
И как вы это делаете?
Купить солнечную панель, посмотреть на напряжение панели, затем посмотреть на график выше и рассчитать таким образом мощность?

Сообщение от Vytorryo Сообщение от sobokymk

Я не вижу значений, которые я измерил сегодня на этом графике,
Под прямыми солнечными лучами панель 6×6 d. 0,52 В и 0,5 А

sobokymk
И как вы это делаете?
Купить солнечную панель, посмотреть на напряжение вашей панели, затем посмотреть на приведенный выше график и рассчитать таким образом мощность?
Представленный здесь график – это “не догма, а руководство к действию”.
Глядя на этот график, вы можете представить, как может выглядеть кривая нагрузки среднего солнечного элемента.
К сожалению, я не смог понять ваши результаты “При прямом солнечном свете панель 6×6 d. 0,52 В и 0,5 А”, и я не могу с этим не согласиться или уточнить.
В этой теме уже говорилось, что максимально возможная мощность от источника может быть получена, если внутреннее сопротивление источника и сопротивление нагрузки согласованы. Другими словами, внутреннее сопротивление источника и внутреннее сопротивление нагрузки должны быть равны.
Вы можете рассчитать внутреннее сопротивление солнечной панели и, следовательно, оптимальное сопротивление нагрузки для получения максимальной мощности от батареи.
Нужно только помнить, что солнечный элемент имеет довольно большое внутреннее сопротивление, а будучи сам полупроводниковым прибором, он является нелинейным элементом.

sobokymk
Вы можете представить себе что угодно, но насколько размытым оно будет?
Там, где требуется точность, я беру измерительные инструменты и делаю расчеты на их основе, и вам советую поступать так же,
Иначе можно нафантазировать себе всякого.

Поэтому КПД зависит от отношения внутреннего сопротивления источника к сопротивлению нагрузки.

При каком условии полная мощность источника максимальна

Из формулы закона Ома для всей цепи (1.5) следует, что индуктивность источника равна сумме падений напряжения во внешней цепи U и внутри источника Uo = I ;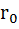

Умножив обе части уравнения на ток I, получим уравнение баланса мощности (1.17)

EI = I 2 r + I 2 R или Rist. = P + Rn 1. 18

Уравнение (1. 18) показывает, что мощность, отдаваемая источником, состоит из потерь мощности на источнике P и мощности, потребляемой нагрузкой Pn. Давайте рассмотрим зависимость мощности ,к нагрузке и КПД источника от величины сопротивления внешней цепи R (от величины тока в цепи I).

В состоянии холостого хода (R = ∞) ток в цепи отсутствует (1=0), поэтому мощность Pn, 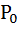и 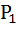равны нулю.

В состоянии короткого замыкания (R=0) ток в цепи достигает значения

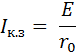
В этом случае источник выдает максимальную мощность, которая полностью потребляется в самом источнике, поскольку мощность, развиваемая во внешней цепи (в нагрузке), равна нулю.

Мощность, развиваемая в токе нагрузки, определяется по формуле

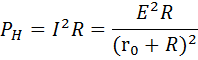
и достигает своего максимального значения, когда фракция

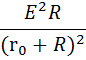
Предполагая, что сопротивление внешней цепи (нагрузки) R является переменным, находим условие максимума функции Pn=f(R)

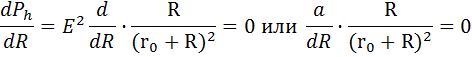
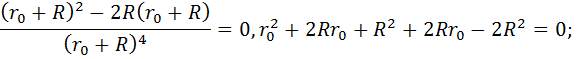
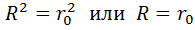
Из этого результата можно сделать вывод, что условием передачи максимальной мощности от источника в нагрузку (во внешнюю цепь) является равенство внутреннего сопротивления источника и сопротивления нагрузки (сечения внешней цепи), поэтому внешняя цепь и источник работают в совместимом режиме при R= .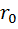

Эффективность источника может быть определена как отношение мощности внешней цепи к мощности источника

= = =

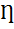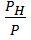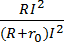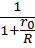
Уравнение (1.20) показывает, что в режиме холостого хода КПД источника 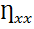= 1; или в режиме короткого замыкания

при R=0 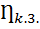= 0 и в режиме согласованной нагрузки при R = r 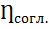= 0,5

График на рис. 12, показывает зависимость Rist 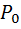, 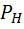и 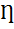как функция тока в цепи I.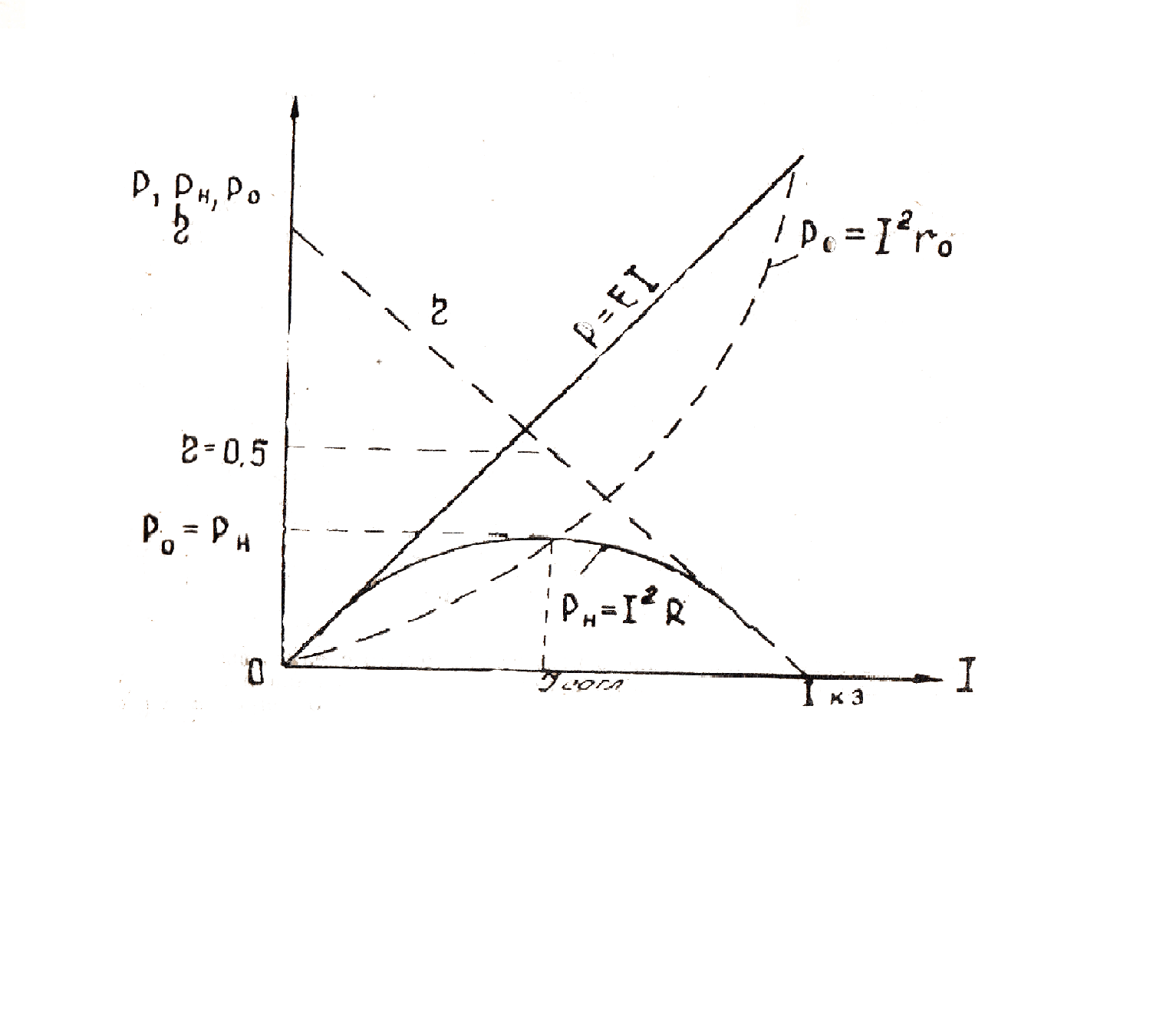

На практике согласованный режим используется только при низком КПД. (0,5) не имеет решающего значения из-за малой мощности цепи и когда максимальная мощность важнее экономических вопросов (радиосхемы, проводная связь, автоматизация и т.д.) – Для передачи большой мощности, когда экономические вопросы очень важны, используются режимы с более высоким КПД. Для этого внутреннее сопротивление источника должно быть намного меньше сопротивления нагрузки (внешней цепи). В этих случаях номинальный режим источника близок к режиму холостого хода, а КПД источника близок к единице.

Дата добавления: 2016-04-06 ; Показано: 2089 ; ОПЕРАТИВНЫЕ ТРЕБОВАНИЯ.

Полная мощность источника тока:

P poln = P полезные + P потери ,

где P мощность – полезная мощность, P полезная = I 2 R ; P потери – потерянная мощность, P потери = I 2 r ; I – ток в цепи; R – сопротивление нагрузки (внешней цепи); r – внутреннее сопротивление источника тока.

Полная мощность может быть рассчитана по одной из трех формул:

P full = I 2 ( R + r ), P full = ℰ 2 R + r , P full = I ℰ,

где ℰ – электродвижущая сила (ЭДС) источника тока.

Полезная мощность – это мощность, которая отдается внешней цепи, т.е. нагрузке (резистору), и может быть использована для какой-либо цели.

Полезная мощность может быть рассчитана по одной из трех формул:

P полезно = I 2 R , P полезно = U 2 R , P полезно = IU ,

где I – ток в цепи; U – напряжение на зажимах источника тока; R – сопротивление нагрузки (внешней цепи).

Мощность потерь – это мощность, которая возникает в источнике тока, т.е. во внутренней цепи, и расходуется на процессы внутри самого источника; ни для каких других целей мощность потерь не может быть использована.

Потери мощности обычно рассчитываются по формуле

P потери = I 2 r ,

где I – ток в цепи; r – внутреннее сопротивление источника тока.

В случае короткого замыкания полезная мощность равна нулю.

поскольку сопротивление нагрузки в условиях короткого замыкания отсутствует: R = 0.

Полная мощность короткого замыкания источника равна мощности потерь и рассчитывается по формуле

где ℰ – электродвижущая сила (ЭДС) источника тока; r – внутреннее сопротивление источника тока.

Полезная мощность максимальна, когда сопротивление нагрузки R равно внутреннему сопротивлению r источника тока:

Максимальная полезная мощность:

P полезная мощность макс = 0,5 P п.е,

где P ample – полная мощность источника тока; P ample = ℰ 2 / 2 r .

Формула для расчета максимальной полезной мощности выглядит следующим образом:

P usable max = ℰ 2 4 r .

Чтобы упростить расчеты, полезно запомнить два момента:

если при двух сопротивлениях нагрузки R 1 и R 2 цепь производит одинаковую полезную мощность, то внутреннее сопротивление источника тока r связано с этими сопротивлениями формулой

Если цепь производит максимальную полезную мощность, то ток I* в цепи равен половине тока короткого замыкания i :

Пример 15 Батарея элементов, закороченных резистором сопротивлением 5,0 Ом, производит ток 2,0 А. Ток короткого замыкания батареи составляет 12 А. Рассчитайте максимальную полезную мощность батареи.

Решение Давайте проанализируем определяющие факторы этой проблемы.

1 Когда батарея подключена к сопротивлению R 1 = 5,0 Ом, в цепи течет ток I 1 = 2,0 А, как показано на схеме a, определяемой из закона Ома для полной цепи:

где ℰ – ЭДС источника тока; r – внутреннее сопротивление источника тока.

2. При коротком замыкании батареи в цепи протекает ток короткого замыкания, как показано на рис. b . Ток короткого замыкания определяется по формуле

где i – ток короткого замыкания, i = 12 A.

Когда батарея подключена к сопротивлению R 2 = r, в цепи течет ток I 2 , как показано на рис. c, определяемый по закону Ома для полной цепи:

I 2 = ℰ R 2 + r = ℰ 2 r ;

в этом случае схема производит максимальную полезную мощность:

P полезный max = I 2 2 R 2 = I 2 2 r .

Поэтому для расчета максимальной полезной мощности необходимо определить внутреннее сопротивление источника тока r и силу тока I 2 .

Чтобы найти силу тока I 2 , напишем систему уравнений:

i = ℰ r , I 2 = ℰ 2 r >.

и разделите уравнения:

I 2 = i 2 = 12 2 = 6,0 A.

Чтобы найти внутреннее сопротивление источника r , напишите систему уравнений:

I 1 = ℰ R 1 + r , i = ℰ r >.

а затем разделите уравнения:

I 1 i = r R 1 + r .

r = I 1 R 1 i – I 1 = 2,0 ⋅ 5,0 12 – 2,0 = 1,0 Ом.

Давайте рассчитаем максимальную полезную мощность:

P полезный max = I 2 2 r = 6,0 2 ⋅ 1,0 = 36 Вт.

Таким образом, максимальная полезная мощность батареи составляет 36 Вт.

Мощность, развиваемая источником тока во всей цепи, называется суммарная мощность.

Она определяется по формуле

где P_всего– это полная мощность, развиваемая источником тока во всей цепи, в ваттах;

E- КПД источника, В;

I- значение тока в цепи, α.

В общем случае цепь состоит из внешней цепи (нагрузки) с сопротивлением R и внутренний контур с сопротивлением R R (сопротивление источника тока).

Подставляя значение ЭДС в выражение для полной мощности по напряжениям в цепи, получаем

Значение UI является мощностью, развиваемой во внешней части цепи (нагрузке) и называется полезная мощность P_пол=UI.

Это значение U_oI это мощность, которая бесполезно рассеивается внутри источника, она называется потеря мощности P_o=U_oI.

Таким образом, полная мощность равна сумме полезной мощности и мощности потерь P_ob=P_пол+P_0.

Отношение полезной мощности к полной мощности, развиваемой источником, называется КПД, сокращенно η.

Его определение выглядит следующим образом

При любых обстоятельствах η ≤ 1.

Если выразить мощность через значения тока и сопротивления участков цепи, то получим

Следовательно, КПД зависит от отношения внутреннего сопротивления источника к сопротивлению нагрузки.

Электрический КПД обычно выражается в процентах.

Для практической электротехники особый интерес представляют два вопроса:

1. условие для получения наибольшей полезной мощности.

2. условие для достижения наивысшей эффективности.

Наибольшая полезная мощность (мощность на нагрузке) развивается электрическим током, когда сопротивление нагрузки равно сопротивлению источника тока.

Эта максимальная мощность равна половине полной мощности (50%), развиваемой источником тока в цепи.

Половина мощности развивается на нагрузке, а половина – на внутреннем сопротивлении источника тока.

Если уменьшить сопротивление нагрузки, то мощность, развиваемая на нагрузке, уменьшится, а мощность, развиваемая на внутреннем сопротивлении источника тока, увеличится.

Если сопротивление нагрузки равно нулю, ток в цепи будет максимальным, т.е. короткое замыкание. Почти вся мощность будет развиваться во внутреннем сопротивлении источника тока. Этот режим опасен как для источника тока, так и для цепи.

Если сопротивление нагрузки увеличивается, ток в цепи уменьшается, и мощность на нагрузке также уменьшается. Если сопротивление нагрузки очень велико, то в цепи вообще не будет тока. Такое сопротивление называется бесконечным. Если цепь разомкнута, то ее сопротивление бесконечно велико. Этот режим работы называется Режим ожидания.

Таким образом, в режимах близкого короткого замыкания и холостого хода полезная мощность мала в первом случае из-за низкого значения напряжения, а во втором – из-за низкого значения тока.

Коэффициент мощности (КПД) равен 100% на холостом ходу (в этом случае полезная мощность отсутствует и энергия от источника не потребляется).

При увеличении тока нагрузки КПД снижается по прямой линии.

В режиме короткого замыкания КПД равен нулю (полезная мощность отсутствует, а мощность, развиваемая источником, полностью расходуется в источнике).

Суммируя вышесказанное, можно сделать выводы.

Получение максимальной полезной мощности (R=R) и максимального КПД (R=∞) – это не одно и то же. Более того, при получении максимальной полезной мощности от источника (работа с согласованной нагрузкой), КПД составляет 50%, т.е. половина мощности, развиваемой источником, бесполезно расходуется в нем.

Режим согласования нагрузки неприемлем в установках большой мощности, так как вызывает большие потери мощности. Поэтому на электростанциях и подстанциях режимы работы генераторов, трансформаторов и выпрямителей разрабатываются таким образом, чтобы обеспечить высокий КПД. (90% и выше).

В слаботочных технологиях ситуация иная. Возьмем, к примеру, телефонную трубку. Разговор перед микрофоном производит электрический сигнал мощностью около 2 мВт. Очевидно, что для достижения максимально возможной дальности связи необходимо передать в линию как можно больше мощности, а это требует режима согласования нагрузки. Является ли в этом случае эффективность линии существенной? Конечно, нет, поскольку потери мощности выражаются в долях или единицах милливатт.

Режим согласования нагрузки используется в радиоаппаратуре. Если генератор и нагрузка не согласованы при прямом подключении, используются меры по согласованию их импедансов.

Зависимость мощности P₁, Р_{мощность, P,P,R} = EI, а коэффициент мощности источника тока показан на рисунке 1.

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равна _{alt=”Статья 34 – Фото 10″ />.}. (9)

Из формулы (8) следует, что

_{alt=”Статья 34 – Фото 11″ />}, (10)

это Р₁ изменяется с изменением тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при _{alt=”Статья 34 – Фото 12″ />.}. Первое значение соответствует разомкнутой цепи (R>> r), второе значение соответствует закороченной цепи (R<< r). Зависимость КПД цепи от силы тока (по формулам (8), (9), (10)) будет выглядеть следующим образом

_{alt=”Статья 34 – Фото 13″ />.} (11)

Следовательно, КПД достигает своего максимального значения h = 1 в случае разомкнутой цепи (I = 0), а затем линейно уменьшается, падая до нуля в случае короткого замыкания.

Зависимость мощности P₁, Р_{мощность, P,R} = EI и эффективность источника тока по отношению к току цепи показана на рис. 1.

alt=”Статья 34 – Фото 14″ />.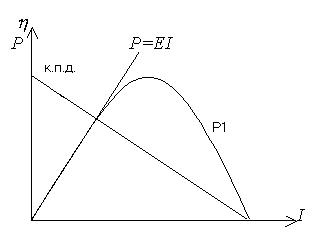

Из графиков видно, что невозможно одновременно получить полезную мощность и КПД. Когда мощность, доступная на внешнем конце цепи P₁достигает своего максимального значения, КПД в этот момент составляет 50%.

P_p=eta IU=0.42 110=462 левая(W/правая).

Формула для среднеквадратичной мощности источника тока

Пусть электрическая цепь состоит из источника тока с сопротивлением $r$ и нагрузки (сопротивление $R$). Мощность источника может быть найдена как:

где $?$ – ЭДС источника тока; $I$ – сила тока. В данном случае $P$ – это полная мощность цепи.

Обозначим $U$ как напряжение на внешнем участке цепи, тогда уравнение (7) будет иметь вид:

где $P_p=UI=I^2R=frac<u^2>(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. В этом случае эффективность источника определяется как:

Максимальная полезная мощность (мощность на нагрузке), которую дает электрический ток, если внешнее сопротивление цепи равно внутреннему сопротивлению источника тока. В этих условиях полезная мощность равна 50% от полной мощности.

В состоянии короткого замыкания (когда $R – 0;;U – 0$) или в режиме холостого хода $(R – 0;;I – 0$) полезная мощность равна нулю.

ЛАБОРАТОРНАЯ РАБОТА 3.7.

В каком состоянии полная мощность источника питания максимальна

ЛАБОРАТОРНАЯ РАБОТА № 3.7.

ПРОВЕРКА ПОЛЕЗНОЙ МОЩНОСТИ И ЭФФЕКТИВНОСТИ ИСТОЧНИКОВ ЭНЕРГИИ

Имя Фамилия _____________ Группа ______ Дата ______

Целью данной работы является экспериментальная проверка теоретических выводов о зависимости полезной мощности и КПД источника тока от сопротивления нагрузки.

Электрическая цепь состоит из источника тока, питающих проводов и нагрузки или токоприемника. Каждый из этих элементов цепи имеет сопротивление.

Сопротивление питающих проводов обычно очень мало, поэтому им можно пренебречь. В каждой части цепи будет расходоваться энергия источника тока. Вопрос правильного использования электрической энергии имеет большое практическое значение.

Полная мощность P, рассеиваемая в цепи, будет равна сумме мощностей, рассеиваемых во внешней и внутренней частях цепи: P = I 2 -R + I 2 -r = I 2 (R + r). С сайта I(R + r) = εтогда P = I-ε,

где R – внешнее сопротивление; r – внутреннее сопротивление; ε – ЭДС источника тока.

Таким образом, полная мощность, излучаемая в цепи, выражается произведением тока и ЭДС элемента. Эта энергия выделяется каким-либо внешним источником энергии; таким источником энергии могут быть, например, химические процессы, происходящие в клетке.

Рассмотрим, как мощность, выделяемая в цепи, зависит от внешнего сопротивления R, к которому закорочен элемент. Предположим, что элемент с заданной ЭДС и заданным внутренним сопротивлением r замкнут внешним сопротивлением R; определите зависимость от R полной мощности P, рассеиваемой в цепи, мощности P_агенерируемый во внешней части схемы, и КПД.

Ток I в цепи выражается по закону Ома следующим образом

Полная мощность, имеющаяся в цепи, будет равна

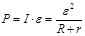
По мере увеличения R мощность будет уменьшаться, стремясь асимптотически к нулю при неограниченном увеличении R.

Мощность, имеющаяся во внешней части цепи, равна

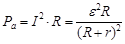
Из этого можно сделать вывод, что эффективная мощность P_а равна нулю в двух случаях R = 0 и R = ∞.

Исследование функции Р_а = f(R) до крайности, мы получаем, что P_а достигает своего максимума в точке R = r, тогда

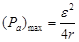
Чтобы быть уверенным, максимальная мощность P_а получена в точке R = r, возьмем производную от P_а на внешнем сопротивлении

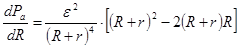
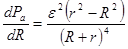
Условие максимума требует, чтобы первая производная была равна нулю

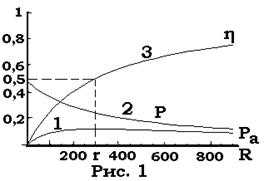
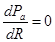r 2 = R 2

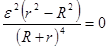R = r

Можно отметить, что при этом условии мы получаем максимум, а не минимум для R_апутем определения знака второй производной .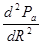

КПД η источника ЭДС – это отношение мощности P_акоторая генерируется во внешней цепи, к полной мощности P, развиваемой источником ЭДС.

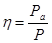
По сути, эффективность источника ЭМП показывает, какая часть работы внешних сил преобразуется в электрическую энергию и передается обратно во внешнюю цепь.

Выражая мощность как функцию тока I, разности потенциалов во внешней цепи U и величины электродвижущей силы ε, получаем

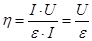
Это означает, что эффективность источника ЭДС равна отношению напряжения внешней цепи к ЭДС. В условиях закона Ома мы можем далее подставить U = IR; ε = I(R + r), то

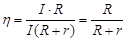
Поэтому в случае, когда вся энергия расходуется в виде тепла Ленца-Джоуля, эффективность источника ЭДС равна отношению внешнего сопротивления к общему сопротивлению цепи.

При R = 0 мы имеем η = 0. При увеличении R эффективность возрастает, что стремится к η = 1 при неограниченном увеличении R, но мощность, рассеиваемая во внешней цепи, стремится к нулю. Поэтому требование одновременного получения максимальной полезной мощности при максимальном КПД не может быть выполнено.

Когда P_а достигает своего максимума, η = 50%. Когда КПД η близок к единице, полезная мощность мала по сравнению с максимальной мощностью, которую можно получить от источника. Поэтому для повышения КПД необходимо как можно больше уменьшить внутреннее сопротивление источника ЭДС, например, батареи или динамо-машины.

В случае, когда R = 0 (короткое замыкание), P_а = 0 и вся мощность генерируется внутри источника. Это может привести к перегреву внутренних деталей источника питания и его выходу из строя. По этой причине недопустимо короткое замыкание источников (динамо, батарейки)!

На рис. 1 кривая 1 показывает зависимость мощности P_агенерируемой во внешней цепи, на сопротивление внешней части цепи R; кривая 2 дает зависимость полной мощности P от R; кривая 3 дает ход КПД η на то же внешнее сопротивление.

Процедура

1. ознакомьтесь со схемой на стенде.

2. с помощью магазина установите сопротивление R = 100 Ом.

3. закройте кнопку K.

4. Измерьте ток в цепи последовательно для различных девяти сопротивлений в магазине резисторов, начиная со 100 Ом и выше. Запишите результаты измерений тока в таблицу, выразив их в амперах.

5. выключите кнопку K.

6. рассчитать для каждого сопротивления P, P_а (в ваттах) и η.

7. построить график P, P_а и η из R.

Обзорные вопросы

1. что называется эффективностью источника ЭМП?

2. Выведите формулу для эффективности источника электромагнитного поля.

3. какова полезная мощность источника ЭМП?

4. выведите формулу для полезной мощности источника ЭМП.

5. какова максимальная мощность, доступная во внешней цепи (Ra)max?

6. при каком значении R полная мощность P, производимая в цепи, максимальна?

7) Какова эффективность источника ЭДС при (Ra)max?

Исследуйте функцию (Ra) f(R) до крайности.

9. Нарисуйте график зависимости P, Ra и η от внешнего сопротивления R.

10. какова ЭДС источника?

11. Почему внешние силы должны быть неэлектрического происхождения?

12. Почему короткое замыкание недопустимо для источников напряжения?

I-10 -3 , A

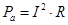, W

, W

</u^2>

Читайте далее: