Электрическое поле; FIZI4KA - услуги электромонтажа, строительства и ремонта

Электрические поля от разных источников существуют в одной и той же точке пространства и действуют на заряд независимо друг от друга.

Содержание

Электрическое поле

Электродинамика – Отрасль физики, занимающаяся изучением свойств и взаимодействия электрических зарядов через электромагнитные поля.

Электростатика Это раздел электродинамики, в котором рассматриваются свойства и взаимодействия электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – Заряженное тело, размер которого мал по сравнению с расстоянием, на котором он измеряется.

Если электрическое поле, создаваемое несколькими заряженными телами, изучается с помощью пробного заряда, то результирующая сила равна геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Поэтому напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрического поля, создаваемого в той же точке зарядами по отдельности:

История открытия электрического поля

Ранним мыслителям было трудно принять концепцию “действия на расстоянии”. Действительно, как один заряд может действовать на другой, если они не находятся в контакте? Даже Ньютону, который применил эту идею в теории всеобщего тяготения, было трудно принять ее.

Однако, как мы видели, эти трудности можно преодолеть с помощью понятия поля, которое ввел английский ученый Майкл Фарадей (1791-1867). Согласно Фарадею, каждый заряд излучает электрическое поле, которое пронизывает все пространство. Когда один заряд приближается к другому, на него действует сила, обусловленная электрическим полем первого заряда.

Поле, создаваемое одним или несколькими зарядами, может быть исследовано с помощью небольшого положительного пробного заряда путем измерения действующей на него силы. Под пробным зарядом мы понимаем достаточно малый заряд, собственное поле которого существенно не изменяет распределение других зарядов в поле.

Сила в точке b меньше, чем в точке a, из-за большего расстояния между зарядами (закон Кулона); в точке c сила еще меньше. Во всех случаях сила направлена радиально от заряда Q.
По определению, напряженность электрического поля (или просто электрического поля) E в любой точке пространства равна отношению силы F, действующей на малый положительный пробный заряд q, к величине этого заряда:

Из приведенного выше определения следует, что направление напряженности электрического поля в любой точке пространства совпадает с направлением силы, действующей в этой точке на положительный образцовый заряд. Напряженность электрического поля – это сила, действующая на единицу заряда; она измеряется в ньютонах на кулон (Н/Кл).

Более конкретно, E определяется как предел отношения F/q при q, который стремится к нулю. Напряженность электрического поля E определяется отношением F/q, чтобы устранить зависимость поля E от величины заряда образца q. Другими словами, E учитывает только те заряды, которые создают данное электрическое поле в данной точке. Поскольку E – векторная величина, электрическое поле является векторным полем.

Поверхности эквипотенциального поля двух одинаковых точечных зарядов показаны на рисунке 1.29.

1.3 электрическое поле. Напряженность поля и потенциал

Вокруг любого электрического заряда всегда существует электрическое поле.

Электрическое поле, создаваемое неподвижным зарядом (или системой неподвижных зарядов), называется электростатический ..

Электростатическое поле – это средство, с помощью которого заряды взаимодействуют друг с другом. Само понятие поля оказалось очень плодотворным и широко используется в современной физике. Появление поля означает, что в окружающем нас пространстве что-то изменилось. Математически поле описывается величиной, которая изменяется от точки к точке. Например, мы можем рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости имеется вектор скорости, который может изменяться со временем (переходный поток) или быть постоянным (стационарный поток). Это пример векторного поля. Поле неподвижных электрических зарядов относится к тому же типу полей.

Запишем выражение для силы, действующей на точечный заряд в результате его взаимодействия с системой точечных зарядов (соотношение из приложения 1)

Это вектор радиуса точки, в которой находится заряд. Нагрузка, на которую действует сила в таких ситуациях, иногда называется “испытательной” нагрузкой и записывается в виде отдельного множителя. Выражение в скобках определяется исключительно свойствами системы зарядов, действующих на заряд . Очевидно, что это действие (сила) зависит от того, где он расположен, поэтому выражение в скобках зависит от радиус-вектора, определяющего положение заряда. В соответствии с вышеизложенной идеей электростатического поля, существующего вокруг каждого заряда и, конечно, системы зарядов, введем силу, характерную для этого поля, называемую интенсивность электрического поля.

Напряженность электрического поля вектор равна отношению силы, действующей на точечный заряд алгебраическому значению этого заряда (рис. 1.12).

Рис. 1.12 Вектор напряженности электрического поля отрицательного и положительного точечных зарядов

Из определения напряженности следует, что напряженность поля любой системы неподвижных зарядов можно записать в виде

В самом деле, сила, с которой система зарядов действует на точечный заряд, равна векторной сумме сил, с которыми каждый из зарядов системы действует на него. Отсюда следует, что напряженность электрического поля системы зарядов определяется следующим образом векторной суммой напряженности поля, создаваемого отдельными зарядами системы. Существует так называемый принцип суперпозиции (независимой суперпозиции). принцип суперпозиции (независимой суперпозиции) электрических полей

Напряженность поля, создаваемого системой неподвижных заряженных тел, равна векторная сумма напряженности поля, создаваемого каждым телом в отдельности:

Принцип суперпозиции является одним из наиболее общих принципов современной физики. Подчеркнем, что интенсивности полей являются векторными суммами.

Рис. 1.13 иллюстрирует принцип суперпозиции полей на примере поля, создаваемого двумя точечными зарядами.

Рис. 1.13. Принцип суперпозиции электрических полей

Для одного заряда , в начале координат, для напряженности поля, создаваемого им в точке с радиус-вектором, получаем (подстрочный индекс 1 опускаем):

Напряженность поля точечного заряда w в разных точках Напряженность поля точечного заряда в разных точках пространства, вообще говоря, отличается как по величине, так и по направлению (рис. 1.14). Поле точечного заряда является центральным полем, центр симметрии поля совпадает с точкой, в которой находится заряд.

Рисунок 1.14: Векторы напряженности электрического поля заряда q в различных точках пространства

В системе СИ единицей напряженности электрического поля является ньютон на кулон (Н/Кл) – т.е. единицей напряженности поля является напряженность поля, при которой на заряд, равный 1 Н, действует сила, равная 1 Кл:

На практике чаще используется другое название этой единицы, “вольт на метр” (В/м) (о единице измерения “вольт(Единица измерения “вольт” будет объяснена чуть позже).

Типичные значения напряженности электрического поля, встречающиеся в нашем мире, показаны на рисунке 1.15.

Рисунок 1.15: Характерные значения напряженности электрического поля, встречающиеся в природе

Обратите внимание на сходство закона Кулона с законом всемирного тяготения

Заряды являются массами, а гравитационная постоянная G подобна коэффициенту Знак минус соответствует тому, что гравитационное взаимодействие всегда является притяжением. Также можно представить вектор напряженности гравитационного поля как отношение силы, например, к массе образца:

Если это масса Земли и ее радиус, то это не что иное, как хорошо известное ускорение свободного падения м/с 2 (к очень малой центробежной силе инерции, содержащейся в гравитационной силе).

Пример 4. Среднее расстояние между электроном и протоном в атоме водорода составляет r = 5,3-10 -11 м (рис. 1.16). Найдите силы электростатического и гравитационного притяжения между ними и определите их соотношение.

Электрон и протон в атоме водорода

Решение. Из закона Кулона

Из закона всемирного тяготения

Соотношение сил не зависит от расстояния между электроном и протоном и равно

Эти расчеты показывают, что в масштабах атомов и молекул гравитационные силы настолько малы по сравнению с электростатическими силами, что ими можно пренебречь.

Так почему же в макромире, в котором мы живем, закон гравитации мы узнаем с первого удара, когда делаем первые шаги в детстве, а закон Кулона остается неизвестным для многих наших сограждан даже после окончания средней школы? Дело в том, что в макромире, как мы видели, положительные и отрицательные электрические заряды в телах компенсируются, так что в обычной жизни мы имеем дело с относительно небольшим избытком зарядов. В то же время все гравитационные массы имеют одинаковый знак, поэтому не происходит компенсации масс и гравитационные силы проявляются в большей степени в макромире.

Электрическое поле можно определить, указав для каждой точки значение и направление вектора напряженности электрического поля. Для визуального представления электрического поля направления силы (или линии векторного поля ).

Линия напряженности электрического поля (линия напряженности поля) представляет собой прямую линию, касательная к которой в каждой точке прямой совпадает по направлению с вектором напряженности электрического поля.

На рисунке 1.17 показана линия электрического поля. Векторы напряженности электрического поля направлены по касательной к линии электрического поля.

Рисунок 1.17: Векторы напряженности электрического поля являются касательными к линиям поля

Количество перпендикулярных линий в единице площади пропорционально значению (модулю) напряженности электрического поля в этом месте. Другими словами, линии поля плотнее там, где модуль напряженности поля больше. Таким образом, конфигурация линий поля позволяет оценить изменение направления и величины вектора в пространстве. Изображение линии векторного поля (не обязательно электрического или магнитного) является очень наглядным графическим способом представления его основных свойств.

Обратим внимание на некоторые важные свойства линий электростатического поля:

Рис. 1.18. линии поля точечного заряда: 1 – q > 0; 2 – q < 0

В первом случае силовые линии начинаются в точке с положительным зарядом и простираются до бесконечности; во втором случае силовые линии простираются от бесконечности и заканчиваются в точке с отрицательным зарядом.

Силовые линии электрического поля, создаваемого двумя одинаковыми точками по модулю показаны на рисунке 1.19.

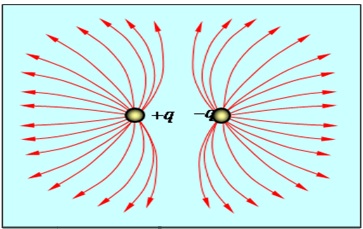
Рисунок 1.19: Линии электрического поля, создаваемые двумя одинаковыми положительными точечными зарядами

Линии электрического поля, создаваемые двумя противоположными зарядами равной модульной величины Заряды показаны на рис. 1.20.

Рис. 1.20: Линии электрического поля, создаваемые двумя противоположными точечными зарядами одинаковой идентичности по модулю

Заметим, что система из двух зарядов одинаковой величины и противоположного знака, показанная (вместе с полем) на рис. 1.20, называется электрическим диполем.

Электрическое поле, напряженность которого одинакова по модулю и направлению во всех точках пространства, называется однородное электрическое поле.

Плотность и направление линий поля во всем объеме однородного электрического поля остаются постоянными. Графически такое поле изображается параллельными прямыми линиями с одинаковым расстоянием между ними.

Далее будет показано, что бесконечная равномерно заряженная плоскость создает вокруг себя однородное электрическое поле. Линии поля перпендикулярны заряженной плоскости и направлены от нее, если плоскость заряжена положительно, и к ней, если она заряжена отрицательно (см. рис. 1.21).

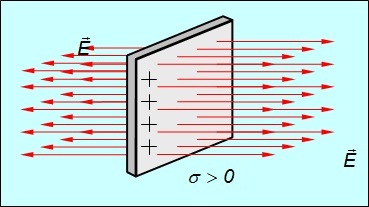
Рисунок 1.21: Электрическое поле равномерно положительно заряженной плоскости

Линии электрического поля можно исследовать экспериментально с помощью установки, показанной на рис. 1.22. Электроды, подключенные к источнику высокого напряжения, погружаются в касторовое масло с суспензией мелких диэлектрических частиц. Когда к электродам прикладывается напряжение, частицы выстраиваются в цепочки вдоль линий поля и показывают распределение поля в пространстве между электродами. Используя электроды различной формы, можно изучать поле точечных зарядов одинакового и разного знака, поле плоских и цилиндрических конденсаторов и т.д.

Рисунок 1.22: Экспериментальное исследование линий электростатического поля

Поведение заряда в электрическом поле описывается вторым законом движения Ньютона

(Предполагается, что на заряд не действуют никакие другие силы, иначе соответствующие члены пришлось бы добавить к правой части).

Один из методов определения заряда электрона (метод Милликена) заключается в наблюдении за движением капель масла в вертикальном электростатическом поле плоского конденсатора (рисунок 1.23). В пространстве между двумя пластинами конденсатора было создано электрическое поле. Здесь вводились капли масла. Под воздействием света воздух между пластинами ионизировался, свободные электроны, образующиеся при этом, передавались каплям, и капли заряжались.

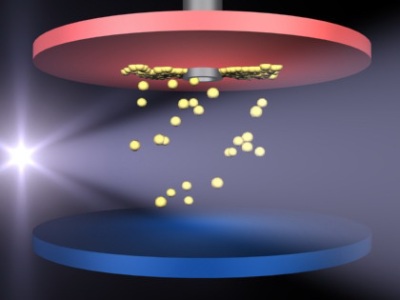
Схема эксперимента Милликена

Наблюдалось движение капли с радиусом 1,64 мкм и плотностью 0,851 г/см 3. Было замечено, что капля перестала падать при напряженности электрического поля 1,95-10 5 В/м. Это означало, что электростатическая сила qE компенсировал силу тяжести мг.

Масса капли равна

Таким образом, мы находим заряд капли

т.е. капля несла пять электронных зарядов. Именно в таких экспериментах было открыто квантование электрического заряда и определено его минимальное значение e.

Движением заряженных частиц можно управлять с помощью электрического поля нужной величины и направления. Это происходит, например, в электронно-лучевом осциллографе.

На рис. 1.24 показано движение электронного пучка, изображающего синусоидальную волну на экране электронно-лучевой трубки с электрическим отклонением. В осциллографе усиленный сигнал подается на вертикальные отклоняющие пластины, а на горизонтальные пластины подается пилообразное напряжение развертки. В результате электронный луч “рисует” на экране осциллографа временную зависимость исследуемого сигнала.

Рис. 1.24. Принцип работы электронно-лучевой трубки

Определение напряженности поля очень часто используется в форме

По определению (или, конечно, это одно и то же) напряженность электрического поля называется его характеристика мощности – она определяет силу, действующую на заряд, помещенный в поле.

Пример 5. Частица, движущаяся параллельно пластинам вдоль оси конденсатора, попадает в пространство между пластинами плоского конденсатора (рис. 1.25). Под действием поля конденсатора частица отклоняется в сторону одной из пластин (в зависимости от знака заряда) и в конце концов падает на нее. Это расстояние можно измерить. Расстояние между пластинами и напряжение на конденсаторе также известны. Можно ли по этим данным определить тип частицы (найдя ее удельный заряд, т.е. отношение заряда к массе)?

Решение. Давайте сначала решим эту задачу, используя метод размерностей. Пройденное расстояние должно быть функцией параметров задачи:

Помня, что произведение потенциала на заряд дает энергию, размерность которой мы получаем

Рис. 1.25. Прохождение заряженной частицы между пластинами плоского конденсатора

Подставляя эту размерность, получаем уравнение:

Сравнивая размерности в обеих частях уравнения, получаем уравнение Eq:

Последнее уравнение, вытекающее из отсутствия размерности времени в левой части количества, сразу дает нам или После этого мы сразу находим: Подставляя найденные значения, получаем:

Произвольная степень (экспонента b не удалось определить) означает, что результат зависит от произвольной функции безразмерного коэффициента

Мы еще не знаем форму этой функции: если задача содержит величины одинаковой размерности, мы, очевидно, не сможем найти функцию их отношения с помощью анализа размерностей. Но мы уже можем ответить на вопрос о задаче: ответ не содержит параметров, характеризующих частицу – ни ее массы, ни заряда. Все частицы в данных условиях отклоняются одинаково, и использовать такое устройство для их идентификации невозможно.

Теперь дадим точное решение этой задачи. Начальная скорость частицы может быть определена из следующего соотношения

В конденсаторе частица находится под действием электрического поля и приобретает поперечное ускорение Расстояние от пластины, через которое она пройдет за время t:

где мы находим время полета:

В продольном направлении за это время частица пройдет расстояние

Мы приходим к такому же выводу относительно независимости характеристик частицы. Кроме того, теперь мы находим функцию, оставшуюся неопределенной в нашем первоначальном результате.

В главе 4 раздела “Механика” было показано, что сила сохранения связана с потенциальной энергией соотношением

Здесь знак – обычное обозначение векторного оператора “набла”, результатом которого на скалярной функции координат является градиент этой функции. Явная форма оператора nabla в декартовых координатах выглядит следующим образом:

Подставляя и деля на , получаем

Скалярная функция называется потенциал электрического поля.

Функция связана с напряженностью электростатического поля соотношением

называется потенциал электростатического поля.

Как видно из (1.13), потенциальная энергия точечного заряда в потенциальном поле равна

а сила, действующая на него, равна

Пример использования этих отношений приведен в Приложении 3.

В системе измерений единицей потенциала электрического поля является вольт (В):

Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал – его потенциальную энергию в этом поле. Поэтому, согласно смыслу соотношения i, напряженность электрического поля называется силовой характеристикой поля, а потенциал – его энергетической характеристикой.

Как и потенциальная энергия, потенциал поля всегда определяется аддитивной константой. Это можно увидеть на примере: Поскольку nabla является дифференциальным оператором, потенциалы и физически идентичны, поскольку соответствуют полю одинаковой напряженности.

Это позволяет нормализовать потенциал путем произвольного выбора некоторой точки и предположения, что потенциал в этой точке равен нулю

Учитывая, что напряженность поля и потенциал поля уменьшаются с увеличением расстояния от системы зарядов, создающих поле, во всех этих случаях, когда конечный заряд распределен по конечной области пространства, естественно и удобно нормировать потенциал к “нулю на бесконечности”, т.е. предполагая, что она равна нулю на бесконечном расстоянии от системы зарядов

Эти идеализированные случаи, когда нормализация к нулю на бесконечности просто в силу идеализации задачи не имеет смысла, будут рассмотрены ниже.

Соотношение (1.13) позволяет нам вычислить напряженность поля из известного потенциала;

Получим “обратное” соотношение: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для (1.18), выражение для вектора бесконечно малых перемещений и выражение для полного дифференциала:

Легко видеть, что скалярное произведение первых двух векторов равно полному дифференциалу потенциала

На самом деле, эти отношения не новы. Если умножить (1.20) на заряд и учесть соотношения (1.14) и (1.15), то получим известное из главы 4 “Механики” соотношение между работой сохранения силы и потерей потенциальной энергии

Там, в главе “Механика”, показано, что стационарное потенциальное поле консервативно. Из (1.18) следует, что электростатическое поле консервативно во всех случаях, когда потенциал поля не зависит от времени.

Интегрируя (1.20) от точки, потенциал которой предполагается равным нулю, до некоторой точки, потенциал которой представляет интерес, вдоль любой удобной кривой (поле консервативно и результат не зависит от формы кривой), получаем

Используем (1.21) для вычисления потенциала поля точечного заряда , расположенного в начале координат, нормируя его к нулю на бесконечном расстоянии от этого заряда. Для этого воспользуемся законом Кулона в форме (1.9):

В вычислениях мы используем тождество , справедливое для любого вектора : и получающееся простым дифференцированием модуля любого вектора: .

Поэтому потенциал поля точечного заряда в начале координат имеет вид

и это поле, как уже упоминалось, является центральным: фактически потенциал поля зависит только от .

Учитывая, что модуль радиус-вектора в знаменателе есть не что иное, как расстояние от заряда, создающего поле, до точки наблюдения поля, эту формулу легко обобщить на случай, когда заряд находится не в начале координат, а в точке с радиус-вектором . В этом случае расстояние от заряда до точки наблюдения равно , а потенциал поля в этой точке (предварительно нормированный на нуль на бесконечности) равен

Связь между напряженностью поля и потенциалом поля линейна, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов в системе. Используя принцип суперпозиции, потенциал поля системы зарядов можно сразу записать :

Здесь указано общее количество зарядов в системе.

Если заряд непрерывно распределен по определенному объему, то получаем

Если заряд распределен непрерывно по некоторой поверхности или кривой, то получим соответственно

где и – соответствующие поверхностная и линейная плотности.

В Дополнении 4 рассматривается пример применения только что выведенных соотношений.

Мы не будем здесь отдельно рассматривать работу электростатических сил при движении точечных зарядов и заряженных тел в электростатическом поле. Электростатическое поле консервативно (рис. 1.26), потенциальная энергия заряда в этом поле равна , поэтому работу электростатических сил всегда можно вычислить из соотношения в виде

Работа электростатических сил зависит только от положения начальной и конечной точек.

Вычислим энергию взаимного взаимодействия зарядов, входящих в состав некоторой системы.

Для нумерации этих зарядов удобно использовать два индекса, например, и . Одни и те же обвинения системы “один раз есть, другой раз будет”. Подчеркнем, что заряд и заряд – это те же 5 зарядов системы. Такие “сложности” необходимы для краткого обозначения выражения для энергии их взаимодействия, и вот почему. Заряды взаимодействуют парами, и энергия взаимодействия и зарядов в унисон составляет

Здесь – потенциал заряда в точке, где находится заряд.

B – не рассматривается взаимодействие заряда с самим собой или его потенциальная энергия в собственном поле.

Поэтому при сложении энергий пар взаимодействующих зарядов мы обязательно должны учитывать, что, во-первых, и во-вторых, каждая пара зарядов должна присутствовать в сумме только один раз. Это можно сделать двумя способами. Первый заключается в том, что при записи двойной суммы мы явно оговариваем, что, например:

Во втором методе, если неравенство выполняется, то суммирование производится по всем все возможные значения и, соответственно, сумма, соответствующая взаимодействию одинаковый пара зарядов присутствует в сумме дважды, поэтому сумма должна быть кратной 2. Получается, что:

В случае непрерывного распределения заряда в определенном объеме плотности , это соотношение принимает, например, вид:

В первой формуле в (1.31) записан потенциал всех зарядов, кроме точки, во втором соотношении этот потенциал записан явно, в третьем соотношении произведена следующая операция: два интеграла для краткости объединены в один и заряды выражены в терминах плотности заряда .

Мы не пишем здесь формулы для случаев распределения заряда по поверхности или вдоль некоторой кривой, они требуют только замены w на i .

Для визуального представления распределения потенциала в пространстве мы используем эквипотенциальные поверхности.

Эквипотенциальная поверхность (эквипотенциальная поверхность) – это множество точек с одинаковым потенциалом.

Рассмотрим систему эквипотенциальных поверхностей определенных полей.

Напомним, что как из физических соображений, так и непосредственно из соотношений следует взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, согласно определению, уравнение эквипотенциальной поверхности имеет вид

Дифференцируя это уравнение, получаем

для всех смещений, касательных к эквипотенциальной поверхности. Это означает, что вектор перпендикулярен эквипотенциальной поверхности. Обратите внимание, что вектор по определению направлен по касательной к линии действия силы. Доказана теорема ортогональности для линий поля и эквипотенциальных поверхностей.

Поверхности эквипотенциального поля точечного заряда представляют собой концентрические сферы с центром в точке, где находится заряд (см. рис. 1.27). Эквипотенциальные поверхности обозначены синими сплошными линиями, силовые линии – красными пунктирными линиями.

Эквипотенциальные поверхности (сферы) (синие сплошные линии) и силовые линии (красные пунктирные линии) поля точечного заряда

Эквивалентные поверхности однородного электрического поля – это плоскости, перпендикулярные линиям поля и лежащие на равных расстояниях друг от друга (см. рис. 1.28).

Рисунок 1.28: Эквипотенциальные поверхности однородного электрического поля

Эквипотенциальные поверхности двух однородных точечных зарядов показаны на рис. 1.29.

Эквипотенциальные поверхности двух одноименных точечных зарядов

Эквипотенциальные поверхности двух противоположных точечных зарядов одинаковых по модулю показаны на рисунке 1.30.

Рис. 1.30: Эквипотенциальные поверхности двух противоположных точечных зарядов с одинаковым модулем

Графическое представление двумерного (в плоскости z = 0) потенциала электрического поля, создаваемого точечным зарядом, помещенным в начало координат, показано на рис. 1.31.

Рис. 1.31: Двумерный (в плоскости z = 0) вид кулоновского потенциала 1/r в окрестности положительного (1) и отрицательного (2) точечного заряда. В случае (1) положительный заряд зонда попадает в бесконечно высокий потенциальный барьер, препятствующий его проникновению в центр. В случае (2) на зондирующий заряд действует притягивающая сила, и он стремится скатиться в образовавшуюся яму потенциала

Экспериментальное исследование потенциала поля вокруг заряженной металлической сферы с помощью “пламенного” зонда показано на рис. 1.32. Используемый зонд присоединен к электрометру. Для выравнивания потенциала зонда с потенциалом точки, в которой он находится, зонд помещается в пламя небольшой газовой горелки, что позволяет воздуху ионизироваться, а зарядам капать и стекать на зонд. Показано, что потенциал уменьшается по мере удаления зонда от центра сферы и что потенциал остается постоянным, когда зонд движется по кругу вокруг центра заряженной сферы.

Рис. 1.32: Экспериментальное исследование потенциала поля вокруг заряженной металлической сферы с помощью “пламенного” зонда.

В Дополнении 7 была получена полезная зависимость градиента скалярной функции от модуля радиус-вектора.

Электрическое поле подчиняется принципу суперпозиции.

Концепция диполей

Электрический диполь – это расположение двух зарядов, одинаковых по модулю, с разными знаками и находящихся на определенном расстоянии друг от друга.

Эта система может служить нам хорошим примером применения принципа суперпозиции полей, а также электрической моделью многих молекул.

Рисунок 1 . 2 . 6 . Линии поля электрического диполя E → = E 1 → + E 2 → .

Дипольный момент p → является одной из наиболее важных характеристик электрического диполя:

Где l → – вектор, направленный от отрицательного заряда к положительному, модуль l → = l .

Например, нейтральная молекула воды (H 2 O) имеет электрический дипольный момент, поскольку центры двух атомов водорода расположены не на одной линии с центром атома кислорода, а под углом 105°. Дипольный момент молекулы воды p = 6 , 2 – 10 – 30 К л – м .

Из приведенного выше определения ясно, как найти напряженность электрического поля в данной точке:

Линии интенсивности

Электрическое поле не видно невооруженным глазом, но его можно визуализировать с помощью линий напряженности. Графически это будут непрерывные линии, соединяющие заряженные объекты. Условная начальная точка такой линии находится на положительном заряде, а конечная – на отрицательном.

Линии интенсивности – это линии, которые совпадают с линиями сил в системе положительных и отрицательных зарядов. Касательные к ним в любой точке электрического поля имеют то же направление, что и напряженность поля.

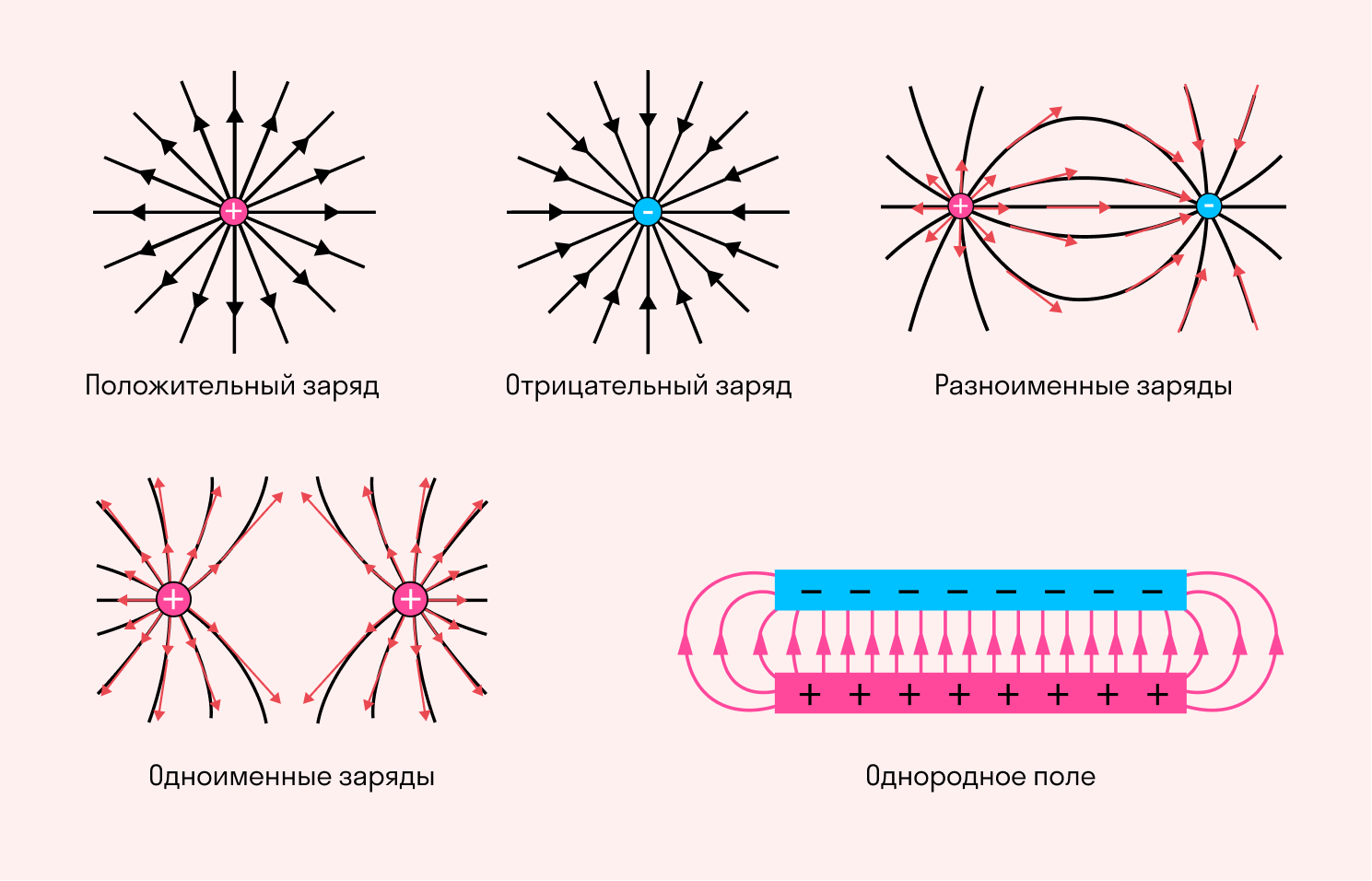
При построении линий поля можно показать не только направление, но и значение напряженности электрического поля (условно, конечно). Там, где модуль интенсивности выше, принято делать более плотный рисунок линии. Существуют также случаи, когда плотность линий не меняется – это относится к представлению однородного поля.

Однородное электрическое поле создается противоположными зарядами одинакового модуля, помещенными на две металлические пластины. Линии напряжения между этими зарядами являются прямыми параллельными линиями везде, кроме краев пластин и пространства за ними.

Основными вехами в истории развития учения об этом феномене являются следующие открытия:

Будущие применения

Многие ученые считают, что электрическое поле – очень важное явление, которое в будущем позволит совершить прорыв в телекоммуникационных технологиях и телепортации объектов на большие расстояния. В настоящее время в этих областях ведутся серьезные исследования и изыскания.

Итак, разобравшись, что такое электрическое поле, можно не только понять и объяснить другим суть и основные особенности этого явления, но и почерпнуть много полезных знаний о том, где оно применяется, какие перспективы имеет в будущем.

Читайте далее: