Электричество и магнетизм - услуги электромонтажа, строительства и ремонта

Спиральное движение заряженной частицы в однородном магнитном поле.

Содержание

5.3 Движение заряженной частицы в однородном магнитном поле

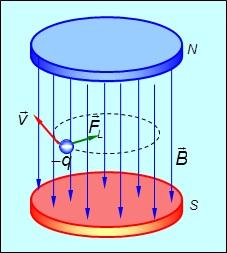
Сила Лоренца создает только нормальное ускорение и поэтому направлена к центру окружности. Поэтому направление вращения положительно заряженной частицы таково, что винт, вращающийся в том же направлении, будет двигаться противоположно направлению поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рисунки 5.14, 5.15).

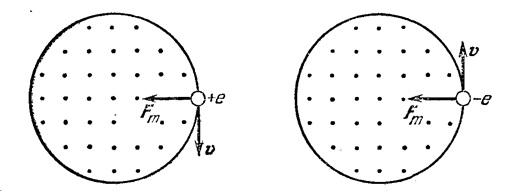
Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля обозначено точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае мы можем представить, что частица входит в однородное магнитное поле со скоростью vкоторый имеет угол q с направлением магнитного поля. Эта скорость может быть разложена на две составляющие, одна из которых

направлена вдоль поля, а другая

перпендикулярно полю. Поэтому движение частицы – это сумма двух движений: равномерного движения вдоль поля со скоростью и вращательного движения по окружности с угловой скоростью . Поэтому траектория частицы представляет собой спираль с радиусом R и наклон h (рис. 5.15):

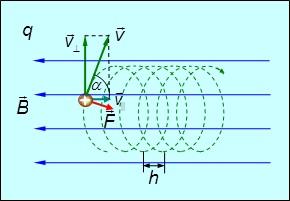
Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. Протон движется в однородном магнитном поле с индукцией 2 Тесла. Траектория его движения представляет собой спиральную линию радиусом 10 см и шагом 60 см. Определите скорость и кинетическую энергию протона. Что такое разность потенциалов ускорения U прошел протон, прежде чем попал в магнитное поле?

Решение. Используя уравнения (5.11), найдите угол между скоростью протона и полем

Пусть жестко закрепленный проводник с током находится в магнитном поле.

Движение заряженных частиц в магнитном поле.

Это уравнение очень сложное, поскольку в общем случае оно зависит от пространственных и временных координат. Более того, сама частица также генерирует свое собственное электромагнитное поле.

Пусть электрическое поле отсутствует, а магнитное поле имеет одну составляющую и является однородным.

Вдоль поля скорость не меняется, движение равномерное.

Поэтому поперечная скорость не изменяется. Поэтому модуль скорости не изменяется вообще. Следовательно, кинетическая энергия частиц не изменяется, поэтому магнитное поле не оказывает на частицы никакого воздействия. Это понятно, потому что магнитная составляющая силы Лоренца всегда перпендикулярна скорости, и сила не совершает никакой работы. Такие силы называются гироскопическими. Если работа не совершается, то изменение магнитного потока равно нулю, а поскольку поле однородно, то площадь фигуры, охватываемая траекторией частицы, не меняется.

Аналогичным образом можно поступить для второй координаты и получить уравнение вида

Поэтому траектория частицы в плоскости XOY является окружностью, и частица движется по этой окружности с циклической частотой

которая называется ларморовской или циклотронной частотой.

Частота и период не зависят от скорости частицы, т.е. от ее кинетической энергии.

Радиус этой окружности равен

Вдоль поля частица движется равномерно. Таким образом, траектория частицы представляет собой спиральную линию с шагом

В ходе эксперимента один из студентов обнаружил, что при замыкании цепи стрелка компаса, находящегося рядом, отклоняется. Это вращение выявило взаимосвязь между электричеством и магнетизмом.

сила Лоренца

Магнитное поле действует на частицу только с силой Ампера. Пока электрон движется хаотично, вокруг него не образуется магнитное поле. Эта сила перпендикулярна проводнику и полю.

Оказывается, сила Ампера вызывается действием некоторой материи на траекторию заряженных частиц, которые начинают двигаться в поле.

Пусть в проводнике есть носители заряда. Их массой в этом случае можно пренебречь. Поскольку эти частицы являются отрицательно заряженными электронами, они движутся в направлении, противоположном направлению тока. На каждый заряд действует сила, которая в сумме составляет силу Ампера.

Если взять воображаемое увеличительное стекло и посмотреть на то, что происходит внутри проводника, то можно увидеть следующее: на окружности тела электрон будет двигаться против тока и испытывать силу, перпендикулярную его движению. Это известно как сила Лоренца. Кратко она определяется следующим образом: результирующая всех ампер-энергий, действующих на заряженные частицы, движущиеся в поле. Он называется Fl.

Кинетическая сила создается только при движении. Если частица нейтральна (нейтрон), она не подвергается воздействию. Чтобы рассчитать эту силу, нам нужно знать длину проводника и скорость носителей заряда. Время, необходимое электрону для изменения положения, задается уравнением: t = L / V.

Сумму частиц, прошедших через центр, можно обозначить как Qob. Это полный заряд, прошедший через радиус проводника в момент времени t. Она будет равна: Qоб = I * t = (I * L) / V.

Учитывая это определение, можно сказать, что Fa = Fl * N. Поскольку число частиц в проводнике равно суммарному заряду в нем N = Qоб / Q, мы можем написать: N = I * L / V * Q. Следовательно, сила в амперах: Fa = Fl * (I * L) / (V * q). Если вместо Fa подставить и выразить силу Лоренца, то формула для ее определения примет вид: Fl = Q * V * B * sin (j), то есть она пропорциональна скорости частицы в магнитном поле, вектору направления индукции и количеству зарядов. А сила Лоренца будет наибольшей, когда V перпендикулярно B.

Кратко рассмотрим природу движения свободного носителя заряда в присутствии электрического и магнитного полей.

Как частица движется в магнитном поле

На заряженную частицу (электрон, дырку), движущуюся в электрическом $vec E$ и магнитном $vec B$ полях, действует сила Лоренца $vec F = m^* ∆dot = qvec E + ¤vec B$ [∗vec v ∗times ∗vec B] $ в СГС, а в СИ: $ ^vec F = m^* ^ddot = qvec E + q[^vec v ^times ^vec B] $ где $m^<*>$ – эффективная масса заряженной частицы, учитывающая влияние периодического поля на движение частицы в веществе, $c$ – скорость света, $q$ – заряд частицы, $vec v$ – скорость частицы, $ddot <>$ – ускорение частицы.

Если пренебречь столкновениями движущейся частицы, то траектория ее движения в электрическом и магнитном полях под действием силы Лоренца может быть найдена с помощью этого уравнения.

В результате действия электрической составляющей поля частица приобретает дополнительную скорость, соответствующую направлению вектора $$. В общем случае, для любой ориентации скорости $<$ и магнитное поле $$, скорость электрона может быть разложена на две составляющие: параллельную $v_ $ и перпендикуляр $v_ $ на поле $$: $ v = (v_,v_); $ тогда сила, действующая на частицу в магнитном поле, $ F_ = =frac B> . $<_ $ изменяет направление скорости $v_$ while $v_ $ остается постоянной и заставляет заряженную частицу двигаться по спирали вдоль магнитного поля. При $v_ =0$ заряженная частица будет вращаться по окружности радиуса $ r=cfrac $ с угловой скоростью $ ™omega = ™frac c> . $

Если электрическое и магнитное поля параллельны, то заряженная частица будет двигаться по спиральной линии с возрастающим шагом, так как электрическое поле изменяет скорость $_ $ и не влияет на $_.$.

Если электрическое и магнитное поля перпендикулярны (скрещенные поля), то при нулевой начальной скорости заряженной частицы, решая уравнение движения частицы под действием силы Лоренца, получаем уравнение циклоиды: частица вращается по окружности радиуса $r$, а центр окружности равномерно движется в направлении, перпендикулярном электрическому и магнитному полям со скоростью дрейфа $ < _.<д>= ∆frac $ Амплитуда периодического движения совпадает с ларморовским радиусом $ = =frac> >$. Обратите внимание, что это справедливо для свободной частицы, которая не сталкивается с другими частицами или любыми другими объектами.

Рассмотрим поведение частицы в отношении столкновений частицы. Из курса молекулярной физики известно, что все частицы совершают хаотическое тепловое движение. Важной характеристикой такого движения является средняя длина свободного пролета $langle langgle$. Зная среднюю (по модулю) тепловую скорость, можно определить среднее время между столкновениями частиц $tau = =frac$. Если на частицы не действует никакая внешняя сила, то средняя проекция тепловой скорости на любое направление равна нулю. Если приложено внешнее постоянное электрическое поле, то на частицу действует постоянная сила. Поэтому в промежутках между столкновениями его движение равномерно ускоряется, и он приобретает дополнительный импульс и, следовательно, дополнительную скорость в направлении действия силы. Если добавление скорость, которую приобретает частица под действием электрического поля в момент времени $tau$. намного меньше, чем его по модулю средней тепловой скорости, такое поле называется слабый. После столкновения частица имеет одинаковую вероятность рассеяния в любом направлении, поэтому в среднем проекция ее скорости на любое направление равна нулю. Двигаясь дальше, он снова испытывает ускорение, приобретает дополнительную скорость и так далее. Поэтому частица, помимо хаотического теплового движения, дрейфует с определенной средней скоростью $v_.$

В в приближении слабого поля Скорость дрейфа $v_ $ намного меньше средней по модулю тепловой скорости, а время $tau$ не зависит от скорости дрейфа и, следовательно, от внешней силы. Дополнительный импульс и скорость, приобретенные частицей, пропорциональны как внешней силе $F_ $ и время действия этой силы $tau$. Таким образом, в слабом электрическом поле скорость дрейфа пропорциональна напряженности электрического поля $<_.=u$, где коэффициент пропорциональности $u$ называется мобильность носителей заряда, в СИ подвижность находится в размерности $frac<м^2><вcdot с="">$, но часто измеряется во внесистемных единицах $<см^2><вcdot с="">$.

Рассмотрим однородный изотропный полупроводник с параллельными стенками. Контакты 1 и 2 будем называть токовыми, а контакты 3 и 4 – потенциальными. В отсутствие магнитного поля, если образец однороден и изотропен, контакты 3 и 4 находятся на эквипотенциальной поверхности, и когда через образец течет ток, падение напряжения между контактами 3 и 4 равно нулю. Поместите наш образец в однородное магнитное поле, вектор магнитного поля $vec B$ перпендикулярен вектору $vec j$. Скорость заряженных частиц состоит из хаотической (тепловой) составляющей и дрейфовой составляющей. Скорость дрейфа возникает в результате действия внешних сил на заряженную частицу (в нашем случае в результате приложенных внешних электрического и магнитного полей $vec E$ и $vec B$). Вследствие линейности силы Лоренца по отношению к скорости имеем: $ ∙vec F = qvec E + ∙frac [T раз $vec B$ + ∙frac [B], $ Поскольку средняя проекция тепловой скорости на любую ось равна нулю, то после усреднения второй член в последней формуле становится равным нулю и средняя сила зависит только от скорости дрейфа. Видно, что магнитная составляющая силы Лоренца отклоняет как положительно, так и отрицательно заряженные частицы в одном и том же направлении, поскольку изменение знака заряда компенсируется изменением направления скорости дрейфа на противоположное.

Предположим, что ток в образце определяется движением заряженных частиц одного типа, например, электронов (иначе пришлось бы учитывать вклад в ток движения заряженных частиц всех типов). В отсутствие магнитного поля ток течет слева направо. При включении магнитного поля на электроны начинает действовать магнитная составляющая силы Лоренца, которая отклоняет их в сторону фронта 3. Таким образом, в течение некоторого времени после включения магнитного поля электроны будут двигаться от поверхности 4 к поверхности 3. Электроны будут создавать отрицательный заряд на поверхности 3 и положительный заряд на поверхности 4, поэтому между этими поверхностями возникнет дополнительное электрическое поле $_H$. Заряд на поверхностях 3 и 4 будет увеличиваться до тех пор, пока магнитная составляющая силы Лоренца не уравновесится дополнительным электрическим полем: $ ecdot _y + efrac ec [_d ™times ™vec B] = 0. $ В этой ситуации мы имеем: $ E_ = =frac<>> B. Поскольку мы рассматриваем движение электрона в свободном пробеге, очевидно, что эта формула означает среднюю скорость дрейфа, определяемую средним временем свободного пробега ансамбля $$ (средним временем релаксации). Поскольку $ j_ =-env_, $ тогда $ E_ =E_ = -frac <>B>. $

Значение $E_H$ называется Поле зала. Таким образом, электрическое поле (для нашей ориентации вектора) имеет компоненты $E_x$ и $E_y$, следовательно, общий вектор электрического поля $Evec E = vec i E_ + vec k E_$ не будет иметь ту же величину и направление, что и исходная, (когда $vec<в>= 0$) между ними будет угол $varphi _H$, называемый Угол Холла. Для тангенса этого угла мы можем написать: $ tg ($varphi _) = =frac $ или $ tg (¯varphi ¯)) = -frac=-u_ B. $

На практике удобнее измерять не напряженность электрического поля, а соответствующую разность потенциалов (между поверхностями 3 и 4 на рисунке), которую мы называем ЭМП зала: $ U_ =E_ -frac <>Bd>. Если выразить полный ток через плотность тока, $I=j_ ddot h$, тогда $ U_ = -frac= =frac <>IB>где $R_ =-(en)^<-1>$ – постоянная Холла.

В случае проводимости полупроводника p-типа в уравнении ($E_ =E_ = -frac <>B>$) должен изменить знак носителей заряда с $-e$ на e$. Тогда мы имеем: $ E_= =frac <>B>=j_ R_ B, $ $ tg (_)= -frac.=-u_

B, $ U_ = -frac= =$frac <>IB>где p – концентрация дырок, $u_p$ – их подвижность, $R_H = (e p)^<-1>$ – постоянная Холла для полупроводника с дырками. Сравнивая последние формулы, можно увидеть, что знак холловских эдс можно использовать для экспериментального определения типа носителей заряда, а величину $R_H$ – для определения их концентрации. Более того, если можно измерить как проводимость, так и постоянную Холла, то на их основе можно определить подвижность носителей: $ u_ =сигма R_ . $

Изучение эффекта Холла в полупроводниках осложняется тем, что в них присутствуют несколько типов носителей заряда. Проводимость, обусловленная движением одинакового количества электронов и дырок, называется внутренней проводимостью. Полупроводники обычно имеют примесную проводимость. В этом типе полупроводников некоторые атомы в базовом кристалле заменены атомами другой валентности. Если валентность примесных атомов выше валентности основного кристалла, то атом примеси имеет “лишний” электрон, слабо связанный с атомной основой, который он может легко отдать в зону проводимости. Такой полупроводник имеет больше электронов, чем дырок, называется полупроводником n-типа и обладает электронной проводимостью. Если валентные соотношения основных и примесных атомов меняются местами, возникает p-тип (дырочный тип) проводимости. В полупроводниках также могут присутствовать оба типа носителей заряда.

Теперь рассмотрим ситуацию, когда в полупроводнике есть и электроны, и дырки. Запишем общий вид уравнений движения для электронов и дырок в электрическом и магнитном полях: $ m frac_n>

=-evec E- frac[для электронов, >> m frac_p>
=-evec E- frac[_p ^vec B] ^mbox < - для дырок.>$ Интегрируя эти уравнения и используя соотношение для подвижности $u_n =frac$, получаем: $ ™vec v_ =-u_ ™vec<>^2> [vec E n n n n B], $ Умножив первое уравнение на $en$, а второе на $ep$, получим уравнения для токов электронов и дырок: $ ¯vec j_ =-en(p)u_ Een(p)¢frac<>^2> [vec E times times times vec B]. $ Отсюда полный ток: $ vec j =e(nu_n + pu_p) vec E+efrac [∗vec E ∗times ∗vec B] $ или в скалярной форме: $ j_x =e(nu_n + pu_p) E_x+e_frac E_y B_z=j, $ $ j_y =e(nu_n + pu_p) E_y+e_frac E_x B_z=0. $ Поскольку магнитное поле слабое, второй член первого уравнения системы намного меньше первого. Учитывая это, если мы решим систему относительно $E_y$, то получим E_=R_ jB, $ R_ = =frac<>
^ <2>-nu_^<2>> <>+pu_

)^2>. $ Из этого выражения видно, что при $n ^ p$: $R_H = (en)^<-1>$, и при $p n$: $R_H = (ep)^<-1>$. В случае собственного полупроводника, где $n = p = n_i$, $ R_= =frac <>

-u_><>(u_ +u_

)>=frac<1-b>.<>(1+b)>, $, где $b = =frac$. Согласно последней формуле $R_H<0$ при $b>1$ (т.е. $u_n>u_p$) и $R_H>0$ при $b<1$ (т.е. $u_n<>

Выше мы предположили, что все носители заряда имеют одинаковое время релаксации, другими словами, мы считали, что вероятность рассеяния не зависит от скорости движения. При строгом рассмотрении необходимо учитывать распределение носителей по скоростям; следствием этого будет зависимость времени релаксации электронов (дырок) от их кинетической энергии. Кинетические явления в ансамбле частиц с учетом их энергетического распределения обычно описываются кинетическим уравнением Больцмана. Следствием рассмотрения эффекта Холла с помощью этого уравнения является появление множителя $r$$ r=frac ^<2> ^<2>> $:

Здесь $langle ^ <2> – среднее время релаксации, $langle ^ <2> – средний квадрат времени релаксации. Поэтому все формулы, полученные выше, где есть множители $(en)^<-1>$ или $(ep)^<-1>$, верны до множителя $r$; в частности, для подвижности: $ u_^ = =frac=ru_; u_

^ =frac=ru_

. Таким образом, подвижность, определяемая эффектом Холла, называется эффектом Холла, в отличие от истинной (дрейфовой) подвижности. Множитель r называется коэффициентом Холла.

Поскольку $r$ определяется временем релаксации $tau$, его значение будет зависеть от механизмов рассеяния носителей заряда. При низких температурах (для Ge $T < $250$ K, для Si $T < $100$ K) обычно доминирует рассеяние носителей на примесных ионах, тогда как при высоких температурах (для Ge и Si - включая комнатную) доминирует рассеяние на колебаниях решетки.

Как отмечалось выше, наши результаты справедливы для случая слабого магнитного поля. Поскольку $tau = ¯frac< ¯langle ¯rangle>< ¯langle v¯rangle>$, связь между длиной свободного пути $ ¯langle ¯rangle$ носителя заряда и радиусом его круговой орбиты в магнитном поле можно заменить следующим образом:

T=frac<2pi><>> ¯mbox < - для слабого поля,>$ ¯tau ¯gg T=frac<2pi><¯omega _.>$ < - для сильного поля,>$ где $T$ – период вращения частицы, $omega _.$ — циклотронная частота (частота вращения носителя заряда по круговой траектории в магнитном поле индукции $vec B$). Поскольку $omega = ¯frac>$ , затем подставляем $omega _$ к приведенному выше выражению, получаем: $frac> <2pi>= frac <2 ¯pi> 1 ¯mbox< - для слабого поля, >$ ¯frac>>>pi>= frac <2 pi> 1 mbox< - для сильного поля. >$

Приведенное выше определение сильного и слабого поля является классическим определением. Изменение энергетического спектра электрона в магнитном поле здесь не учитывается.

Слово “электричество” происходит от греческого слова electron – янтарь, который электризуется при трении о шерстяную ткань. В природе известны два типа электрического заряда, условно называемые положительным и отрицательным зарядом. Их взаимодействие также известно: заряды с одинаковыми названиями отталкиваются друг от друга, а заряды с противоположными названиями притягиваются друг к другу.

Физика B1.B8.

Электростатика 1. Электрические заряды

Слово “электричество” происходит от греческого слова “электрон”. янтарь, который электризуется при трении о шерстяную ткань. В природе существует два типа электрических зарядов, которые условно называются положительным и отрицательным зарядами. Их взаимодействие также известно: одноименные заряды отталкиваются друг от друга, а разноименные притягиваются.

Электрический заряд любого тела состоит из числа элементарных зарядов, равных приблизительно Этот заряд – заряд отрицательно заряженной частицы, называемой электроном. Масса покоя электрона составляет ок. . Кроме отрицательно заряженного электрона существуют частицы с положительным элементарным зарядом. Стабильной частицей с положительным элементарным зарядом является протон. Протон является ядром атома водорода, самого легкого элемента таблицы Менделеева. Масса протона в 1836 раз больше массы электрона . Протон – это частица, образующая ядра всех элементов и определяющая заряд ядра. Электроны в атомах образуют электронную оболочку атома. Они могут покидать электронную оболочку атома или молекулы, превращая ее в положительный ион; они также могут присоединяться к другому атому или молекуле, превращая эти молекулы в отрицательный ион. Перенос электронов может происходить не только между атомами или молекулами, но и между телами, например, при их контакте друг с другом. Это явление называется электризацией тел при контакте. В результате электризации одни тела имеют избыток электронов, и эти тела заряжены отрицательно, а в других телах электронов не хватает, и эти тела заряжены положительно. Однако во всех случаях выполняется один из основных законов физики – закон сохранения электрического заряда: алгебраическая сумма зарядов частиц или тел, образующих электрически изолированную (замкнутую) систему, не меняется ни для каких процессов, происходящих в этой системе. Электрически изолированная система – это система тел (частиц), которые не обмениваются зарядами с телами, не входящими в эту систему.

Используя магнитные поля, можно разделить заряженные частицы в соответствии с их удельными зарядами и точно определить их массу. Разделение частиц должно осуществляться в масс-спектрографы 1 .

11 класс

Сила Лоренца.

Движение заряженных частиц в пространстве с одновременными электрическими и магнитными полями представляет большой интерес. Для этого случая Лоренц получил выражение для силы, которая в его честь была названа силой Лоренца. Это сумма сил, действующих на заряженную частицу, движущуюся в электрическом и магнитном поле.

Пусть заряженная частица с зарядом q движется со скоростью в однородном магнитном поле индукции и в однородном электрическом поле напряженности . Электрическое поле действует на заряд q с силой, модуль которой равен F_э = qE. Эта составляющая силы Лоренца называется электрический компонент. В магнитном поле на движущуюся частицу действуют магнитный компонент Сила Лоренца.

Его модуль можно найти с помощью закона Ампера. Предположим, что проводник с током находится в однородном магнитном поле. Заряженные частицы движутся вдоль проводника. Рассмотрим длину проводника Δl и площадь поперечного сечения S (рис. 3.38).

На него действует амперная сила от магнитного поля. В В § 1 “Условия существования электрического тока. Электрический ток в проводниках”. Выведена формула для определения силы тока в проводнике:

Подставив это выражение в формулу для модуля силы Ампера F_A = BIΔlsin αполучаем

где N = nSΔl – число заряженных частиц в рассматриваемом объеме SΔl. Магнитная составляющая силы Лоренца равна по модулю

где α – угол между векторами i .

Магнитная составляющая силы Лоренца всегда перпендикулярна плоскости, в которой расположены вектор скорости заряженной частицы и вектор магнитной индукции.

Поскольку эта сила перпендикулярна скорости частицы, она не совершает никакой работы.

Поэтому, если существует электрическое и магнитное поле, то полная сила, действующая на движущуюся частицу, равна

Для определения направления магнитной составляющей силы Лоренца правило левой руки.

Если вы положите левую руку так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены в направлении скорости положительно заряженной частицы, то большой палец, согнутый (в плоскости руки) на 90°, будет направлен в сторону магнитной составляющей силы Лоренца, действующей на заряженную частицу.

Если отрицательно заряженные частицы движутся в магнитном поле, пальцы левой руки должны быть расположены в направлении, противоположном направлению вектора скорости. Чтобы проиллюстрировать применение правила левой руки, см. рисунок 3.39.

Пунктирные линии на нем показывают траектории движения зарядов (на рисунке 3.39, a – положительный заряд, рис. 3,39, b – отрицательный заряд).

Движение заряженной частицы в однородном магнитном поле.

Рассмотрим простейший случай движения заряженной частицы в магнитном поле – это движение в однородном магнитном поле с индукцией, перпендикулярной начальной скорости частицы (рис. 3.40).

Поскольку магнитное поле не изменяет модуль скорости заряженной частицы, модуль магнитной составляющей силы Лоренца остается неизменным. Поскольку эта сила перпендикулярна скорости, частица движется с центростремительным ускорением. Модульно постоянное центростремительное ускорение частицы, движущейся с постоянной по модулю скоростью, означает, что радиус кривизны R траектории частицы является постоянной. Частица движется равномерно по окружности радиуса R. Согласно второму закону движения Ньютона,

Поэтому, измеряя R известного υ и Вмы можем определить удельный заряд отдельных частиц.

Масс-спектрограф.

Используя магнитное поле, можно разделить заряженные частицы в соответствии с их удельными зарядами и точно определить их массу. Разделение частиц осуществляется в С помощью масс-спектрографа 1 .

1 Масс-спектрограф был впервые построен в 1919 году учеником Дж. Дж. Томсона Фрэнсисом Астоном (1877-1945). С помощью этого прибора он провел точные измерения масс и дефектов масс ряда изотопов.

На рисунке 3.41, а показана схема простого масс-спектрографа, а на рисунке 3.41, б – внешний вид современного прибора. Вакуумная камера масс-спектрографа помещена в магнитное поле (вектор магнитной индукции перпендикулярен рисунку). Заряженные частицы (электроны или ионы), ускоренные электрическим полем, после зажигания дуги попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории R. По этому радиусу можно определить удельный заряд иона и, следовательно, его массу.

Циклотрон.

Используя формулу для радиуса траектории, находим время прохождения заряженной частицы через полукруг:

т.е. Δt зависит только от свойств частицы и индукции магнитного поля.

Этот факт был использован американским физиком Эрнестом Лоуренсом (1901 – 1958), который в 1931 году создал циклотрон. Это устройство позволяет ускорять заряженные частицы с помощью относительно небольшого электрического поля в течение нескольких циклов. Рассмотрим устройство циклотрон (рисунок 3.42).

Два электрода специальной формы – дуанты – помещаются в камеру, в которой поддерживается вакуум (рисунок 3.43).

Дуанты помещаются между полюсами сильного магнита, и к ним прикладывается переменная разность потенциалов. В центре камеры между дуантами помещается источник заряженных частиц. Когда между нитями существует большая разность потенциалов, электрическое поле между ними ускоряет заряженные частицы.

Ускоренные частицы влетают во внутреннюю часть дуанта, где электрическое поле практически отсутствует. Двигаясь под действием магнитной составляющей силы Лоренца вдоль окружности, заряженные частицы вновь появляются в зазоре между дуантами через пол-оборота.

Те частицы, которые двигались с соответствующей скоростью, проходят через зазор как раз в тот момент (после полупериода изменения напряжения, приложенного к дуантам), когда там электрическое поле успевает изменить свое направление на противоположное. Эти частицы снова ускоряются, описывают полукруг еще большего радиуса внутри второго дуанта и снова приближаются к ускоряющей щели в нужный момент (время прохождения частиц через полукруг остается постоянным, так как не зависит от скорости частиц) и т.д. Другие частицы ускоряются слабо или вообще не ускоряются.

Циклотроны и другие более мощные ускорители заряженных частиц (например, фазотроны, синхротроны, синхрофазотроны) широко используются в ядерной физике и физике частиц. Изучая столкновения между ускоренными частицами и частицами-мишенями, физики могут исследовать структуру микрочастиц, действующие между ними силы и взаимные превращения элементарных частиц.

Магнитный щит Земли.

Магнитное поле Земли оказывает сильное влияние на поток заряженных частиц из космоса (космические лучи). Он образует третий “защитный щит” над атмосферой и ионосферой, который защищает живые организмы на Земле от вредного воздействия космических лучей.

На больших высотах магнитное поле Земли невелико, но охватывает огромные пространства. Воздействуя на заряженную частицу в течение длительного времени, он существенно изменяет ее траекторию. Вместо прямой линии она становится спиральной, навитой вдоль линии индукции магнитного поля (рис. 3.44).

Сила Лоренца не действует на частицу, летящую вдоль линий магнитной индукции. Поэтому частицы могут свободно приближаться к полюсам, от которых расходятся линии магнитной индукции.

Кроме того, магнитное поле Земли удерживает низкоэнергетические заряженные частицы на больших высотах. Эти области высокой концентрации заряженных частиц, окружающие Землю, называются радиационными поясами. Большинство частиц во внешнем радиационном поясе Земли – это электроны, а внутренний радиационный пояс состоит из протонов (рис. 3.45).

Протоны задерживаются более сильным магнитным полем во внутреннем радиационном поясе. В радиационных поясах заряженные частицы перемещаются от одного полюса к другому, оставаясь в “магнитной ловушке”.

Вопросы:

(a) электрическая составляющая силы Лоренца;

(b) магнитная составляющая силы Лоренца?

(2) В каком случае магнитная составляющая силы Лоренца будет максимальной?

3. как определить направление магнитной составляющей силы Лоренца.

a) на положительно заряженной частице;

(b) на отрицательно заряженной частице?

4. то, к чему привыкли:

5. Как магнитное поле Земли влияет на поток космических лучей?

Вопросы для обсуждения:

1. Действует ли магнитная составляющая силы Лоренца:

(a) на незаряженной частице в однородном магнитном поле;

(b) на заряженной частице, покоящейся в магнитном поле;

(c) на заряженной частице, движущейся вдоль линии магнитного поля?

(2) Как будет двигаться положительно заряженная частица в параллельных электрическом и магнитном полях, если ее начальная скорость направлена под некоторым углом к и от ?

Пример решения проблемы

Электрон входит в однородное магнитное поле с индукцией 10 -3 Тесла перпендикулярно линии магнитного потока и под углом α = π/4 до границы поля (рис. 3.46, а).

Модуль скорости электрона равен 10 6 м/с. В направлении X и Y направлении магнитное поле бесконечно. На каком расстоянии от точки входа электрон вылетит из поля? Отношение заряда электрона к его массе д/м = 1,76 ∙ 10 11 кл/кг.

В магнитном поле, под действием магнитной составляющей силы Лоренца, электрон образует дугу окружности. Найдите его радиус R. Запишите второй закон движения Ньютона:

Ответ: l = 8 мм.

Упражнения:

1. протон в магнитном поле с индукцией 0,01 Тесла обогнул окружность радиусом 10 см. Какова скорость протона?

Найти ускорение протона, движущегося со скоростью 2 м/с в магнитном поле индукцией 3 мТл перпендикулярно линии магнитной индукции.

Определите кинетическую энергию электрона, движущегося по окружности радиусом 1 см в однородном магнитном поле с индукцией 0,03 Тесла. Дайте свой ответ в Дж и эВ.

4. Протон с энергией 600 эВ входит в однородное магнитное поле индукцией 0,33 Тесла в направлении, перпендикулярном линии магнитной индукции. Найдите радиус траектории протона. Изменится ли кинетическая энергия протона при его движении через это магнитное поле?

Электрон входит в однородное магнитное поле индукцией 9,4 мТл так, что его вектор скорости образует угол 30° с направлением линии магнитной индукции (рис. 3.47).

Определите радиус поворота траектории электрона и расстояние, пройденное вдоль линии магнитного потока за три оборота. Скорость электрона равна 2,5 ∙ 10 6 м/с. 6.

Электрон, попавший в однородное магнитное поле под углом 60° к линии магнитной индукции, движется по спирали диаметром 10 см с периодом вращения 6 ∙ 10 -5 с. Определите скорость электрона, индукцию магнитного поля и отклонение спирали.

Читайте далее: