Линейные электрические цепи.
- Основные теоремы теории электромагнитного поля и их применение к теории электрических цепей.
- Свойства линейных электрических цепей и методы их расчета. Электрические цепи постоянного тока.
- Электрические цепи однофазного синусоидального тока.
- Четырехполюсные цепи. Схемы управляемых источников. Круговые диаграммы.
- Электрические фильтры.
- Трехфазные цепи.
- Несинусоидальные периодические токи в линейных электрических цепях.
- Переходные процессы в линейных электрических цепях.
- Интеграл Фурье. Спектральный метод. Сигналы.
- Синтез электрических цепей.
- Стационарные процессы в электрических и магнитных цепях, содержащих линии с распределенными параметрами.
- Переходные процессы в электрических цепях, содержащих линии с распределенными параметрами.
- Нелинейные электрические цепи постоянного тока.
- Магнитные цепи.
- Нелинейные электрические цепи переменного тока.
- Переходные процессы в нелинейных электрических цепях.
- Основы теории устойчивости нелинейных цепей.
- Электрические цепи с изменяющимися во времени параметрами.
- Электростатическое поле.
- Электрическое поле постоянного тока в проводящей среде.
- Магнитное поле постоянного тока.
- Основные уравнения переменного электромагнитного поля.
- Переменное электромагнитное поле в однородных и изотропных проводящих средах.
- Распространение электромагнитных волн в однородных и изотропных диэлектриках, в полупроводниковых и гиротропных средах.
- Потенциалы задержки переменных электромагнитных полей и излучения электромагнитной энергии.
- Электромагнитные волны в направляющих системах.
- Движение заряженных частиц в магнитном и электрическом полях.
- Основы магнитной гидродинамики.
- Сверхпроводящие среды в электромагнитных полях.
Сила F пропорциональна произведению вышеуказанных величин, но это не значит, что она просто равна произведению. Чтобы найти значение силы, произведение индукции B, длины и тока необходимо умножить на коэффициент (множитель) k. Последний коэффициент k зависит от единицы измерения магнитной индукции, тока и длины проводника, а также от единицы измерения силы.
Закон Ленца
Русский ученый Э.Х.Ленц еще в 1834 году установил свой знаменитый закон, который позволяет легко найти направление ЭДС, индуцированной магнитным полем: Наведенная ЭДС всегда направлена таким образом, чтобы создать ток, который противодействует происходящим изменениям.
Давайте объясним это на примерах:
Примечание Направление магнитного поля, создаваемого токами обмоток, во всех примерах определяется по правилу штопора.
Пример № 33
В первой обмотке ток увеличивается и создает магнитное поле, направление которого указано стрелкой 1 (рис. 3-36а). Электродвижущая сила, индуцированная во второй обмотке, создает в ней ток. Согласно закону Ленца, магнитное поле тока второй катушки должно быть направлено в сторону возрастания магнитного поля первой катушки. Магнитное поле индуцированного тока противостоит восходящему полю. Сравните сказанное здесь с направлениями токов, показанными на рисунке 3-32.
Пример № 34
В первой обмотке ток 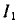 уменьшается, поэтому магнитное поле в направлении, указанном стрелкой
уменьшается, поэтому магнитное поле в направлении, указанном стрелкой 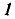 (рис. 3-36б). Электродвижущая сила, индуцированная во второй катушке, создает в ней ток
(рис. 3-36б). Электродвижущая сила, индуцированная во второй катушке, создает в ней ток 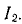
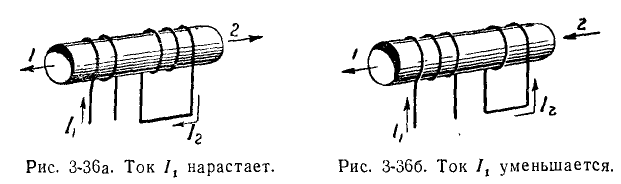
Магнитное поле тока второй обмотки, согласно закону Ленда, должно иметь то же направление, что и магнитное поле первой обмотки. Магнитное поле индуцированного тока поддерживает уменьшающееся поле, то есть противодействует происходящему изменению.
Сравните то, что было сказано здесь, с направлением токов, показанных на рис. 3-31.
Пример 35
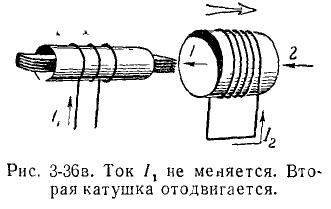
Обмотка, образующая замкнутый контур, удаляется из магнитного поля другой (первой) обмотки, подключенной к источнику тока. Направление магнитного поля неподвижной обмотки указано стрелкой 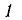 (Рисунок 3-30c) электродвижущая сила, индуцированная во второй обмотке, вызывает ток во второй обмотке. Магнитное поле второй обмотки, согласно закону Ленца, должно быть в том же направлении, что и первой обмотки Магнитное поле, которое исчезает во второй обмотке из-за ее удаления, поддерживается током, индуцированным во второй обмотке.
(Рисунок 3-30c) электродвижущая сила, индуцированная во второй обмотке, вызывает ток во второй обмотке. Магнитное поле второй обмотки, согласно закону Ленца, должно быть в том же направлении, что и первой обмотки Магнитное поле, которое исчезает во второй обмотке из-за ее удаления, поддерживается током, индуцированным во второй обмотке.
Пример № 36
Убедитесь, что направление тока, индуцированного во второй обмотке в условиях эксперимента, показанного на рис. 3-33, соответствует закону Ленца.
Магнитный поток
Для того чтобы понять смысл нового термина “магнитный поток”, мы подробно рассмотрим несколько экспериментов по индукции ЭДС, обращая внимание на количественную сторону сделанных наблюдений.
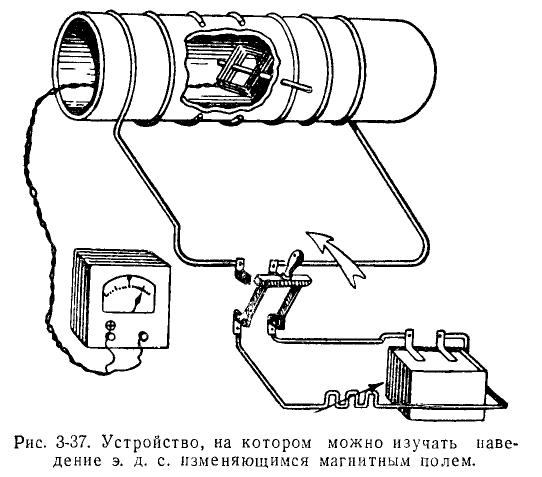
В наших экспериментах мы будем использовать схему, показанную на рис. 3-37, которая состоит из большой катушки, намотанной, скажем, на трубку из толстого клееного картона. Катушка питается от аккумулятора через переключатель и регулируемое сопротивление. О силе тока, протекающего в катушке, можно судить по амперметру (не показан на Рис. 3-37).
Внутри большой катушки может быть установлена еще одна маленькая катушка, концы которой соединены с магнитоэлектрическим гальванометром. Для наглядности часть катушки показана вырезанной, чтобы показать расположение маленькой катушки. Когда переключатель замкнут или разомкнут, на маленькую катушку подается напряжение. с., и стрелка гальванометра кратковременно отбрасывается из нулевого положения.
По величине обнуления можно судить о том, больше или меньше индуцированная ЭДС. Наблюдая за количеством делений, на которое стрелка отбрасывается назад, можно количественно сравнить действие, вызванное индуцированной ЭДС. 1
Первое наблюдение. Вставьте малую катушку внутрь большой, закрепите их на месте и пока ничего не меняйте в их расположении. 1 Обратите внимание, что в лаборатории мы обычно используем зеркальный, а не сагиттальный гальванометр. В этом случае выбирайте медленно осциллирующие гальванометры – требуется 10-20 секунд, чтобы зеркало и оправа вышли из равновесия (влево, вправо и обратно влево), очень легко считать крайнее положение светового индикатора (луча).
Включим выключатель и, изменяя сопротивление, подключенное за батареей, установим определенное значение тока, например: 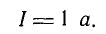
Теперь давайте выключим выключатель, наблюдая за гальванометром. Пусть бросает 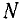 на 5 делений вправо:
на 5 делений вправо: 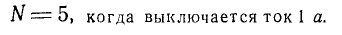
Снова включите выключатель и, изменяя сопротивление, увеличьте ток в большой катушке до 4 а.
Подождите, пока гальванометр стабилизируется, а затем снова выключите выключатель, наблюдая за показаниями гальванометра.
Если при выключении тока на 1 a его слабина составляла 5 делений, то теперь мы наблюдаем, что при выключении тока на 4 a слабина увеличилась в 4 раза:
N = 20 при отключении тока до значения 4а. Продолжая подобные наблюдения, легко прийти к выводу, что отдача гальванометра, а значит и наведенная ЭДС, увеличивается пропорционально увеличению выключенного тока. Однако мы знаем, что изменение тока вызывает изменение магнитного поля (его индукции), поэтому правильный вывод из нашего наблюдения следующий: Индуцированная ЭДС пропорциональна скорости изменения магнитной индукции.
Более детальные наблюдения подтверждают справедливость этого вывода.
Второе наблюдение. Продолжим наблюдение за отдачей гальванометра, выключив тот же самый ток, скажем 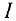 = 4 а. Однако мы изменим количество витков в маленькой катушке, оставив ее положение и размер неизменными.
= 4 а. Однако мы изменим количество витков в маленькой катушке, оставив ее положение и размер неизменными.
Предположим, мы наблюдали, как гальванометр выключается при 100 (сто витков на маленькой катушке).
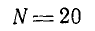 1 Включение выключателя должно сопровождаться перемещением гальванометра на 5 делений влево (см. почему). И тогда при регулировке тока игла гальванометра будет отклоняться с каждым изменением тока, потому что изменение тока сопровождается изменением магнитного поля, а значит, и изменением индукции электромагнитного тока в маленькой катушке.
1 Включение выключателя должно сопровождаться перемещением гальванометра на 5 делений влево (см. почему). И тогда при регулировке тока игла гальванометра будет отклоняться с каждым изменением тока, потому что изменение тока сопровождается изменением магнитного поля, а значит, и изменением индукции электромагнитного тока в маленькой катушке.
Как изменится отклонение гальванометра, если количество витков увеличить вдвое? Эксперимент показал, что
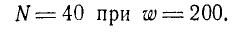 Это именно то, чего вы ожидаете. Фактически, все витки маленькой катушки находятся под воздействием одного и того же магнитного поля, и в каждом из них должна индуцироваться одна и та же ЭДС.
Это именно то, чего вы ожидаете. Фактически, все витки маленькой катушки находятся под воздействием одного и того же магнитного поля, и в каждом из них должна индуцироваться одна и та же ЭДС.
Назовем ЭДС одной катушки 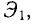 это е.ф. 100 катушек, соединенных последовательно, одна за другой, должно быть в 100 раз больше, чем
это е.ф. 100 катушек, соединенных последовательно, одна за другой, должно быть в 100 раз больше, чем
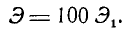 Для 200 оборотов
Для 200 оборотов 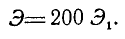 Для любого другого числа оборотов
Для любого другого числа оборотов 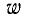
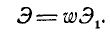
Если выходная мощность увеличивается пропорционально количеству витков, то очевидно, что реакция гальванометра также должна быть пропорциональна количеству витков.
Это то, что показывает опыт. Таким образом, – Наведенная ЭДС пропорциональна количеству катушек. Мы еще раз подчеркиваем, что размер маленькой катушки и ее положение оставались неизменными во время нашего эксперимента. Само собой разумеется, эксперимент проводился в той же большой катушке с тем же выключенным током.
Третье наблюдение. После проведения нескольких экспериментов с одной и той же маленькой катушкой при одном и том же коммутируемом токе легко убедиться, что величина наведенной ЭДС зависит от положения маленькой катушки.
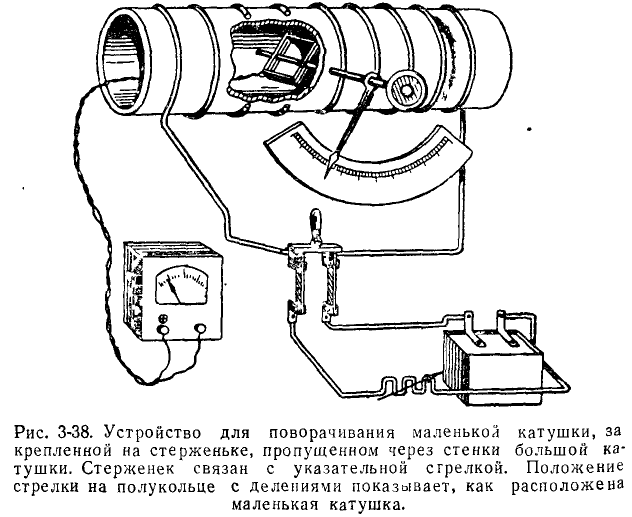
Для того чтобы пронаблюдать зависимость наведенной ЭДС от положения маленькой катушки, давайте немного подкорректируем нашу установку (рис. 3-38). К внешнему концу оси маленькой катушки прикрепляем стрелку-указатель и градуированный круг (подобный тем, что встречаются на радиоприемниках). После поворота штифта мы теперь знаем положение указательной стрелки на маленькой катушке внутри большой катушки.
Из наблюдений следует, что Из наблюдений следует, что малая катушка находится в самом высоком положении э.д.с., когда ее ось расположена в том же направлении, что и магнитное поле.
Другими словами, когда оси большой и малой катушек параллельны. Такое расположение малой катушки показано на рис. 3-39, А и Б. По мере вращения катушки индуцированная в ней электродвижущая сила будет становиться все меньше и меньше. Наконец, если плоскость маленькой катушки станет параллельной линиям поля, то в ней не будет индуцированной ЭДС. Может возникнуть вопрос, что произойдет при дальнейшем вращении маленькой катушки? Если мы повернем катушку более чем на 90 0 (относительно ее первоначального положения), знак индуцированного электрического поля изменится. Линии поля войдут в катушку с другой стороны.
Четвертое наблюдение. Важно сделать последнее замечание. Давайте выберем определенное положение, в которое поместим маленькую катушку.
Договоримся, например, всегда размещать его в таком положении, чтобы индуктируемый переменный ток был как можно выше (конечно, для данного числа витков и данного значения тока выключения). Сделайте несколько небольших катушек разного диаметра, но с одинаковым количеством витков.
Поместите эти катушки в то же положение и, выключив ток, наблюдайте за отдачей гальванометра.
Эксперимент покажет нам, что Наведенная ЭДС пропорциональна площади поперечного сечения катушек.
Магнитный поток. Все наблюдения приводят нас к выводу, что индуцированная ЭДС всегда пропорциональна изменению магнитного потока.
Но что такое магнитный поток?
Сначала мы рассмотрим магнитный поток через плоскую поверхность 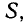 которая образует прямой угол с направлением магнитного поля. В этом случае магнитный поток равен произведению площади поверхности на индукцию или
которая образует прямой угол с направлением магнитного поля. В этом случае магнитный поток равен произведению площади поверхности на индукцию или
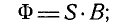 здесь S – площадь нашего квадрата, см 2 ;
здесь S – площадь нашего квадрата, см 2 ;
- B – индукция,
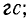
- Ф – магнитный поток, максвелл (мкс).
Единицей измерения потока является максвелл. Представляя магнитное поле линией, мы можем сказать, что магнитный поток пропорционален числу линий поля, проходящих через данную площадь.
Если линии поля проведены таким образом, что их количество на 1 см2 в поперечной плоскости равно индукции поля B, выраженной в гауссианах, то можно прямо сказать, что поток равен количеству таких (одиночных) линий.
Если линии поля расположены таким образом, что их количество на 1 см2 в поперечной плоскости равно индукции поля B, выраженной в тысячных долях гауссзатем равна количеству этих строк, умноженному на тысячу.
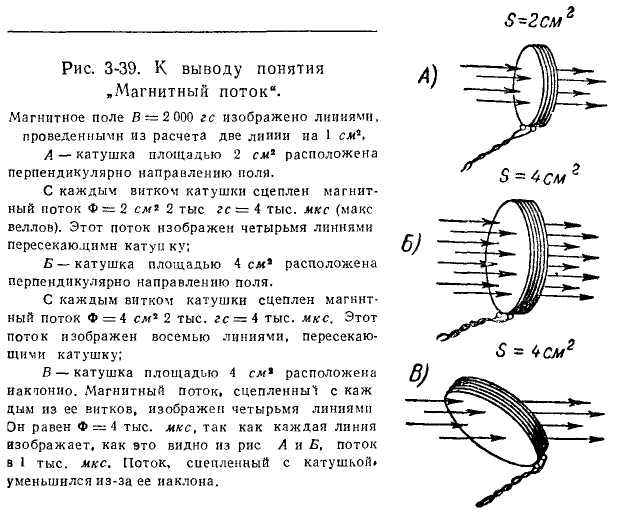
На рисунке 3-39 магнитное поле при 2 000 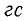 представлена линиями, проведенными с частотой две линии на 1sl 2 . Таким образом, в случае A магнитный поток на площади 2 см2 , поперечной к полю, составляет
представлена линиями, проведенными с частотой две линии на 1sl 2 . Таким образом, в случае A магнитный поток на площади 2 см2 , поперечной к полю, составляет
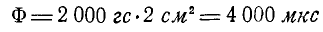
что составляет 4 строки, умноженные на тысячу.
В случае B, на том же рисунке 3-39, магнитный поток через поперечную площадку площадью 4 см 2 при индукции 2 000 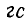 это:
это: 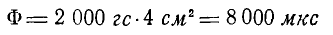
т.е. 8 строк, умноженных на тысячу.
Можно также сказать так: магнитный поток равен 8000 единичным линиям.
Магнитный поток, связанный с катушкой. Говоря об индуцированном ВЧД, мы должны иметь в виду поток, связанный с катушкой. Поток, связанный с катушкой, – это поток, который проникает в поверхность, окруженную катушкой.
На рис. 3-39 поток, подключенный к каждой обмотке катушки в случае A, составляет 4 000 мкс, а в случае B – 8 000 мкс. Если площадь поверхности не является поперечной по отношению к магнитным линиям, поток больше не может быть определен просто произведением площади поверхности и индукции. Мы определяем поток в этом случае как произведение индукции на площадь поверхности проекции нашего квадрата.
Это проекция на плоскость, перпендикулярную линиям поля, так сказать, тень, отбрасываемая площадкой (Рисунок 3-40).
Однако для любой квадратной формы поток по-прежнему пропорционален числу линий, проходящих через него, или равен числу единичных линий, пронизывающих квадрат.
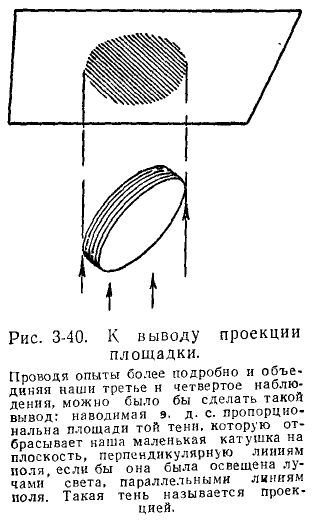
Так, для случая B на рис. 3-39 поток через площадь 4 см2 при индукции 2 000 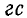 составляет всего 4 000 мкс (4 строки по 1 000 мкс каждая). Представление магнитного поля линиями очень помогает в определении потока.
составляет всего 4 000 мкс (4 строки по 1 000 мкс каждая). Представление магнитного поля линиями очень помогает в определении потока.
Если поток Ф связан с каждой из обмоток катушки, то это произведение можно назвать 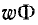 общая мощность потока в катушке. Индукционная концепция особенно удобна в использовании, когда разные потоки подключены к разным катушкам. В этом случае общая коэрцитивная сила катушки равна сумме потоков, подключенных к каждой катушке.
общая мощность потока в катушке. Индукционная концепция особенно удобна в использовании, когда разные потоки подключены к разным катушкам. В этом случае общая коэрцитивная сила катушки равна сумме потоков, подключенных к каждой катушке.
Несколько комментариев по поводу слова “поток”. Почему мы говорим о флюсе? Связана ли с этим словом идея потока чего-то магнитного? Действительно, когда мы говорим “электрический ток”, мы представляем себе движение (поток) электрических зарядов. То же самое с магнитным потоком? Нет, когда мы говорим “магнитный поток”, мы имеем в виду только меру магнитного поля (произведение напряженности поля на площадь поверхности), подобную той, которую используют инженеры и ученые, изучающие движение жидкостей. Когда вода движется, ее поток называется произведением скорости воды и площади поперечного сечения (поток воды в трубе равен отношению ее скорости к площади поперечного сечения трубы).
Конечно, само магнитное поле, которое является разновидностью материи, также связано с определенной формой движения. У нас пока нет достаточно четкого понимания и знания природы этого движения, хотя современным ученым многое известно о свойствах магнитного поля: магнитное поле связано с существованием определенной формы энергии, его основной мерой является индукция, другой очень важной мерой является магнитный поток.
Закон индукции
Все эксперименты с индукцией, а также теоретические соображения приводят к следующему выводу: ЭДС, индуцированная в электрической цепи, равна скорости изменения потока, связанного с ней.
Выразим это с помощью математической формулы. Для этого мы вводим новый знак 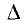 или d. Первый – это греческая буква
или d. Первый – это греческая буква 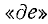 (читается как дельта), вторая – просто латинская буква d. Каждая из этих букв, будучи поставленной перед обозначением некоторого количества, выражает его изменение. Так, например, если время обозначается через t, то
(читается как дельта), вторая – просто латинская буква d. Каждая из этих букв, будучи поставленной перед обозначением некоторого количества, выражает его изменение. Так, например, если время обозначается через t, то 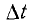 это изменение во времени или период времени. Если по
это изменение во времени или период времени. Если по 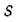 обозначает путь, тогда
обозначает путь, тогда 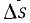 означает путь или пройденное расстояние. В этом случае соотношение
означает путь или пройденное расстояние. В этом случае соотношение 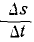 выражает скорость
выражает скорость 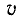
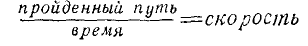
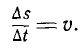
Пусть для временного интервала 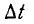 магнитный поток, подключенный к катушке, изменяется равномерно на
магнитный поток, подключенный к катушке, изменяется равномерно на 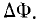 В этом случае скорость изменения потока может быть задана соотношением
В этом случае скорость изменения потока может быть задана соотношением 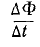 . Это отношение равно индуцированной э.д.с,
. Это отношение равно индуцированной э.д.с,
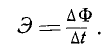
Эта формула является математическим выражением одного из важнейших законов электротехники.
Направление э.д.с. всегда можно определить из закона Ленца. О единицах измерения магнитного потока и э.м.с. Например, для 0,01 с 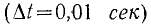 поток, запутанный в катушке, постоянно увеличиваясь, изменяется на 20 000 Максвеллов
поток, запутанный в катушке, постоянно увеличиваясь, изменяется на 20 000 Максвеллов 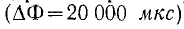 Поэтому в это время в катушке индуцировалась электродвижущая сила.
Поэтому в это время в катушке индуцировалась электродвижущая сила.
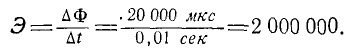
Электродвижущая сила равна 2 млн. Все правильно, только здесь э.ф.к. выражена в неизвестных единицах: э.ф.к. равна 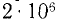 (2 миллиона) неизвестных единиц, не
(2 миллиона) неизвестных единиц, не 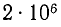 в. Эти единицы используются для выражения э.д.с. были введены около 70 лет назад одновременно с единицами Гаусса и Максвелла для магнитной индукции и магнитного потока. Физики по-прежнему часто используют эти единицы, поэтому здесь мы будем называть их физическими единицами 1 . Однако физические единицы для индукции и потока достаточно удобны, и на практике они часто используются. Напротив, физическая единица для напряжения практически неприемлема, и вместо нее была введена единица 1v, равная 100 миллионам физических единиц:
в. Эти единицы используются для выражения э.д.с. были введены около 70 лет назад одновременно с единицами Гаусса и Максвелла для магнитной индукции и магнитного потока. Физики по-прежнему часто используют эти единицы, поэтому здесь мы будем называть их физическими единицами 1 . Однако физические единицы для индукции и потока достаточно удобны, и на практике они часто используются. Напротив, физическая единица для напряжения практически неприемлема, и вместо нее была введена единица 1v, равная 100 миллионам физических единиц:
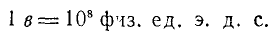 Поэтому, если мы хотим выразить, например, магнитный поток в вольтах, а магнитный поток в Максвеллах, то в формулу для ведущего закона нужно ввести множитель 10 -8, например
Поэтому, если мы хотим выразить, например, магнитный поток в вольтах, а магнитный поток в Максвеллах, то в формулу для ведущего закона нужно ввести множитель 10 -8, например 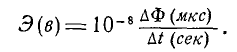
 1 Их полные названия – это единицы магнитной системы: сантиметр, грамм, секунда.
1 Их полные названия – это единицы магнитной системы: сантиметр, грамм, секунда.
Пример № 37
Катушка площадью 4 см2 помещена в магнитное поле. Напряженность поля (индукция) увеличивается от нуля до 2 000 gsi за 0,05 с. Плоскость катушки образует угол 90 0 с направлением поля. Каково значение индукции в катушке?
Решение:
Поток, подключенный к катушке, достигает значения
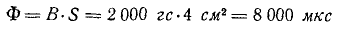
за 0,05 секунды, так что 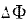 =8000 мкс (поток начал увеличиваться с нуля) и
=8000 мкс (поток начал увеличиваться с нуля) и 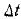 =0,05 сек. Наведенный Vs.
=0,05 сек. Наведенный Vs.
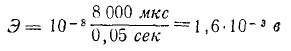 Или 1,6 мВ (милливольт).
Или 1,6 мВ (милливольт).
Пример № 38
Катушка состоит из 500 витков.
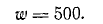 Каждая катушка соединена с магнитным потоком, который увеличивается на
Каждая катушка соединена с магнитным потоком, который увеличивается на 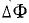 = 8.000 мкс во времени
= 8.000 мкс во времени 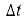 = 0,05 сек. Какова полная ЭДС, индуцированная в катушке?
= 0,05 сек. Какова полная ЭДС, индуцированная в катушке?
Решение:
В каждой катушке индуцируется ток 1,6 мВ (см. предыдущий пример). Это означает, что во всей катушке индуцируется электромагнитная волна. 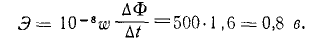
Пример 39
Катушка состоит из 200 витков. Площадь каждого витка составляет 400 см2 . Магнитная индукция направлена вдоль оси катушки и равномерно возрастает от 5 000 до 12 000 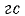 за 0,01 с времени. Какова индукция в катушке?
за 0,01 с времени. Какова индукция в катушке?
Решение:
В каждой катушке поток изменяется на
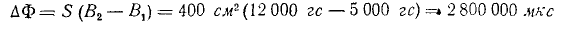
(два миллиона восемьсот тысяч Максвеллов) или 2800 кмс (две тысячи восемьсот киломаксвеллов, или одна тысяча Максвеллов). Здесь новое значение индукции 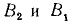 означает новое значение индукции
означает новое значение индукции 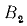 = 12000
= 12000 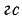 и старое значение
и старое значение 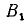 = 5 600
= 5 600 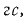 из которого начало расти поле. Индуцированные э.д.с.
из которого начало расти поле. Индуцированные э.д.с.
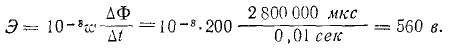
Пример № 40
Катушка площадью 500 см2 помещена в магнитное поле так, что ее ось образует угол 45 0 с направлением поля. Индукция магнитного поля равна 800 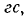 равномерно сводится к нулю за 0,1 с. Каково значение электродвижущей силы, индуцированной в катушке?
равномерно сводится к нулю за 0,1 с. Каково значение электродвижущей силы, индуцированной в катушке?
Решение Проведите 10 параллельных линий, равноудаленных друг от друга и проходящих через катушку, которая находится поперек поля (ось катушки совпадает с направлением поля). Нарисуем спираль, наклоненную под углом 45° C, и подсчитаем количество прямых, проходящих через эту спираль. Из рисунка легко увидеть, что при наклоне катушки она будет лететь с 7 линиями вместо 10 (ср. рис. 3-39 и 3-40).
Но 10 линий соответствуют потоку
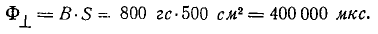
Таким образом, поток соответствует 7 строкам
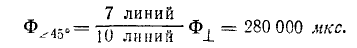
С помощью знаков 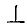 и
и 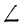 45° указывают поток в положении, перпендикулярном нити накала и под углом 45°.
45° указывают поток в положении, перпендикулярном нити накала и под углом 45°.
Дополнительные примечания по магнитным единицам измерения. В целях обеспечения возможности выражения в законе поведения e.f.c. 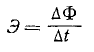 может быть выражен в вольтах, а поток в максвеллах, мы ввели множитель 10 -8 (одна сотая миллионной). Но мы могли бы поступить иначе – мы могли бы ввести новую единицу магнитного потока на 100 миллионов больше максвелла. В этом случае мы получили бы непосредственно среднеквадратичное значение в вольтах в левой части. Такую единицу удобно называть вольт-секунда*
может быть выражен в вольтах, а поток в максвеллах, мы ввели множитель 10 -8 (одна сотая миллионной). Но мы могли бы поступить иначе – мы могли бы ввести новую единицу магнитного потока на 100 миллионов больше максвелла. В этом случае мы получили бы непосредственно среднеквадратичное значение в вольтах в левой части. Такую единицу удобно называть вольт-секунда* 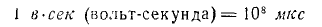
(сто миллионов максвелловцев) или
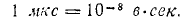
В правой части выражения для E вольт-секунда находится в числителе, а секунда – в знаменателе. Второй и второй могут быть уменьшены. После этого уменьшения остается только число, умноженное на вольт. Возьмем цифры из примера 3:
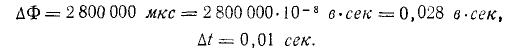
Рассчитайте э.д.с., индуцированную в одной катушке
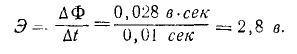
Создание новой единицы для потока влечет за собой создание новой единицы для магнитной индукции. Формула для определения магнитного потока
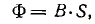

* Для этого устройства также используется другое название – Weber.
можно также использовать для определения индукции B по потоку
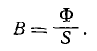 Если
Если 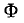 выражается в
выражается в 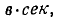 и S в см 2 , новая единица для индукции определяется как отношение единичного потока к единичной площади. Если мы определим площадь поверхности S в квадратных метрах
и S в см 2 , новая единица для индукции определяется как отношение единичного потока к единичной площади. Если мы определим площадь поверхности S в квадратных метрах 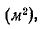 мы получаем еще одну единицу индукции:
мы получаем еще одну единицу индукции: 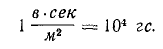
Э.Д.С. индукция в прямолинейном проводнике, движущемся в поле
В современных машинах – генераторах – генерация э.д.с. основана на только что рассмотренном законе. Однако, в отличие от примеров в предыдущем параграфе, в электрических машинах изменение магнитного потока вызвано движением проводника в магнитном поле.
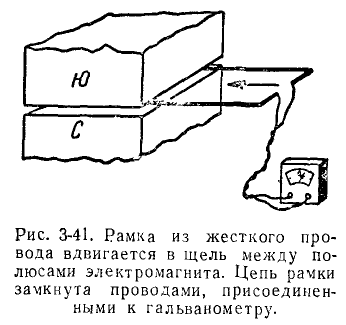
Представьте, что в узком зазоре между полюсами большого электромагнита находится отрезок жесткой прямоугольной рамки, согнутой из толстой проволоки (рис. 3-41 и 3-42). Эта рама не полностью закрыта, и ее концы соединены с гибким проводом. Провод подключен к гальванометру. При движении рамки в направлении, указанном стрелкой, магнитный поток, связанный с рамкой, изменяется. При изменении магнитного потока возникает ЭДС. Величина ЭДС отображается отклонением гальванометра.
На рисунке 3-42 для наглядности показано отклонение гальванометра. 3-42, верхняя часть электромагнита (южный полюс) для наглядности вообще не показана. На этом же рисунке магнитное поле показано в виде серии маленьких стрелок. Поле между полюсами направлено точно так, как показывают маленькие стрелки, В пространстве между полюсами поле имеет постоянную индукцию. По мере удаления от полюсов поле очень быстро ослабевает. Можно даже предположить, что за пределами зазора нет поля.
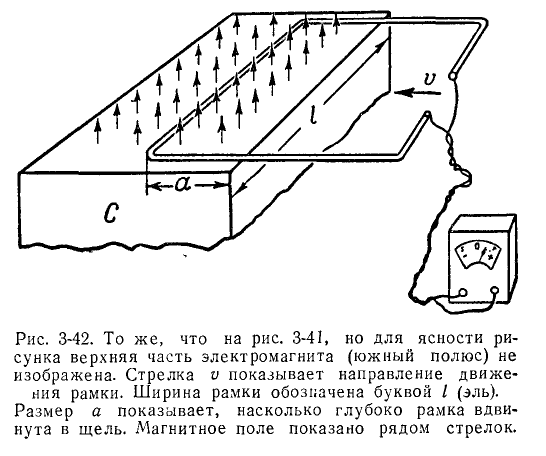
Вычислим магнитный поток F, содержащийся в рамке.
Для этого нужно умножить магнитную индукцию B на площадь рамки между полюсами. Если рама широкая 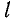 и вставляется на глубину a (рис. 3-42) область
и вставляется на глубину a (рис. 3-42) область 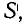 пронизанный полем:
пронизанный полем: 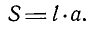 Магнитный поток, связанный с рамой
Магнитный поток, связанный с рамой 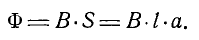 Чем глубже вставлена рамка, тем больше поток.
Чем глубже вставлена рамка, тем больше поток.
Пусть рама удлинится до половины ширины шеста, как показано на рисунке. В этом случае связанный поток представлен 16 линиями. Давайте передвинем рамку еще глубже, чтобы она достигла 3/4 ширины колонны. Тогда поток будет состоять из 24 линий. Когда рамка охватывает весь полюс, поток увеличивается до 32 линий.
Но какова скорость увеличения потока? Это, конечно, зависит от скорости, с которой рама скользит в зазор между столбами.
Однако скорость роста потока можно определить и более точно. Когда рамка перемещается в формуле 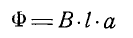 изменяется только расстояние a (глубина, на которую вставляется рамка), поэтому изменение потока
изменяется только расстояние a (глубина, на которую вставляется рамка), поэтому изменение потока 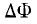 зависит от изменения этой размерности a. В течение определенного периода времени
зависит от изменения этой размерности a. В течение определенного периода времени 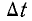 интервал времени, в течение которого эта величина увеличивается, можно определить по следующей формуле
интервал времени, в течение которого эта величина увеличивается, можно определить по следующей формуле 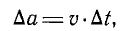 где
где 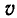 – это скорость, с которой движется кадр 1. Но если мы знаем, что изменение размера
– это скорость, с которой движется кадр 1. Но если мы знаем, что изменение размера 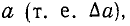 то нетрудно вычислить соответствующее изменение потока
то нетрудно вычислить соответствующее изменение потока 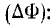
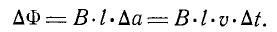 Таким образом, мы почти подошли к концу формулы для индукционного тока. Нам по-прежнему нужно определить только скорость изменения потока
Таким образом, мы почти подошли к концу формулы для индукционного тока. Нам по-прежнему нужно определить только скорость изменения потока 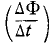 . Разделив левую и правую части последнего уравнения на
. Разделив левую и правую части последнего уравнения на 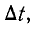 мы находим:
мы находим:
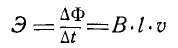 или
или
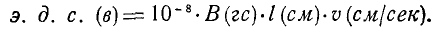 Это формула для расчета наведенной ЭДС, индуцированная в прямолинейном проводнике, движущемся в магнитном поле со скоростью
Это формула для расчета наведенной ЭДС, индуцированная в прямолинейном проводнике, движущемся в магнитном поле со скоростью 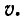
Полученная формула действительна, если: 1) проводник находится под прямым углом к направлению магнитного поля и к направлению скорости, и когда 2) скорость 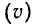 также перпендикулярно полю.
также перпендикулярно полю.
1 Скорость определяется как расстояние, пройденное за единицу времени. Если скорость составляет, например, 5 см в секунду, то за 1 с пройденное расстояние составит 5 см, а за 0,1 с – 0,5 см.
Выводы, сделанные здесь, также верны, если провод неподвижен, но сами полюса движутся вместе с магнитным полем, которое они генерируют.
Мы нашли формулу для движения рамки и применили ее как формулу, скажем, для индукции в прямолинейном проводнике, движущемся по полю. Это легко объяснить: в боковых проводниках, параллельных направлению скорости, не индуцируется электрический ток. Вся электрическая энергия индуцируется в поперечном проводнике длиной 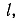 движущиеся в магнитном поле. На самом деле, если этот поперечный провод выходит за пределы поля, то при движении рамки связанный лоток достигнет своего наибольшего значения (32 линии) и не изменится. Конечно, только до тех пор, пока обратная сторона рамы не войдет в зазор между стойками. Поэтому в боковых (параллельных) проводах не индуцируется электрический ток, даже если они движутся в магнитном поле.
движущиеся в магнитном поле. На самом деле, если этот поперечный провод выходит за пределы поля, то при движении рамки связанный лоток достигнет своего наибольшего значения (32 линии) и не изменится. Конечно, только до тех пор, пока обратная сторона рамы не войдет в зазор между стойками. Поэтому в боковых (параллельных) проводах не индуцируется электрический ток, даже если они движутся в магнитном поле.
Правило правой руки. Величину ЭДС, наведенной движущимся проводом, можно определить с помощью правила правой руки (рис. 3-43). Если правая рука расположена так, что линии поля входят в ладонь, а согнутый большой палец совпадает с направлением движения, то четыре вытянутых пальца показывают направление индуцированной ЭДС.
Направление индуцированной ЭДС – это направление, в котором должен протекать ток в замкнутой цепи под ее действием. Легко видеть, что правило правой руки полностью соответствует закону Ленца. Мы предоставляем читателю самому разобраться в этом.
Пример № 41
Проволока перемещается между полюсами, как показано на рис. 3-41 и 3-42. Магнитная индукция B = 112 000 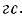 Длина провода
Длина провода 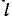 – 80 см. Скорость
– 80 см. Скорость 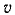 = 50 м/с (или 5 000 см/с). Найдите э.д.с., индуцированную в проводе.
= 50 м/с (или 5 000 см/с). Найдите э.д.с., индуцированную в проводе.
Решение:
Используя формулу 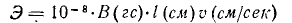 мы находим
мы находим 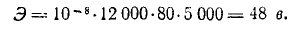
Конечно, такая ЭДС индуцируется в проводнике только в тот промежуток времени, когда проводник находится между полюсами. Магнитные поля, скорости и размеры, подобные показанным в этом примере, можно встретить в электрических машинах.
Взаимная индукция
В наших первых экспериментах с индукцией мы наблюдали индукцию, например, в одной цепи под действием изменения тока в другой. Однако первая цепь принципиально не отличалась от второй, и поэтому, изменяя ток во второй цепи, мы, естественно, обнаруживали индукционные э.д.с. в первой цепи.
Индукция в одной цепи, вызванная изменением тока в другой цепи, называется взаимной индукцией (индукцией). Величина индукции прямо пропорциональна скорости изменения тока.
Коэффициент пропорциональности между скоростью изменения тока в первой цепи и скоростью изменения тока во второй цепи называется взаимной индуктивностью и обычно обозначается буквой M.
Единица измерения индуктивности. Если мы выражаем скорость изменения тока в амперах в секунду (ампер/с), а отношение между этими величинами М оказывается выраженным в единицах, которые мы называем genri 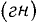 . Если M = 1
. Если M = 1 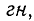 то э.д.с., индуцированная в одной цепи изменением тока в другой цепи, численно равна скорости изменения тока. Представим скорость изменения тока соотношением
то э.д.с., индуцированная в одной цепи изменением тока в другой цепи, численно равна скорости изменения тока. Представим скорость изменения тока соотношением 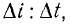 где
где 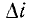 – приращение тока в интервале времени
– приращение тока в интервале времени 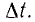
Тогда все вышесказанное можно записать с помощью формулы
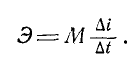 Явление взаимной индукции очень важно в современной электротехнике. Явление взаимной индукции лежит в основе работы трансформаторов.
Явление взаимной индукции очень важно в современной электротехнике. Явление взаимной индукции лежит в основе работы трансформаторов.
Пример № 42
Взаимная индуктивность между двумя катушками составляет 2 миллигенри (мгм), или две тысячные доли генри. Ток в первой катушке изменяется со скоростью 800 а/с. Каково среднеквадратичное значение переменного тока, индуцированного во второй катушке?
Решение:
Электродвижущая сила E равна скорости изменения тока 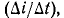 умноженное на обратную величину индуктивности M, или
умноженное на обратную величину индуктивности M, или
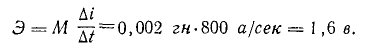
Пример 43
Если бы рядом с мощной ЛЭП на километр проходила воздушная телефонная линия (мн. телеграфная линия), между ними возникла бы значительная индуктивная связь – магнитный поток, создаваемый током в ЛЭП, пробивал бы петлю проводов ЛЭП. Для случая одного такого сближения двух линий, взаимная индуктивность M была рассчитана как 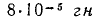 (восемьсот тысячных долей Генри). В случае короткого замыкания в линии электропередачи скорость нарастания тока
(восемьсот тысячных долей Генри). В случае короткого замыкания в линии электропередачи скорость нарастания тока 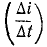 может достигать очень высокого значения
может достигать очень высокого значения 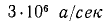 (З млн. ом в секунду). Следует отметить, что такая скорость изменения наблюдается, когда ток короткого замыкания достигает пикового значения порядка 10 000 А. За тысячную долю секунды
(З млн. ом в секунду). Следует отметить, что такая скорость изменения наблюдается, когда ток короткого замыкания достигает пикового значения порядка 10 000 А. За тысячную долю секунды 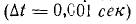 ток может увеличиться на 3 000 а
ток может увеличиться на 3 000 а 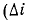 – 3000 а). Необходимо ли находить величину тока в линии в случае короткого замыкания в линии электропередачи?
– 3000 а). Необходимо ли находить величину тока в линии в случае короткого замыкания в линии электропередачи?
Решение:
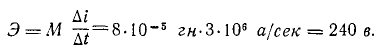 Из ответа совершенно ясно, что необходимо отделить линию связи от линии электропередачи или принять другие меры. Обратите внимание, что даже гораздо меньшая индукция э.к. мешает хорошей работе связи. Электродвижущая сила взаимной индукции возникает потому, что, как уже говорилось, изменение тока связано с изменением потока. Поэтому взаимную индуктивность M можно также рассматривать как отношение между током одного контура и потоком, связанным с другим контуром.
Из ответа совершенно ясно, что необходимо отделить линию связи от линии электропередачи или принять другие меры. Обратите внимание, что даже гораздо меньшая индукция э.к. мешает хорошей работе связи. Электродвижущая сила взаимной индукции возникает потому, что, как уже говорилось, изменение тока связано с изменением потока. Поэтому взаимную индуктивность M можно также рассматривать как отношение между током одного контура и потоком, связанным с другим контуром.
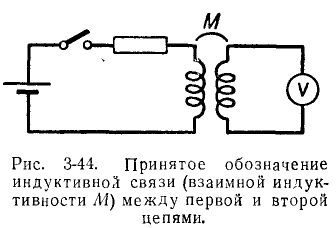
На рисунке 3-44 показана принципиальная схема. 3-44 схематично показана индуктивная связь двух контуров,
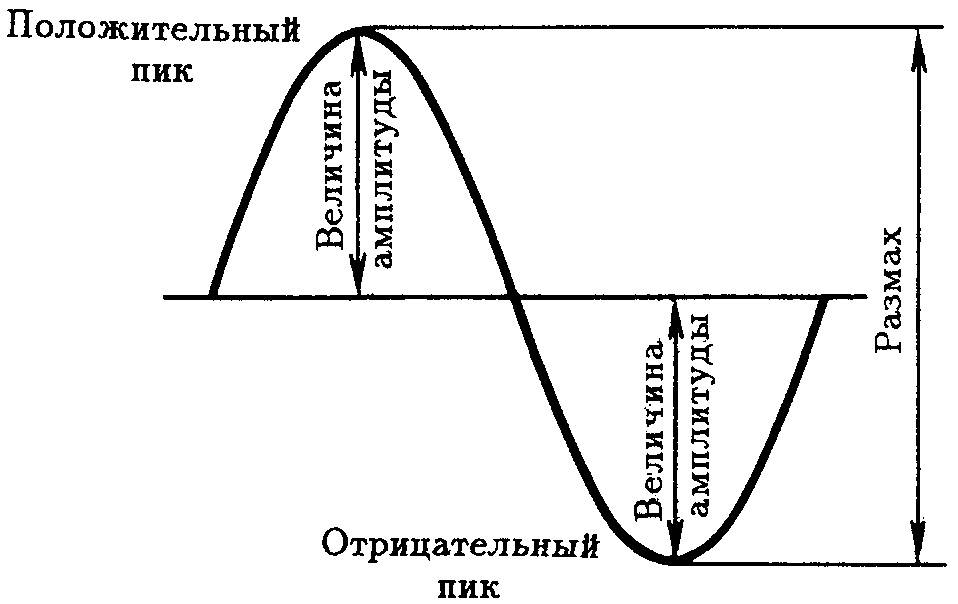
Переменный ток – это электрический ток, направление и сила которого периодически меняются. Поскольку переменный ток обычно изменяется синусоидально, переменный ток представляет собой синусоидальные колебания напряжения и тока. Поэтому все, что относится к синусоидальным электрическим колебаниям, относится к переменному току. В этой статье мы расскажем о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону.
Что такое переменный ток?
 Переменный ток – это электрический ток, направление и сила которого периодически меняются. Поскольку переменный ток обычно изменяется синусоидально, переменный ток – это синусоидальное изменение напряжения и силы тока. Поэтому все, что относится к синусоидальным электрическим колебаниям, относится к переменному току. В этой статье мы расскажем о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону.
Переменный ток – это электрический ток, направление и сила которого периодически меняются. Поскольку переменный ток обычно изменяется синусоидально, переменный ток – это синусоидальное изменение напряжения и силы тока. Поэтому все, что относится к синусоидальным электрическим колебаниям, относится к переменному току. В этой статье мы расскажем о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону.
 Переменный ток широко используется в промышленности. Почти вся электроэнергия вырабатывается генераторами переменного тока. Его легко преобразовать с помощью трансформаторов, он легко передается на большие расстояния по линиям электропередач, а широко используемые двигатели переменного тока проще в производстве и эксплуатации. В цепи с резистором ток и напряжение, как было показано ранее, находятся в фазе друг с другом. Если начальная фаза тока равна нулю, то начальная фаза напряжения на резисторе также будет равна нулю. Мгновенное значение мощности в цепи равно .
Переменный ток широко используется в промышленности. Почти вся электроэнергия вырабатывается генераторами переменного тока. Его легко преобразовать с помощью трансформаторов, он легко передается на большие расстояния по линиям электропередач, а широко используемые двигатели переменного тока проще в производстве и эксплуатации. В цепи с резистором ток и напряжение, как было показано ранее, находятся в фазе друг с другом. Если начальная фаза тока равна нулю, то начальная фаза напряжения на резисторе также будет равна нулю. Мгновенное значение мощности в цепи равно .
 Причина, которая разделяет заряды и заставляет их двигаться по замкнутому контуру, называется электродвижущей силой (ЭДС, EMF). ЭДС любого источника, в котором происходит разделение зарядов, оценивается по работе, совершаемой полем при перемещении единичного заряда от электрода с наименьшим потенциалом к электроду с большим потенциалом. Согласно определению потенциала, эта работа равна разности потенциалов разделенных зарядов, которая, как и причина, разделяющая заряды, называется электродвижущей силой.
Причина, которая разделяет заряды и заставляет их двигаться по замкнутому контуру, называется электродвижущей силой (ЭДС, EMF). ЭДС любого источника, в котором происходит разделение зарядов, оценивается по работе, совершаемой полем при перемещении единичного заряда от электрода с наименьшим потенциалом к электроду с большим потенциалом. Согласно определению потенциала, эта работа равна разности потенциалов разделенных зарядов, которая, как и причина, разделяющая заряды, называется электродвижущей силой.
 Частицы и поля – это два типа материи. Особенностью взаимодействия частиц является то, что оно происходит не при непосредственном контакте между ними, а на некотором расстоянии от них. Это происходит потому, что частицы связаны с полем, которое их окружает и вызывает взаимодействие между ними. Таким образом, частицы взаимодействуют друг с другом через свои поля. В отличие от дискретных частиц, поля распределены в пространстве непрерывно. Некоторые взаимодействия имеют двойственную природу. Например, электромагнитное поле, распространяющееся через пространство в виде волн.
Частицы и поля – это два типа материи. Особенностью взаимодействия частиц является то, что оно происходит не при непосредственном контакте между ними, а на некотором расстоянии от них. Это происходит потому, что частицы связаны с полем, которое их окружает и вызывает взаимодействие между ними. Таким образом, частицы взаимодействуют друг с другом через свои поля. В отличие от дискретных частиц, поля распределены в пространстве непрерывно. Некоторые взаимодействия имеют двойственную природу. Например, электромагнитное поле, распространяющееся через пространство в виде волн.
 Каждая батарея, в зависимости от ее типа, имеет определенные номиналы: номинальное напряжение, максимальный ток, оптимальный ток, номинальная емкость. Следует отметить, что эти значения верны только при соблюдении условий эксплуатации, рекомендованных производителем, и только для батарей, срок службы которых еще далеко не исчерпан. Иногда, однако, необходимо получить от батареи больше, чем она способна по техническим характеристикам. Поэтому для увеличения емкости необходимо увеличить рабочий ток или напряжение.
Каждая батарея, в зависимости от ее типа, имеет определенные номиналы: номинальное напряжение, максимальный ток, оптимальный ток, номинальная емкость. Следует отметить, что эти значения верны только при соблюдении условий эксплуатации, рекомендованных производителем, и только для батарей, срок службы которых еще далеко не исчерпан. Иногда, однако, необходимо получить от батареи больше, чем она способна по техническим характеристикам. Поэтому для увеличения емкости необходимо увеличить рабочий ток или напряжение.
 Физические величины могут быть определены двумя способами: одни могут быть определены только числовым значением, а другие – как числовым значением, так и направлением (положением) в пространстве. К первым относятся такие величины, как масса, температура, электрический ток, электрический заряд, работа и т.д. Эти величины называются скалярными величинами (или скалярами). Скалярная величина может быть выражена только в виде одного именованного числового значения. Вторичные величины, называемые векторными, включают длину, площадь, силу, скорость, ускорение и т.д. Длина вектора в данном масштабе равна .
Физические величины могут быть определены двумя способами: одни могут быть определены только числовым значением, а другие – как числовым значением, так и направлением (положением) в пространстве. К первым относятся такие величины, как масса, температура, электрический ток, электрический заряд, работа и т.д. Эти величины называются скалярными величинами (или скалярами). Скалярная величина может быть выражена только в виде одного именованного числового значения. Вторичные величины, называемые векторными, включают длину, площадь, силу, скорость, ускорение и т.д. Длина вектора в данном масштабе равна .
 Существует множество типов задач по расчету магнитного поля. Помимо проблем определения индуктивности цепей, работающих в магнитном поле, существуют также проблемы расчета магнитных полей в сложных ферромагнитных структурах, проблемы распределения токов в заданном объеме для получения магнитного поля заданной напряженности и т.д. Методы расчета магнитных полей можно разделить на аналитические, графические и экспериментальные. Аналитические методы используют интегрирование уравнения Пуассона (для областей, где течет ток), интегрирование уровня Лапласа.
Существует множество типов задач по расчету магнитного поля. Помимо проблем определения индуктивности цепей, работающих в магнитном поле, существуют также проблемы расчета магнитных полей в сложных ферромагнитных структурах, проблемы распределения токов в заданном объеме для получения магнитного поля заданной напряженности и т.д. Методы расчета магнитных полей можно разделить на аналитические, графические и экспериментальные. Аналитические методы используют интегрирование уравнения Пуассона (для областей, где течет ток), интегрирование уровня Лапласа.
 Для определения в определенной точке пространства вектора индукции магнитного поля B, создаваемого постоянным током I, можно использовать закон Био-Савара. Это делается путем сложения всех вкладов в магнитное поле от отдельных элементов тока. Одной из типичных задач является дальнейшее определение силы взаимодействия между двумя параллельными токами. Ведь известно, что токи генерируют собственные магнитные поля, а ток в магнитном поле (другого тока) подчиняется силе Ампера. Под действием силы Ампера противоположно направленные токи отталкиваются друг от друга.
Для определения в определенной точке пространства вектора индукции магнитного поля B, создаваемого постоянным током I, можно использовать закон Био-Савара. Это делается путем сложения всех вкладов в магнитное поле от отдельных элементов тока. Одной из типичных задач является дальнейшее определение силы взаимодействия между двумя параллельными токами. Ведь известно, что токи генерируют собственные магнитные поля, а ток в магнитном поле (другого тока) подчиняется силе Ампера. Под действием силы Ампера противоположно направленные токи отталкиваются друг от друга.
 Важность электродинамики в современном мире обусловлена главным образом техническими возможностями, которые она предоставляет для передачи электроэнергии на большие расстояния по проводам, а также способами распределения и преобразования электроэнергии в другие формы, такие как механическая, тепловая, световая и т.д. Выработанное на электростанциях электричество передается на многие километры по линиям электропередач – в дома и на промышленные предприятия, где электромагнитные силы приводят в движение двигатели различных приборов.
Важность электродинамики в современном мире обусловлена главным образом техническими возможностями, которые она предоставляет для передачи электроэнергии на большие расстояния по проводам, а также способами распределения и преобразования электроэнергии в другие формы, такие как механическая, тепловая, световая и т.д. Выработанное на электростанциях электричество передается на многие километры по линиям электропередач – в дома и на промышленные предприятия, где электромагнитные силы приводят в движение двигатели различных приборов.
 Во второй половине 19 века английский физик Джон Хопкинсон и его брат Эдвард Хопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, названную “формулой Хопкинсона” или законом Хопкинсона, которая является аналогом закона Ома (используется для расчета электрических цепей). Таким образом, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Хопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).
Во второй половине 19 века английский физик Джон Хопкинсон и его брат Эдвард Хопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, названную “формулой Хопкинсона” или законом Хопкинсона, которая является аналогом закона Ома (используется для расчета электрических цепей). Таким образом, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Хопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).
 уменьшается, поэтому магнитное поле в направлении, указанном стрелкой
уменьшается, поэтому магнитное поле в направлении, указанном стрелкой 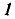 (рис. 3-36б). Электродвижущая сила, индуцированная во второй катушке, создает в ней ток
(рис. 3-36б). Электродвижущая сила, индуцированная во второй катушке, создает в ней ток 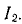


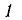 (Рисунок 3-30c) электродвижущая сила, индуцированная во второй обмотке, вызывает ток во второй обмотке. Магнитное поле второй обмотки, согласно закону Ленца, должно быть в том же направлении, что и первой обмотки Магнитное поле, которое исчезает во второй обмотке из-за ее удаления, поддерживается током, индуцированным во второй обмотке.
(Рисунок 3-30c) электродвижущая сила, индуцированная во второй обмотке, вызывает ток во второй обмотке. Магнитное поле второй обмотки, согласно закону Ленца, должно быть в том же направлении, что и первой обмотки Магнитное поле, которое исчезает во второй обмотке из-за ее удаления, поддерживается током, индуцированным во второй обмотке.
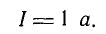
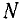 на 5 делений вправо:
на 5 делений вправо: 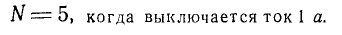
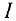 = 4 а. Однако мы изменим количество витков в маленькой катушке, оставив ее положение и размер неизменными.
= 4 а. Однако мы изменим количество витков в маленькой катушке, оставив ее положение и размер неизменными.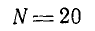 1 Включение выключателя должно сопровождаться перемещением гальванометра на 5 делений влево (см. почему). И тогда при регулировке тока игла гальванометра будет отклоняться с каждым изменением тока, потому что изменение тока сопровождается изменением магнитного поля, а значит, и изменением индукции электромагнитного тока в маленькой катушке.
1 Включение выключателя должно сопровождаться перемещением гальванометра на 5 делений влево (см. почему). И тогда при регулировке тока игла гальванометра будет отклоняться с каждым изменением тока, потому что изменение тока сопровождается изменением магнитного поля, а значит, и изменением индукции электромагнитного тока в маленькой катушке. 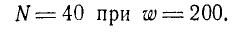 Это именно то, чего вы ожидаете. Фактически, все витки маленькой катушки находятся под воздействием одного и того же магнитного поля, и в каждом из них должна индуцироваться одна и та же ЭДС.
Это именно то, чего вы ожидаете. Фактически, все витки маленькой катушки находятся под воздействием одного и того же магнитного поля, и в каждом из них должна индуцироваться одна и та же ЭДС.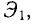 это е.ф. 100 катушек, соединенных последовательно, одна за другой, должно быть в 100 раз больше, чем
это е.ф. 100 катушек, соединенных последовательно, одна за другой, должно быть в 100 раз больше, чем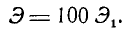 Для 200 оборотов
Для 200 оборотов 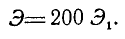 Для любого другого числа оборотов
Для любого другого числа оборотов 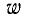
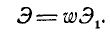


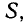 которая образует прямой угол с направлением магнитного поля. В этом случае магнитный поток равен произведению площади поверхности на индукцию или
которая образует прямой угол с направлением магнитного поля. В этом случае магнитный поток равен произведению площади поверхности на индукцию или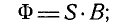 здесь S – площадь нашего квадрата, см 2 ;
здесь S – площадь нашего квадрата, см 2 ;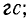
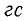 представлена линиями, проведенными с частотой две линии на 1sl 2 . Таким образом, в случае A магнитный поток на площади 2 см2 , поперечной к полю, составляет
представлена линиями, проведенными с частотой две линии на 1sl 2 . Таким образом, в случае A магнитный поток на площади 2 см2 , поперечной к полю, составляет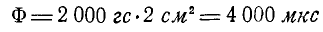
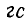 это:
это: 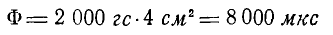

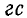 составляет всего 4 000 мкс (4 строки по 1 000 мкс каждая). Представление магнитного поля линиями очень помогает в определении потока.
составляет всего 4 000 мкс (4 строки по 1 000 мкс каждая). Представление магнитного поля линиями очень помогает в определении потока.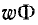 общая мощность потока в катушке. Индукционная концепция особенно удобна в использовании, когда разные потоки подключены к разным катушкам. В этом случае общая коэрцитивная сила катушки равна сумме потоков, подключенных к каждой катушке.
общая мощность потока в катушке. Индукционная концепция особенно удобна в использовании, когда разные потоки подключены к разным катушкам. В этом случае общая коэрцитивная сила катушки равна сумме потоков, подключенных к каждой катушке.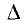 или d. Первый – это греческая буква
или d. Первый – это греческая буква 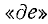 (читается как дельта), вторая – просто латинская буква d. Каждая из этих букв, будучи поставленной перед обозначением некоторого количества, выражает его изменение. Так, например, если время обозначается через t, то
(читается как дельта), вторая – просто латинская буква d. Каждая из этих букв, будучи поставленной перед обозначением некоторого количества, выражает его изменение. Так, например, если время обозначается через t, то 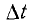 это изменение во времени или период времени. Если по
это изменение во времени или период времени. Если по 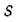 обозначает путь, тогда
обозначает путь, тогда 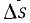 означает путь или пройденное расстояние. В этом случае соотношение
означает путь или пройденное расстояние. В этом случае соотношение 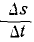 выражает скорость
выражает скорость 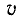
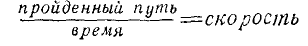
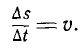
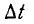 магнитный поток, подключенный к катушке, изменяется равномерно на
магнитный поток, подключенный к катушке, изменяется равномерно на 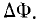 В этом случае скорость изменения потока может быть задана соотношением
В этом случае скорость изменения потока может быть задана соотношением 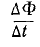 . Это отношение равно индуцированной э.д.с,
. Это отношение равно индуцированной э.д.с,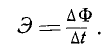
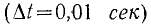 поток, запутанный в катушке, постоянно увеличиваясь, изменяется на 20 000 Максвеллов
поток, запутанный в катушке, постоянно увеличиваясь, изменяется на 20 000 Максвеллов 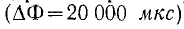 Поэтому в это время в катушке индуцировалась электродвижущая сила.
Поэтому в это время в катушке индуцировалась электродвижущая сила.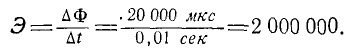
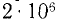 (2 миллиона) неизвестных единиц, не
(2 миллиона) неизвестных единиц, не 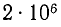 в. Эти единицы используются для выражения э.д.с. были введены около 70 лет назад одновременно с единицами Гаусса и Максвелла для магнитной индукции и магнитного потока. Физики по-прежнему часто используют эти единицы, поэтому здесь мы будем называть их физическими единицами 1 . Однако физические единицы для индукции и потока достаточно удобны, и на практике они часто используются. Напротив, физическая единица для напряжения практически неприемлема, и вместо нее была введена единица 1v, равная 100 миллионам физических единиц:
в. Эти единицы используются для выражения э.д.с. были введены около 70 лет назад одновременно с единицами Гаусса и Максвелла для магнитной индукции и магнитного потока. Физики по-прежнему часто используют эти единицы, поэтому здесь мы будем называть их физическими единицами 1 . Однако физические единицы для индукции и потока достаточно удобны, и на практике они часто используются. Напротив, физическая единица для напряжения практически неприемлема, и вместо нее была введена единица 1v, равная 100 миллионам физических единиц: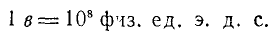 Поэтому, если мы хотим выразить, например, магнитный поток в вольтах, а магнитный поток в Максвеллах, то в формулу для ведущего закона нужно ввести множитель 10 -8, например
Поэтому, если мы хотим выразить, например, магнитный поток в вольтах, а магнитный поток в Максвеллах, то в формулу для ведущего закона нужно ввести множитель 10 -8, например 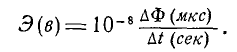
 1 Их полные названия – это единицы магнитной системы: сантиметр, грамм, секунда.
1 Их полные названия – это единицы магнитной системы: сантиметр, грамм, секунда.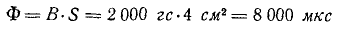
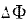 =8000 мкс (поток начал увеличиваться с нуля) и
=8000 мкс (поток начал увеличиваться с нуля) и 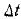 =0,05 сек. Наведенный Vs.
=0,05 сек. Наведенный Vs.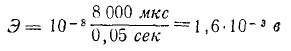 Или 1,6 мВ (милливольт).
Или 1,6 мВ (милливольт).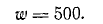 Каждая катушка соединена с магнитным потоком, который увеличивается на
Каждая катушка соединена с магнитным потоком, который увеличивается на 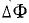 = 8.000 мкс во времени
= 8.000 мкс во времени 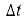 = 0,05 сек. Какова полная ЭДС, индуцированная в катушке?
= 0,05 сек. Какова полная ЭДС, индуцированная в катушке?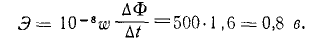
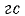 за 0,01 с времени. Какова индукция в катушке?
за 0,01 с времени. Какова индукция в катушке?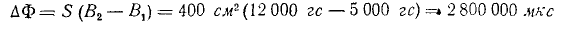
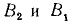 означает новое значение индукции
означает новое значение индукции 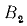 = 12000
= 12000 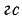 и старое значение
и старое значение 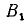 = 5 600
= 5 600 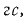 из которого начало расти поле. Индуцированные э.д.с.
из которого начало расти поле. Индуцированные э.д.с.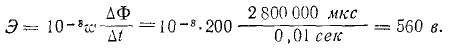
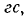 равномерно сводится к нулю за 0,1 с. Каково значение электродвижущей силы, индуцированной в катушке?
равномерно сводится к нулю за 0,1 с. Каково значение электродвижущей силы, индуцированной в катушке?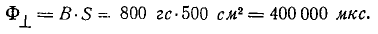
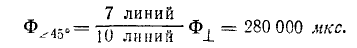
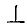 и
и 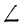 45° указывают поток в положении, перпендикулярном нити накала и под углом 45°.
45° указывают поток в положении, перпендикулярном нити накала и под углом 45°.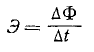 может быть выражен в вольтах, а поток в максвеллах, мы ввели множитель 10 -8 (одна сотая миллионной). Но мы могли бы поступить иначе – мы могли бы ввести новую единицу магнитного потока на 100 миллионов больше максвелла. В этом случае мы получили бы непосредственно среднеквадратичное значение в вольтах в левой части. Такую единицу удобно называть вольт-секунда*
может быть выражен в вольтах, а поток в максвеллах, мы ввели множитель 10 -8 (одна сотая миллионной). Но мы могли бы поступить иначе – мы могли бы ввести новую единицу магнитного потока на 100 миллионов больше максвелла. В этом случае мы получили бы непосредственно среднеквадратичное значение в вольтах в левой части. Такую единицу удобно называть вольт-секунда* 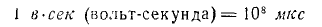
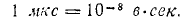
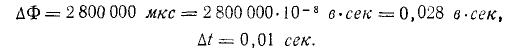
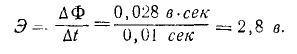
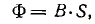

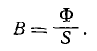 Если
Если 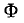 выражается в
выражается в 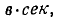 и S в см 2 , новая единица для индукции определяется как отношение единичного потока к единичной площади. Если мы определим площадь поверхности S в квадратных метрах
и S в см 2 , новая единица для индукции определяется как отношение единичного потока к единичной площади. Если мы определим площадь поверхности S в квадратных метрах 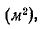 мы получаем еще одну единицу индукции:
мы получаем еще одну единицу индукции: 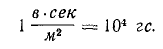


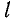 и вставляется на глубину a (рис. 3-42) область
и вставляется на глубину a (рис. 3-42) область 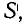 пронизанный полем:
пронизанный полем: 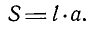 Магнитный поток, связанный с рамой
Магнитный поток, связанный с рамой 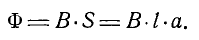 Чем глубже вставлена рамка, тем больше поток.
Чем глубже вставлена рамка, тем больше поток.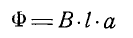 изменяется только расстояние a (глубина, на которую вставляется рамка), поэтому изменение потока
изменяется только расстояние a (глубина, на которую вставляется рамка), поэтому изменение потока 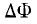 зависит от изменения этой размерности a. В течение определенного периода времени
зависит от изменения этой размерности a. В течение определенного периода времени 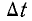 интервал времени, в течение которого эта величина увеличивается, можно определить по следующей формуле
интервал времени, в течение которого эта величина увеличивается, можно определить по следующей формуле 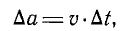 где
где 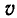 – это скорость, с которой движется кадр 1. Но если мы знаем, что изменение размера
– это скорость, с которой движется кадр 1. Но если мы знаем, что изменение размера 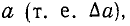 то нетрудно вычислить соответствующее изменение потока
то нетрудно вычислить соответствующее изменение потока 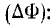
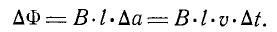 Таким образом, мы почти подошли к концу формулы для индукционного тока. Нам по-прежнему нужно определить только скорость изменения потока
Таким образом, мы почти подошли к концу формулы для индукционного тока. Нам по-прежнему нужно определить только скорость изменения потока 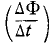 . Разделив левую и правую части последнего уравнения на
. Разделив левую и правую части последнего уравнения на 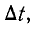 мы находим:
мы находим: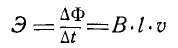 или
или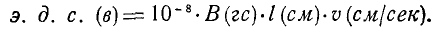 Это формула для расчета наведенной ЭДС, индуцированная в прямолинейном проводнике, движущемся в магнитном поле со скоростью
Это формула для расчета наведенной ЭДС, индуцированная в прямолинейном проводнике, движущемся в магнитном поле со скоростью 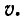
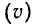 также перпендикулярно полю.
также перпендикулярно полю.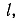 движущиеся в магнитном поле. На самом деле, если этот поперечный провод выходит за пределы поля, то при движении рамки связанный лоток достигнет своего наибольшего значения (32 линии) и не изменится. Конечно, только до тех пор, пока обратная сторона рамы не войдет в зазор между стойками. Поэтому в боковых (параллельных) проводах не индуцируется электрический ток, даже если они движутся в магнитном поле.
движущиеся в магнитном поле. На самом деле, если этот поперечный провод выходит за пределы поля, то при движении рамки связанный лоток достигнет своего наибольшего значения (32 линии) и не изменится. Конечно, только до тех пор, пока обратная сторона рамы не войдет в зазор между стойками. Поэтому в боковых (параллельных) проводах не индуцируется электрический ток, даже если они движутся в магнитном поле.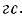 Длина провода
Длина провода 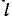 – 80 см. Скорость
– 80 см. Скорость 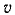 = 50 м/с (или 5 000 см/с). Найдите э.д.с., индуцированную в проводе.
= 50 м/с (или 5 000 см/с). Найдите э.д.с., индуцированную в проводе.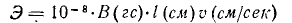 мы находим
мы находим 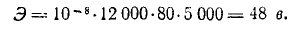
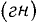 . Если M = 1
. Если M = 1 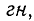 то э.д.с., индуцированная в одной цепи изменением тока в другой цепи, численно равна скорости изменения тока. Представим скорость изменения тока соотношением
то э.д.с., индуцированная в одной цепи изменением тока в другой цепи, численно равна скорости изменения тока. Представим скорость изменения тока соотношением 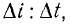 где
где 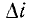 – приращение тока в интервале времени
– приращение тока в интервале времени 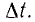
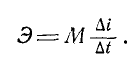 Явление взаимной индукции очень важно в современной электротехнике. Явление взаимной индукции лежит в основе работы трансформаторов.
Явление взаимной индукции очень важно в современной электротехнике. Явление взаимной индукции лежит в основе работы трансформаторов.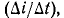 умноженное на обратную величину индуктивности M, или
умноженное на обратную величину индуктивности M, или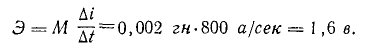
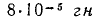 (восемьсот тысячных долей Генри). В случае короткого замыкания в линии электропередачи скорость нарастания тока
(восемьсот тысячных долей Генри). В случае короткого замыкания в линии электропередачи скорость нарастания тока 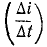 может достигать очень высокого значения
может достигать очень высокого значения 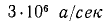 (З млн. ом в секунду). Следует отметить, что такая скорость изменения наблюдается, когда ток короткого замыкания достигает пикового значения порядка 10 000 А. За тысячную долю секунды
(З млн. ом в секунду). Следует отметить, что такая скорость изменения наблюдается, когда ток короткого замыкания достигает пикового значения порядка 10 000 А. За тысячную долю секунды 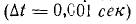 ток может увеличиться на 3 000 а
ток может увеличиться на 3 000 а 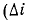 – 3000 а). Необходимо ли находить величину тока в линии в случае короткого замыкания в линии электропередачи?
– 3000 а). Необходимо ли находить величину тока в линии в случае короткого замыкания в линии электропередачи?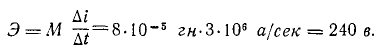 Из ответа совершенно ясно, что необходимо отделить линию связи от линии электропередачи или принять другие меры. Обратите внимание, что даже гораздо меньшая индукция э.к. мешает хорошей работе связи. Электродвижущая сила взаимной индукции возникает потому, что, как уже говорилось, изменение тока связано с изменением потока. Поэтому взаимную индуктивность M можно также рассматривать как отношение между током одного контура и потоком, связанным с другим контуром.
Из ответа совершенно ясно, что необходимо отделить линию связи от линии электропередачи или принять другие меры. Обратите внимание, что даже гораздо меньшая индукция э.к. мешает хорошей работе связи. Электродвижущая сила взаимной индукции возникает потому, что, как уже говорилось, изменение тока связано с изменением потока. Поэтому взаимную индуктивность M можно также рассматривать как отношение между током одного контура и потоком, связанным с другим контуром.
 Переменный ток – это электрический ток, направление и сила которого периодически меняются. Поскольку переменный ток обычно изменяется синусоидально, переменный ток – это синусоидальное изменение напряжения и силы тока. Поэтому все, что относится к синусоидальным электрическим колебаниям, относится к переменному току. В этой статье мы расскажем о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону.
Переменный ток – это электрический ток, направление и сила которого периодически меняются. Поскольку переменный ток обычно изменяется синусоидально, переменный ток – это синусоидальное изменение напряжения и силы тока. Поэтому все, что относится к синусоидальным электрическим колебаниям, относится к переменному току. В этой статье мы расскажем о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. Переменный ток широко используется в промышленности. Почти вся электроэнергия вырабатывается генераторами переменного тока. Его легко преобразовать с помощью трансформаторов, он легко передается на большие расстояния по линиям электропередач, а широко используемые двигатели переменного тока проще в производстве и эксплуатации. В цепи с резистором ток и напряжение, как было показано ранее, находятся в фазе друг с другом. Если начальная фаза тока равна нулю, то начальная фаза напряжения на резисторе также будет равна нулю. Мгновенное значение мощности в цепи равно .
Переменный ток широко используется в промышленности. Почти вся электроэнергия вырабатывается генераторами переменного тока. Его легко преобразовать с помощью трансформаторов, он легко передается на большие расстояния по линиям электропередач, а широко используемые двигатели переменного тока проще в производстве и эксплуатации. В цепи с резистором ток и напряжение, как было показано ранее, находятся в фазе друг с другом. Если начальная фаза тока равна нулю, то начальная фаза напряжения на резисторе также будет равна нулю. Мгновенное значение мощности в цепи равно . Причина, которая разделяет заряды и заставляет их двигаться по замкнутому контуру, называется электродвижущей силой (ЭДС, EMF). ЭДС любого источника, в котором происходит разделение зарядов, оценивается по работе, совершаемой полем при перемещении единичного заряда от электрода с наименьшим потенциалом к электроду с большим потенциалом. Согласно определению потенциала, эта работа равна разности потенциалов разделенных зарядов, которая, как и причина, разделяющая заряды, называется электродвижущей силой.
Причина, которая разделяет заряды и заставляет их двигаться по замкнутому контуру, называется электродвижущей силой (ЭДС, EMF). ЭДС любого источника, в котором происходит разделение зарядов, оценивается по работе, совершаемой полем при перемещении единичного заряда от электрода с наименьшим потенциалом к электроду с большим потенциалом. Согласно определению потенциала, эта работа равна разности потенциалов разделенных зарядов, которая, как и причина, разделяющая заряды, называется электродвижущей силой. Частицы и поля – это два типа материи. Особенностью взаимодействия частиц является то, что оно происходит не при непосредственном контакте между ними, а на некотором расстоянии от них. Это происходит потому, что частицы связаны с полем, которое их окружает и вызывает взаимодействие между ними. Таким образом, частицы взаимодействуют друг с другом через свои поля. В отличие от дискретных частиц, поля распределены в пространстве непрерывно. Некоторые взаимодействия имеют двойственную природу. Например, электромагнитное поле, распространяющееся через пространство в виде волн.
Частицы и поля – это два типа материи. Особенностью взаимодействия частиц является то, что оно происходит не при непосредственном контакте между ними, а на некотором расстоянии от них. Это происходит потому, что частицы связаны с полем, которое их окружает и вызывает взаимодействие между ними. Таким образом, частицы взаимодействуют друг с другом через свои поля. В отличие от дискретных частиц, поля распределены в пространстве непрерывно. Некоторые взаимодействия имеют двойственную природу. Например, электромагнитное поле, распространяющееся через пространство в виде волн. Каждая батарея, в зависимости от ее типа, имеет определенные номиналы: номинальное напряжение, максимальный ток, оптимальный ток, номинальная емкость. Следует отметить, что эти значения верны только при соблюдении условий эксплуатации, рекомендованных производителем, и только для батарей, срок службы которых еще далеко не исчерпан. Иногда, однако, необходимо получить от батареи больше, чем она способна по техническим характеристикам. Поэтому для увеличения емкости необходимо увеличить рабочий ток или напряжение.
Каждая батарея, в зависимости от ее типа, имеет определенные номиналы: номинальное напряжение, максимальный ток, оптимальный ток, номинальная емкость. Следует отметить, что эти значения верны только при соблюдении условий эксплуатации, рекомендованных производителем, и только для батарей, срок службы которых еще далеко не исчерпан. Иногда, однако, необходимо получить от батареи больше, чем она способна по техническим характеристикам. Поэтому для увеличения емкости необходимо увеличить рабочий ток или напряжение. Физические величины могут быть определены двумя способами: одни могут быть определены только числовым значением, а другие – как числовым значением, так и направлением (положением) в пространстве. К первым относятся такие величины, как масса, температура, электрический ток, электрический заряд, работа и т.д. Эти величины называются скалярными величинами (или скалярами). Скалярная величина может быть выражена только в виде одного именованного числового значения. Вторичные величины, называемые векторными, включают длину, площадь, силу, скорость, ускорение и т.д. Длина вектора в данном масштабе равна .
Физические величины могут быть определены двумя способами: одни могут быть определены только числовым значением, а другие – как числовым значением, так и направлением (положением) в пространстве. К первым относятся такие величины, как масса, температура, электрический ток, электрический заряд, работа и т.д. Эти величины называются скалярными величинами (или скалярами). Скалярная величина может быть выражена только в виде одного именованного числового значения. Вторичные величины, называемые векторными, включают длину, площадь, силу, скорость, ускорение и т.д. Длина вектора в данном масштабе равна . Существует множество типов задач по расчету магнитного поля. Помимо проблем определения индуктивности цепей, работающих в магнитном поле, существуют также проблемы расчета магнитных полей в сложных ферромагнитных структурах, проблемы распределения токов в заданном объеме для получения магнитного поля заданной напряженности и т.д. Методы расчета магнитных полей можно разделить на аналитические, графические и экспериментальные. Аналитические методы используют интегрирование уравнения Пуассона (для областей, где течет ток), интегрирование уровня Лапласа.
Существует множество типов задач по расчету магнитного поля. Помимо проблем определения индуктивности цепей, работающих в магнитном поле, существуют также проблемы расчета магнитных полей в сложных ферромагнитных структурах, проблемы распределения токов в заданном объеме для получения магнитного поля заданной напряженности и т.д. Методы расчета магнитных полей можно разделить на аналитические, графические и экспериментальные. Аналитические методы используют интегрирование уравнения Пуассона (для областей, где течет ток), интегрирование уровня Лапласа. Для определения в определенной точке пространства вектора индукции магнитного поля B, создаваемого постоянным током I, можно использовать закон Био-Савара. Это делается путем сложения всех вкладов в магнитное поле от отдельных элементов тока. Одной из типичных задач является дальнейшее определение силы взаимодействия между двумя параллельными токами. Ведь известно, что токи генерируют собственные магнитные поля, а ток в магнитном поле (другого тока) подчиняется силе Ампера. Под действием силы Ампера противоположно направленные токи отталкиваются друг от друга.
Для определения в определенной точке пространства вектора индукции магнитного поля B, создаваемого постоянным током I, можно использовать закон Био-Савара. Это делается путем сложения всех вкладов в магнитное поле от отдельных элементов тока. Одной из типичных задач является дальнейшее определение силы взаимодействия между двумя параллельными токами. Ведь известно, что токи генерируют собственные магнитные поля, а ток в магнитном поле (другого тока) подчиняется силе Ампера. Под действием силы Ампера противоположно направленные токи отталкиваются друг от друга. Важность электродинамики в современном мире обусловлена главным образом техническими возможностями, которые она предоставляет для передачи электроэнергии на большие расстояния по проводам, а также способами распределения и преобразования электроэнергии в другие формы, такие как механическая, тепловая, световая и т.д. Выработанное на электростанциях электричество передается на многие километры по линиям электропередач – в дома и на промышленные предприятия, где электромагнитные силы приводят в движение двигатели различных приборов.
Важность электродинамики в современном мире обусловлена главным образом техническими возможностями, которые она предоставляет для передачи электроэнергии на большие расстояния по проводам, а также способами распределения и преобразования электроэнергии в другие формы, такие как механическая, тепловая, световая и т.д. Выработанное на электростанциях электричество передается на многие километры по линиям электропередач – в дома и на промышленные предприятия, где электромагнитные силы приводят в движение двигатели различных приборов. Во второй половине 19 века английский физик Джон Хопкинсон и его брат Эдвард Хопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, названную “формулой Хопкинсона” или законом Хопкинсона, которая является аналогом закона Ома (используется для расчета электрических цепей). Таким образом, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Хопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).
Во второй половине 19 века английский физик Джон Хопкинсон и его брат Эдвард Хопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, названную “формулой Хопкинсона” или законом Хопкинсона, которая является аналогом закона Ома (используется для расчета электрических цепей). Таким образом, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Хопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).