Емкостное и индуктивное сопротивление в цепи переменного тока; Школа для электриков: Электротехника и электроника - услуги электромонтажа, строительства и ремонта

Емкостное и индуктивное сопротивления называются пассивными сопротивлениями. Энергия не тратится на реактивное сопротивление, как на активное. Энергия, запасенная в конденсаторе, периодически отдается обратно источнику, когда электрическое поле в конденсаторе исчезает.

Содержание

Емкостное и индуктивное сопротивление в цепи переменного тока

Если мы включим конденсатор в цепь постоянного тока, то обнаружим, что он имеет бесконечное сопротивление, потому что постоянный ток просто не может пройти через диэлектрик между витками, так как диэлектрик по определению не проводит постоянный ток.

Конденсатор разрывает цепь постоянного тока. Однако если тот же конденсатор включить в цепь переменного тока, мы обнаружим, что конденсатор не разрывается полностью, а попеременно заряжается и разряжается, т.е. Электрический заряд перемещается, а ток во внешней цепи поддерживается.

Исходя из теории Максвелла, в этом случае можно сказать, что переменный ток, проходящий внутри конденсатора, замыкается, за исключением того, что в данном случае это реактивный ток. Таким образом, конденсатор в цепи переменного тока действует как своего рода сопротивление конечной величины. Это сопротивление называется емкость ..

Практика давно показала, что величина переменного тока, протекающего через провод, зависит от формы провода и магнитных свойств окружающей среды. Прямой провод будет иметь наибольший ток, но если тот же провод намотать в катушку с большим количеством витков, сила тока будет меньше.

А если в ту же катушку вставить ферромагнитный сердечник, ток еще больше уменьшится. Поэтому проводник имеет не только омическое (активное) сопротивление переменному току, но и некоторое дополнительное сопротивление, которое зависит от индуктивности проводника. Это сопротивление называется индуктивное сопротивление ..

Его физический смысл заключается в том, что изменение тока в проводнике, обладающем определенной индуктивностью, вызывает в этом проводнике ЭДС самоиндукции, которая стремится предотвратить изменение тока, то есть стремится уменьшить ток. Это эквивалентно увеличению сопротивления проводника.

Емкость в цепи переменного тока

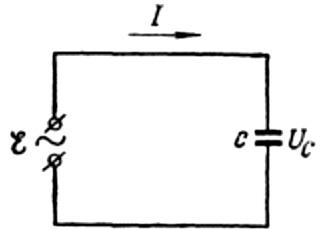
Давайте сначала подробнее рассмотрим емкостное сопротивление. Предположим, что конденсатор емкостью C подключен к источнику синусоидально переменного тока, ЭДС этого источника будет описываться следующей формулой:

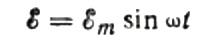
Падение напряжения на соединительных проводах будет опущено, так как оно обычно очень мало и при необходимости может быть рассмотрено отдельно. Теперь предположим, что напряжение на катушках конденсатора равно напряжению источника переменного тока. Следующий:

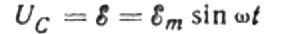
В любой момент времени заряд на конденсаторе зависит от его емкости и напряжения между его катушками. Затем, для заданного известного источника, о котором говорилось выше, мы получаем выражение для нахождения заряда на катушках конденсатора через напряжение источника:

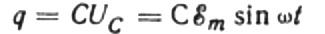
Пусть за бесконечно долгое время dt заряд на конденсаторе изменится на величину dq, тогда ток I будет равен току, который течет по проводам от источника к конденсатору:

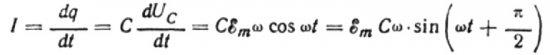
Значение амплитуды тока будет равно:

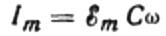
Тогда окончательное выражение для тока будет выглядеть следующим образом:

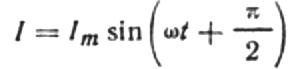
Перепишем формулу для амплитуды тока следующим образом:

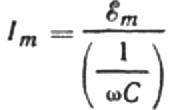
Это уравнение является законом Ома, где обратная величина угловой частоты, умноженная на емкость, играет роль сопротивления, и по сути является выражением для нахождения емкости конденсатора в цепи синусоидально переменного тока:

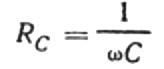
Таким образом, емкость обратно пропорциональна угловой частоте тока и емкости конденсатора. Легко понять и физический смысл этих отношений.

Чем больше емкость конденсатора в цепи переменного тока и чем чаще меняется направление тока в цепи, тем больше общий заряд, который в итоге проходит за единицу времени через поперечное сечение проводников, соединяющих конденсатор с источником переменного тока. Таким образом, ток пропорционален произведению емкости и угловой частоты.

В качестве примера рассчитаем емкость конденсатора 10 мкФ для цепи синусоидально переменного тока с частотой 50 Гц:

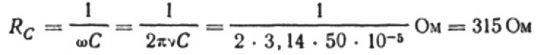
Если бы частота была 5000 Гц, тот же конденсатор представлял бы собой сопротивление около 3 Ом.

Из приведенных выше формул ясно, что ток и напряжение в цепи переменного тока с конденсатором всегда изменяются в разных фазах. Фаза тока на пи/2 (90 градусов) раньше, чем фаза напряжения. Это означает, что максимальный ток по времени всегда на четверть периода опережает максимальное напряжение. Поэтому в емкостном резисторе ток находится на четверть периода по времени или на 90 градусов по фазе перед напряжением.

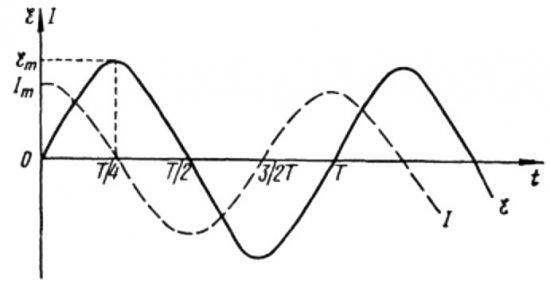
Давайте объясним физическое значение этого явления. В первый момент конденсатор полностью разряжен, поэтому малейшее приложенное к нему напряжение перемещает заряды на пластинах конденсатора, создавая ток.

По мере заряда конденсатора напряжение на его катушках увеличивается, что препятствует дальнейшему протеканию заряда, поэтому ток в цепи уменьшается независимо от дальнейшего увеличения напряжения, приложенного к катушкам.

Таким образом, если ток был максимальным в начальный момент времени, то когда напряжение достигнет максимума через четверть периода, ток вообще перестанет течь.

В начале периода ток максимален, а напряжение минимально и начинает расти, но через четверть периода напряжение достигает максимума, а ток к тому времени падает до нуля. Поэтому ток на четверть периода раньше, чем напряжение.

Индуктивное сопротивление в цепи переменного тока

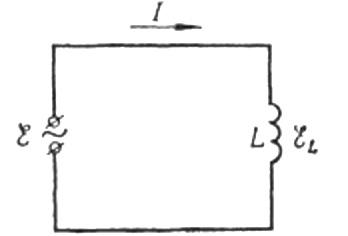
Давайте теперь вернемся к индуктивному сопротивлению. Предположим, что через катушку индуктивности протекает синусоидально переменный ток. Это можно выразить следующим образом:

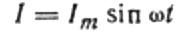
Ток вызывается изменяющимся напряжением, приложенным к катушке. Это означает, что катушка будет иметь ЭДС самоиндукции, которая выражается следующим образом:

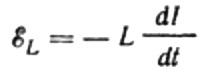
Опять же, давайте пренебрежем падением напряжения на проводах, соединяющих источник ЭДС с катушкой. Их омическое сопротивление очень мало.

Пусть изменяющееся напряжение, приложенное к катушке, в каждый момент времени полностью уравновешивается результирующей ЭДС самоиндукции, равной по величине, но противоположной по направлению:

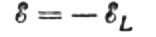
Тогда у нас есть закон обозначений:

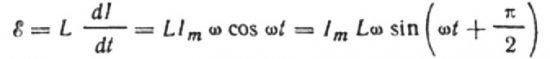
Поскольку амплитуда напряжения, приложенного к катушке, равна:

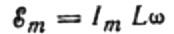
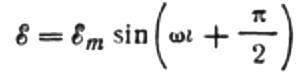
Выразим максимальный ток следующим образом:

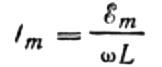
Это выражение на самом деле является законом Ома. Величина, равная произведению индуктивности на угловую частоту, здесь выступает как сопротивление и является ничем иным, как индуктивным сопротивлением катушки индуктивности:

Поэтому индуктивное сопротивление пропорционально индуктивности катушки и угловой частоте переменного тока, протекающего через катушку.

Это происходит потому, что индуктивное сопротивление обусловлено влиянием самоиндуцированного электромагнитного поля на напряжение источника – самоиндуцированное электромагнитное поле стремится уменьшить ток и тем самым вносит сопротивление в цепь. Известно, что величина ЭДС самоиндукции пропорциональна индуктивности катушки и скорости изменения протекающего через нее тока.

В качестве примера рассчитаем индуктивное сопротивление катушки с индуктивностью 1 Гн, включенной в цепь с частотой тока 50 Гц:

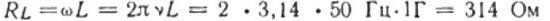
Если бы частота была 5000 Гц, то сопротивление той же катушки было бы около 31400 Ом. Напомним, что омическое сопротивление провода катушки обычно указывается в единицах Ом.

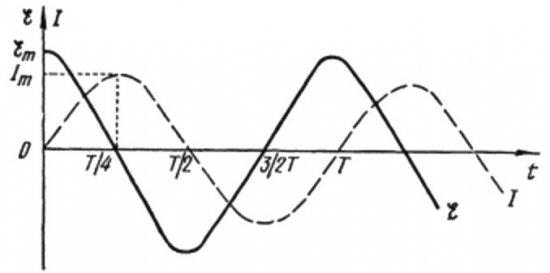
Из приведенных формул видно, что изменения тока и напряжения в катушке происходят в разных фазах, причем фаза тока всегда меньше фазы напряжения на pi/2. Поэтому максимум тока наступает на четверть периода позже, чем максимум напряжения.

В индуктивном резисторе ток отстает от напряжения на 90 градусов из-за тормозящего эффекта ЭДС самоиндукции, которая препятствует изменению тока (как увеличению, так и уменьшению), поэтому максимальный ток в цепи катушки наступает позже, чем максимальное напряжение.

Катушка и конденсатор работают вместе

Когда индуктор и конденсатор соединены последовательно в цепи переменного тока, напряжение на индукторе будет превышать напряжение на конденсаторе на половину периода, т.е. 180 градусов по фазе.

Емкостное и индуктивное сопротивления называются пассивными сопротивлениями. В реактивном сопротивлении энергия расходуется не так, как в активном. Энергия, запасенная в конденсаторе, периодически отдается обратно источнику, когда электрическое поле в конденсаторе исчезает.

То же самое справедливо и для катушки: пока магнитное поле катушки создается током, энергия накапливается в катушке в течение четверти периода, а затем возвращается к источнику в течение следующей четверти периода. В этой статье мы рассматриваем синусоидально переменный ток, для которого эти положения строго соблюдаются.

В цепях синусоидального переменного тока для ограничения тока традиционно используются индукционные катушки с сердечниками, называемые дросселями. Их преимущество перед реостатами заключается в том, что энергия не рассеивается в больших количествах в виде тепла.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это поможет нашему сайту сильно вырасти!

C – размер конденсатора в фарадах.

От чего зависит сопротивление конденсаторов в цепях переменного тока?

Его величина зависит не только от емкостных характеристик последнего, но и от частотной характеристики электрического тока, протекающего по цепи. Когда мы говорим о сопротивлении резистора, мы имеем в виду параметры самого резистора, например, материал, форму, но нет абсолютно никакой связи между его сопротивлением и электрической частотой цепи (мы говорим об идеальном резисторе, который не характеризуется паразитными параметрами). Когда мы говорим об устройстве для хранения энергии и зарядки электрическим полем – все по-другому. Конденсатор с одинаковой емкостью имеет разный уровень сопротивления при разных частотах тока. Амплитуда тока, протекающего через него при постоянной амплитуде напряжения, имеет другое значение.

Расчет Xc

Какие выводы можно сделать из этой формулы для сопротивления конденсатора в цепи переменного тока? По мере увеличения частоты сигнала электрическое сопротивление конденсатора уменьшается.

По мере увеличения емкости накопителя заряда энергия электрического поля Xc переменного электричества, протекающего через него, будет иметь тенденцию к уменьшению.

График, представляющий величину этого конденсатора при непостоянном токе в цепи, имеет форму гиперболы

По мере приближения значений частоты к нулю на оси (когда переменный ток становится похожим по своим параметрам на постоянный), это сопровождается увеличением Xc конденсатора до бесконечных значений. Это действительно так: известно, что конденсатор в сети постоянного тока на самом деле является разомкнутой цепью. Фактическое электрическое сопротивление, конечно, не бесконечно; оно ограничено коэффициентом утечки конденсатора. Однако его ценности остаются на высоком уровне, который нельзя игнорировать.

При увеличении числа частот до бесконечных значений емкость электрического конденсатора стремится к нулю. Это характеризует идеальные модели. В реальной жизни конденсатор обладает неприятными свойствами (такими как индуктивность и сопротивление утечки), поэтому емкость уменьшается до определенных значений, а затем увеличивается.

Пожалуйста, обратите внимание! Когда конденсатор подключен к переменной электрической цепи, его энергия не расходуется, поскольку фазовые характеристики напряжения и тока сдвинуты на 90° относительно друг друга. В течение одной четверти периода конденсатор заряжен (энергия накапливается в его электрическом поле), в течение следующего он разряжен, энергия отдается обратно в цепь. Его электрическое сопротивление без ваты, реактивное.

В этом случае сопротивление конденсатора в цепи переменного тока составляет 96,5 кОм. Если мы запишем все расчеты, то получим следующие результаты.

Векторное представление емкости

Для простого понимания процессов, происходящих в конденсаторе под воздействием источника переменного тока, удобно использовать векторное представление емкости.

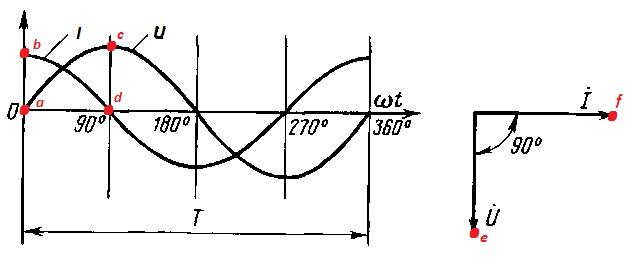
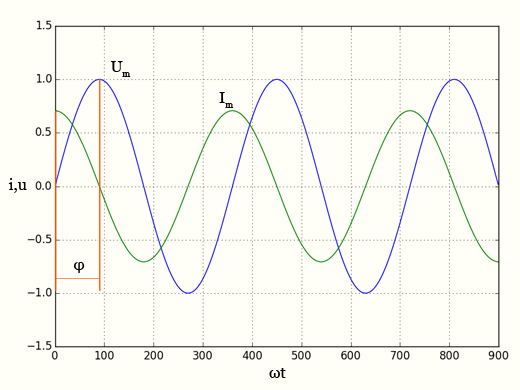
В начальный момент зарядки конденсатора потенциал U на его катушках равен нулю (точка a). В то же время ток I имеет максимальное значение (точка b). В этот момент уже заметна задержка. Ток начинает уменьшаться от своего пикового значения (точка bd). Напряжение в этой точке еще не увеличилось и только приближается к своему максимальному значению (ac).

То же самое отражено на диаграмме справа. В точке, где напряжение U имеет наименьшее значение (e), ток I только начал переходить в отрицательную область (f).

Таким образом, в конце второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет своего наибольшего, амплитудного значения.

Емкость конденсатора

Мы уже видели, что ток в цепи с конденсатором может течь только при изменении приложенного к нему напряжения, и ток, протекающий через цепь при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.

Конденсатор в цепи переменного тока влияет на ток, протекающий через цепь, то есть ведет себя как сопротивление. Чем выше емкость и чем выше частота переменного тока, тем меньше значение емкостного сопротивления. И наоборот, сопротивление конденсатора для переменного тока увеличивается с уменьшением емкости и снижением частоты.

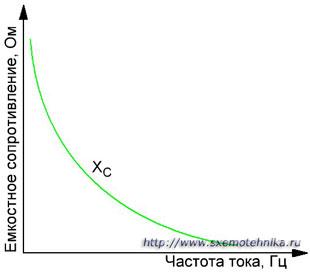
Рисунок 2. Зависимость емкости конденсатора от частоты.

Для постоянного тока, т.е. когда его частота равна нулю, емкостное сопротивление бесконечно велико; поэтому постоянный ток не может протекать через цепь с емкостью.

Значение емкости определяется по следующей формуле:

где Xc – емкость конденсатора в Ом;

f – частота переменного тока в гц;

ω – угловая частота переменного тока;

C – емкость конденсатора в ф.

Когда конденсатор подключен к цепи переменного тока, в нем не расходуется энергия, как в индуктивности, поскольку фазы тока и напряжения смещены на 90° относительно друг друга. Энергия накапливается в электрическом поле конденсатора в течение одной четверти периода – когда конденсатор заряжается – и в течение другой четверти периода – когда конденсатор разряжается – она высвобождается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.

Следует отметить, однако, что практически в каждом конденсаторе, когда через него проходит переменный ток, потребляется больше или меньше активной мощности из-за изменений в диэлектрическом состоянии конденсатора. Кроме того, между пластинами конденсатора никогда не бывает абсолютно идеальной изоляции; утечки в изоляции между пластинами приводят к тому, что конденсатор подключается параллельно с каким-либо активным сопротивлением, через которое протекает ток, и, следовательно, потребляется некоторая мощность. В обоих случаях мощность бесполезно расходуется на нагрев диэлектрика и поэтому называется мощностью потерь.

Потери из-за изменения состояния диэлектрика называются диэлектрическими потерями, а потери из-за несовершенства изоляции между пластинами – потерями утечки.

Ранее мы сравнивали электрическую емкость с емкостью герметично закрытого сосуда или с площадью дна открытого сосуда с вертикальными стенками.

Конденсатор в цепи переменного тока можно сравнить с упругостью пружины. Чтобы избежать возможного недопонимания, под упругостью следует понимать не эластичность (“твердость”) пружины, а ее противоположность, “мягкость” или “податливость” пружины.

Представьте себе, что мы периодически сжимаем и растягиваем свернутую пружину, которая одним концом плотно прикреплена к стене. Время, которое нам потребуется для завершения полного цикла сжатия и растяжения пружины, будет соответствовать периоду переменного тока.

Таким образом, мы сожмем пружину в первом квартале периода, отпустим ее во втором квартале периода, растянем в третьем квартале периода и снова отпустим в четвертом квартале периода.

Кроме того, предположим, что наши усилия в течение периода будут неравномерными, а именно, они будут увеличиваться от нуля до максимума в первом и третьем кварталах периода и уменьшаться от максимума до нуля во втором и четвертом кварталах периода.

Сжимая и растягивая пружину таким образом, вы заметите, что в начале первой четверти периода свободный конец пружины будет двигаться довольно быстро при относительно небольшом усилии с нашей стороны.

В конце первой четверти периода (когда пружина сжата), наоборот, несмотря на увеличение силы, неприкрепленный конец пружины будет двигаться очень медленно.

Во второй четверти периода, когда мы постепенно уменьшаем давление на пружину, свободный конец пружины будет отходить от стены в нашу сторону, несмотря на то, что наши сдерживающие силы направлены в сторону стены. В этом случае наши силы в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины – наименьшей. В конце второй четверти периода, когда наши силы будут наименьшими, скорость пружины будет наибольшей, и так далее.

Продолжая аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и строя графики (рис. 1, б) изменения нашей силы и скорости движения незакрепленного конца пружины, мы увидим, что эти графики точно соответствуют графикам ЭДС и тока емкостной цепи (рис. 1, а), график силы будет соответствовать графику ЭДС, а график скорости – графику тока.

Рисунок 3. (a) Процессы, происходящие в цепи переменного тока с конденсатором и (b) Сравнение между конденсатором и пружиной.

Легко видеть, что пружина, как и конденсатор, накапливает энергию за одну четверть периода и отдает ее за другую четверть периода.

Также очевидно, что чем менее упругой является пружина, тем более упругой она является и тем большую силу она будет оказывать на нас. То же самое верно и для электрической цепи: чем меньше емкость, тем больше сопротивление цепи на данной частоте.

Наконец, чем медленнее мы сжимаем и растягиваем пружину, тем меньше скорость движения ее свободного конца. Аналогично, чем ниже частота, тем меньше ток при данной ЭДС.

При постоянном давлении пружина будет только сжиматься и тем самым останавливать свое движение, так же как при постоянной ЭДС конденсатор будет только заряжаться и тем самым останавливать дальнейшее движение электронов в цепи.

Теперь вы можете увидеть, как ведет себя конденсатор в цепи переменного тока на видео ниже:

ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Если R = 0, то напряжение на конденсаторе равно приложенному напряжению и u = q/C. Мгновенное значение тока задается выражением:

Емкость

Конденсатор с емкостью C имеет бесконечное сопротивление в цепи постоянного тока. Однако если к конденсатору приложить переменное напряжение, он будет периодически заряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает своего максимального значения в те моменты, когда ток равен нулю.

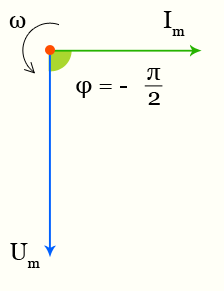
Между напряжением и током существует разность фаз -π/2.

В чисто емкостной цепи переменного тока ток превышает напряжение на π/2 (или T/4).

Из приведенного выше уравнения следует, что амплитуда тока I_m = ωCU_m. Сравнение с законом Ома U = RI показывает, что 1/ωC действует как сопротивление.

Цепь переменного тока, содержащая емкость C, имеет сопротивление переменному току; это называется емкость Х_C.

Единица СИ для емкостного сопротивления: [X_C] = Ом.

Х_C	емкость цепи переменного тока,	Ом
ω = 2πf	круговая частота переменного тока,	радиан/секунда
C	емкость,	Фарад

С увеличением частоты емкость уменьшается. Для постоянного тока (f = 0) она бесконечно велика.

Ток в цепи с одной только емкостью дается выражением

После этого можно легко определить значение емкости или реактивного сопротивления конденсатора: xc = 1/2π x f x C = 1/ ω x C. Этот показатель рассчитывается, когда конденсатор подключен к цепи переменного тока. Поэтому, согласно закону Ома, в цепи переменного тока с подключенным конденсатором значение тока будет следующим: I = U/xc, а напряжение на катушках составит: Uc = Ic x xc.

Емкость в цепи переменного тока

Когда конденсатор подключается к цепи постоянного тока, через него в течение короткого периода времени протекает зарядный ток. После завершения зарядки, когда напряжение конденсатора совпадет с напряжением источника тока, протекание тока в цепи на короткое время прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет представлять собой своего рода разомкнутую цепь или сопротивление бесконечной величины. При переменном токе конденсатор будет вести себя совсем по-другому. В такой цепи он будет заряжаться в переменном направлении. Протекание переменного тока в цепи не прерывается в этой точке.

Более внимательное рассмотрение этого процесса показывает, что в момент включения конденсатор имеет нулевое напряжение. При подаче напряжения сети переменного тока начинается зарядка. В это время напряжение в сети будет расти в течение первой четверти этого периода. По мере накопления заряда на катушках напряжение самого конденсатора будет увеличиваться. Когда напряжение в сети достигнет максимума в конце первого квартала, зарядка закончится, и ток в цепи будет равен нулю.

Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q – количество электроэнергии, протекающей через цепь в момент времени t. Согласно законам электростатики, количество электричества в приборе составит: q = C x Uc = C x U. В этой формуле C – емкость конденсатора, U – напряжение сети, а Uc – напряжение на катушках элемента. Окончательная формула для тока в цепи будет такой: i = C x (∆Uc/∆t) = C x (∆U/∆t).

В начале второго квартала напряжение в сети упадет, и конденсатор начнет разряжаться. Ток в цепи изменит направление и потечет в противоположном направлении. В следующем полупериоде напряжение сети изменит направление, ячейка зарядится, а затем снова начнет разряжаться. Ток, присутствующий в цепи конденсатора, будет опережать напряжение на катушках на 90 градусов.

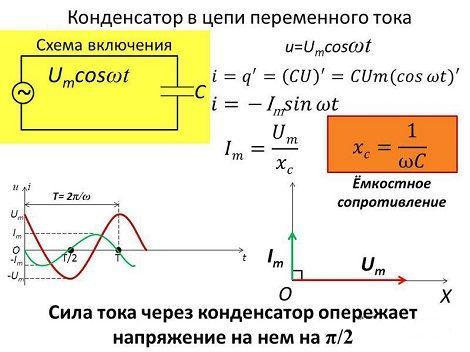
Установлено, что ток конденсатора изменяется со скоростью, пропорциональной угловой частоте ω. Поэтому, согласно уже известной формуле для тока в цепи i = C x (∆U/∆t), по аналогии получается, что среднеквадратичное значение тока также является пропорциональной зависимостью между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.

Часть сетевого напряжения, падающая на конденсатор, называется емкостным падением напряжения. Она также известна как реактивная составляющая напряжения, обозначаемая символом Uc. Значение емкости xc и значение индуктивного сопротивления xi напрямую зависят от частоты переменного тока.

Читайте далее: