Формула частоты в физике

Формулы (4) – (6) являются приближенными. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, рассчитанное с их помощью.

С помощью частоты характеризуются колебания. В данном случае частота – это физическая величина, обратная периоду колебаний $(T).

Частота в данном случае – это количество полных колебаний ($N$), происходящих в единицу времени:

где $Delta t$ – время, за которое происходит $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная величина секунды:

Герц – это единица частоты периодического процесса, при котором один цикл процесса происходит за время, равное одной секунде. Единица частоты периодического процесса названа в честь немецкого ученого Г. Герца.

Частота грохота, возникающего при двух колебаниях, происходящих вдоль одной линии с разными, но одинаковыми частотами ($_1$ i $_2$) равна:

Другой величиной, характеризующей колебательный процесс, является циклическая частота ($_0$), связанная с частотой как:

Циклическая частота измеряется в радианах, деленных на секунду:

Частота колебаний тела массой $ m,$, подвешенного на пружине с коэффициентом упругости $k$, равна:

Формула (4) верна для упругих малых колебаний. Кроме того, масса пружины должна быть мала по сравнению с массой тела, прикрепленного к пружине.

Для математического маятника частота колебаний рассчитывается как: длина струны:

где $g$ – ускорение свободного падения; $l$ – длина струны (длина подвеса) маятника.

Физический маятник колеблется с частотой:

где $J$ – момент инерции колеблющегося тела вокруг оси; $d$ – расстояние центра масс маятника от оси колебаний.

Уравнения (4) – (6) являются приближенными. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, рассчитанное с их помощью.

Однако, как показывает практика, не всегда удобно делить единицу на число, что может быть довольно хлопотно, а параллельно еще – манипулировать нулями при переводе значений из одних единиц в другие. Итак, давайте дополним то, что мы узнали, с помощью простых онлайн-калькуляторов.

Как связаны частота и период?

Частота (F) в физическом смысле слова – это характеристика, равная количеству повторений периодического процесса (в нашем случае вибрации) в единицу времени.
Частота рассчитывается как отношение числа колебаний (повторений) к периоду времени, в течение которого они происходят.

Период колебаний (T) – период времени, в течение которого совершается 1 полное колебание.

Формула, связывающая эти параметры, чрезвычайно проста и в системе СИ выглядит следующим образом:
F_(Гц) = 1/T_(с) и соответственно: T_(с) = 1/F_(Гц)

Однако практика показывает, что не всегда удобно делить единицу на число, что может быть довольно громоздко, а также параллельно манипулировать нулями при переводе значений из одних единиц в другие. Поэтому давайте оживим ситуацию с помощью простых онлайн-калькуляторов.

ОНЛАЙН-КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ

А теперь все то же самое, но в обратном порядке:

ОНЛАЙН-КАЛЬКУЛЯТОР ЧАСТОТЫ ДЛЯ РАСЧЕТА ПЕРИОДА КОЛЕБАНИЙ

В некоторых прикладных электрических расчетах (для простоты) используется дополнительная величина – циклическая частота (круговая, радиальная, угловая), обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а ее числовое значение равно: ω _(рад/с) = 2πF_(Гц) .

Синусоидальные волны имеют разные частоты. Более низкие имеют более высокие частоты, а горизонтальная ось представляет собой время.

Частота периодического движения лучше всего представлена угловой частотой – ω. Он относится к угловому смещению в единицу времени или скорости изменения состояния синусоидальной формы волны. В виде формулы:

Колеса, вращающиеся с частотой Механическая связь позволяет линейным колебаниям поршней паровой машины приводить в движение колеса.

Частота и циклическая частота связаны формулой:

Примеры решения проблем

Заказ	Определите частоту колебаний железнодорожного вагона, если период его вертикальных колебаний равен 0,5 с.
Решение	Частота колебаний является обратной величиной периода:

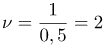Гц

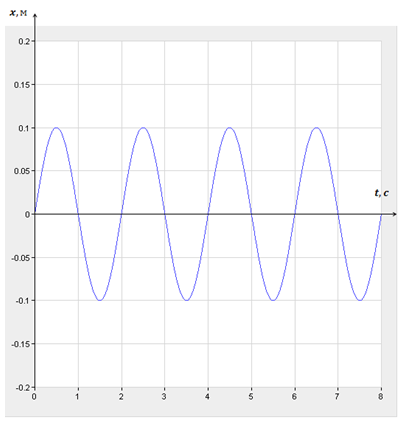
Задача	Маятник колеблется 9 раз за 18 секунд. Определите период и частоту колебаний. Напишите уравнение гармонического колебания и постройте график колебаний маятника, если амплитуда равна 10 см.
Решение	Частота колебаний задается формулой:

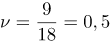Гц

В данном случае:

Назначение	Период колебаний крыльев шмеля составляет 5 мс, а частота колебаний крыльев комара – 600 Гц. Найдите количество взмахов крыльями, сделанных насекомым за одну минуту, и на сколько больше.
Решение	Определим частоту колебаний крыльев шмеля:

С другой стороны, частота:

Приравнивая правые части уравнений, получаем количество закрылков крыла шмеля во времени :

Количество взмахов крыльями, которые комар сделает за определенное время находим непосредственно из формулы:

Переведем единицы измерения в систему СИ: мс min .

Амплитуда кинетической энергии маятника составляет EKmax = $frac <2>Pot A^2 ¯omega^2$ , где

17 Механика Читать 0 мин.

Качели – это процесс, в ходе которого состояние системы изменяется, повторяясь во времени и перемещаясь в ту или иную сторону от равновесного состояния.

Период – это время, в течение которого состояние системы повторяется, т.е. система совершает одно полное колебание. Период выражается в секундах.

Частота – обратная величина периода: количество полных колебаний в единицу времени. Частота измеряется в герцах (Гц).Гц] = [c-1]. Частота равна v = $frac<1>$ , где

Если известно, что организм производит N вибрации во время tтогда частота его колебаний может быть определена как v = $frac$ , где

N – число колебаний;

Для описания колебательных систем, реализующих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят в течение 2π секунд и равна ω = 2πvили ω = $frac<2$ , где

ω – циклическая частота [рад/с];

Гармонические колебания – колебания, при которых физические величины изменяются по закону синусов или косинусов. Кинематическое уравнение для гармонических колебаний выглядит следующим образом:

ω – циклическая частота [рад/с];

φ0 – начальная фаза колебаний, [rad];

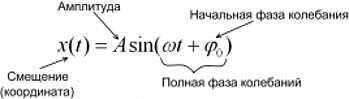
Смещение (x) – это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать его от положения равновесия.

Амплитуда колебаний (A) – это максимальное отклонение колеблющейся величины от положения равновесия, т.е. максимальное смещение равно амплитуде колебаний xmax = A.

Начальная фаза колебания (φ0) определяет смещение в начальный момент времени, выраженное в радианах.

Фаза колебаний (φ) или полная фаза колебания, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебания равна φ = ωt + φ0, где

φ – полная фаза колебаний [rad];

φ0 – начальная фаза колебаний, [rad];

ω – циклическая частота [рад/с];

Пример анализа гармонического колебания точки

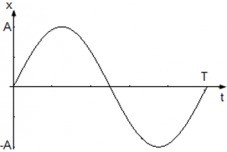
Рассмотрим гармоническое колебание, в котором уравнение движения точки имеет вид x(t) = Asin(ωt), где

ω – циклическая частота [рад/с].

Из уравнения x(t) = Asin(ωt) следует, что нет начального смещения (φ0 = 0) и колебания начинаются из положения равновесия. Смена x достигает своего максимального значения xmax и равна амплитуде xmax = Aв момент, когда модуль синусоидальной волны равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний составляет φ = $frac <2>+2pi n$, когда x = –A фаза колебаний принимает значения φ = $frac<3pi> <2>+2pi n$ , где n = 0, 1 , 2, … N.

График колебаний координат точки имеет вид:

Определите уравнение и график колебания скорости. Скорость – производная по времени от координаты: v = xt‘, где

v – скорость точки [м/с];

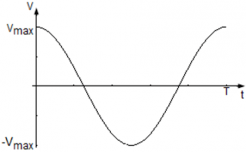
Поскольку мы знаем закон изменения координат x(t) = Asin(ωt), скорость колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).

Уравнение для скорости точки имеет вид v(t) = Acos(ωt), где

v – скорость точки [м/с];

ω – циклическая частота [рад/с];

Сравнительное уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко видеть, что Aω – амплитуда изменения скорости, и ωt – фаза колебания скорости. Таким образом, максимальное значение скорости составляет vmax = Aωи достигается при | cos(ωt) | = 1, т.е. когда фаза скорости составляет φ = πnгде n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

Таким же образом определяются уравнение и график колебания ускорения точки, движущейся по гармоническому закону.

Ускорение – производная скорости по времени: a = vt‘, где

a – ускорение движения точки [м/с2];

v – скорость точки [м/с];

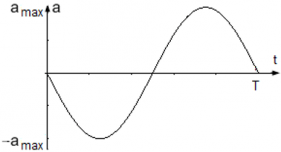
Поскольку закон изменения скорости определен выше v(t) = Aωcos(ωt), определите ускорение колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).

Уравнение ускорения точки имеет вид a(t) = –Aω2sin(ωt), где

a – ускорение точки [м/с2];

ω – циклическая частота [рад/с];

Модуль ускорения точки максимален, когда |sin(ωt)| = 1 – в тот самый момент, когда смещение точки достигает максимума. Максимальное ускорение, т.е. амплитуда ускорения точки составляет amax = Aω .2.

Диаграмма колебательного ускорения точки выглядит следующим образом:

При гармонических колебаниях энергетические формы колебательной системы постоянно находятся в процессе взаимного преобразования. В механической колебательной системе происходит преобразование механической энергии: потенциальной энергии в кинетическую, а затем кинетической энергии в потенциальную. Полная механическая энергия колебательной системы постоянна, и закон сохранения энергии действует в любое время. E = EP + EKгде

E – полная механическая энергия системы, E = const, [J];

EP – потенциальная энергия системы, изменяющаяся со временем, [J];

EK – кинетическая энергия системы, изменяющаяся со временем, [J].

Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется в соответствии с гармоническим уравнением x(t) = Asin(ωt).

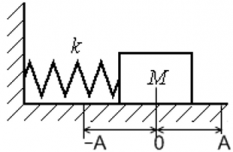
Потенциальная энергия деформированной пружины равна EP = $frac<kx^2><2>$ , где

EP – потенциальная энергия деформированной пружины, [Джоули];

k – коэффициент упругости пружины [Н/м];

x – Прогиб пружины (степень растяжения или сжатия) [м].

В случае пружинного маятника натяжение пружины является переменной величиной, зависящей от времени. Кинематическое уравнение движения для точки, принадлежащей этому маятнику, имеет вид x(t) = Asin(ωt). Поэтому потенциальная энергия пружинного маятника может быть записана как EP = $frac<k(x(t))^2><2> $ = $frac<k(asin(omega t))^2=””><2> $ = $frac <2> ^2 ^sin^2 (^omega t)$ .

Уравнение потенциальной энергии пружинного маятника EP = $frac <2>cdot A^2 ^sin^2 (^omega t)$ , где

EP – потенциальная энергия пружинного маятника, [J];

k – коэффициент упругости пружины [Н/м];

ω – циклическая частота [рад/с];

Амплитуда потенциальной энергии пружинного маятника составляет EPmax = $frac<2>A^2$ , где

EPmax – максимальная потенциальная энергия пружинного маятника, [J];

k – коэффициент упругости пружины [Н/м];

Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0, когда маятник проходит через положение равновесия, и достигает максимума, когда sin(ωt) = 1 – когда маятник находится в крайних положениях, т.е. когда его смещение равно его амплитуде.

График колебательной потенциальной энергии пружинного маятника:

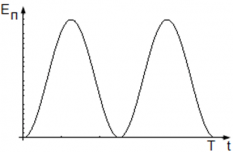
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eq = $frac<mv^2><2>$ , где

Eq – кинетическая энергия тела, [Джоули];

v – скорость движения тела, [м/с].

В теле, которое колеблется, скорость является переменной величиной.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), уравнение для скорости точки v(t) = Aωcos(ωt). Следовательно, кинетическая энергия маятника равна Eq = $frac<m(v(t))^2><2> $ = $frac <2>cdot (Aomega cos(™omega t))^2$ = $frac <2> ^2 ^cdot A^2 ^cos^2 (^omega t)$ .

Уравнение кинетической энергии маятника Eq = $frac <2>cdot A^2 ^cos^2 (^omega t)$ , где

Eq – кинетическая энергия маятника, [J];

ω – циклическая частота [рад/с];

Амплитуда кинетической энергии маятника составляет EKmax = $frac <2>Pot A^2 $ , где

EKmax – максимальная кинетическая энергия маятника, [J];

ω – циклическая частота [рад/с].

Максимальная кинетическая энергия маятника достигается, когда cos2(ωt) = 1 – маятник проходит через положение равновесия и равен нулю, когда маятник находится в крайнем положении.

Диаграмма колебательной кинетической энергии маятника:

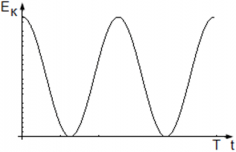
Математический маятник – Математический маятник – это колебательная система, состоящая из материальной точки, подвешенной на разматывающейся струне или стержне.

Период колебаний математического маятника равен T = $2 ∆sqrt<frac>$ , где

l – длина нити математического маятника [м];

g – ускорение свободного падения [м/с2].

Период колебаний пружинного маятника равен T = $2 и 2qrt<frac>$ , где

Существует особый тип осцилляции вынужденные колебания. Вынужденные колебания возникают только при постоянном периодическом внешнем воздействии, и их характеристики зависят от характеристик этого воздействия.

Если частота внешней силы, вызывающей вынужденное колебание, совпадает с собственной внутренней частотой колебательной системы – возникает явление резонанса. При наступлении резонанса амплитуда колебаний системы быстро увеличивается. Частота, при которой происходит явление резонанса, называется резонансной частотой.

На графике показана кривая резонанса – увеличение амплитуды, когда частота внешнего взаимодействия совпадает с внутренней частотой системы.

Где:

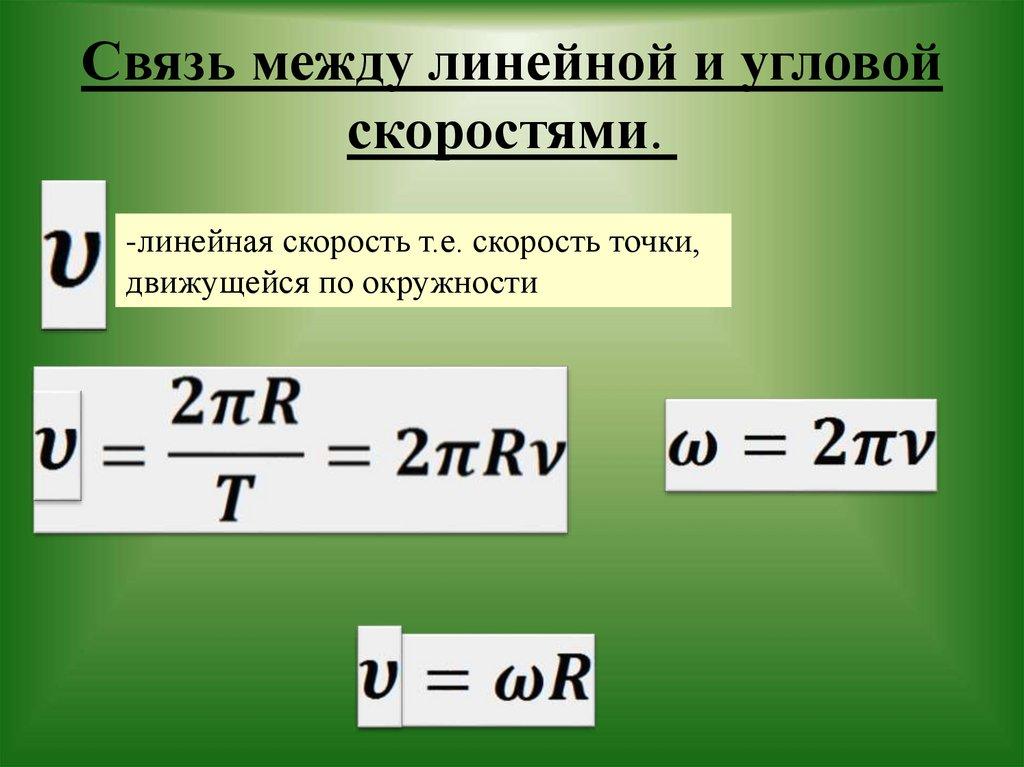
Переход от угловой скорости к линейной скорости

Существует разница между линейной скоростью точки и угловой скоростью. Сравнивая значения в выражениях, описывающих принципы вращения, можно увидеть сходство между этими двумя понятиями. Любая точка B, принадлежащая окружности радиуса R, проходит расстояние, равное 2*π*R. Таким образом, он совершает одну революцию. Учитывая, что время, необходимое для этого, составляет период T, модульное значение линейной скорости точки B определяется следующим образом:

ν = 2*π*R / T = 2*π*R* ν.

Поскольку ω = 2*π*ν, то получается, что:

Следовательно, линейная скорость точки B тем больше, чем дальше от центра вращения она находится.

В качестве напоминания. Если в качестве такой точки рассматривать города на широте Санкт-Петербурга, то их линейная скорость относительно земной оси составляет 233 м/с. Для объектов на экваторе она составляет 465 м/с.

Численное значение вектора ускорения точки B, движущейся равномерно, выражается формулой R и угловую скорость, таким образом:

a = ν2/ R, подставляя сюда ν = ω* R, получаем: a = ν2/ R = ω2* R.

Это означает, что чем больше радиус окружности, по которой движется точка B, тем больше значение ее ускорения по модулю. Чем дальше точка твердого тела находится от оси вращения, тем больше ее ускорение.

Это позволяет вычислить ускорения, модули скорости необходимых точек тела и их положения в любой момент времени.

Понимание и умение пользоваться расчетами и не путать определения поможет на практике вычислять линейные и угловые скорости, а также свободно переходить от одной величины к другой в расчетах.

</m(v(t))^2></mv^2></k(asin(omega></k(x(t))^2></kx^2>

Читайте далее:

• Механические колебания и волны; FIZI4KA.
• Затухающие колебания – это. Что такое затухающие колебания?.
• Значение слова "амплитуда" в 11 словарях.
• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• Начальная фаза колебаний, теория и онлайн-калькуляторы.
• Шаговые двигатели: свойства и практические схемы управления. Часть 2.
• Принцип работы колебательного контура.