В случае препятствия эквивалентного заряда при параллельном соединении его можно определить на основе закона Ома с преобразованием расчетной формулы. Поэтому необходимые расчеты могут быть проведены по следующей формуле: R – R / N-R = R / N.
В физике не существует точного термина. Оно может быть выведено из ряда других терминов и из формулировки закона Ома. Из этого следует, что эквивалентное сопротивление резистора является полным барьером для сменных реактивных элементов в электрической сети, чтобы позволить заряду пройти в проводник.

Сопротивление резисторов
Для справки. Одно число дает выходное значение удельного сопротивления, на которое не влияет ряд внешних факторов.

Подробное объяснение эквивалентного сопротивленияВозьмем пример двух резисторов, соединенных параллельно. Ток, протекающий через каждый резистор (I1 и I2), будет разным, потому что сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, входящий в цепь в точке “А”, должен выйти из нее в точке “В”.
Параллельное соединение резисторов. Калькулятор
Параллельное соединение резисторов – Один из двух типов электрического соединения, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Резисторы часто соединяют последовательно или параллельно для создания более сложных электронных схем.
Схема параллельного соединения резисторов показана на рисунке ниже. Если резисторы соединены параллельно, напряжение на всех резисторах будет одинаковым, а ток, протекающий через них, будет пропорционален их сопротивлению:
Формула для параллельного соединения резисторов
Общее сопротивление нескольких резисторов, соединенных параллельно, определяется по следующей формуле:
Ток, протекающий через один резистор, согласно закону Ома, можно найти по формуле:
Пример 1
При проектировании устройства возникла необходимость установки резистора с сопротивлением 8 Ом. Если вы проверите весь диапазон стандартных резисторов, то обнаружите, что резистор 8 Ом не входит в этот диапазон.
Выходом из этой ситуации является использование двух резисторов, соединенных параллельно. Значение эквивалентного сопротивления для двух параллельно соединенных резисторов рассчитывается следующим образом:
Из этого уравнения следует, что если R1 равно R2, то сопротивление R равно половине сопротивления одного из двух резисторов. Если R = 8 Ом, то R1 и R2 должны быть 2 × 8 = 16 Ом. Теперь проведите тест, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета 2
Найдите общее сопротивление R трех резисторов, соединенных параллельно:
Полное сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использован для расчета любого количества отдельных резисторов, соединенных параллельно.
При расчете параллельно соединенных резисторов следует помнить одну важную вещь: общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в соединении.
Как рассчитать сложные соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематического объединения резисторов в группы. На рисунке ниже рассчитайте общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчетов давайте сначала сгруппируем резисторы по типам параллельного и последовательного подключения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 рассчитывается как сумма резисторов R2 и R3:
Поэтому мы упрощаем схему как два параллельных резистора. Теперь общее сопротивление всей цепи можно рассчитать следующим образом:
Расчеты более сложных соединений резисторов могут быть выполнены с использованием законов Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторов
Общий ток I, протекающий в цепи параллельных резисторов, равен сумме отдельных токов, протекающих во всех параллельных ветвях, но ток в отдельной ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одинаковое напряжение. Поскольку значение сопротивления в параллельной цепи может меняться, количество тока, протекающего через каждый резистор, также будет меняться (в соответствии с законом Ома).
Рассмотрим это на примере двух резисторов, соединенных параллельно. Ток, протекающий через каждый резистор (I1 и I2), будет разным, потому что резисторы R1 и R2 не равны. Однако мы знаем, что ток, входящий в цепь в точке “A”, должен выйти из цепи в точке “B”.
R = R1 + R2. При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого количества последовательно соединенных проводников.
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально току, протекающему через него. Формула для определения сопротивления по закону Ома, если известны ток и напряжение: R = U I <r=></r=>> R=IU, где R – сопротивление, U – напряжение и I – ток.
Pv = cx-S-v2-ρ/2, где S – площадь фронтальной проекции автомобиля, м2; v – скорость автомобиля относительно воздуха, м/с; ρ – плотность воздуха, кг/м3; sk – коэффициент аэродинамического сопротивления.
S = P1/cosφ
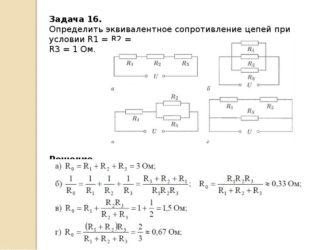
Как определить эквивалентное сопротивление
При наличии в электрической сети нескольких источников сопротивления для расчета тока, напряжения и мощности должен использоваться единый сменный индекс сопротивления физической цепи.
Каждый показатель последовательного или параллельного соединения может быть преобразован с помощью эквивалентного резистора и одного источника электродвижущей силы. Сопротивление в этом случае будет равно сумме всех пассивных препятствий для заряда электрической сети. Электродвижущая сила сменного источника будет равна сумме всех источников, включенных в цепь.
Формула для определения соотношения
Обратите внимание! Собирая схему с использованием преобразований проводников, соединенных последовательно или параллельно, можно максимально упростить дальнейшие расчеты в любой цепи. Исключением могут быть схемы, содержащие сопротивления в виде звезды и треугольника.
Формула расчета для смешанного соединения устройств
Как правильно произвести расчет для кабелей со смешанным режимом работы
Соединение устройств в смешанном режиме – это тип соединения, при котором некоторые из сменных компонентов соединены последовательно, а некоторые – параллельно. Для соединения со смешанным режимом несложно определить значение эквивалентного сопротивления. Достаточно использовать следующую формулу: (R1 + R2) R3 / (R1 + R2 + R3) + R4.
Эта комбинация используется для изменения сопротивления в пусковых резисторах с питанием от постоянного тока. Для расчета используются специальные онлайн-сервисы. Это помогает быстрее вычислять, упрощать и ускорять электрические расчеты.
Формула расчета для смешанного соединения устройств
Поэтому, чтобы рассчитать эквивалентное сопротивление цепи, вспомните закон Ома и используйте приведенные выше формулы. Только в случае смешанного подключения рекомендуется выполнять расчет с помощью онлайн-калькулятора, так как существует риск ошибок в расчетах.
Гирляндная цепочка из n соединенных элементов имеет свои особенности.
Инструмент 3: Преобразование дельты в звезду
Предположим, что у нас есть дельта-сегмент в цепи (рис. 3, слева). Нужно заменить его сегментом такой формы – “звездой”. (рис. 3, справа), причем сопротивление между сторонами “звезды” такое же, как между соответствующими радиусами “треугольника”. Почему это необходимо? Вы узнаете об этом позже.
Давайте рассмотрим “звезда”
на рис. 3. Предположим, что нам известны сопротивления между точками A и B, что составляет (Ra+Rb); A и C, что составляет (Ra+Rc); B и C, что составляет (Rb+Rc). Каковы сопротивления Ra, Rb, Rc?
Зная все сопротивления между концами звезды, мы можем рассчитать сопротивление каждой отдельной балки.
Теперь мы рассчитаем сопротивления между точками A, B и C (звезды) через известные нам сопротивления треугольника (рис. 3-2). Сначала рассчитаем сопротивление между точками A и B звезды (рис. 3-2 верхний ряд). В нашем треугольнике есть два параллельных сопротивления, Rab и (Rac+Rbc). Мы знаем, как рассчитать их полное сопротивление (ответы на вопросы 3 и 4). Рассчитайте сопротивления между точками A и C и B и C (линии 2 и 3). Обратите внимание, что во всех формулах знаменатель один и тот же.
Теперь вы можете рассчитать сопротивление одного луча (Рисунок 3-3). Формула очень громоздкая, но мы сократим ее.
И получается такая стройная и элегантная формула (рис. 3-4, верхний ряд). Аналогичным образом рассчитайте сопротивления других лучей звезды.
Сформулируйте формулу на рисунке 3-4 своими словами, чтобы лучше ее запомнить.
Чтобы найти сопротивление луча звезды, умножьте сопротивления сторон “треугольника”, которые являются “смежными”. (“имеют одну и ту же букву”) и разделить на сумму сопротивлений всех сторон “треугольника”.
Читайте далее:
- Как найти напряжение источника.
- Звезда или треугольник – Советы электрикам – Electro Genius.
- Топология электрической цепи (Лекция N 2).
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Как найти начало и конец обмотки электродвигателя – ООО "СЗЭМО Электродвигатель".
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
- Электричество. Сила электричества.