Формулы для параллельного, последовательного и смешанного соединения резисторов - услуги электромонтажа, строительства и ремонта

Сложные цепи рассчитываются путем группировки по методам параллельного и последовательного соединения.

Резистор – это пассивный элемент электрической цепи, который поглощает энергию тока и преобразует ее в тепло, оказывая сопротивление потоку электронов в цепи.

Связь между током и сопротивлением описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух типов – фиксированные и переменные, в последнем случае сопротивление проводника изменяется механически (вручную).

Последовательное и параллельное соединение резисторов являются основными способами соединения резистивных элементов.

Внимание! Резистор не имеет полярности, а длина проводов одинакова с обоих концов, поэтому предлагается назвать провода для лучшего понимания соединения:

На правом конце, точно.
В левом конце, слева.

_________________
Перестаньте жить так, как вы хотите жить, и живите так, как вы хотите жить.

Содержание

Как изменяется мощность при параллельном подключении

_________________
Не живите так, как есть, живите так, как вы хотите жить.

_________________
Указывайте на ошибки других прямо, а не косвенно.
Дорогие кошки, ПАМЯТЬ и ОНА пишутся одинаково.
Унижая другого человека, вы унижаете себя.

JLCPCB, всего $2 за прототип печатной платы! Любой цвет!

Подпишитесь и получите два купона на $5 каждый: https://jlcpcb.com/cwc

Сборка печатной платы от $30 + БЕСПЛАТНАЯ доставка по всему миру + шаблон

_________________
Перестаньте жить так, как вы знаете, живите так, как вы хотите.

Модули Navigator могут значительно сократить время разработки программного обеспечения. Во время вебинара 17 ноября вы сможете узнать о новых семействах Teseo-LIV3x, Teseo-VIC3x и Teseo-LIV4F. Вы узнаете, как легко добавить функциональность позиционирования с повышенной точностью с помощью двухдиапазонного приемника и MEMS Sensor Navigation. Работайте с программным обеспечением Teseo Suite и ознакомьтесь с результатами полевых испытаний.

Резисторы одинаковой мощности и мощности можно легко соединить параллельно, а согласно здравому смыслу и закону Ома, любые резисторы можно соединить и последовательно.

PS. Это мне недавно понадобилось для освещения лампой постоянного тока 310В. посчитал, нашел, что нужен резистор 21 ком на 5 ватт. взял 4 резистора 24 ком на 2 ватта каждый. Спаял два последовательно параллельно. Лампа 8 Вт, 24 кОм горит, а резисторы слегка теплые.
И мне не пришлось ничего искать.

Компания Infineon представила 40-вольтовые МОП-транзисторы семейства OptiMOS 5. Эти транзисторы являются МОП-транзисторами нормального уровня и имеют более высокое пороговое напряжение (чем другие низковольтные МОП-транзисторы), что обеспечивает защиту от ложных срабатываний в условиях повышенного шума.

Осмелюсь предположить (под пиво) следующее:
Если поставить параллельно резисторы 1Вт=100 Ом и 0,25Вт=10кОм, очевидно, что более слабым звеном будет резистор большей мощности.
Если их соединить последовательно, то самый слабый резистор останется тем же резистором. Даже если незначительно, он будет иметь более высокую выходную мощность за счет меньшего сопротивления.

На самом деле, если я правильно понимаю aFFturator (я не могу назвать его иначе), с набором резисторов то же самое номинальная мощность и значения сопротивления:
– параллельно – мощность складывается как a+b+c+d=d;
– Последовательно – нужно xitro считать, потому что падение на первом резисторе дает слабину на втором, а затем сумма первых двух дает слабину на третьем, и так далее.

Извините, если я ошибаюсь. Но именно так я построил свое первое “зарядное устройство” около 15 лет назад (транс мост-конденсатор-резисторы). Сначала был 10-омный резистор мощностью 1 Вт с 5 плашками, затем 0,5 Вт той же мощности с 5 плашками и, наконец, 0,125 Вт той же мощности.

P.S.: Пожалуйста, уточните, о чем вы просите. Иначе “где бы я, черт возьми, нашел то, что было бы. “

q_общий= q1 = q2 = q3

Питание при последовательном подключении

Когда резисторы соединены последовательно, электрический ток проходит через каждый резистор по очереди. Значение тока в каждой точке цепи будет одинаковым. Этот факт определяется законом Ома. Если мы сложим все резисторы в этой цепи, то получим следующий результат: R = 200+100+51+39 = 390 Ом.

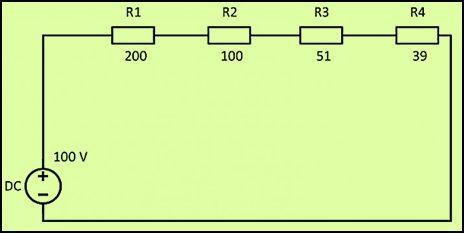
При напряжении в цепи 100 В, согласно закону Ома, сила тока равна I = U/R = 100/390 = 0,256 А. Исходя из полученных данных, мощность последовательно соединенных резисторов можно рассчитать по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

Мощность каждого отдельного резистора может быть рассчитана аналогичным образом:

P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если мы сложим полученные мощности, то получим общее число P: P = 13,11+6,55+3,34+2,55 = 25,55 W.

Помимо функции управления током, резисторы используются в схемах делителя напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что при увеличении сопротивления напряжение увеличивается. Это принцип, на котором основаны все устройства делителя напряжения. В делителях тока используется параллельное соединение резисторов, а в делителях напряжения – последовательное.

Резисторы показаны на схемах в виде прямоугольника размером 10×4 мм. Для маркировки используется символ R, который может быть дополнен значением мощности элемента. Для мощностей более 2 Вт обозначение производится римскими цифрами. Соответствующая надпись нанесена на схеме рядом с символом резистора. Мощность также включена в маркировку на корпусе компонента. Единицами измерения сопротивления являются омы (1 Ом), килоомы (1000 Ом) и мегаомы (100 000 000 000 Ом). Резисторы выпускаются в диапазоне от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать эти компоненты с достаточно точными значениями сопротивления.

Мощность в параллельном режиме

При параллельном соединении все резисторы подключены к одному узлу, а концы – к другому. В этом случае ток разветвляется и начинает протекать через каждый элемент. Согласно закону Ома, ток будет обратно пропорционален всем подключенным резисторам, а напряжение на всех резисторах будет одинаковым.

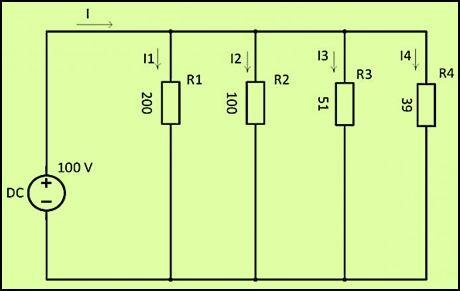
Перед расчетом тока рассчитайте общую проводимость всех резисторов по следующей формуле:

1/R = 1/R₁+1/R₂+1/R₃+1/R₄ = 1/200+1/100+1/51+1/39 = 0.005+0.01+0.0196+0.0256 = 0.06024 1/Ω.
Поскольку сопротивление – величина, обратно пропорциональная проводимости, его значение будет: R = 1/0,06024 = 16,6 Ом.
Предполагая значение напряжения 100 В, ток рассчитывается по закону Ома: I = U/R = 100 x 0,06024 = 6,024 А.
Зная силу тока, мощность параллельно соединенных резисторов определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
Рассчитайте ток для каждого резистора, используя формулы: I₁ = U/R₁ = 100/200 = 0,5A; I₂ = U/R₂ = 100/100 = 1A; I₃ = U/R₃ = 100/51 = 1,96A; I₄ = U/R₄ = 100/39 = 2,56A. На примере этих резисторов видно, что при уменьшении сопротивления ток увеличивается.

Существует еще одна формула для расчета мощности при параллельном соединении резисторов: P₁ = U 2 /R₁ = 100 2 /200 = 50 ВТ; P₂ = U 2 /R₂ = 100 2 /100 = 100 ВТ; P₃ = U 2 /R₃ = 100 2 /51 = 195,9 ВТ; P₄ = U 2 /R₄ = 100 2 /39 = 256.4 W. Объединив мощности отдельных резисторов, мы получим общую мощность: P = P₁+Р₂+Р₃+Р₄ = 50+100+195.9+256.4 = 602.3 W.

Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить наиболее точные результаты.

Параллельное соединение резисторов

Параллельное соединение резисторов

Параллельное соединение резисторов (или потребителей энергии, ветвей, сопротивлений) – это такое соединение, при котором несколько резисторов (ветвей) подключены к одним и тем же двум узлам электрической цепи (рис. 1).

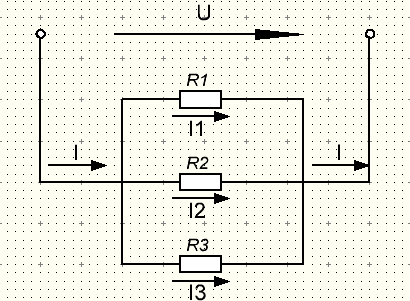
Рисунок 1 Параллельное соединение трех резисторов

Проводимость для параллельного соединения

Сопротивление для параллельного подключения:

За три Резисторы, соединенные параллельно

На два Резисторы, соединенные параллельно

Для филиалов с одинамическое сопротивление где n – количество ветвей

Ток при параллельном подключении

Питание при параллельном подключении

Доказательство

Поскольку резисторы подключены к одним и тем же узлам, каждый резистор находится под одним и тем же напряжением U. В соответствии с законом Ома, токи в резисторах даются в виде

Из этих формул следует, что токи в параллельных резистивных ветвях распределяются прямо пропорционально проводимости ветвей или обратно пропорционально их сопротивлению. Серия параллельно соединенных резисторов может быть заменена эквивалентным резистором с сопротивлением R, величина которого должна быть такой, чтобы при одном и том же напряжении на зажимах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

Т.е. Эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Поэтому эквивалентное сопротивление будет меньше, чем наименьшее из параллельно соединенных резисторов.
Уравнение (1) также позволяет определить эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление

Для двух резисторов

Если сопротивление ветвей одинаковые R1 = R2 = R3, тогда можно использовать формулу

в общем случае, когда n резисторов с одинаковым сопротивлением соединены вместе равное сопротивление R1 эквивалентное сопротивление равно

Мощность параллельно соединенных резисторов равна сумме мощностей всех резисторов

Реальные электрические цепи чаще всего содержат не один проводник, а несколько проводников, соединенных определенным образом. В своей простейшей форме электрическая цепь имеет только “вход” и “выход”, т.е. две клеммы для подключения к другим проводникам, через которые заряд (ток) может входить в цепь и выходить из нее. Когда в цепи существует установившийся ток, значения входного и выходного токов будут одинаковыми.

Ток и напряжение в параллельных, последовательных и смешанных соединениях проводников

Реальные электрические цепи чаще всего содержат не один проводник, а несколько проводников, каким-то образом соединенных вместе. В своей простейшей форме электрическая цепь имеет только “вход” и “выход”, то есть две клеммы для подключения к другим проводникам, через которые заряд (ток) может входить в цепь и выходить из нее. При установившемся токе в цепи значения входного и выходного токов будут одинаковыми.

Если мы рассмотрим электрическую цепь, состоящую из нескольких различных проводников, и рассмотрим пару точек на ней (вход и выход), то в принципе остальную часть цепи можно рассматривать как один резистор (по его эквивалентному сопротивлению).

При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на клеммах, т.е. разность электрических потенциалов между точками “входа” и “выхода”, то отношение U/I можно рассматривать как значение эквивалентного сопротивления R цепи в целом.

Если закон Ома выполняется, эквивалентное сопротивление может быть вычислено довольно легко.

Ток и напряжение при последовательном соединении проводников

В простейшем случае, когда два или более проводников соединены вместе в последовательную цепь, ток в каждом проводнике будет одинаковым, а напряжение между “выходом” и “входом”, то есть на клеммах всей цепи, будет равно сумме напряжений резисторов, образующих цепь. А поскольку закон Ома действует для каждого из резисторов, мы можем написать:

Таким образом, следующие формулы характерны для последовательного соединения проводников:

Чтобы найти общее сопротивление цепи, сопротивления проводников, образующих цепь, складываются вместе;

Ток, протекающий через цепь, равен току, протекающему через каждый из проводников, образующих цепь;

Напряжение на зажимах цепи равно сумме напряжений на каждом из проводников, составляющих цепь.

Ток и напряжение при параллельном соединении проводников

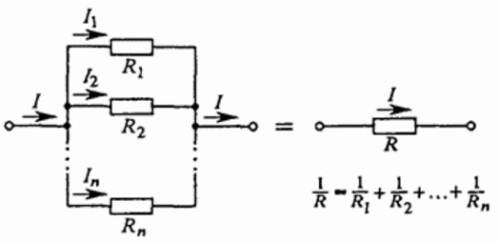
Когда несколько проводников соединены параллельно, напряжение на зажимах такой цепи равно напряжению на каждом из проводников, образующих цепь.

Напряжения на всех проводниках равны между собой и равны приложенному напряжению (U). Ток, протекающий через всю цепь – на “входе” и “выходе” – равна сумме токов в каждой из ветвей цепи, соединенных параллельно и образующих цепь. Зная, что I = U/R, получаем, что:

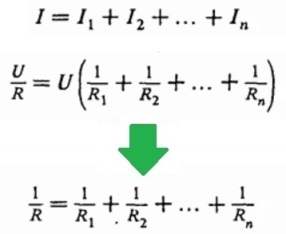
Таким образом, для параллельного соединения проводников характерны следующие формулы:

Чтобы найти общее сопротивление цепи, сложите инверсные сопротивления проводников, образующих цепь;

Ток, протекающий через цепь, равен сумме токов, протекающих через каждый из проводников, образующих цепь;

Напряжение на зажимах цепи равно напряжению на каждом из проводников, составляющих цепь.

Эквивалентные электрические схемы для простых и сложных цепей

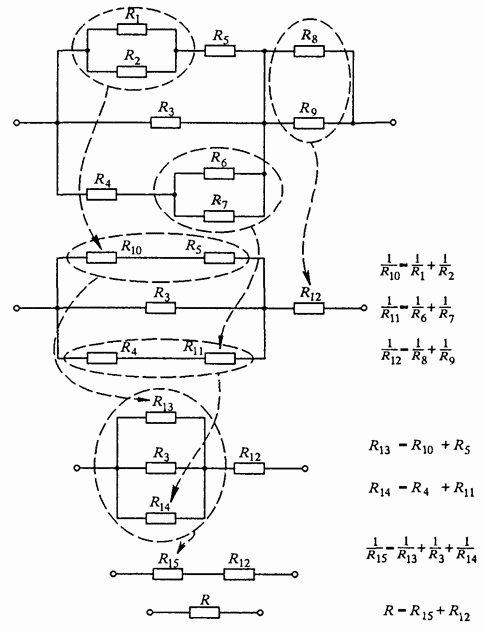
В большинстве случаев электрические схемы, будучи соединенными комбинациями проводников, поддаются пошаговому упрощению.

Группы частей схемы, соединенных последовательно и параллельно, заменяются эквивалентными сопротивлениями по вышеуказанному принципу, рассчитывая шаг за шагом эквивалентные сопротивления отдельных частей и затем сводя их к единому значению эквивалентного сопротивления всей схемы.

И если поначалу схема выглядит довольно запутанной, упрощаясь шаг за шагом, она может быть разбита на более мелкие цепочки проводников, соединенных последовательно и параллельно, и таким образом в конечном итоге значительно упрощена.

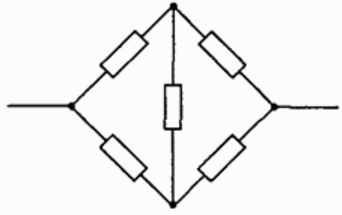
Между тем, не все схемы поддаются такому упрощению. Кажущаяся простой “мостовая” цепь из проводников не может быть проверена таким образом. Необходимо соблюдать несколько правил:

Для каждого резистора выполняется закон Ома;

В каждом узле, т.е. в точке схождения двух или более токов, алгебраическая сумма токов равна нулю: сумма токов, входящих в узел, равна сумме токов, выходящих из узла (первое правило Кирхгофа);

Сумма напряжений на участках цепи на любом пути от “входа” до “выхода” равна напряжению, приложенному к цепи (второе правило Кирхгофа).

Мостовое соединение проводов

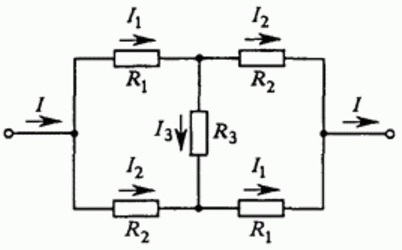
Чтобы рассмотреть пример применения вышеуказанных принципов, мы рассчитаем цепь, состоящую из проводников, соединенных вместе и образующих мостовую схему. Чтобы не усложнять расчет, предположим, что некоторые сопротивления проводников равны друг другу.

Обозначим направления токов I, I1, I2, I3 на пути от “входа” в цепь к “выходу” цепи. Вы видите, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. На самом деле, если поменять местами “вход” и “выход” схемы, то схема будет неотличима от исходной.

Для каждого узла можно написать уравнения тока, исходя из того, что сумма токов, входящих в узел, равна сумме токов, вытекающих из узла (закон сохранения электрического заряда), что дает два уравнения:

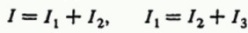
Следующий шаг – написать уравнения для суммы напряжений для каждого участка цепи, когда цепь шунтируется от входа к выходу различными способами. Поскольку в данном примере цепь симметрична, достаточно двух уравнений:

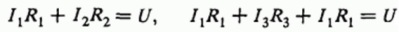
Решение системы линейных уравнений дает формулу для нахождения величины тока I между “входной” и “выходной” клеммами, исходя из заданного приложенного напряжения U и сопротивления проводников в цепи:

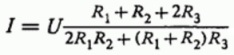
А для общего эквивалентного сопротивления цепи, предполагая R = U/I, формула выглядит следующим образом:

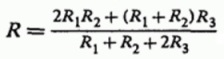
Можно даже проверить правильность решения, например, приведя значения сопротивления к пределам и особым случаям:

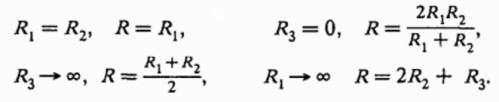
Теперь вы знаете, как найти ток и напряжение в параллельных, последовательных, смешанных и даже мостовых соединениях, используя закон Ома и правила Кирхгофа. Эти правила очень просты, и даже самые сложные схемы в конечном итоге могут быть сведены к элементарной схеме с помощью нескольких простых математических операций.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Читайте далее: