Гармонические напряжения и токи в электротехнике (TE) - формулы и определения с примерами - услуги электромонтажа, строительства и ремонта

Во многих практических приложениях важно знать фазовые соотношения между гармониками одной и той же частоты. Фазовые отношения характеризуются Разность фаз сравниваемых колебаний.

Содержание

Гармонические напряжения и токи

В предыдущих лекциях мы рассматривали электрические цепи, предполагая, что в них существуют постоянные напряжения и токи. В действительности токи и напряжения, действующие в электрических цепях, являются переменными, т.е. это электрические колебания. колебания. Обратите внимание, что колебания – это процессы, которые характеризуются определенным повторением во времени. Мы различаем непериодические и периодические колебания.

Простейшими и наиболее важными типами периодических колебаний являются гармонический, когда осциллирующая величина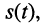

Уникальная роль гармонических колебаний в радиотехнической теории и практике обусловлена следующими обстоятельствами:

они обычно используются для передачи сигналов и электрической энергии (например, промышленный ток 50 Гц)
они используются в качестве простейшего тестового сигнала
они являются единственным типом колебаний, форма которых не меняется при движении через любую линейную систему
Каждое периодическое негармоническое колебание можно представить как сумму (суперпозицию) различных гармонических колебаний (такое представление называется спектром негармонических колебаний).

Если временной интервал ограничен 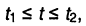то существует сегмент гармонического колебания, который уже будет иметь свойства, отличные от свойств гармонического колебания; чем длиннее интервал, тем ближе свойства сегмента будут к свойствам самого гармонического колебания; во всех лекциях предполагается, что интервал отсчитывается от нуля до бесконечности: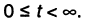

Колебание напряжения на конденсаторе в цепи переменного тока описывается уравнением, в котором все величины выражены в СИ. Емкость конденсатора равна амплитуде тока. (Дайте ответ в амперах).

Формула для амплитуды тока в цепи

Электромагнитные колебания – это взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания возникают в различных электрических цепях. Они вызывают изменения заряда, напряжения, тока, напряженности электрического поля, индукции магнитного поля и других электродинамических величин.

Свободные электромагнитные колебания возникают в электромагнитной системе, когда она выводится из состояния равновесия, например, при зарядке конденсатора или изменении тока в цепи.

Эти колебания затухают, поскольку энергия, поступающая в систему, расходуется на нагрев и другие процессы.

Вынужденные электромагнитные колебания – это невозмущенные колебания в цепи, вызванные внешним периодически меняющимся синусоидальным переменным током.

Электромагнитные колебания описываются теми же законами, что и механические колебания, хотя физическая природа колебаний совершенно иная.

Электрические колебания являются частным случаем электромагнитных колебаний, когда рассматриваются только электрические величины. В этом случае мы говорим о переменном токе, напряжении, мощности и т.д.

Колебательный контур – это электрическая цепь, состоящая из последовательно соединенных конденсатора C, катушки индуктивности L и резистора сопротивления R.

Устойчивое равновесное состояние колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку не течет).

Величины, выражающие свойства самой системы (параметры системы): L i m, 1/C i k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в цепи – это

где q” – вторая производная заряда по времени. Значение

циклическая частота. Те же уравнения описывают колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре задается формулой (Томсона):

Значение φ = ώt + φ под знаком синуса или косинуса является фазой колебания.

Фаза определяет состояние колебательного контура в каждый момент времени t.

Ток в цепи равен производной заряда по времени и может быть выражен как

Чтобы лучше выразить сдвиг фаз, давайте заменим косинус на синус

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, вращающейся с постоянной угловой скоростью в однородном магнитном поле индукции B. Магнитный поток Ф проникновение рамы с поверхностью S ,

где – угол между нормалью к рамке и вектором магнитной индукции .

Согласно закону электромагнитной индукции Фарадея, ЭДС индукции равна

где – скорость изменения магнитного потока.

Гармонически изменяющийся магнитный поток создает синусоидальную ЭДС индукции

где – значение амплитуды ЭДС индукции.

Если источник внешней гармонической ЭДС подключен к цепи

то в нем возникнет вынужденное колебание, протекающее с циклической частотой ώ, совпадающей с частотой источника.

В этом случае вынужденные колебания совершаются зарядом q, разностью потенциалов u текущий i и другие физические величины. Колебания являются незатухающими, поскольку энергия поступает в цепь из источника, компенсирующего потери. Гармонически изменяющиеся ток, напряжение и другие величины в цепи называются переменными. Естественно, они различаются по величине и направлению. Токи и напряжения, которые изменяются только по величине, называются пульсирующими.

В промышленных цепях переменного тока в России предполагается частота 50 Гц.

Для расчета количества тепла Q, выделяемого переменным током, протекающим по проводнику с активным сопротивлением R, нельзя использовать значение максимальной мощности, так как она достигается только в определенные моменты времени. Необходимо использовать среднюю мощность за период – отношение полной энергии W, поступающей в цепь в данный период, к значению за период:

Таким образом, количество тепла будет выделено в момент времени T:

Значение I переменного тока равно силе такого постоянного тока, который выделяет такое же количество тепла, как и переменный ток, за время, равное периоду T:

Следовательно, среднеквадратичное значение тока

Аналогично, среднеквадратичное значение напряжения

Трансформатор – это устройство, которое увеличивает или уменьшает напряжение в несколько раз с незначительной потерей энергии или без нее.

Трансформатор состоит из стального сердечника, изготовленного из отдельных листов, на котором закреплены две катушки с проволочными обмотками. Первичная катушка подключается к источнику переменного напряжения, а вторичная катушка – к оборудованию, потребляющему электроэнергию.

называется коэффициентом трансформации. Для понижающего трансформатора K > 1, для повышающего трансформатора K > 1.

Пример. Заряд на пластинах конденсатора в колебательном контуре изменяется во времени в соответствии с уравнением . Найдите период и частоту колебаний в цепи, циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний тока. Напишите уравнение, выражающее зависимость тока от времени.

Из уравнения следует, что . Период задается формулой для циклической частоты

Временная зависимость тока выглядит следующим образом:

Амплитуда силы тока.

Ответ: Заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, что соответствует циклической частоте 100 рад/с, амплитуда силы колебательного тока составляет 510 3 А, ток изменяется по закону:

i=-5000 sin100t

Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис. 1) состоит из индукционной катушки L (рассмотрим идеальный случай, когда катушка не имеет омического сопротивления) и конденсатор C и называется закрытой катушкой. Характерной особенностью катушки является ее индуктивность, которая обозначается через L и измеряется в генри (Гн), конденсатор характеризуется емкостью Cкоторый измеряется в фарадах (F).

Пусть конденсатор изначально заряжен (рис. 1), так что на одной из его стенок имеется заряд +Q а на другой стороне есть зарядQ . Таким образом, между пластинами конденсатора создается электрическое поле с энергией

где – амплитуда (максимум) напряжения или разности потенциалов на катушках конденсатора.

При замыкании цепи конденсатор начнет разряжаться, и в цепи потечет электрический ток (рис. 2), величина которого будет увеличиваться от нуля до максимального значения. Поскольку ток, протекающий в цепи, имеет переменную величину, в катушке наводится ЭДС самоиндукции, которая препятствует разрядке конденсатора. Поэтому процесс разрядки конденсатора происходит не мгновенно, а постепенно. В каждый момент времени разность потенциалов на витках конденсатора

(где – заряд конденсатора в данный момент времени) равна разности потенциалов на катушке, т.е. равна ЭДС

Рис.1

Рис.2

Когда конденсатор полностью разряжен и , ток в катушке достигает своего максимального значения (рис.3). В этот момент индукция магнитного поля катушки также достигнет максимального значения, а энергия магнитного поля составит

Ток начнет уменьшаться, а на пластинах конденсатора будет накапливаться заряд (рис.4). Когда ток упадет до нуля, заряд конденсатора достигнет своего максимального значения Q но катушка, ранее положительно заряженная, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор снова начинает разряжаться, и ток в цепи течет в обратном направлении.

Таким образом, процесс перетекания заряда с одной пластины конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в схеме есть электромагнитные колебания. Этот процесс включает не только изменение величины заряда и напряжения на конденсаторе и тока в катушке, но и перенос энергии из электрического поля в магнитное и обратно.

Рис. 3

Рис.4

Зарядка конденсатора до максимального напряжения происходит только в том случае, если в колебательном контуре нет потерь энергии. Этот тип цепи называется идеальной цепью.

В реальных цепях происходят следующие потери энергии:

1) тепловые потери, потому что R ¹ 0;

2) диэлектрические потери в конденсаторе

3) Гистерезисные потери в сердечнике катушки

4) радиационные потери и т.д. Если пренебречь этими потерями энергии, то можно записать, что , т.е.

Колебания, возникающие в идеальном колебательном контуре, в котором выполняется это условие, называются бесплатноили натуральныйколебания контура.

В этом случае напряжение U (i обвинение Q) на конденсаторе изменяется по гармоническому закону:

где n – собственная частота колебательного контура, w = 2pn – собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в цепи определяется как

период T – время, в течение которого происходит одно полное колебание напряжения конденсатора и тока в цепи, определяемое как в соответствии с формулой Томсона

Ток в цепи также изменяется по гармоническому закону, но с задержкой по отношению к напряжению на . Поэтому зависимость тока в цепи от времени имеет вид

На рис. 6 напряжение U на конденсаторе и ток I для идеального колебательного контура.

В реальной цепи энергия будет уменьшаться с каждым колебанием. Амплитуды напряжения конденсатора и тока в цепи будут уменьшаться, эти колебания называются затухающими колебаниями. Их не следует использовать в осцилляторах, так как устройство будет работать максимум в импульсном режиме.

Рис.5

Рис.6

Для достижения затухающих колебаний необходимо компенсировать потери энергии на различных частотах устройств, в том числе используемых в медицине.

Не нашли то, что искали? Используйте поиск:

Лучшие высказывания: Увлекаться девушкой – отращивать хвосты, учиться – отращивать рога. 10034 – | 7811 – или прочитать их все.

91.146.8.87 © studopedia.ru Не является автором размещенных материалов. Но это дает возможность использовать его бесплатно. Было ли нарушено авторское право? Свяжитесь с нами | Обратная связь.

Снова активируйте AdBlock!
и обновите страницу (F5)
Мне это очень нужно

07.06.2019

5 июня. Что нужно решить по физике

30 мая Решения вчерашних экзаменов по математике

Общий вид зависимости напряжения конденсатора в колебательном контуре: где – значение амплитуды напряжения. Сравнивая с находим, что значение максимального заряда на витках конденсатора равно Амплитуда тока колебательной силы связана с частотой колебаний и максимальным значением заряда конденсатора соотношением Отсюда находим

Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой имеется конденсатор, выполняется соотношение Im=Um/Xc, где под током и напряжением понимаются их амплитудные значения, а Xc – емкость конденсатора, равная Xc=1/w*C. Подставляя вторую формулу в первую, получаем: Im=Um*w*C. Подставив значения из условия, вы получите значение амплитуды тока, которое совпадает с вашим.

P. С. Мой способ решения кажется мне более логичным, потому что обе формулы приведены в учебнике физики, в отличие от последней формулы в предложенном вами способе решения.

Спасибо. Хороший вариант.

Но формула, используемая в конце, явно дана в школьном курсе. Ведь, насколько я знаю, на этом этапе школьной физики уже начинают использовать производные. Формула следует из закона изменения заряда со временем в гармонических колебаниях и того факта, что ток является производной заряда

Подобно механическому резонансу, резонанс в колебательном контуре создает оптимальные условия для потока энергии от внешнего источника в контур. Мощность в цепи максимальна, когда ток находится в фазе с напряжением. Здесь наблюдается полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).

§ 35 Резонанс в электрической цепи

При изучении вынужденных механических колебаний мы познакомились с явлением резонанса. Резонанс наблюдается, когда собственная частота колебательной системы совпадает с частотой изменяющейся внешней силы. Если трение мало, то амплитуда вынужденных колебаний в устойчивом состоянии при резонансе резко возрастает. Совпадение форм уравнений для описания механических и электромагнитных колебаний позволяет сделать вывод о возможности резонанса и в электрической цепи, если эта цепь является колебательным контуром, имеющим определенную собственную частоту.

В механических колебаниях резонанс ярко выражен при малых значениях коэффициента трения μ. В электрической цепи коэффициент трения равен ее активному сопротивлению R. Именно наличие этого сопротивления в цепи приводит к тому, что энергия тока преобразуется во внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном контуре должен быть хорошо заметен, если активное сопротивление R мало.

Мы уже знаем, что если активное сопротивление мало, то собственная частота в цепи задается формулой

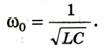
Сила тока вынужденных колебаний должна достигать максимальных значений, когда частота переменного напряжения, приложенного к цепи, равна собственной частоте цепи:

Резонанс в электрическом колебательном контуре это явление внезапного увеличения амплитуды вынужденного колебательного тока, когда частота внешнего переменного напряжения совпадает с собственной частотой колебательного контура.

Амплитуда тока при резонансе

Подобно механическому резонансу, резонанс в колебательном контуре создает оптимальные условия для поступления энергии из внешнего источника в контур. Мощность в цепи максимальна, когда ток находится в фазе с напряжением. Здесь прослеживается полная аналогия с механическими колебаниями: когда в механической колебательной системе возникает резонанс, внешняя сила (аналог напряжения в цепи) находится в фазе со скоростью (аналог тока).

Не сразу после включения внешнего переменного напряжения в цепи устанавливается резонансное значение силы тока. Амплитуда колебаний тока постепенно увеличивается – до тех пор, пока энергия, выделяемая за один период на резисторе, не сравняется с энергией, поступающей в цепь за то же время:

Больше проблем, связанных с ЭМП, в нашем блоге.

Вопросы по теме “Переменный ток”

Вопрос 1. Какой тип тока называется переменным?

Ответ.

Переменный ток – это электрический ток, который изменяется во времени по гармоническому закону.

Вопрос 2. В чем преимущества переменного тока перед постоянным?

Ответ. Переменный ток имеет много преимуществ перед постоянным током:

Генератор переменного тока намного проще и дешевле;
Переменный ток можно передавать на большие расстояния с меньшими потерями.
Переменный ток может быть преобразован;
Переменный ток может быть легко преобразован в постоянный;
Двигатели переменного тока намного проще и дешевле, чем двигатели постоянного тока.

Вопрос 3. Кто популяризировал использование переменного тока?

Ответ. Никола Тесла был сторонником активного использования переменного тока. Подробнее о текущей войне между Теслой и Эдисоном вы можете прочитать в нашей отдельной статье.

Вопрос 4. В обычной бытовой розетке частота электроэнергии составляет 50 Гц. Что это значит?

Ответ. Это означает, что ток меняет свое направление 50 раз за одну секунду.

Вопрос 5. Сформулируйте закон Ома для переменного тока.

Ответ. Закон Ома для цепи переменного тока гласит:

Величина тока в цепи переменного тока прямо пропорциональна напряжению в цепи и обратно пропорциональна полному сопротивлению цепи.

Вам трудно решать задачи и выполнять другие учебные задания? Добро пожаловать в профессиональный сервис для студентов по решению их проблем!

Курсовая работа от 1 дня / от 120 страниц Изучить стоимость
Диссертация от 7 дней / от 9540 р. Узнайте больше о расходах
Курсовая работа от 5 дней / от 2160 р. Узнайте больше о стоимости
Коллективная работа от 1 дня / от 840 р. Смета расходов

Иван Колобков, также известный как Джони. Маркетолог, аналитик и копирайтер в компании Zaochnik. Многообещающий молодой писатель. Любитель физики, редких вещей и произведений С. Буковски.

В законе изменения тока в колебательном контуре величина имеет значение амплитуды тока и циклической частоты. Сначала определим амплитуду колебаний заряда; она связана с амплитудой тока и циклической частотой следующим соотношением

Как определить амплитуду тока

Задача 26, № 3450

Емкость конденсатора в колебательном контуре равна 50 мкФ. Меняющаяся во времени сила тока в индукционной катушке имеет следующий вид: где а = 1,5 A и Найти амплитуду напряжения, колеблющегося через конденсатор. Ответ дайте в вольтах.

В законе переменного тока в колебательном контуре эта величина имеет значение амплитуды тока и значение циклической частоты. Сначала определим амплитуду колебаний заряда; она связана с амплитудой тока и циклической частотой соотношением

Дается полное решение, включающее следующие элементы:

I) записываются положения физических теорий и законов, закономерности, применение которых необходимо для решения задачи выбранным способом;

II) описаны все буквенные обозначения физических величин, вновь введенных в решение (кроме обозначений констант, указанных в варианте КИМ, обозначений, использованных в описании задачи, и стандартных обозначений величин, используемых в обозначениях физических законов)

III) должны быть представлены необходимые математические преобразования и вычисления, приводящие к правильному числовому ответу (допускаются частичные решения с промежуточными вычислениями);

Все необходимые теоремы, физические законы, закономерности записаны правильно, преобразования для решения задачи выполнены, но присутствует одна или несколько из следующих ошибок.

Записи, соответствующие пункту II, представлены не полностью или не представлены вообще.

В решении имеются дополнительные записи, не являющиеся частью решения (возможно, неправильные), которые не отделены от решения и не зачеркнуты.

Имеются ошибки в необходимых математических преобразованиях или вычислениях и/или в математических преобразованиях/вычислениях отсутствуют логически важные шаги.

(или собственные), если они происходят за счет энергии, которая поступает в колебательную систему один раз и больше никаких внешних воздействий на эту систему нет.

§ 2.9 Закон Ома для цепи переменного тока

Какова амплитуда тока в таком контуре (колебательном контуре), если на его концах поддерживается напряжение u(t) = U sin ωt?

Мы видели, что когда проводник с сопротивлением R, конденсатор с емкостью C или индуктор с индуктивностью L соединены в цепь по отдельности, амплитуда тока определяется формулами (2.6.2), (2.7.3) и (2.8.4) соответственно. Амплитуды напряжений на резисторе, индукторе и конденсаторе связаны с амплитудой тока следующим образом:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных участках цепи, соединенных последовательно. Однако если мы измерим результирующее напряжение в цепи и напряжения на отдельных элементах цепи переменного тока, то обнаружим, что напряжение в цепи (среднеквадратичное значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Причина в том, что гармонические колебания напряжения в разных частях цепи сдвинуты по фазе друг относительно друга.

Действительно, квазистационарный ток одинаков во всех частях цепи в любой момент времени. Это означает, что амплитуды и фазы токов, протекающих через емкостную, индуктивную и активную части резистора, одинаковы. Однако только на участке активного сопротивления изменения напряжения и тока совпадают по фазе. На конденсаторе колебание напряжения происходит на π/2 позже колебания тока (см. §2.7), а на индукторе колебание напряжения происходит на π/2 раньше колебания тока (см. §2.8).

Векторная диаграмма электрической цепи

Чтобы вывести закон Ома для цепи переменного тока, показанной на рисунке 2.20, необходимо уметь складывать мгновенные колебания фазосдвинутых относительно друг друга напряжений. Самый простой способ выполнить сложение нескольких гармонических колебаний – использовать векторные диаграммы, рассмотренные в §1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду тока как функцию амплитуды напряжения и сдвиг фаз между током и напряжением.

Поскольку сила тока одинакова во всех частях цепи, удобно начать векторную диаграмму с вектора тока

m. Этот вектор изображен вертикальной стрелкой (рис. 2.21). Напряжение на резисторе находится в фазе с током. Поэтому вектор mR должен совпадать по направлению с вектором m. Его модуль равен UmR = ImR.

Колебания напряжения на индукционной катушке предшествуют колебаниям тока на π/2, и соответствующий вектор i

mL должен быть повернут относительно вектора m на π/2. Его модуль равен UmL = IωL. Если считать, что положительный сдвиг фазы соответствует повороту вектора против часовой стрелки, то вектор mL должен быть повернут влево на π/2. (Можно, конечно, сделать и наоборот).

Вектор напряжения на конденсаторе

mC находится на π/2 позади вектора m, поэтому он повернут на этот угол по отношению к вектору m вправо. Его модуль составляет .

Чтобы найти вектор полного напряжения

три вектора, mR, mL и mC, должны быть сложены вместе. Удобнее сначала сложить два вектора mL и mC (рис. 2.22).

Модуль этой суммы равен

, если . Именно такой случай показан на рисунке. Затем, добавив вектор mL + mC к вектору mR, получаем вектор m, который характеризует колебания сетевого напряжения.

По теореме Пифагора (из треугольника AOB):

Из уравнения (2.9.2) можно найти амплитуду тока в цепи:

Это закон Ома для электрической цепи переменного тока, показанной на рисунке 2.20.

Из-за сдвига фаз между напряжениями в разных частях цепи полное сопротивление Z цепи (см. рис. 2.20) выражается следующим образом:

Исходя из амплитуды тока и напряжения, можно перейти к среднеквадратичным значениям этих величин. Они связаны друг с другом так же, как амплитуды в (2.9.3):

Среднеквадратичное значение тока изменяется гармонически с течением времени:

где φc – разность фаз между силой тока и напряжением сети. Она зависит от частоты z и параметров цепи R, L, C.

Сдвиг фаз между током и напряжением

Сдвиг фаз φc между переменным током и напряжением равен по модулю углу φ между векторами

м и м (см. рис. 2.22). Как видно на этом рисунке,

Согласно рисунку 2.22, ток отстает от напряжения по фазе, если

. Поэтому фазовый сдвиг φc = -φ i

В частных случаях цепей с активными, емкостными и индуктивными сопротивлениями правильные значения фазового сдвига получаются из этой формулы.

Читайте далее: