ИНДУКТИВНОСТЬ это. Что такое ИНДУКТИВНОСТЬ? - услуги электромонтажа, строительства и ремонта

Коэффициент. L и Лназ. I. Размер L измеряется в генах, L – w ci = d/dt(LI) (в системе СИ), E ci = -(1/s 2 )(d/dt)(LI)(2) (в системе СГС).

Содержание

ИНДУКТИВНОСТЬ .

ИНДУКТИВНОСТЬ

Физический энциклопедический словарь. – Москва: Советская энциклопедия . Главный редактор А. М. Прохоров . 1983 .

В электродинамике (коэффициент самоиндукции) (от лат. inductio – индукция, возбуждение) – параметр электрической цепи, определяющий величину красной самоиндукции, наводимой в цепи при протекании по ней тока и/или при ее деформации. Оно также используется для определения цилиндрического (биполярного) элемента, определяющего его индуктивные свойства (синоним – катушка самоиндукции).I. – это количественная характеристика эффекта самоиндукции, открытая независимо друг от друга Дж. Генри в 1832 году и Фарадеем в 1835 году. При изменении тока в цепи и/или деформации цепи изменяется намагниченность. поле, которое, согласно закону индукции, создает вращающееся электрическое поле E(r, t )с ненулевой циркуляцией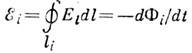

на замкнутых циклах л и прошел через магнитный поток Ф i . Внутри проводника вращательное поле Е взаимодействует с порождающим его током и противодействует изменению магнитного потока (правило Ленца). Циркулирующий E i и магнитный поток Ф i существенно зависит от выбора схемы l i внутри проводника конечной толщины. Однако для медленного движения и квазистатических процессов, когда общий ток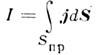

на замкнутых циклах л и прошел через магнитный поток Ф i . Внутри проводника вращательное поле Е взаимодействует с порождающим его током и противодействует изменению магнитного потока (правило Ленца). Циркулирующий E i и магнитный поток Ф i существенно зависит от выбора схемы l i внутри проводника конечной толщины. Однако для медленного движения и квазистатических процессов, когда общий ток

(j – плотность тока) одинакова для всех нормальных сечений проводника S пр , можно перейти к усредненной характеристике: эдс самоиндукции E si =<E i > ) и магнитный поток F=F i > . Предположим, что токопроводы замыкаются при прохождении одной петли,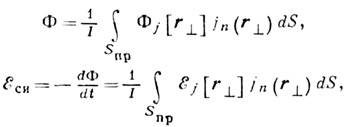

где r ^ , – векторы радиусов нормальных точек сечения проводника, F j (r ^ ) – магнитный поток на поверхности, ограниченной линией тока, проходящей через точку r ^ , E j (r ^ ) – векторная циркуляция E вдоль этой линии тока, j n – нормаль к S np компонента j. В более сложных случаях, когда линии тока замыкаются через несколько петель или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнения, но в любом случае должна удовлетворять энергетическому соотношению: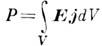
где r ^ , – векторы радиусов нормальных точек сечения проводника, F j (r ^ ) – магнитный поток на поверхности, ограниченной линией тока, проходящей через точку r ^ , E j (r ^ ) – векторная циркуляция E вдоль этой линии тока, j n – нормаль к S np компонента j. В более сложных случаях, когда линии тока замыкаются через несколько петель или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнения, но в любом случае должна удовлетворять энергетическому соотношению: =E si I ( Р– Для квазистационарных процессов усредненный магнитный поток пропорционален току:

F=L.I (в системе СИ), F= 1 / c (LI) (в системе СГС). (1)

Коэфф. L и Лназ. L. Value L измеряется в генах, L – В см. si = d/dt(LI) (в СИ), E si = -(1/s 2 )(d/dt)(LI)(2) (в СГС).

Производная времени I. определяет ту часть E ci, которая связана с деформацией проводящего контура; в случае недеформируемых контуров и квазистационарных процессов I. можно вынести за знак дифференцирования. m = 1 / 2 LI 2 (в системе СИ), W m = 1 / 2 c 2 LI 2 (в системе СГС). (3)

Соотношение (3) позволяет провести различие между I. внутренним Л и , которая представляет собой энергию магнитного поля, сосредоточенную в проводниках, и внешнюю L Л е , которое связано с внешним магнитным полем (L=L i +L e , L=L i +L e ). В частном случае токовых цепей из проводов, толщина которых мала по сравнению с радиусами изгиба или расстоянием между соседними проводами, можно считать, что структура токов и ближнего поля такая же, как у прямого провода того же сечения (такие цепи мы называем квазилинейными). Приблизительно, для заданной структуры токов, не зависящей от способа их наведения, I. зависит только от геометрии проводящей цепи (толщины и длины проводника и его формы). Для квазилинейного проводника с круглым сечением L i =(m 0 /8p)m i l (l – длина проводника, m i – величина. проницаемости проводника) и внешней И. можно представить в виде взаимная индуктивность двух параллельных бесконечно тонких проводящих нитей, одна из которых (l 1 ) совмещен с осевой линией проводника, а другой (l 2 ) выравнивается с его поверхностью: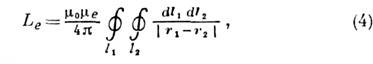

где r 1 , r 2 – векторы радиусов точек на окружности l l , l 2 ,m е – проницаемость окружающей среды [по аналогии, соотношение в СГС L “(m 0 /4p)L]. Из (4) следует, что L e логарифмически расходится по мере приближения радиуса провода к нулю, поэтому идеализация бесконечно тонкого провода не может быть использована для описания явления самоиндукции. Приблизительное вычисление интеграла в (4) с учетом внутреннего I. дает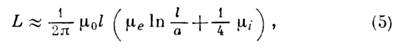

где r 1 , r 2 – векторы радиусов точек на окружности l l , l 2 ,m е – проницаемость окружающей среды [по аналогии, соотношение в СГС L “(m 0 /4p)L]. Из (4) следует, что L e логарифмически расходится по мере приближения радиуса провода к нулю, поэтому идеализация бесконечно тонкого провода не может быть использована для описания явления самоиндукции. Приблизительное вычисление интеграла в (4) с учетом внутреннего I. дает

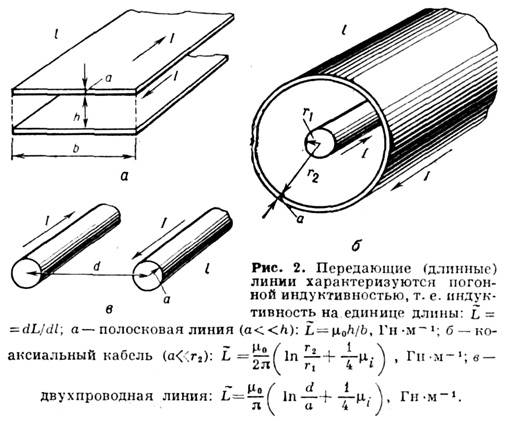
где l и а – длина и радиус провода. Это выражение логарифмически точно – его относительная погрешность порядка величины l/ln(Относительная погрешность этого выражения имеет порядок величины l/ln( l/a). Типичные примеры электрических цепей и выражения для их I, показаны на рисунках 1 и 2.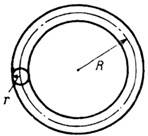

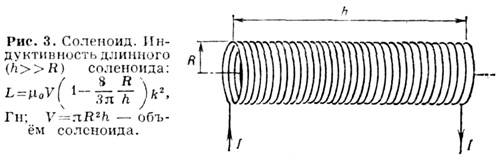
Рис. 1: Круговая катушка. Индуктивность катушки (проводящего тора): L=m 0 R(ln(8R/r)-2+ 1 / 4 m i ), Gn, r<<>

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с соответствующими плотными витками – соленоиды (рис. 3), которые используются для увеличения ИС. Поскольку ИБ цепей, в которых используются соленоиды, зависит в основном от них, принято говорить об ИБ соленоида. Считается, что идеальный соленоид эквивалентен выходу проводящей поверхности с азимутальными поверхностными токами плотности j pov = Ik (I – ток в соленоиде, k – (I – ток в катушке, k – число витков на единицу длины).

Понятие I может быть обобщено на быстро меняющиеся гармонические процессы 2xr(iwt)-, которые нельзя описать, пренебрегая задержкой магнитного взаимодействия, скин-эффектом в проводниках и дисперсией среды. Комплексные амплитуды тока I w и самоиндуцированной электромагнитной индуктивности E w связаны соотношением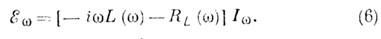

И. L(w) зависит от частоты (обычно уменьшается с увеличением частоты). Эффективный импеданс R L (w) определяет часть потерь энергии, включая потери на излучение, и связан с L(w) формулой связана с L(w) соотношением Крамерса-Кронига: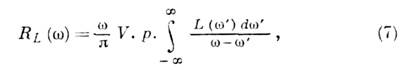

И. L(w) зависит от частоты (обычно уменьшается с увеличением частоты). Эффективный импеданс R L (w) определяет часть потерь энергии, включая потери на излучение, и связан с L(w) формулой связана с L(w) соотношением Крамерса-Кронига:

где интеграл берется по главному значению. На низких частотах сопротивлением R L (w) можно пренебречь, в этом случае E w и I w сдвинуты по фазе на p/2. Уравнение (3) для высокочастотных процессов преобразуется к виду: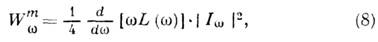

где W m w – энергия ближнего (квазистационарного) магнитного поля, усредненная за период осцилляции (полная магнитная энергия поля неопределенна из-за линейно возрастающей во времени энергии поля излучения).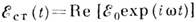
где W m w – энергия ближнего (квазистационарного) магнитного поля, усредненная за период осцилляции (полная магнитная энергия поля неопределенна из-за линейно возрастающей во времени энергии поля излучения). можно перенести (с изменением знака) в правую часть уравнения:

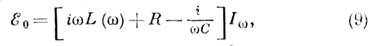
где C –емкость контура. Коэффициент (9) позволяет нам рассматривать значение Z L =iwLas индуктивная часть импеданса цепи (атомная Z C =-i/w С –емкостной, а Z R =R– является активной частью всего импеданс Z=Z L +Z C +Z R ). Принято считать, что двухполярное сопротивление является индуктивным, если его мнимая часть больше нуля [если рассматривать эхр (-iwt)-процессы, то она меньше нуля]. В технике принято называть И. любой двухполюсник, импеданс которого имеет индуктивный характер и линейно зависит в определенном диапазоне частот. Если индуктивные элементы являются катушками самоиндукции, то их можно рассматривать как биполярные, в общем случае, только если взаимодействие через магнитные поля между ними и другими элементами цепи пренебрежимо мало. Затем их импедансы могут быть добавлены в соответствии с принципами Кирхгофа: при последовательном соединении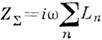
где C –емкость контура. Коэффициент (9) позволяет нам рассматривать значение Z L =iwLas индуктивная часть импеданса цепи (атомная Z C =-i/w С –емкостной, а Z R =R– является активной частью всего импеданс Z=Z L +Z C +Z R ). Принято считать, что двухполярное сопротивление является индуктивным, если его мнимая часть больше нуля [если рассматривать эхр (-iwt)-процессы, то она меньше нуля]. В технике принято называть И. любой двухполюсник, импеданс которого имеет индуктивный характер и линейно зависит в определенном диапазоне частот. Если индуктивные элементы являются катушками самоиндукции, то их можно рассматривать как биполярные, в общем случае, только если взаимодействие через магнитные поля между ними и другими элементами цепи пренебрежимо мало. Затем их импедансы могут быть добавлены в соответствии с принципами Кирхгофа: при последовательном соединении и, в случае параллельного соединения 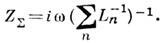При описании сильноточных цепей часто возникает необходимость обобщить понятие И. на случай нелинейных систем. Если неподвижный проводящий контур расположен в пространстве, где вектор магнитной индукции равен В и напряженность магнитного поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то магнитный поток, связанный с контуром, можно рассматривать как однозначную функцию тока F=F(I). Согласно закону индукции Фарадея, ЭДС самоиндукции в цепи равна:
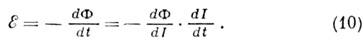При описании сильноточных цепей часто возникает необходимость обобщить понятие И. на случай нелинейных систем. Если неподвижный проводящий контур расположен в пространстве, где вектор магнитной индукции равен В и напряженность магнитного поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то магнитный поток, связанный с контуром, можно рассматривать как однозначную функцию тока F=F(I). Согласно закону индукции Фарадея, ЭДС самоиндукции в цепи равна:

L E (I)=d Ф /dИназ. Дифференциальная (или иногда динамическая) I. Выражение для накопленной энергии постоянного тока имеет вид: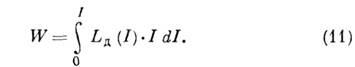

В линейном приближении (при I “0) L Д “L и выражения (10), (11) могут быть преобразованы в (2) и (3) соответственно. Лит: I. Е. Тамм, Основы теории электричества, 9-е издание, М., 1976; П. Л. Калантаров и Л. А. Цейтлин, Расчет индуктивностей, 3-е издание, Л., 1986; Л. Д. Ландау и Е. М. Лифшиц, Электродинамика сплошных сред, 2-е издание, М., 1982. M. A. Миллер, Г. В. Пермитин.

Энциклопедия физики. В пяти томах. – Москва: Советская энциклопедия . Под редакцией А. М. Прохорова . 1988 .

В этом случае процесс происходит следующим образом. Когда клавиша S4 замкнута, цепь будет замкнута, и ток должен течь. Однако индукционная катушка препятствует изменению тока, и в первый момент после замыкания ключа ток останется равным 0! Фактически, катушка в этой точке представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке в целом. Другой способ посмотреть на это – Ur=I*R. Падение напряжения на резисторе равно I*R, I равно 0, поэтому напряжение на резисторе также равно 0, и к катушке будет приложено общее напряжение U. Тогда ток в катушке увеличится. В области 0 линейно по способу (см. рис. 19 ~~“Переход Суворова через Альпы”~~ “Экспонента проходит через 0 под углом 45 градусов”). Ток увеличится, и падение напряжения на резисторе также увеличится. А на катушке падение соответственно увеличится, потому что часть напряжения будет забираться резистором. Поэтому со временем линейность увеличения тока в цепи будет нарушена. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U, ток перестанет увеличиваться, потому что напряжение на катушке станет равным 0 (все напряжение упадет на резисторе).

Индуктивность

Выше мы рассмотрели два основных понятия в электротехнике – идеальный генератор напряжения и идеальный генератор тока.

Идеальный генератор напряжения производит определенное напряжение U (давление в аналогии с гидравликой) при любой нагрузке (внешнее сопротивление цепи).

Согласно закону Ома I=U/R, даже если R обратится в ноль, а ток увеличится до бесконечности.

Внутреннее сопротивление идеального генератора напряжения равно 0.

Идеальный генератор тока производит заданный ток I (поток в аналогии с гидравликой), даже если сопротивление внешней цепи уходит в бесконечность. Напряжение на нагрузке также стремится к бесконечности U=I*R.

Внутреннее сопротивление идеального генератора тока равно ∞.

Здесь прослеживается определенная симметрия, двойственность.

Мы рассматриваем конденсатор C, который может накапливать заряд (отсюда его название – емкость) C=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление), когда в конденсатор закачивается заряд U=Q/C.

Если емкость заряда очень велика (стремится к бесконечности), то такая конденсатор с бесконечной емкостью будет идеальным генератором напряжения. Он никогда не разряжается, может выдавать любой ток, и напряжение на нем остается постоянным.

Симметричным по отношению к конденсатору является индуктивность. Индуктивность обозначается буквой L (см. схему ниже).

Обычно сам электронный компонент называется индуктори его параметром является индуктивность L.

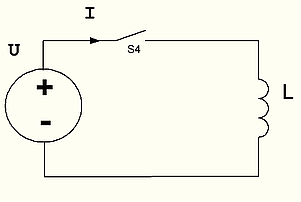
Рисунок 13: Подключение индуктора к генератору напряжения.

В то время как конденсатор является генератором напряжения, индуктивность является генератором тока. Индуктивность стремится сохранить ток в цепи постоянным, т.е. предотвращает изменение тока в цепи.

Индуктивность бесконечного размера является идеальным генератором токаТ.е. он будет бесконечно управлять заданным током I независимо от сопротивления нагрузки.

Как хорошо сказано в Вики – “Сравнивая электрический ток со скоростью в механике и электрическую индуктивность с массой в механике, ЭДС самоиндукции похожа на сила инерции.”

Это как если бы вы подошли к тележке, стоящей на рельсах, и начали толкать ее (прикладывать к ней силу). Тележка начнет медленно разгоняться, и “ток будет течь по проводам все быстрее и быстрее”. Затем попробуйте затормозить тележку, и она медленно остановится.

Аналогично в индуктивности, при подаче напряжения ток будет постепенно увеличиваться (тележка разгоняется), а при подаче напряжения другой полярности – постепенно уменьшаться (тележка тормозит).

Отсюда вывод, что “~~Поезд не может быть остановлен немедленно!”.~~

“Ток в индуктивности не может быть остановлен немедленно!

Это означает, что даже если вы повернете переключатель S4 на схеме и разомкнете цепь, ток все равно будет течь в течение первого мгновения после этого! На практике это приводит к искрению между контактами в выключателе, когда он размыкается.

Сопротивление при размыкании контактов возрастет до бесконечности (фактически до очень больших значений), а протекающий ток создаст на этом сопротивлении очень большое напряжение, так что воздушный зазор между контактами будет пробит.

В гидравлической аналогии это явление можно сравнить с гидравлическим ударом, когда масса воды в гидравлической системе набирает скорость, и при резком закрытии крана вода, продолжая свое инерционное движение, создает высокое давление, которое может привести к разрыву трубы.

Причины, по которым индуктивность обладает такими свойствами (сохранение тока в цепи), хорошо описаны в Вики -. https://ru.wikipedia.org/wiki/Самоиндукция

“Когда ток в цепи изменяется, магнитный поток через поверхность, ограниченную этой цепью, также изменяется пропорционально. Изменение этого магнитного потока, согласно закону электромагнитной индукции, приводит к индуктивному возбуждению ЭДС в этой цепи. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда таково, что когда ток в цепи увеличивается, ЭДС самоиндукции препятствует этому увеличению (направлена против тока), а когда ток уменьшается, она препятствует его уменьшению (в том же направлении, что и ток). Явление самоиндукции можно наблюдать в замедлении процессов угасания и восстановления тока.”

Что касается конденсатора, то основное отличие от индуктивности, говоря простым языком, заключается в том, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность, наоборот, пропускает постоянный ток и не пропускает переменный.

Здесь есть один момент – постоянный ток – это ток, который не изменяется со временем, то, что мы называем “компонентом постоянного тока” с частотой 0 Гц. Конденсатор не пропускает его. Это не так.

Но индуктивность вообще не пропускает переменный ток бесконечной частоты. И только переменный ток любой конечной частоты пропускает его немного.

Однако к понятию напряжения переменного тока мы вернемся позже.

Рассмотрим схему на рисунке 13 – комбинацию индукционной катушки и генератора напряжения.
Ниже приведен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.

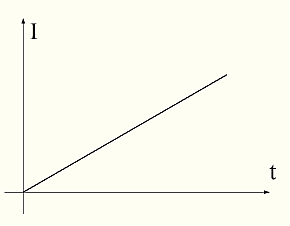
Рис. 14 График тока в катушке индуктивности при подаче на нее постоянного напряжения.

При подаче постоянного напряжения на индукционную катушку ток в ней линейно увеличивается со временем.

Мы помним аналогичную картину для конденсатора.

Напряжение на конденсаторе линейно увеличивается при подаче на него постоянного тока.

Что произойдет, если мы запитаем индуктивность от генератора тока?

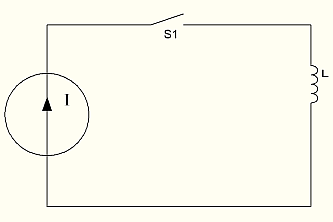
Рисунок 15: Подключение индуктивности к генератору тока.

Это немного похоже на ситуацию “слон или кит”.

Попробуйте проанализировать, как работает схема (подсказка – обычно схема показана с ошибкой. Что это такое? Как правильно нарисовать схему?)

Цепи, содержащие конденсатор и индуктивность

Как упоминалось выше, индуктивность играет ту же роль в электротехнике, что и масса в механике. А что является эквивалентом конденсатора в механике? Конденсатор – это генератор напряжения, т.е. он создает силу, которая перемещает поток заряда по проводникам. Выше мы привели аналог конденсатора в виде напорной башни, которая наполняется водой (заряд) и в ней повышается давление (напряжение).

Но можно также представить конденсатор в виде пружины – когда он заряжен, пружина сжимается, и сжимающая сила (напряжение) увеличивается. Мощность в этом случае является обратной величиной жесткости пружины. Чем жестче пружина, тем быстрее увеличивается сила сжатия. То есть, комбинация конденсатора и индуктивности эквивалентна каретке, прикрепленной к пружине. )

Что произойдет, если конденсатор подключить к индуктору, например, как в схеме на рисунке 16?

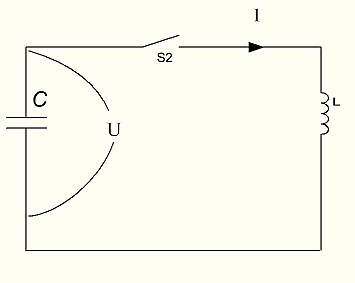
Рисунок 16: Параллельное соединение конденсатора и индуктора.

Пусть конденсатор C заряжен до напряжения U. Выключатель S2 замыкается, и в цепи начинает течь ток. Это эквивалентно сжатию пружины и последующему ее отпусканию в определенный момент (закрытие ключа S2).

В первый момент после замыкания ключа ток в цепи будет равен 0, поскольку индуктивность препятствует изменению тока. На тележку действует сила, но в первый момент ее скорость равна 0. Затем сила тока начинает увеличиваться (тележка ускоряется). Пружина все больше разряжается, скорость каретки (ток) увеличивается, и в какой-то момент пружина оказывается разжатой. Конденсатор разрядился до 0. Но. Мы помним, что “ток в индуктивности не может быть остановлен немедленно!”. Повозка ускорилась, и даже если мы не будем ее толкать, она будет двигаться по инерции. Это означает, что индуктивность будет удерживать ток при зарядке конденсатора, но в другой полярности – заряд теперь будет накапливаться на другой стороне конденсатора. Возрастающее напряжение противоположного знака на конденсаторе будет препятствовать перемещению зарядов, и в конечном итоге ток в цепи станет равным нулю. Но конденсатор уже был заряжен напряжением U другой полярности!

Таким образом, цепь достигла состояния, когда конденсатор заряжен, а ток в цепи равен нулю.
Хммм… но это то же самое состояние, с которого мы начали, только полярность напряжения обратная. Поэтому процесс повторится, но ток потечет в другом направлении, и система вернется в исходное состояние. Каретка переместится назад, минуя положение равновесия, и инерция снова сожмет пружину.

Возникает колебательный процесс. Это означает, что тележка на пружине будет катиться вперед и назад, и в отсутствие потери энергии (трения) этот процесс будет продолжаться бесконечно.

Таким образом, комбинация конденсатора и индуктивности создает колебательный элемент. Такие элементы широко используются в электротехнике для создания генераторов переменного тока и фильтров переменного напряжения.

Концепцию переменного тока мы обсудим в следующей статье.

UPD.
Поскольку возник спор о том, увеличивается ли ток экспоненциально при подключении индукционной катушки к генератору напряжения или линейно, я скажу еще несколько слов по этому вопросу.

Откуда берется экспоненциальное увеличение тока в цепи рис.13?
Ответ находится ниоткуда. Его там нет. Ток увеличивается линейно, а зависимость между током и напряжением описывается формулой

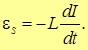
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения тока в цепи.
Чтобы обеспечить U=const (а U – это производная тока катушки), ток должен увеличиваться линейно.

Так откуда же взялись разговоры об экспоненциальных показателях? Это связано с тем, что ток растет линейно только в идеальном случае – в цепи с идеальным генератором напряжения (с бесконечной мощностью и нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае, с учетом внутреннего сопротивления, схема будет выглядеть следующим образом.

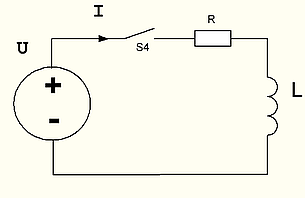
Рис. 17: подключение индуктора к генератору напряжения с учетом внутреннего сопротивления.

В схеме рис.17, R – внутреннее сопротивление генератора и индукционной катушки. (Они по-прежнему соединены последовательно, поэтому вы можете использовать одно R как сумму этих сопротивлений).

В этом случае процесс происходит следующим образом. Когда клавиша S4 замкнута, цепь будет замкнута, и ток должен течь. Однако индукционная катушка препятствует изменению тока, и в первый момент после замыкания ключа ток останется равным 0! Фактически, катушка в этой точке представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке в целом. Другой способ посмотреть на это – Ur=I*R. Падение напряжения на резисторе равно I*R, I равно 0, поэтому напряжение на резисторе также равно 0, и к катушке будет приложено общее напряжение U. Тогда ток в катушке увеличится. В области 0 линейно по способу (см. рис. 19 ~~“Переход Суворова через Альпы”~~ “Экспонента проходит через 0 под углом 45 градусов”). Ток увеличится, и падение напряжения на резисторе также увеличится. А на катушке соответственно уменьшиться, так как часть напряжения будет забираться резистором. Поэтому со временем линейность увеличения тока в цепи будет нарушена. Когда падение напряжения на резисторе I*R будет равно напряжению генератора U, ток перестанет увеличиваться, потому что напряжение на индукторе будет равно 0 (все напряжение упадет на резисторе).

В этом случае мы получаем экспоненциальный график увеличения тока в индуктивности.

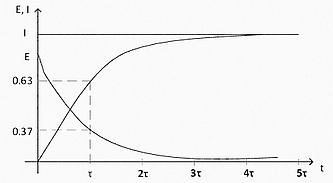Рис. 18 Экспоненциальный график нарастания тока в индуктивности. 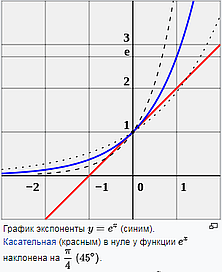Рис. 18 Экспоненциальный график нарастания тока в индуктивности. Рис. 19 “Экспонента проходит через 0 под углом 45 градусов”.

зы. В интернете так много различной ереси об индукционных катушках. Это невероятно.
“Индукционная катушка также обладает очень интересным свойством. Когда к катушке прикладывается постоянное напряжение, в течение короткого времени в ней возникает противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от величины индуктивности катушки. Поэтому при подаче напряжения на катушку ток плавно изменяется от 0 до некоторого значения в течение долей секунды, так как напряжение при подаче электрического тока также изменяет свое значение от нуля до фиксированного значения.”
Ну… поскольку здесь ничего не говорится о резисторе в цепи, это не на короткое время, а до тех пор, пока входное напряжение не будет снято. Вторая часть звучит неверно, но направление правильное – ток из цепи увеличивается от нуля до….. без резистора – до бесконечности, с резистором – I=Uin/R.

Предположим, что обычная индукционная катушка подключена к источнику напряжения через ключ. Когда ключ закрыт, напряжение подается на индуктивность, вызывая быстрое изменение тока, протекающего через нее. Когда приложенное напряжение увеличивается от нуля до своего пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение противоположной полярности приложенному напряжению. Напряжение, индуцируемое при подаче энергии на индуктор, называется обратной ЭДС и определяется уравнением 1:

VL = – L*(di/dt), (1)
Где:
VL – это напряжение (обратное ЭДС), индуцированное на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.

По-видимому, здесь пытались описать начальный момент самоиндуцированного электромагнитного поля, но это оказалось бессмыслицей. Сказать, что “индуцированное напряжение имеет полярность, противоположную приложенному напряжению” – это то же самое, что сказать: “Падение напряженияпадение напряжения на резисторе противоположно полярности приложенного напряжения.” Да, все верно, приложенное напряжение складывается с падением напряжения, и за резистором получается 0. Правильно, лол.
“ЭДС самоиндукции” в катушке аналогична “падению напряжения” на резисторе. Только в резисторе электрическая энергия рассеивается, преобразуясь в тепло, тогда как в индукторе она сохраняется, преобразуясь в энергию магнитного поля. В гидравлической аналогии индуктор похож на турбину, вставленную в водопроводную трубу и обладающую моментом инерции. Турбина пропускает воду только при вращении. Итак, открывается кран, давление подается на турбину, она начинает вращаться, и ток течет по трубе. Чем быстрее вращается турбина, тем больше ее мощность. Турбина вращается, ток увеличивается и так до бесконечности. Это происходит в том случае, если нет потерь энергии – резистор. Но если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся затраченная энергия будет израсходована на трение, турбина перестанет разгоняться, а сила тока достигнет своего максимального значения.

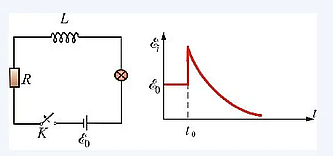
Рисунок 20 Переходный процесс в цепи с индуктивностью

Изображение неправильное. В правильном варианте при отключении источника резистор подключается, и цепь остается замкнутой.

Рассмотрим следующую схему

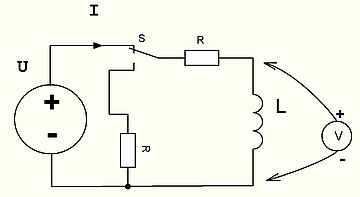
Рис.21 Цепь с индуктивностью и переключателем

Вопрос для загадки: Каково напряжение на индуктивности в первый момент, когда переключатель S переключается из положения “вверх” в положение “вниз”?

Совет: Не ломайте голову, пытаясь понять, каким будет знак самоиндукции ЭМП и что с ним произойдет дальше. Вам нужно применять простое эмпирическое правило:
В первый момент после переключения ток в индуктивности остается неизменным.
Затем примените закон Ома.

Индуктивность – это элемент цепи, в котором энергия накапливается за счет магнитного поля. Таким образом, поле накапливается или преобразуется в другие виды энергии. Самый идеальный пример – индукционная катушка. Он накапливает поле и преобразует его в другие виды энергии, включая тепловую. Способность сохранять магнитное поле – это индуктивность. Индуктивность напрямую связана с электромагнитной индукцией, о которой у нас на сайте также есть статья. В этой статье мы опишем это физическое явление, как оно возникает, как используется на практике, как его измеряют и как можно рассчитать его физические свойства. К ним будут добавлены два клипа и одна статья на тему по вашему выбору.

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и ЭДС в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, как правило, различны. Таким образом, если предположить, что начальная фаза тока равна нулю, то начальные фазы напряжения и электродвижущей силы будут иметь определенные значения ϕ и ψ, соответственно. При этих условиях мгновенные значения тока, напряжения и ЭДС будут выражаться следующими формулами:

u = Um sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

Сопротивление цепи, учитывающее невозвратные потери электроэнергии из-за теплового воздействия тока, называется активным сопротивлением. Можно предположить, что это сопротивление для тока низкой частоты равно сопротивлению R того же проводника для постоянного тока и может быть найдена по формуле:

В цепи переменного тока с единственным активным сопротивлением, например, в лампочках, нагревательных приборах и т.д., сдвиг фаз между напряжением и током равен нулю, т.е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одной и той же фазе, а электрическая энергия полностью расходуется на тепловой эффект тока.

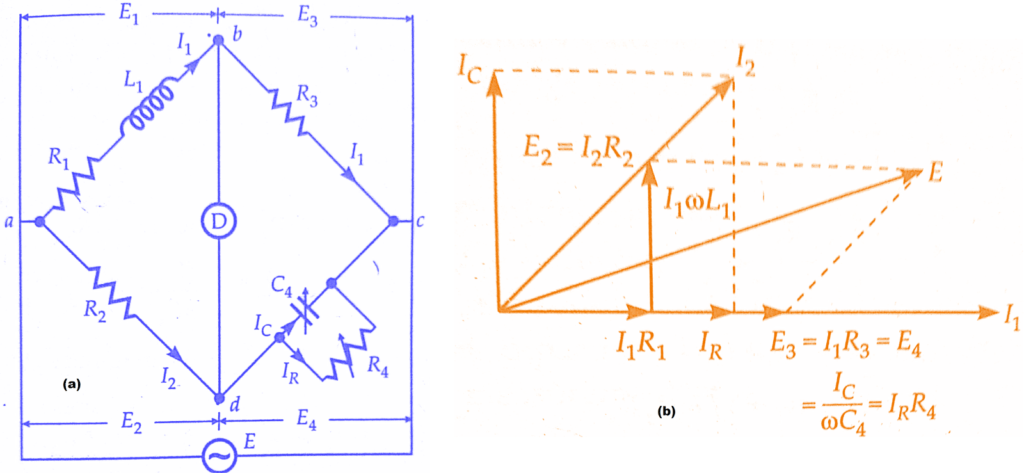
Включение катушки индуктивности L в цепь переменного тока приводит к увеличению сопротивления цепи. Это связано с тем, что при переменном токе в катушке постоянно действует э.д.с. самоиндукции, которая ослабляет ток. Сопротивление X_Lкоторое обусловлено явлением самоиндукции, называется индуктивным сопротивлением. Поскольку чем больше индуктивность цепи и чем быстрее изменяется ток, индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

Влияние индуктивного сопротивления на ток в цепи наглядно иллюстрирует эксперимент, показанный на рис. 26.6. Когда в катушку вставляют ферромагнитный сердечник, лампа гаснет, а когда сердечник вынимают, она снова загорается. Это происходит потому, что индуктивность катушки значительно увеличивается, когда в нее вставляется сердечник. Обратите внимание, что напряжение на индуктивном резисторе опережает ток по фазе.

Постоянный ток не протекает через конденсатор, потому что между катушками находится диэлектрик. Если конденсатор подключен к цепи постоянного тока, ток в цепи прекратится, когда конденсатор зарядится.

Пусть конденсатор подключен к цепи переменного тока. Заряд конденсатора (q=CU) постоянно меняется из-за изменения напряжения, поэтому в цепи течет переменный ток. Чем больше емкость конденсатора и чем чаще он заряжается, тем выше частота переменного тока. Сопротивление, обусловленное емкостью в цепи переменного тока, называется емкостью Xc. Она обратно пропорциональна емкости C и круговой частоте ω;

Сравнение уравнений (26.11) и (26.12) показывает, что индукторы представляют собой очень большое сопротивление для высокочастотного тока и малое сопротивление для низкочастотного тока, а конденсаторы – наоборот. Напряжение на емкостном сопротивлении Xa задерживается в фазе относительно тока. Индуктивный X_L и емкость Резисторы Xc обозначаются как pреактивные резисторы. Теория переменного тока доказывает, что при последовательном соединении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

и является индуктивным в точке X_L > Xc и является емкостным при X_L < Xc.

Подводя итоги, отметим, что средняя активная мощность переменного тока, которая показывает, какое количество энергии в единицу времени передается электрическим током на данном участке цепи, задается формулой:

Мощность, потребляемая только за счет теплового воздействия тока, выражается формулой:

Для того чтобы увеличить активную мощность переменного тока, необходимо увеличить cos ϕ. (Объясните, почему cos ϕ имеет наибольшее значение в точке X_L=X_C.)

Источник (печатная версия): Словарь русского языка : в 4-х томах / РАН, Институт лингвистических исследований ; под ред. А. П. Евгеньевой. – 4-е изд. – М.: Рус. яз; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Значение слова “индуктивность”.

Источник (печатная версия): Словарь русского языка: в 4-х томах / РАН, Институт лингвистических исследований; под ред. А. П. Евгеньевой. – 4-е изд. – М.: Русс. Джаз; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Индуктивность (или коэффициент самоиндукции) – это отношение пропорциональности между электрическим током, протекающим в замкнутом контуре, и общим магнитным потоком, также называемым потоком катушки, создаваемым этим током через поверхность, краем которой является контур.

– ток в цепи,

Нередко говорят об индуктивности прямого длинного провода (см.). В этом случае и в других (особенно в неквазистационарных случаях), где замкнутый контур нелегко определить адекватно и однозначно, приведенное выше определение требует специального уточнения; подход (упомянутый ниже), связывающий индуктивность с энергией магнитного поля, кажется частично полезным для этой цели.

Индуктивность используется для выражения самоиндукции ЭДС в цепи, возникающей при изменении тока в цепи:

Угол j, под которым расположена проволока, определяется соотношением

Индукционные катушки

Индукционные катушки обладают свойством обеспечивать реактивное сопротивление для переменного тока и незначительное сопротивление для постоянного тока. Вместе с конденсаторами они используются для создания фильтров для частотной селекции электрических сигналов, для создания элементов задержки и памяти, для соединения цепей с помощью магнитного потока и т.д. В отличие от резисторов и конденсаторов, они не являются стандартизированными изделиями, а изготавливаются для конкретных целей и имеют такие параметры, которые необходимы для выполнения конкретных преобразований электрических сигналов, токов и напряжений.

Работа индукторов основана на взаимодействии тока и магнитного потока. Известно, что при изменении магнитного потока Ф в проводнике в магнитном поле возникает ЭДС, которая определяется скоростью изменения магнитного потока

Поэтому, когда источник постоянного напряжения подключается к проводнику, ток в проводнике устанавливается не сразу, так как при включении изменяется магнитный поток и в проводнике индуцируется ЭДС, которая препятствует увеличению тока, но через некоторое время, когда магнитный поток перестает изменяться. Если к проводнику подключен источник переменного напряжения, то ток и магнитный поток будут непрерывно изменяться, а наведенная в проводнике ЭДС будет препятствовать протеканию переменного тока, что эквивалентно увеличению сопротивления проводника. Чем выше частота изменения напряжения, приложенного к проводнику, тем больше величина наведенной в нем ЭДС, и, следовательно, тем большее сопротивление оказывает проводник протекающему току. Это сопротивление X L не связано с потерей энергии и поэтому является реактивным. Если ток изменяется синусоидально, то индуцированная ЭДС будет равна

Она пропорциональна частоте w , а коэффициентом пропорциональности является индуктивность L. Следовательно, индуктивность характеризует способность проводника сопротивляться переменному току. Значение этого сопротивления X L = w L

Индуктивность короткого проводника (мкГн) определяется его размером:

где l – длина проволоки в см, d – диаметр проволоки в см.

Если провод намотать на каркас, образуется катушка индуктивности. В этом случае магнитный поток концентрируется, и значение индуктивности увеличивается.

2.3.2.Конструкции индукционных катушек.

Конструктивной основой индукционной катушки является диэлектрический каркас, на который намотан провод в виде спирали. Обмотка может быть однослойной (рис.2.21,а) или многослойной (рис.2.21,6). В некоторых случаях многослойная намотка выполняется в поперечном сечении (рис.2.21,в). Плоские спиральные индукторы используются в интегральных схемах (рис.2.21,г).

Магнитные сердечники используются для увеличения индуктивности. Сердечник, помещенный внутрь катушки, концентрирует магнитное поле и тем самым увеличивает ее индуктивность. Перемещая сердечник внутри каркаса, можно изменять индуктивность. На рисунке 2.22 показаны три различных типа цилиндрических сердечников: С-образные, Т-образные и PR-резьбовые, а также два типа бронированных стержней. Бронированные сердечники состоят из двух чашек 2, изготовленных из карбонильного железа или феррита.

Они могут быть закрытыми (тип SB – a) или открытыми (тип SB – b). Для изменения индуктивности используется обрезанный цилиндрический сердечник 1. Кроме цилиндрических и броневых сердечников используются также тороидальные (кольцевые) сердечники. На высоких частотах (десятки – сотни МГц) используются цилиндрические диамагнитные сердечники (латунь, медь). Вставка этих сердечников в катушку уменьшает индуктивность.

В индукторах, работающих при низких напряжениях, в качестве сердечников используются пермаллои. Эти сердечники изготавливаются из тонких пластин толщиной 0,002-0,1 мм.

Чтобы уменьшить влияние электромагнитного поля катушки на другие элементы схемы и уменьшить влияние внешних полей на катушку индуктивности, ее помещают внутрь металлического экрана, как показано на рис. 2.23 (1 – вилка, 2 – экран, 3 – корпус, 4 – обмотка, 5 – каркас, 6 – настроечный стержень, 7 – чашечный сердечник, 8 – основание, 9 – отливка).

2.3.3 Индуктивность и емкость индукторов.

Индуктивность – это основной параметр индуктора. Его значение (µTn) определяется следующим образом

L=L 0 W 2 D . 10 -3

где W – число витков, D – диаметр катушки в см, L 0 – коэффициент, зависящий от отношения длины катушки / к ее диаметру O.

Для однослойных катушек L 0 определяется следующим соотношением

Оптимальным диаметром катушки в этом случае является соотношение, а диаметр катушки составляет от 1 до 2 см. Для расчетов диаметр катушки D принимается равным диаметру сепаратора D 0

В случае многослойных катушек значение L 0 зависит не только от величины 1/D , но и от отношения толщины обмотки t к диаметру катушки D. Оно определяется по графикам (рис. 2.24). В этом случае внешний диаметр катушки D=D 0 + 2t

При расчете индукционной катушки сначала определяют геометрические размеры катушки и определяют коэффициент L 0, затем находят число витков в зависимости от заданного значения индуктивности L:

где I – в мкГн, D – в см.

Обычно катушка наматывается на оптимальный диаметр провода, который рассчитывается с помощью эмпирических формул и графиков. Для этого используйте график S=f(t/D; l /D) (рисунок 2.25) и найдите вспомогательный коэффициент S. Затем вычисляется коэффициент

где f – в мкГц, D – в см. Затем выведите коэффициент a 1

где f – частота в Гц. Затем по графику b 1 = f (a 1) (рис. 2.26) находят вспомогательный коэффициент b 1S и рассчитывают оптимальный диаметр проволоки (мм).

Полученное значение округляется до ближайшего стандартного значения (см. табл. 2.6) и выбирается марка проволоки диаметром d.

Основные параметры обмоточных проводов

Максимальный диаметр в изоляции , мм

После выбора оптимального диаметра проволоки необходимо проверить возможность укладки обмотки с заданными размерами l и t . Для однослойных катушек шаг намотки следует рассчитывать следующим образом

Если t> d of, то обмотка будет размещена. В противном случае задается большее значение l, и расчет повторяется.

Для многослойных катушек рассчитывается толщина катушки

где a – коэффициент провисания обмотки (a = 1,05. 1,3), и найти действительное значение внешнего диаметра катушки D=D 0 +2t. Если это значение отличается от выбранного в начале расчета более чем на 10%, то определяются новые значения для l и t и расчет повторяется. Размещение катушки в корпусе уменьшает индуктивность катушки

где h – коэффициент, зависящий от соотношения l /D (рис. 2.27).

D – диаметр катушки,

D eq – диаметр щита.

Чем меньше диаметр экрана, тем больше уменьшается индуктивность. В большинстве случаев D ek /D >1,6yo1,8. В этом случае индуктивность уменьшается максимум на 20%.

Многослойные катушки обычно строятся с бронированными сердечниками, в которых большая часть линий магнитного поля катушки замыкается сердечником, а меньшая часть – воздухом, так что влияние экрана на индуктивность катушки значительно уменьшается.

Использование сердечников из магнитных материалов уменьшает количество витков индукционной катушки и, следовательно, ее размер. Основным параметром сердечника является магнитная проницаемость m c Таким образом, индуктивность катушки составляет

Поскольку расчетные формулы содержат эмпирические коэффициенты, индуктивность изготовленной катушки отличается от расчетной. Использование обрезанных магнитопроводов позволяет получить необходимое значение индуктивности.

Индуктивная емкость является паразитным параметром индуктора, ограничивающим его применение. Его возникновение обусловлено конструкцией индуктора: емкость возникает между отдельными витками, между витками и сердечником, между витками и экраном, между витками и другими элементами конструкции. Все эти распределенные емкости могут быть объединены в одну, называемую собственной емкостью индуктора C L

Однослойные индукторы имеют наименьшую внутреннюю емкость Это приближение рассчитывается по формуле (pF)

где D – диаметр катушки в см. Обычно он не превышает 1-2пФ.

Емкость многослойных катушек намного выше. В многослойной последовательной обмотке он достигает ZOpF, в обмотке “в стену” он несколько меньше. Значительное снижение емкости многослойных катушек достигается за счет использования универсальной намотки, при которой провод укладывается под определенным углом к цилиндрической форме каркаса. Схема такой обмотки показана на рис. 2.28. Когда провод достигает края катушки, направление выравнивания меняется на противоположное. Цикл универсальной обмотки таков, что, сделав один оборот вокруг каркаса, проволока возвращается в положение, отличающееся от первоначального на угол b . Этот угол выбирается таким образом, чтобы каждый последующий виток примыкал к предыдущему.

Угол j, под которым располагается проволока, определяется соотношением

где l – осевая длина катушки,

D – диаметр катушки.

Наименьшее значение угла j получается для витков с наименьшим диаметром, равным диаметру рамы D 0.

Как правило, при использовании универсальной обмотки длина катушки принимается равной от 2 до 10 мм. Число циклов обмотки связано с расчетным числом витков W с помощью соотношения

Значение удельной емкости катушки с универсальной обмоткой варьируется от 3 до 8пФ. Дополнительное снижение емкости достигается за счет змеевидной намотки, как показано на рис. 2.21c.

Совместное влияние индуктивности и емкости можно учесть, введя понятие эквивалентной индуктивности катушки, определяемой из уравнения.

где – собственная резонансная частота индукционной катушки.

Если рабочая частота намного ниже собственной резонансной частоты в L , то можно считать, что L e =L.

В процессе эксплуатации на катушку воздействуют различные внешние факторы, такие как температура, влажность и другие, которые влияют на ее индуктивность, причем наиболее существенным является влияние температуры, которое оценивается температурным коэффициентом .

Температурная нестабильность индуктивности вызвана несколькими факторами: при нагревании увеличивается длина и диаметр провода катушки, увеличивается длина и диаметр каркаса, что вызывает изменение шага и диаметра витков; кроме того, изменение температуры вызывает изменение диэлектрической проницаемости материала каркаса, что приводит к изменению емкости катушки.

Для повышения температурной стабильности используются рамы, изготовленные из материала с низким коэффициентом линейного расширения. Этим требованиям лучше всего отвечает керамика. Температурная стабильность катушки повышается благодаря прочному сцеплению обмотки с каркасом катушки. Для этого намотка осуществляется путем обжига серебра в керамический каркас. В этом случае изменение размера проводящего слоя определяется только линейным расширением каркаса. Такие индукторы имеют ТКЛ >(5-100) . 10 -6 Стабильность многослойных индукторов гораздо хуже, поскольку невозможно избежать изменения линейных размеров обмоточного провода. Многослойные катушки имеют TKL > (50-100) . 10 -6

2.3.4 Потери в индукционных катушках.

В индукционных катушках, помимо основного эффекта взаимодействия тока и магнитного поля, существуют паразитные эффекты, благодаря которым сопротивление катушки не является чисто реактивным и равно X L . Наличие паразитных эффектов приводит к потерям в катушке, оцениваемым сопротивлением потерь R P , которое определяет коэффициент качества индукционной катушки

Потери состоят из потерь в проводниках, диэлектрике, сердечнике и экране.

Потери в проводах обусловлены тремя причинами.

Во-первых, провода обмотки имеют омическое сопротивление

где l – длина проволоки катушки, d – диаметр проволоки, p – удельное сопротивление.

Это сопротивление (Ом) может быть выражено как функция числа витков W и среднего диаметра катушки D CP

где – диаметр проволоки в см.

Во-вторых, сопротивление провода катушки переменного тока увеличивается с ростом частоты, что обусловлено поверхностным эффектом, суть которого заключается в том, что ток протекает не через все сечение проводника, а через кольцевую часть сечения (рис. 2.29), ширина которой (мм) равна

где f – частота в МГц,

r – удельное сопротивление в мкОм-м.

Следовательно, провод длиной l имеет сопротивление переменного тока, равное

где S EF – площадь кольца, которая равна

После преобразования получаем

В-третьих, в обмотках возникает эффект близости (рис.2.30), суть которого заключается в смещении тока под действием вихревых токов и магнитного поля к краям провода, прилегающим к каркасу, в результате чего участок, по которому течет ток, принимает форму серпа, что приводит к дополнительному увеличению сопротивления провода.

Сопротивление r B, возникающее в результате эффекта близости, прямо пропорционально диаметру проволоки, в то время как сопротивление r P, возникающее в результате этого эффекта, обратно пропорционально диаметру проволоки (рис. 2.31).

Существует оптимальный диаметр проволоки d opt , при котором сопротивление проволоки

провода для высокочастотного тока r f = r B + r P минимальна. Для однослойных катушек d opt = 0,2-0,6 мм, для многослойных катушек d opt = 0,08-0,2 мм. Можно значительно снизить потери в проводниках, используя “литиевый провод”, состоящий из большего количества проводников, скрученных в жгут. При малых диаметрах тонких нитей поверхностный эффект подавляется, а скручивание нитей в пучок подавляет эффект близости.

Существует процедура расчета сопротивления r f , при которой сначала рассчитывается вспомогательный коэффициент

где f – частота в Гц,

d – диаметр проводника в см.

Затем по таблице вычисляем коэффициенты F(z) и G(z).

Затем по диаграмме (рис. 2.32) определяется вспомогательный коэффициент K z, который зависит от геометрии катушки.

Согласно (2.50), сопротивление провода катушки высокочастотному току вычисляется

где D – внешний диаметр катушки в см,

d – диаметр провода в см.

Если однослойная катушка намотана проводом оптимального диаметра с параметром z > 5, то сопротивление r f можно определить по формуле

где D в см, d в см, f в МГц.

Диэлектрические потери являются результатом того, что между соседними витками катушки существует емкость, которая имеет две составляющие: воздушную емкость C ov и диэлектрическую емкость C od (рис.2.33).

Диэлектрические потери определяются величиной tg d, зная которую можно рассчитать сопротивление потерь

r D = 0,25 C od tg d L 2 f 3 . 10 -3

где C od – в пф, L – в мкГн, f – в МГц.

Потери в сердечнике состоят из потерь на вихревые токи d in, гистерезисные потери d d и начальные потери d p, и учитываются как тангенс угла потерь в сердечнике

tg d c = d в f + d g H + d p

В справочниках приводятся значения . tg d c для различных типов сердечников. Сопротивление потерь определяется по формуле

r c = tg d в L

Потери в экране обусловлены тем, что ток, протекающий в катушке, индуцирует ток в экране. Потери на экране определяются

где D e – диаметр экрана в см,

l – длина экрана в см,

f – частота в МГц.

Значение h = f(l/D) определяется по графику (рис. 2.27).

Таким образом, полное сопротивление потерь индуктора, определяющее его коэффициент качества, равно

R p = r f + r e + r c + r e

На практике коэффициент качества варьируется от 30 до 200. Коэффициент Q увеличивается за счет оптимизации выбора диаметра провода, увеличения размера индукционной катушки и использования сердечников с высокой магнитной проницаемостью и низкими потерями. С учетом потерь и паразитных емкостей индукционная катушка может быть представлена в виде эквивалентной схемы (рис. 2).

схема (рис.2.34,а), где R n = r f + r e + r c + r e. Эту схему можно привести к более удобному виду (рис.2.34,б), где L e – эквивалентная индуктивность с учетом собственной емкости. Значения. L e и R n , и, следовательно, коэффициент качества Q = w L / R n зависят от температуры. Температурная зависимость Q задается температурным коэффициентом качества TKD= D Q / Q D T

2.3.5.Разновидности индукторов.

Катушки с круговой индуктивностью. Эти индукторы используются вместе с конденсаторами для создания резонансных контуров. Они должны обладать высокой стабильностью, точностью и коэффициентом качества. В диапазоне длинных и средних волн эти катушки являются многослойными, обычно с универсальными обмотками. Для повышения коэффициента качества используются многожильные литиевые провода. Цилиндрические сердечники из альсифера или карбонильного железа используются для изменения индуктивности.

В коротковолновом и ультракоротковолновом диапазонах используются однослойные катушки с индуктивностью порядка единиц микрогенри и коэффициентом добротности от 50 до 100. Число витков таких катушек не превышает одного-двух десятков, диаметр каркаса 10-20 мм. В качестве каркасов используются керамика, полиэтилен и полистирол. Ребристые рамки используются для уменьшения внутренней емкости. Обмотка выполнена из одножильного медного провода диаметром около 1 мм. На УКВ используются бескаркасные катушки из голого провода.

Катушки связи. Эти катушки используются для обеспечения индуктивной связи между отдельными контурами и каскадами. Это позволяет разделить постоянный ток между цепями базы и коллектора и т.д.

К таким катушкам не предъявляются жесткие требования по качеству и точности, поэтому они изготавливаются из тонкой проволоки в виде двух небольших витков. Основными параметрами этих катушек являются индуктивность и коэффициент связи.

где L 1 и L 2 – индуктивности соединенных катушек,

M – взаимная индуктивность между ними. Значение коэффициента связи зависит от расстояния между катушками, чем оно меньше, тем больше k.

Вариометры. Это катушки, в которых индуктивность может быть изменена во время работы для компенсации колебательных контуров.

Они состоят из двух катушек, соединенных последовательно. Одна катушка неподвижна (статор), другая находится внутри первой катушки и вращается (ротор). Изменение положения ротора относительно статора изменяет величину взаимной индукции и, следовательно, индуктивность вариометра.

L = L 1 + L 2 + 2M

В этой системе индуктивность может быть изменена в 4-5 раз.

Дроссели. Это индукторы с высоким сопротивлением для переменного тока и низким сопротивлением для постоянного тока. Обычно они включаются в схемы усилителей мощности. Они используются для защиты источников питания от высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические сердечники.

Индукционные катушки для ГИС. Тонкопленочные спиральные катушки используются на частотах порядка 10-100 МГц. На площади в 1 квадратный сантиметр не более 10 витков. Коэффициент качества этих катушек не превышает 20-30. Поэтому они имеют ограниченное применение. В ГИС предпочтительны миниатюрные тороидальные катушки на ферритовых сердечниках с индуктивностью до десятков тысяч микросеток.

В последнее время наметилась тенденция замены катушек специальными схемами на транзисторах (гираторами) и электромеханическими, пьезоэлектрическими и акустическими фильтрами, основанными на принципе механических упругих колебаний и механического резонанса. Скорость распространения упругих колебаний в твердых телах примерно в 100 000 раз меньше скорости распространения электромагнитных волн, что позволяет создавать очень компактные механические резонаторы с распределенными параметрами, коэффициент добротности которых составляет около 10 3 . Развитие микроэлектроники привело к созданию фильтров на основе приборов с зарядовой связью и фильтров на основе поверхностных акустических волн. Кроме того, активные RC-фильтры, в которых используются операционные усилители с глубокой частотно-зависимой обратной связью, широко применяются в интегральных схемах.

Давайте начнем перемещать проводник в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, в нашем проводнике возникает электродвижущая сила (ЭДС). Или наоборот, проводник остается на месте, а магнит перемещается так, чтобы силовые линии магнита пересекали проводник. Теперь у нас есть пример электромагнитной индукции. Величина электродвижущей силы, индуцированной в проводнике, прямо пропорциональна индукции магнитного поля, скорости движения и длине проводника.

Что такое дроссель

Дроссель – это тип индуктора, который обладает высоким сопротивлением для переменного тока и низким сопротивлением для постоянного тока.

Дроссели используются в следующих областях применения:

Для защиты оборудования от внезапных скачков напряжения;

Для снижения скорости нарастания тока короткого замыкания ;

Для уменьшения импульсных помех;

И это лишь малая часть мест, где используются душители.

Представьте, что у нас есть дроссель перед электродвигателем. И в какой-то момент происходит скачок тока, что происходит: Мы знаем, что когда ток проходит через дроссель, вокруг катушки создается электромагнитное поле. А для формирования поля необходима энергия, поэтому в самом начале протекания тока энергия расходуется на формирование электромагнитного поля. Согласно закону Ленца, мы знаем, что ток в катушке не может измениться мгновенно. А явление самоиндукции, когда ток меняется, направлено в сторону основного тока. Поэтому дроссель просто съест всплеск тока в сети.

Читайте далее: