Как найти напряжение источника

Из формулы следует, что чем больше внутреннее сопротивление источника тока, тем меньше внутренний ток I_w и большая часть тока I₀ подается на нагрузку. В пределе при R_w = ∞ весь ток I₀ подается на нагрузку, и ток нагрузки не зависит от напряжения нагрузки. В данном случае мы имеем дело с идеальным источником тока. Таким образом, в идеальном источнике тока внутреннее сопротивление бесконечно. В идеальном источнике тока с бесконечным сопротивлением нагрузки (разрыв цепи нагрузки) на его зажимах будет напряжение бесконечной величины.

Содержание

На источник понимается как элемент, снабжающий цепь электромагнитной энергией. Эта энергия потребляется пассивными элементами цепи – накапливается в индуктивностях и емкостях и рассеивается в активных сопротивлениях. Примерами реальных источников электромагнитной энергии являются генераторы постоянных, синусоидальных и импульсных сигналов различной формы, сигналы, получаемые от различных датчиков, антенн радиоприемников, источников питания, сигналы, поступающие с выходов электронных устройств и т.д.

Для анализа цепей удобно ввести идеализированные источники двух типов: источник напряжения и источник тока, которые учитывают основные свойства реальных источников. Соответствующим образом дополнив идеализированные источники пассивными элементами, можно передать все свойства реальных источников по отношению к их внешним выходам.

Источник напряжения. Источник напряжения определяется какисточник напряжения понимается как элемент с двумя клеммами (полюсами), между которыми прикладывается напряжение как функция времени независимо от тока, приложенного к внешней цепи. Зависимость напряжения от тока в идеальном источнике напряжения показана на рис. 1.3. Такой идеальный источник способен выдавать неограниченную мощность. Наиболее часто используемые графические представления источника напряжения показаны на одном рисунке, где предполагаемая положительная полярность напряжения источника обозначена либо стрелкой внутри круга, либо знаками “+”, “-“.

Реальные источники Источники сигналов имеют внутреннее сопротивление. Внутреннее сопротивление подключено последовательно с источником напряжения. На рисунке 1.4 показана вольт-токовая характеристика и схема реального источника напряжения. Для реального источника напряжения выходное напряжение составит

Из приведенной выше формулы следует, что выходное напряжение реального источника тока зависит от тока нагрузки I_н. Чем больше ток нагрузки, тем больше падение напряжения на внутреннем сопротивлении источника и тем меньше часть напряжения U₀ подается на нагрузку (выход). С другой стороны, чем больше внутреннее сопротивление R чем больше падает напряжение на нем, тем ниже напряжение на выходе источника питания. В электронных схемах внутреннее сопротивление источника часто называют выходное сопротивление.

Для идеального источника напряжения его внутреннее сопротивление равно 0, а напряжение на нагрузке не зависит от тока нагрузки. В этом случае ток нагрузки может возрастать до бесконечности, если сопротивление нагрузки стремится к 0. В действительности невозможно построить идеальный источник напряжения во всем диапазоне выходных токов. Однако во многих случаях, для ограниченного диапазона изменения выходного тока, некоторые источники можно считать идеальными.

Например, источник питания в диапазоне рабочих токов имеет очень маленькое внутреннее сопротивление, которым можно пренебречь, по сравнению с сопротивлением нагрузки. Другой пример: выходное сопротивление операционного усилителя с отрицательной обратной связью может достигать нескольких сотых долей ома. Этим внутренним сопротивлением можно пренебречь и рассматривать выход операционного усилителя как идеальный источник напряжения в диапазоне допустимых выходных токов.

Источник тока. Под идеальный источник тока определяется как элемент цепи, по выводам которого течет ток с определенным, зависящим от времени изменением напряжения между выводами. Вольт-амперные характеристики и графики идеального источника тока показаны на рис. 1.5. Независимость тока от напряжения означает, что внутренняя проводимость источника, в котором может протекать ток, равна 0, а его внутреннее сопротивление бесконечно. Вольт-амперная диаграмма и схема реального источника тока показаны на рис. 1.5.

Принципиальная схема реального источника тока показана на рис. 6. Когда напряжение нагрузки увеличивается за счет увеличения сопротивления нагрузки, внутренний ток источника тока увеличивается. Меньшая часть тока I₀ поступает в нагрузку. Выходной ток I_н будет равна

Из формулы следует, что чем больше внутреннее сопротивление источника тока, тем меньше внутренний ток I_w и большая часть тока I₀ подается на нагрузку. В пределе при R_w = ∞ весь ток I₀ подается на нагрузку, и ток нагрузки не зависит от напряжения нагрузки. В данном случае мы имеем дело с идеальным источником тока. Таким образом, в идеальном источнике тока внутреннее сопротивление бесконечно. В идеальном источнике тока, если сопротивление нагрузки бесконечно (разрыв цепи нагрузки), на его зажимах появится напряжение бесконечной величины.

Конечно, это идеализация – невозможно построить источник тока с внутренним сопротивлением бесконечности. На практике, однако, используются источники тока, построенные на транзисторах, с внутренними сопротивлениями, достигающими значений во много мегаом и более, работающие в ограниченном диапазоне выходных напряжений. Такие источники тока широко используются в дифференциальных и операционных усилителях, цифро-аналоговых преобразователях, токовых петлях и т.д.

Фактические источники напряжения и тока эквивалентны. Это означает, что цепи ведут себя одинаково по отношению к своим клеммам, т.е. один и тот же источник при анализе цепи может рассматриваться как реальный источник напряжения или реальный источник тока. Условия эквивалентности могут быть получены из выражения для напряжения реального источника напряжения

Разделите правую и левую части уравнения на R_wполучаем

Введем обозначение U₀ /R_w = I₀ = const; U₀ /R = I_w и запишите уравнение в следующем виде

И с сопротивлениями R_{за пределами} и Р_н падает на одно и то же напряжение U_нт.е. они соединены параллельно

Это приводит нас к схеме реального источника тока, показанной на рисунке 1.6.

Поскольку цепи реальных источников напряжения и тока эквивалентны, возникает вопрос, когда использовать один или другой источник при анализе цепи? Ответ прост. Используйте тот тип источника, который облегчает анализ работы схемы. На практике это часто бывает именно так. Если внутреннее сопротивление источника намного меньше сопротивления нагрузки, целесообразно рассматривать его как источник напряжения. В качестве первого приближения величиной внутреннего сопротивления можно пренебречь. Если внутреннее сопротивление намного больше, чем сопротивление нагрузки, такой источник следует рассматривать как источник тока. В предварительном анализе он считается идеальным. Более детальный анализ схемы учитывает неидеальный характер источника тока.

Не нашли то, что искали? Используйте поиск:

Лучшие высказывания: Самое главное для студента – не сдать экзамен, а вовремя его вспомнить. 10070 – | 7511 – или прочитать их все.

78.85.5.224 © studopedia.ru Я не являюсь автором размещенного материала. Но я обеспечиваю его бесплатное использование. Было ли нарушено авторское право? Свяжитесь с нами | Обратная связь.

Снова активируйте AdBlock!
и обновите страницу (F5)
срочно требуется

Давайте посмотрим, не сможем ли мы выяснить, что за источник питания и как он называется в различных схемах.

Обычно источник питания условно представляется так, как показано на схеме ниже:

Однако на диаграммах это отображается следующим образом:

Здесь показан источник питания. источник тока в составе генератора тока, собранного с использованием биполярных транзисторов.

Источником тока или генератором тока обычно называют двухполярный генератор тока, который вырабатывает ток независимо от сопротивления подключенной к нему нагрузки. И так часто называют любой источник электрического напряжения (розетка, генератор, аккумулятор и т.д.). Однако только в физическом смысле это не совсем корректный термин; напротив, источники напряжения, используемые в бытовых целях, чаще называют источниками ЭМП.

Приведенная выше диаграмма включает источник тока как часть эквивалента трехполярного транзистора. Стрелка указывает на положительное направление тока. Однако ток, генерируемый этим источником, зависит от напряжения на другом конце этой цепи.

Закон Кулона

Чему равно напряжение.

Напряжение напрямую связано с работой тока, заряда и сопротивления. Для непосредственного измерения напряжения в электрической цепи необходимо подключить к ней вольтметр. Он подключается к цепи параллельно, в отличие от амперметра, который подключается последовательно. Клеммы измерительного прибора подключаются к точкам, между которыми необходимо рассчитать напряжение. Чтобы он показывал правильное значение, цепь должна быть включена. Вольтметр обозначается на схемах буквой V, обведенной кружком.

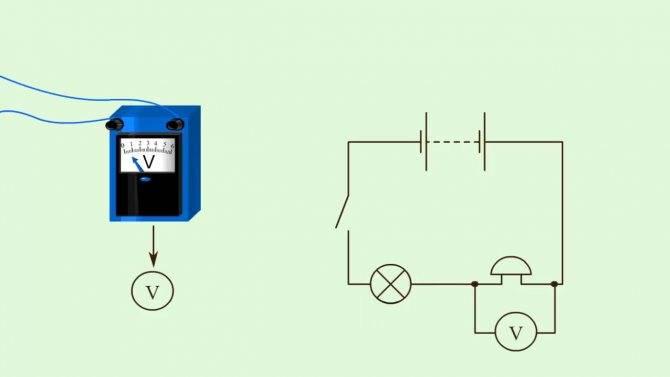
Фотография вольтметра и схемы

Напряжение обозначается латинской аббревиатурой [U] и измеряется в [В]. Она равна работе, которую совершает поле при перемещении единичного заряда. Формула для напряжения тока – U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Вас интересуют особенности дифференциального тока

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.

Электрическое поле

Согласно законам Кирхгофа, подсистема уравнений топологической схемы выглядит следующим образом

РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

В Цепи постоянного тока Применяются постоянные напряжения, протекают постоянные токи и присутствуют только резистивные элементы (резисторы).

Идеальный источник напряжения это источник, в котором напряжение на зажимах, создаваемое внутренней электродвижущей силой (ЭДС), не зависит от тока, который он производит в нагрузке (рис. 6.1a). В этом случае имеет место равенство. Вольт-амперная характеристика идеального источника напряжения показана на рис. 6.1б.

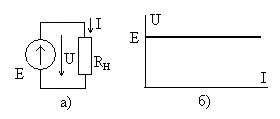
Идеальный источник тока это источник, который подает в нагрузку ток, не зависящий от напряжения на зажимах источника, рис. 6.2a. Его вольт-амперная характеристика показана на рис. 6.2б.

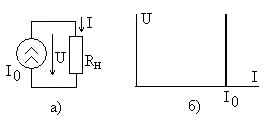
В сопротивление Связь между напряжением и током определяется законом Ома в форме

Пример электрической цепи показан на рис. 6.3. Она состоит из следующих частей Филиалыкоторые заключаются в последовательном соединении нескольких элементов (источник E и сопротивление ) или одного элемента ( и ) и узлы – точки соединения трех и более ветвей обозначены жирными точками. В приведенном примере есть ветвь и узел.

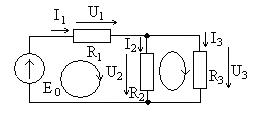
Кроме того, схема обозначена независимые замкнутые контурыкоторые не содержат идеальных источников тока. Их количество равно . В примере на рис. 6.3 их количество , например, цепей с ветвями E и , показано на рис. 6.3 овалами и стрелками, обозначающими позитивное направление Связь между токами и напряжениями в цепях показана стрелками на рис. 6.3.

Связь между токами и напряжениями в цепи определяется законами Кирхгофа.

Первый Первый закон Кирхгофа: Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю,

Токи, втекающие в узел, имеют знак плюс, а токи, вытекающие из узла, имеют знак минус.

Второй закон КирхгофаВторой закон Кирхгофа: алгебраическая сумма напряжений на элементах замкнутой независимой цепи равна алгебраической сумме ЭДС идеальных источников напряжения, включенных в эту цепь,

Напряжения и ЭДС берутся со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в противном случае используется знак минус.

Для примера, показанного на рис. 6.3, получаем подсистему определяющих уравнений, следующих закону Ома

Согласно закону Кирхгофа, подсистема уравнений топологической цепи имеет вид

Расчеты в соответствии с законом Ома

Этот метод удобен для расчета относительно простых цепей с одним источником. Он заключается в вычислении сопротивления тех участков цепи, для которых известен ток (или напряжение).

цепь, для которой известен ток (или напряжение), а затем определить неизвестное напряжение (или ток). Возьмем схему, показанную на рис. 6.4, с током идеального источника A и сопротивлениями Ом, Ом, Ом. Необходимо определить токи ветвей и , и напряжения на сопротивлениях , и .

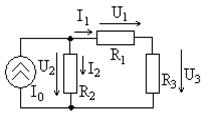Если нам известен ток источника, мы можем рассчитать сопротивление цепи относительно клемм источника тока (параллельное соединение сопротивлений и последовательное соединение резисторов).

Рис. 6.4 сопротивление i ),

Напряжение на источнике тока (на сопротивлении ) равно

Затем мы можем найти токи ветвей.

Полученные результаты можно проверить, используя первый закон Кирхгофа в форме . Подставляя вычисленные значения, получаем A, которое совпадает со значением тока источника.

Зная токи ветвей, нетрудно найти напряжения на резисторах (значение уже найдено).

Согласно второму закону Кирхгофа . Суммируя результаты, проверяем, выполнен ли он.

Расчет электрической цепи с использованием уравнений Кирхгофа

Давайте рассчитаем токи и напряжения в цепи, показанной на рис. 6.3 w и . Цепь описывается системой уравнений (6.4) и (6.5), из которых для токов ветвей получаем

Из первого уравнения выражаем , а из третьего уравнения получаем

Из второго уравнения следует, что

Из уравнения закона Ома получаем

Легко видеть, что второй закон Кирхгофа выполняется

Подставив числовые значения, получаем

Те же результаты можно получить, используя только закон Ома.

Мощность в цепи постоянного тока

Применение к цепи идеальные источники отдают энергию в подключенную к ним цепь (нагрузку). Для схемы на рис. 6.1а мощность, отдаваемая идеальным источником напряжения, равна

Для цепи на рис. 6.2а идеальный источник тока отдает мощность в нагрузку

Внешний резистивный контур, подключенный к источнику, принимает энергию от источника и преобразует ее в другие формы энергии, чаще всего в тепло.

Если через сопротивление течет ток, а приложенное к нему напряжение равно , то для мощности, потребляемой сопротивлением, получим

Принимая во внимание уравнения закона Ома (6.1), мы можем написать

Если в цепи имеется более одного сопротивления, то сумма потребляемых ими мощностей равна полной мощности, отдаваемой в цепь всеми действующими в ней источниками. Это условие равновесия сил.

Например, для схемы на рис. 6.3 в общем случае получаем

Подставляя в левую часть уравнения (6.11) полученные ранее выражения для токов, получаем

Это соответствует правой части выражения (6.11).

Аналогичный расчет можно выполнить для схемы на рис. 6.4.

Условие баланса мощности позволяет нам дополнительно проверить правильность расчетов.

В последнем примере мы рассчитаем напряжение, выдаваемое батареей, учитывая значения тока (I) и сопротивления (R):

Формула закона Ома

Фундаментальное открытие Ома заключалось в том, что электрический ток, протекающий через металлический проводник в цепи при любой температуре, прямо пропорционален приложенному к нему напряжению. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь между напряжением, током и сопротивлением:

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в два других варианта, решив для I и R соответственно:

В соответствии с выражением, написанным выше,

Электрическая цепь с двумя источниками

Электрическая цепь может содержать несколько источников или потребителей электроэнергии. Такие схемы называются сложные схемыДля расчета основных величин в таких схемах используются специальные методы.

На рисунке 1 показана цепь с двумя источниками переменного тока: E₁ и E₂. Источники имеют внутреннее сопротивление r₁ и r₂. Нагрузка обозначается как резистор с сопротивлением R. Поскольку цепь не разветвлена, ток во всех ветвях будет одинаков и равен I

Рисунок 1: Схема электрической цепи с двумя источниками электромагнитного поля

Помимо закона Ома, для расчета сложных цепей используются два закона Кирхгофа.

Одним из самых простых способов расчета цепи с двумя источниками электрического тока является метод Метод суперпозиции токов. Этот метод основан на аддитивное свойство токовсогласно которому ток в цепи равен алгебраической сумме токов, производимых каждым источником независимо друг от друга. Это правило применимо к любой линейной цепи (т.е. цепи, в которой сопротивления всех участков постоянны).

Предположим, что цепь имеет только один источник переменного тока E₁тогда ток в цепи будет

Давайте теперь предположим противоположную ситуацию, что существует только один источник ЭДС E₂и источник E₁ присутствует, но не вырабатывает ток. Тогда ток в цепи будет равен

Два источника электромагнитного поля в цепи направлены в противоположные стороны, поэтому полный ток I будет равна разности токов I₁ и I₂

Из свойства аддитивности токов можно сделать важный вывод: если ЭМП E₁ и E₂

Если значения E₁ и E₂ различны, цепь генерирует ток, направление которого совпадает с направлением тока, генерируемого “bо“большее” ЭМП. Другими словами, если E₁ > E₂направление тока совпадает с ЭДС E₁если E₁ < E₂направление тока меняется на противоположное. На рисунке 1 выбранное направление тока соответствует первой ситуации (E₁ > E₂).

Электродвижущая сила E₂направленный в направлении, противоположном току I направление называется счетчик или счетчик ЭМП ..

Давайте рассмотрим процессы и перечислим основные взаимосвязи, которые соответствуют каждому участку схемы.

W ab существует сопротивление источника ЭДС r₁а действие самого источника совпадает с направлением тока I. Таким образом, источник действует как генератор (источник энергии). Поэтому ЭДС источника равна сумме напряжения на его зажимах и внутреннего падения напряжения

В соответствии с выражением, написанным выше,

Другими словами, напряжение на клеммах источника, отдающего энергию в цепь, равно разности между ЭДС источника и внутренним падением напряжения.

Согласно закону Ома, при bc падение напряжения равно

Следует также отметить, что на отрезке прямой bc электрическая энергия преобразуется в тепловую, выделяя мощность, равную

В последнем рассматриваемом сегменте последний рассматриваемый сегмент ca источник ЭМП E₂ действует противоположно направлению тока I. Источник имеет сопротивление r₂. На этом участке происходит потеря мощности (нагрев), равная r₂ ⋅ I 2 . Кроме того, источник ЭМП генерирует собственную энергию E₂⋅ Iчтобы преодолеть силы противодействующего ЭМП. Оказалось, что источник со счетчиком ЭДС выступает в качестве потребителя (приемника) в схеме.

Мощность, излучаемая при ca равна .

Таким образом, напряжение в этой точке составляет

Исходя из вышеприведенного утверждения, можно сделать вывод, что напряжение на выход источника, действующего на равна сумме самой ЭДС и внутреннего падения напряжения на нем.

Рассмотрим в качестве примера схему на рис. 4.11, а, которая используется для измерения сопротивления (схема моста Уитстоуна).

Законы Кирхгофа

Два закона Кирхгофа, вытекающие из закона сохранения энергии, используются для расчета электрических цепей в дополнение к закону Ома.

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к разъемам в электрических цепях:
В ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

В эту сумму входят токи разных знаков, в зависимости от их направления относительно узла. На основе первого закона Кирхгофа можно рассчитать уравнение для токов для каждого узла. Например, для точки 3 на рис. 3.16 уравнение имеет вид
I₁ + I₂ – I₄ – I₇ = 0.
В этом уравнении токи, направленные к узлу, считаются положительными, а токи, направленные от узла, считаются отрицательными:
I₁ + I₂ = I₄ + I₇. (4.2)

Уравнение (4.2) дает другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу в электрической цепи, равна сумме токов, направленных от этого узла.

Этот закон следует из принципа непрерывности тока. Если допустить преобладание токов одного направления в узле, то заряд одного знака должен накапливаться и потенциал узловой точки должен изменяться непрерывно, чего не происходит в реальных цепях.

Второй закон Кирхгофа

Второй закон Кирхгофа применим к электрическим цепям:
В электрической цепи алгебраическая сумма напряжений на ее ветвях равна нулю:

Чтобы доказать второй закон Кирхгофа, давайте обойдем контур 1-2-3-4-5-6-1 на рис. 3.16 по часовой стрелке и напишем выражения для потенциалов точек контура при указанных направлениях токов в ветвях (выбираются произвольно). Начнем с точки 1, потенциал которой V₁. Выразим потенциал каждой последующей точки по отношению к предыдущей: V₂ = V₁ + Е₁; V₃ = V₂ – I₁R₁; V₄ = V₃ – I₄R₄; V₅ = V₄ – E₃; V₆ = V₅ + I₆R₆; V₁ = V₆ – I₃R₃.
Изменение потенциала вдоль выбранной цепи должно быть равно нулю, поскольку оно выражает работу, затраченную на перемещение частиц, имеющих вместе единичный заряд, по замкнутому пути в электрических полях источников и потребителей энергии. Таким образом, в замкнутом контуре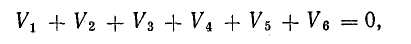

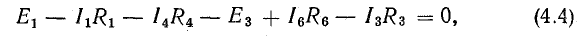
или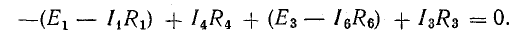

В этом уравнении напряжения ветвей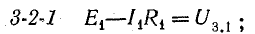

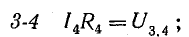
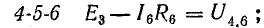
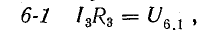
поэтому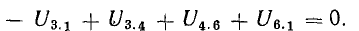

В уравнении (4.4) напряжение, направленное вокруг цепи, считается положительным, а направленное в сторону от цепи – отрицательным.
Запишем уравнение (4.4) в следующем виде: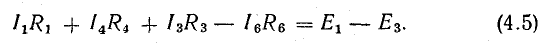

Уравнение (4.5) позволяет по-другому сформулировать второй закон Кирхгофа:
В электрической цепи алгебраическая сумма падений напряжения на реактивных элементах равна алгебраической сумме э.д.с. этой цепи:

Другие петли соответствуют другим уравнениям, которые нетрудно написать без необходимости выражать потенциалы точек петли.

Для этого можно использовать следующее правило. В левой части уравнения напишите алгебраическую сумму падений напряжения на реактивных элементах цепи, а в правой – алгебраическую сумму э.д.с., возникающих при прохождении цепи.

Токи и э.д.с., направление которых совпадает с направлением обхода, считаются положительными.
Следуя этому правилу, напишем уравнения для двух других контуров схемы, показанной на рис. 3.16:
для 1-2-3-6-1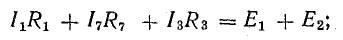

для 3-4-6-3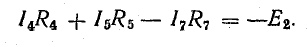

Неразветвленная цепь

Элементы неразветвленной электрической цепи соединяются последовательно.

Отличительной особенностью последовательного соединения является то, что электрический ток одинаков во всех частях цепи.

Общий случай последовательного соединения

Рассмотрим общий случай последовательного соединения источников и потребителей электроэнергии (рис.4.1), пренебрегая внутренними сопротивлениями источников. Приравняем цепь по второму закону Кирхгофа с любым направлением тока в цепи и направлением обхода цепи (например. по часовой стрелке):

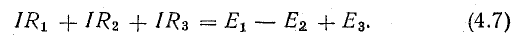
Ток в цепи

Для петли округления видно, что относительно направления округления, уравнение.₁ и Е₃ находятся в одном направлении, т.е. в одном направлении и E₂ – находятся относительно друг друга.
Ток в цепи определяется действием всех трех э.д.с., а учитывая направления э.д.с. и тока, нетрудно заключить, что элементы с э.д.с. E₁ и Е₃ вырабатывают электроэнергию, а элемент с E₂ потребляет его. Если источники э.ф.к. в данном случае предполагаются как батареи, то источники E₁ и Е₃ разряжается, а источник E₂ загружается.
В элементах цепи, характеризующихся сопротивлениями R₁, R₂ и Р₃Электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера диаграмму на рисунке 4.1, легко увидеть, что второй закон Кирхгофа. 4.1 в качестве примера, легко увидеть, что второй закон Кирхгофа является следствием закона сохранения энергии в применении к цепи.

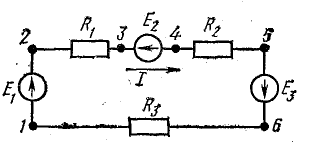
Рисунок 4.1: Схема неразветвленной цепи

Для этого просто умножьте уравнение (4.7) на I, переведя ранее E₂ на левую сторону: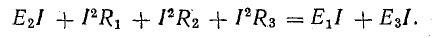

Выведем уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электроэнергии равна сумме мощностей нагрузок.

Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощности сохранится, если переставить элементы цепи, сгруппировав уравнения и сопротивления, как показано на рис. 4.2. 4.2, а.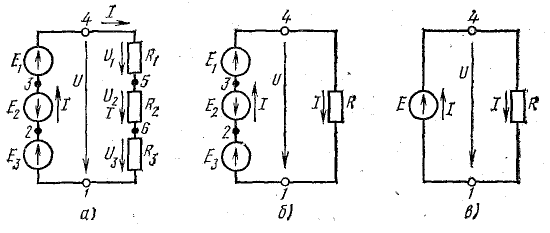

Рисунок 4.2: Преобразование неразветвленной цепи

Последовательное соединение пассивных элементов

Цепь 4-5-6-1 представляет собой последовательное соединение резисторов. К данному участку прикладывается напряжение U, которое равно алгебраической сумме э.д.с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение также равно сумме падений напряжения в правой части цепи [см. левую часть уравнения (4.7)].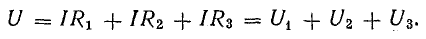

Выбросив I за скобки, получаем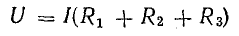

или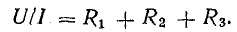

Отношение U/I = R – это некоторое сопротивление, эквивалентное всем трем сопротивлениям: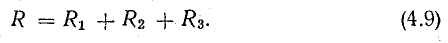

Это равенство позволяет заменить три сопротивления на участке 4-5-6-1 одним (эквивалентным) и получить более простую схему (рис. 4.2, б), при условии, что ток в цепи не изменится и сохранится тот же баланс мощностей. Этот вывод можно распространить на любое количество последовательно соединенных реактивных элементов:

т.е. Полное сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.

Последовательное подключение источников ЭДС.

Участок 1-2-3-4 схемы на рисунке 4.2 4.2, a представляет собой последовательное соединение источников ЭДС. Напряжение между точками 4-1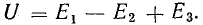
Последнее уравнение позволяет нам заменить отрезок 1-2-3-4 на три (эквивалентных), например.

и получаем более простую схему (рис. 4.2, c), в которых имеется только одна (эквивалентная) э.м.ф. E.

Это можно распространить на любое количество источников, соединенных последовательно. Если э.ф. всех источников равны и правильно направлены, как в случае с батареей внутри батареи, то суммарная э.ф. может быть определена по формуле

где E_n – э.д.с. одного элемента; n – количество элементов в батарее.

Как показано на эквивалентной диаграмме (рис. 4.2, в),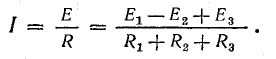

Диаграмма потенциалов

В системе, показанной на рис. 4.1, от точки 1 до точки 2 потенциал увеличивается на E₁а от точки 2 к точке 3 уменьшается на U_2.3 = IR₁. При переходе от точки 3 к точке 4 потенциал уменьшается на U_3.4 = -E₂.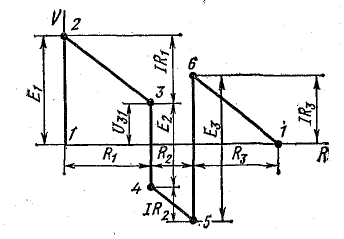

Рисунок 4.3: Потенциальная диаграмма электрической цепи

Изменение потенциала в электрической цепи может быть графически проиллюстрировано в виде потенциальной диаграммы.

Потенциальная диаграмма – это график изменения потенциала при прохождении через цепь, построенный в прямоугольной системе координат, в которой ось абсцисс представляет собой сопротивление участков цепи, а ось ординат – потенциалы соответствующих точек на определенной шкале. Потенциальная диаграмма цепи, показанной на рис. 4.1, приведена на рис. 4.3.

Потенциалы точек в цепи определяются в соответствии с уравнениями

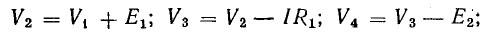
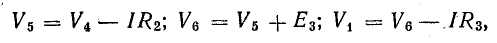
Потенциал в точке 1 принимается равным нулю.

Поскольку собственное сопротивление источников, например, предполагается равным нулю, потенциалы при прохождении через эти элементы изменяются ступенчато.

Проблема 4.3.

Генератор постоянного тока, батарея и два резистора постоянного сопротивления образуют неразветвленную цепь._г = 120 В; внутреннее сопротивление r_г = 1,0 Ом, эффективность батареи E_а = 72 В; внутреннее сопротивление r_а = 3 Ом, R₁ = 16 Ом, R₂ = 12 Ом.
Определите силу тока в цепи, выполните баланс мощности и постройте график потенциала цепи.
Решение. Прослеживая схему цепи (рис. 4.4), мы видим, что и батарея, и генератор включаются в соответствии: относительно произвольного направления обхода цепи обе э.д.с. направлены в одну сторону.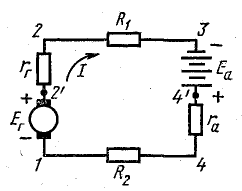

Рисунок 4.4 К задаче 4.3

Эквивалентное внутреннее сопротивление цепи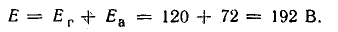

Эквивалентное внутреннее сопротивление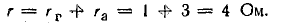

Эквивалентное сопротивление нагрузки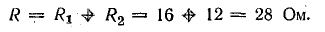

Ток в цепи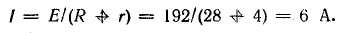

Чтобы получить баланс мощности, найдите мощность каждого элемента в цепи:
генератор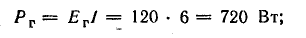

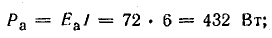
потери внутри генератора

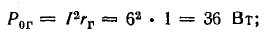
потери внутри батареи

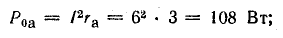
расход энергии в резисторе R₁

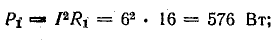
расход энергии в резисторе R₂

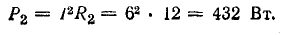
Баланс мощности (суммарная мощность источников энергии равна суммарной мощности потребления)

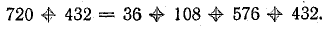
Чтобы построить потенциальную диаграмму, найдите потенциалы точек цепи, принимая потенциал точки 1 V₁ = 0:

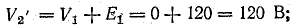
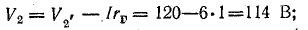
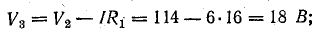
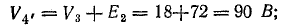
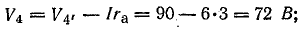
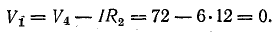
Потенциальная диаграмма показана на рис. 4.5.

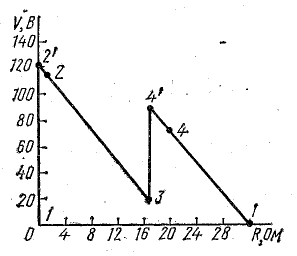
Рисунок 4.5: Потенциальная диаграмма.

Разветвленная электрическая цепь с двумя узлами

Разветвленная электрическая цепь, как следует из названия, состоит из нескольких ветвей.

Ветви, подключенные к одной паре узлов, соединяются параллельно (рис. 4.7, а). Характеристика параллельного соединения заключается в том, что на все ветви подается одинаковое напряжение.

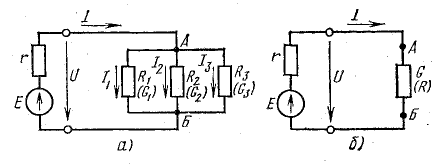
Рисунок 4.7: Преобразование цепи с параллельным соединением нагрузок

Параллельное соединение пассивных компонентов

Потребители электроэнергии, показанные на схеме рис.4.7, и с сопротивлениями R₁, R₂, R₃ и источник электричества E с внутренним сопротивлением r подключены к одной и той же паре узлов (точки A и B). Сформулируем уравнение токов для узла A в соответствии с первым законом Кирхгофа: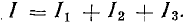
Токи потребителей могут быть выражены в терминах напряжения между узлами и проводимости ветвей: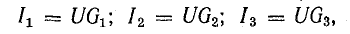

где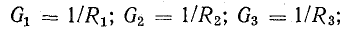

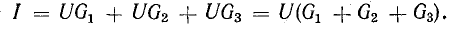
Разделите это уравнение на U: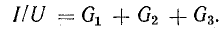

Отношение UU – это проводимость G, соответствующая общему току цепи и общему напряжению:

Этот вывод можно распространить на любое число n приемников, соединенных параллельно:

Когда пассивные ветви соединены параллельно, общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.

Исходя из уравнений (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).

Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из следующего уравнения

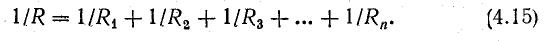
Очень часто два ответвления подключаются параллельно. В этом случае эквивалентный импеданс задается формулой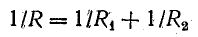

Схема на рис. 4.7, б, полученная заменой трех проводимостей одной (эквивалентной) проводимостью, является простейшей схемой электрической цепи.
Ток в цепи, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле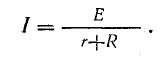

Цель этой схемы – определить не только общий ток, но и ток в каждой ветви.

Если даны все сопротивления и общий ток, то после определения напряжения между узлами и токами ветвей с помощью закона Ома (3.15), необходимо определить напряжение между узлами и токами ветвей: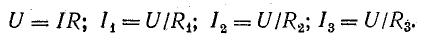

Параллельное подключение источников питания

На практике часто встречаются случаи, когда источники энергии подключены параллельно с одной или несколькими нагрузками (рис. 4.8).

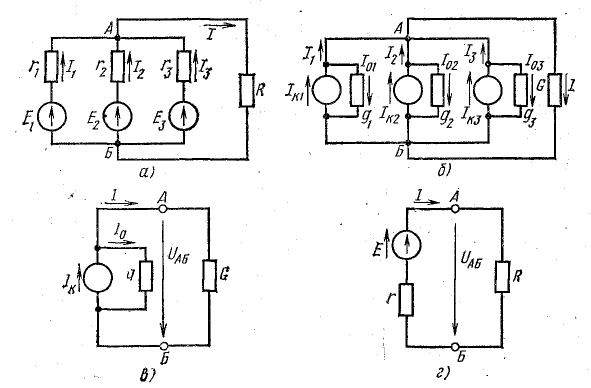
Рисунок 4.8: Преобразование цепи с параллельным соединением источников

В таких случаях определение токов в источниках решает важную проблему распределения нагрузки между ними.

Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

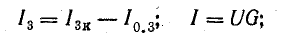
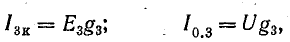
где U = U_ab – напряжение между узловыми точками A и B.

Согласно первому закону Кирхгофа, для узла A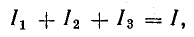

или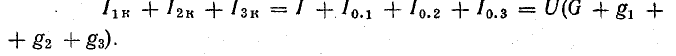

Это равенство позволяет заменить три источника тока одним (эквивалентным) и заменить рис. 4.8, б на более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания, равным

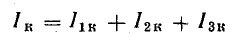
и внутренняя проводимость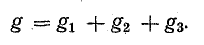

Для схемы на рис. 4.8, в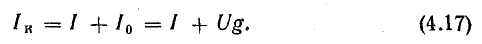

Напряжение между узлами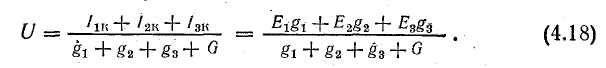

Токи ветвей могут быть определены по следующим формулам:

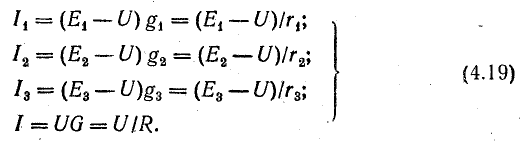
Эти выражения показывают, что источники с относительно большей э.д.с. и меньшим внутренним сопротивлением имеют больший ток, т.е. несут большую нагрузку. Если э.д.с. и внутренние сопротивления источников одинаковы, то нагрузка равномерно распределяется между ними.

Полный ток в этом случае определяется произведением тока одного источника I_n раз больше количества источников, подключенных параллельно:

Величина тока каждого источника ограничена его номинальным значением I_номвыше которого источник не может быть перегружен. Параллельное соединение источников используется для увеличения общего тока, что увеличивает потребляемую мощность без изменения напряжения.

От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником мощности (рис. 4.8, г), разделив уравнение (4.17) на g: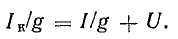

Поскольку l/g = r – внутреннее сопротивление эквивалентного источника ЭДС, I_кr = Ir + U.
Но я_кr – E – ЭДС эквивалентного источника; Ir – падение напряжения на внутреннем сопротивлении, поэтому E = U + Ir.

Рассматривается метод расчета разветвленных электрических цепей, который предполагает замену всех источников электроэнергии одним (эквивалентным) источником, обычно называемым эквивалентным генератором.

Общий случай параллельного соединения источников и потребителей электроэнергии.

Полученные ранее выводы и формулы могут быть применены для расчета электрических цепей с двумя узлами, между которыми имеется любое количество параллельных ветвей с источниками и потребителями энергии, включая также такие ветви, которые имеют несколько последовательно соединенных элементов (например, цепь рис. 4.9).

Процедура расчета таких цепей, которая заключается в предварительном определении напряжения между узловыми точками, называется методом узловых напряжений.

Для применения этого метода необходимо определить проводимости источника и ветвей (последняя может быть определена, если определены сопротивления каждой ветви).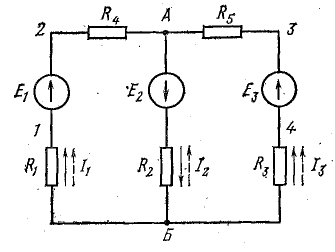

Рисунок 4.9: Схема с двумя узлами

В общем случае токи ветвей и э.д.с. могут иметь разные направления, поэтому при определении узлового напряжения возьмите алгебраическую сумму произведений э.д.с., и уравнение (4.18) примет следующий вид

Признак э.д.с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от B к A).

Выход ветви считается положительным, если его направление совпадает с положительным направлением тока. В противном случае он подставляется со знаком минус в формулу (4.21), а также при определении токов по формуле (4.19).

Задача 4.8.

Для цепи, показанной на рис. 4.7, а, известно: E = 130 В, r = 0,5 Ом, R₁ = 30 Ом, R₂ = 20 Ом, R₃ = 12 Ом. Определите токи в цепи, мощность, передаваемую приемникам, и КПД источника.
Решение. Сначала определите эквивалентное сопротивление между точкой A и точкой B: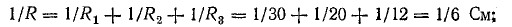

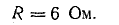
Ток в неразветвленной части цепи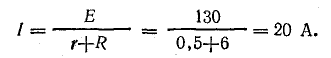

Для определения токов параллельной ветви между узловыми точками определите напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках: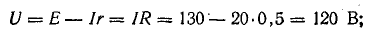

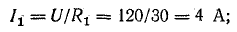
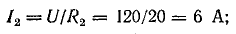
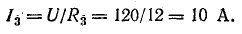
Проверим правильность определения токов с помощью уравнения (4.1):

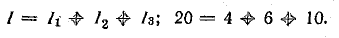
Передача электроэнергии потребителям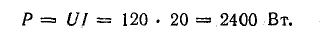

Энергоэффективность источника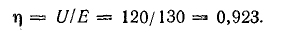

Проблема 4.10.

Для цепи, показанной на рис. 4.7, а, известны следующие свойства: R₁ = 10 Ом; R₂ = 15 Ом; R₃ = 6 Ом, r = 0,5 Ом, l₃ = 10 А. Определите токи в цепи, мощность и КПД источника.
Решение. Используя заданные условия для третьей ветви, определите напряжение между узлами A и B, используя закон Ома: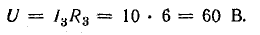

Напряжение U является общим для всех ветвей, подключенных к точкам A и B. Это позволяет нам использовать одну и ту же формулу для определения токов в обеих ветвях: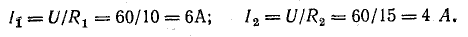

Ток в неразветвленной части цепи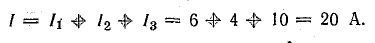

выход источника.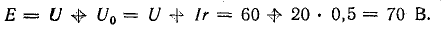

Мощность источника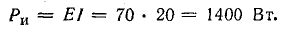

Потребляемая мощность нагрузок

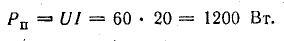
Исходный выход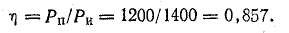

Задание 4.12.

Определите токи и выполните баланс мощности для цепи, показанной на рис. 4.9, если известны следующие данные: E₁ = 120 В; E₂ = 80 В; E₃ = 60 В; r₁ = 0,5 Ом; r₂ = 0,4 Ом; r₃ = 0,2 Ом; R₁ = 2 Ом; R₂ = 15,6 Ом; R₃ = 12,4 Ом; R₄ = 7,5 Ом; R₅ = 7,4 Ом.
Решение. Используя метод узловых напряжений, найдите U_AB в соответствии с формулой (4.21). Заранее определим положительное направление токов от B к A и рассчитаем проводимости ветви: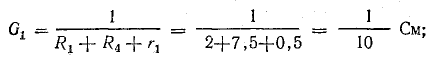

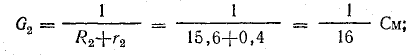
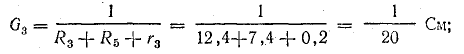
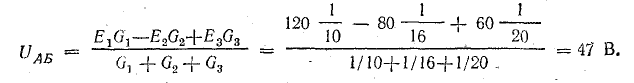
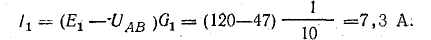
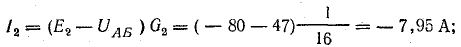
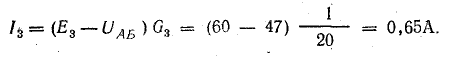
Токи l₁ и l₃ являются положительными. Их направление совпадает с ранее выбранным условно положительным направлением от узла B к узлу A. Направление тока l₂ противоположно положительному направлению; результирующий ток отрицательный. В схеме на рис. 4.9 пунктирная линия показывает положительное направление токов в ветвях, а сплошная стрелка – их фактическое направление.

Для баланса мощности необходимо рассчитать мощность каждого элемента схемы, включая мощность потерь внутри источников. Обратите внимание, что направления тока и силы тока во всех ветвях одинаковы – источники тока являются источниками энергии.
Мощность источников составляет P_1.1 = E₁I₁ = 120 – 7,3 = 876 ВТ; P_1.2 = Е₂I₂ = 80 – 7,95 = 636 W; P_1.3 = E₃I₃ = 60 – 0.65 = 39 W.
Общая мощность источников составляет 1 551 Вт.

При определении мощности источников можно не задаваться вопросом, в каком режиме работает источник. Ответ на этот вопрос дает знак полученной мощности, если заменить токи и выходные мощности на знаки, принятые или полученные при расчете. Например, мощность второго источника положительна: P_1.2 = -80 – (-7.95) = 636 W. Это означает, что в этой ветви работает источник питания. Ранее Е₂ и я₂ были сразу же признаны положительными, поскольку направления напряжения и тока совпадали.

Потери энергии в источниках: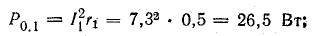
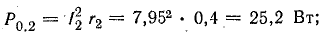
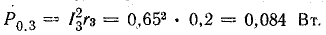
Общая потеря мощности в источниках составляет около 52 Вт. Мощность приемников: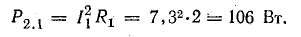

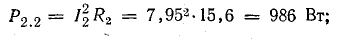
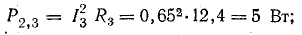
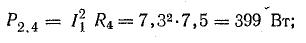
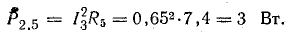
Общая мощность приемников составляет 1499 Вт.
Баланс мощности (мощность источников равна мощности приемников плюс потери мощности в источниках) 1551 Вт = 1499 + 52 Вт.

Расчет электрических цепей методом эквивалентного импеданса (метод свертки)

Метод эквивалентного сопротивления используется для расчета электрических цепей, в которых пассивные элементы соединены последовательно, параллельно или смешанно.

Как определить эквивалентные сопротивления

В схеме на рис. 4.10 сопротивления R₃ и Р₄ соединены последовательно: между ними нет тока ответвления (точка 3), поэтому I₃ = I₄. Эти два сопротивления могут быть заменены одним (эквивалентным) сопротивлением, определяемым как сумма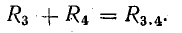
После этой замены мы получим более простую диаграмму (рис. 4.10, б). Сопротивления R₂ и Р_3.4 подключены параллельно, их можно заменить одним (эквивалентным) и он будет рассчитан по формуле (4.16):

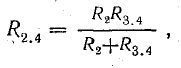
R и получается более простая схема (рисунок 4.10, в).

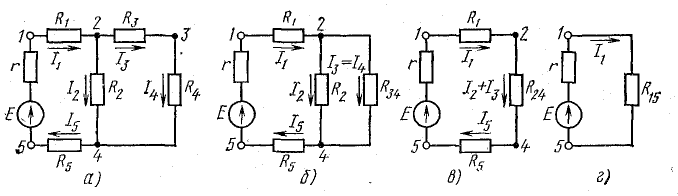
Рисунок 4.10: Метод эквивалентного сопротивления

В цепи рис. 4.10, c сопротивления R₁, К_2.4, К₅ соединены последовательно. Заменив эти сопротивления на одно (эквивалентное) сопротивление между точками 1 и 5, получим простейшую схему (рис. 4.10, г).

Путем аналогичных преобразований смешанная комбинация пассивных элементов с одним источником энергии в большинстве случаев может быть сведена к простейшей схеме. В более сложных схемах метод эквивалентного сопротивления позволяет добиться упрощения, что значительно облегчает расчеты.

Определение токов

В простейшей цепи (рис. 4.10, г) ток I определяется по закону Ома с помощью формулы (3.15). Токи в других ветвях исходной цепи определяются путем перехода от цепи к цепи в обратном порядке.
Из схемы на рис. 4.10, c следует, что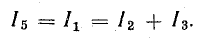

Кроме того, напряжение между точками 2 и 4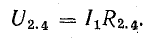

Зная это напряжение, легко определить токи I₂ и я₃ = I₄:

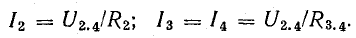
Когда токи I₁ и я₅ напряжение U_2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого мы предполагаем, что V₄ известно (например, равно нулю), а V₂ находим так же, как и в потенциальной диаграмме, опуская из точки 4 неразветвленную часть цепи с током I₁ =I₅: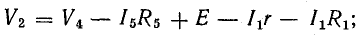

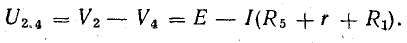
Метод преобразования сопротивления по дельте и звезде

Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах группы из трех элементов можно выделить, чтобы сформировать сопротивление в виде треугольника или звезды.
При расчете таких цепей упрощение схемы производится известным методом эквивалентных сопротивлений, но предварительно производится преобразование сопротивления треугольника в эквивалентную звезду или наоборот.

Схемы с сопротивлением “треугольник” и “звезда

В этой схеме нет элементов, соединенных последовательно или параллельно, вместо этого есть замкнутые цепи из трех резисторов (треугольники сопротивления), точки, разделяющие каждую пару соседних резисторов, являются узлами.

В узловых точках a, b, c треугольник сопротивлений R_ab, R_bc, R_ca. Его можно заменить эквивалентной трехлучевой звездой с сопротивлением R_a, R_b, R_c (обозначены на рисунке пунктирными линиями), соединенные, с одной стороны, с одинаковыми точками a, b, c, а с другой – с общей узловой точкой e.

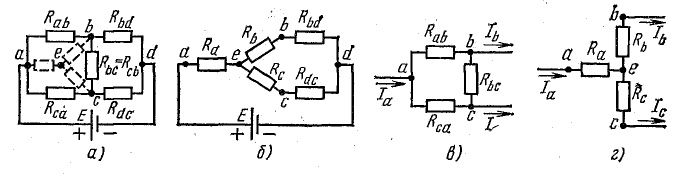
Рисунок 4.11: Преобразование треугольника сопротивления в звезду замещения

Значение этой замены становится понятным, когда мы рассмотрим схему, эквивалентную 4.11, b, где сопротивление R_b и Р_bd соединены последовательно, а b – сопротивление R_c и Р_{dc .}.
Две ветви между узлами e и d с этими парами сопротивлений соединены параллельно. С помощью соответствующих преобразований схему можно свести к ее простейшей форме.

Преобразование треугольника сопротивления в эквивалентную звезду

Замена треугольника сопротивления на эквивалентную звезду и наоборот, при условии, что такая замена не изменяет потенциалы узлов a, b, c, которые являются вершинами треугольника и эквивалентной звезды.
При этом предполагается, что остальная часть схемы, на которую не влияет преобразование, не меняет свой режим работы (не меняет токи, напряжения, мощности). Чтобы доказать возможность преобразования из треугольника в звезду и наоборот, рассмотрим схемы на рис. 4.11, c, d.
Эти схемы остаются эквивалентными для всех режимов, включая режим, в котором I_a = 0, что соответствует обрыву общего провода, ведущего к a. В этом случае схема треугольника имеет две ветви, соединенные параллельно между точками b и c, с резисторами R_bc и Р_ab + R_ca
Полное сопротивление между этими точками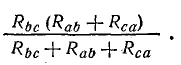

В звездной системе сопротивление R_b и Р_c. Полное сопротивление между этими точками R_b + R_c.
Если условие эквивалентности выполняется, то напряжение между точками b и c и токи I_b и я_c должны быть одинаковыми в обеих схемах. Следовательно, сопротивления между b и c одинаковы в обеих схемах, т.е.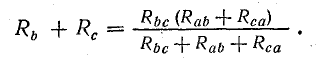

Предполагая, что я_b =0 и тогда I_c = 0, получаем: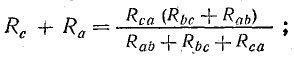

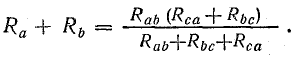
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые используются для определения сопротивления трехрукавной звезды по известному эквивалентному сопротивлению треугольника: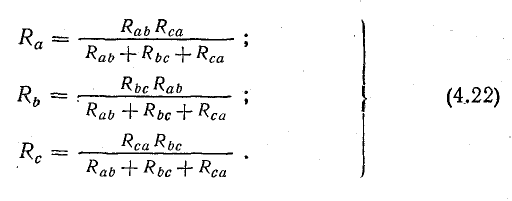

Преобразование импеданса звезды в эквивалентный импеданс треугольника

Преобразование трехлучевой звезды в эквивалентный треугольник используется для расчета некоторых схем, как показано на рис. 4.12, а, где схема выполнена так же, как на рис. 4.11, а.

Чтобы определить параметры треугольника по заданным параметрам звезды, воспользуйтесь формулами, которые написаны для диаграмм на рис. 4.12, a, b: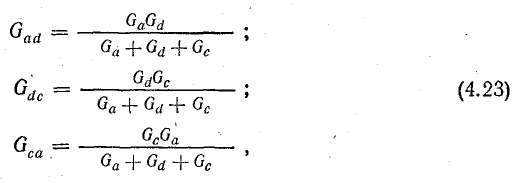

где G_{реклама}; G_dc; G_ca – проводимости сторон треугольника; G_a; G_d; G_c – это проводимости лучей звезды.

Зная проводимости, нетрудно определить сопротивления треугольников, если это необходимо.

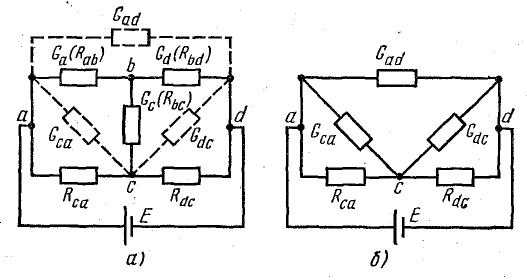
Рисунок 4.12: Преобразование трехконечной звезды в эквивалентный треугольник

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан группой преподавателей на некоммерческой основе для дополнительного образования молодежи.

Сайт написан, поддерживается и управляется командой учителей

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.

Читайте далее: