- Цифровая обработка сигналов
Фонд Викимедиа . 2010 .
Полезная страница
Смотреть что такое “Дискретизация” в других словарях
Дискретизация – Процесс преобразования непрерывного сигнала в цифровой сигнал путем измерения численных значений амплитуды сигнала через равные промежутки времени. См. также Обработка сигналов Финансовый словарь Финам… Финансовый словарь
отбор проб – [http://www.iks media.ru/glossary/index.html?glossid=2400324] Темы телекоммуникации, основные понятия EN дискретизации … Словарь технического переводчика
дискретизация . – (лат.; см. дискретизация) то же, что квантование. Новый словарь иностранных слов. By EdwART, , 2009. дискретизация i, множественное число, ж. ( … Словарь иностранных языков
дискретизация – дискретизация, я … Русский орфографический словарь
дискретизация – Преобразование, включающее замену непрерывного множества дискретным множеством … Политехнический терминологический словарь
передискретизация – Передискретизация частоты по частоте в методе шумоподавления квантования выборки – [Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: Центральный научно-исследовательский институт информационных технологий государственного предприятия, 2003.]] Тематика информационных технологий в целом Синонимы … Руководство технического переводчика
дискретизация телеметрических сообщений – Дискретизация Процесс преобразования телеметрического сообщения, описываемого непрерывной функцией времени, в форму, представленную набором координат. [ГОСТ 19619 74] Темы телемеханика, телеметрия Синонимы дискретизация EN… … Руководство технического переводчика
Дискретизация в значительные моменты времени – Дискретизация в моменты времени, когда исходный сигнал меняет состояние. [Л.М. Невдяев. Телекоммуникационные технологии. Англо-русский толковый словарь. Под редакцией Ю.М. Горностаева. Москва, 2002] Телекоммуникации,. Руководство переводчика
временная дискретизация телекоммуникационного сигнала – Преобразование телекоммуникационного сигнала, при котором сигнал представляется в виде набора его значений в дискретные моменты времени. [ГОСТ 22670 77] Сеть данных Темы Синонимы Дискретизация EN выборка … Руководство технического переводчика
дискретизация уровней – квантование квантование – [Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: Государственное предприятие ЦНИИС, 2003] Темы Информационные технологии в целом Синонимы количественная оценка количественная оценка количественная оценка EN количественная оценка … Справочник технического переводчика
Согласно этой теореме, любой непрерывный сигнал с конечным частотным спектром полностью определяется его дискретными значениями в опорных точках, удаленных друг от друга на временные интервалы ∆t = l/(2Fmax), где Fmax – максимальная частота в спектре сигнала. Иначе, выборка во времени не влечет за собой потерю информации, если частота выборки f discr = 1/∆t в два раза больше верхней частоты сигнала Fмакс.
Дискретизация
Дискретизация – Переход от непрерывного сигнала к близкому (в некотором смысле) дискретному сигналу, описываемый функцией прерывного времени. Примером дискретного сигнала является последовательность коротких импульсов с переменной амплитудой (последняя в данном случае выступает в качестве информационного параметра).
Обработка и передача дискретной информации имеет много преимуществ по сравнению с непрерывной информацией. Дискретные сигналы менее подвержены искажениям при передаче и хранении, легко преобразуются в двоичный цифровой код и могут обрабатываться цифровыми вычислительными устройствами.
Процесс отбора проб обычно состоит из двух этапов: отбор проб по времени и отбор проб по уровню (квантификация).
Аналоговая выборка времени – Процесс выборки аналогового сигнала с периодами, кратными периоду последовательности выборки ∆t.
Последовательность выборки – это периодическая последовательность временных выборок, определяющая дискретную временную сетку.
Период выборки ∆t – интервал времени между двумя последовательными выборками аналогового сигнала (шаг выборки времени).
При выборе частоты дискретизации времени можно воспользоваться теоремой В.А. Теорема Котельникова.
Теорема о частоте дискретизации (теорема Котельникова) – это теорема, определяющая выбор периода дискретизации ∆t аналогового сигнала в зависимости от его спектральных характеристик.
Согласно этой теореме, любой непрерывный сигнал с ограниченным частотным спектром полностью определяется его дискретными значениями в точках выборки, удаленных друг от друга на временные интервалы ∆t = l/(2Fmax), где Fmax – максимальная частота в спектре сигнала. Иначе, выборка во времени не влечет за собой потерю информации, если частота выборки f discr = 1/∆t в два раза больше верхней частоты сигнала Fмакс.
Согласно теореме Котельникова, нет необходимости передавать бесконечное множество всех значений непрерывного сигнала x(t), достаточно передать только те значения (рис. 3.52), которые ∆t = l/(2Fmax). Для восстановления сигнала x(t) на вход идеального фильтра низких частот с полосой пропускания от 0 до Fmsx, должна быть подана последовательность узких импульсов амплитудой, соответствующей дискретным выборкам сигнала x(t(i) в моменты времени ti = i ∆t.
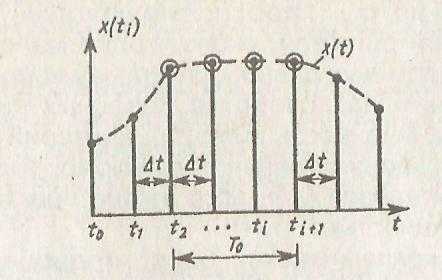
Рисунок 3.52: Образцы дискретных сигналов
Поскольку теорема счета (теорема Котельникова) сформулирована для сигнала с ограниченным спектром, а реальные сигналы имеют неограниченную спектральную плотность, то при вычислении ∆t =1/(2Fmax) приближение Fmax (например, активная ширина спектра, определяемая критерием амплитуды, критерием 90% энергетического содержания или средней мощностью сигнала). Кроме того, идеальный фильтр низких частот, необходимый для воспроизведения сигнала в соответствии с теоремой, также физически нереален, поскольку требования (идеально прямоугольная форма волны, отсутствие сдвига фазы в рассматриваемой полосе от 0 до Fmax) оказываются противоречивыми и могут быть выполнены только с определенной погрешностью. Следовательно, частота дискретизации по времени обычно принимается в 1,5-2,5 раза больше значения, рассчитанного по теореме Котельникова.
Существуют и другие способы выбора частоты дискретизации сигнала (с учетом времени корреляции передаваемого сообщения, значения наибольшего или среднеквадратичного отклонения процесса). Таким образом, согласно критерию Н.А. Железнова, которая удовлетворяется для случайных сигналов конечной длительности Тс неограниченным частотным спектром, рекомендуется принять шаг дискретизации ∆tравный максимальному интервалу корреляции сигнала φ0. Предполагается, что параметр φ0, характеризует интервал времени, в котором отдельные значения случайного процесса можно рассматривать как статистически зависимые (коррелированные), где φ0Тс. Таким образом, исходный непрерывный сигнал заменяется набором N=Тc/φ0 некоррелированных выборок (импульсов), происходящих с частотой fдискриминация=1/∆t= φ0. В этом случае восстановление сигнала x(t) осуществляется линейным предиктивным фильтром со среднеквадратичной ошибкой, как можно меньше отклоняющейся от нуля на временном интервале, равном интервалу корреляции φ0.
Однако, учитывая более полно свойства реальных сигналов (конечная длительность, неограниченный спектр), критерий Железнова предполагает, что корреляционная функция сигнала равна нулю Кx(φ) вне интервала [-φ0; φ0], что на практике выполняется с некоторой погрешностью.
При наличии более подробной информации об изменчивости сигнала частота дискретизации может быть выбрана на основе допустимой ошибки аппроксимации функции x(t) в каждом из интервалов отбора проб. Рис. 3.53 показан пример линейной аппроксимации, когда соседние образцы функции x(t), взятые в разные моменты времени ti и ti+1, соединены прямыми отрезками.
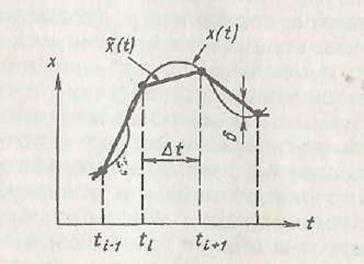
Рисунок 3.53: Шестилинейная аппроксимация
Рассмотренные методы равномерной выборки (при ∆t=const) может иногда приводить к избыточным выборкам, не оказывая существенного влияния на процесс реконструкции исходного сообщения. Например, если функция x(t) мало изменяется в течение некоторого достаточно большого интервала времени Тo, соответствующие дискретные выборки сигнала практически неотличимы друг от друга, и поэтому нет необходимости использовать все эти выборки для хранения или передачи информации по линии связи. Сокращение избыточной информации возможно на основе адаптивных (неравномерных) методов выборки, обеспечивающих, что ∆t между соседними выборками на основе фактического изменения характеристик сигнала (например, скорости изменения).
Выборка уровня сигнала – Процесс отображения бесконечного множества значений аналогового сигнала на некоторое конечное множество (определяемое количеством уровней квантования).
Характерной особенностью дискретизации уровней является замена непрерывной шкалы уровней сигнала x(t) на дискретной шкале хi (i = 1, 2, . m), в котором отдельные значения сигнала отличаются, по крайней мере, на константу (или значение, выбранное в процессе квантования) ∆tназывается этапом квантования.
этап квантификации – это величина, равная интервалу между двумя соседними уровнями квантования (определяется только для случая равномерного квантования).
Причина необходимости квантования заключается в том, что цифровые вычислительные устройства могут оперировать только числами с конечным числом цифр. Поэтому квантификация подразумевает округление передаваемых значений до заданной точности. При равномерном квантовании (∆x=const) число допустимых дискретных уровней x равно
m = (xмаксимум – xмин)/∆x,
где xмаксимум и xmin – верхняя и нижняя границы диапазона изменения сигнала, соответственно.
Ошибка квантования – это величина, определяемая как ξ(х) = х – хei, где х – дискретное значение, подлежащее кодированию, хei – дискретизированный сигнал.
Квантификационный шум – случайная функция времени, определяемая как зависимость ошибки квантования от времени.
Чем меньше значение ∆хтем меньше результирующая ошибка. Если в результате квантования любое из значений сигнала x(t), попадающих в интервал (хei – ∆х/2; хei + хei х/2), с округлением до хe, результирующая ошибка ξ(х) не превышает половины шага квантования, т.е. max|ξ(х)|=0,5∆х. На практике шаг квантования ∆х выбирается на основе помех, возникающих в той или иной форме при измерении, передаче и обработке реальных сигналов.
Если функция x(t) заранее неизвестен, а шаг квантования ∆х достаточно мал по сравнению с диапазоном изменения сигнала (хмаксимум – хmin), предполагается, что ошибка квантования ξ(х) как случайная величина, подчиняющаяся закону равномерного распределения. Тогда, как показано на рис. 3.54, плотность вероятности f1(ξ) для случайной переменной ξ, принимает значение 1/(∆х) в интервале (-∆х/2; +∆х/2) и равна нулю вне этого интервала.
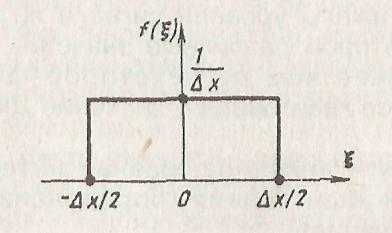
Рисунок 3.54. Равномерный закон распределения ошибки квантования
При ∆x=const относительная ошибка квантования ∆х=ξ(х)/х сильно зависит от текущего значения сигнала x(t). По этой причине, когда необходимо обрабатывать и передавать сигналы с широким диапазоном, часто используется неравномерное (нелинейное) квантование, при котором шаг ∆х предполагается малым для сигналов низкого уровня и увеличивается с ростом вклада сигнала (например, ∆х выбирается пропорционально логарифму |x(t)|). Выбор шага ∆хi =хei – хei-1 также учитывает плотность распределения случайного сигнала (меньший шаг квантования для более вероятных значений сигнала, больший – для менее вероятных). Это обеспечивает высокую точность преобразования при ограниченном (не слишком большом) количестве допустимых уровней дискретных сигналов. x(t).
Процесс преобразования дискретного сигнала в цифровой называется кодированием информации, а набор различных кодовых комбинаций, созданных по определенному правилу кодирования, называется кодом.. Важной характеристикой кода является его основание (или разряд) – количество возможных значений, которые могут принимать элементы кодовой комбинации. Предположим, что необходимо передать сигнал, уровень которого изменяется в диапазоне от 0 до 10 В. Если шаг квантования данных составляет 10 мВ, то каждый образец сигнала можно рассматривать как одно из 1000 возможных сообщений. Для передачи этой информации могут быть предложены различные методы:
– для присвоения каждому сообщению определенного уровня напряжения, с кодовой базой m = 1000, а длина кодовой комбинации (слова) принимает минимальное значение n=1;
– двоичное (бинарное) представление амплитуды сигнала может быть использовано путем m = 2, но тогда длина комбинации n = 10 (210=1024, поэтому некоторые комбинации здесь не используются).
Для выполнения полиномиальной интерполяции достаточно, используя выражение (5.4.1), построить систему линейных уравнений для n последовательных выборок и определить n значений коэффициентов a и . При глобальной интерполяции для всех N точек функции степень полинома равна N-1. Глобальная интерполяция обычно выполняется для достаточно коротких (не более 8-10 выборок) наборов данных. Пример глобальной интерполяции показан на рис. 5.4.1.
Дискретизация сигналов и функций
В первой половине 20-го века аналоговые приборы и устройства реального времени использовались в основном для записи и обработки информации, и даже преобразование дискретных сигналов в аналоговую форму применялось к величинам дискретного характера. Это изменилось с распространением микропроцессорной технологии и компьютеров. Цифровая запись и обработка информации оказалась более совершенной и точной, более универсальной, многофункциональной и гибкой. Мощность и простота цифровой обработки сигналов настолько превзошла аналоговую, что преобразование аналоговых сигналов в цифровую форму уже давно стало промышленным стандартом.
Дискретизация сигнала – это преобразование функций непрерывных переменных в функции дискретных переменных, из которых исходные непрерывные функции могут быть восстановлены с заданной точностью. Роль дискретных отсчетов обычно играют квантованные значения функций на дискретной шкале координат. Квантование относится к преобразованию непрерывного значения величины в дискретное значение величины из конечного набора допустимых значений, которые называются уровнями квантования. Если уровни квантования пронумерованы, то результатом преобразования является число, которое может быть выражено в любой системе счисления. Округление мгновенных значений непрерывной аналоговой величины с шагом равного аргумента с заданной разрядностью является простейшим случаем дискретизации и квантования сигналов при их преобразовании в цифровые сигналы.
Задачи обработки производственных данных обычно требуют гораздо меньше информации, чем та, которая доступна от измерительных датчиков в виде непрерывного аналогового сигнала. Из-за статистических флуктуаций измеряемых величин и конечной погрешности измерительных приборов информация о величине сигнала всегда ограничена. Рационально выполняя выборку и количественную обработку исходных данных, можно снизить затраты на хранение и обработку информации. Использование цифровых сигналов позволяет применять методы кодирования информации с возможностью последующего обнаружения и исправления ошибок при обработке информации. Цифровая форма сигналов также способствует унификации операций по обработке информации на всех этапах ее циркуляции.
Задачи функции выборки. Принципы дискретизации
Суть дискретизации аналоговых сигналов заключается в замене непрерывной во времени аналоговой функции s(t) последовательностью коротких импульсов, амплитудные значения которых c n определяются весовыми функциями или непосредственно выборками (отсчетами) мгновенных значений сигнала s(t) в момент времени t n . Представление сигнала s(t) в интервале времени T множеством дискретных значений c n имеет вид
(c 1 , c 2 , … c N ) = A[s(t)],
где A – оператор выборки. Запишите операцию восстановления сигнала s(t):
s'(t) = B[(s 1 , s 2 , . . . , c N )].
Выбор операторов A и B зависит от требуемой точности восстановления сигнала. Линейные операторы являются самыми простыми. В общем случае:
Где q n (t) – массив весовых функций.
Числа в выражении (5.1.1) связаны с операцией интегрирования, которая обеспечивает высокую устойчивость к шумам выборки. Однако из-за сложности технической реализации “взвешенного” интегрирования, последнее используется довольно редко, при высоких уровнях шума. Более распространенными являются методы, в которых сигнал s(t) заменяется набором его мгновенных значений s(t n ) в моменты времени t n . Роль весовых функций в этом случае играют гребенчатые (решетчатые) функции. Интервал времени D t между соседними выборками называется шагом выборки. Частота дискретизации F=1/ D t называется равномерной, если значение D t постоянно во всем диапазоне обработки сигнала. При неравномерной выборке значение D t между выборками может меняться в соответствии с определенной программой или в зависимости от изменения параметров сигнала.
Непрерывное воспроизведение
Выборка непрерывного сигнала может быть выполнена с использованием как ортогональных, так и неортогональных базисных функций. Функция восстановления s'(t) соответствующим образом представлена аппроксимирующим полиномом:
где v n (t) – набор базисных функций. Ортогональные базисные функции гарантируют, что ряд сходится к s(t) при n Ґ . Оптимальные методы выборки – это те, которые обеспечивают минимальный числовой ряд для заданной ошибки реконструкции сигнала. Для неортогональных базисных функций в основном используются полиномы степенной формы:
Если значения аппроксимирующего полинома совпадают со значениями образцов в моменты их счета, то такой полином называется интерполирующим полиномом. Полиномы Лагранжа обычно используются в качестве интерполирующих полиномов. Реализация интерполирующих полиномов требует задержки сигнала на интервал дискретизации, что в системах реального времени требует определенных технических решений. Полиномы Тейлора обычно используются в качестве экстраполирующих полиномов.
Естественным требованием при выборе частоты дискретизации является внесение минимальных искажений в динамику функции сигнала. Логично предположить, что чем ниже частота дискретизации F, тем меньше искажение информации. С другой стороны, также очевидно, что чем выше значение F, тем больше цифровых данных будет отображаться и тем больше времени придется потратить на обработку сигнала. В оптимальном варианте частота дискретизации F должна быть необходимой и достаточной для обработки информационного сигнала с заданной точностью, т.е. обеспечивать приемлемую ошибку восстановления аналоговой формы сигнала (среднеквадратичное значение на всем интервале сигнала или по максимальным отклонениям от реальной формы в характерных информационных точках сигналов).
Равномерная выборка. Спектр дискретного сигнала
Предположим, что для обработки задан произвольный аналоговый сигнал s(t) с конечным и достаточно компактным Фурье-образом S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг D t = 1/F) с математических позиций означает умножение функции s(t) на гребенчатую функцию Sh D t (t) = d (t-k D t) – непрерывную последовательность импульсов Кронекера:
s D t (t) = s(t) Ch D D t (t) = s(t) d (t-k D t) =s(k D t) d (t-k D t). (5.2.1)
Принимая во внимание известное преобразование Фурье гребенчатой функции
Sh D t (t) Y (1/T) d (f-nF) = F-sh F (f), (5.2.2)
это преобразование Фурье дискретной функции s D t (t):
Следовательно, для спектра дискретного сигнала имеем:
S F (f) = F × S(f) * d (f-nF) = FS(f-nF). (5.2.4)
Из этого выражения следует, что спектр дискретного сигнала – это непрерывная периодическая функция с периодом F, совпадающая (при определенных условиях конечности спектра непрерывного сигнала) с функцией непрерывного сигнала F × S(f) s(t) в центральном интервале от -f N до f N , где f N = 1/2 D t = F/2. Частота f N (или для круговой частоты в N = p / D t) называется частотой Найквиста. Центральный период функции S F (f) называется диапазоном основной частоты.
Интуитивно понятно, что если спектр полосы основной частоты совпадает со спектром непрерывного сигнала в диапазоне постоянных коэффициентов, то этот спектр может быть использован для воспроизведения не только формы дискретного сигнала, но и формы исходного непрерывного сигнала. Шаг дискретизации и соответствующая частота Найквиста должны иметь решающее значение.
Как правило, условно принимается, что шаг дискретизации сигнала (шаг числовых таблиц) составляет D t = 1, и что основной частотный диапазон занимает интервал -0,5 J f J 0,5, или по шкале угловых частот соответственно – p J в J p .
Физическая суть формирования дискретных спектров сигналов достаточно проста. Наиболее наглядно это можно увидеть в Mathcad (см. рис. 5.2.1).
Сначала представим себе непрерывный сигнал с постоянной единичной амплитудой c(t) = const = 1 на любом интервале времени 0-T, например, при T=100. Начнем дискретизировать сигнал с равномерным шагом D t = 1. Вычислим спектр первой дискретной выборки c 0 = 1. При N = 1 сигнал является импульсом Кронекера и, следовательно, модуль спектра стандарта c 0 = 1 представляет собой непрерывное частотное распределение |C( w )| = const в диапазоне от – Ґ до + Ґ (показан только отрезок от -6 p до +6 p, нормированный на N для наглядного сравнения спектров). Все частоты сигнала имеют нулевую фазу и, кроме того, взаимно смещены во всех временных точках, кроме t=0, где амплитуды частот суммируются, образуя единую выборку со значением 0.
Добавим к сигналу вторую дискретную выборку со значением 1 =1 (N=2). Если вычислить спектр только второго образца, то его модуль будет равен модулю первого образца (так как z 1 = z 0 ), но нулевые фазы гармоник этого спектра сместятся к t = 1, то есть относительно t = 0 фазы гармоник второго образца изменятся на – wD t по теореме задержки преобразования Фурье. При сложении двух спектров первого и второго образцов наблюдается интерференция частот и возникают пульсации частотного спектра с максимумами на частотах, кратных F=1/ D t или в угловых единицах 2 p / D t, где фазы первого и второго образцов совпадают и равны нулю. Форма результирующего модуля спектра для N=2 показана на рис.
При дальнейшем увеличении числа образцов периодичность совпадения нулевой фазы и положения максимумов остаются неизменными, в то время как частотная интерференция между максимумами становится более сложной, при этом ширина основных пиков постепенно сужается во всем диапазоне частот спектра от минус до плюс бесконечности. Рис. В 5.2.1 приведены примеры спектров сигналов при N=10 и N=50. В пределе, при двусторонней шкале времени ±T ® ± Ґ и N ® Ґ , гребенчатая функция от импульсов Кронекера во временной области c t ® Sch D t (t) = d (t-k D t) превращается в идеальную гребенчатую функцию (1/T) d (f-nF) = F Sch F (f) в частотной области (уравнение 5.2.2). Этот спектр является непрерывным и физически реальным в диапазоне частот от – Ґ до + Ґ .
Физический смысл частотной интерференции остается тем же, если определить любой сигнал, например, синусоиду u(t) U(f), на любом временном интервале T и дискретизировать его, т.е. умножить сигнал на непрерывную последовательность импульсов Кронекера c(t) × u(t) ® u(t) d (t-k D t) = u(t) × Sch D t (t). А поскольку каждый дискретный образец в этом случае имеет свою определенную амплитуду и, соответственно, свой гармонический амплитудный уровень своего спектра, то при частотном суммировании получается более сложная интерференционная картина с разделением общего спектра сигнала всех дискретных образцов на две зеркальные составляющие относительно кратных 2 p/D t.
Математически, произведение двух функций во временной области представляется путем сращивания спектров этих функций в частотном представлении, т.е. путем сращивания спектра сигнала u(t) с частотной гребенчатой функцией спектра, порожденного гребенчатой функцией временной дискретизации u(t)W D t (t) BY U(f) * F W F (f), из чего следует уравнение (5.2.4). Пример выборки одного периода синусоидальной волны показан на рис. 5.2.2.
Давайте вернемся к важности и роли частоты Найквиста при дискретизации сигнала.
На рисунках 5.2.3 и 5.2.4 показаны примеры равномерной выборки аналоговых сигналов s 1 (t) = exp(-a|t|) и s 2 (t) = exp(-bt 2 ) (дискретные выборки обведены кружками) и спектры этих дискретных сигналов.
Рисунок 5.2.3 Дискретные сигналы. Рис. 5.2.4 Спектры дискретных сигналов.
Для того чтобы периодическое спектральное повторение, вызванное дискретизацией аналогового сигнала, не изменяло спектр в основном диапазоне частот (относительно спектра исходного аналогового сигнала), необходимо и достаточно, чтобы максимальные частотные составляющие f max в спектре аналогового сигнала не превышали частоту Найквиста (f max Ј f N = F/2). Это означает, что частота дискретизации сигнала должна быть как минимум в два раза больше максимальной частотной составляющей в спектре сигнала:
что гарантирует, что на концах основной полосы спектр дает нулевые значения, как это имеет место для спектра S 2 ( w ) на рис. 5.2.4.
Другими словами, для каждого периода колебаний с частотой f max должны существовать как минимум две опорные точки. Это понятно – невозможно определить три неизвестных параметра данной гармоники (амплитуда, частота, фаза) из одной точки отсчета в пределах периода гармонического сигнала.
При нарушении условия (5.2.5) неизбежно искажение частотного спектра исходного аналогового сигнала. На рис. 5.2.4 хорошо видно, что частота дискретизации сигнала s 1 (t) не удовлетворяет условию, спектры периодов перекрываются, и результирующий спектр дискретных выборок сигнала s 1 (t) отличается от реального спектра сигнала s 2 (t) (реальный спектр и его периодические повторения в области перекрытия спектра основной полосы частот с боковыми полосами спектра показаны пунктиром).
Характер искажений во временной области при нарушении условия (5.2.5) наглядно показан на рис. 5.2.5. На рисунке показаны три возможных соотношения частот гармонических сигналов при постоянной частоте дискретизации.
1. график A – частота гармонического сигнала меньше частоты Найквиста. Дискретным образцам может соответствовать только та исходная гармоника, амплитуда, частота и фаза которой могут быть однозначно определены из любых трех последовательных точек (три уравнения, три неизвестных).
2 График B – частота гармонического сигнала равна частоте Найквиста. Это означает, что каждая пара последовательных выборок периодически повторяется, поэтому для решения необходимо только два уравнения с тремя неизвестными, а определить можно только частоту, при условии, что начальная фаза сигнала не совпадает с начальной фазой частоты дискретизации (тогда все выборки равны нулю). Амплитуда и фаза сигнала однозначно определяются только в том случае, если выборки совпадают с экстремумами гармоник.
Рисунок 5.2.5: Дискретизация гармоник с различными частотами.
График C – частота гармонического сигнала больше частоты Найквиста. Решение трех уравнений в трех последовательных точках позволяет определить амплитуду гармоники, но дает искаженные значения частоты и фазы (показаны пунктирной линией). Это известно как эффект алиасинга. Гармонические частоты выше частоты Найквиста “отражаются” в основной диапазон частот от его границ (на частоте Найквиста), как видно на рис. 5.2.4 для фактического спектра сигнала S 1 ( w ), отмеченного точками. Этот эффект аналогичен хорошо известному эффекту обратного вращения автомобильных колес (и любого другого быстро вращающегося объекта) на кино- и телеэкранах, когда скорость их вращения начинает превышать частоту кадров.
Интерполяционный ряд Котельникова-Шеннона
Спектр дискретизированного сигнала (5.2.4) представляет собой сумму сдвинутых копий исходного аналогового сигнала с шагом сдвига, равным частоте дискретизации. Конечно, если спектры копий не перекрываются, можно с абсолютной точностью восстановить исходный аналоговый сигнал по центральной копии дискретного спектра. Умножая функцию (5.2.3) на прямоугольную весовую функцию P F (f), равную 1 в основном диапазоне частот [-F/2,F/2] и нулю вне его, получаем непрерывный спектр в бесконечных частотных пределах, равный спектру F × S(f) в основном диапазоне частот:
F × S(f) = F × [S(f) * S F (f)] × P F (f). (5.2.6)
Обратное преобразование Фурье такого спектра должно давать конечный и непрерывный сигнал. Выполним обратное преобразование обеих частей равенства (5.2.6):
F-[S(f) * W F (f)] BY s D t (t), P F (f) BY F Ch sinc( p Ft).
F ´ s(t) = s D t (t) * F ´ sinc( p Ft).
s(t) = sinc( p Ft) * s(k D t) d (t-k D t),
Дискретизированный сигнал s D t (t) =s(k D t) d (t-k D t) представляет собой сумму последовательных весовых импульсов Кронекера, сдвинутых на интервал D t, с весовыми значениями, равными отсчетам функции s(t) в моменты k D t. Когда такой сигнал проходит через систему с импульсной характеристикой h(t)= sinc( p Ft)= sin( p Ft)/ p Ft, каждый импульс с весом Кронекера будет возбуждать на выходе соответствующую последовательную серию сдвинутых и масштабированных копий оператора фильтра. Следовательно, принимая во внимание очевидное равенство
d (t-k D t) * sinc( p Ft) = sinc[ p F(t-k D t)],
выходной сигнал будет представлять собой сумму сдвинутых взвешенных импульсных откликов системы, где значение веса определяется отсчетами дискретного сигнала:
s(t) =s(k D t) sinc[ p F(t-k D t)] =s(k D t) sinc[ p (t/ D t-k)]. (5.2.7)
Эта конечная формулировка называется интерполяционным рядом Котельникова-Шеннона. Из этого следует, что если наибольшая частота в спектре произвольной непрерывной функции s(t) не превышает частоты ее дискретизации, то ее можно представить в виде числовой последовательности дискретных значений s(k D t), k = 0,1,2, без потери точности. и однозначно реконструируется из этой последовательности. В этом заключается суть теоремы Котельникова о выборке. В зарубежной литературе ее также называют теоремой Шеннона или теоремой выборки.
Академик В.А.Котельников, 1908-2005 Выдающийся ученый в области радиотехники, радиофизики и информатики. В 1931 году он окончил Московский институт энергетического машиностроения. С 1931 по 1941 год он читает лекции в МЭИ и проводит исследования в Центральном научно-исследовательском институте связи. В 1933 году он формулирует знаменитую теорему счета, которая носит его имя. Во время Великой Отечественной войны (1941-1945 гг.) он занимался разработкой аппаратуры специальной связи. С 1948 по 1953 год. Директор и главный конструктор ОКБ МЭИ. В 1953 году он был избран членом Академии наук СССР. С 1954 года – директор Института радио и электроники Академии наук СССР. Он занимался теорией помех в радиосвязи и радиолокацией, радиолокационным исследованием планет. Лауреат Ленинской премии, дважды лауреат Государственной премии СССР. Он был дважды удостоен звания Героя Социалистического Труда, награжден шестью орденами Ленина и орденом “За заслуги перед Отечеством” I степени.
Фактически, ряд (5.2.7) является частным случаем разложения сигнала по формуле (5.1.2) системой ортогональных интегральных синусоидальных функций v(t, k D t)= sinc( p F(t-k D t))= sinc( p (t/ D t – k)), которые образуют базис сигнального пространства s(t). Для проверки ортогональности достаточно вычислить скалярное произведение базисных функций:
v(t,n D t) v(t,m D t) dt = .
Разложение (5.2.7) проще и нагляднее, чем разложение ряда Фурье, что видно на рис. 5.2.6 Вес каждой выборки функции sinc[ p F(t-k D t)] создает в каждой текущей точке t= k D t пиковое значение интегрального синуса, равное значению сигнала s(k D t), а во всех остальных точках дискретных выборок sinc[ p F(t-(k±j) D t)], j= 1,2,….. значения интегрального синуса равны нулю. Ряд числовых значений интегрального синуса для дискретных значений t= n D t при суммировании по k полностью эквивалентен гребенчатой функции:
sinc[ p F(n D t-k D t)] є Sch D t (t).
Однако, в отличие от гребенчатой функции, в интервале между дискретными выборками интеграл синуса имеет не нулевые, а определенные колебательные значения. Накладывая эти значения на текущие t-значения от всех синус-интегралов, которые колеблются до данного t-значения, генерируются аналоговые значения сигнала в интервале между выборками.
Рисунок 5.2.6: Реконструкция непрерывного сигнала из дискретных выборок.
В принципе, функции дискретизации имеют бесконечные колебания и восстанавливают аналоговый сигнал, который является бесконечным по аргументу. Амплитуда колебаний функций образца уменьшается довольно медленно (см. рис. 5.2.7). Однако на рис. 5.2.6 легко заметить, что из-за изменения знака выборочной функции в интервалах дискретизации колебания восстановленных кривых конечного спектра довольно быстро затухают и для данных без значительных выбросов и больших перепадов значений определяются в основном выборками, ближайшими к интервалу интерполяции. Таким образом, интервал суммирования в формуле (2.5.7) может быть ограничен некоторой окрестностью текущих точек интерполяции.
Работа 1 – Исследование и разработка основных принципов укладки интервальных ограничений при интерполяции данных по Котельникову-Шеннону.
Ряд (5.2.7) позволяет просто ввести масштабный коэффициент в аргумент интеграла синуса, чтобы изменить представление сигнала на оси времени, растягивая или сжимая сигнал:
s(t) =s(k D t) sinc[ p F(m-t-k D t)].
Аналогичная формула может быть использована для преобразования дискретных данных в другой интервал выборки:
s(n- D t new ) = s(k D t) sinc[ p F(n- D t new -k D t)].
Примеры восстановления аналоговой формы произвольно конечного сигнала и изменения шага дискретизации данных показаны на рис. 5.2.9.
Рис. 5.2.9: Интерполяция Котельникова-Шеннона.
На рис. 5.2.10 показана имитация дискретизации аналогового сигнала, эффект наложения спектров боковых периодов на спектр основного диапазона дискретного сигнала и восстановление формы аналогового сигнала по этому спектру.
Графики A и B на рисунке показывают модельный аналоговый сигнал, точки его дискретизации и модуль спектра дискретного сигнала. Спектр рассчитывается с помощью быстрого преобразования Фурье (БПФ) и отображает диапазон частот 0-2f N , соответственно. Дискретизация была выполнена правильно при выполнении условия (5.2.5), что также можно оценить по спектру дискретного сигнала (график B, выход на незначительные значения до частоты Найквиста f N ).
Кривая S1 на графике C – это спектр дискретного сигнала модели при нарушении условия (5.2.5). В данном случае это произойдет при увеличении шага дискретизации в 2 раза, что приведет к уменьшению новой частоты Найквиста в 2 раза и смещению границы основной полосы до 0,5f N на графике B, с наложением спектров подполос. Кривые S1a и S1b строятся как отдельные спектры правой половины основной полосы без суммирования со спектром правой боковой полосы (диапазон 0-2f N , где f N – частота Найквиста новой выборки), и левой половины правой боковой полосы в том же диапазоне 0-2f N без суммирования со спектром основной полосы. Хорошо видны “хвосты” спектров, которые выходят за пределы интервала Найквиста от центров полос и в соседние полосы. Сложив эти спектры при 0 -2f N, легко увидеть, что результат будет точно таким же, как спектр S1 вновь дискретизированного исходного сигнала. Обратите внимание, что сложение спектров соседних полос может вызвать не только увеличение высокочастотных составляющих (как видно на рисунке 5.2.4 – спектр S1), но и их взаимную компенсацию, что и происходит в данном случае для спектра S1 (пунктирная кривая на рисунке B).
Наложение спектров полос искажает аналоговую форму сигнала, восстановленную из дискретных выборок, что видно на кривой D – s2. В данном случае, при частичной взаимной компенсации перекрывающихся частей спектра, наиболее сильное искажение произошло во второй, высокочастотной части сигнала.
Рисунок 5.2.10: Моделирование выборки аналогового сигнала.
Выборочные сигналы обычно содержат широкополосный шум, высокочастотные компоненты которого неизбежно перекрываются при периодизации спектра и увеличивают ошибку реконструкции сигнала. Чтобы устранить этот фактор, все частоты выше частоты Найквиста должны быть подавлены перед выборкой, т.е. должна быть выполнена низкочастотная фильтрация сигнала. Если последнее не сделано, рекомендуется уменьшить интервал выборки в 2-4 раза от оптимального интервала выборки и выполнить низкочастотную цифровую фильтрацию в качестве первой операции обработки данных, после чего можно выполнить децимацию данных.
Увеличение интервала дискретизации сигналов – довольно распространенная операция в цифровой обработке данных, и не только при подготовке данных к хранению с целью уменьшения их количества. При комплексной обработке данных различной природы интервалы дискретизации этих данных могут быть разными, и они сводятся к одному значению. Подобная операция обычно выполняется при создании многоуровневых информационных пакетов. В таких случаях уменьшение интервала выборки данных является необходимостью, даже с потерей некоторых высокочастотных компонентов информации. Предварительная фильтрация отброшенных данных перед децимацией (чтобы избежать их попадания в основной частотный диапазон и искажения основной информации) в этом случае обязательна, особенно если энергия этих компонентов сигнала достаточно высока. Пример такой децимации показан на рис. 5.2.10 На рисунках C и D показаны спектры децимированных данных S2(f) и аналогового сигнала s2(t), восстановленного из дискретных выборок sd(k D t) ↔ S2(f). Децимация выполняется непосредственно в частотной области путем замыкания на частотной части 0-f N спектра sm(f) исходного сигнала sm(m D m) связанной части на интервале 1.5f N – f N , что уменьшает новый интервал Найквиста в два раза и создает спектр S2(f), соответствующий дискретному сигналу с удвоенным интервалом дискретизации данных с полностью подавленной частью спектральных компонент от 0.5f N до 1.5f N . Этот метод можно использовать для десэмплирования (передискретизации) данных любой кратности.
Дискретизация с усреднением
Если сигнал дискретизируется импульсами конечной ширины, то импульсы соответствуют средним значениям сигнала за интервал длительности импульса. Для ширины импульса r мы имеем:
s(k D t) = (1/r)s(t) dt. (5.2.8)
С помощью функций селектора и гребенки эта операция представлена следующим образом:
s D t (t) = (1/r)[s(t) * P r (t)]S D t (t). (5.2.9)
Соответственно, спектр дискретной функции имеет вид:
S F (f) = [S(f) Ch sinc( p fr)] * F Ch F (f). (5.2.10)
Отсюда следует, что для выборки с усреднением спектр S(f) заменяется спектром S(f) × sinc( p fr), периодическое продолжение которого образует спектр дискретной функции. Применяя обратное преобразование Фурье и используя интерполяционную формулу Котельникова-Шеннона, вместо исходной функции s(t) получаем функцию s'(t) = s(t) * P r (t)/r, что эквивалентно прохождению сигнала через фильтр с откликом h(t) = P r (t)/r, то есть низкочастотный сглаживающий “скользящий” усредняющий фильтр с окном r.
Предположим, что r= lD t, lJ 1, F=2 a f max , ai 1. Для этих условий частотная передаточная функция фильтра записывается в следующем виде: H(f) = sip[(pl /2 a )(f/f max )]. Если потери компонентов сигнала на всех частотах не должны превышать 3%, то должно выполняться условие: sinc( pl /2 a ) и 0,97. Из a = 1 следует, что значение l должно быть Ј 0,27, т.е. ширина импульса выборки может составлять до 27 % от интервала выборки.
Обратите внимание, что в выражении (5.2.8) отсчеты относятся к центру интервала дискретизации r. Если отсчеты относятся к концу r интервалов, что имеет место при обработке информации в реальном времени, то в выходной функции (5.2.9) будет сдвиг на r/2 интервала и соответствующий сдвиг фазы на r/2 в ее спектре (в правую часть выражения (5.2.10) будет добавлен множитель exp(-j p fr)).
Дискретизация спектров
Теоремы, доказанные для прямого преобразования Фурье, в равной степени справедливы и для обратного преобразования. Когда спектр сигнала дискретизируется с шагом D f, динамическое представление сигнала также становится периодическим с периодом T = 1/ D f. Шаг частоты дискретизации должен удовлетворять условию, чтобы сигнал мог быть точно воспроизведен в основном периоде (без наложения сигналов из соседних периодов):
Отметим попутно, что для временной формы причинного сигнала в качестве основного периода берется интервал от 0 до T, хотя при компьютерной обработке это не имеет значения и основной период может быть задан от -T/2 до T/2.
Информационная идентичность динамической и частотной форм представления дискретного сигнала следует непосредственно из теоремы Котельникова-Шеннона.
Основой любого преобразования при обработке данных обычно является конечный (конечной длины) сигнал, записанный в интервале 0-T и состоящий из определенных частотных составляющих от 0 до f max . Оптимальная выборка аналогового сигнала без потери точности, как обсуждалось выше, соответствует двум отсчетам на период максимальной частотной составляющей:
D t = 1/2f max , N t = T/ D t. (5.2.12)
где N t – общее число выборок сигнала в интервале времени Т. Если сигнал записывается непосредственно в дискретном виде, то он автоматически ограничивается максимальной частотой, т.е. максимальные частоты в таком сигнале равны f max Ј 1/2 D t.
Когда дискретный сигнал преобразуется в частотную форму, спектр сигнала становится непрерывным и периодическим с периодом 1/ D t = 2f N . Для оптимальной выборки частоты без потери точности восстановления непрерывного спектра необходимо выполнение следующих условий:
D f = 1/T = 1/( D tN t ), f N = 1/2 D t, (5.2.13)
N f = 2f N / D f = N t . (5.2.14)
Спектр сигнала подвергается некоторому преобразованию (обработке), обычно только в основном диапазоне частот, и таким образом становится непериодическим сигналом, возникающим только в интервале 2f N (от -f N до f N ). Спектральные значения за пределами основной полосы неявно принимаются равными нулю. Когда такой сигнал преобразуется обратно из частотной формы в динамическую, сигнал также является непрерывным и периодическим с периодом 1/ D f = T, с оптимальной дискретизацией по координатам без потери точности при восстановлении непрерывной формы:
Для преобразований s(k D t) TO S(n D f), а также S(n D f) TO s(k D t) условие N f = N t является необходимым и достаточным для полного сохранения информации при преобразовании сигнала из одной формы представления в другую. Условия (5.2.12-5.2.16) определяют оптимальность преобразований без потерь. Если исходный сигнал дискретизирован оптимально и представлен N выборками, то уменьшение числа выборок при преобразовании неизбежно приводит к некоторой потере информации.
Что касается увеличения числа выборок при преобразовании функции (уменьшения интервала дискретизации), то это всегда возможно, поскольку выход конечного преобразования сигнала является непрерывной функцией, и в принципе интервал дискретизации может быть установлен бесконечно малым. Однако увеличение числа выборок не увеличивает ни количество информации, содержащейся в исходном сигнале, ни точность ее представления. Фактически, такая операция полностью эквивалентна интерполяции исходного сигнала по ряду Котельникова-Шеннона. Пример такой операции показан на рис. 5.2.11.
Выборки s(k D t) и их огибающая кривая на рис. 5.2.11 воспроизводят (в более детальном масштабе) сигнал s 1 (t) рис. 5.2.3, дискретизированный с шагом D t = 1. Как уже отмечалось, интервал дискретизации этого сигнала оказался передискретизированным и спектр сигнала искажен (рис. 5.2.4). Операция s(k D t) S(n D f) увеличила количество точек выборки спектра S(n D f) в 5 раз по сравнению с количеством точек сигнала s(k D t), т.е. N f = 5N t . При обратном преобразовании S(n D f) в z(k D t) выполнялись условия (5.2.15 – 5.2.16) и шаг дискретизации сигнала при его восстановлении также был в 5 раз меньше исходного (D t = 0,2). Результат можно увидеть на рис. 5.2.11 (кривая z(k D t)). Интерполяция сигнала s(k D t) с помощью ряда Котельникова-Шеннона с шагом D t = 0,2 дает точно такой же результат. Искажение аналогового сигнала вносится при его дискретизации, если шаг дискретизации не удовлетворяет условию (5.2.5) и не может быть исправлен никакими дальнейшими преобразованиями, так как информация об исходной форме аналогового сигнала безвозвратно теряется при неправильной дискретизации.
Дискретизация усеченных сигналов
Согласно условию (5.2.5) для сигналов с ограниченным спектром, аналоговая форма сигнала может быть восстановлена из дискретных выборок, если сигнал в интервале T его задания конечен или, по крайней мере, затухает настолько быстро, что выборки сигнала вне интервала T практически равны нулю. Проблема выборки усложняется для медленно затухающих сигналов, сигналов бесконечной длительности и сигналов с неограниченным по частоте спектром. Последняя ситуация возникает, когда в сигнале присутствуют разрывы и резкие скачки.
В общем случае длительность сигнала и ширина его спектра не могут быть одновременно ограничены конечными интервалами. Если длительность сигнала ограничена и сигнал усечен в ненулевой области, то спектр сигнала неограничен, и наоборот. Однако обработка реальных сигналов возможна только при ограниченном спектре, как по координатам, так и по ширине. В этом случае в качестве оценки правильности ограничения сигнала используется энергетический критерий, согласно которому длительность сигнала T и практическая спектральная ширина W выбираются таким образом, чтобы в них было сосредоточено подавляющее большинство энергии сигнала. Это достигается при соблюдении условий:
|s(t)| 2 dt = k|s(t)| 2 dt, (5.2.17)
|S( w )| 2 d w = k|S( w )| 2 d w , (5.2.17′)
где k – коэффициент репрезентативности (качества) присвоения сигнала, значение которого может быть установлено от 0,9 до 0,99, в зависимости от целей обработки сигнала.
Предположим, что любой сигнал s(t) рассматривается на конечном интервале [0, T] и предполагается равным нулю за его пределами. Такой сигнал можно получить путем умножения сигнала s(t) на прямоугольную весовую функцию P T (t):
s T (t) = s(t) P T (t).
Для спектра S T (f) функции s T (f) соответственно имеем:
S T (f) = S(f) * T C sinc( p fT). (5.2.18)
Спектр S T (f) является неограниченным, потому что носитель функции sinc( p fT) является неограниченным. Из этого следует, что частота дискретизации функции s T (t) в принципе должна быть бесконечно большой, т.е. правильная дискретизация невозможна. На практике предполагается, что спектр S T (f) также определен в конечной области [- W , W ]:
S’ T (f) = S T (f) × P 2 W (f),
а за пределами этой области, согласно оценке Шеннона, формула для спектра S T (f) имеет вид
|S T (f)| ” 1/ W T , f P (- W , W ). (5.2.19)
Но усеченная часть спектра определяет разницу между исходной функцией s T (t) и функцией s’ T (t), восстановленной из усеченного спектра S’ T (f), поскольку усеченных гармоник спектра недостаточно для полного восстановления функции s T (f):
e T (t) = s T (t) – s’ T (t).
Соответственно, оценка дисперсии ошибки аппроксимации дается выражением:
s 2 = e 2 T (t) ” 1/ W T, s ” 1/. (5.2.20)
Эти выражения определяют порядок среднеквадратичной ошибки аппроксимации, которая является интегралом по интервалу T, а не локальной разницей значений s T (t)-s’ T (t). Типичная форма ошибки аппроксимации для усеченных сигналов показана на рис. Ошибка равна нулю в точках дискретизации, максимальна в центрах интервалов дискретизации и увеличивается по мере приближения к границам интервала T.
Физические данные обычно записываются через определенные интервалы времени T и обычно не достигают нуля на границах интервалов. В этом случае усечение ширины спектра может быть выполнено в соответствии с (5.2.20) с учетом допустимой среднеквадратичной ошибки аппроксимации данных. Частота W при усечении спектра может рассматриваться как частота Найквиста для сигнала s T (t) при его дискретизации, что определяет частоту дискретизации не менее F=2 W и число точек дискретизации не менее N=TF=2 W T.
Поскольку свойства прямого и обратного преобразования Фурье идентичны, для оценки условий выборки спектров можно использовать аналогичную технику.
Поэтому дискретизация усеченных сигналов возможна, но при обработке усеченных сигналов необходимо соблюдать осторожность и контролировать как среднеквадратичное значение ошибки, так и характер возникающих искажений сигнала и спектра. Например, когда автокорреляционная функция усечена, в спектре мощности сигнала могут появиться отрицательные значения, поскольку функция выборки sinc( p fT) в (5.2.18) является знакопеременной. Другим примером является проектирование полосовых фильтров. Рассматривая передаточную функцию H(f) в частотной области как функцию P H(f) = P r (f), обратное преобразование Фурье дает импульсный ответ фильтра h(t) с H(f) бесконечной длины. Усечение отклика h T (t) = h(t)P T (t) вызывает изменение передаточной функции фильтра (явление Гиббса): H T (f) = P r (f) * P T (f) J P r (f) Ch T sinc( p fT), где на краях скачков функции P появляются затухающие колебания амплитуды первого скачка до 9% от значения коэффициента усиления полосы пропускания фильтра.
Поскольку частотный характер искажений, возникающих при обрезании сигнала, определяется весовой функцией P T (t) Y T C sinc( p fT), приемлемый уровень и форма искажений сигнала могут быть определены не только выбором интервала T, но и использованием других весовых функций. Поэтому, чтобы исключить появление отрицательных значений в спектрах мощности, целесообразно провести усечение автокорреляционной функции путем взвешивания функций, не имеющих отрицательных значений в своих спектрах. Одной из таких функций является, например, треугольная весовая функция (окно Бартлетта).
Спектральная корреляция одиночных и периодических сигналов
Спектр S T (f) = S(k D f) периодического сигнала s T (t) с периодом T является дискретным (D f = 1/T). Спектр S(f) одиночного сигнала s(t), заданного интервалом T, является непрерывным и представляет собой спектральную плотность сигнала в момент времени T Ґ . Но периодический сигнал также можно представить как свертку одного периода с функцией Дирака:
s T (t) = s(t) * Sch T (t).
Если мы перейдем в частотную область, то получим :
S T (f) = (1/T) Ch S(f) Ch 1/T (f) = S(k D f),
Из этого следует, что спектр периодического сигнала – это дискретизированный спектр единичного сигнала, нормированный на длину периода.
С другой стороны, одиночный сигнал s(t) может быть получен из периодического сигнала s T (t) путем умножения на селективный прямоугольный импульс P T (t):
s(t) = s T (t) × P T (t).
Спектр одиночного сигнала:
S(f) = T C S T (f) * P T (f) = T S(k D f) C sinc[ p T(f-k/T)], (5.2.22)
то есть непрерывный спектр одиночного сигнала однозначно сопоставляется со спектром периодического сигнала (интерполяция с помощью ряда Котельникова-Шеннона в частотной области).
Выборка по критерию максимального отклонения
Проблема абсолютно точной реконструкции сигнала на практике обычно не ставится, в отличие от проблемы минимального физического объема информации, при котором сохраняется возможность ее восстановления в непрерывном виде с определенной приемлемой величиной погрешности. Эта проблема существует всегда, особенно при дистанционных методах записи и обработки информации, передачи сигналов по каналам связи и подготовки информации к длительному хранению. Одним из методов решения этой проблемы является дискретизация сигналов по критерию наибольшего отклонения.
В процессе дискретизации по критерию наибольшего отклонения определяется допустимое значение ошибки восстановления сигнала s. При восстановлении сигнала непрерывная функция s(t) обычно аппроксимируется степенными полиномами порядка n. Ошибка восстановления функции s(t) полиномом s a (t) определяется остаточным членом L(t):
L(t) = s(t) – s a (t) = s (t).
Шаг дискретизации выбирается из условия, что L(t) < s на всем интервале детерминации функции s(t). В принципе, динамика функции s(t) может значительно изменяться в различные моменты времени в пределах интервала обнаружения, и шаг выборки также может изменяться, при условии, что фиксированная ошибка не превышается на каждом шаге. Для заданного значения s количество выборок уменьшается за счет увеличения мощности аппроксимирующего полинома. На практике обычно ограничиваются ступенчатой, линейной и параболической аппроксимацией с полиномами нулевой, первой и второй степеней, соответственно.
Полиномы Лагранжа используются в качестве интерполирующих полиномов. Для полинома Лагранжа нулевой степени предполагается, что значение s a (t) в момент времени t в интервале t i
Полиномы Тейлора используются в качестве экстраполирующих полиномов. Для полинома Тейлора нулевой степени условия восстановления сигнала практически такие же, как и для полинома Лагранжа, за исключением направления (от текущей записанной опорной точки и вперед на t). Для более мощных полиномов Тейлора, помимо опорного значения s(t i ), для реконструкции сигнала используются также соответствующие производные значения в опорной точке. Восстановление сигнала с помощью полиномов Тейлора выполняется без временной задержки. Однако при использовании полиномов степени выше нуля точная реконструкция сигнала требует вдвое большей частоты дискретизации по сравнению с методами интерполяции.
Адаптивная выборка
Единая частота дискретизации рассчитывается на основе предельных значений частотных характеристик сигналов. Адаптивная выборка ориентируется на динамические характеристики сигнала, позволяя реконструировать его с минимальным количеством выборок. Принципы адаптивной выборки основаны на отслеживании текущей ошибки реконструкции сигнала. Наиболее часто используемые алгоритмы выборки – это алгоритмы с адаптивной длиной интервала аппроксимации. Суть дискретизации заключается в последовательно увеличивающемся интервале аппроксимации с непрерывным сравнением сигнала s(t) с функцией отображения s a (t). При достижении заданного значения s приращение интервала останавливается и подсчитывается значение s(t i ), т.е. выборка становится нерегулярной. Для восстановления нерегулярно дискретизированных сигналов обычно используются алгебраические полиномы мощности степени ноль и степени один в вариантах интерполяции или экстраполяции.
Простейшей техникой является адаптивная выборка с использованием полинома нулевой степени. В момент времени t и в начале каждого интервала аппроксимирующий полином s a (t) принимает значение, равное s(t i ), вычисляется текущая разность L(t) = s(t)-s a (t) и ее значение сравнивается с заданным значением s . После установления равенства L(t) = s снимается еще одно показание и начинается следующий временной интервал.
Если используется аппроксимация полиномом первой степени, то вычисляется значение s a (t) = s(t i )+s'(t i ), где s'(t) – производная сигнала. Момент следующего отсчета определяется выполнением равенства s(t)-s(t i )-s'( t i ) = s . Обратите внимание, что этот алгоритм неэффективен в присутствии высокочастотного шума, к которому операция дифференцирования очень чувствительна.
Задание 2 – Исследовать и разработать программу для оценки спектра дискретного сигнала с неравномерным шагом дискретизации.
Простейшими методами восстановления сигнала при адаптивной выборке являются линейная и квадратичная интерполяция, которые реализуются уравнениями:
f(x) lin = a 0 + a 1 x. f(x) kv = a 0 + a 1 x + a 2 x 2 .
Эти уравнения являются частным случаем полиномиальной интерполяции с использованием аппроксимирующего полинома:
f(x) = a 0 + a 1 x + a 2 x 2 + … + a n x n = a i -x i . (5.4.1)
Для выполнения полиномиальной интерполяции достаточно, используя выражение (5.4.1), построить систему линейных уравнений для n последовательных выборок и определить n значений коэффициентов a и . При глобальной интерполяции для всех N точек функции степень полинома равна N-1. Глобальная интерполяция обычно выполняется для достаточно коротких (не более 8-10 выборок) наборов данных. Пример глобальной интерполяции показан на рисунке 5.4.1.
Рисунок 5.4.1: Интерполяция данных.
Большие наборы данных интерполируются в последовательных локальных частях или в скользящем интерполяционном окне, обычно нечетного значения N, с вычислением желаемых значений сигнала в некотором интервале средней части окна.
Курсовая работа 3 – Исследовать и обосновать оптимальный метод полиномиальной интерполяции для произвольных данных с равномерным шагом выборки. Разработайте программу для интерполяции.
Курсовая работа 4 – Исследовать и обосновать оптимальный метод полиномиальной интерполяции для произвольных данных с неравномерным шагом выборки. Разработайте программу для интерполяции.
Аппроксимационные формулы, не требующие предварительного определения коэффициентов аппроксимирующих полиномов, более удобны в практическом применении. К таким формулам относится интерполирующий полином Лагранжа /30/. Когда функция y(x) аппроксимируется полиномом n-й степени f(x):
Пример интерполяции Лагранжа показан на рисунке 5.4.2. 5.4.2.
Рисунок 1.2.2: Лагранжева интерполяция.
Курсовая работа 5 – Исследовать и обосновать оптимальный метод интерполяции Лагранжа для произвольных данных с неравномерным шагом дискретизации. Разработайте программу для интерполяции.
Квантование сигнала
Дискретизация аналоговых сигналов вместе с их преобразованием в цифровую форму связана с квантованием сигнала. Суть квантования заключается в замене бесчисленного множества возможных значений функции, в общем случае случайных, конечным множеством цифровых показаний, что осуществляется путем округления мгновенных значений входной функции s(t i ) в моменты времени t i до ближайших значений s i (t i ) = n i Ds , где Ds – шаг квантования шкалы цифровых показаний. Квантование с фиксированным шагом Ds называется равномерным квантованием. Математически операция квантования может быть выражена формулой:
где скобки […] обозначают целую часть значения, указанного в скобках.
При квантовании сигналов в большом динамическом диапазоне значений шаг квантования также может быть неравномерным, например, логарифмическим, т.е. пропорциональным логарифму значения входного сигнала. Установленный диапазон шкалы квантования от s min до s max и шаг квантования Ds определяют количество делений шкалы N s = (s max -s min )/ Ds и цифровое разрешение квантования, соответственно. В результате дискретизации и квантования непрерывная функция s(t) заменяется числовой последовательностью . Ошибка округления e i = s(k D t)-s i (k D t) находится в диапазоне – Ds /2< e < Ds /2 и называется шумом квантования. Требуемая точность квантования оценивается по влиянию возникающего шума квантования на дальнейшую обработку сигнала.
Если шаг квантования достаточно мал, можно предположить, что каждое значение в его пределах одинаково вероятно, так что значения e распределены по закону равномерности:
p( e ) = 1/ Ds , – Ds /2 Ј e Ј Ds /2.
Дисперсия и среднеквадратичное значение шума квантования, соответственно:
e 2 = Ds 2 /12, ” 0,3 Ds . (5.5.1)
При определении уровня шума квантования с помощью выражения (5.5.1) несложно определить приемлемый шаг квантования.
Входной сигнал обычно содержит аддитивную смесь собственно сигнала s(t) и помехи q(t) с дисперсией s q 2 , соответственно. Если шум не коррелирует с сигналом, то после квантования общая дисперсия шума
s 2 = s q 2 + e 2 .
На практике шаг квантования обычно выбирается таким образом, чтобы не происходило значительного изменения отношения сигнал/шум, т.е. e 2 << s q 2 .
Децимация и интерполяция данных
Децимация (уменьшение, сокращение) цифровых данных обычно называется уплотнением данных с удалением избыточной информации. Последнее происходит, если шаг выборки данных был установлен слишком подробным, а сигнал f N = 1/2 D t >> f max. Информация о высокочастотной части сигнала может оказаться ненужной, если основная энергия полезной части сигнала содержится в низкочастотной области. Децимация также может потребоваться, если наборы данных представлены с разной частотой дискретизации.
Децимации должна предшествовать низкочастотная фильтрация данных. Это связано с тем, что во время децимации шаг выборки D t заменяется новым шагом D t’ = p D t, где p>1, с соответствующим сжатием основной полосы частот, и существует риск, что отбракованные частотные компоненты и высокочастотный шум отражаются в основной полосе (как в случае неправильного выбора шага выборки). Точка среза фильтра низких частот устанавливается на новую частоту Найквиста: f N ‘=1/(2p D t).
Значение p коэффициента децимации может быть любым, но обычно используются целые значения, и децимация производит простое прореживание данных. Когда p не является целым числом, децимация может быть выполнена с помощью интерполяционного ряда Котельникова-Шеннона (а также любого другого интерполяционного полинома) или преобразования Фурье. Последнее осуществляется путем преобразования сигнала в частотную форму и возврата в координатную форму с новым шагом D t’ = p D t, так что фильтрация низких частот может быть выполнена непосредственно по частоте. Возможно также прямое усечение основной полосы частот от N точек до N’ = N/p обратно до новой полосы частот в координатной форме с числом точек N’, но в этом случае необходимо учитывать последствия усечения спектральной функции (умножение на прямоугольное селективное окно) на восстановленную из нее форму сигнала (свертка исходного сигнала с Фурье-образом прямоугольного селективного окна).
Интерполяция данных отличается от децимации только коэффициентом p<1, с соответствующим увеличением частоты Найквиста, и не требует фильтрации низких частот.
Для децимации и интерполяции данных также были разработаны специальные быстрые методы и алгоритмы (цифровые фильтры) – экспандеры и компрессоры /4,5/.
Литература
4 Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочное пособие. – М.: Радио и связь, 1985.
5. Гольденберг Л.М. и др. Цифровая обработка сигналов: учебник для средних школ.- М.: Радио и связь, 1990 г. – 256 с.
10. Дмитриев В.И. Прикладная теория информации: учебник для вузов. – Москва: Высшая школа, 1989.
16. Максим Ж. Методы и техника обработки сигналов в физических измерениях. – Москва: Мир, 1983.
17. Никитин А.А. Теоретические основы обработки геофизической информации: учебник для вузов – М.: Недра, 1986.- 342 с.
21 . Рапопорт М.Б. Компьютерная техника в промысловой геофизике: учебник для вузов.- М.: Недра, 1993 г. – 350 с.
30. Корн Г., Корн Э. Справочник по математике для ученых и инженеров. – Москва: Наука, 1984.
Дискретизация сигналов означает преобразование функций непрерывных переменных в функции дискретных переменных, из которых исходные непрерывные функции могут быть восстановлены с определенной точностью. Роль дискретных образцов обычно играют квантованные значения функции на дискретной шкале координат. Под квантификацией понимается преобразование непрерывной величины в величину с дискретной шкалой значений из конечного множества допустимых значений, которые называются уровнями квантификации. Если уровни квантования пронумерованы, то результатом преобразования является число, которое может быть выражено в любой системе счисления. Округление мгновенных значений непрерывной аналоговой величины с шагом аргумента с некоторым разрешением является простейшим случаем дискретизации и квантования сигналов при их преобразовании в цифровые сигналы.
2.2 Цифровой сигнал
Цифровой сигнал – это сигнал данных, каждый из параметров которого описывается дискретной функцией времени и имеет конечное множество возможных значений.
Сигналы – это дискретные электрические или световые импульсы. В этом методе вся пропускная способность канала связи используется для передачи одного сигнала. Цифровой сигнал использует всю полосу пропускания кабеля. Полоса пропускания – это разница между максимальной и минимальной частотой, которая может быть передана по кабелю. Каждое устройство в такой сети отправляет данные в обоих направлениях, а некоторые могут принимать и передавать их одновременно. Узкополосные (baseband) системы передают данные в виде цифрового сигнала одной частоты.
Дискретные цифровые сигналы сложнее передавать на большие расстояния, чем аналоговые, поэтому они предварительно модулируются на стороне передатчика и демодулируются на стороне приемника. Использование алгоритмов проверки и восстановления цифровой информации в цифровых системах может значительно повысить надежность передачи информации.
Предупреждение. Обратите внимание, что реальный цифровой сигнал по своей физической природе является аналоговым. Он имеет колебания амплитуды, фазы/частоты (джиттер) и поляризации из-за шума и изменения параметров линии передачи. Однако этому аналоговому сигналу (импульсному и дискретному) придаются численные свойства. Поэтому для его обработки можно применять численные методы (компьютерная обработка).
Познакомьтесь с цифровой синусоидой частотой 15 кГц с одинаковой амплитудой и частотой. Красивый узор, не правда ли? Как вы видите, амплитуда меняется с частотой. Это уже интермодуляционные искажения. Наш истинный сигнал 15 кГц модулируется с частотой, кратной 44,1 кГц.
Подводя итог
Конечно, никто не умер из-за плохих высоких частот, и, возможно, я преувеличиваю, говоря, что частота дискретизации 44,1 кГц настолько плоха, но, как видите, особым качеством на высоких частотах не блещет.
Мне гораздо интереснее слушать винил дома. Но вы не попадете в андеграунд с проигрывателем… Поэтому вам придется удовлетворить свои потребности любителя музыки с помощью цифрового плеера.
Всем хорошего звука!
(P.S. – не стесняйтесь комментировать 
Привет! В этом блоке авторы блогов любят измерять крутость своих биографий. С другой стороны, я предпочитаю выслушивать критику статей и блогов в комментариях. Обычный человек, который любит музыку, копается в аппаратуре, электронике и программном обеспечении, особенно когда эти вещи переплетаются и образуют единое целое, отсюда и название – Audiogeek. Материалы на этой странице – это мой собственный опыт, который, я надеюсь, будет полезен и вам. Я рад, что вы читаете это 
Ну, вы не можете бороться с логикой, потому что при 20000 Гц с дискретизацией 40000 это будет тупой треугольный сигнал…
Я никогда не читал о звуковых хитросплетениях в такой простой форме, спасибо!
Я рада, что вам понравилось. Так вот, я не думал о частоте дискретизации, я больше обращал внимание на битрейт, но когда я случайно обнаружил, что синус на самом деле не синус, я понял, какая куча(((
Спасибо за ваш комментарий  !
!
Спасибо, я немного не хочу покупать дорогое оборудование)))
Спасибо за четкое объяснение!
Спасибо за тему, я не обращал внимания на дискретность звука, всегда выбирал после битрейта, так точно на картинках в наше время не видел, лет 20 назад натыкался на такие темы, но как-то не воспринимал всерьез, потому что выбор осциллографа был нормой, а со звуком это никак не вязалось, уважуха!
Спасибо за комментарий!
Я заинтересовался этим после того, как решил использовать осциллограф для проверки выхода плеера на высоких частотах…..
Я сделал тракт со ступенчатым изменением частоты от 10кГц до 20кГц за минуту, подал выходной сигнал на осциллограф и смотрел, как все это красиво крутится…..
Добрый вечер, Эндрю.
Случайно наткнулся на вашу статью, давно интересуюсь этим вопросом, могу объяснить некоторые ваши интересные наблюдения:
1) Мало кто это знает и понимает, но для восстановления сигнала в теореме Котельникова необходимо строгое неравенство, согласно обозначениям в вашей статье это должно быть f > 2F. Поэтому при частоте дискретизации 44,1 кГц вы не сможете правильно восстановить синусоиду с частотой 22,05 Гц.
2) При выборке на частоте, не являющейся кратной, интермодуляционные искажения отсутствуют. Согласно теореме Котельникова, сигнал будет восстановлен теоретически точно, без ошибок. Однако это будет возможно только в том случае, если мы будем использовать фильтры с идеальными характеристиками. Поскольку все реальные фильтры имеют неидеальные АЧХ, сигнал восстанавливается с искажениями. Чем выше частота дискретизации, тем ниже искажения. Поэтому при частоте дискретизации 192 кГц качество звучания высокочастотных сигналов на порядок выше.
Здравствуйте Дмитрий!
Спасибо за ваш исчерпывающий комментарий.
1 Да, согласен, должно быть строгое неравенство, а начиная с 22.05 кГц – это условие не выполняется.
На том же википедия цитируется следующий отрывок из статьи Котельникова:
Любая функция f(t), состоящая из частот от 0 до fc, может быть передана непрерывно с любой точностью числами, следующими за 1/2fc секунды.
Это означает, что частота fc может быть передана с любой точностью при удвоенной частоте дискретизации самой fc.
В любом случае, те же 20 кГц также очень далеки от вероятности.
2) И здесь я с вами согласен!) В идеале на выходе ЦАПа должны быть фильтры 6-8 порядка, которые не только трудно реализуемы, но и вносят существенный вклад в искажение частотной и фазовой характеристики. Поэтому в качестве альтернативы обычно достаточно фильтров 2-го порядка. Но он все равно не может отсечь все ненужное.
По крайней мере, глядя осциллографом на выход моего HiFiMan HM-601, я наблюдал слегка сглаженные, но в целом такие же изображения, как приведены в статье.
Однако сейчас существуют не только аналоговые, но и цифровые фильтры, которые могут обеспечить очень крутой срез всех частот выше слышимых частот. Однако это уже несколько сложнее и дороже.
__________
Так почему же не интермодуляционные искажения? Если вы посмотрите на фотографии частот, которые не кратны частоте дискретизации, вы можете ясно увидеть, что точки идут волнами. А частота этих волн – это частота дискретизации. Поэтому полезный сигнал модулируется частотой дискретизации.
Более того, если вы генерируете сигнал, который плавно изменяется от 20 Гц до 20 кГц, это даже становится слышимым, примерно с 10 кГц и далее вы можете почувствовать, как он начинает плавать туда-сюда вместо плавного нарастания.
Добрый вечер, вы также не учли, что аудиосигнал при оцифровке не будет синхронизирован с дискретизацией, например, если разница в частоте дискретизации составляет полпериода, то вы получите плоскую линию вместо треугольников.
Некоторые люди получают от Бога уши, а некоторые – теорему Котельникова.
С вашего позволения, я расскажу вам одну историю из старых времен. Кажется, что это было сто лет назад, но на самом деле чуть меньше. Это был расцвет аналогового аудио. Я случайно оказался перед стендом на ярмарке в нечетное время. Сама выставка еще не была открыта, и стенды только собирались. Это был конец дня. На стенде стояла акустическая система с усилителем. Верхняя частота колонок составляла 70 кГц, а усилителя – 100 кГц. Через эту систему воспроизводилась музыка с катушечного магнитофона, стоявшего в углу. Рядом со мной сидел пожилой японец, слушал музыку и пил что-то принесенное в термосе. Звук, надо сказать, был впечатляющим. Такова была атмосфера. И вот я, такой умный, такой знающий – второй Котельников. Я спросил – а в чем проблема у вас, уважаемый гражданин – усилитель на 100 кГц, колонки – на 70, а слышим мы на 20? Японец оказался не только представителем производителя, но и инженером-разработчиком. Он позвал переводчика, тот перевел мой вопрос, и, что удивительно, японец ответил. Первая часть его ответа заключалась в том, что вибрационные помехи создают суммарные и разностные частоты. Если мы делаем трак с частотной характеристикой в слышимом диапазоне, скажем, до 20 кГц, мы потеряем 5 кГц, если подадим на вход две частоты – 20 кГц и 25 кГц. В этот момент переводчика увели, но японец почему-то хотел, чтобы я понял его концепцию. Уже на плохом английском, жестикулируя и рисуя в блокноте, он говорил о передаче фазовой информации в звуке, о влиянии фазовых искажений на звуковой образ, об альтернативном видении окружающей среды с помощью слуха…
Теорема Котельникова должна применяться после понимания того, какую информацию мы хотим извлечь из вибраций. А если у вас есть уши, то им нужно на порядок больше информации о звуке. Саундстейдж, окружающее пространство – это фазированная информация, которая начинает проявляться только при разрешении 18 бит 96 кГц. Желаю вам удачи!
Спасибо за ваш полезный и глубокий комментарий!
Вы, несомненно, правы! Почему-то я не думал об этом с такой точки зрения. Так что спасибо еще раз:)
треугольный сигнал с частотой 20 кГц, есть гармоники, которые портят звук….. Очень интересно… имеют ли гармоники частоту выше 20 кГц или ниже? ….a? Каким ухом вы их услышите?
Конечно, на выходе любого ЦАП есть фильтр LPF, который огибает этот треугольник, приближая его к синусу.
Настолько, что для избавления от лишнего цифрового мусора, генерируемого ЦАПом, вам понадобится LPF с частотой среза 20 кГц, обеспечивающий 30-40 дБ затухания при частоте дискретизации 44 кГц. Создание такого аналогового фильтра технически очень сложная и громоздкая задача, поэтому все чаще прибегают к цифровым фильтрам и псевдодублированию частот затухания.
Все это делается для удаления гармоник, лежащих на частотах, кратных частотам дескрипторов 44k, 88k….. Которые находятся за пределами слышимого диапазона, но влияют на него.
Я думаю, что все это делается не просто так, а?
“Имеют ли гармоники частоту выше или ниже 20 кГц? ….a? Каким ухом вы их услышите?”. – Дмитрий, она называется “Я не читатель, я писатель”. Извините.
Если мы говорим о гармониках, связанных с АЦП, то в вашем примере они будут занимать весь спектр от 0 Гц до нескольких МГц, из-за их странности и способности складывать, вычитать (также с исходным сигналом) и многое другое в нелинейной цепи. Вы можете увидеть спектральное распределение шума, подключив анализатор. Неплохо избавиться от него с помощью специальных алгоритмов, которые в несколько итераций вычитают из исходного сигнала спектр, создаваемый гармониками. Недостатком этого метода является то, что он дорогостоящий и привязан к конкретному аппаратному тракту. Существуют также менее точные, но более универсальные аппаратные аналоги этого решения (Burr-Brown, Tripath…), которые используют введение обратной связи, но, тем не менее, являются общепризнанными стандартами высокого качества, прежде всего, при передаче звука.



