Лекции ITE-№55 Законы коммутации в переходных цепях - услуги электромонтажа, строительства и ремонта

и мощность, поглощаемая электрическим полем конденсатора:

Содержание

№ 55 Законы (принципы) коммутации.

Первый закон коммутации гласит, что ток iL в цепи с индуктором L не должен изменяться с шагом в момент коммутации, т.е.

Предположим, наоборот, что ток iL изменяется с шагом, т.е:

Из этого следует, что напряжение на катушке:

и мощность, потребляемая магнитным полем катушки:

Полученные выводы противоречат законам физики, поскольку невозможно получить напряжение u=∞, а в природе не существует источников энергии, способных развивать бесконечную мощность. Поэтому наше первоначальное предположение неверно, и мы вправе утверждать, что diL/dt≠0, т.е. ток iL в цепи с катушкой L в момент переключения не может изменяться ступенчато.

Второй закон коммутации гласит, что напряжение uC на выводах конденсатора C не должно изменяться ступенчато при коммутации, т.е.

Предположим вместо этого, что напряжение uC изменяется скачкообразно, т.е.

Из этого следует, что ток в конденсаторе

и мощность, потребляемая электрическим полем конденсатора:

Полученные выводы противоречат законам физики, так как невозможно получить ток i=∞ и не существует источников энергии с бесконечной мощностью. Поэтому наше первоначальное предположение неверно, и мы вправе утверждать, что duC/dt≠0, т.е. напряжение uC на зажимах конденсатора C в момент коммутации не может изменяться ступенчато.

Законы переключения используются на практике для определения начальных условий при расчете переходных процессов.

Если мы продолжим упрощать схему (исключая внутреннее сопротивление источника /? 6.1, c), то перемещение ключа из одного положения в другое всегда будет представлять собой неправильную коммутацию.

Закон коммутации.

В реальной цепи переход из одного устойчивого состояния в другое не может быть мгновенным, в мгновение ока. Это происходит потому, что энергия, запасенная в электрическом и магнитном полях, имеет определенное значение, соответствующее каждому устойчивому состоянию. Для ступенчатого перехода из одного устойчивого состояния в другое потребуется ступенчатое изменение запасенной энергии, что, учитывая выражение (1.5), возможно только в том случае, если источники энергии бесконечно мощные, т.е. токи или напряжения, которые они могут подавать, могут принимать бесконечно большие значения. В связи с тем, что каждый реальный источник энергии может отдавать только конечную мощность, общая энергия, запасенная в цепи, может изменяться только плавно, т.е. является непрерывной функцией времени.

Следовательно, Возникновение переходных процессов при переходе электрической цепи из одного устойчивого состояния в другое связано с тем, что энергия, запасенная реактивными элементами в цепи, не может изменяться скачком, а изменяется только плавно, т.е. с конечной скоростью.

Из этого следует, что в резистивной цепи (в нереактивной цепи) переход из одного устойчивого состояния в другое должен быть мгновенным. Таким образом, в нереактивных цепях переходные процессы отсутствуют. Понятно, что такие цепи можно рассматривать только как очень упрощенные модели реальных цепей, поэтому процесс перехода от одного устойчивого состояния к другому в любой реальной цепи всегда будет сопровождаться переходными процессами.

Хорошо известно, что энергия, запасенная реактивными элементами в цепи, определяется токами индуктивности и напряжениями емкости. Предполагая, что запасенная энергия является непрерывной функцией времени, мы делаем вывод, что токи индуктивности и напряжения емкости непрерывны во времени. Этот вывод чрезвычайно важен в теории цепей и формулируется в виде законов (правил) коммутации.

Первый закон коммутации: В начальный момент времени после переключения индукционный ток сохраняет прежнее значение, как это было непосредственно перед переключением

а затем плавно переходит, начиная с этого значения.

Второй закон коммутации: В начальный момент времени после переключения емкостное напряжение сохраняет прежнее значение, как это было непосредственно перед переходом

а затем плавно переходит, начиная с этого значения.

Законы коммутации не накладывают ограничений на характер изменения емкостных токов, индуктивных напряжений и токов или резистивных напряжений, которые могут изменяться произвольно, в том числе ступенчато.

Хорошо известно, что теория цепей рассматривает процессы, происходящие в идеализированных цепях под влиянием идеализированных внешних взаимодействий. Использование слишком упрощенных моделей элементов схемы и внешних взаимодействий может привести к нарушению предположений, сделанных при формулировке законов коммутации, и, следовательно, к нарушению самих законов. Например, интерес представляют случаи, когда идеализированные источники энергии могут обеспечить бесконечно большой ток или напряжение за бесконечно короткое время, т.е. развивать бесконечно большую мощность. Под влиянием таких внешних воздействий законы коммутации нарушаются, и токи индуктивности или напряжения емкости изменяются скачкообразно (см. раздел 6.5).

Законы коммутации также могут не выполняться для некоторых коммутаций с ветвями, содержащими реактивные элементы. Выключатели такого типа называются неправильные коммутации. Анализ процессов, происходящих в цепях с неправильной коммутацией, проводится с использованием принципов непрерывности цепи потока и электрического заряда, которые являются более общими, чем законы коммутации: Алгебраическая сумма индуктивности контура потока в любом замкнутом контуре электрической цепи и алгебраической суммы зарядов конденсатора, подключен к любому узлу электрической цепи, являются непрерывными функциями времени

Следует подчеркнуть, что Неправильная коммутация возникает в результате чрезмерного упрощения процесса коммутации или чрезмерного упрощения модели элемента и может быть устранена более строгим анализом.

Таким образом, термин “неправильная коммутация” не совсем корректен: правильнее говорить не о неправильной коммутации, а о неправильной постановке проблемы коммутации.

Пример 6.1 Рассмотрим процесс зарядки конденсатора от гальванического элемента. Если конденсатор и источник энергии соединены последовательно (рис. 6.1, а), а затем переключить клавишу S из положения 1 в положение 2 (или наоборот) является действительной операцией переключения.

Действительно, пусть в исходном состоянии ключ находится в положении 1, а емкость С полностью разряжен и в момент времени t = Если в результате коммутации напряжение на конденсаторе внезапно увеличилось, то согласно уравнению составляющих конденсатора

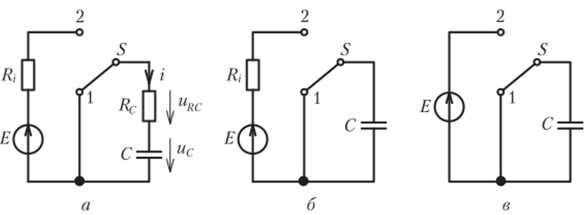
Рисунок 6.1. Например, 6.1

(1.13), ток в цепи достигнет бесконечно большого значения, в результате чего левая часть уравнения баланса напряжений для цепи будет получена после переключения, ис+ (R_c + Rj)i – E_> не будет равна правой части.

Таким образом, предположение, что второй закон коммутации нарушается в ceni, приводит к однозначно неверному результату. Поэтому напряжение на конденсаторе в начальный момент времени после коммутации сохраняет то же значение, что и в момент, непосредственно предшествующий коммутации: m_с uq = E).

Если в исходном состоянии ключ находится в положении 2, а емкость C заряжена до значения Ето при переключении ключа в положение 1 напряжение на емкости сохраняет значение, которое оно имело в момент, непосредственно предшествующий изменению, напряжение на сопротивлении /?_с(0+)= -Е, и ток сопротивления перескакивает на -i’c(0+) = -E/R_c. Затем напряжение и ток конденсатора плавно уменьшаются, стремясь к нулю.

Если мы упростим схему конденсатора и исключим сопротивление потерь R_c. (рис. 6.1, б), то перемещение ключа из положения 1 в положение 2 будет по-прежнему правильной коммутацией, а перемещение ключа из положения 2 в положение 1 – неправильной коммутацией (неправильная коммутация связана с тем, что в рассмотренной эквивалентной схеме не учтены потери энергии в конденсаторе и соединительных проводах, а также энергия, выделяемая при искре между контактами ключа. В зависимости от точности анализа, следует либо предположить, что напряжение на конденсаторе скакнуло от is(O-) = E к нулю или использовать более сложную эквивалентную схему для конденсатора, выключателя и соединительных проводов).

Если продолжать упрощать схему (исключая внутреннее сопротивление источника /?,) (рис. 6.1, в), то переключение ключа из одного положения в другое всегда будет неправильным.

Пример 6.2. Рассмотрим идеализированную цепь (рис. 6.2). Предположим, что в начальном состоянии ключ S находится в положении 1, а ток, протекающий через индуктивность, имеет постоянное значение i_Li(0_) =

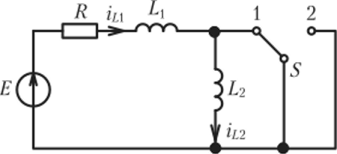
Рисунок 6.2. Пример 6.2

Если в момент t = 0 ключ S переключается из положения 1 в положение 2, индуктивности L_< и L₂ будут включены последовательно, и их токи должны быть немедленно уравнены (для баланса токов). Очевидно, что такая коммутация неверна и что начальное значение тока индукторов rD (0+) = ii2(0.)) = i_L(0+) после коммутации можно определить из принципа непрерывности протекающих токов: L_<i_Ll(0₊) + L₂i_L2(0+) = (L_< + L₂)i_L<0₊) = L_<i_Ll(0_)_y следовательно

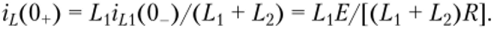
При анализе такой оценки обычно предполагается, что токи индуктивности L и Ь₂ варьироваться ступенчато в зависимости от уровня i_L (0+), а затем плавно увеличивается (начиная с этого уровня) до фиксированного значения ii = E/R.

Нетрудно заметить, что энергия данной цепи сразу после переключения

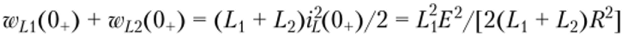
меньше, чем энергия, накопленная в индукторе L перед переключением:

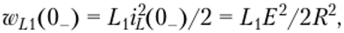
где разница между этими значениями равна энергии коммутационных потерь, т.е. потерь, связанных с образованием дуги или искры между контактами. Рассматриваемая коммутационная операция может быть скорректирована путем включения в анализ конечного времени коммутации, использования более точной модели индукторов, содержащей не только сопротивления потерь, но и паразитные емкости, а также учета явления дуги между контактами. Конечно, учет этих явлений значительно усложняет анализ.

Общий подход к анализу переходных процессов. Задача анализа переходных процессов обычно заключается в определении мгновенных значений токов и напряжений всей или части ветви цепи в любой момент времени после коммутации. Для этого необходимо найти общее решение основной системы электрических уравнений цепи или системы электрических уравнений, составленной любым другим способом, в точке t > 0. Исключив из системы уравнений все неизвестные, кроме одного, можно получить дифференциальное уравнение цепи относительно этой величины. Таким образом, задача анализа переходного процесса может быть сведена к решению дифференциального уравнения цепи при t > 0. В частности, задача анализа переходных процессов в линейной инвариантной во времени системе с сосредоточенными параметрами порядка v сводится к нахождению общего решения линейного неоднородного дифференциального уравнения порядка v вида (1.46).

Общее решение такого уравнения содержит v произвольных констант, для которых должны быть заданы значения искомой функции s и его v – 1 первых производных в начальный момент времени после коммутации, т.е. при t = 0+. Эти величины определяются законами переключения на основе анализа процессов, происходящих в цене до переключения. Проанализируйте цепь перед переключением, рассчитав токи всех индуктивностей и напряжения всех емкостей за время непосредственно перед переключением. Затем, используя законы коммутации (в более общем случае принципы непрерывности цепи потоков и электрических зарядов), найдите токи индуктивности и напряжения емкости в начальный момент времени после коммутации. Очевидно, что для определения v начальных условий законы коммутации должны быть применены к v независимо включенным реактивным элементам, то есть ко всем реактивным элементам, включенным таким образом, что их энергетическое состояние может быть задано независимо. Сумма начальных значений токов независимо включенных индуктивностей и напряжений независимо включенных емкостей составляет являются независимыми начальными условиями системы. Используя независимые начальные условия и уравнения электрического равновесия цепи после переключения, найдите зависимые начальные условият.е. значения токов и напряжений любых ветвей и их производных в момент времени t = 0₊.

Если энергия, запасенная в цепи за время, непосредственно предшествующее коммутации, равна нулю, то цепь анализируется при нулевых начальных условиях. Если начальная запасенная энергия ненулевая, цепь должна быть проанализирована при ненулевых начальных условиях. (В первом случае все независимые начальные условия равны нулю, во втором случае хотя бы одно из них имеет ненулевое значение).

Следует отметить, что независимые начальные условия, и поэтому_у токи и напряжения ветвей цепи после коммутации определяются на основе энергетического состояния цепи только во время, непосредственно перед расслаблением (С = 0 ), и не зависит от характера процессов, происходящие в цепи до переключения (в момент времени t и два независимых индуктивных сечения <>_f ?₂“Az>” <аз» 4=”” as=””>* Порядок сложности схемы v =. фик

2) Закон коммутации:

Законы коммутации в электрических цепях

Переключение – это кратковременное или прерывистое изменение структуры или параметров цепи (включение, выключение, переключение).

Результатом переключения является так называемый “переходный процесс”. процесс перехода состояния электрической цепи из одного устойчивого состояния в другое, при этом мы различаем принудительно (проводка) процесс перехода и бесплатно (например, при отключении электропитания).

В отличие от процесса переключения, переходный процесс не может быть ступенчатым, поскольку ступенчатое изменение энергии цепи потребовало бы бесконечной мощности (p = dW/dt). А поскольку электрическая энергия в реактивных элементах не может быть запасена мгновенно, то при постоянных значениях = const действуют два закона коммутации:

1) Закон о коммутации:

Ток в индуктивном элементе не должен изменяться ступенчато, т.е. ток перед коммутацией должен быть равен току при коммутации: .

2-й закон о коммутации:

Напряжение на емкостном элементе не должно меняться скачками, т.е. до коммутации и в момент коммутации должно быть одинаковым: = .

Все остальные напряжения и токи могут изменяться ступенчато.

В анализе переходных процессов начальное устойчивое состояние называется начальные условиякоторые описывают внутреннее состояние системы в некоторый фиксированный момент времени. По условию, значение желаемой функции и ее производные определяются в момент времени t=0. Они могут быть нулевыми (ток через индуктор и напряжение на конденсаторе, когда система включена) и ненулевыми (те же параметры, когда система выключена). Согласно законам коммутации, при нулевых начальных условиях (1-й закон) индуктивный элемент является разрывом в цепи; аналогично емкостной элемент при включении в тех же начальных условиях (2-й закон) является коротким замыканием в цепи.

Следует отметить, что резкое увеличение тока в цепи при резонансе соответствует увеличению Xl и Xc. Эти напряжения могут быть намного выше, чем напряжение U на клеммах цепи, поэтому резонанс напряжений является опасным явлением в электроустановках.

Переходные процессы в цепях переменного тока, законы коммутации, явления резонанса

Стационарные электрические цепи – это цепи, в которых параметры цепи, такие как напряжение, ток, сопротивление и т.д., постоянны. Если напряжение изменится после достижения устойчивого состояния, ток также изменится. Переход из одного устойчивого состояния в другое происходит не мгновенно, а занимает некоторое время (рис. 1).

Процессы, происходящие в цепях при переходе из одного устойчивого состояния в другое, называются переходными. Переходные процессы возникают при резком изменении параметров цепи. Момент внезапного изменения в цепи рассматривается как начальный момент, по отношению к которому характеризуется состояние цепи и который описывает сам переходный процесс.

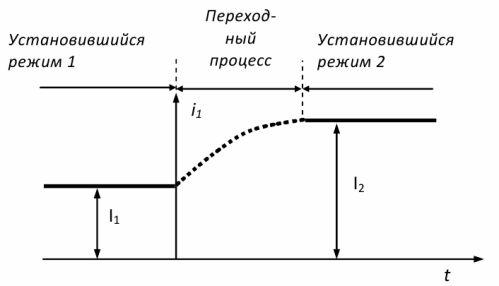
Рисунок 1: Режимы, возникающие в цепи переменного тока

Продолжительность переходного процесса может быть очень короткой, измеряемой долями секунд, но токи и напряжения или другие параметры, описывающие процесс, могут быть очень высокими. Переходные процессы возникают в результате переключения в цепи.

Переключение – это замыкание или размыкание контактов в коммутационных устройствах. При анализе переходных процессов используются два закона коммутации.

Первый закон коммутации: ток, протекающий через индукционную катушку до коммутации, равен току, протекающему через ту же катушку сразу после коммутации. Это означает, что ток в индукционной катушке не может изменяться ступенчато.

Второй закон коммутации: напряжение на емкостном элементе до коммутации равно напряжению на том же элементе после коммутации. Это означает, что напряжение на емкостном элементе не может изменяться ступенчато. Для резистора, индуктора и конденсатора, соединенных последовательно, применимо следующее

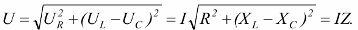
В рассматриваемой цепи, когда реактивности Xl и Xc равны, возникает так называемый резонанс напряжения. Поскольку эти сопротивления зависят от частоты, резонанс возникает при определенной резонансной частоте ωo .

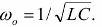
В этом случае импеданс цепи минимален и чисто активен Z = R, а ток максимален. При ω ωo нагрузка является активно-конденсаторной, а при ω > ωo – активно-индуктивной.

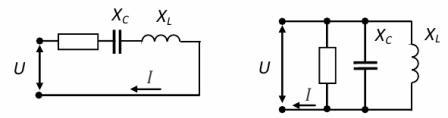
Обратите внимание, что резкое увеличение тока в цепи при резонансе соответствует увеличению Xl и Xc. Эти напряжения могут быть намного выше, чем напряжение U на клеммах цепи, поэтому резонанс напряжения является опасным явлением в электроустановках.

Токи в ветвях параллельно соединенной цепи имеют соответствующий сдвиг фаз по отношению к общему напряжению цепи. Поэтому общий ток цепи равен сумме токов отдельных ветвей, включая сдвиг фаз, и определяется по формуле

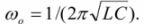
Когда реактивности Xl и Xc равны, токи в цепи с параллельными элементами являются резонансными. Ток при резонансе максимален, а коэффициент мощности максимален (cos φ = 1). Значение резонансной частоты задается формулой

Токи в ветвях, содержащих L и C, при резонансе могут быть больше, чем общий ток цепи. Индуктивный и емкостной токи противоположны по фазе, равны по величине и взаимно компенсированы по отношению к источнику питания. Другими словами, в цепи между индуктором и конденсатором происходит обмен энергией.

Этот режим работы, близкий к резонансу токов, широко используется для повышения коэффициента мощности электрических нагрузок. Это дает значительный экономический эффект благодаря снятию нагрузки на проводники, снижению потерь, экономии материалов и электроэнергии.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

В электрических цепях могут включаться и выключаться пассивные или активные ветви, замыкаться отдельные участки, выполняться различные переключения, внезапно изменяться параметры и т.д. В результате таких изменений, часто называемых переключением или просто коммутацией, которые мы будем рассматривать как происходящие мгновенно, в цепи возникают переходные процессы, заканчивающиеся через некоторое (теоретически бесконечно долгое) время после переключения. Если это не указано в явном виде, мы предполагаем, что время перехода t=0 начинается в момент переключения. Обозначим момент непосредственно перед мгновенной коммутацией через 0 – , а момент непосредственно после мгновенной коммутации через 0 + .

Два закона коммутации

В индуктивном элементе ток (и магнитный поток) сразу после коммутации, в момент, который мы называем моментом коммутации t=0+ , или сокращенно t=0, сохраняет значение, которое он имел непосредственно перед коммутацией, т.е. в момент t=0- , а затем начинает изменяться от этого значения:

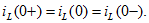
Таким образом, после включения ветви с катушкой, в которой не было тока, ток в этой ветви в момент включения равен нулю. Если для такой ветви предположить, что в момент коммутации ток изменяется ступенчато, то напряжение на индуктивном элементе 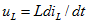будет бесконечно большим, и цепь не будет удовлетворять второму закону Кирхгофа.

В емкостном элементе напряжение (и заряд) в момент переключения остается таким же, каким оно было непосредственно перед переключением, а затем изменяется от этого значения:

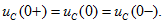
Поэтому если мы включаем ветвь с незаряженным конденсатором, то в момент включения напряжение на конденсаторе равно нулю. Если предположить, что в момент коммутации напряжение на емкостном элементе изменяется ступенчато, то ток 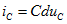будет бесконечно большой, и цепь снова не будет удовлетворять второму закону Кирхгофа.

С энергетической точки зрения, невозможность немедленного изменения текущей 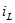и напряжение 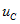обусловлено невозможностью резкого изменения энергии, запасенной в индуктивных и емкостных элементах (энергия магнитного поля 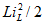и энергия электрического поля 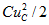). Действительно, ступенчатое изменение энергии требует бесконечно большой мощности, что не имеет физического смысла, поскольку реальные источники питания не имеют бесконечно большой мощности и не могут ее обеспечить.

В этой главе мы обсудим переходные процессы в линейных электрических цепях с сосредоточенными параметрами. Поэтому мы исключаем из рассмотрения нелинейный элемент – электрическую дугу, которая может возникнуть при коммутационных операциях. Для того чтобы исключить эффект дуги, будем считать, что длительность переключения очень мала по сравнению с длительностью переходного процесса, т.е. теоретически мгновенна.

Законы переключения для тока 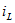и напряжение 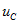для ветвей, содержащих реактивные элементы, может применяться неправильно для некоторых коммутаций. Такие коммутации называются “некоммутативными” (это вызывает скачки тока и напряжения) 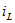и напряжения 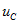). Расчет переходных процессов в таких цепях обсуждается в гл.

В некоторых случаях переходные процессы в электрических цепях являются нежелательными и опасными (например, короткие замыкания в энергосистемах). В других случаях переходные процессы являются естественными, нормальными режимами работы, как, например, в радиопередающем и приемном оборудовании, системах автоматического управления и других цепях.

Переходные процессы в электрических цепях. Классический метод расчета

Возникновение переходных процессов:

В предыдущих главах мы рассматривали стационарные процессы в линейных электрических цепях, т.е. в тех, где напряжения и токи постоянны во времени (цепи постоянного тока) или являются периодическими функциями времени (цепи переменного тока).

Появлению установившегося процесса, отличного от первоначальной работы схемы, обычно предшествует переходный процесс, при котором напряжения и токи изменяются непериодически.

Переход от одного режима работы к другому может быть вызван изменением параметров схемы или ее конструкции, что в электротехнике обычно называют коммутацией.

Теоретически можно предположить, что переключение происходит мгновенно, т.е. нет времени на включение, выключение или переключение цепи. Однако переход от начального режима работы схемы к последующему установившемуся процессу происходит не мгновенно, а занимает некоторое время. Это происходит потому, что каждому состоянию контура соответствует определенный запас энергии электрического и магнитного полей. Переход в новое состояние связан с увеличением или уменьшением энергии этих полей. Энергия 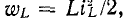запасенная в магнитном поле индуктивности L и энергия 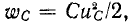энергия может изменяться непрерывно, без скачков, так как в противном случае мощность, равная производной энергии по времени, достигла бы бесконечного значения, что физически невозможно. Поэтому, например, при размыкании ветви с индукционной катушкой в месте размыкания неизбежно возникает искра, сопротивление которой расходует энергию, запасенную в магнитном поле индукционной катушки. Аналогично, если концы конденсатора, который был предварительно заряжен, закорочены, накопленная электрическая энергия рассеивается в сопротивлении соединительного провода и между контактами.

Если пренебречь индуктивностью разомкнутой цепи и емкостью короткого замыкания и рассматривать цепи, в которых энергия, запасенная в магнитном или электрическом поле, может быть рассеяна в виде тепла в сопротивлениях, то, предполагая, что переключение происходит мгновенно, искрением можно пренебречь.

Теоретически, для завершения переходных и установившихся процессов требуется бесконечно долгое время. На практике, однако, переходный процесс определяется коротким периодом, после которого токи и напряжения настолько близки к своим установившимся значениям, что разница почти незаметна. Чем больше энергии рассеивается в резисторах, тем быстрее переходный процесс.

Если бы электрическая цепь состояла только из сопротивлений и не включала индуктивность и емкость, то переход из одного устойчивого состояния в другое был бы мгновенным, без затрат времени. В реальном электрооборудовании тепловые потери из-за тока, магнитного и электрического полей сопровождают друг друга. Используя специальные схемы и выбирая соответствующие параметры схемы, можно ускорить или замедлить переходный процесс в зависимости от необходимости.

В некоторых случаях переходные процессы в электрических цепях являются нежелательными и опасными (например, короткие замыкания в энергосистемах). В других случаях переходные процессы являются естественными, нормальными режимами работы, например, в радиопередающем и приемном оборудовании, системах автоматического управления и других цепях.

Существуют различные методы расчета переходных процессов в линейных электрических цепях. В этой главе рассматривается классический метод решения дифференциальных уравнений, описывающих переходные процессы.

Законы коммутации и начальные условия

Приведенные выше утверждения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени индуктивности контура потока и электрического заряда емкости и называются законами коммутации.

Невозможность ступенчатого изменения тока в катушке обусловлена тем, что в противном случае на индуктивности возникло бы бесконечно высокое напряжение 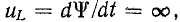что не имеет никакого физического смысла. Ввиду уравнения. 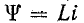Принцип непрерывности тока индуктора означает, что при неизменном L ток i не может измениться скачком. Таким образом, в начальный момент после переключения ток в индуктивности остается таким же, как непосредственно перед переключением, а затем плавно изменяется.

Аналогичная невозможность ступенчатого изменения электрического заряда q вытекает из того факта, что в противном случае через емкость протекал бы бесконечно большой ток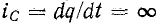что также не имеет физического смысла. Ввиду уравнения. 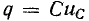принцип непрерывности электрического заряда означает, что при постоянном C напряжение 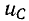не может изменяться ступенчато. Таким образом, в начальный момент после переключения напряжение на емкости остается таким же, как непосредственно перед переключением, а затем плавно изменяется.

Заметим, однако, что в цепях с идеализированными сосредоточенными параметрами токи в резисторах и конденсаторах 1) и напряжения в резисторах и индукторах 2) могут изменяться скачкообразно.

Значения токов в индуктивностях и напряжений на конденсаторах в момент коммутации называются независимыми начальными условиями.

Обычно предполагается, что переключение происходит в момент времени t = 0; тогда ток в индуктивности и напряжение на конденсаторе в момент времени непосредственно перед переключением обозначаются через 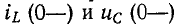и, в начальный момент переходного процесса после переключения, по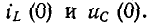

На основании закона о коммутации:

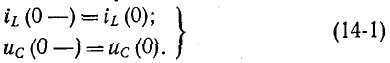
Эти уравнения выражают начальные условия цепи, в которой происходит переключение.

При нулевых начальных условиях, т.е. cos.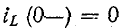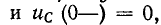индуктивность в начальный момент после переключения равна разрыву цепи, а емкость равна короткому замыканию.

Для ненулевых начальных условий, т.е. когда 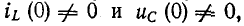индуктивность в первый момент эквивалентна источнику тока 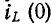а емкость эквивалентна источнику электрического тока. 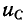(0).

Независимые начальные условия описывают энергию магнитного и электрического полей, накопленную в момент коммутации, и расчет переходных процессов требует знания этих начальных условий и не имеет значения, как эти условия создаются в цепи.

При расчете переходных процессов в цепях ответвлений, помимо независимых начальных условий, используются так называемые зависимые начальные условия, т.е. значения токов, напряжений и их производных в начальный момент времени (t = 0).
До сих пор мы исключали из рассмотрения случаи коммутации, при которых между контактами неизбежно возникает искра или электрическая дуга. Один из таких случаев показан на рис. 14-1 а. Перед переключением ток протекает через индуктивность 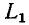и контакт, который шунтирует индуктивность 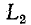текущий w 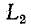равна нулю. В момент времени t = 0 контакт размыкается, и индуктивность 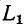и 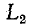соединены последовательно; ток в них обязательно одинаков. Поскольку в момент коммутации ток w 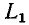не изменяется, а текущее значение w 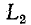равен нулю, то в соответствии с первым законом Кирхгофа ток должен замыкаться в дуге, образованной между контактами. Более того, если по 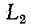является настоящей индукционной катушкой, ток может частично

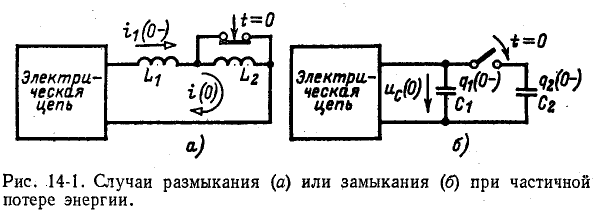
частично через межобмоточную емкость. После того, как дуга быстро гаснет, токи в 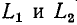уравнивать. Эта начальная фаза переходного процесса настолько быстрая, что ею можно почти пренебречь, поскольку токи в немедленно уравниваются. Именно в этом смысле можно условно говорить о ступенчатом изменении токов в индуктивностях, которое предшествует исследуемому переходному процессу в цепи. Для расчета переходного процесса используется принцип непрерывности общего контура ток-ток во время коммутации, т.е. 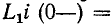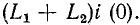. Ступенчатое изменение токов и соответствующих потоков в Lx и L2 в момент коммутации не влечет за собой введение бесконечно большой суммарной индуктивности, так как контур ток-ток не претерпевает ступенчатого изменения. При новых значениях токов w 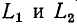магнитная энергия, запасенная в катушках, будет меньше, чем энергия, запасенная в первой катушке до переключения. Часть энергии будет преобразована в тепло в искре, а также излучена.

Сила тока найдена таким образом 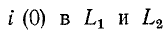может быть принято в качестве независимого начального условия для расчета переходного процесса через цепь на рис. 14-1, а после разрыва дуги.

Во время коммутации в цепях с емкостями при отсутствии сопротивления также возможны очень быстрые перераспределения заряда, которые традиционно считаются мгновенными. В этом случае действует принцип непрерывности полного заряда. Полученные значения зарядов и напряжений на отдельных конденсаторах используются при расчете последующих переходных процессов как независимые начальные условия.

Например, для схемы на рис.14-1, б принцип непрерывности полного заряда до и после коммутации выражается уравнением.

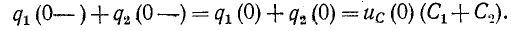
При таком предположении остальная часть цепи, подключенная к конденсаторам, не производит бесконечно большой ток, поскольку общий заряд не изменяется ступенчато в момент времени t=0.

Во время данной коммутации энергия электрического поля уменьшится, поскольку часть ее будет преобразована в тепло в очень малом сопротивлении проводника при очень большом токе и может быть выделена в искре и излучена.

Стационарный и свободный режимы

В общем случае анализ переходных процессов линейной цепи с сосредоточенными параметрами r, L, C и M сводится к решению неоднородных линейных обыкновенных дифференциальных уравнений, выражающих законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.

Например, если определенная ЭДС e (t) включена в цепь, состоящую из r, L и C, соединенных последовательно, то дифференциальное интегральное уравнение имеет вид:

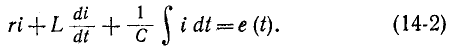
Это уравнение при дифференцировании сводится к неоднородному дифференциальному уравнению второй степени

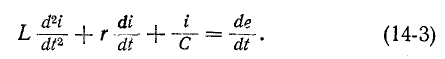
Известно, что интеграл такого уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.

Частичное решение выражает устойчивое состояние, заданное источником.

Расчет установившихся токов обсуждался в предыдущих главах.

Общее решение физически определяет поведение цепи при отсутствии внешних источников электричества и заданных начальных условиях. Функции, определяемые общим решением, называются свободными компонентами (токи, напряжения и т.д.).

В рассматриваемом случае однородное уравнение имеет вид:

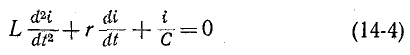
и соответствующее характеристическое уравнение

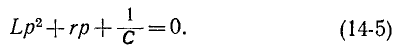
Если корни характеристического уравнения обозначить через 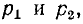, тогда интегральное решение запишется в виде

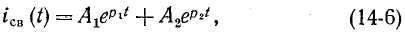
где 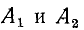– константы интегрирования, определяемые из начальных условий .

Общий переходный ток в цепи равен сумме установившегося и свободного тока:

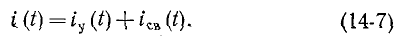
Аналогичным образом, напряжение, заряд, магнитный поток и другие функции в любом переходном процессе цепи состоят из стационарной и свободной составляющих.

Из закона коммутации мы можем найти начальные независимые условия 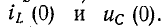Тогда его можно записать в соответствии с (14-7):

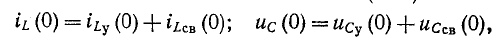
где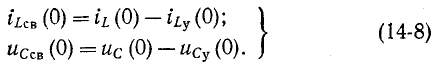

Поэтому начальные значения свободных функци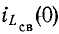й и 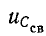(0) определяются изменениями момента переключения соответствующих установившихся функций.

В особом случае нулевых начальных условий:

В зависимости от порядка дифференциальных уравнений, описывающих изучаемые переходные процессы, различают схемы первого, второго и более высокого порядка.

В цепях первого порядка энергия хранится только в одном элементе, L или C, в виде магнитной или электрической энергии. Один контур, содержащий элементы, в которых хранится как магнитная, так и электрическая энергия, является контуром второго порядка. Разветвленные цепи могут быть более высокого порядка.

Переходный процесс в цепи r, L

Предположим, что в момент времени t = 0 цепь, состоящая из последовательно соединенных сопротивления r и индуктивности L, подключена к источнику e (t) (рис. 14-2).

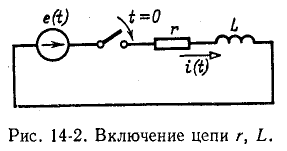
Дифференциальное уравнение для времени 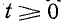записывается как

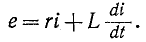
Характеристическое уравнение имеет вид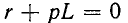и, следовательно, корень уравнения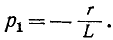

Следовательно, свободный ток

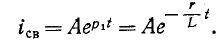
Переходный ток в цепи будет определяться суммой установившегося и свободного тока:

Стационарный ток может быть найден, если задано e (t).

Рассмотрим три случая:

1) включение в цепь d, L постоянной э.ф. £;

2) цепь короткого замыкания d, L

3) введение синусоидального переменного тока в цепь d, L.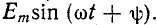

1. введение постоянного выходного тока в d, L.

Когда мы вводим постоянную ЭДС E в цепь d, L, установившийся ток равен E’/r. Поэтому, согласно (14-9)

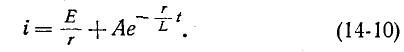
Константа интегрирования A определяется из начального условия

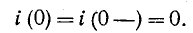
Согласно уравнению (14-10), в момент времени t – 0

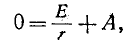
где 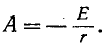Поэтому,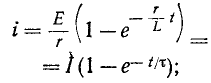

здесь 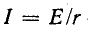– это предел, к которому стремится ток i (t) при увеличении t до бесконечности, называемый установившимся током.

В начальный момент времени t = 0 индуктивная э.д.с. самоиндукции 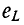= 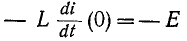i полностью компенсируется ЭДС источника, так как ток i (0) равен нулю.

С течением времени э.ф.к. Индуктивность уменьшается, а ток в цепи увеличивается, приближаясь асимптотически к установившемуся значению.

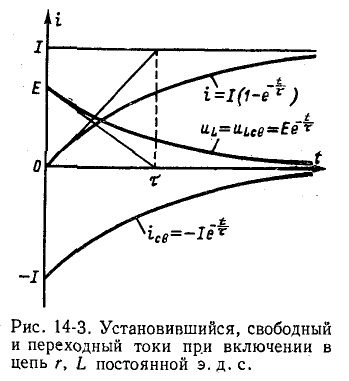
На рисунке 14-3 показаны кривые тока в установившемся, свободном и переходном режимах; на этом же рисунке показана кривая напряжения на индуктивности

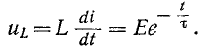
Из потока математического анализа известно, что если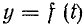недостаточный ток 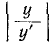. В этом случае при любом значении t

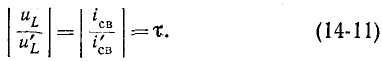
значение 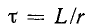называется постоянной времени. Постоянная времени измеряется в секундах:

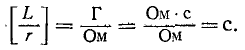
Из выражения (14-11) следует, что постоянная времени определяется графически длиной подкриво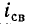й или 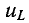при любом значении t.

Чем быстрее нарастает ток, тем меньше постоянная времени, и, следовательно, тем быстрее уменьшается ЭДС самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах от конечного значения (при установившемся режиме), составляет:

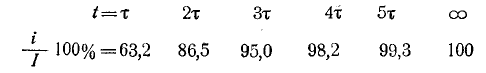
Поэтому постоянная времени цепи r, L равна интервалу времени, в течение которого свободная составляющая тока уменьшается в e = 2,718 раз и, соответственно, ток в этой цепи с коммутацией постоянного тока достигает 63,2% от своего установившегося значения.

Как видно из рисунка 14-3 и приведенной выше таблицы, процесс перехода теоретически продолжается бесконечно. На практике можно считать, что он заканчивается после приблизительно.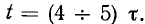

2. короткое замыкание r, L.

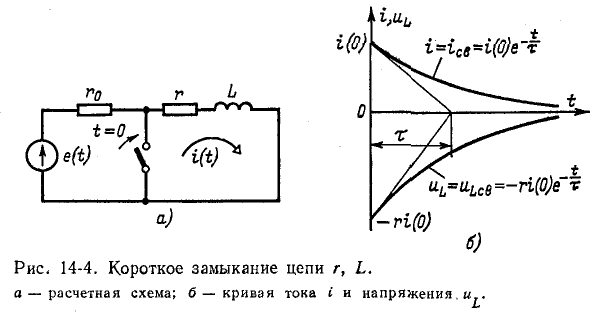
Предположим, что цепь r, L, подключенная к источнику постоянного или переменного напряжения, закорочена в момент времени t = 0 (рис. 14-4, a). В результирующем контуре r, L, обусловленном магнитным полем катушки индуктивности, ток исчезает не сразу: эффективность самоиндукции из-за уменьшения магнитного потока стремится поддерживать ток в контуре за счет энергии исчезающего магнитного поля.

Поскольку энергия магнитного поля постепенно рассеивается и преобразуется в тепло в сопротивлении d, ток в цепи приближается к нулю.

Процесс в компактной цепи d, L является свободным; установившийся ток в этом случае равен нулю.

Предполагая, что в (14-9) 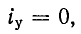получаем:

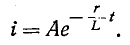
Константа интегрирования A определяется из начального условия

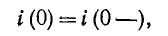
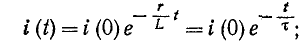
здесь i(0-) – значение тока в индукторе в момент, непосредственно предшествующий короткому замыканию; оно может быть положительным или отрицательным.

На рисунке 14-4, б показаны кривая затухания тока короткого замыкания и кривая напряжения на индуктивности

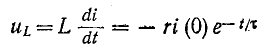предполагая, что i (0) > 0.

Постоянная времени цепи 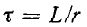можно найти графически как подкривую кривой i (t) (например, в момент времени t = 0).

Переходный процесс в коротком замыкании теоретически заканчивается при 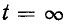. В это время в резисторе g энергия выделяется в виде тепла, т.е.

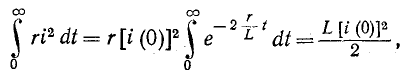
то есть вся энергия, запасенная в магнитном поле катушки до переключения.

Как и в предыдущем случае, переходный процесс в короткозамкнутой цепи практически можно считать завершенным после того, как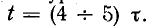

3. Включение синусоидального электрического сигнала в цепь r, L.

Когда r, L подключено к синусоидальной ЭДС. 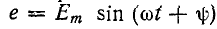ток в установившемся режиме будет:

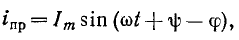
где

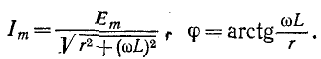
На основании (14-9)

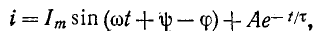
где

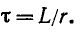
Константа интегрирования определяется начальным условием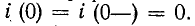

Поэтому, 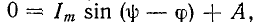где A =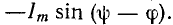Следовательно, желаемый ток будет:

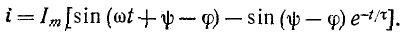
Рисунок 14-5, и показывает кривые 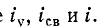Ординаты начального 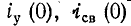одинаковы и противоположны по знаку, поэтому ток в начальный момент равен нулю. Свободный ток уменьшается по экспоненциальному закону. После временной задержки 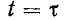свободный ток уменьшается в e=2,718 раз от своего первоначального значения 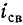(0). Постоянная времени прямо пропорциональна коэффициенту качества
Q и обратно пропорционально частоте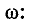
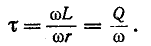
Если в момент коммутации (t = 0) ток 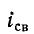проходит через ноль, т.е. выполняется условие 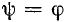или 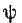= 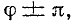или , свободный ток не возникает, и цепь немедленно достигает устойчивого состояния без переходного процесса.

Если, с другой стороны, коммутация происходит при 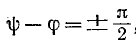начальный свободный ток не более (рис. 14-5, б),

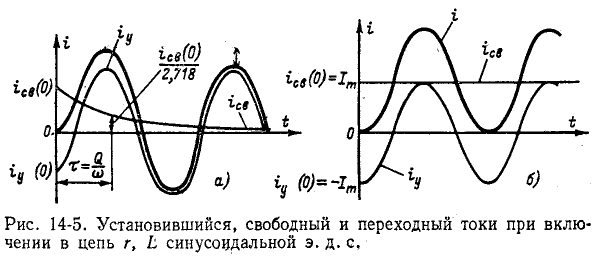
а именно 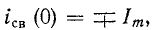и переходный ток достигает значения

В конце первого полуцикла переходный ток достигает экстремального значения (положительного или отрицательного). Однако даже в предельном случае, когда r = 0 и, следовательно, 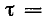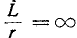ток не может превышать амплитуду установившегося режима более чем в два раза.

Если постоянная времени достаточно велика 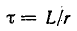первый член правой части дифференциального уравнения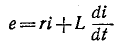
можно пренебречь по сравнению со вторым членом, предполагая, что приблизительно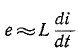с какой стороны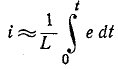и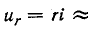

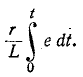
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующий элемент.

С другой стороны, если постоянная времени достаточно мала, то пренебрегая вторым членом уравнения, мы аппроксимируем

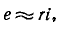
откуда
.
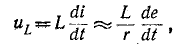
т.е. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени является дифференцируемым элементом.

В обоих случаях функция e(t) может быть произвольной.

Интегральные и дифференциальные схемы являются элементами систем автоматического управления.

Переходный процесс в цепи r, C

Предположим, что в момент времени t = O цепь, состоящая из сопротивления r и емкости C, соединенных последовательно, подключена к источнику e(t) (рис. 14-6).

На основе второго закона Кирхгофа уравнение для времени t 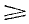0 является следующим:

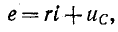
где 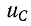– напряжение на конденсаторе.
Принимая во внимание, что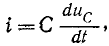
получаем:

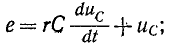
Здесь искомое значение – это напряжение на конденсаторе.

Характеристическое уравнение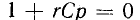и, следовательно, корень уравнения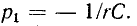Поэтому свободная составляющая напряжения на конденсаторе

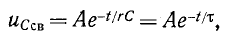где 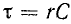– постоянная времени r, C (измеряется в секундах: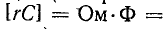

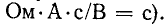
Переходное напряжение на конденсаторе равно сумме вынуждающего и свободного напряжений:

В свою очередь, ток в цепи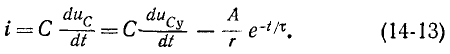

Рассмотрим три случая:

(1) рассмотрение постоянного тока в цепи r, C.

2) цепь короткого замыкания r, C

3) подключение в цепь r, C синусоидального тока.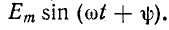

Учитывая постоянную ЭДС в цепи r, C.

Включим постоянную э.ф. E в цепь с сопротивлением r и предварительно заряженной емкостью C (полюса заряженной емкости обозначены + и – на рис. 14-6); начальное напряжение на емкости

(0) для простоты будем обозначать U.

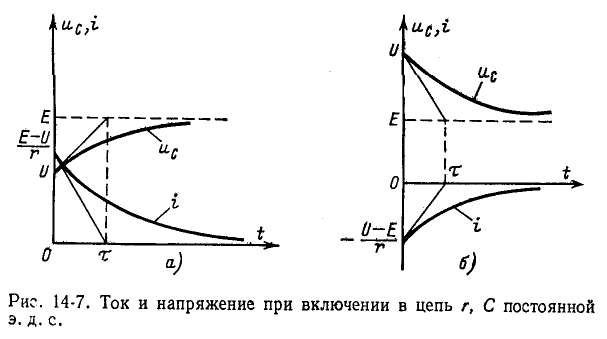
Стационарное напряжение на конденсаторе равно емкости источника. Поэтому, согласно (14-12)

Константа интегрирования A в (14-14) находится из начального условия:

В момент времени t = 0 мы имеем где Следовательно,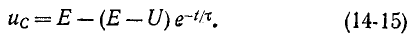

Согласно (14-13) ток в контуре

Если E > U, напряжение на конденсаторе увеличивается со временем, двигаясь к установившемуся значению E, а ток уменьшается, двигаясь к нулевой границе; на рисунке 14-7a показан рост напряжения на конденсаторе. 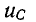и распад i. Чем больше постоянная времени, тем медленнее увеличение 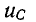и распад i.

Если E 0), убывающая (c 0) или убывающая (c 1) Когда э.ф.к. изменяется как импульс аналитической формы, часто представляется целесообразным использовать интеграл Дюамеля

токи, с другой стороны 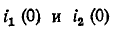– из уравнений Кирхгофа после коммутации: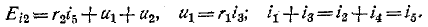

Подставляя в эти уравнения найденные значения 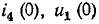и

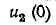урожайность:

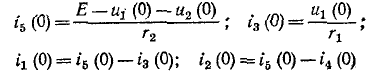
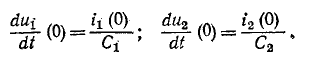
Начальное значение производной тока в индуктивности также определяется из уравнения Кирхгофа:

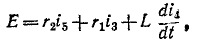
Где в t = O

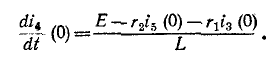
Пример (4-2. Определите ток i в jepi с рисунка 14-17, если известно, что e = E = 100 В,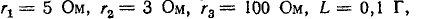

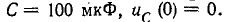
Подставив данные значения в вышеприведенное характеристическое уравнение, получим:

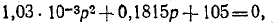
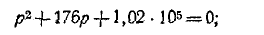
Корни характеристического уравнения являются комплексными:

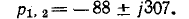
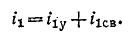
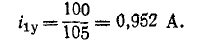
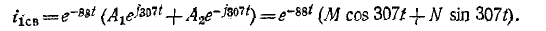
В начальный момент 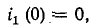поэтому 0 = 0,952 + M, из которых M = – 0,952.

Производная от тока по времени

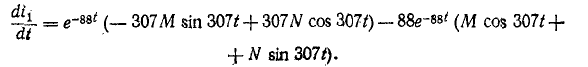
В начальный момент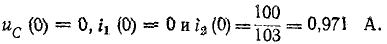

Поэтому в начальный момент напряжение в ветви 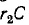(и его параллельная ветвь 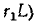равен 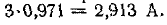Начальное значение

производная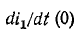) определяется из уравнений 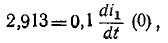где

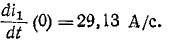
Следовательно, подставив значение 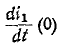к выражению для производной в момент времени t = 0, получаем

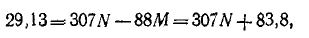
следовательно

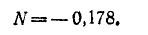
Таким образом,

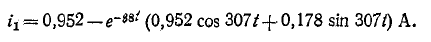
Переходные процессы в распределенных цепях

Переходные процессы в распределенных сетях (линиях, обмотках машин и т.д.) возникают при коммутации, передаче непериодических сигналов или наличии внешнего электромагнитного поля (например, молнии). Частные дифференциальные уравнения (11-2) используются для исследования переходных процессов в однородных цепях с распределенными параметрами:

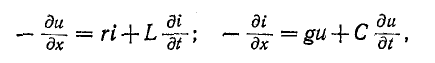
где r, L, g и C – параметры цепи на единицу длины; x – координата данной точки, измеренная от начала цепи.

В целом, решение этих дифференциальных уравнений довольно сложное. Решение упрощается, если пренебречь потерями.
То есть, предположим, что r и g равны нулю.

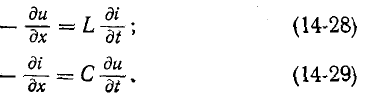
Дифференцируя (14-28) относительно x

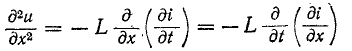
и, используя (14-29), получаем:

Дифференциальное уравнение (14-30) известно в математической физике как уравнение коокуррентности струн. Его решение дано Далембером и имеет вид:

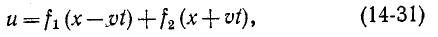
где

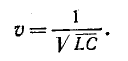
Первый член представляет собой одну волну прямого натяжения, которая движется без изменений в направлении увеличения x, т.е. от начала к концу струны. Для всех значений x, при которых 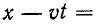const, эта константа имеет одно и то же значение, т.е. волна движется со скоростью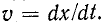

Вторая сплошная – это одиночная инвертированная волна напряжения, которая проходит без изменений в противоположном направлении.

Чтобы найти ток, заменим переменные на знак 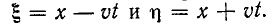На основании (14-29) и (14-31)

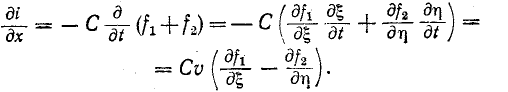
Но

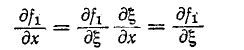
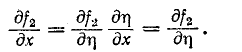
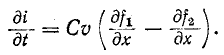
Интегрирование последнего уравнения дает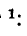

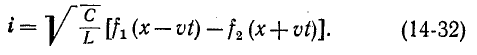
Выражения (14-31) и (14-32) запишем в сокращенном виде:

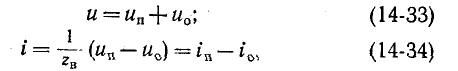
здесь 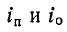– это ток прямой и обратной бегущей волны; 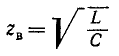– волновое сопротивление.

Следовательно, напряжения и токи в прямой и обратной волнах, соответственно, связаны законом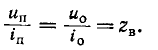
Аналогичный результат был получен для устойчивых прямых и обратных волн при рассмотрении синусоидальной моды в однородной линии. Физически, установившиеся волны представляют собой бесконечную сумму отдельных прямых и обратных волн, отраженных от обоих концов линии.

Таким образом, в однородной цепи без потерь с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 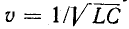в противоположных напряжениях, не изменяя их формы. В любой точке однородной цепи отношение напряжения и тока для прямой и обратной волн равно волновому сопротивлению gv.

Когда на пути распространения волны встречаются неоднородности, например, воздушная линия переходит в кабельную или волна достигает конца линии (открытого или закороченного сопротивлением), происходит отражение волны. В зависимости от характера неоднородности, отражение может быть частичным или полным. В первом случае, помимо отраженной волны, за точкой нарушения однородности распространяется преломленная волна; во втором случае преломленной волны нет.

Обозначим через 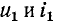– напряжение и ток в точке отражения;

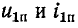– напряжение и ток падающей (прямой) волны;

Константа интегрирования может быть связана с функциями

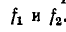
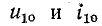– напряжение и ток отраженной (обратной) волны;

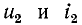– напряжение и ток преломленной (прямой) волны;

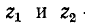– волновые сопротивления для прямой и обратной волны 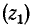и преломленной волны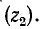

В точке неоднородности выполняется условие равенства
напряжений и токов:

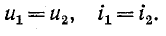
Следовательно,

Подставив в (14-36) значения 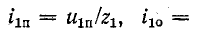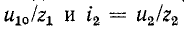урожайность:

В результате совместного решения уравнений (14-35) – (14-37) получаем отраженное 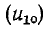и преломляется 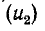волны:

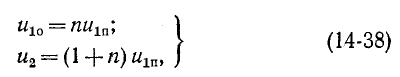
где 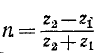– коэффициент отражения.

Соответственно, ток отраженной волны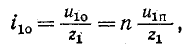

и ток преломленной волны.

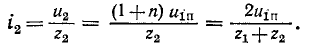
Из последнего выражения следует, что ток в конце линии после отражения может быть найден как ток в эквивалентной цепи, которая содержит напряжение, равное удвоенному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 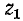и последовательно соединенное с ним сопротивление нагрузки (которое содержит вторую линию в своем волновом сопротивлении).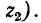

Опишем процесс подключения однородной линии без потерь. Когда линия подключается к источнику питания, по ней начинает распространяться волна заряда, создавая напряжение и ток. Если на конце линии подключена нагрузка, равная импедансу линии,

то падающая волна не будет отражена, когда она достигнет конца линии, и линия сразу же перейдет в устойчивое состояние. Если нагрузка не подключена к линии, падающая волна заряда будет отражена, когда достигнет конца линии. Распространяясь в обратном направлении, отраженная волна объединится с падающей волной, напряжения этих волн будут складываться, а токи вычитаться (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника тока, как и от закороченного конца; возникнет новая простая волна напряжения и тока, которая также отразится от конца, и так далее. Этот процесс будет продолжаться до тех пор, пока не будет достигнуто устойчивое состояние. Теоретически, в идеальной линии без потерь с чисто реактивной нагрузкой процесс колебаний будет продолжаться бесконечно. В реальной линии, при наличии потерь, волны напряжения и тока будут постепенно исчезать в направлении распространения.

Напряжение и ток линии в любой момент времени определяются как алгебраические суммы и разности прямого и обратного напряжений и токов соответственно.

Используя формулы и приведенную выше схему, можно найти напряжение и ток в точке подключения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).

Обратите внимание, что индуктивность, подключенная последовательно с линией, или емкость, подключенная параллельно проводникам линии, сгладит фронт преломленной волны; активное сопротивление, подключенное параллельно линии, уменьшит преломленную волну.

Пример 14-3. На конце линии, имеющей волновое сопротивление 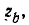подключен к индукционной катушке r, L. Определите ток в катушке и напряжение на ней под действием прямоугольной волны U

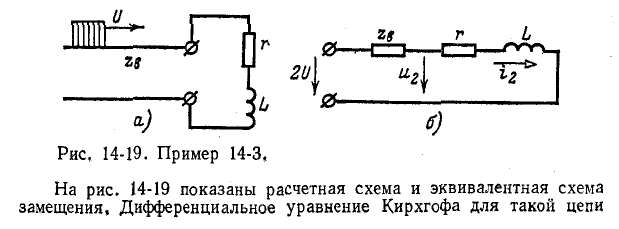
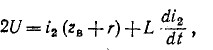
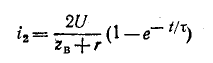
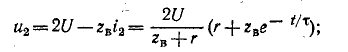
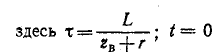соответствует моменту падения волны на катушку

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан командой учителей на некоммерческой основе с целью дальнейшего образования молодежи.

Сайт написан, поддерживается и управляется командой преподавателей

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.

</аз»>

Читайте далее: