Лекции по ТЭ – #27 Явление резонанса в электрических цепях

В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным сопротивлениями, резонанс называется резонансом напряжений. Рассмотрим простую цепь, часто называемую последовательной цепью. Для него резонанс наступает, когда x = xL – xC = 0 или xL = xC, следовательно:

No. 27 Явление резонанса в электрических цепях.

Резонанс – это когда в цепи, содержащей индуктивность и емкость, ток находится в фазе с напряжением. Входные реактивность и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь является чисто активной: Z = R; сдвиг фаз отсутствует (φ=0).

В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным сопротивлениями, резонанс называется резонансом напряжений. Рассмотрим простую цепь, часто называемую последовательной цепью. Для него резонанс наступает при x = xL – xC = 0 или xL = xC, следовательно:

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все напряжение, приложенное к цепи, обусловлено ее активным сопротивлением (рисунок 27.1, a).

Рисунок 27.1 – Векторные диаграммы резонансных напряжений (a) и токов (b)

Напряжения на индуктивности и емкости могут быть намного больше, чем напряжения на входе схемы. Их соотношение, называемое коэффициентом качества Q, зависит от величины индуктивного (или емкостного) и активного сопротивления:

Коэффициент добротности показывает, во сколько раз напряжения на индуктивности и емкости превышают напряжения, приложенные к контуру при резонансе. В радиочастотных цепях он может достигать нескольких сотен единиц.

Из приведенного выше условия следует, что резонанс может быть достигнут путем изменения любого из параметров – частоты, индуктивности, емкости. Это изменяет реактивность и импеданс цепи, а значит, ток, напряжение на элементах и сдвиг фаз. Не анализируя формулы, покажем графическую зависимость между некоторыми из этих величин и емкостью (рис. 27.2). Емкость C0, при которой возникает резонанс, можно определить по формуле: C0=1/(ω2L).

Рис. 27.2 – Взаимосвязь между параметрами режима и емкостью

Аналогичные соображения можно сделать для цепи, состоящей из R, L и C, соединенных параллельно. Векторная диаграмма его резонансного режима показана на рис. 27.1, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активное и реактивное сопротивления (рис. 27.3, а).

Рисунок 27.3 – Разветвленная схема (a) и ее эквивалентная схема (b)

Для него условием резонанса является равенство нулю его реактивной проводимости: ImY = 0. Это равенство означает, что мы должны приравнять мнимую часть комплексного выражения Y к нулю.

Определите комплексную проводимость цепи. Это равно сумме проводимостей составных ветвей:

Уравновесив выражение в скобках нулем, получаем:

Левая и правая части этого последнего выражения – не что иное, как пассивные проводимости первой и второй ветвей B1 и B2. Подставляя схему на рис. 27.3, а в эквивалентную схему (рис. 27.3, б), рассчитанную по формулам, и используя условие резонанса (B = B1 – B2 = 0), мы снова приходим к окончательному выражению.

Диаграмма на рис. 27.3, б соответствует векторной диаграмме на рис. 27.4.

Рисунок 27.4 – Векторная диаграмма резонанса разветвленной цепи

Резонанс в разветвленной цепи называется резонансом тока. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.

алгебраическая форма

Рекомендуемые файлы

2. ток в цепи будет наибольшим, а следовательно P_max = I 2 _maxR также максимальна, а реактивная мощность равна нулю.

3 Резонансная частота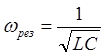

4.

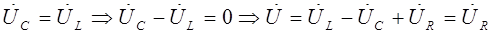
Резонанс может быть достигнут путем изменения L, C или ω.

Векторные диаграммы при резонансе напряжения

LC схема RLC схема

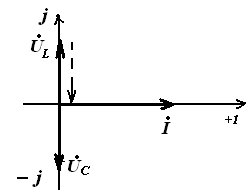
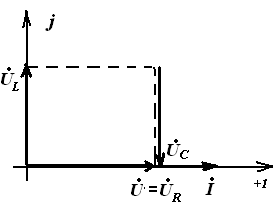
Случаи других режимов работы RLC схема

1. Если X_L>X_C тогда есть

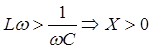
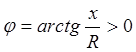
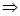U обгоняет Iозначает, что цепь является активно-индуктивной.

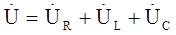Напряжение на индукторе больше, чем напряжение на конденсаторе.

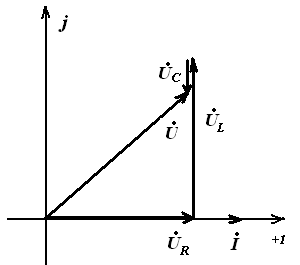
1. Если X_L<X_C , т.е.

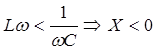
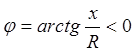
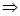U отстаёт IЭто означает, что схема имеет активно-конденсаторную природу.

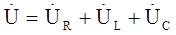Напряжение на конденсаторе больше, чем напряжение на индукторе.

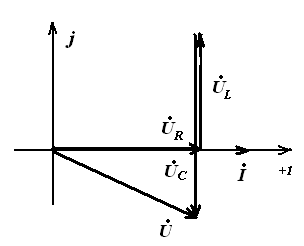
Параллельное соединение элементов в цепи синусоидального тока

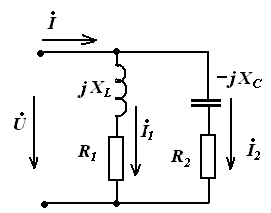
На входе параллельной цепи напряжение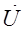

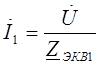
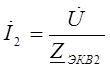
Эквивалентные сопротивления ветвей: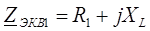

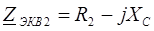
Запишем эквивалентные проводимости:

;

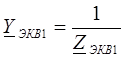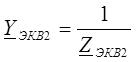
Согласно первому закону Кирхгофа: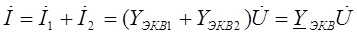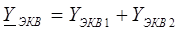

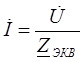где

где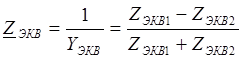

Треугольники проводимостей и токов

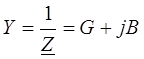алгебраическая форма

G – реальная часть, активный компонент

B – мнимая часть, реактивная составляющая.

; ;;

; ;

;

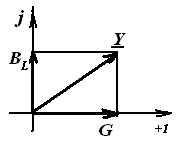
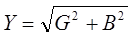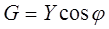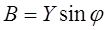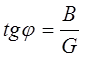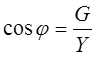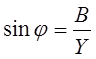
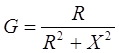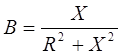
или ;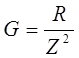

; ;

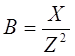
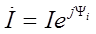
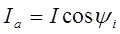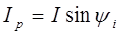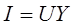
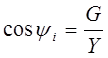
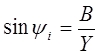
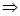
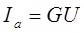
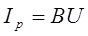
Резонанс токов

Режим, при котором в цепи, содержащей параллельные индуктивную и емкостную ветви, ток в неразветвленной части цепи находится в фазе с напряжением (φ=0), называется токовый резонанс.

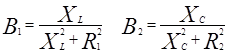Условие резонанса токов: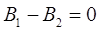

В₁ – реактивная проводимость первой ветви,

В₂ – реактивная проводимость второй ветви

Признаки резонанса токов:

1. Реактивными составляющими токов ветвей являются I_ПК = I_PL и находятся в противофазе, когда входное напряжение является чисто активным;
2. Токи ветвей больше, чем общий ток цепи, который имеет минимальное значение;
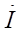3. и 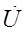находятся в фазе друг с другом.

RLC – контур Векторная диаграмма

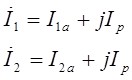
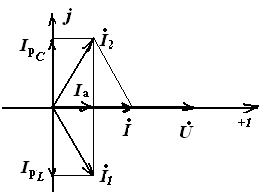
LC – контур Векторная диаграмма

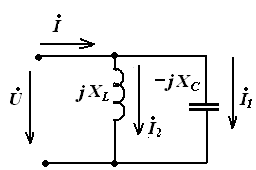
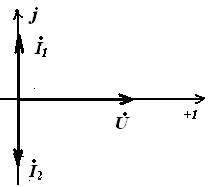
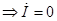
Резонансная частота

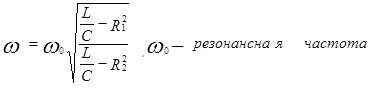Случаи резонансных контуров

схемы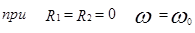

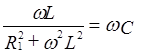Если R₂=0 возникнет резонанс, при

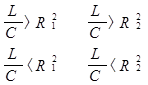Случай резонансных токов

Случай 1. Один резонанс в цепи, при условии:

Случай 2. Два резонанса в цепи при заданном соотношении сопротивлений элементов

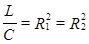Случай 3 В цепи нет резонанса – частота неопределенная, с

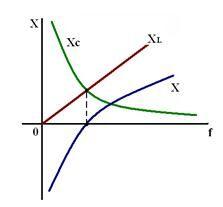
Частотная характеристика колебательного контура

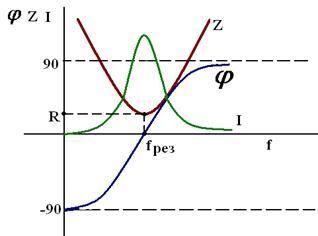
Баланс мощности в цепях переменного тока

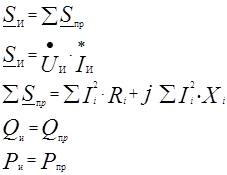Коэффициент мощности

– Работа генератора или электроприбора энергетически выгодна, если он совершает максимальное количество работы. Работа в электрической цепи определяется активной мощностью P.

– Коэффициент мощности показывает, насколько эффективно используется генератор или электроприбор.

При снижении коэффициента мощности стоимость используемой электроэнергии увеличивается. .

Способы увеличения коэффициента мощности

– Коэффициент мощности достигает максимума, когда Р = Sт.е. в случае резистивной цепи.

– В режиме максимальной мощности генератор осуществляет только необратимое преобразование энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем нагрузки.

– Потребители электроэнергии в основном имеют схему замещения РЛ поэтому увеличение коэффициента мощности возможно при компенсации реактивной мощности путем подключения емкостного элемента (Q_L–Q_С)Подключение емкостного элемента уменьшает ток в линии передачи, что уменьшает площадь поперечного сечения электрических проводников и, таким образом, экономит проводящие материалы.

– Значение коэффициента мощности в энергосистеме зависит от того, насколько правильно эксплуатируются электроустановки и оборудование.

• сosφ может быть снижена, когда системы работают в режиме холостого хода или недогружены.

Когда напряжение резонирует или близко к резонансу, ток в цепи быстро увеличивается. В теоретическом случае, когда R=0, она уходит в бесконечность. Соответственно возрастающий ток вызывает увеличение напряжения индуктивных и емкостных компонентов, которое может многократно превышать напряжение питания.

Векторная диаграмма резонансного напряжения

Резонанс – это действие цепи, состоящей из индуктивных и емкостных элементов, таким образом, что ее входное сопротивление (входная проводимость) является реальным. Следствием этого является то, что ток на входе цепи находится в фазе с входным напряжением.

Резонанс в цепи с последовательно соединенными элементами
(резонанс напряжения).

Для схемы, изображенной на рис. 1, применимо следующее

;

(1)

.

(2)

В зависимости от соотношения значений i возможны три различных случая.

1. в цепи преобладает индуктивность, т.е. . и, следовательно,

. Этот режим соответствует векторной диаграмме на рис. 2а.

2.В цепи преобладает емкость, т.е. . , и, следовательно, . Этот случай отражен на векторной диаграмме на рис. 2,б.

3.- Случай резонанса напряжений (рис. 2,в).

Условие резонанса

В этом случае, как следует из (1) и (2), .

При резонансе напряжения или вблизи него ток в цепи быстро возрастает. В теоретическом случае при R=0 его значение стремится к бесконечности. Следовательно, увеличение тока вызывает увеличение напряжения на индуктивных и емкостных элементах, которое может многократно превышать величину напряжения источника питания.

Например, предположим, что в схеме рис. 1 . Тогда , и , соответственно.

Явление резонанса находит полезное применение на практике, особенно в радиотехнике. Однако, если оно возникает спонтанно, то может привести к несчастным случаям из-за возникновения высокого перенапряжения и сверхтоков.

Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем индуктора и электрическим полем конденсатора, в то время как сумма энергий этих полей остается постоянной.

Суть дела не меняется, если в цепи есть несколько индуктивных и емкостных элементов. Действительно, в этом случае , и уравнение (3) справедливо для эквивалентных значений L_Э и C_Э .

Как видно из анализа уравнения (3), резонансный режим может быть получен путем изменения параметров L и C и частоты. Основываясь на (3) для резонансной частоты, мы можем написать

Резонансные кривые зависимости тока и напряжения от частоты. В качестве примера на рис. 3 приведены типичные кривые I(f), а для схемы на рис. 1 при U=const.

Важной характеристикой резонансного контура является коэффициент качества Q, определяется как отношение напряжения на индуктивном (емкостном) элементе к входному напряжению:

– и охарактеризовать “селективные” свойства резонансного контура, в частности его пропускная способность .

Другим параметром резонансного контура является характеристический импедансс учетом коэффициента качества в соответствии с формулой

или из (4) и (5) мы можем написать

Резонанс в цепи с параллельно соединенными элементами
(резонанс токов)

Для схемы на рис. 4 имеем

;

(8)

.

(9)

В зависимости от соотношения и , как и в приведенном выше случае последовательно соединенных элементов, возможны три различных случая.

В цепи доминирует индуктивность, т.е. и поэтому . Этому режиму соответствует векторная диаграмма на рис. 5,а.

В цепи преобладает емкость, т.е. поэтому . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.

– Случай резонанса токов (рис. 5,в).

Условие для резонанса токов или

Поэтому, как следует из (8) и (9), . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, напротив, максимально. В частности, при отсутствии резистора R в цепи на рис. 4 ее входное сопротивление в режиме резонанса уходит в бесконечность, т.е. при резонансе токов ток на входе цепи минимален.

Из тождества соотношений (3) и (5) следует, что в обоих случаях резонансная частота задается (4). Однако выражение (4) не следует использовать для любого резонансного контура. Он действителен только для простейших цепей с индуктивными и емкостными элементами, соединенными последовательно или параллельно.

При определении резонансной частоты в цепи любой конфигурации или, в общем случае, зависимости параметров цепи в резонансном режиме, следует исходить из условия, что входное сопротивление (входная проводимость) цепи вещественное.

Например, для схемы на рис. 6 мы имеем

Поскольку в резонансном режиме мнимая часть должна быть равна нулю, условие резонанса имеет вид

где, в частности, – резонансная частота.

Резонанс в сложной цепи

Условие резонанса в цепи, состоящей из смешанных индуктивных и емкостных элементов, в которой мнимая часть входного сопротивления или входной проводимости равна нулю, порождает несколько действительных корней, т.е. в таких цепях существует несколько резонансных частот.

При определении резонансных частот для цепи с двухполярным реактивным сопротивлением аналитическое выражение для ее входного реактивного сопротивления или входной проводимости должно быть представлено как отношение двух полиномов в степени , то есть или . Тогда корни уравнения дадут частоты, соответствующие резонансам напряжения, а корни уравнения дадут частоты, при которых возникают резонансы тока. Общее число резонансных частот в цепи на единицу меньше числа индуктивных и емкостных элементов в цепи, полученной из исходной схемы путем приведения ее к схеме (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерно, что резонансные моды напряжений и токов переплетаются.

В качестве примера определим резонансные частоты для цепи на рис. 7. Выражение для входного сопротивления этой цепи имеет вид

Из решения уравнения получаем частоту , соответствующую резонансу напряжения, а из решения уравнения получаем частоту , соответствующую резонансу тока.

1. Основы Теория цепей : учебник для средних школ / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. -Пятое издание, пересмотренное. -М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А.. Теоретические основы электротехники: Электрические цепи. Учебник для студентов вузов, изучающих электротехнику, энергетику и приборостроение. 7-е издание, переработанное и дополненное. -М.: Выш. шк., 1978. -528с.

Вопросы и контрольные задания

1. Что такое резонанс напряжения и каковы его характеристики?
2. Что такое резонанс тока и каковы его характеристики?
3. Какова физическая природа резонансных режимов?
4. Какие условия используются для определения резонансных частот в общем случае?
5. Цепь на рис. 1 имеет R=1 Ом; L=10 мГн; C=10 мкФ. Определите резонансную частоту и коэффициент добротности контура.

Напряжение на катушке опережает ток на pi /2, поэтому мы размещаем ее под прямым углом вверх, перпендикулярно вектору напряжения на активном резисторе. Предположим, что для нашего примера UL>UC.

Как построить векторную диаграмму токов и напряжений

Векторные диаграммы – это метод графического расчета напряжений и токов в цепях переменного тока, в котором переменные напряжения и токи символически (условно) представлены векторами.

Метод основан на том, что любая переменная, изменяющаяся по синусоидальному закону (см. синусоидальные колебания), может быть определена как проекция в некотором выбранном направлении вектора, вращающегося вокруг своей начальной точки с угловой скоростью, равной угловой частоте изображаемой переменной.

Поэтому любое переменное напряжение (или переменный ток), изменяющееся по синусоидальному закону, может быть представлено таким вектором, вращающимся с угловой скоростью, равной угловой частоте представляемого тока, длина вектора представляет амплитуду напряжения в определенном масштабе, а угол – начальную фазу этого напряжения.

Если мы рассмотрим электрическую цепь, состоящую из источника переменного тока, резистора, индуктора и конденсатора, соединенных последовательно, где U – мгновенное значение переменного напряжения, а i – сила тока в данный момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно написать

Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Поэтому на каждом элементе будет падение напряжения: UR на активном резисторе, UC на конденсаторе и UL на индукторе. Согласно второму закону Кирхгофа, напряжение источника будет равно сумме падений напряжения на элементах цепи, поэтому мы имеем записанный закон:

Обратите внимание, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления величина R зависит только от свойств проводника, она не зависит от тока или момента времени, следовательно, ток находится в фазе с напряжением, и мы можем написать:

Но конденсатор в цепи переменного тока имеет реактивную емкость, и напряжение на конденсаторе всегда находится в фазе с током на Pi / 2 , поэтому мы пишем:

Индуктор с индуктивностью действует как индуктивное реактивное сопротивление в цепи переменного тока, и напряжение на индукторе все время опережает ток по фазе на Pi / 2 , следовательно, для индуктора мы пишем:

Теперь можно записать сумму падений напряжения, но в общем случае для напряжения, приложенного к цепи, мы можем написать:

Видно, что существует некоторый фазовый сдвиг, связанный с реактивной составляющей полного сопротивления цепи, когда по ней течет переменный ток.

Поскольку в цепях переменного тока и ток, и напряжение изменяются по закону косинуса, а мгновенные значения отличаются только по фазе, физики придумали рассматривать токи и напряжения в цепях переменного тока как векторы в математических расчетах, поскольку тригонометрические функции могут быть описаны векторами. Поэтому давайте запишем напряжения в виде векторов:

Используя метод векторных диаграмм, можно вывести, например, закон Ома для заданной последовательной цепи в условиях протекающего через нее переменного тока.

Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, поэтому отложим векторы токов и построим векторную диаграмму токов:

Пусть ток Im – амплитудное значение тока в цепи – откладывается в направлении оси X. Напряжение на активном резисторе совпадает по фазе с током, поэтому эти векторы будут сонаправлены, поэтому переведем их из одной точки.

Напряжение на конденсаторе задержано на PiНапряжение на конденсаторе задержано относительно тока на Pi /2, поэтому положим его под прямым углом вниз, перпендикулярно вектору напряжения на активном резисторе.

Напряжение на индукторе опережает ток на pi /2, поэтому мы строим график под прямым углом вверх, перпендикулярно вектору напряжения на активном резисторе. Предположим, что для нашего примера UL>UC.

Поскольку мы имеем дело с векторным уравнением, мы складываем векторы напряжений на реактивных элементах и получаем разность. В нашем примере (мы предположили, что UL>UC) она будет направлена вверх.

Теперь мы складываем вектор напряжения на активном сопротивлении и получаем, согласно правилу сложения векторов, вектор общего напряжения. Поскольку мы взяли максимальные значения, мы получаем вектор значений суммарной амплитуды напряжения.

Поскольку ток изменяется по косинусу, напряжение также изменяется по косинусу, но со сдвигом фаз. Между током и напряжением существует постоянный сдвиг фаз.

Запишем закон Ома для полного сопротивления Z (импеданса):

Из векторных изображений, используя теорему Пифагора, мы можем написать:

После элементарных преобразований мы получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:

Затем мы получим выражение для закона Ома для цепи переменного тока:

Заметим, что наибольшее значение тока получается в цепи, находящейся в резонансе, при условиях, когда:

Из наших геометрических построений мы получаем косинус фи:

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

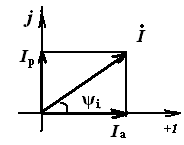
При построении векторной диаграммы вектор напряжения ? используется в качестве начального вектора, за ним следуют векторы тока ?_а и ?_р. В этом случае текущий ?_а будет находиться в фазе с напряжением ?, а ток ?_р – задерживается по отношению к нему на угол 90°. Ток I сдвинут относительно напряжения ?

22.Цепь переменного тока с параллельно соединенными проводниками. Векторная диаграмма.

Простейшая параллельная схема. Рассмотрим простую цепь, состоящую из активного сопротивления R и реактивного сопротивления X, соединенных параллельно (рис. 194,a). В этой схеме как

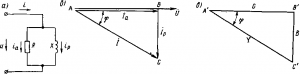Рис. 194.Схема простой параллельной цепи переменного тока (a), векторная диаграмма (b) и треугольник проводимости (c)

Предполагается, что индуктивное сопротивление является реактивным, но оно также может быть емкостным. Для каждой ветви этой цепи можно, используя закон Ома, определить токи I_а и я_р в ветвях и их фазовые углы относительно напряжения, а затем, построив векторную диаграмму (рис. 194,б), можно найти ток в неразветвленной части цепи, используя принцип векторного сложения:

? = ?_а+ ?_р

При построении векторной диаграммы вектор напряжения ? принимается за начальный вектор, а затем векторы тока ?_а и ?_р. В этом случае ток ?_а будет находиться в фазе с напряжением ?, а ток ?_р – задерживается по отношению к нему на угол 90°. Ток I сдвинут относительно напряжения ?

Из треугольника токов LAN имеем:

I_а = I cos ?; I_р = I sin ?; I = ?(I 2 _а + I 2 _р)

Общий случай параллельного соединения резисторов. В случае, когда в каждой ветви имеется активное сопротивление R и реактивное сопротивление X (рис. 195, а), необходимо определить токи I₁ и я₂ в параллельных прямых и их фазовые углы ?₁ и ?₂ в зависимости от напряжения U, а затем, построив векторную диаграмму (рис. 195,b), найдите, согласно принципу векторного сложения, силу тока в неразветвленной части цепи ? = ?₁+?₂ и его фазовый угол ? по отношению к напряжению U.

Можно также определить эквивалентную активную проводимость всей цепи:

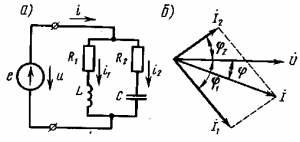Рисунок 195. Схема параллельной цепи переменного тока с активным, индуктивным и емкостным сопротивлениями (a) и векторная диаграмма (b)

эквивалентная реактивная проводимость

общая проводимость контура

а затем найти ток в неразветвленной части цепи.

В общем случае, при определении эквивалентной реактивной проводимости нескольких параллельных ветвей, емкостные проводимости ветвей В_С берутся со знаком плюс, а индуктивные B_L – со знаком минус.

Предположим, что конденсатор емкостью C получил от источника энергии

Резонанс в электрических цепях

Резонансные (колебательные) контуры:

Резонансные или осциллирующие цепи – это электрические цепи, в которых может возникнуть явление резонанса напряжений или токов.

Резонанс – это пассивная электрическая цепь, содержащая индуктивности и емкости, в которой реактивное сопротивление и реактивная проводимость цепи равны нулю; реактивная мощность на зажимах цепи соответственно равна нулю.

Резонанс напряжения наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов r, L и C, является одним из простейших случаев такой цепи. В радиотехнике это называется последовательным колебательным контуром.

При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой части, включенной последовательно с первой. В результате реактивное сопротивление и реактивная мощность на зажимах цепи равны нулю.

Резонанс токов, с другой стороны, наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Одним из простейших примеров такой цепи является цепь, состоящая из параллельно соединенных элементов r, L и C. В радиотехнике такая схема называется параллельным колебательным контуром.

Когда токи резонируют, индуктивная проводимость одной части цепи компенсируется емкостной проводимостью другой части, которая подключена параллельно первой. В результате реактивная проводимость и реактивная мощность на зажимах цепи равны нулю.

Частоты, на которых происходит явление резонанса, называются резонансными частотами.

Исследование резонансных режимов в электрических цепях основано на поиске резонансных частот,

зависимость различных величин от частоты или параметры L и C, а также рассмотреть энергетические соотношения в резонансе.

Резонансные контуры очень широко используются в электротехнике и являются неотъемлемой частью всех радиотехнических устройств. Эта глава посвящена изучению резонанса, свойств и частотных характеристик простейших резонансных цепей.

Последовательный колебательный контур. Резонанс напряжения

Резонансная схема с последовательно соединенными элементами r, L и C (рис. 5-1) является простейшей схемой для изучения явления резонанса напряжения и подробно рассматривается ниже. Комплексное сопротивление такой цепи является функцией частоты: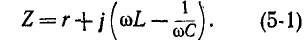

Резонанс напряжения возникает на частотах 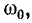когда

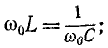
следовательно

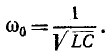
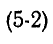
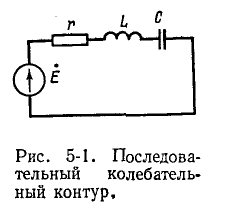
Мгновенные энергии даются по формулам: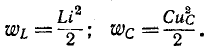

Если мы предположим, что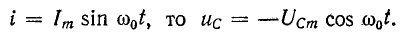

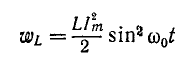
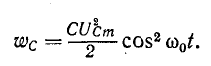
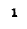Эти соотношения называются частотной характеристикой

Максимальные значения этих энергий равны друг другу, потому что

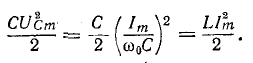
Это также связано с тем, что реактивность цепи, содержащей индуктивность и емкость, пропорциональна разности между максимальной энергией, запасенной в магнитном и электрическом полях в любой системе соединения:

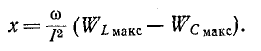
Поэтому условие резонанса (x = 0) соответствует уравнению.

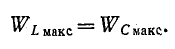
Мгновенные значения 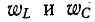колеблются с удвоенной частотой вокруг среднего значения 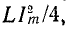и происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарная величина которых постоянна:

.

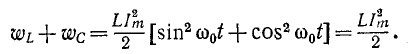В рассматриваемом случае (резонанс напряжений, рис. 5-1) между источником и пассивными элементами цепи нет обмена энергией, и вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r.

Мы уже познакомились с понятием коэффициента добротности индуктора 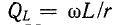и конденсатор 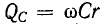. Умножение и деление выражения для 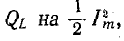получаем :

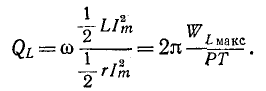
Здесь 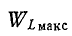– максимальная энергия, периодически накапливаемая в индуктивности L; P – активная мощность, потребляемая в сопротивлении при амплитуде тока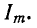

Рассуждение аналогичным образом, т.е. путем умножения и деления выражения 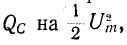получаем:

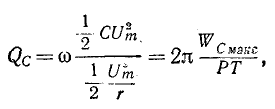
где 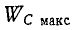– максимальная энергия, периодически накапливаемая в емкости C, а P – активная мощность, теряемая в параллельном резисторе r при амплитуде напряжения на емкости 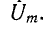Следовательно, в обоих случаях коэффициент качества определяется как отношение максимальной энергии реактивного элемента к энергии РТ, выделяемой в виде тепла в течение периода.

В случае резонансного контура также используется термин коэффициент качества, который обычно означает

здесь 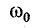– является резонансной частотой; 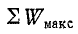– сумма максимальной энергии, периодически накапливаемой при резонансе в индуктивных (или емкостных) элементах; P – активная мощность на зажимах контура при резонансе.

Подпишитесь в (5-3) относится к случаю, когда число индуктивных (или емкостных) элементов превышает единицу. В случае резонанса напряжений в цепи рис. 5-1 знак 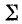опущен.

Для схемы рис. 5-1, исходя из (5-3), получаем:

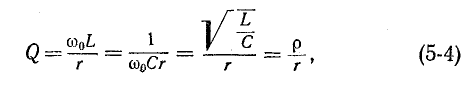
где

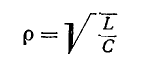
называется характеристическим (а также волновым) сопротивлением резонансного контура.

Назовем это относительным отклонением частоты относительно резонанса
частота контура составляет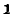

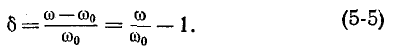
Сопротивление петли согласно (5-1) и с учетом (5-2) и (5-4)

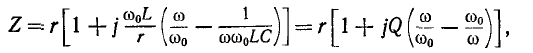
откуда, используя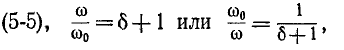получаем:

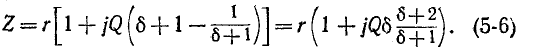
Следовательно, полное сопротивление цепи

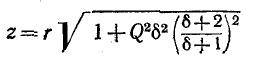
и угол

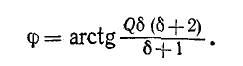
Ток в цепи

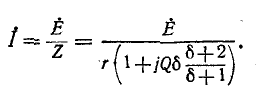
На частоте, близкой к резонансной, 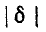значительно меньше единицы, и поэтому приблизительно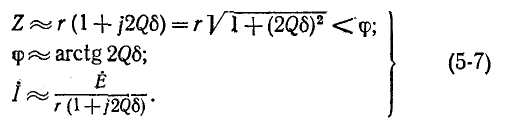

Выражения (5-7) почти достаточно точны при 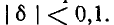. На 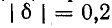ошибка в сопротивлении z составляет менее 10%.

На рис. 5-2 кривые приведены в относительных величинах: по оси абсцисс указаны относительные сдвиги частоты 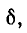По оси ординат откладывается отношение импеданса z к сопротивлению r (рис. 5-2, а) и угол. 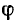(рис. 5-2, б).

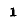Обратите внимание, что частоты выше резонанса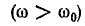являются положительными значениями настройки 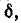и частоты ниже резонанса 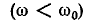– отрицательные значения 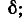нулевая частота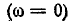соответствует 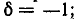на резонансной частоте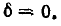

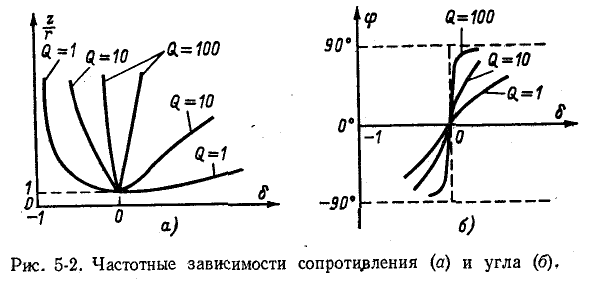
Сопротивление цепи минимально при резонансе напряжений, при этом ток в цепи достигает максимального значения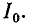

На рис. 5-3 показаны кривые резонансных токов в относительных величинах: по оси абсцисс, как и на предыдущих графиках, величина 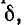по оси ординат – отношение токов к максимальному току при резонансе:

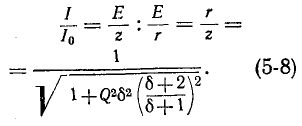
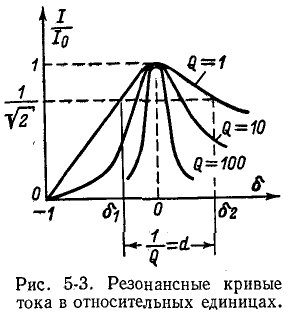
Чем выше коэффициент добротности Q контура, тем острее резонансные кривые. Следовательно, Q характеризует резкость резонансной кривой (“резкость настройки”); согласно (5-3), чем выше отношение максимальной энергии поля реактивного элемента к количеству тепла, рассеиваемого за период в резонансном контуре, тем резче резонансная кривая.

Резонансные кривые построены здесь как функция относительного разброса частот. 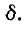Это возможно

вывести расчетные выражения и построить резонансные кривые в зависимости от 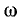или относительная частота 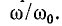Обратите внимание, что максимумы резонансных кривых на рисунке 5-3 равны, поскольку по оси ординат отношение 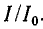Если построить график тока I, то при разных r максимумы резонансных кривых, очевидно, не будут совпадать в одной точке.

Полоса частот вблизи резонанса, на границе которой ток уменьшается до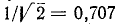до максимального (резонансного) значения 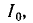называется полосой пропускания резонансного контура. В настоящее время 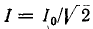мощность, рассеиваемая в резисторе r, равна:

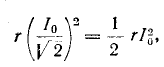
tj. составляет половину мощности, поглощаемой при резонансе. Поэтому полоса пропускания определяется как полоса, границы которой соответствуют половине максимальной мощности. На границах резонансной полосы активное и реактивное сопротивления составляют 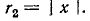Это следует из условия

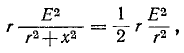
что даёт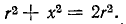

Соответственно, сдвиг фаз между напряжением на зажимах цепи и током составляет 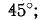на нижней границе комплексного сопротивления цепи является емкостным (ток проводит напряжение) и 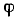= -45°; на верхней границе комплексное сопротивление цепи является индуктивным (ток отстает от напряжения) и 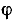= 45°.

Исходя из (5-8), условие для границы полосы записывается в следующем виде:

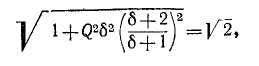
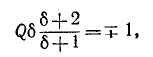
следовательно

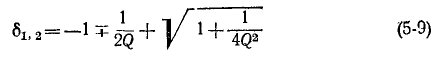
(знак минус перед корнем, полученным в результате решения квадратного уравнения, опущен как несущественный). Подписи 1 и 2 и знаки минус и плюс в выражении (5-9) относятся к пределам ниже и выше резонанса, соответственно.

Из определения следует, что полоса пропускания резонансного контура определяется условием

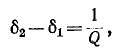
Величина d, обратная коэффициенту качества контура, называется демпфированием контура.

Если коэффициент качества резонансного контура достаточно высок 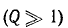выражение для подрешетки (5-9) можно приравнять к единице, где 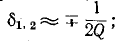т.е. демпфирование почти симметрично относительно резонансной частоты.
В радиотехнических приложениях один из реактивных элементов колебательного контура, например, конденсатор, подключается к нагрузке в виде сопротивления 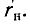Это приводит к увеличению потерь в цепи и соответствующему снижению коэффициента добротности цепи. Чтобы определить коэффициент качества нагруженной цепи, параллельное соединение 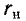и C можно заменить эквивалентным последовательным соединением емкости и “импеданса” на резонансной частоте. 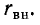Для этого используются условия эквивалентности последовательных и параллельных цепей.

Поскольку обычно 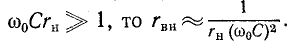Принимая во внимание, что 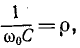получаем: 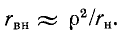Следовательно, как было отмечено в конце, емкости эквивалентных схем могут быть практически приравнены друг к другу.

Таким образом, коэффициент качества нагруженного контура равен:

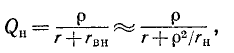
а затухание увеличивается за счет вносимых потерь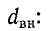

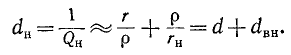
Если вносимые потери 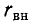намного больше, чем импеданс k, тогда

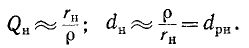
Внутреннее сопротивление источника тока. 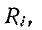добавленное к сопротивлению r, влияет на коэффициент качества и полосу пропускания колебательного контура: чем больше значение, тем ниже коэффициент качества и шире полоса пропускания. 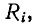тем ниже коэффициент качества и тем шире полоса пропускания.

чем выше коэффициент качества, тем шире полоса пропускания. Поэтому, с точки зрения уменьшения полосы пропускания последовательного колебательного контура, источник напряжения с низким внутренним сопротивлением является преимуществом.

В условиях близких к резонансу напряжения на индуктивности и емкости могут быть очень высокими, что необходимо учитывать во избежание повреждения изоляции.

Рис. 5-4 показана векторная диаграмма токов и напряжений при резонансе. Напряжения реактивных элементов при резонансе определяются выражением

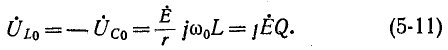
Когда Q > 1, эти напряжения больше, чем напряжение U – E, приложенное к резонансному контуру. Однако значения, полученные из (5-11), не являются максимальными: максимальное напряжение 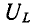это

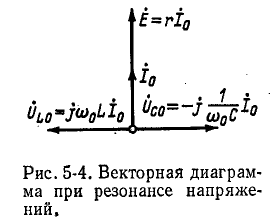
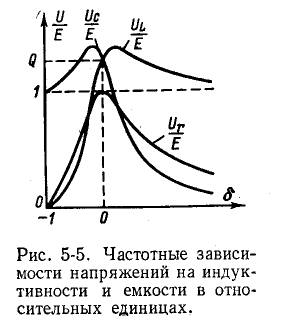
Максимальное напряжение находится немного выше (справа), а максимальное Uc – ниже (слева) резонансной частоты (рис. 5-5).

Напряжение на индукционной катушке 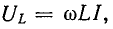который равен нулю w 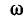= 0, с увеличением 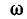может увеличиваться только до тех пор, пока ток не начнет уменьшаться быстрее, чем увеличиваться 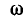. Затем 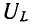уменьшается, стремясь в пределе к E. Напряжение на конденсаторе 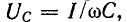равный w 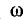= O к приложенному напряжению U = E, увеличивается, и ток растет быстрее, ч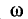ем затем 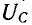уменьшается, достигая нуля в пределе. Кривые 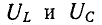пересекаются в резонансе, а ордината точки пересечения согласно (5-11) равна QE.

Это также следует из анализа следующих выражений, полученных из (5-5) и (5-6):

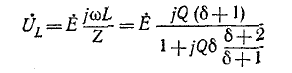
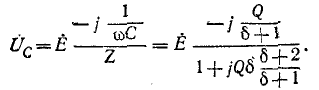
Напряжение 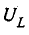достигает максимума при

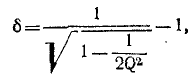
и напряжение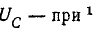

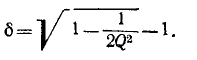
Пренебрежение 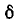выше, получаем приближенную формулу

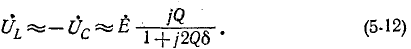
Возвращаясь к определению коэффициента качества рассматриваемого резонансного контура, мы видим, что вместе с формулами (5-3) и (5-4) коэффициент качества контура характеризуется выражениями (5-10) и (5-11), а именно:

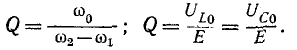
Из последней формулы коэффициент качества рассматриваемой цепи определяется как кратное значение перенапряжения на L и C на резонансной частоте.

Выше была рассмотрена неразветвленная электрическая цепь с r, L и C, соединенными последовательно. Для изучения явления резонанса в более сложных цепях разветвления, где резонанс напряжения может возникать на одной или нескольких частотах, полезно использовать метод геометрической локализации в дополнение к аналитическому методу расчета, показанному выше.

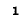Следует отметить, что в 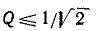максимум функции 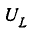происходит в 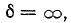т.е. в данном случае 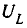с увеличением частоты непрерывно стремится к значению приложенного напряжения U – E, в то время как максимум функции 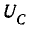в рассматриваемом случае происходит при 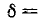= -1, т.е. при нулевой частоте 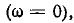когда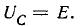

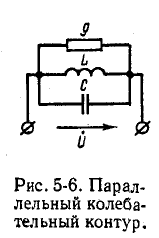
Параллельный колебательный контур и резонанс токов

Удобно исследовать резонанс токов в электрической цепи с r, L и C, соединенными параллельно (рис. 5-6), поскольку можно использовать результаты, полученные в предыдущей главе.

Фактически, выражение для комплексной проводимости такой цепи

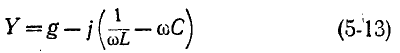
имеет структуру, аналогичную (5-1), а резонансная частота определяется в соответствии с (5-2).

Коэффициент качества резонансного контура на основе (5-3)

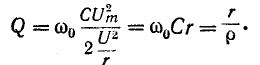
По аналогии с предыдущим, выражение (5-13) сводится к виду:
Сравнивая результат с (5-6), мы видим, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение 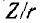для системы на рис. 5-1.

Поэтому кривые на рис. 5-2 применимы и в этом случае: кривые на рис. 5-2, а выражают зависимость от 6 Коэффициент y/g, а кривые на рис. 5-2, б – зависимость от угла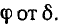

Кривые на рис. 5-2, а показывают, что при резонансе токов общая проводимость цепи минимальна, т.е. входное сопротивление достигает максимума.

При заданном напряжении 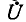на выходах цепи, ток, протекающий от источника к цепи, равен:

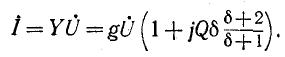
Этот ток достигает минимума на резонансной частоте, потому что на этой частоте

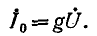
Поэтому отношение токов 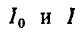определяется выражением

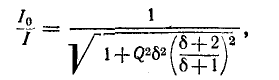
правая часть которого полностью совпадает с (5-8).

Поэтому резонансные кривые с рис. 5-3 выражают по отношению к диаграмме с рис. 5-6 соотношение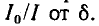

Ибо резонансные токи в индуктивном и емкостном элементах рис. 5-6 равны и противоположны по знаку:

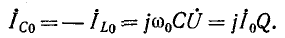
Из приведенного выше выражения следует, что коэффициент качества данной цепи определяется как кратное отношение токов в L и C к общему току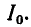

При Q > 1 эти токи больше, чем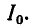

Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением 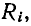тем меньше сопротивление 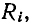к параллельному соединению с сопротивлением r, тем меньше коэффициент качества и тем шире полоса пропускания контура. Поэтому, в отличие от последовательного колебательного контура, с точки зрения уменьшения. Источник тока с высоким внутренним сопротивлением благоприятно влияет на полосу пропускания параллельного колебательного контура.

Для схемы на рисунке 5-6 для резонансных токов вывод из предыдущего параграфа о непрерывном обмене энергией между индуктивными и емкостными элементами при резонансных напряжениях остается в силе.

Схема на рисунке 5-6 является идеализированной. 5-6 является идеализированным, поскольку не учитывает активные потери в ветвях L и C. Поэтому следует рассмотреть другие схемы, “принимая во внимание активные сопротивления в ветвях L и C (рис. 5-7, a и b).

Условие резонанса токов для цепи рис. 5-7, а записывается в терминах равенства реактивных проводимостей:

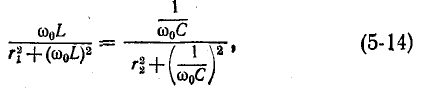
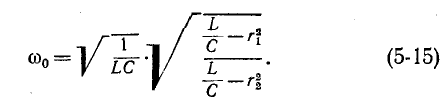
Явление резонанса возможно в этом случае только в том случае, если подчиненное выражение (5-15) имеет положительное значение

знак или, что то же самое, величины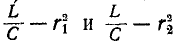имеют одинаковый знак Если 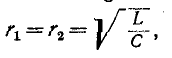то контур резонирует на любой частоте.

.
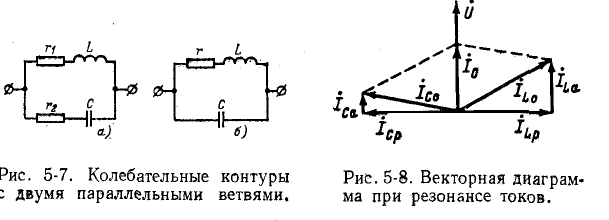
На рис. 5-8 показана векторная диаграмма для резонансных токов в цепи рис. 5-7, а. Индуктивные и емкостные токи ветвей состоят из активных 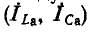и реактивный 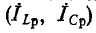элементы, при этом

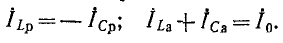
Меньше 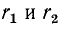по сравнению с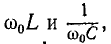и ближе к

к 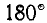фазовый угол между 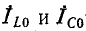в этом случае токи в ветвях образуют своего рода циркулирующий ток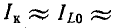 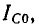замыкание в колебательном контуре

В резонансе вся цепь имеет только активную проводимость

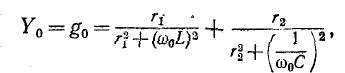
где z (5-14)

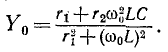
Для колебательного контура с малыми потерями член 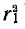по сравнению с 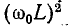и рассмотреть

что 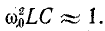В этом случае проводимость колебательного контура будет приблизительно выражаться формулой, которая обычно используется в радиотехнической практике:

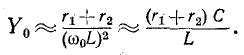
На сайте 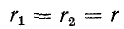(5-15)

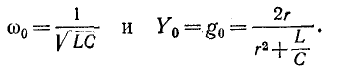
Кроме того, если 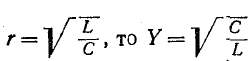в каждом

частота (резонанс в такой цепи называется “нейтральным” резонансом).

Легко видеть, что даже для резонансного контура с двумя параллельными ветвями (см. рис. 5-7) условие 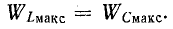Для этого достаточно

умножить обе части уравнения (5-14) на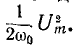

Выше было указано, что в цепи с r, L и C, соединенными параллельно (см. рис. 5-6) общая проводимость цепи имеет минимум на резонансной частоте.

Для цепи на рис. 5-7, б легко показать, что при изменении частоты (о) или индуктивности L минимум общей проводимости цепи и минимум общего тока не возникают на резонансной частоте. В том же случае, когда переменной величиной является емкость C, проводимость и полный ток достигают минимума при резонансе токов.
Коэффициент качества параллельного колебательного контура, исходя из (5-3), равен:

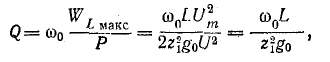
но

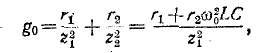
где

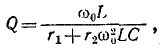
где резонансная частота 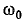получается из уравнения (5-15).

Часто в ветви с емкостью сопротивление 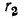можно опустить. После этого формулы значительно упрощаются.

Рассмотрим этот случай (см. рисунок 5-7, б).

Резонансная частота такого контура в соответствии с (5-15)

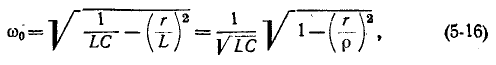
и коэффициент качества цепи в соответствии с приведенным выше выражением

Сравнение (5-16) и (5-2) показывает, что при одинаковых параметрах r, L и C резонансные частоты для схем рис. 5-1 и 5-7, b отличаются в раз

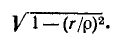
На 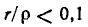разница в резонансных частотах составляет менее 1%. Более того, выражение (5-16) показывает, что резонанс токов возможен в цепи рис. 5-7,6 только при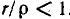

Полное сопротивление колебательного контура (см. рисунок 5-7, б)

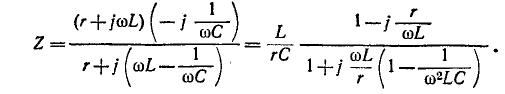
Из соотношений (5-16) и (5-17) можно сделать вывод, что:

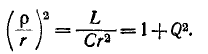
Принимая во внимание также отношения

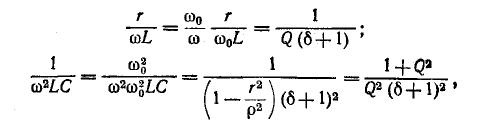
мы получаем выражение для сопротивления колебательного контура:

.

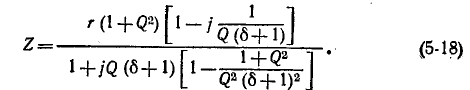На резонансной частоте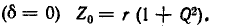

На резонансной частоте 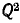больше единицы, то выражение (5-18) упрощается:

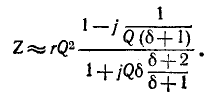
Вблизи резонанса, когда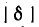несоизмеримо меньше единицы, выражение заменяется приближенным:

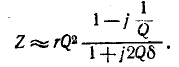
Если коэффициент качества колебательного контура высок

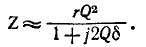
В этом случае токи ветвей

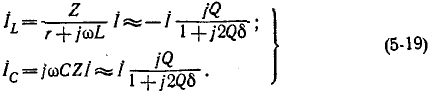
Здесь 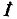– ток, входящий в цепь.

Напряжение на проводах цепи 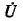связана с током I следующим образом:

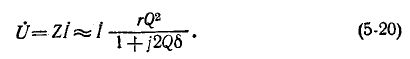
Приближенные выражения (5-19) и (5-20) для заданного Q аналогичны выражениям (5-12) и (5-7), полученным для схемы рис. 5-1, при условии, что напряжения заменены токами и наоборот. Поэтому кривые сопротивлений, токов и напряжений, соответствующие схеме рис. 5-1, в известном масштабе приближенно соответствуют проводимостям, напряжениям и токам в схеме рис. 5-7, б.

Заметим, что в цепи рис. 5-6 мгновенная мощность в цепи во время резонанса токов равна мгновенной мощности, рассеиваемой в сопротивлении r; в цепях с двумя параллельными ветвями (рис. 5-7) мгновенная мощность на зажимах цепи отличается от мгновенной мощности, рассеиваемой в сопротивлениях ветвей. Например, в момент, когда ток, входящий в цепь, проходит через ноль, мгновенная мощность на зажимах цепи равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно общего тока цепи, отличны от нуля, и поэтому мгновенная мощность, затраченная в сопротивлениях ветвей, также не равна нулю. Это объясняется тем, что на диаграммах

На рис. 5-7a и b энергия, запасенная реакторами, периодически частично преобразуется в тепло (в сопротивлениях ветвей), а затем восполняется источником.
Для увеличения крутизны резонансной характеристики, что необходимо для более четкого разделения колебаний разных частот, в радиотехнике широко используются двухконтурные резонансные контуры: два резонансных контура, каждый из которых отдельно настроен на одну частоту, индуктивно или электрически соединены. В отличие от резонансной кривой одиночного контура, соединенные контуры создают кривые с двойными горбами; например, ток в каждом контуре может иметь максимум на двух частотах ниже и выше резонансной частоты одиночного контура.

Частотная характеристика сопротивления и проводимости реактивных биполей

Двухполюсник – это любая электрическая цепь или часть электрической цепи, имеющая два проводника. Далее рассматриваются только линейные биполярные машины, т.е. состоящие из линейных элементов.

Различают активные и пассивные биполярные полюса.

Активный двухполюсник – это двухполюсник, содержащий источники электрической энергии, которые не взаимно компенсируются в пределах этого двухполюсника.

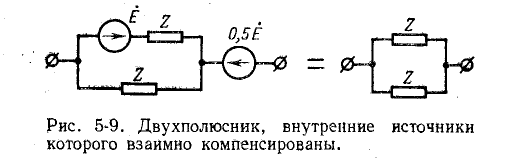
Двухполюсником называется пассивный двухполюсник, который не содержит источников электричества; в случае линейного двухполюсника он может содержать источники электричества, которые взаимно компенсируются так, что напряжение на его открытых клеммах равно нулю. Такой линейный двухполюсник является пассивным; его сопротивление, измеренное на его клеммах, не изменится, если источники электричества в нем заменить пассивными элементами – внутренними сопротивлениями источников ЭДС или внутренними проводимостями источников тока, соответственно. Пример биполя, содержащего компенсированные источники, показан на рисунке 5-9.

В зависимости от количества элементов, входящих в состав двухполюсника, различают одноэлементные, двухэлементные и многоэлементные двухполюсники.

По характеру этих элементов двухполюсники делятся на двухполюсники с реактивностью, т.е. содержащие индуктивности и емкости, и двухполюсники с потерями, содержащие активные сопротивления. Реактивные двухполюсные цепи – это идеализированные электрические системы, которые приближаются к свойствам физически существующих цепей с малыми потерями.

Частотные характеристики сопротивления или проводимости двухполюсных элементов, составляющих электрическую цепь, определяют частотные и резонансные свойства цепи, то есть частотную зависимость амплитуд и фаз токов и напряжений.

В этом разделе рассматриваются частотные характеристики реактивных пассивных двухполюсников.

Одноэлементные реактивные биполи

Индуктивность и емкость являются простейшими одноэлементными реактивными двухполюсниками. Знак комплексного сопротивления и комплексной проводимости каждого из этих двух полюсов не зависит от частоты; это существенно отличает их от других, более сложных реактивных двухполюсников, содержащих разнородные элементы реактивности, т.е. индуктивность и емкость в различных комбинациях.

Комплексное сопротивление индуктивного элемента имеет положительный знак во всем частотном спектре, а комплексная проводимость – отрицательный знак:

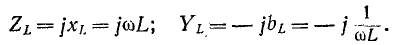
Комплексное сопротивление емкостного элемента имеет отрицательный знак во всем частотном спектре, в то время как комплексная проводимость имеет положительный знак:

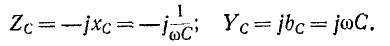
Для реактивных биполярных элементов комплексные сопротивления и проводимости являются мнимыми. Поэтому, чтобы сохранить знаки, удобно рисовать частотные характеристики сопротивления и проводимости в прямоугольной системе координат, где мнимые величины обозначены сверху плюсом, а мнимые величины – снизу минусом.

Частотная характеристика 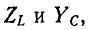в прямоугольной системе координат являются прямыми линиями, а частотная характеристика 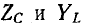– равносторонняя гипербола (рис. 5-10). Поэтому кривые 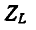и 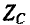похожи на кривые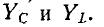

Отметим, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных биполей увеличиваются (с учетом знака) с ростом частоты, т.е.

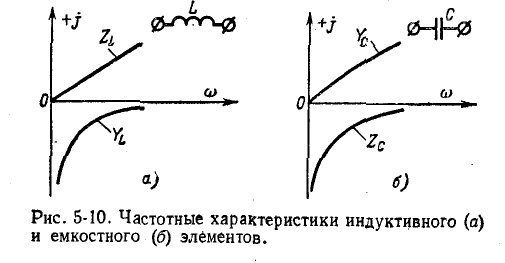
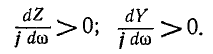
Это общее свойство всех реактивных биполей, а не только одноэлементных.

Двухполюсник, состоящий из однородных элементов (индуктивности или емкости), соединенных последовательно или параллельно, относится к одноэлементному двухполюснику, поскольку однородные элементы, соединенные последовательно или параллельно, могут быть заменены эквивалентным реактивным элементом той же природы.

Двухэлементные биполярные реактивные элементы

Двухэлементные биполярные цепи, состоящие из индуктивности и емкости, являются простейшими резонансными цепями.

Когда индуктивность и емкость соединены последовательно, комплексные сопротивления складываются алгебраически. На рис. 5-11, а, жирной линией показана частотная характеристика двухполюсной цепи, полученная путем графического сложения кривых 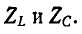Она пересекает ось абсцисс на резонансной частоте 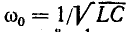(резонанс напряжения). Это частота, на которой функция Z 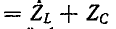называется нулем этой функции, точка на абсциссе, соответствующая нулю функции, отмечается кружком.

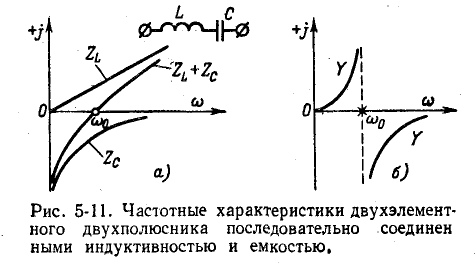
Частотная характеристика проводимости одного и того же двухполюсника является обратной функцией сопротивления: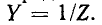

Кривая Y показана на рис. 5-11, б.

На резонансной частоте проводимость данного биполя переходит в бесконечность; эта точка называется полюсом функции Y и обозначена крестиком на рисунке

Частотные характеристики Z и Y1, построенные таким образом, соответствуют уравнениям

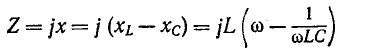
и

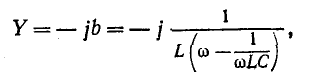
или с (5-2):

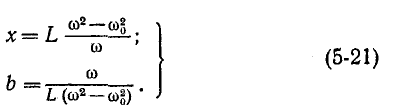
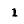По оси ординат частотной характеристики цепей с чистым реактивным сопротивлением откладываются мнимые значения сопротивления и проводимости.

В диапазоне частот ниже резонанса 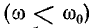сопротивление емкостного элемента по абсолютной величине больше, чем сопротивление индуктивного элемента; в этом случае сопротивление двухполюсной цепи является емкостным.

В диапазоне частот выше резонансной частоты абсолютное значение емкостного сопротивления меньше индуктивного сопротивления; сопротивление двухполюсника индуктивное.

Когда индуктивность и емкость соединены параллельно, их комплексные проводимости складываются алгебраически. На рисунке 5-12, а, жирной линией показана частотная характеристика двухполюсника.

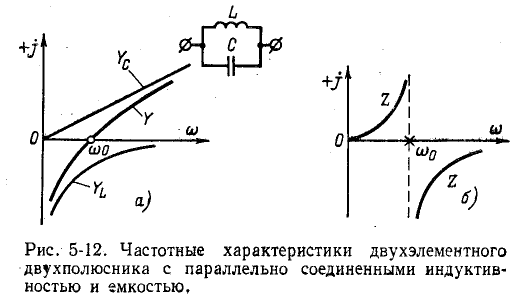
Частотная характеристика двухполюсника, полученная путем графического сложения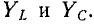

Частотная характеристика сопротивления того же двухполюсника является обратной функцией проводимости: Z – 1/Y. Кривая Z показана на рисунке 5-12, б.

Частота, при которой характеристика Y пересекает ось абсцисс (нуль функции Y), а характеристика Z уходит в бесконечность (полюс функции Z), является резонансной частотой (резонансом токов).

Частотная характеристика, построенная на рисунке 5-12, соответствует уравнениям:

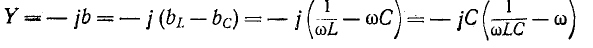
И

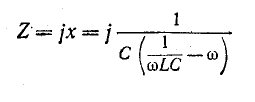
или с учетом (5-22)

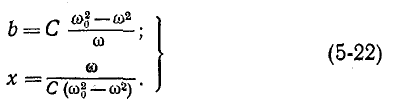
В области частот ниже резонанса проводимость индуктивного элемента более чем компенсирует проводимость емкостного элемента, и сопротивление двухполюсника оказывается индуктивным. В области частот выше резонанса происходит обратное, и сопротивление двухполюсника становится емкостным.

Таким образом, в зависимости от частоты двухэлементный двухполюсник с реактивным сопротивлением может иметь либо индуктивное, либо емкостное сопротивление. В этом случае, как и в случае одноэлементного реактивного биполя, кривые Z и Y увеличиваются, т.е. производные 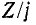и 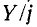положительны по отношению к частоте.

В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только частотой тока, сопротивления двухэлементных реактивных двухполюсников зависят также от разности квадратов резонансной частоты и частоты тока (уравнения (5-21) и (5-22)1.

Как видно из выражений (5-21), для построения частотных характеристик двухполюсника, состоящего из последовательно соединенных элементов L и C, достаточно знать нуль функции Z или, эквивалентно, полюс функции Y. Параметр L, содержащийся в (5-21), влияет только на выбор масштабов Z и Y по оси ординат.

Аналогично, согласно (5-22), для построения частотной характеристики двухполюсника, состоящего из параллельно соединенных элементов L и C, достаточно знать полюс Z или, эквивалентно, ноль Y, при этом параметр C влияет только на шкалы Z и Y.

Двухполюсники с одинаковыми частотными характеристиками Z или Y эквивалентны.

Многоэлементный реактивный биполярный

Многоэлементный двухполюсник с реактивным сопротивлением может быть результатом различных комбинаций одноэлементного и двухэлементного двухполюсников. Используя приведенные выше данные частотных характеристик, можно построить данные частотных характеристик для трех-, четырех- и многоэлементных двухполюсников с реактивным сопротивлением. В этом процессе однофункциональные элементы (или группы элементов с одинаковыми резонансными частотами) сначала должны быть заменены одним элементом (или эквивалентной группой элементов) в параллельном или последовательном расположении.

Одиночные элементы (или группы элементов с одинаковыми резонансными частотами), соединенные параллельно или последовательно, должны быть сначала заменены одним элементом (или эквивалентной группой элементов, как, например, показано на рис. 5-13. 5-13).

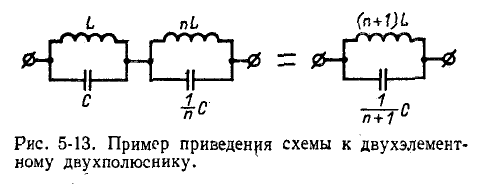
Такие биполярные полюса будут называться “редуцированными”.

Из свойства положительности производно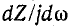й (или 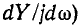следует, что нули и полюса функции Z (или Y) должны переплетаться, так как если бы было два последовательных нуля, не разделенных полюсом, то возник бы участок характеристики с отрицательной производной.

В общем, если в 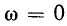сопротивление пассивного двухполюсника равно нулю, то есть если есть путь для постоянного тока, то сначала возникает резонанс тока, затем резонанс напряжения и так далее.

В противном случае порядок резонансов меняется на противоположный: резонанс напряжения – первый, резонанс тока – второй, и так далее.

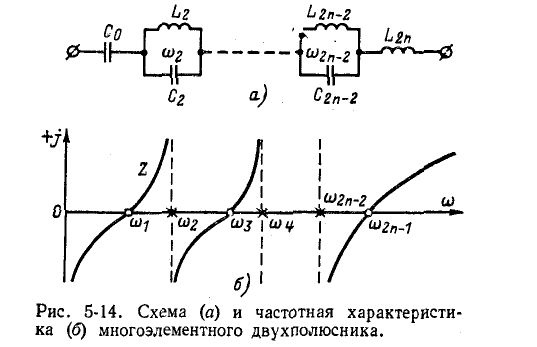
На рисунке 5-14, а показана схема многоэлементного двухполюсника, а на рисунке 5-14, б – соответствующая импедансная частотная характеристика.

В реактивных двухполюсниках сумма чисел полюсов и нулей (без учета точек 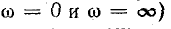на единицу меньше, чем число элементов данного “редуцированного” биполя.

Расположение нулей и полюсов, как указано выше, является переменным, и все ветви частотной характеристики увеличиваются по мере того, как 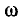СУБЪЕКТ.

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан командой педагогов на некоммерческой основе для дополнительного образования молодежи.

Сайт написан, поддерживается и управляется командой учителей

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.

Читайте далее:

• Полное сопротивление цепи переменного тока – Основы электроники.
• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• 56 Резонанс напряжения и резонанс тока.
• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• Форум RadioCat; Просмотр темы – Измерение индуктивности простыми методами.
• Топология электрической цепи (Лекция N 2).
• Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.