Образно-логическое мышление (Наглядно-образное мышление) – Различные мыслительные процессы так называемого “пикториального” решения задач, которое предполагает визуальное представление ситуаций и операций с помощью изображений составляющих объектов. Зрительное воображение, по сути, является синонимом слова “фантазия”, которое позволяет нам наиболее четко и ярко воспроизводить различные реальные черты предмета или явления. Этот вид мыслительной деятельности человека формируется в детстве, начиная примерно с 1,5 лет.
Логическое мышление – логическое развитие
 Каждый день мы сталкиваемся с множеством задач, которые требуют умения логически мыслить. Логика, как способность мыслить и рассуждать связно и последовательно, необходима во многих жизненных ситуациях, от решения сложных технических и деловых проблем до убеждения других людей и совершения покупок.
Каждый день мы сталкиваемся с множеством задач, которые требуют умения логически мыслить. Логика, как способность мыслить и рассуждать связно и последовательно, необходима во многих жизненных ситуациях, от решения сложных технических и деловых проблем до убеждения других людей и совершения покупок.
Однако, несмотря на высокую востребованность этого навыка, мы часто совершаем логические ошибки, не осознавая этого. Среди многих людей бытует мнение, что правильное мышление основано на жизненном опыте и так называемом здравом смысле, без использования законов и специальных приемов “формальной логики”. Для простых логических операций, вынесения элементарных суждений и простых выводов здравого смысла может быть достаточно, но когда нужно узнать или объяснить что-то более сложное, здравый смысл часто сбивает нас с пути.
Причины этих иллюзий кроются в принципах развития и формирования основ логического мышления человека, которые формируются уже в детстве. Логическое мышление не преподается целенаправленно, а отождествляется с уроками математики (для детей в школе или для студентов в университете) и с решением и прохождением различных игр, тестов, задач и головоломок. Однако такие занятия способствуют развитию лишь небольшой части процессов логического мышления. Кроме того, они объясняют нам принципы поиска решений задач довольно примитивным способом. Почему-то нас не учат развивать вербально-логическое (т.е. словесно-логическое) мышление, умение правильно выполнять мыслительные операции и последовательно делать выводы. Поэтому уровень логического мышления людей недостаточно высок.
Мы считаем, что логическое мышление людей и их способность к познанию необходимо развивать систематически и на основе специального терминологического аппарата и логических инструментов. В этом онлайн-тренинге вы изучите методы самообучения для развития логического мышления, познакомитесь с основными категориями, принципами, свойствами и законами логики, найдете примеры и упражнения для применения полученных знаний и навыков.
Оглавление:
l Тождество (полное совпадение объемов понятий);
Логические операции
Утверждение, содержащее другие утверждения, называется комплекс. Для создания сложных утверждений мы используем логические операции (снопы). Рассмотрим некоторые из них (в порядке приоритета при вычислении логических выражений).
Инверсия (отрицание)
Инверсия – это логическая операция, создающая составное высказывание, которое является истинным тогда и только тогда, когда исходное высказывание ложно.
В выражениях это обозначается ¬A или Ā.
Там написано “НЕ” (например, “не А”).
Конъюнкция (логическое умножение)
Конъюнкция – это логическая операция, которая производит составное предложение, которое истинно тогда и только тогда, когда истинны оба исходных предложения.
В выражениях он обозначается AÙ B или A&B (знак может быть не указан – AB).
Здесь написано “И”. (например, A и B).
дизъюнкция (логическое сложение)
Дисъюнкция – это логическая операция, создающая составное высказывание, которое истинно, если истинно хотя бы одно из исходных высказываний.
В выражениях он обозначается AÚ B, иногда A+B.
Он читается как ИЛИ (например, A или B).
Импликация (следующая)
Импликация – это логическая операция, в результате которой получается составное высказывание, которое ложно тогда и только тогда, когда первое исходное высказывание истинно, а второе ложно.
В выражениях это обозначается как A Þ B или A ® B.
Там написано: “ЕСЛИ. ТОГДА” (например, “если А, то Б”).
Эквивалентность (эквивалентность)
Эквивалентность – это логическая операция, в результате которой получается составное высказывание, которое истинно тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях это обозначается как A Û B или A º B.
Она гласит: “КОГДА И ТОЛЬКО КОГДА”. (например, “А, если и только если В”).
Таблицы истинности для логических операций
Таблица истинности Массив, содержащий значения логической функции для всех возможных комбинаций значений ее аргументов.
Количество комбинаций (строк в таблице) определяется как 2 N , где N – количество аргументов (т.е. при двух аргументах количество строк равно 4, при трех аргументах количество строк равно 8 и т.д.).
Соответственно, Петров успешно прошел логику.
2 Понятие и слово.
Будучи отражением объектов действительности, понятие неотделимо от слово. Слово – это материальный носитель понятия, языковое средство фиксации идеи, ее хранения и передачи другим людям. Кроме слов, не существует никаких понятий.
В соответствии с двумя сторонами понятия – его содержанием и объемом – в слове различают смысл и значение. На основании значение это знание об объектах, составляющих содержание понятия. И по обозначающий обозначает объекты, стоящие за словом, которые образуют объем понятия.
Отношения между понятием и словом не являются соответствием один к одному. Они мобильны и многогранны. С одной стороны, Каждое понятие выражается словом (или слова), а с другой стороны Не каждое слово выражает понятие.. Понятие может быть выражено либо одним словом (напр. “государство”), или фраза, состоящая из двух или более слов: “правовое государство”, “федеральное правовое государство”, “демократическое федеральное правовое государство” или даже “демократическое федеральное правовое государство с республиканской формой правления”. Последнее словосочетание используется в действующей Конституции Российской Федерации для характеристики ее государственного устройства и выражения соответствующего понятия (см. статью 1).
Однако, если, как уже говорилось выше, каждое понятие выражается словом (или фразой), то не каждое слово выражает понятие. Таковы, например, междометия, которые непосредственно фиксируют не мысли, а чувства (“ах”, “ай”, “эге-ге” и т.д.), хотя чувства тоже могут быть объектом мысли и о них возможны собственные понятия (“ужас”, “изумление”, “недоумение” и т.д.). Это также вспомогательные слова – союзы, частицы и т.д. (“когда”, “не”).
Далее, Одно и то же понятие может быть выражено разными словами.. Например, понятие преступления в разных языках оформляется в разных словесных формах: “преступление” в русском языке, “правонарушение” в английском, “Verbrechen” в немецком и т.д. И даже в одном и том же языке понятие может быть выражено разными словами, напр: “отечество” – “отечество”; “конституция” – “основной закон государства”; “юрист” – “правовед”; “адвокат” – “защитник” – “защитник”. В русском языке такие слова называются синонимы.
В свою очередь, Одно и то же слово может содержать в себе несколько понятий.. Например, “коса” – это инструмент фермера, полоса песка на берегу реки или моря, а также разновидность женской прически. “Закон” – это как объективный закон природы или общества, так и юридический закон. Такие слова называются омонимы.
Необходимым условием правильного мышления является точная языковая формулировка понятий, выражение их в соответствующих словах и словосочетаниях. И наоборот, условием правильной речи является использование слов в соответствии с понятиями, которые они выражают. Поэтому синонимия важна для выражения различных оттенков мысли, для выделения разных сторон отраженного в ней предмета. Однако это таит в себе опасность логических ошибок: смешение понятий, подмена понятий и т.д.
Это особенно важно учитывать в юридической практике. Как неоднократно отмечалось в юридической литературе, нередко в качестве синонимов используются слова, обозначающие разные понятия.
Например, в чем разница между “ответчиком” и “обвиняемым”? Они настолько близки, что кажутся синонимами, но на самом деле обозначают качественно разные стадии следственного и судебного процесса и поэтому выражают разные понятия. Так объясняется в Уголовно-процессуальном кодексе Российской Федерации:
“1. Обвиняемый – это лицо, в отношении которого:
1) принято решение о привлечении его к суду;
2) было вынесено обвинительное заключение.
2. Обвиняемый, по уголовному делу которого назначено судебное разбирательство, именуется обвиняемым”. (Статья 47). И далее: “Подсудимый, признанный виновным, именуется осужденным. Подсудимый, в отношении которого вынесен оправдательный приговор, именуется оправданным”. (там же).
Иногда используются синонимы: “подстрекатель” и “подстрекатель” (хотя не все подстрекатели являются подстрекателями и, наоборот, не все подстрекатели являются подстрекателями); “кровотечение” и “кровотечение” (может быть кровотечение без кровотечения и может быть кровотечение без кровотечения); “крайняя необходимость” и “необходимая оборона”. Нередко путают “заявление” и “жалобу”, “донос” и “заговор”, “помилование” и “амнистию”. С введением судов присяжных может возникнуть путаница в терминах “вердикт” и “судебное решение”. И такая путаница слов усложняет дело, вызывает непонимание и влияет на людей.
Что касается омонимов, то, как и все совпадения, они неизбежны в языке. Но их использование также требует осторожности, иначе и здесь возможны логические ошибки. Например, если мы скажем: “Закон всемирного тяготения”, но “Закон брака и семьи”, такое использование словесного омонима “закон” будет правильным в соответствии с различиями между понятиями “объективный закон” и “юридический закон”. Если, с другой стороны, мы скажем: “Закон всемирного тяготения” и “Закон брака и семьи”, то в обоих случаях сочетание слова “закон” с другими словами будет казаться странным и даже непоследовательным. Но разве до недавнего времени в социальных науках не звучали столь же странно и абсурдно следующие формулировки: “Закон решающей роли материального производства в жизни и развитии общества”, “Закон решающей роли общественного бытия по отношению к общественному сознанию”, “Закон соответствия (или еще хуже: обязательного соответствия!) производственных отношений характеру и уровню развития производительных сил”? Сознательно или бессознательно, но произошло смешение объективных законов, которые не зависят от людей (законы ), с человеческими, юридическими правами (права o). Результатом этого стала путаница в их понимании.
Если одно и то же слово одновременно используется в разных значениях, то такая ошибка называется в логике амфиболия (двусмысленность). Такие омонимичные слова часто становятся основой для шуток, розыгрышей и анекдотов. Их прекрасно использовал Льюис Кэрролл в своих знаменитых книгах “Приключения Алисы в стране чудес” и “Алиса в стране чудес”. Козьма Прутков был экспертом по амфиболам (см. его “Плоды размышлений”). Многие габровские анекдоты были основаны на них.
В преддверии референдума по проекту новой Конституции Российской Федерации в одной из центральных газет появилась статья под названием “Конституция мадам Грицацуевой – самая демократическая в мире”. Название предполагало, что речь в статье идет о другой, женской, альтернативной версии проекта конституции. Но оказалось, что статья была о строительстве женского тела! В статье отмечается, что мода на худых красавиц проходит, и что рацион многих моделей содержит всевозможные мучные изделия. А с точки зрения одного известного модельера, фигура вообще не нужна.
Правда” привела совершенно анекдотичный случай, когда один высокопоставленный московский чиновник, находясь в провинции, после сытного обеда мечтал о “колхознике”. (сорт дыни), и они хотели привести к нему женщину (правда, не колхозницу, а сельскую учительницу).
Многозначность слов создает значительные трудности в науке и технике. Поэтому они стремятся к однозначности в использовании определенных слов, за которыми стоят очень конкретные понятия. Это достигается путем создания системы понятий – слов, имеющих одинаковое значение, по крайней мере, в рамках данной науки или отрасли техники.
Как показывает практика, разработка научной терминологии – дело долгое и трудное, но очень важное. Особенно важным является правильность слов, которые вводятся или используются в законе. Над этим работают целые команды ученых и юристов-практиков.
Современная логика разработала стройную теорию “именования” объектов – учение об именах, и были созданы специальные искусственные языки, свободные от всякой двусмысленности и двусмысленности и состоящие из однозначных символов.
Для тех, кто пропустил математику в школе, поясню: тождество – это равенство.
Законы логики (логические знания)
Законы логики – это правила, из которых можно вывести правильный вывод..
Существует 4 закона. Иногда они нарушаются случайно, что приводит к неправильному выводу – паралогизму. Иногда намеренно, чтобы запутать собеседника и привести его к неправильному убеждению. К этому добавляются софизмы – недостоверные выводы, которые кажутся логически верными.
Закон идентичности
Для тех, кто пропустил математику в школе, поясню: идентичность – это равенство.
Этот закон гласит следующее: понятие должно сохранять свое первоначальное значение в ходе логических рассуждений.
Язык многогранен, почти каждое слово имеет несколько значений. Если в процессе подменить одно значение другим, то получится ложный логический вывод.
Приведу пример известной юмористической загадки: “Почему в стакане вода? Чтобы выпить, конечно. Но нет, он находится за стеклом. Есть игра смыслов, нет идентичности. Нельзя путать понятия и обязательно нужно избегать двусмысленности.
В истории европейской логики можно выделить этапы:
Металогия
Метатеоретические проблемы логики
- формализованные теории
- Независимость аксиом формализованных теорий
- Детерминированность
- Сравнительный анализ логических теорий
Концепции логики
Концепции логики различаются прежде всего тем, как они относятся к метатеоретическим проблемам логики, связанным с основаниями математики:
Проблемы аксиоматизации теории множеств
- Логические парадоксы
- Семантические парадоксы
Решение. В соответствии с порядком следования операций, сначала сравнение, затем отрицание, а затем конъюнкция. Отрицанием утверждения M ≥ 10 является M < 10. Получаем выражение M < 10 ∧ M > 3. Чтобы это выражение (конъюнкция) было истинным, оба неравенства должны быть выполнены (т.е. быть истинными). Поэтому значение М должно быть больше 3, но меньше 10. Среди предложенных значений только одно удовлетворяет этому условию – число 4.
Ответ: 4) 4.
Что это значит в логике
Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Ее интересует не содержание мышления, а его форма, поэтому ее часто называют формальной логикой.
Форма мышления – Это способ выражения мысли, то есть форма, в которой она построена.
Форма, обозначающая некоторый объект или его отличительный признак, называется зачатие. Примерами концепций являются: “компьютер”, “планета”, “длина”, “профессия”.
Форма, утверждающая или отрицающая что-либо о свойствах понятий и отношениях между ними, называется утверждение (заявление, решение). Примерами логических утверждений являются: “Декодирование – это процесс восстановления информации из закодированного представления”; “В двоичной системе используются две цифры, 0 и 1”; “Париж – столица Франции”. Утверждения могут быть истинными или ложными. Например, утверждение “Шанхай – столица Франции” является ложным.
Форма, в которой новое утверждение выводится из двух или более утверждений, называется умозаключением. Примером умозаключения является: “Периферийные устройства компьютера – это устройства ввода или вывода информации. Сканер – это устройство, используемое для переноса текста и изображений с бумаги на компьютер. Поэтому сканер является периферийным устройством”.
Правила, которым необходимо следовать, чтобы прийти к истинным выводам из истинных суждений, являются законами мышления. Логика изучает эти законы и то, как вывести новые теоремы из существующих.
Математическая логика использует математические методы для определения истинности или ложности утверждений. В ней используется специальный символический язык, похожий на язык математики, поэтому ее часто называют символической логикой.
Алгебра логики – Ветвь математической логики, использующая алгебраические методы для логических преобразований. Изучает логические утверждения и методы определения их истинности или ложности с помощью алгебраических методов.
Логическое утверждение – это любое повествовательное предложение, о котором мы можем однозначно сказать, что его содержание истинно или ложно. Вопросительные и командные предложения не являются логическими высказываниями. Но и каждое повествовательное предложение не является логическим утверждением. Например, утверждение “Летом было очень дождливо” не является однозначным, поскольку утверждение “Существует несколько вселенных” не может быть однозначно определено как истинное; следовательно, эти предложения не являются логическими утверждениями (ассерциями).
Отличительной особенностью логических высказываний является то, что они могут принимать одно из двух значений правда и ложный. Истинность или ложность высказывания определяется вне алгебры логики – путем наблюдения, научных исследований, практических экспериментов и т.д.
Алгебра логики различает простые высказывания и сложные высказывания, состоящие из нескольких простых. Если в высказывании нельзя выделить какую-то часть, которая не тождественна по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т.д.
Сложные высказывания представляют собой комбинации простых высказываний с помощью логические разъемы. Слова “не”, “и”, “или”, “тогда и только тогда”, “если … тогда” используются в качестве логических соединителей. Истинность или ложность полученных таким образом составных высказываний определяется значением простых высказываний. Например, простые утверждения “Офис компании находится в Мадриде” и “Офис компании находится в Берлине” можно объединить в составные утверждения “Офис компании находится в Мадриде или Берлине”, “Офис компании находится в Мадриде и Берлине”, “Если офис компании находится в Мадриде, то он также находится в Берлине”. Истинность первого из них означает, что офис компании находится в одном из указанных городов или что офисы есть в обоих городах. Ложь означает, что ни в одном из городов нет офиса. Второе составное утверждение верно, если компания имеет офис в обоих городах. Если офис есть только в Берлине или только в Мадриде, то второе сложноподчиненное предложение ложно.
В классической двоичной булевой алгебре существует только два булевых значения – True и False. Они соответствуют числовому представлению – 1 и 0. Иногда эти значения записываются как “да” и “нет”. Тот факт, что некоторое высказывание A истинно или ложно, записывается как A = 1 или A = 0, соответственно.
Логические операции
В булевой алгебре логические коннекторы рассматриваются как логические операции. Они имеют свои собственные имена и обозначения. Результаты применения каждой операции над логическими высказываниями (истина или ложь) можно представить в виде таблицы. Он определяет все возможные комбинации начальных значений логических высказываний и истинность или ложность результата. Такие таблицы называются таблицы истинности операции. Обычно они используют обозначения логических значений 0 и 1 или false и true.
Основными логическими операциями являются отрицание, соединение, дизъюнкция, эксклюзивная дизъюнкция, следствие и эквивалентность.
Логическое отрицание (инверсия) – Логическая операция, когда из заданного высказывания создается новое высказывание – отрицание исходного высказывания. Обозначается символически тире над (Ā) или обозначением ¬A, не A, не A (читается как “отрицание A”, “не A”, “A ложно”, “ложно, что A”).
Высказывание ¬A ложно, когда A истинно, и истинно, когда A ложно.
Таблица истинности операции отрицания

Если мы обозначим через A утверждение “Арбуз – ягода”, то ¬A соответствует утверждению “Арбуз – не ягода”. (“Неправда, что арбуз – это ягода”).
Отрицание – это унарная операция. Унарная (сингулярная) операция – это операция, которая относится к одному операнду.
Другие логические операции являются бинарными (двоичными). Бинарная операция – это операция, которая выполняется над двумя операндами.
Логическое умножение (конъюнкция) – Операция, объединяющая два или более утверждений с помощью связки “и”. Эта конъюнкция символически обозначается ∧ и читается как “A и B”. Для обозначения союзов также используются следующие знаки: A – B, A & B, A и B, A и B, A и B, а иногда между предложениями знак не ставится: AB.
Утверждение A ∧ B истинно только в том случае, если истинны и A, и B. Утверждение A ∧ B ложно только в том случае, если хотя бы одно из утверждений A или B ложно.
Таблица истинности конъюнкции

Например, утверждения “Лондон находится к северу от Лиссабона” и “Лондон находится к востоку от Лиссабона” являются истинными. Тогда составное логическое утверждение “Лондон находится к северу и востоку от Лиссабона” также истинно. ‘London is neither north nor east of Lisbon’, ‘London is north or east of Lisbon’ или ‘London is neither north nor east of Lisbon’ являются ложными.
Логическое сложение (дизъюнкция) – Операция, объединяющая два или более утверждений с помощью связки “или”. Эта конъюнкция символически обозначается v и читается как “A или B”. Следующие знаки также используются для обозначения дизъюнкции: A + B, A или B, A или B, A | B.
Утверждение A v B истинно только в том случае, если хотя бы одно из утверждений A или B истинно. Утверждение A v B ложно только в том случае, если и A, и B ложны.
Таблица истинности операций дизъюнкции

Например, утверждения “Виктор старше Ольги” и “Виктор – однофамилец Ольги” являются истинными. Тогда логические составные высказывания также истинны: “Виктор старше Ольги или Виктор – однофамилец Ольги”, “Виктор младше Ольги или Виктор – однофамилец Ольги”, “Виктор старше Ольги или Виктор не однофамилец Ольги”. Утверждение “Виктор моложе Ольги или Виктор не однофамилец Ольги” ложно, потому что оба простых утверждения, из которых оно состоит, ложны.
Исключение добавки (exclusive disjunction, strict disjunction, addition modulo two, strictly disjunctive disjunction) – логическая операция, соединяющая два высказывания с помощью связки “или”, используемой в исключительном смысле (также называемой эксклюзивным “или”). Операция символически обозначается ⊕ и читается как “либо A, либо B”.
Высказывание A ⊕ B истинно только в том случае, если высказывания A и B имеют разные значения.
Таблица истинности для операций строгой дизъюнкции

Например, результат эксклюзивной дизъюнкции двух высказываний “Виктор не старше Ольги” и “Виктор моложе Ольги” всегда будет истинным, независимо от того, кто из них старше.
Логическое следствие (импликация) – это логическая операция, которая соединяет два утверждения с помощью “если…”. тогда” в составное высказывание. Эта операция символически обозначается → и читается как “Если A, то B”, “A влечет B”, “Из A следует B”, “A подразумевает B”. Импликация также обозначается ⊃ или ⇒. Первое логическое утверждение является условием (посылкой), а второе – следствием (выводом).
Для операции импликации верно, что из лжи может следовать что угодно, но из истины может следовать только истина. Таким образом, импликация A → B ложна только в том случае, если A истинно, а B ложно (за истинным высказыванием следует ложное). Во всех остальных случаях следствие верно.
Таблица истинности операции импликации

Для утверждений “Луна – спутник Земли” и “Сумма углов треугольника не равна 180°” (первое – истинно, второе – ложно) составное высказывание “Если Луна – спутник Земли, то сумма углов треугольника не равна 180°” будет ложным. С другой стороны, эти утверждения истинны: “Если Луна – спутник Земли, то сумма углов треугольника равна 180°”, “Если Луна – не спутник Земли, то сумма углов треугольника не равна 180°” и “Если Луна – не спутник Земли, то сумма углов треугольника равна 180°”. Этот пример ясно показывает, что в алгебре логики смысл высказываний не принимается во внимание, только их истинность или ложность.
Эквивалентность (эквивалентность, последовательность, двойная импликация, эквивалентность) – это логическая операция, которая из двух высказываний A и B дает новое высказывание A ≡ B (читается “A эквивалентно B”). Эта операция может быть выражена конъюнкциями “тогда и только тогда”, “необходимый и достаточный”, “эквивалентный”. Для обозначения эквивалентности используются следующие знаки
Если два высказывания имеют разные логические значения, то результат операции эквивалентности всегда будет ложным. Если оба простых высказывания ложны или оба истинны, то сложное логическое высказывание всегда будет истинным.
Таблица истинности для операции эквивалентности

Для высказываний “Линейное уравнение всегда имеет решение” и “Кит – млекопитающее” операция эквивалентности всегда будет истинной, потому что оба простых высказывания истинны.
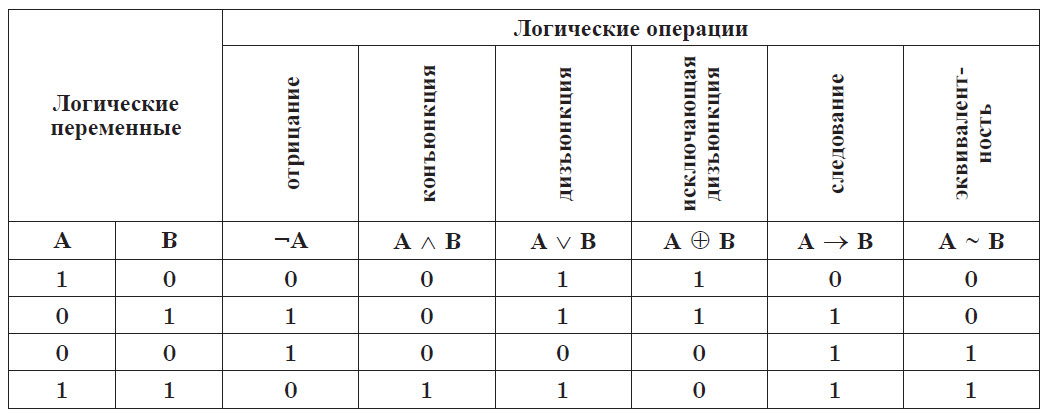
Таким образом, сводная таблица истинности для всех основных логических операций выглядит следующим образом:
Булевы выражения
Логические выражения могут быть записаны в виде формул (логических выражений). Булевы выражения содержат логические переменные, символы логических операций, логические константы (true и false) и круглые скобки. Булевы выражения принимают значения true или false.
Правила построения логических выражений следующие:
- каждая логическая переменная или константа (true и false) является логическим выражением;
- Если A является , то ¬ A также является логическим выражением;
- если A и B – логические выражения, то A ∧ B; A v B ; A ⊕ B; A → B; A
Например, A ⊕ true v B v false является логическим выражением; A v ⊕ B v false не является логическим выражением.
Логическое выражение, которое принимает значение правда для всех значений составляющих его переменных называется личность – истинное выражение (тавтология). Например, A v B v ¬A; (A ∧ ¬A) → B.
Логическое выражение, которое принимает значение ложный для любого значения составляющих его переменных называется является тождественно ложным выражением (противоречие). Например, A ∧ ¬A; B
Булево выражение, которое принимает как значение false, так и значение true при различных значениях составляющих его переменных, называется булевым выражением исполняемое выражение.
ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Для сложных логических выражений, содержащих несколько логических операций, определяется порядок операций (приоритет): сначала операции отрицания, затем операции логического умножения, затем операции логического сложения и исключающего сложения, затем операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения можно изменить с помощью круглых скобок.
Приоритет логических операций в логических выражениях

Пример 1
Определение старшинства логических операций в выражении.
Вычислите его значение, если A = 1, B = 0, C = 1.
¬ A ∧ C v (A ⊕ B) ∧ B
Решение. Значения в скобках вычисляются в первую очередь. Затем операции выполняются в соответствии с приоритетом: операция отрицания имеет наивысший приоритет, за ней следует операция умножения, а затем операция сложения, как и в математике. Таким образом, порядок будет следующим: 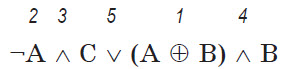
Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и скобочного выражения: 0 ∧ 1 v 1 ∧ 0, после операции умножения: 0 v 0. Итого: 0.
Ответ: логическое выражение ложно.
Пример 2
Для какого из приведенных слов верно следующее утверждение?
(Вторая буква – гласная) ИЛИ (Первая буква – гласная) И НЕ (Длина имени 5 букв или меньше)
1) Олег 2) Марианна 3) Светлана 4) Ольга.
- В соответствии с иерархией старшинства операций, сначала вычислите результат операции отрицания: “длина имени больше 5 букв”. К таким названиям относятся. Марианна, Светлана.
- Затем вычислите результат конъюнкции (соединения И) второго и третьего выражений. Конъюнкция истинна только в том случае, если оба высказывания истинны. Следовательно, мы должны выбрать имена, в которых и первая буква является гласной, и длина имени больше 5 букв – таких имен среди предложений нет.
- Результат дизъюнкции (OR-связка) истинен только в том случае, если одно, другое или оба простых высказывания истинны одновременно. Первое простое утверждение верно для Марианны, второе – ложно для данных имен. Поэтому правильный ответ – 2.
Ответ: 2) Марианна.
СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ
Между логическими операциями существует взаимосвязь. Операции исключающего “или”, наследования и эквивалентности могут быть выражены операциями отрицания, логического сложения и умножения, как показано в таблице ниже.
Взаимосвязь между логическими операциями

Поэтому операции отрицания, логического сложения и логического умножения называются базовыми логическими операциями: их достаточно для построения любого логического выражения.
Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, то говорят, что выражение находится в нормальной форме.
ЭКВИВАЛЕНТНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ
Булевы выражения, значения которых одинаковы для всех наборов переменных, входящих в них, называются эквивалентными, или равносильными.
Чтобы убедиться, что два выражения эквивалентны, можно построить для них таблицы истинности. Если все значения в таблицах совпадают, то они эквивалентны.
Пример 3
Проверьте эквивалентность выражений A
E и (Ā ∧ Ē) v (A ∧ E).
Решение. Для проверки создайте таблицу истинности, содержащую как можно больше строк наборов значений переменных, содержащихся в выражении. Для двух переменных (A и E) количество наборов равно четырем. Для двух столбцов для значений переменных (A и E) добавьте количество столбцов, равное количеству операций в выражении. Поэтому нам нужно создать таблицу с 4 строками и 7 столбцами.
Заполните первые 2 столбца (A и E) всеми комбинациями значений переменных. Запишите в качестве заголовков столбцов все операции в выражении в том порядке, в котором они выполняются (по приоритету и в круглых скобках). Вычислите значения этих операций: сначала выражения в скобках, затем результат их сложения.
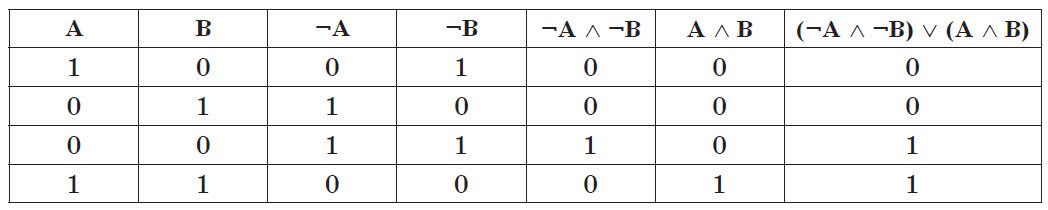
Последний столбец содержит значение результата выражения. Она совпадает с таблицей истинности для операции эквивалентности. Таким образом, эти выражения эквивалентны.
Основные законы булевой алгебры
Для сложных логических выражений с большим количеством переменных определение их истинностных значений путем построения таблиц истинности становится громоздким. В таких случаях используются методы упрощения выражений. Под упрощением мы понимаем эквивалентное преобразование выражения к его нормальной форме.
Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойного отрицания.
Эквивалентные преобразования, иначе известные как базовые преобразования, служат для упрощения Законы булевой алгебры.
Идентичные преобразования логических выражений
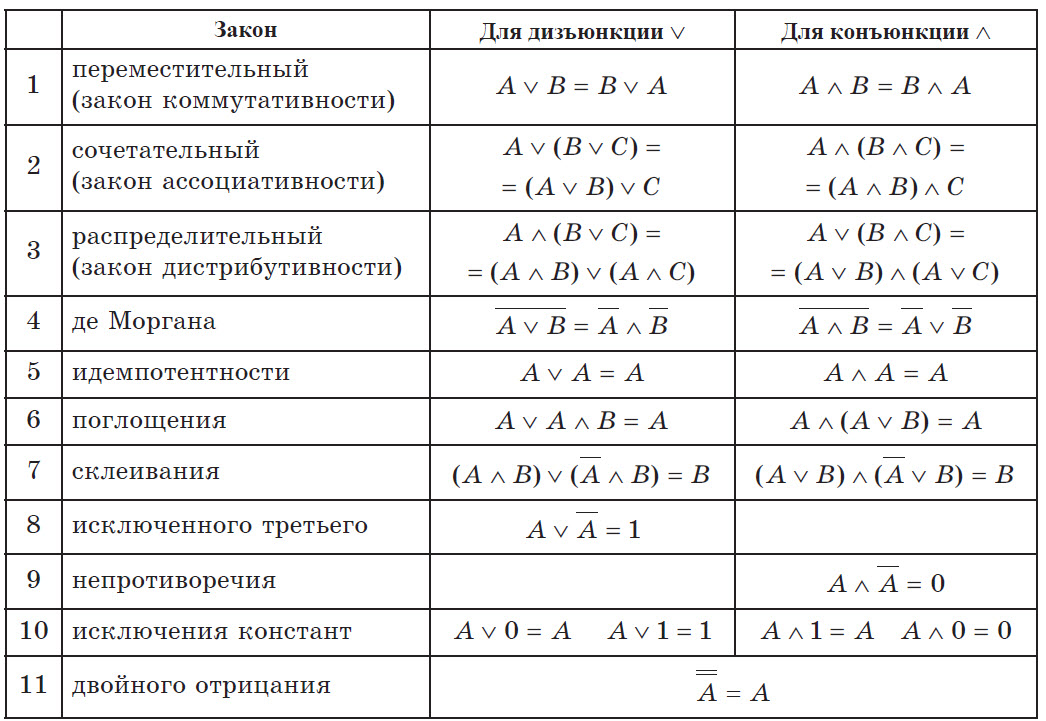
Для всех одинаковых преобразований Закон двойственностиЕсли мы преобразуем конъюнкцию в дизъюнкцию, дизъюнкцию в конъюнкцию, 1 в 0, 0 в 1, то закон, данный для конъюнкции, будет таким же и для дизъюнкции, и наоборот.
Прежде всего, при выполнении преобразований равенства избавьтесь от отрицания, а затем от логических операций исключительной дизъюнкции, наследования и эквивалентности. Затем используйте законы булевой алгебры, чтобы уменьшить количество переменных в выражении.
Пример 4
Выберите выражение, которое эквивалентно выражению (A ∧ B) v (Ā ∧ B).
1) A 2) A ∧ B 3) Ā ∧ B 4) B
Решение. По закону конкатенации (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение эквивалентно B.
Ответ: 4) B.
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Выражения, которые принимают логические значения (true или false) в результате операций сравнения (больше >, меньше <, больше или равно ≥, меньше или равно ≤, равно =, не равно ≠), также являются логическими выражениями. Помимо сравнения и логических операций, такие выражения могут содержать алгебраические функции и операции. Приоритет этих операций следующий:
- Вычисление значений функций.
- Выполнение алгебраических операций (сначала экспоненция, затем умножение и деление, затем вычитание и сложение).
- Выполнение операций сравнения (в порядке нотации).
- Логические операции (сначала операции отрицания, затем операции логического умножения, затем операции логического сложения, затем операции импликации и эквивалентности).
Если в логическом выражении используются круглые скобки, то сначала выполняются операции, содержащиеся в них.
Пример 5
Для какого из следующих значений M верно следующее выражение?
¬M ≥ 10 ∧ M > 3
1) 1 2) 2 3) 3 4) 4
Решение. В соответствии с приоритетом операций, сначала должны выполняться операции сравнения, затем отрицания, а затем конъюнкции. Отрицанием высказывания M ≥ 10 является высказывание M < 10. Получаем выражение M < 10 ∧ M > 3. Чтобы это выражение (конъюнкция) было истинным, оба неравенства должны быть выполнены (т.е. быть истинными). Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений только одно удовлетворяет этому условию – число 4.
Ответ: 4) 4.
Задачи, аналогичные предыдущему примеру, также можно решать с помощью таблиц истинности.
Пример 6.
Для какого из следующих значений M верно следующее выражение?
¬M ≥ 10 ∧ M > 3
1) 1 2) 2 3) 3 4) 4
Решение. Составьте таблицу истинности: все операции выражения приведены в столбцах таблицы, а все предполагаемые значения M – в строках таблицы. Рассчитайте значения таблицы:
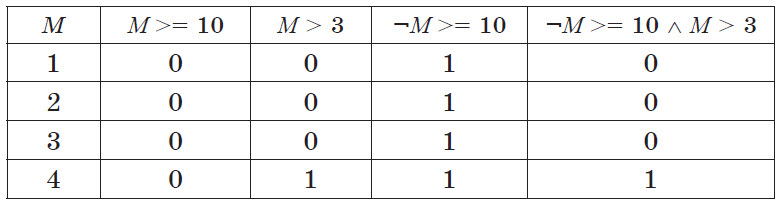
Последний столбец содержит результат всего выражения. Это будет верно только для значения M, равного 4.
Ответ: 4) 4.
Пример 7.
В таблице показаны ежемесячные продажи групп товаров за период в шесть месяцев. Сколько товарных групп показали рост продаж в весенние месяцы или достигли более 80% в июне?
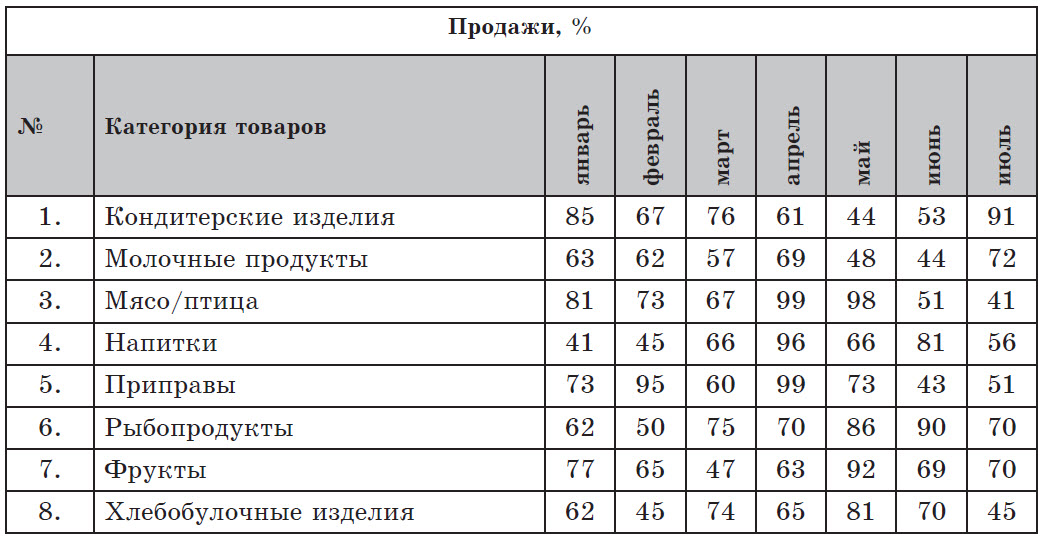
Решение. Переформулируем условие задачи: найти такие товарные группы, для которых (март < апрель) ∧ (апрель < май) v (июнь > 80).
Введем обозначения:
A = (март < апрель).
B = (апрель < май)
C = (июнь > 80)
Тогда выражение можно записать как A ∧ B v C.
Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только в том случае, если оба простых выражения, входящих в него ((март < апрель) и (апрель < май)), истинны. Значение выражения дизъюнкции будет истинным, если хотя бы одно из составляющих его простых предложений истинно.
Составьте таблицу истинности для исходных данных.
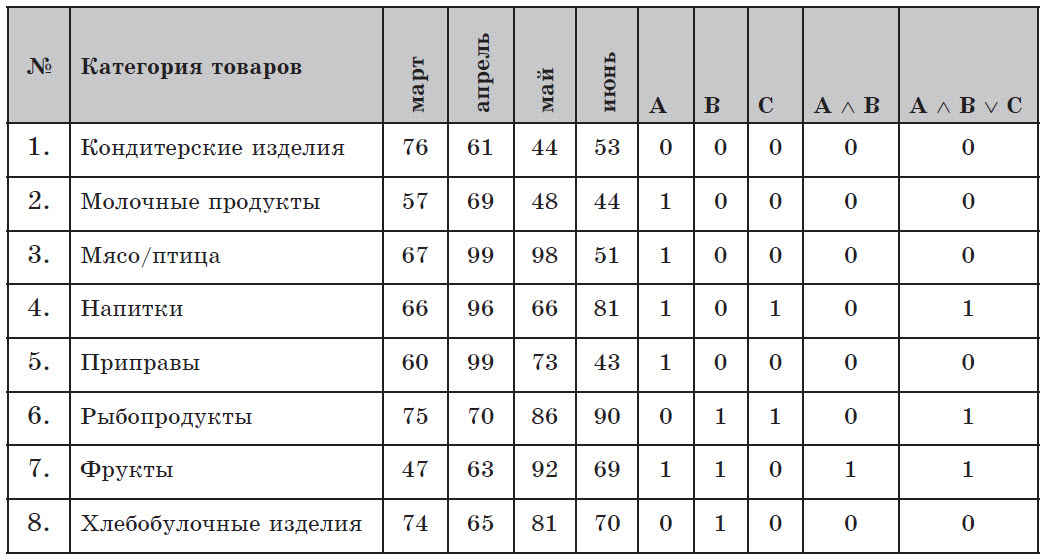
Есть 3 записи, удовлетворяющие логическому выражению – 4, 6 и 7.
Ответ: 3.
Конспект урока по информатике “Логические значения, операции, выражения”.
Читайте далее: