В повседневной жизни мы часто слышим и используем термины “логично”, “хорошо развитое логическое мышление”, “логически”. Так что же такое “логическое мышление”? Термин “логика” происходит от древнегреческого logos – “слово, мысль, понятие, рассуждение, закон”. Логика – одна из дисциплин, формирующих математическую основу информатики. Логика – это наука о законах и формах мышления. Поскольку это знание вытекает из разума, логику также называют наукой о правильном мышлении.
Логика в компьютерных науках
В повседневной жизни мы часто слышим и используем термины “логично”, “развитое логическое мышление”, “логически”. Что именно является “логическим мышлением”? Термин “логика” происходит от древнегреческого logos – “слово, мысль, понятие, рассуждение, закон”. Логика – одна из дисциплин, формирующих математическую основу информатики. Логика – это наука о законах и формах мышления. Поскольку эти знания вытекают из разума, логику также называют наукой о правильном мышлении.
Логика как наука возникла в 4 веке до нашей эры. Аристотель считается основателем логики. . Он систематизировал имеющиеся знания по логике, обосновал формы и правила логического мышления. Аристотель сформулировал законы формальной логики, согласно которым можно определить истинность высказываний. В 19 веке английский математик Джордж Буль основал новую ветвь математики – алгебру логики. Булева алгебра (или булева алгебра) оперирует логическими величинами, которые могут принимать только два значения: true или false.
Концепции логики используются в компьютерных науках. Здесь используются логические схемы – устройства, преобразующие двоичные сигналы. Анализ и проектирование логических схем основаны на законах булевой алгебры.
Каждый язык программирования содержит логические переменные и инструменты для описания и вычисления логических выражений.
Логические методы также используются при работе с базами данных.
В школьном курсе информатики в восьмом классе на раздел “Логика” отводится всего 4 часа. Практика показывает, что дети плохо усваивают эти темы. Поэтому целесообразно изучать этот раздел информатики в начале 9 класса. Детей знакомят с такими базовыми понятиями:
Что такое логическая переменная? Логическая переменная имеет имя и значение 0 или 1 (true или false). Несколько переменных, связанных друг с другом логическими операциями, называются логическая функция . Существует три основных логических операции: конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и инверсия (отрицание). Если составное высказывание (логическую функцию) выразить в виде формулы, то получится логическое выражение. Значение логического выражения также может быть истинным (1) или ложным (0).
Это очень важная тема для студентов GCSE, и логические задачи в A2 требуют, чтобы вы увидели, какое утверждение ложно, а какое истинно. В задании A12 рассматриваются основные логические операции. Задание A18 – одно из заданий повышенной сложности, практика показывает, что процент выполнения этого задания в IO не высок. Это задание предполагает знание логических операций и их специфики.
В настоящее время на вступительных экзаменах по информатике (ГИА и ЕГЭ) встречается много заданий из “Булевой алгебры”. А целью учителя должно стать закрепление умения решать задания ЕГЭ и ГИА по информатике с использованием элементов булевой алгебры.
5) ¬B = false = true; ¬truth = false;
Булевы выражения
Булева алгебра (англ. алгебра логики) – одна из основных ветвей математической логики, использующая методы алгебры в логических преобразованиях.
Основателем алгебраической логики является английский математик и логик Дж. Буль (1815-1864), который основывал свое логическое учение на аналогии между алгеброй и логикой. Он записывал любую теорему с помощью символов разработанного им языка и получал “уравнения”, истинность или ложность которых можно было доказать на основе определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и т.д.
Современный алгебра логики является ветвью математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истинно, ложно). Утверждения могут быть истинными, ложными или содержать истину и ложь в разных пропорциях.
Логическое утверждение – это любое повествовательное предложение, для которого мы можем однозначно утверждать, что его содержание истинно или ложно.
Например, “3 умножить на 3 равно 9”, “Архангельск находится севернее Вологды” являются истинными высказываниями, а “Пять меньше трех”, “Марс – звезда” – ложными.
Конечно, не каждое тезисное утверждение может быть логическим утверждением, потому что не всегда можно сказать, что оно ложно или истинно. Например, утверждение “Информатика – интересный предмет” является расплывчатым и требует дополнительной информации, а утверждение “Информатика – интересный предмет для ученика 10 класса, А.А. Иванов” может иметь значение “истинный” или “ложный”, в зависимости от интересов Иванова.
В дополнение к двумерная алгебра теоремгде принимаются только два значения – “истинно” и “ложно”, существует многозначная алгебра высказываний. В такой алгебре, помимо “истинно” и “ложно”, используются такие истинностные значения, как “вероятно”, “возможно”, “невозможно” и т.д.
В алгебре логики мы проводим различие между простой (элементарно) заявленияобозначаемые латинскими буквами (A, B, C, D, …), и комплекс составные (сложные) предложения, которые состоят из нескольких простых предложений с использованием логических соединителей, напр. “Не”, “и”, “или”, “тогда и только тогда”, “если .. Истинность или ложность таких составных высказываний определяется значением простых высказываний.
Обозначим через А утверждение “Алгебра логики успешно используется в теории электрических цепей”, и по В – “Применение алгебры логики в синтезе релейно-контактных схем”.
Тогда составное утверждение “Булева алгебра успешно применяется в теории электрических цепей и при синтезе лестничных и контакторных схем” можно записать как A и B; здесь “и” – это логическая связка. Очевидно, что поскольку элементарные утверждения A и B истинны, то составное высказывание A и B.
Каждая логическая связка рассматривается как операция над логическими выражениями и имеет собственное имя и обозначение.
Есть только два логических значения: True (TRUE) и false (ЛОЖЬ).. Это соответствует числовому представлению – 1 и 0. Результаты каждой логической операции можно хранить в таблице. Такие таблицы называются таблицами истинности.
Основные операции булевой алгебры
1 Логическое отрицание, инверсия (лат. инверсия – это логическая операция, в результате которой из данного высказывания (например, A) мы получаем новое высказывание (не A), который называется отрицание первоначального утвержденияСимволически это обозначается чертой сверху ($A<->$) или условными обозначениями, например. ¬, “неи гласит: “не A”, “A ложно”, “ложно, что A”, “отрицание A”.. Например: “Марс – это планета в Солнечной системе”. (утверждение А); “Марс не является планетой Солнечной системы”. ($A<->$); утверждение “10 – простое число” (утверждение B) ложно; утверждение “10 не является простым числом” (утверждение B ) истинно.
Операция, применяемая к одной величине, называется унарный. Массив значений данной операции выглядит следующим образом
| A | ¬A |
| правда | ложный |
| ложный | правда |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A<->$ ложно, когда A истинно, и истинно, когда A ложно.
Геометрически отрицание можно представить следующим образом: если A – это некоторое множество точек, то $A<->$ – это дополнение множества A, то есть все точки, которые не принадлежат множеству A.
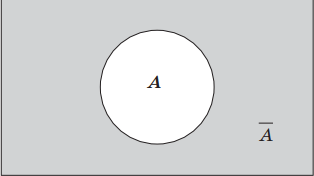
2. Конъюнктура (лат. conjunctio – конъюнкция) – это логическое умножение, операция, требующая по крайней мере двух логических значений (операндов) и объединяющая два или более высказываний путем “и” (например, “А и Б”), которую мы символически обозначим через ∧ (A ∧ B) и прочитаем: “А и Б”. Следующие символы также используются для обозначения конъюнкции: A ∙ B; A & B, A и BИногда между высказываниями нет знака: AB. Пример логической связки: “Этот треугольник равнобедренный и прямоугольный”. Высказывание может быть истинным только при выполнении обоих условий, в противном случае высказывание ложно.
Таблица истинности для этой операции
| A | B | A ∧ B |
| правда | ложный | ложь |
| ложь | правда | ложь |
| ложь | ложь | ложь |
| правда | правда | правда |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Предложение А ∧ В истинно только в том случае, если оба утверждения А и В оба верны.
Геометрически конъюнкция может быть представлена следующим образом: если A, B А ∧ В является пересечением множеств А и В.
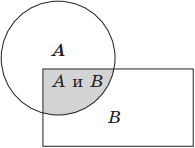
3. Дисъюнкция (лат. дизъюнкция – деление) – это логическое сложение, операция, которая соединяет два или более высказываний посредством “или” (например, “А или Б”), который символически обозначается ∨. (А ∨ В) и гласит: “А или Б”.. Следующие символы также используются для обозначения дизъюнкции: A + B; A или B; A | B. Пример логического сложения: “Число x делится на 3 или на 5”. Это утверждение будет истинным, если выполнены оба или хотя бы одно из условий.
Таблица истинности этой операции выглядит следующим образом
| A | B | A ∨ B |
| правда | ложный | правда |
| ложь | правда | правда |
| ложь | ложь | ложь |
| правда | правда | правда |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Заявление А ∨ В ложно только в том случае, если оба утверждения А и В оба ложны.
Геометрически логическое сложение можно представить следующим образом: если A, B А ∨ В – является объединением множеств А и Вт.е. фигура, сочетающая в себе и квадрат, и круг.
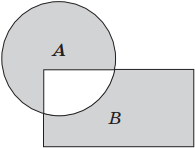
4. Строго разделимая дизъюнкция, по модулю два дополнения – это логическая операция, которая объединяет два выражения, используя “или”используется в исключительном смысле, символически обозначается ∨ ∨ или ⊕ (А ∨ ∨ B, A ⊕ В) и читайте: “либо А, либо Б”.. Примером сложения по модулю два является утверждение “Этот треугольник раздвоенный или остроугольный”. Утверждение истинно, если выполняется одно из условий.
Таблица истинности этой операции выглядит следующим образом
| А | В | А ⊕ B |
| правда | ложный | правда |
| ложь | правда | правда |
| ложь | ложь | ложь |
| правда | правда | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Утверждение A ⊕ B истинно только в том случае, если утверждения A и B имеют разные значения.
5. Импликация (лат. implisito – (лат. implisito) – это логическая операция, соединяющая два высказывания с помощью связки “если. то” в составное предложение, которое символически обозначается → (А → В) и гласит: “если А, то В”, “А влечет за собой В”, “из А следует В”, “А подразумевает В”.. Для обозначения импликации также используется символ ⊃ (A ⊃ B). Примером импликации является: “Если полученный четырехугольник является квадратом, то вокруг него можно нарисовать круг”. Эта операция объединяет два простых логических выражения, первое из которых является условием, а второе – следствием. Результат операции ложен только в том случае, если посылка истинна, а следствие ложно. Например, “Если 3 * 3 = 9 (A), то Солнце – планета (B)”, результат импликации A → B является ложным.
Таблица истинности для этой операции
| А | В | А → В |
| правда | ложь | ложь |
| ложь | правда | правда |
| ложь | ложь | правда |
| правда | правда | правда |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации верно, что из лжи может следовать что угодно, но из истины может следовать только истина.
6. Эквивалентность, двойная импликация, эквивалентность (лат. aequalis – равный и валентис – действительный) – это логическая операция, которая позволяет вывести два утверждения А и В для получения новой выписки A ≡ B, который гласит следующее: “A эквивалентно B”.. Для обозначения эквивалентности также используются следующие знаки: ⇔, ∼. Эта операция может быть выражена конъюнкцией “тогда и только тогда”, “необходимый и достаточный”, “эквивалентный” .. Примером эквивалентности является утверждение: “Треугольник является правильным тогда и только тогда, когда один из его углов равен 90 градусам.
Таблица законов эквивалентности выглядит следующим образом
| А | В | А ∼ В |
| правда | ложь | ложь |
| ложь | правда | ложь |
| ложь | ложь | правда |
| правда | правда | правда |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат “истина” тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, мы можем использовать таблицы истинности для определения значений сложных высказываний. Важно знать, что для представления любой функции в булевой алгебре достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | A ⊕ B | $(A <->∧B) ∧ (A ∧ B<->)$ |
| Импликация | A → B | $A <->∨ B$ |
| Эквивалентность | A ∼ B | $(A <->∧ B<->) ∨ (A ∧ B)$ |
Приоритет логических операций следующий: отрицание (“нет”) имеет наивысший приоритет, за ним следует конъюнкция (“и”), после конъюнкции – дизъюнкция (“или”).
С помощью логических переменных и логических операций любое логическое высказывание может быть формализовано, то есть заменено логической формулой. Таким образом, элементарные высказывания, составляющие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определить истинность или ложность составного высказывания. Например, утверждение “Если пять больше двух (А), то вторник всегда следует за понедельником (В)” является импликацией А → Ви результатом операции в данном случае будет ‘true’. В логических операциях смысл высказываний не рассматривается, только их истинность или ложность.
Рассмотрим, например, построение высказывания, состоящего из утверждений А и Вкоторое будет ложным тогда и только тогда, когда оба утверждения истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А утверждение может быть, например, таким: “Этот шар полностью красный или полностью синий”. Следовательно, если утверждение А “Этот шар полностью красный” – истинно, а утверждение В “Этот шар полностью синий” истинно, тогда составное высказывание ложно, потому что шар не может быть одновременно красным и синим.
Примеры решений
Пример 1. Найдите для заданных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Порядок операций следующий: сначала выполняется операция парентетического сравнения, затем операция дизъюнкции и, наконец, операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации такова
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
((1 > 3) ∨ (1 < 3)) → (1 < 4) = false ∨ true → true
((12 > 3) ∨ (12 < 3) → (12 < 4) = true ∨ false → true → false = false;
((3 > 3) ∨ (3 < 3)) → (3<4) = false ∨ false → true → false = true.
Пример 2. Найдите множество целых значений X, для которых верно выражение ¬((X > 2) → (X > 5)).
Решение. Операция отрицания применяется ко всему выражению ((X > 2) → (X > 5)) Таким образом, когда ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) → (X > 5)) ложно. Поэтому мы должны определить, для каких значений X выражение ((X > 2) → (X > 5)) является ложным. Операция импликации принимает значение “false” только в одном случае: когда за истиной следует ложь. И это верно только для X = 3; X = 4; X = 5.
Пример 3. Для какого из приведенных слов утверждение ¬(гласная первая буква ∧ гласная третья буква) ⇔ строка из 4 символов является ложным? 1) assa; 2) cucu; 3) corn; 4) error; 5) strongman.
Решение. Рассмотрите все предложенные слова по очереди:
1) для слова assa мы получаем: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 – высказывание истинно;
2) для слова кукушка мы получаем: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 – утверждение истинно;
3) для слова кукуруза мы получаем: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 – утверждение ложно;
4) для слова ошибка получаем ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 – утверждение истинно;
5) для слова strongman получаем: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 – утверждение ложно.
Логические выражения и их преобразования
На сайте логическое выражение это обозначение, которое может принимать логическое значение ‘true’ или ‘false’. В этом определении необходимо провести различие между логическими выражениями:
- выражения, которые используют операции сравнения (“больше”, “меньше”, “равно”, “не равно” и т.д.) и принимают логические значения (например, выражение a > b , где a = 5 и b = 7, равно значению “false”);
- прямые логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ B ∧ C, где A = true, B = false и C = true).
Булевы выражения могут содержать функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения операций следующий:
- вычисление существующих функциональных связей;
- выполнение алгебраических операций (сначала умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в любом порядке);
- Выполнение логических операций (сначала операции отрицания, затем логическое умножение, логическое сложение, а затем операции импликации и эквивалентности).
Круглые скобки можно использовать в логическом выражении, чтобы изменить порядок выполнения операций.
Пример. Найдите значение этого выражения:
$1 ≤ a ∨ A ∨ sin(π/a – π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для a = 2, b = 3, A = true, B = false.
Решение. Порядок подсчета значений следующий:
1) b a + a b > a + b, после подстановки получаем: 3 2 + 2 3 > 2 + 3, т.е. 17 > 2 + 3 = верно;
2) A ∧ B = true ∧ false = false.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = true ∨ false = true;
3) 1≤ a = 1 ≤ 2 = верно;
4) sin(π/a – π/b) < 1 = sin(π/2 – π/3) < 1 = верно.
После этих вычислений мы получаем: true ∨ A ∧ true ∧ ¬B ∧ ∧ true.
Теперь выполните операции отрицания, а затем логического умножения и сложения:
5) ¬B = ¬false = true; ¬truth = false;
6) A ∧ true ∧ true ∧ false ∧ false = true ∧ true ∧ true ∧ true ∧ false = false;
7) true ∨ false = true.
Таким образом, результатом булева выражения с заданными значениями является “true”.
Примечание. Учитывая, что выходное выражение в итоге является суммой двух слагаемых, а значение одного из них 1 ≤ a = 1 ≤ 2 = true, без дальнейших вычислений можно сказать, что результат для всего выражения также “true”.
Идентичные преобразования логических выражений
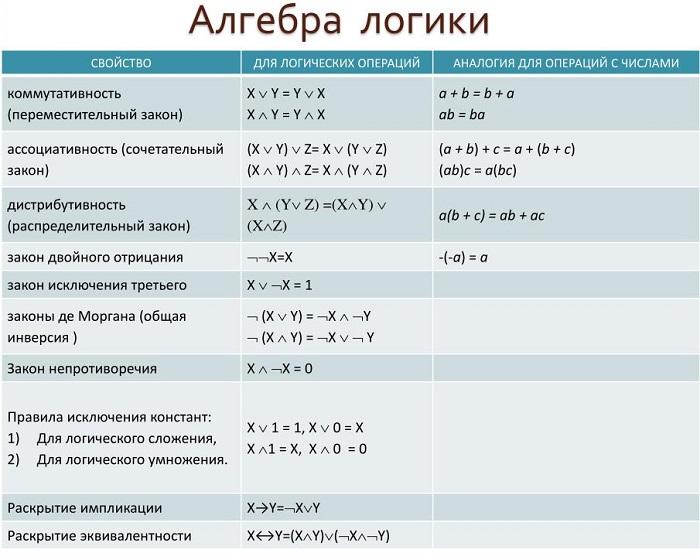
В алгебре логики выполняются основные законы, допускающие тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| пермутативный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Комбинаторика | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | $<->$ = $A <->∧ B<->$ | $<->$ = $A <->∨ B<->$ |
| Идемпотентность | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Связывание | (A ∧ B) ∨ (A <->∧ B) = B | (A ∨ B) ∧ (A <->∨ B) = B |
| Переменный режим работы с его реверсированием | $A ∨ A<->$ = 1 | $A ∧ A<->$ = 0 |
| Операции с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойное отрицание | $A<=>$ = A | |
Доказательства этих теорем проводятся путем построения таблиц истинности для соответствующих записей.
Эквивалентные преобразования логических формул имеют ту же цель, что и преобразования формул в обычной алгебре. Они используются для упрощения формул или приведения их к определенной форме с помощью основных законов булевой алгебры. На сайте упрощение формулыкоторая не содержит операций импликации и эквивалентности, является эквивалентным преобразованием, приводящим к формуле, которая содержит либо меньше операций по сравнению с исходной формулой, либо меньше переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование перестановок и законов комбинаторики и т.д.), другие основаны на свойствах, которыми не обладают операции в обычной алгебре (использование закона делимости для конъюнкции, закона поглощения, склеивания, де Моргана и т.д.).
Рассмотрим в качестве примеров некоторые приемы и методы, используемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Здесь для преобразований можно использовать закон идемпотентности, закон делимости, операцию переменной с инверсией и операцию константы.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для простоты используется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
Преобразования используют правило Де Моргана, операцию над переменной с ее инверсией, операцию над константой
Примеры решений
Пример 1. Найдите логическое выражение, которое равно A ∧ ¬(¬B ∨ C) .
Решение. Примените правило де Моргана для B и C: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равное исходному выражению: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Пример 2. Напишите значения логических переменных A, B, C, для которых логическое выражение (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации является ложной только в том случае, если истинная посылка ложна. Следовательно, для данного выражения посылка A ∨ B должна быть истинной, а следствие, то есть выражение B ∨ ¬C ∨ B, должно быть ложным.
1) A ∨ B – результат дизъюнкции является “истинным”, если хотя бы один из операндов является “истинным”;
2) B ∨ ¬C ∨ B – выражение ложно, если все слагаемые ложны, т.е. B – ‘false’; ¬C – ‘false’, и поэтому переменная C имеет значение ‘true’;
3) если мы рассмотрим посылку и обнаружим, что B “ложно”, то получим, что значение A “истинно”.
Ответ: A – истинно, B – ложно, C – истинно.
Пример 3. Каково наибольшее целое число X, при котором теорема (35
0
3 | Формальная и неформальная логика
Первоначальное деление логики таково формальные и неформальные.. Формальная логика отличается от неформальной тем, что она записывается в виде уравнений. Неформальная логика записывается в выражениях в форме языка, поэтому она подходит для риторики, в то время как формальная логика подходит для абстрактных наук.
Формальная логика в равной степени делится на дедуктивные и индуктивные.. Они отличаются тем, что в дедуктивной аргументации истинность условий гарантирует истинность умозаключения или заключения. В индуктивном рассуждении, если условия истинны, то ложный и истинный вывод одинаково возможны.
Законы формальной логики таковы:
1. закон одинаковости (A = A): не допускается двусмысленность или расплывчатость. Не допускается подмена одного понятия другим.
2. закон непротиворечия (A ∧ ¬A = 0): одно и то же утверждение не может быть истинным и ложным одновременно.
3. закон исключения третьего или бивалентность (A ∨ ¬A = 1): высказывание может быть либо истинным, либо ложным – третьего не дано.
Принципы формальной логики:
1. принцип достаточного обоснования: достаточными являются те фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.
Язык запросов SQL для реляционных баз данных состоит из операторов для определения, запроса и обработки информации в базах данных. Операторы поиска информации содержат логические условия поиска, которые могут быть простыми и сложными.
Логика и логическое программирование
‘Логическое программирование – Парадигма программирования, основанная на автоматическом доказательстве утверждений с использованием механизмов логического вывода на основе заданных фактов и правил вывода. Язык Пролог и логическое программирование и широко используются для создания баз знаний и экспертных систем и исследований в области искусственного интеллекта, основанных на логических моделях баз знаний и логических процедурах вывода и принятия решений.
Язык и система логического программирования Prolog основана на языке исчисления предикатов, который является подмножеством логики первого порядка. Основой языка Prolog являются понятия фактов и правил логического вывода, а также запросы для поиска и извлечения информации в базах знаний.
Процедуры логических выводов и принятия решенийПроцедуры, которые система логического программирования Prolog использует для того, чтобы делать логические умозаключения и давать осмысленные ответы. Факты в Prolog описываются логическими предикатами с определенными значениями. Правила в Prolog записываются в виде правил логического вывода с логическими умозаключениями и списком логических условий.
Обратите внимание, что эта операция является ложной только в том случае, если из первого ложного утверждения следует ложный результат. На компьютерном языке этот процесс определяется формулой: if. then.
Логические выражения
В информатике существует два типа утверждений: простые и сложные.
Простой – Простое утверждение – это утверждение, которое обычно дается в форме предложения, и вы можете сказать, истинно оно или ложно.
Нью-Йорк является столицей США (ложно);
В России 1117 городов (правда).
Комплекс Сложное высказывание относится к набору простых высказываний, которые связаны между собой логическими процессами.
Идет дождь, а у меня нет зонтика.
В разговорной речи используются логические союзы “не”, “и”, “или”, “если… то”, “тогда и только тогда” и т.д. Эта фраза называется составной фразой. Высказывания, образованные из других высказываний, называются составными высказываниями. Высказывание, любая часть которого не является высказыванием, называется элементарным высказыванием. Например, из двух простых утверждений (какие?) можно составить следующее составное утверждение: “Алгебра логики является основой для построения логических схем компьютера и служит математическим фундаментом для решения сложных логических задач”. Истинность или ложность составных высказываний зависит от истинности или ложности образуемых ими высказываний и от определенного обращения с конъюнкциями (логическими операциями над высказываниями).
Урок 11: Алгебра логики. Таблицы истинности
Список тем, рассматриваемых в теме: теорема, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквивалентность), логические выражения, предикаты и их истинностные множества, таблицы истинности и их анализ.
Глоссарий по теме: импликация, эквивалентность, предикат, примеры законов алгебры логики.
Основная литература по теме урока:
Л. Л. Босова, А. Босова. Компьютерные науки. Базовый уровень: Учебник для 10 класса
– М.: БИНОМ. Лаборатория знаний, 2017 (с. 174-197).
Открытые электронные ресурсы по теме:
Теоретический материал для самостоятельного изучения:
Алгебра логики – Раздел математики, занимающийся изучением утверждений, рассматриваемых с точки зрения их логических значений (истинно или ложно) и логических операций над ними.
Алгебра логики появилась в середине 19 века в трудах английского математика Джорджа Буля. Его истоком была попытка решить традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил булеву алгебру для описания работы релейных схем и схем электронных ламп. Логическое утверждение – это повествовательное предложение, о котором можно однозначно сказать, что оно истинно или ложно.
Например, предложение “Джордж Буль – основатель алгебраической логики” является истинным, а “Солнце – спутник Земли” – ложным.
Обычные логические союзы, используемые в речи “не”, “и”, “или”, “если … тогда”, “тогда и только тогда” и т.д. позволяют строить новые утверждения на основе уже заданных данных. Высказывания, образованные из других высказываний, называются составными высказываниями. Высказывание, любая часть которого не является высказыванием, называется элементарным высказыванием. Например, из двух простых утверждений (какие?) можно получить следующее составное утверждение: “Алгебра логики является основой для построения логических схем компьютеров и служит математической базой для решения сложных логических задач”. Истинность или ложность составных высказываний зависит от истинности или ложности составляющих их высказываний и от определенного обращения с коннективами (логическими операциями над высказываниями).
Обоснование истинности или ложности элементарных теорем не является задачей логической алгебры. Этими вопросами занимаются науки, которые имеют дело с элементарными теоремами. Такое сужение круга интересов позволяет нам маркировать утверждения символическими именами (например, A, B, C).
Логическая переменная – это переменная, которая обозначает любое утверждение и может принимать логические значения “true” или “false”. Для логических значений типа true-false можно использовать следующие обозначения: И – Л, истинно – ложно, да – нет, 1 – 0.
Логическая операция может быть полностью описана с помощью таблица истинностикоторый указывает, какие значения принимает составное высказывание при всех возможных значениях составляющих его элементарных высказываний.
В булевой алгебре существует шесть логических операций. Из курса информатики 8-9 класса вы знаете три из них:
– Отрицание (инверсия, логическое НЕ).
Новое утверждение присваивается тому утверждению, значение которого противоположно исходному значению.
– Конъюнкция (логическое умножение, логическое И).
Высказывание истинно тогда и только тогда, когда оба исходных высказывания истинны.
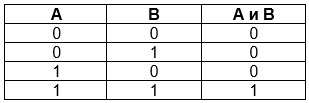
– Дисъюнкция (логическое сложение, логическое ИЛИ).
Высказывание ложно тогда и только тогда, когда оба исходных высказывания ложны.
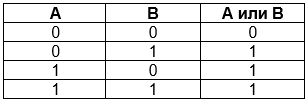
Рассмотрим новые логические операции.
– Логическая операция сопоставления двух высказываний с новым высказыванием, которое ложно тогда и только тогда, когда первое высказывание (посылка) истинно, а второе высказывание (следствие) ложно, называется импликацией (от лат. implicatio – опутывание, тесная связь) или логическим следствием.
Операция импликации обозначается символом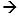 
и определяется следующей таблицей истинности:
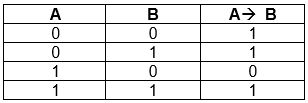
В повседневной речи импликация соответствует предложениям, содержащим связку “если…, то”. Обычно мы используем эту связку, когда хотим показать зависимость одного события от другого.
Импликацию можно заменить выражением, используя ранее изученные операции NOT и OR: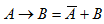 
– Логическая операция, которая сопоставляет два высказывания с новым высказыванием, которое истинно тогда и только тогда, когда истинно только одно из двух высказываний, называется строгой (эксклюзивной) дизъюнкцией.
Строгая дизъюнкция обозначается символом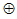
и определяется следующей таблицей истинности:
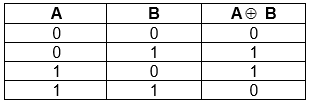
В русском языке строгая дизъюнкция соответствует связке “или”. Например, в пословице “Или получишь, или потеряешь” оба условия не могут быть выполнены одновременно. В отличие от обычной дизъюнкции, в высказывании, содержащем строгую дизъюнкцию, мы гарантируем, что произойдет только одно событие.
Строгая дизъюнкция может быть представлена с помощью следующих базовых операций:
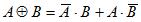
Для доказательства равенства достаточно для всех возможных комбинаций вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения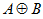 
для одних и тех же исходных данных.
– Логическая операция, которая сопоставляет два высказывания с новым высказыванием, которое истинно, если оба исходных высказывания истинны, или оба исходных высказывания ложны, называется эквивалентностью или равносильностью.
В логике эквивалентность обозначается символом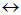 
и определяется следующей таблицей истинности:
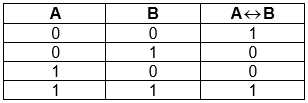
В разговорной речи эквивалентность соответствует “тогда и только тогда”, а в математике – “необходимо и достаточно”.
Если мы внимательно посмотрим на таблицы истинности для двух последних логических операций, то увидим, что эквивалентность является обратной операцией исключающего ИЛИ, т.е.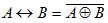 
Можно заменить эквивалентность выражением, которое содержит только основные логические операции: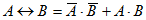 
Сложное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и круглых скобок.
Это верно для логического выражения:
- каждая логическая переменная, а также логические константы (0,1) являются логическими выражениями;
- Если
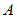– является логическим выражением, тогда 
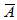– является логическим выражением; - если A и B – являются выражениями, то соединенные любой бинарной операцией, они также являются логическими выражениями.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
- отрицание;
- соединение;
- дизъюнкция; строгая дизъюнкция;
- Импликация; эквивалентность.
Операции с одинаковым приоритетом выполняются в порядке слева направо. Как и в математике, круглые скобки изменяют порядок выполнения операций.
Читайте далее: