Механические колебания и волны; FIZI4KA - услуги электромонтажа, строительства и ремонта

свободная вибрация – Колебание, которое совершает тело под действием внутренних сил системы, вызванное начальным запасом энергии после того, как оно было выведено из положения устойчивого равновесия.

Содержание

Механические колебания и волны

Механические колебания – Периодическое смещение материальной точки при ее движении по определенной траектории попеременно в двух противоположных направлениях относительно устойчивого положения равновесия.

Отличительными характеристиками колебательного движения являются

Повторение движений;
Взаимность движения.

Для существования механических колебаний необходимо:

наличие возвращающей силы – силы, которая стремится вернуть тело в положение равновесия (при небольших смещениях от положения равновесия);
Наличие небольшого количества трения в системе.

Механические волны – это процесс распространения колебаний в упругой среде.

Типы волн

Поперечный – это волна, в которой частицы среды колеблются перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны создаются слоями среды, движущимися относительно друг друга, поэтому они распространяются в твердых телах.

Продольный – это волна, в которой частицы среды совершают колебания в направлении распространения волны.

Продольная волна представляет собой чередование областей сгущения и расширения.
Продольные волны возникают при сжатии и расширении среды, поэтому они могут возникать в жидкостях, твердых телах и газах.

Важно!
Механические волны не переносят материю в среде. Они несут энергию, которая представляет собой сумму кинетической энергии молекул среды и потенциальной энергии ее упругих деформаций.

1. Найдите массу заряда, который совершает 20 колебаний за 16 с на пружине с жесткостью 250 Н/м.

Урок 1: Механические колебания

Механические колебания – это физические процессы, которые повторяются точно или приблизительно через равные промежутки времени.

Колебания, возникающие под действием внутренних сил в колебательной системе, называются свободными колебаниями.

Вынужденная вибрация – это вибрация, возникающая под действием внешней, периодически изменяющейся силы.

Амплитуда – это максимальное смещение колеблющейся величины из положения равновесия.

Период – это длительность одного полного колебания.

Частота – это количество колебаний в единицу времени.

Фаза колебания – это физическая величина, которая описывает отклонение колеблющейся величины от положения равновесия в данный момент времени.

Резонанс – это явление быстрого увеличения амплитуды вынужденного колебания, когда частота изменения внешней силы, действующей на систему, совпадает с частотой свободных колебаний.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика, 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017 – С. 53 – 73.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. – Москва: Дрофа, 2009 – С. 59 – 61.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. Москва, Просвещение 1999.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. Москва, Просвещение, 2004.

Основное содержание урока

Мир удивителен и разнообразен. Каждый день мы наблюдаем различные движения тел. Мы все видели, как ветка качается на ветру, лодка на волнах, качели, деревья на ветру. Чем эти движения отличаются от движения тележки, движущейся по прямой? Мы видим, что, в отличие от движения тележки, движущейся по прямой, движение всех этих тел повторяется через некоторое время.

Колебания играют огромную роль в нашей жизни. Примерами вибраций в нашем теле являются биение сердца и движение голосовых связок. Колебания также происходят в жизни нашей планеты (приливы, ветры, землетрясения) и в астрономических явлениях (пульсация звезд). Одним из самых удивительных природных явлений являются землетрясения – сотрясения земной поверхности. Строители рассчитывают устойчивость возводимых ими сооружений во время землетрясения.

Без знания законов колебаний невозможно было бы создать телевидение, радио и многие современные приборы и машины. Неучтенные вибрации могут привести к разрушению сложных технических конструкций и вызвать серьезные заболевания у людей. Все это делает необходимым их всестороннее изучение.

Основной характеристикой колебательного движения является его периодичность. За одно колебание колеблющееся тело дважды проходит через положение равновесия. Колебание характеризуется периодом, частотой, амплитудой и фазой.

Амплитуда – это наибольшее смещение величины, колеблющейся от положения равновесия.

Для малых амплитуд расстояние, проходимое телом за одно полное колебание, составляет около четырех амплитуд.

Интервал, в течение которого тело совершает одно полное колебание, называется периодом колебаний.

Период – это время, необходимое для одного полного колебания.

Чтобы найти период колебания, разделите время колебания на число колебаний.

Частота колебаний – это количество колебаний в единицу времени.

Единица частоты названа в честь немецкого ученого Г. Герца.

Фаза колебания – это физическая величина, определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени.

Во всех колебательных системах существуют силы, которые пытаются вернуть тело к равновесию. Существует несколько типов маятников: струнные, пружинные и т.д. Слово “маятник” относится к твердому телу, которое под действием приложенных сил может колебаться вокруг неподвижной точки или вокруг оси.

Мы рассмотрим пружинный маятник и математический маятник.

Пружинный маятник. В данном случае колебательная система представляет собой тело, прикрепленное к пружине. Колебания этого маятника вызваны упругостью пружины и силой тяжести.

Период колебаний пружинного маятника:

T – период колебаний пружинного маятника

m – масса подвешенного груза

Математический маятник.

Математический маятник – это материальная точка, подвешенная на длинной нерастяжимой нити.

Математический маятник – это идеализированная модель. Настоящий маятник можно считать математическим, если длина нити намного больше размера подвешенного тела, а масса нити пренебрежимо мала по сравнению с массой тела. Колебания такого маятника вызываются силой натяжения струны и силой тяжести. Формула для расчета периода колебаний математического маятника была выведена Гюйгенсом.

T – период колебаний математического маятника

? – длина хорды маятника

? – ускорение силы тяжести

Гюйгенс доказал, что период малых колебаний маятника не зависит от времени. Используя это свойство, называемое изохронностью маятника, Гюйгенс в тысяча шестьсот пятьдесят седьмом году сконструировал первые маятниковые часы. Это свойство маятника было обнаружено 19-летним Галилео Галилеем более чем за 20 лет до открытия Гюйгенса. Наблюдая за раскачивающимися соборными светильниками, подвешенными на струнах одинаковой длины, он заметил, что период их колебаний не зависит от времени. В те времена не было наручных часов, и молодой Галилей придумал решение, которое послужит примером блеска и остроумия человеческой мысли для последующих поколений: он сравнил колебания маятника с частотой биения собственного сердца.

Гармонические колебания – это колебания, возникающие под действием силы, пропорциональной смещению колеблющейся точки и направленной в сторону, противоположную этому смещению. Уравнение для гармонических колебаний:

x – координата колеблющейся величины

– амплитуда колебаний

ω – циклическая частота

Если в системе есть силы трения, колебания будут затухать. Амплитуда колебаний в этом случае уменьшается со временем. Иногда может потребоваться гашение вибраций, например, колебаний тела на рессорах при движении автомобиля. Для гашения вибраций используются специальные амортизаторы. Поршень соединен с корпусом и при вибрации перемещается в цилиндре, который заполнен жидкостью. Высокое сопротивление жидкости гасит колебания.

Колебания, происходящие под воздействием внешней периодической силы, называются вынужденными колебаниями.

Если частота изменения внешней силы не равна частоте свободных колебаний системы, то внешняя сила будет действовать с частотой, отличной от частоты свободных колебаний самой системы. Тогда амплитуда колебаний будет определяться максимальным значением внешней силы, действующей на систему.

Если частота изменения внешней силы совпадает с частотой свободных колебаний, то мы будем наблюдать резкое увеличение амплитуды колебаний, так как внешняя сила в этом случае будет действовать в такт со свободными колебаниями системы.

ω – частота изменения внешней силы.

ω₀ – частота свободных колебаний системы.

Явление резонанса было впервые описано Галилео Галилеем. Явление резонанса играет большую роль в природе, технике и науке. Большинство конструкций и машин, обладая определенной упругостью, способны свободно вибрировать. Поэтому внешние периодические воздействия могут вызвать их резонанс, что может привести к катастрофам. Известно много случаев, когда люди, идущие строем, были источником опасных вибраций. Например, в 1831 году в Манчестере обрушился мост, когда колонна солдат пересекла его в пешем темпе. Аналогичный случай произошел в Санкт-Петербурге в 1905 году. Когда кавалерийский эскадрон переходил мост через реку Фонтанку, мост рухнул. Для предотвращения явления резонанса используются различные методы гашения вынужденных колебаний. Одним из способов является изменение частоты свободных колебаний в системе. Другой способ – увеличить трение в системе: чем выше трение, тем меньше амплитуда резонансных колебаний.

Тематическое исследование

1. Найдите массу груза, который совершает 20 колебаний за 16 секунд на пружине жесткостью 250 Н/м.

Напишите формулу для периода пружинного маятника

Из этой формулы выразите массу

Найдите период колебаний заряда по времени и числу колебаний по формуле:

Подставьте числовые значения

Следовательно, масса равна :

2. Шарик массой 0,1 кг подвешен на нити. Мяч отклоняется на высоту 2,5 см (относительно положения равновесия) и отпускается. Определите максимальную скорость шарика.

Скорость колеблющегося шарика максимальна, когда он проходит положение равновесия.

Используйте закон сохранения энергии для решения задачи:

Подставьте числовые значения для этих величин:

Ответ:

Математический маятник – это маленькое тело, подвешенное на невесомой, нерастяжимой нити (рис. 5). Математический маятник может колебаться в вертикальной плоскости в поле силы тяжести.

Уравнение гармонических колебаний.

Вернемся к общему гармоническому закону (1) . Продифференцируем это уравнение:

Теперь продифференцируем полученное уравнение (4) :

Сравним выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты только мультипликативным коэффициентом :

Это соотношение называется с уравнением гармонических колебаний. Его также можно записать в такой форме:

С математической точки зрения, уравнение (7) имеет вид является дифференциальным уравнением. Решениями дифференциальных уравнений являются функции (а не числа, как в обычной алгебре).
Таким образом, можно доказать, что:

-решением уравнения (7) является любая функция вида (1) с любым ;

-ни одна другая функция не является решением уравнения.

Другими словами, соотношения (6), (7) описывают гармонические колебания циклической частоты и только их. Эти две константы определяются из начальных условий – по начальным значениям координаты и скорости.

Где , , , и – определенные числа.

Глава 11 Вибрации и механические волны

Колебательное движение – это любое периодически повторяющееся движение. Следовательно, координата и скорость тела ко времени в колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются колебания, в которых соотношения и скорости тела тригонометрические функции , или их комбинации, где – это число. Такие колебания называются гармоническими колебаниями (функции и часто называют гармоническими функциями). Для решения задач по колебаниям, включенных в программу Единого государственного экзамена по физике, необходимо знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Приведем эти определения и свяжем указанные величины с параметрами координатно-временного отношения которая в случае гармонических колебаний всегда может быть представлена как

где , и – это несколько номеров.

Амплитуда колебаний – это максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значения косинуса в (11.1) равны ±1, амплитуда колебаний колеблющегося тела (11.1) составляет . Период колебаний – это минимальное время, через которое движение тела повторяется. Для соотношения (11.1) период может быть определен из следующих соображений. Косинус является периодической функцией с периодом . Поэтому движение полностью повторяется после достижения такого значения такой, что . . Следовательно, мы получаем

Частота колебаний тела – это число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний связан с периодом колебаний в соответствии с формулой

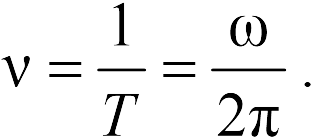
Круговая (или циклическая) частота – это количество колебаний на единицу времени. Из уравнения (11.3) мы заключаем, что круговая частота равна из уравнения (11.1).

Фаза колебания является аргументом тригонометрической функции, описывающей временную зависимость координаты. Из уравнения (11.1) следует, что фаза вибрирующего тела, движение которого описывается уравнением (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для уравнения (11.1) начальная фаза колебаний имеет вид . Конечно, начальная фаза колебаний зависит от выбора отсчета времени (момент = 0), которая всегда условна. Изменяя отсчет времени, всегда можно “приравнять” начальную фазу к нулю, а синус из уравнения (11.1) можно “преобразовать” в косинус или наоборот.

Экзамен также включает знание уравнений для частоты колебаний пружинного маятника и математического маятника. Пружинный маятник – это тело, которое может колебаться на гладкой горизонтальной поверхности под действием пружины, другой конец которой неподвижен (левый рисунок). Математический маятник – это массивное тело, размерами которого можно пренебречь, колеблющееся на длинной, невесомой и нерастяжимой струне (правый рисунок). Название “математический маятник” происходит от того, что он является абстрактным математический модель реального (физическая) маятник. Необходимо запомнить формулы для периода (или частоты) колебаний пружинного и математического маятника. Для пружинного маятника

где – коэффициент жесткости пружины, – масса груза. Период колебаний математического маятника определяется следующим соотношением

где – длина цепи, – ускорение свободного падения. Давайте рассмотрим применение этих определений и законов через решение задач.

Чтобы найти циклическую частоту колебаний нагрузки в Проблема 11.1.1 сначала найти период колебаний, а затем использовать уравнение (11.2). Поскольку 10 м 28 с – это 628 с, а за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Следовательно, циклическая частота колебаний равна 1 c -1 (ответ 2). В Проблема 11.1.2 Груз совершает 60 колебаний за 600 с, поэтому частота колебаний равна 0,1 с -1 (Ответ ). 1).

Чтобы найти расстояние, пройденное движущимся объектом за 2,5 периода (задание 11.1.3), давайте проследим его движение. Через некоторое время элемент вернется обратно в точку максимального прогиба, совершив полное колебание. Таким образом, за это время вес пройдет расстояние, равное четырем амплитудам: до положения равновесия – одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону – вторая, обратно до положения равновесия – третья, от положения равновесия до исходной точки – четвертая. Во второй период груз будет двигаться по четырем амплитудам, а в оставшуюся половину периода по двум амплитудам. Следовательно, пройденное расстояние равно десяти амплитудам (ответ 4).

Величина движения тела – это расстояние от начальной до конечной точки. В период 2,5 периодов в из ссылки 11.1.4. тело успевает совершить два полных и одно неполное колебание, т.е. оно будет находиться при максимальном прогибе, но по другую сторону от положения равновесия. Таким образом, величина смещения равна двум амплитудам (ответ 3).

Фаза колебания по определению является аргументом тригонометрической функции, которая описывает зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в Проблема 11.1.5. — 3.

Период – это время полного колебания. Это означает, что возвращение тела в ту же точку, из которой оно стартовало, не означает, что период прошел: тело должно вернуться в ту же точку с той же скоростью. Например, тело, которое начинает колебаться из положения равновесия, в течение периода будет отклоняться на максимальную величину в одном направлении, отклоняться на максимальную величину в другом направлении и снова отклоняться. Поэтому за это время тело успевает удвоить максимальное отклонение от положения равновесия и вернуться в него. Следовательно, для перехода из положения равновесия в точку максимального прогиба требуется время (проблема 11.1.6) тело занимает одну четверть периода (ответ 3).

Гармонические колебания – это колебания, при которых временная зависимость координаты вибрирующего тела описывается тригонометрической (синус или косинус) функцией времени. В проблема 11.1.7. являются функциями и несмотря на то, что их входные параметры обозначаются как 2 и 2 . Функция – является тригонометрической функцией квадрата времени. Поэтому только колебания величин и (Ответ 4).

При гармонических колебаниях скорость тела изменяется по закону где – амплитуда колебания скорости (начало времени выбирается так, чтобы начальная фаза колебания была равна нулю). Отсюда получаем зависимость кинетической энергии тела от времени (проблема 11.1.8). Используя далее известную тригонометрическую формулу, получаем

Из этой формулы следует, что кинетическая энергия тела при гармонических колебаниях также изменяется по гармоническому закону, но с вдвое большей частотой (ответ 2).

Связь между кинетической энергией заряда и потенциальной энергией пружины (проблема 11.1.9) можно легко понять из следующих соображений. Когда тело максимально отклонено от положения равновесия, скорость тела равна нулю, поэтому потенциальная энергия пружины больше кинетической энергии веса. Напротив, когда тело перемещается в положение равновесия, потенциальная энергия пружины равна нулю, и поэтому кинетическая энергия больше потенциальной. Поэтому между достижением положения равновесия и максимальным отклонением кинетическая и потенциальная энергии сравниваются один раз. А поскольку за один период тело проходит путь от положения равновесия до максимального отклонения или обратно четыре раза, то кинетическая энергия гири и потенциальная энергия пружины сравниваются друг с другом четыре раза за период (ответ 2).

Амплитуда колебания скорости (проблема 11.1.10) легче всего выводится из закона сохранения энергии. В точке максимального прогиба энергия колебательной системы равна потенциальной энергии пружины где – коэффициент жесткости пружины, – амплитуда колебаний. В положении равновесия энергия тела равна его кинетической энергии где – масса тела, – это скорость тела при прохождении через положение равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебательной скорости. Приравнивая эти энергии, получаем

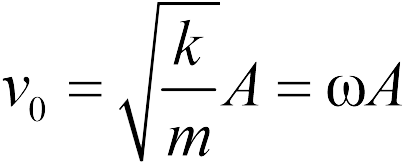
(ответ 1), где используется выражение для частоты круговых колебаний груза на пружине:

Из формулы (11.4) получаем в задание 11.2.1

Из уравнения (11.5) мы заключаем, что (проблема 11.2.2), что масса математического маятника не определяет его период, и что когда его длина в 4 раза больше, то период колебаний в 2 раза больше (ответ 1).

Часы – это колебательный процесс, который используется для измерения интервалов времени (проблема 11.2.3). Слова “спешка” в часах означают, что период этого процесса короче, чем должен быть. Поэтому для объяснения хода этих часов необходимо увеличить период процесса. Согласно уравнению (11.5), чтобы увеличить период колебаний математического маятника, необходимо увеличить его длину (ответ 3).

Чтобы найти амплитуду колебаний в маятника в задаче 11.2.4.необходимо представить временную зависимость координаты тела в терминах одной тригонометрической функции. Для функции, заданной в задаче это можно сделать, введя дополнительный угол. Умножение и деление этой функции на и, используя формулу для сложения тригонометрических функций, получаем

где – это такой угол, что . Из этой формулы следует, что амплитуда колебаний тела составляет (ответ 4).

В значение в задаче 11.2.5 у нас есть в см. Откуда см (ответ 2).

Проблема 11.2.6 и 11.2.7 касаются механических волн. Волна – это некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка в среде вибрирует вокруг определенного положения и в среднем не перемещается в пространстве. Волна характеризуется своим периодом (или связанная с ним частота ), скорость и длина волны который определяется как минимальное расстояние между двумя точками, колеблющимися в одной и той же фазе. Для решения заданий ЕГЭ по этой теме вам необходимо запомнить формулу, дающую зависимость между параметрами волны

Это легко запомнить, потому что зависимость имеет ту же форму, что и обычная зависимость между расстоянием, скоростью и временем. Например, в проблема 11.2.6. Используя формулу (11.6), находим длину волны м (ответ 2).

Как следует из рисунка в проблема 11.2.7 длина волны, распространяющейся вдоль провода, равна м. Поэтому, согласно формуле (11.6), имеем Гц (ответ 4).

Поскольку в момент максимального отклонения пружинного маятника механическая энергия системы равна потенциальной энергии пружины, то

где – амплитуда колебаний, – жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличится на времена (проблема 11.2.8 – ответ 1).

Используя известную тригонометрическую формулу, получаем в проблема 11.2.9

Это отношение является гармонической функцией, но колеблющейся вокруг точки . Амплитуда этого колебания является множителем перед косинусом (потому что сам косинус изменяется в пределах от -1 до 1). Циклическая частота – это значение (ответ 4).

Вертикальный пружинный маятник отличается от горизонтального маятника (проблема 11.2.10) из-за присутствия гравитации. Однако гравитация только смещает положение равновесия маятника, и возвращающая сила по-прежнему будет зависеть от смещения маятника. из положения равновесия в соответствии с законом (Потому что возвращающая сила будет равна разнице между силой упругости и постоянной силой тяжести). Поэтому период колебаний гири на вертикальной и горизонтальной пружине одинаков (при условии, конечно, что и гиря, и пружины одинаковы). Правильным ответом на это задание является. 3.

g.Schwingungsausschlag m, Schwingungsbreite f, Schwingungsweite f

АМПЛИТУДА ВИБРАЦИИ

Энциклопедический словарь по физике. – Москва: Советская энциклопедия. Главный редактор А. М. Прохоров 1983 .

Смотреть что такое “АМПЛИТУДА ВИБРАЦИИ” в других словарях:

АМПЛИТУДА КОЛЕБАНИЙ

наибольшее отклонение периодически изменяющейся величины от ее нулевого значения (болгарский; билгарский) – амплитуда по трептению [колебаниям] (чеш. watch.

АМПЛИТУДА КОЛЕБАНИЙ

Амплитуда колебаний – наибольшее отклонение периодически изменяющейся величины от ее нулевого значения (болгарский язык; б’олгарски) – амплитуда тр. смотреть

АМПЛИТУДА КОЛЕБАНИЙ

АМПЛИТУДА ВИБРАЦИИ Разница между максимальным и минимальным значением, достигнутым во время регулярного колебания. Если

АМПЛИТУДА КОЛЕБАНИЙ

Амплитуда колебаний – это максимальное отклонение вибратора от нейтрального положения. Амплитуда вибратора прямо пропорциональна массе эксцентрика и e. смотреть.

АМПЛИТУДА КОЛЕБАНИЙ

амплитуда колебаний, амплитуда вибрации* *амплитуда колебаний

АМПЛИТУДА КОЛЕБАНИЙ

g.Schwingungsausschlag m, Schwingungsbreite f, Schwingungsweite f

АМПЛИТУДА КОЛЕБАНИЙ

ампицца ди осцилляционе; ампицца ди вибрационе

АМПЛИТУДА ВИБРАЦИИ

амплитуда колебаний; амплитуда вибрации

АМПЛИТУДА ВИБРАЦИИ

f.ast. амплитуда тербелистера; амплитуда тербелиса

АМПЛИТУДА ВИБРАЦИИ

амплитуда колебаний

АМПЛИТУДА ВИБРАЦИИ

АМПЛИТУДА КОЛЕБАНИЙ

амплитуда колебаний

АМПЛИТУДА КОЛЕБАНИЙ

Амплитуда колебаний

АМПЛИТУДА КОЛЕБАНИЙ

АМПЛИТУДА ВИБРАЦИИ

АМПЛИТУДА КОЛЕБАНИЙ КРИСТАЛЛИЗАТОРА

АМПЛИТУДА ВИБРАЦИИ УРОВЕНЬ ВОДЫ

амплитуда вибрации уровня воды амплитуда вибрации уровня воды амплитуда вибрации уровня воды

АМПЛИТУДА КОЛЕБАНИЙ УРОВНЯ ВОДЫ

амплитуда колебаний уровня воды (амплитуда колебаний уровня воды)

АМПЛИТУДА КОЛЕБАНИЙ ЦЕН (ЗА ВЕСЬ ПЕРИОД ПРОДАЖ)

Амплитуда колебаний цен, в пределах которой торговались акции, облигации или товары с момента их первичного размещения. Волатильные акции будут иметь более высокую амплитуду колебаний цен, чем более стабильные акции. Технические аналитики всегда рассматривают верхний уровень существующей амплитуды как уровень сопротивления, а нижний – как уровень поддержки. Они считают значимым событием, когда цена акции поднимается выше уровня сопротивления или опускается ниже уровня поддержки. Обычно такое изменение означает, что цены на акции достигли новых рекордных максимумов или рекордных минимумов, что увеличивает амплитуду волатильности.

Математический маятник это небольшой предмет, подвешенный на тонкой, длинной, нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой предмета. Только в случае малых колебаний математический маятник является гармоническим маятником осцилляторто есть система, способная совершать гармонические (по закону sin или cos) колебания. Практически это приближение справедливо для углов порядка 5-10°. Колебания маятника с большими амплитудами не являются гармоническими.

Что такое амплитуда в физике

В инженерном деле и в окружающем нас мире мы часто имеем дело с периодический Процессы, повторяющиеся через регулярные промежутки времени. Эти процессы называются осцилляция. Осцилляция это изменения физической величины, которые происходят по определенному закону с течением времени. Колебательные явления различной физической природы управляются общими законами. Колебания тока в электрической цепи и колебания математического маятника, например, могут быть описаны одним и тем же уравнением. Общие колебательные закономерности позволяют унифицировать представление о колебательных процессах в различных природах.

Механическое колебание – это движение тела это движение тел, повторяющееся через абсолютно одинаковые промежутки времени. Примерами простых колебательных систем являются гиря на пружине или математический маятник. Для существования в системе гармонические колебания необходимо, чтобы система имела устойчивое положение равновесия, т.е. положение, из которого на систему действует восстанавливающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть бесплатно и принудительно. Свободные вибрации Колебания вызываются внутренними силами системы, после того как система была выведена из равновесия. Колебание груза на пружине или колебание маятника – это свободные колебания. Колебания, вызванные внешними, периодически изменяющимися силами, называются вынужденными колебаниями. принудительно.

Простейшим типом колебательного процесса является процесс, происходящий по закону синуса или косинуса, называемый гармонические колебания. Уравнение, описывающее физическую систему, основано на способности колебаться в гармоническом ритме с циклической частотой ω₀ дается следующим образом:

Решением предыдущего уравнения является уравнение движения для гармонических колебаний, которая имеет вид:

Где: x – смещение тела из положения равновесия A – амплитуда колебаний, т.е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Значение под знаком косинуса: φ = ωt + φ₀называется фаза гармонического процесса. Значение фазы колебания: фаза, в которой находится колебание в данный момент времени. На t = 0 мы получаем, что φ = φ₀поэтому φ₀ называется начальный этап (т.е. фаза, с которой началось колебание).

Минимальный интервал времени, в течение которого движение тела повторяется, называется период колебаний T. Если число осцилляций Nи их время tпериод определяется как:

Физическая величина, обратная периоду колебаний, называется частота колебаний:

Частота колебаний ν показывает, сколько колебаний совершается в секунду. Единицей измерения частоты является герц (Гц). Частота колебаний связана с циклической частотой ω и период колебаний T по следующему уравнению:

Временная зависимость скорости в гармонических механических колебаниях выражается следующим уравнением:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные значения по модулю для скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Ускорение определяется аналогичным образом a = a_x тела в гармонических колебаниях. Временная зависимость ускорения для гармонических механических колебаний:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет противоположный знак по отношению к смещению x(t), и поэтому возвращает тело в исходное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует отметить, что:

Физические свойства колебательной системы определяют только собственную частоту ω₀ или период T.
Параметры процесса колебаний, такие как амплитуда A = x_m и начальная фаза φ₀зависит от того, как система выведена из равновесия в начальный момент времени, т.е. от начальных условий.
При колебательном движении тело проходит расстояние, равное 4 амплитудам, за время, равное периоду. При этом тело возвращается в исходную точку, т.е. его движение будет равно нулю. Следовательно, путь, равный амплитуде, будет пройден телом за время, равное четверти периода.

Чтобы определить, когда подставлять синус и когда подставлять косинус в уравнение колебаний, необходимо учитывать следующие факторы:

Самый простой способ сделать это – сказать, что колебание является синусоидальным или косинусоидальным.
Если мы говорим, что тело выталкивается из положения равновесия, мы предполагаем синус с начальной фазой, равной нулю.
Если говорят, что тело отклоняется и отпускается, то это косинус с начальной фазой, равной нулю.
Если тело выталкивается из положения равновесия, то начальная фаза не равна нулю и можно взять как синус, так и косинус.

Математический маятник

Математический маятник это тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой струне, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим маятником осцилляторто есть система, способная совершать гармонические (по закону sin или cos) колебания. Практически это приближение справедливо для углов порядка 5-10°. Колебания маятника с большими амплитудами не являются гармоническими.

Циклическая частота колеблющегося математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная таким образом формула называется формулой Гюйгенса и является действительной, когда точка подвеса маятника неподвижна. Обратите внимание, что период малых колебаний математического маятника не зависит от амплитуды этих колебаний. Это свойство маятника называется изохронность. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника применимы следующие соотношения:

Путь от положения равновесия до экстремальной точки (или обратно) проходит за одну четверть периода.
Путь от крайней точки до половины амплитуды (или обратно) проходит за одну шестую периода.
Путь от положения равновесия до половины амплитуды (или обратно) проходит за одну двенадцатую периода.

Пружинный маятник

Свободные колебания возникают под действием внутренних сил системы, когда она выводится из состояния равновесия. Для того чтобы свободные колебания происходили по гармоническому закону, необходимо, чтобы сила, возвращающая тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную этому смещению. Это свойство силы упругости.

Поэтому заряд некоторой массы mприкрепленный к пружине с жесткостью k, другой конец которого неподвижен, представляют собой систему, способную к свободным гармоническим колебаниям в отсутствие трения. Вес на пружине называется пружинный маятник.

Циклическая частота пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

Для малых амплитуд период колебаний пружинного маятника не зависит от амплитуды (как в случае математического маятника). Если пружинная система расположена горизонтально, сила тяжести, действующая на груз, компенсируется силой реакции опоры. Если груз подвешен к пружине, гравитационная сила направлена вдоль линии движения груза. В положении равновесия пружина растягивается на x₀, равный:

И колебания происходят вокруг этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и период колебаний T также действительны в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

В свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а значит и кинетическая энергия, обращается в ноль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника это энергия, содержащаяся в гравитационном поле Земли.

Когда тело в своем движении проходит через положение равновесия, его скорость максимальна. Тело перескакивает через свое равновесное положение из-за инерции. В этот момент он обладает максимальной кинетической энергией и минимальной потенциальной энергией (потенциальная энергия в положении равновесия обычно принимается равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении потенциальная энергия начинает увеличиваться за счет уменьшения кинетической энергии, и так далее.

Таким образом, в гармонических колебаниях происходит периодическое преобразование кинетической энергии в потенциальную и наоборот. Если в колебательной системе нет трения, то полная механическая энергия при свободных колебаниях остается неизменной. В этом случае максимальное значение кинетической энергии в механических гармонических колебаниях дается формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергии, а также сумме кинетической и потенциальной энергии в произвольно выбранный момент времени):

Механические волны

Если в любой точке твердой, жидкой или газообразной среды возбуждаются колебания молекул, то в результате взаимодействия атомов и молекул среды эти колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волна.

Механические волны бывают разных форм. При распространении волны молекулы среды испытывают смещение в направлении, перпендикулярном направлению распространения волны, эта волна называется поперечный. Если частицы среды движутся в направлении распространения, мы называем волну продольный.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. Во время распространения частицы среды совершают только колебания вокруг равновесных положений. Однако волны передают колебательную энергию из одной точки среды в другую.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газовых). Существуют немеханические волны, которые также могут распространяться в вакууме (например, световые волны, или электромагнитные волны могут распространяться в вакууме).

Продольные механические волны могут распространяться во всех средах – твердых, жидких и газообразных.
Поперечные волны не не могут существовать в жидких или газообразных средах.

Большой интерес на практике представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебаний частиц, частота ν и длина волны λ. Синусоидальные волны распространяются в однородной среде с определенной постоянной скоростью υ.

Длина волны λ расстояние между двумя соседними точками, колеблющимися в одной и той же фазе. Расстояние, равное длине волны λволна проходит путь за время, равное периоду T, поэтому длина волны может быть рассчитана по формуле:

Где: υ – скорость распространения волны. Когда волна переходит из одной среды в другую, длина волны и скорость распространения изменяются. Неизменными остаются только частота и период волны.

Разница в фазе колебаний двух точек волны, расстояние между ними l рассчитывается по формуле:

Электрическая цепь

В электрических цепях, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является серия LC-контур. В отсутствие демпфирования свободные колебания в электрической цепи являются гармоническими. Энергетические характеристики и их корреляция колебаний в электрической цепи:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Временная зависимость заряда на конденсаторе во время колебаний в электрической цепи описывается законом:

Временная зависимость электрического тока, протекающего через индукционную катушку во время колебаний в электрической цепи:

Зависимость напряжения на конденсаторе от времени во время колебаний в электрической цепи:

Максимальное значение тока при гармонических колебаниях в электрической цепи можно рассчитать по формуле:

Максимальное значение напряжения на конденсаторе во время гармонических колебаний в электрической цепи:

Все реальные цепи содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. В течение каждого периода колебаний часть электромагнитной энергии, накопленной в цепи, преобразуется в тепло, которое выделяется в резисторе, и колебания подавляются.

Переменный ток. Трансформатор

Сегодня большая часть электроэнергии в мире вырабатывается генераторами переменного тока, которые производят синусоидальное напряжение. Они обеспечивают наиболее простую и экономичную передачу, распределение и использование электроэнергии.

Устройство, преобразующее механическую энергию в энергию переменного тока, называется генератор переменного тока. Он характеризуется переменным напряжением U(t) (наведенная ЭДС) на его клеммах. Работа генератора основана на явлении электромагнитной индукции.

Переменный ток это электрический ток, который изменяется во времени по гармоническому закону. Значения U₀, I₀ = U₀/R называются амплитуда значения напряжения и тока. Значения напряжения U(t) и текущий I(t), которые зависят от времени, называются мгновенный.

Переменный ток характеризуется эффективный значения тока и напряжения. Среднеквадратичное значение переменного тока – это количество постоянного тока, которое, протекая по цепи, выделит такое же количество тепла, как и данный переменный ток за единицу времени. Для переменного тока эффективное значение текущего можно рассчитать по формуле:

Аналогично, вы можете ввести действующее значение напряжениякоторый рассчитывается по формуле:

Таким образом, выражения для мощности постоянного тока остаются действительными и для мощности переменного тока, если используются эффективные значения тока и напряжения:

Обратите внимание, что когда речь идет о напряжении переменного тока или мощности переменного тока, имеется в виду среднеквадратичное значение (если не указано иное). Поэтому напряжение 220 В является действующим напряжением в бытовой электроустановке.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор не проводит электричество (в том смысле, что через него не проходят носители заряда). Поэтому, когда конденсатор подключен в цепь постоянного тока, ток в любой точке цепи равен нулю в любой момент времени. Когда конденсатор подключен к цепи переменного тока, он заряжается из-за постоянного изменения ЭДС. Через него не течет ток, но ток в цепи существует. Поэтому конденсатор условно называют проводником переменного тока. В этом случае концепция сопротивления конденсатора в цепи переменного тока (или емкость). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Он принципиально отличается от сопротивления R, к которому мы привыкли. Например, сопротивление R выделяет тепло (поэтому его часто называют активным сопротивлением), тогда как емкостное сопротивление не выделяет тепла. Активное сопротивление связано с взаимодействием носителей заряда при протекании тока, а емкостное сопротивление связано с процессами зарядки конденсатора.

Индуктор в цепи переменного тока

Когда в катушке течет переменный ток, возникает самоиндукция и, следовательно, ЭДС. Из-за этого напряжение и ток в катушке не находятся в фазе (когда ток равен нулю, напряжение максимально, и наоборот). Из-за этого несоответствия средняя тепловая мощность, генерируемая в катушке, равна нулю. В этом случае термин сопротивление катушки в цепи переменного тока (или индуктивное сопротивление). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и при емкостном сопротивлении, при индуктивном сопротивлении не выделяется тепло. Индуктивное сопротивление обусловлено явлением самоиндукции в катушке.

Трансформеры

Среди устройств переменного тока, нашедших широкое применение в технике, важное место занимают следующие устройства трансформаторы. Трансформаторы для повышения или понижения напряжения переменного тока основаны на явлении электромагнитной индукции. Простейший трансформатор состоит из закрытого сердечника с двумя обмотками: основной и дополнительно. Первичная обмотка подключена к источнику переменного тока с заданным напряжением U₁а вторичная обмотка подключена к нагрузке, где напряжение U₂. В этом случае, если число витков в первичной обмотке равно n₁а во вторичной обмотке n₂применяется следующее соотношение:

Коэффициент трансформации рассчитывается по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (входная и выходная мощности равны):

В неидеальном трансформаторе вводится понятие эффективности:

Электромагнитные волны

Электромагнитные волны – это электромагнитные поля, распространяющиеся во времени и пространстве. Электромагнитные волны являются поперечными – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которую можно вычислить по формуле:

Где: ε и μ – это диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрические и магнитные постоянные: ε₀ = 8,85419-10 -12 Ф/м, μ₀ = 1,25664-10 -6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) является постоянной и равна с = 3∙10 8 м/с, его также можно рассчитать по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических констант. Если электромагнитная волна распространяется в среде, то ее скорость распространения также выражается следующим соотношением:

где: n – показатель преломления материи, физическая величина, определяющая, во сколько раз скорость света в данной среде ниже, чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

Электромагнитные волны передают энергию. При распространении волн создается поток электромагнитной энергии.
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с постоянной скоростью, не являются источником электромагнитных волн. Однако цепи переменного тока, т.е. цепи, в которых носители заряда постоянно меняют направление, т.е. движутся с ускорением, являются источником электромагнитных волн. В современной радиотехнике электромагнитные волны излучаются с помощью антенн различных конструкций, в которых возбуждаются быстрые переменные токи.

Назад
К фронту

Как эффективно подготовиться к экзамену CT по физике и математике?

Для успешной подготовки к сдаче КТ по физике и математике существуют, помимо прочего, три важных предварительных условия:

Изучите все темы и выполните все тесты и задания, приведенные в учебных материалах на этом сайте. Вам достаточно уделять три-четыре часа в день на подготовку к КТ по физике и математике, изучение теории и решение задач. Дело в том, что CT – это экзамен, для которого недостаточно просто знать физику или математику; необходимо также уметь быстро и эффективно решать большое количество заданий на разные темы и разной степени сложности. Последнему можно научиться только путем решения тысяч задач.
Изучите все формулы и законы в физике, а также формулы и методы в математике. На самом деле это тоже очень легко сделать, всего около 200 формул требуется в физике и чуть меньше в математике. В каждом из этих предметов есть около десятка стандартных методов решения задач на базовом уровне, которые вы также можете изучить, и таким образом легко решить большинство задач в этом томе, когда придет время. После этого вам придется думать только о самых сложных проблемах.
Пройдите все три этапа пробных экзаменов по физике и математике. Вы можете посещать каждый ПТ дважды, чтобы решить оба вопроса. Опять же, в CT, помимо умения быстро и эффективно решать задачи и знания формул и методов, вы также должны уметь правильно планировать свое время, распределять силы и, прежде всего, правильно заполнять бланк ответов, не путая номера ответов и задач и свое имя. Также важно привыкнуть к стилю постановки вопросов в проблемах, который может показаться очень непривычным для неподготовленного человека в CT.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная практика на итоговых тренировочных тестах, позволит вам явиться на CT с отличным баллом, лучшим из тех, которые вы можете себе позволить.

Вы нашли ошибку?

Если вы считаете, что нашли ошибку в учебных материалах, пожалуйста, напишите нам (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название или номер темы или теста, номер задания или место в тексте (страницу), где, по вашему мнению, допущена ошибка. Также объясните, в чем, по вашему мнению, заключается ошибка. Ваше письмо не останется незамеченным, и ошибка будет исправлена или вам объяснят, почему это не ошибка.

Материал или его части НЕ могут быть использованы в коммерческих целях, а также скопированы, перепечатаны, опубликованы или воспроизведены в любой форме. Нарушение прав владельцев авторских прав будет преследоваться по закону. Читать далее.

Читайте далее: