Мощность в цепи постоянного тока

Давайте начнем с абстрактного примера, чтобы было легче понять концепции, которые я буду использовать. Предположим, есть магазин товаров (условно это можно считать напряжением), есть деньги (условно это электричество), есть совесть, которая не позволяет вам тратить много или, наоборот, побуждает тратить много (это можно считать сопротивлением), и есть купленные товары или продукты, которые вы несете домой (это энергия). На самом деле, многие законы, связанные с электричеством, можно объяснить на этом примере. Все приведенные величины связаны друг с другом законом Ома, который гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи, следующим образом:

Содержание

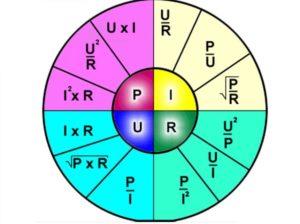
Здравствуйте, эту статью можно рассматривать как начало знакомства с электричеством. Напряжение, ток и сопротивление – это три основные величины, на которых основаны основные законы электротехники, и у этих величин есть еще одна общая черта – мощность. Чтобы помочь вам узнать об электротехнике, мы рассмотрим следующие вопросы мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока возникает довольно много условий. Однако все в порядке, и вы быстро освоитесь.

Для удобства я запишу международные обозначения этих четырех величин:

U – напряжение (В, вольт)

R – сопротивление (ом, Ом)

P – мощность (ватты, watt – не путать с вольтами, которые обозначаются только буквой V)

Я начну с абстрактного примера, чтобы было легче понять концепции, которые я буду использовать. Предположим, есть магазин с товарами (условно это можно считать напряжением), есть деньги (условно это электричество), есть совесть, которая не позволяет вам тратить много или, наоборот, побуждает тратить много (это можно считать сопротивлением), есть купленные товары или продукты, которые вы несете домой (это энергия). На самом деле, многие законы, связанные с электричеством, можно объяснить на этом примере. Все приведенные величины связаны между собой законом Ома, который гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи, следующим образом:

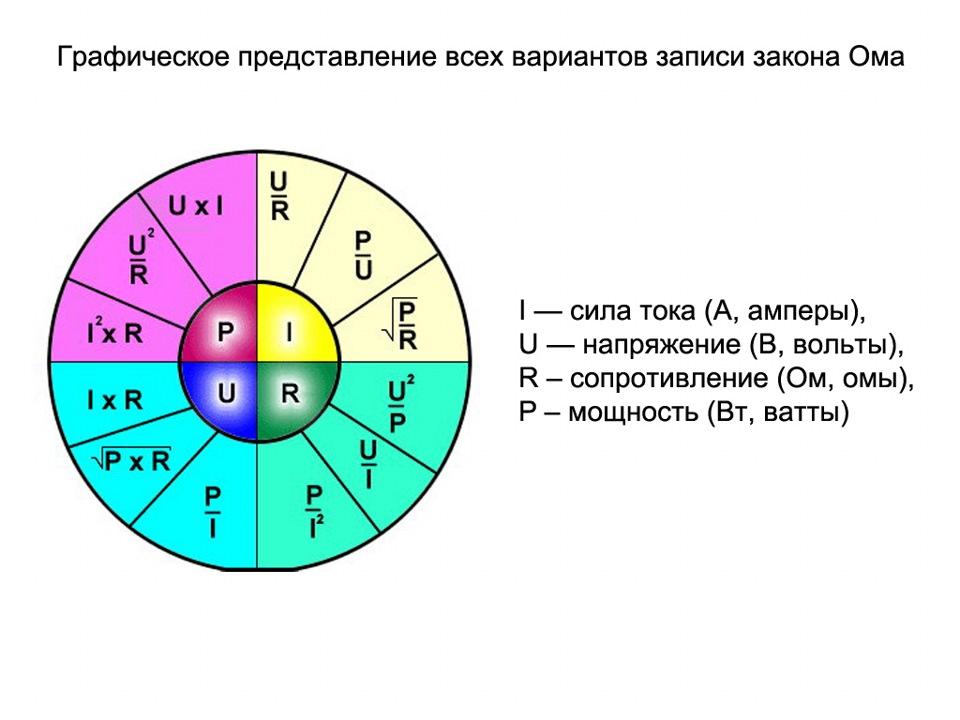
В абстрактном примере – чем больше магазин (напряжение) и чем меньше шепчет вам совесть (сопротивление), тем больше денег вы тратите (сила тока), а неся купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока – это работа, совершаемая электричеством. Мощность – это произведение тока и напряжения, и если вы подставите соответствующие значения тока или напряжения, то получите мнемоническую таблицу:

Как видите, мощность в цепи постоянного тока – довольно простая концепция, если немного подумать над материалом. По сути, это просто две формулы с подставленными значениями. Как это выглядит: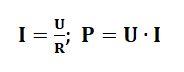

Если мы теперь подставим формулу для значения тока в формулу для мощности, то получим следующие результаты: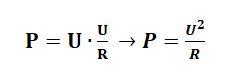

Это дает нам 12 формул, основанных на законе Ома, которые мы видим в мнемонической таблице. Мы уже более или менее разобрались с тем, что такое мощность в цепях постоянного тока, но есть еще один момент.

Небольшая разница в значениях обусловлена округлением при расчете.

Баланс мощности в источнике тока

При решении электрических проблем часто необходимо проверить правильность найденных значений. Для этой цели в науке технологии существует так называемая баланс сил.

Баланс сил – это выражение закона сохранения энергии в электрической цепи. Баланс мощности определяется следующим образом: сумма мощностей, потребляемых нагрузками, равна сумме мощностей, отдаваемых источниками. Это означает, что если источник ЭМП в цепи излучает 100 Вт, то нагрузки в этой цепи потребляют точно такую же мощность.

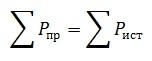
Или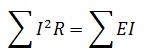

Давайте проверим эту взаимосвязь на простом примере.

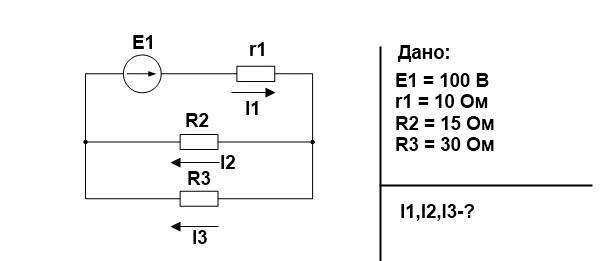
Сначала давайте разложим схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

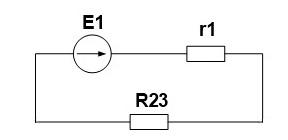
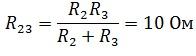
Используя закон Ома, находим ток источника и напряжение на R₂₃предполагая, что r₁ и Р₂₃ соединены последовательно, поэтому ток одинаковый.

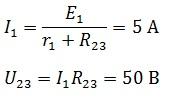
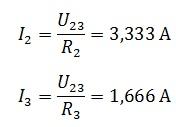
Теперь проверим правильность с помощью баланса мощности.

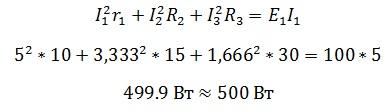
Небольшая разница в значениях объясняется округлением при расчетах.

С помощью баланса мощности можно проверить не только простую, но и сложную схему. Проверим сложную цепь из статьи Метод контурного тока.

Как видите, независимо от сложности схемы, равновесие сходится, и должно сходиться в каждой схеме!

Равновесие мощности в электрической цепи означает, что мощность, которую отдают все источники энергии, равна мощности, которую потребляют все потребители энергии в той же цепи:

где – мощность i-мощность i-го источника ЭДС или тока, W j-сопротивление, W.

Очевидно, что баланс мощности следует из закона сохранения энергии.

Запишем для анализируемой цепи с рис. 2.15 сумму мощностей, выделяемых всеми источниками энергии. Будем считать мощность, излучаемую ЭДС и источниками тока, положительной, если ток в ветви, в которой установлен ЭДС или источник тока, совпадает с направлением тока в источнике (со стрелкой в обозначении ЭДС или источника тока), и отрицательной, если направление тока в ветви противоположно направлению тока в источнике. Затем, составив соответствующее уравнение для расчета полной мощности, подводимой источниками ЭДС и тока к анализируемой цепи, и подставив в него числовые значения, получают полную мощность источников:

, при этом токи ветвей подставляются в уравнение (2.70) со своим знаком, который был получен при их расчете.

Полная мощность, рассеиваемая в цепи резисторами (потребителями энергии), для той же цепи рис. 2.15 может быть найдена следующим образом:

Результат расчета (2.70), мощности, рассеиваемой источниками, и (2.71), мощности, потребляемой резисторами в цепи, должен быть одинаковым.

Потенциальная диаграмма электрической цепи

Потенциальная диаграмма цепи постоянного тока – это графическое представление второго закона Кирхгофа, в котором вместо падений напряжения записаны потенциалы узлов цепи. Она показывает общий потенциал и общее сопротивление в данной точке цепи, для которой строится диаграмма, считая от опорного узла, потенциал которого принимается за ноль. Другими словами, потенциальная диаграмма показывает распределение потенциалов и сопротивлений в цепи, для которой она построена.

Графически это полилиния в декартовой системе координат, где горизонтальная ось (абсцисса) – ось сопротивления, а вертикальная ось (ордината) – ось потенциала.

Процесс построения потенциальной диаграммы электрической цепи будет рассмотрен для той же электрической цепи, показанной на рис. 2.3, и изменен для удобства построения потенциальной диаграммы, как на рис. 2.15.

Поскольку построение потенциальной диаграммы требует знания численных значений токов ветвей и сопротивлений ветвей, приведем эти численные значения для цепи на рисунке 2.15, предполагая, что исходные данные для расчета этой цепи следующие: Ом, Ом, Ом, Ом, Ом; значения источников электромагнитного поля: B, B; значения источников тока: A, A. Значения токов ветвей, рассчитанные путем прямого применения законов Кирхгофа (сам расчет здесь не приводится), следующие: [A]; [A]; [A]; [A]; [A]; [A]; [A].

Построение потенциальной диаграммы мы начинаем с выбора контура, для которого эта диаграмма будет построена. На наш взгляд, наиболее информативным является построение потенциальной диаграммы для контура d-b-m-a-c-s-dтак как этот контур содержит все источники ЭДС и источники тока анализируемой цепи и при таком переходе потенциальная диаграмма будет показывать потенциалы всех узлов анализируемой цепи. Затем необходимо выбрать опорный узел, потенциал которого принимается равным нулю. Имеет смысл взять в качестве опорного узла dкак и ранее при расчете анализируемой цепи. Потенциал этого узла будет равен нулю, как и ранее (2.44).

Определим численные значения потенциалов узлов и точек анализируемой цепи, которые находятся на пути выбранной нами цепи d-b-m-a-c-s-d. Поскольку потенциал узла d равен нулю (2.44), тогда потенциал узла b будут определены следующим образом:

Знак плюс в произведении означает, что потенциал узла b увеличивается при переходе от узла d анализируемой цепи к узлу b (см. полярность падения напряжения на сопротивлении в зависимости от тока на рис. 2.15).

Далее мы определяем потенциал точки m анализируемой цепи:

Знаки w и соответствуют полярностям, показанным на диаграмме на рисунке 2.15.

Далее, после точки m анализируемой цепи является узел a. Его потенциал равен:

Рисунок 2.15: Эквивалентная схема анализируемой цепи для потенциальной диаграммы

Далее мы определяем потенциал узла c, значение которого будет равно:

Потенциал точки sза узлом c вдоль выбранного нами контура, равна:

Пройдя таким образом весь контур d-b-m-a-c-s-dмы возвращаемся к узлу d. Таким образом, потенциал узла d должна стать равной нулю. Это действительно так, поскольку при приближении из узла c к узлу dПотенциал последних станет равным:

Вычислив численные значения потенциалов для петель d-b-m-a-c-s-d можно построить саму потенциальную диаграмму. Эта диаграмма показана на рисунке 2.16.

Техника построения потенциальной диаграммы следующая. По осям декартовой системы координат откладываются потенциалы и сопротивления для цепи (системы), выбранной ранее для построения потенциальной диаграммы. В нашем примере, рис. 2.15, это контур d-b-m-a-c-s-d. Значения ранее рассчитанных потенциалов для каждой точки на этом контуре откладываются на вертикальной оси (ось ординат) в диапазоне положительных или отрицательных значений, в зависимости от знака потенциала, полученного ранее при расчете. В нашем примере это будут потенциалы , , , , , , и снова точки d-b-m-a-c-s-dсоответственно. Порядок расположения значений потенциала на потенциальной диаграмме соответствует их порядку при расчете значения потенциала. d-b-m-a-c-s-d .. Значения сопротивления откладываются на горизонтальной оси (ось абсцисс) декартовой системы координат. За нулевое (начальное) значение сопротивления в потенциальной диаграмме принимается значение в опорном узле; в нашем примере с рис. 2.15 это значение сопротивления в узле d. Затем, при шунтировании цепи, цепь, выбранная для потенциальной диаграммы (в нашем примере цепь d-b-m-a-c-s-d), значения сопротивления в каждой последующей точке прибавляются к значениям сопротивления в предыдущей точке.

Таким образом, сопротивление в каждой точке контурной потенциальной диаграммы оказывается суммарным для этой точки, начиная с опорного узла, где значение сопротивления принимается за ноль. Если в цепи нет сопротивления при переходе от одной точки к другой, к предыдущему значению сопротивления добавляется ноль (это происходит при прохождении источника ЭДС с нулевым внутренним сопротивлением).

Рисунок 2.8.2 Потенциальная диаграмма цепи d-b-m-a-c-s-d тестируемой цепи

В нашем примере значения сопротивления в точках потенциальной диаграммы d-b-m-a-c-s-d являются:

Таким образом, При построении потенциального графика электрической цепи на вертикальной оси декартовой системы координат откладываются потенциалы узлов по мере их перечисления в траверсе цепи, а на горизонтальной оси – возрастающие полные сопротивления также по мере их перечисления в этой траверсе. Потенциальная схема используется для визуального представления распределения потенциалов и соответствующих им сопротивлений вдоль цепи.

Библиография

Основы теории цепей 1. Методические указания и контрольные задания для студентов радиотехнической специальности 0701 “Радиотехника”. A. Мантейфельд, А.Д. Суслов. Москва: МИРЭА. -1980.-48 стр.

Основы теории электрических цепей. Инструкция по выполнению расчетно-графических заданий № 1-2 для студентов радиотехнических специальностей. Составлено. В.И. Вепринцев. Красноярск: Издательство КГТУ, 2000. 64 с.

3) Шебес, М.Р., Каблукова, М.В.. Задачник по теории линейных электрических цепей: учебник для электротехнических, радиотехнических специальностей высших учебных заведений.- Четвертое издание, переработанное и дополненное.- Москва: Общеобразовательный лицей, 1990.-544 с.: иллюстрации.

Основы теории цепей: учебник для средних школ / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. – 5-е издание, пересмотренное. – М.: Энергоатомиздат, 1989 г. – 528 с.

5. 5) Теория линейных электрических цепей: учебник для вузов / Б.П. Афанасьев, О.Е. Гольдин, И.Г. Клацкин, Г.Я. Кузнецов. – М.: Высшая школа, 1973 – 592 с.

Оглавление

1. ЗАДАНИЕ И ВЫБОР ВАРИАНТОВ ДЛЯ ЕГО РЕАЛИЗАЦИИ. 4

2. РАСЧЕТ ЗНАЧЕНИЙ ТОКА ПУТЕМ ПРЯМОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА, МЕТОДОВ КОНТУРНЫХ ТОКОВ, УЗЛОВЫХ ПОТЕНЦИАЛОВ И МЕТОДА ЗАМЕЩАЮЩЕГО ГЕНЕРАТОРА … 9

2.2 Анализ (расчет) сложных электрических цепей 19

используя метод контурного тока 19

2.6.3 Анализ (расчет) сложных электрических цепей 25

метод узловых потенциалов. 25

2.6.4 Анализ (расчет) сложных электрических цепей 31

Использование метода эквивалентного осциллятора. 31

2.5 Баланс мощности в электрической цепи постоянного тока. 40

2.6 Потенциальная диаграмма электрической цепи. 41

Цепь постоянного тока. 41

40 Библиография. 47

Дата добавления: 2018-02-15 ; Дисплеи: 2258 ; ЗАКАЗНАЯ РАБОТА

Равновесие сил является следствием закона сохранения энергии – общая мощность, вырабатываемая (производимая) источниками электроэнергии, равна сумме мощностей, потребляемых в цепи.

Источники E1 и E2 производят электричество, потому что направления электромагнитного поля и тока в ветвях источников одинаковы (если электромагнитное поле и ток в ветвях направлены одинаково). напротив направлении, источник ЭМП потребляет энергию и записывается с минус). Баланс мощности для данной цепи будет записан следующим образом:

С учетом погрешности вычислений, баланс мощности получается следующим образом.

Баланс мощности в электрической цепи

В каждой электрической цепи должен существовать энергетический баланс, баланс мощности: алгебраическая сумма мощностей всех источников энергии (источников напряжения и источников тока) равна арифметической сумме мощностей всех потребителей энергии, т.е.

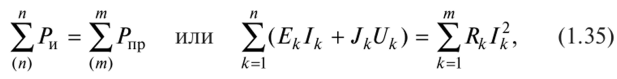
где п – количество источников энергии; т – количество резистивных элементов в цепи; Е_ки1_к — ЭДС и ток источника напряжения; J_k и (J_k — это ток и напряжение на клеммах источника тока.

После учета внутреннего сопротивления источников мощность каждого источника напряжения меньше развиваемой им мощности ?_И (US/_И источники тока) на потери мощности R_mI_H (G_BTU_H).

Мощность HI следует рассматривать как положительную и записывать в уравнение баланса мощности (1.35) со знаком плюс, если направление тока положительное /._и совпадает с направлением ЭМП Е, и для ИТ, если направления тока не совпадают J и напряжение U_K на своих терминалах. В других случаях эти силы следует рассматривать как отрицательные и записывать со знаком минус (например, для заряженной батареи).

Упражнение 1.4. Проверьте расчет токов (/, = 11 A, /₂ = 1 А, / = 10 А) цепи (рис. 1.28) с параметрами Е_х = 14,4 В, Е₂ = 12 В, /?_wt1 = /?_wt2 = 0,2 Ом, R= 12,2 Ом в соответствии с балансом мощности.

Выполним баланс мощности с учетом взаимных направлений ЭДС и токов активных элементов.

1. мощность источников напряжения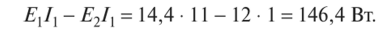

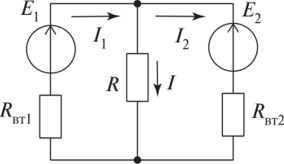
Активный элемент Е₂, где направление тока противоположно направлению ЭДС, является приемник энергия, поскольку ее мощность отрицательна (Р_н2 = Е₂1₂ 0).

2 Потребители энергии (пассивные элементы)

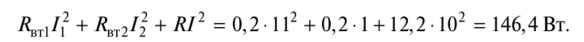
Емкости активного и пассивного элементов равны, поэтому расчет токов в цепи верен.

Сначала мы свернем цепь и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

Баланс сил

При решении электрических проблем часто необходимо проверить правильность найденных значений. Для этого в науке о технике существует так называемая баланс сил.

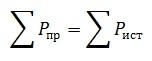
Или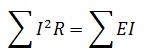

Давайте проверим эту взаимосвязь на простом примере.

Давайте сначала разложим схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

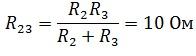
Используя закон Ома, находим ток источника и напряжение на R₂₃предполагая, что r₁ и Р₂₃ соединены последовательно, поэтому ток одинаков.

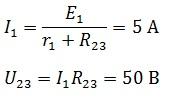
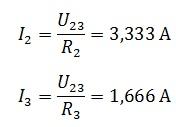
Теперь проверьте правильность с помощью баланса мощности.

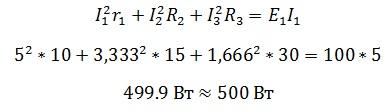
Небольшая разница в значениях обусловлена округлением при расчете.

Как видите, независимо от сложности схемы, баланс сходится, и он должен сходиться в каждой схеме!

мощность, доступная у j-го источника тока или силы тока, Вт; – мощность, доступная у j-го источника тока или силы тока, Вт
j-
сопротивление, W.

Определение баланса сил

Институт информационных технологий

Специализация “Программное обеспечение для информационных технологий”.

ТЕСТОВАЯ РАБОТА №2

По курсу “Теория электрических цепей”

Полное имя Галина Дубровская

Адрес: Гомель, ул. 4-я Рабочая, 301

Представьте баланс сил. Найдите силу тока в сопротивлении R3. Найдите напряжение между узлами 5 и 6 (U56)

Номер филиала

Начало – Конец

Сопротивление

источник ЭДС, V

Источники тока, A

Давайте построим график этой цепи. Расположите узлы таким образом, чтобы их ветви не пересекались (Рисунок 1)

Включите источники сопротивления и ЭДС в ветви цепи. Подключите источники тока параллельно к соответствующим ветвям (рис.2).

Расчет токов с использованием метода преобразования

В схеме (рис.2) преобразуем источник тока J02 в источник напряжения E02:

Источник тока J06 к источнику напряжения E06:

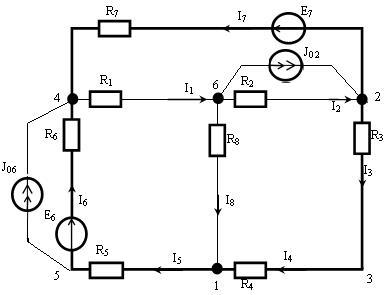
Полученная схема показана на рис. 3. В этой схеме источники напряжения E6 и E06 подключены к источнику напряжения E’6:

последовательно соединенные резисторы

Рисунок 3: Схема преобразованной цепи.

Чтобы создать пассивный треугольник 3-1-6, мы заменим источник напряжения E02 на источник тока J’2

Преобразуем пассивную дельту 3-1-6 в пассивную звезду (рис.4), где

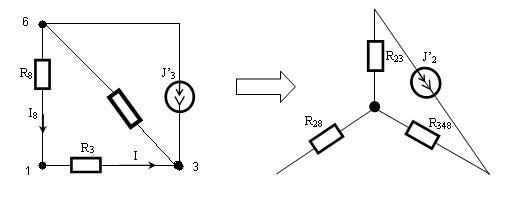
Рис.4 Дельта-звездное преобразование.

Преобразуем источник тока J’2 в источник напряжения:

В результате этих преобразований схема будет иметь следующий вид, показанный на рисунке 5.

Рисунок 5: Преобразованная электрическая схема

Чтобы еще больше упростить схему, давайте объединим источники напряжения и сопротивления:

Теперь схема выглядит следующим образом (рис.6):

Рисунок 6. преобразованная электрическая схема

Далее применяем метод узловых напряжений. Для определения напряжения U02 необходимо одно уравнение:

Давайте определим токи на рисунке 6 на основе второго закона Кирхгофа:

Запишем уравнение согласно второму закону Кирхгофа для цепи 4-6-1-5 (рис. 3):

Для определения неизвестных токов

, , , , , составим уравнения для узлов 6, 2, 1, 4 по первому закону Кирхгофа (рис.2):

Определение баланса сил

ЭДС положительна, если направления ЭДС и тока ветви равны, и отрицательна, если ЭДС и ток ветви противоположны.

Мощность источника тока определяется произведением тока этого источника и напряжения на его зажимах. Он положителен, когда направления клемм источника и тока источника противоположны.

Мощность, рассеиваемая в активных резисторах, всегда положительна и равна:

Баланс сил записывается как

Где m – количество источников ЭДС в цепи;

n – количество источников тока в цепи;

f – количество активных резисторов в цепи.

Давайте сделаем баланс мощности для схемы на рисунке 2:

Поскольку мощность источников равна мощности тепловых потерь, значения рассчитанных токов верны.

Источник статьи https://lektsii.org/5-47550.html

Стандартная форма полного бухгалтерского баланса содержит пункты, которые могут потребоваться бухгалтеру для заполнения формы. Балансовый отчет составляется с учетом специфики бизнеса и наличия или отсутствия определенных видов данных. Поэтому не все строки могут быть заполнены. Кроме того, строки могут быть уточнены, добавлены при необходимости. Об этом говорится в ПБУ 4/99 (п. 11), приказе № 66н п. 3. 3.

Как заполнять строки

Рассмотрим, какие счета и как используются при составлении баланса, в соответствии с Планом счетов бухгалтерского учета (Приказ Минфина № 94н).

Активы

Раздел 1 актива баланса “Внеоборотные активы” заполняется таким образом:

Нематериальные активы (НМА), стр. 1110. Дт. 04 – Дт. 05. Затраты на исследования и разработки не показаны.
Результаты исследований и разработок, с. 1120. дт. 04 для НИОКР.
Нематериальные активы геологоразведки (НА), стр. 1130. dt. 08 – Дт. 05 (оба счета учитываются для нематериальных ПА).
Нематериальные ПА, стр. 1140. Дт 08-Кт 02 (оба счета используются для материальных основных средств).
Основные средства, стр. 1150 Дт. 01 по Дт. 02 (без учета амортизации прибыльных инвестиций в основные средства).
Выгодные инвестиции в ценности, с. 1160. Дт. 03-Кт. 02 (без учета амортизации основных средств).
Инвестиции, стр. 1170. Дт. 58 – Дт. 59 (только для долгосрочных финансовых инвестиций) + Дт. 73/1 (только для долгосрочных процентных займов, счет 73/1 – расчеты по займам, предоставленным работникам).
Отложенные налоговые активы (ОНА), стр. 1180. dt. 09.
Прочие внеоборотные активы, стр. 1190. Дт 07 + Дт 08 (за исключением поисковых активов) + Дт 97 (затраты с датой списания более 12 месяцев после отчетной даты).

Порядок заполнения 2-й части актива баланса “Оборотные активы”:

Инвентаризация, стр. 1210. Часть 10 + Часть 11 – Кт 14 + Кт 15 + Кт 16 + Кт 20 + Кт 21 + Кт 23 + Кт 28 + Кт 29 + Кт 41 – Кт 42 + Кт 43 + Кт 44 + Кт 45 + Кт 97 (в отношении затрат, не превышающих 12 месяцев с отчетной даты).
НДС на приобретенные ценности, с. 1220; Pwt 19.
Дебиторская задолженность, стр. 1230. 1230. Дт 46 + Дт 60 + Дт 62 – Кт 63 + Дт 68 + Дт 69 + Дт 70 + Дт 71 + Дт 73 (субсчет 73-1 не учитывается) + Дт 75 + Дт 76 (без учета НДС, отраженного на счетах расчетов по авансам выданным и полученным).
Финансовые инвестиции (за исключением денежных эквивалентов), стр. 1240. Дт 58 – Кт 59 (только краткосрочные финансовые инвестиции) + Дт 55/3 (счет 55/3 – депозитные счета) + Дт 73/1 (только краткосрочные процентные займы).
Денежные средства и их эквиваленты, стр. 1250. часть 50 + часть 51 + часть 52 + часть 55 + часть 57. субсчет 50/3 и сальдо субсчета 55/3 не должны признаваться.
Прочие оборотные активы, стр. 1260. 1260. Дт 50/3 + Дт 94.

Обязательства

Таким образом, заполняется третий раздел статьи баланса “Капитал и резервы”:

Уставный капитал (и его юридически определенные варианты), с. 1310. ct 80.
Собственные акции, стр. 1320. dt 81 (в скобках указать, вычтено или не вычтено).
Переоценка основных средств, стр. 1340. Дт 83 (для суммы переоценки).
Дополнительные взносы капитала (без переоценки), стр. 1350. ct 83 (без переоценки).
Резервный капитал, с. 1360. ct 82.
Нераспределенная прибыль (непокрытый убыток), стр. 1370. Кт 99 + Кт 84 (или Кт 99 + Кт 84 указывается в скобках; Кт 84 – Кт 99, Кт 99 – Кт 84, если отрицательный, указывается в скобках).

Порядок заполнения 4-го раздела обязательств “Долгосрочные обязательства”:

Читайте далее: