Определение постоянной времени. Переходные процессы в цепи R-L-C (Лекция № 26) - услуги электромонтажа, строительства и ремонта

В этом случае и

Содержание

Какова постоянная времени

Переходные процессы в цепи с одним накопителем энергии и любым количеством резисторов

Как отмечалось в предыдущей лекции, линейная цепь подвержена одному переходному процессу. Поэтому в рассматриваемом одиночном накопителе энергии (индукторе или конденсаторе), системы первого порядка, постоянная времени будет одинаковой для всех свободных составляющих напряжений и токов ветвей цепи, параметры которых входят в характеристическое уравнение.

Общий подход к переходным процессам в таких цепях основан на теореме об активном двухполюснике: накопительная ветвь удаляется из цепи, а остальная часть цепи рассматривается как активный двухполюсник А (эквивалентный осциллятор) (см. рис. 1, а) со схемой на рис. 1, б.

Совершенно очевидно, что постоянная времени для цепей с индуктивным элементом определяется здесь как:

, а с емкостным как:

где – входное сопротивление цепи относительно клемм подключения ветви 1-2, содержащей накопитель энергии.

Например, для напряжения на конденсаторе в схеме на рисунке 2 можно написать

где, в соответствии с вышеизложенным

Переходные процессы при последовательном соединении
R-L-C цепь к источнику напряжения

Рассмотрим два случая:

В соответствии с процедурой расчета переходных процессов классическим методом, описанной в предыдущей лекции, для напряжения на конденсаторе в цепи рис. 3 можно написать

Тогда, для первого случая, вынужденная составляющая этого напряжения

характеристическое уравнение цепи

решая это уравнение, получаем

В зависимости от соотношения параметров цепи возможны три типа корней, и, соответственно, три варианта выражения для свободного компонента:

1. или , где -. критическое сопротивление контура, ниже которого свободный процесс становится колебательным.

2 – Предельный случай апериодического режима.

В этом случае и

3. – Периодический (осциллирующий) характер переходного процесса.

В этом случае i

где – коэффициент демпфирования; -. угловая частота собственных колебаний; – период естественных колебаний.

Из-за апериодического характера переходного процесса, после подстановки (2) и (3) в уравнение

Чтобы найти константы интегрирования, учитывая, что в общем случае и согласно первому закону коммутации , мы напишем два уравнения для t = 0:

решая, получаем

Тогда ток в цепи

и напряжение на индукционной катушке

На рис. 4 показаны кривые качества для , и , соответствующие апериодическому переходному процессу в .

Для критического режима на основе (2) и (4) можно написать

Для колебательных переходных процессов в соответствии с (2) и (5) имеем

Чтобы найти константы интегрирования, напишите

На рис. 5 показаны кривые качества и , соответствующие колебательному переходному процессу при .

При подключении R-L-C цепи к источнику синусоидального напряжения для нахождения вынужденных составляющих тока в цепи и напряжения на конденсаторе используйте символический метод расчета, согласно которому

Здесь также возможны три режима работы:

1. ;

Наиболее интересным является третий режим, связанный с появлением в переходном процессе собственных колебаний с частотой . В этом случае, в зависимости от соотношения собственной частоты и напряжения источника, возможны три варианта характеристик: 1 – ; 2 – ; 3 – , – которые показаны на рис. 6,а … 6,c, соответственно.

Основы Теория цепей : учебник для средних школ / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. -Пятое издание, пересмотренное. -М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учебник для студентов вузов, изучающих электротехнику, энергетику и приборостроение. -Седьмое издание, переработанное и дополненное. М.: Высшая школа, 1978. -528с.
Теоретический Основы электротехники. Учебник для высших учебных заведений. В трех томах. Под общей редакцией К.М. Поливанова. Том 1. К.М. Поливанов. Линейные электрические цепи с сосредоточенными константами (на русском языке). -М.: Энергия, 1972. -240с.

Обзорные вопросы

Как определить постоянную времени цепи с одним аккумулятором энергии, глядя на осциллограмму тока или напряжения в любой ветви?
Определите, какой процесс, зарядка или разрядка конденсатора в цепи рис. 2, будет происходить быстрее?

Эта константа цепи называется “tau”, измеряется в секундах и обозначается соответствующей греческой буквой. Численно для RC-цепи он равен R*C, где R выражается в омах, а C – в фарадах.

Постоянная времени электрической цепи – что это такое и где она используется

Для природы характерны периодические процессы: день сменяется ночью, теплые времена года сменяются холодными и т.д. Период этих событий практически постоянен и поэтому может быть строго определен. Более того, мы вправе сказать, что периодические природные процессы, приведенные в качестве примера, не подавляются, по крайней мере, в отношении времени жизни отдельного человека.

Однако в технике, и особенно в электротехнике и электронике, не все процессы являются периодическими и незатухающими. Как правило, электромагнитный процесс сначала увеличивается, а затем уменьшается. Часто она ограничивается фазой начала колебания, которая никогда не достигает своей полной величины.

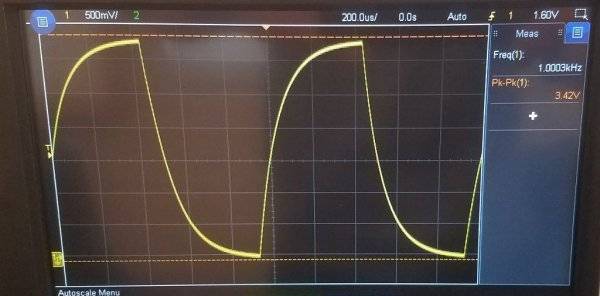
В электротехнике мы очень часто сталкиваемся с так называемыми экспоненциальными переходными процессами, суть которых заключается в том, что система просто стремится достичь определенного равновесного состояния, которое в конечном итоге выглядит как состояние покоя. Такое переходное состояние может быть возрастающим или убывающим.

Внешняя сила сначала выводит динамическую систему из состояния равновесия, а затем не препятствует естественному возвращению системы в исходное состояние. Эта последняя фаза называется переходным процессом и характеризуется определенной продолжительностью. Кроме того, процесс вывода системы из равновесия также является переходным процессом с характерной продолжительностью.

В любом случае, постоянная времени переходного процесса – это временная характеристика процесса, которая определяет время, в течение которого параметр процесса изменяется на коэффициент “e”, то есть увеличивается или уменьшается примерно в 2,718 раза по отношению к начальному состоянию.

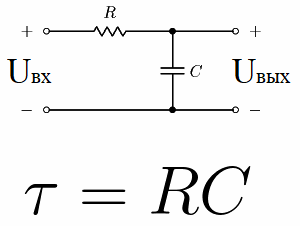
Рассмотрим, например, электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Этот тип цепи, в которой резистор соединен последовательно с конденсатором, называется интегрирующей RC-цепью.

Если к такой цепи в начальный момент приложить мощность, т.е. постоянное напряжение Uin, то Uout, т.е. напряжение на конденсаторе, начнет расти по экспоненте.

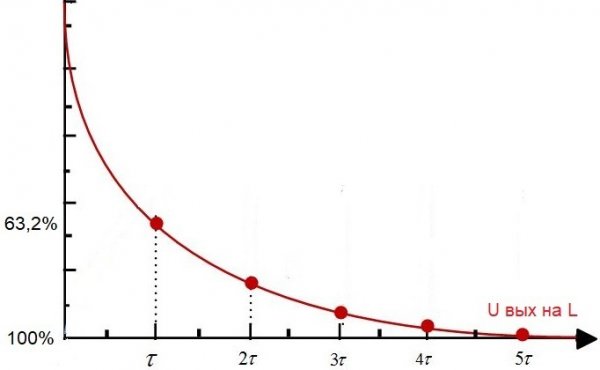
Через время t1 напряжение на конденсаторе достигнет 63,2% от входного напряжения. Таким образом, интервал времени от начального момента до t1 будет постоянной времени этой RC-цепи.

Интегрирующие RC-цепочки используются в электронике в качестве фильтров низких частот, когда высокие частоты должны быть отсечены (ослаблены), а низкие частоты должны быть пропущены.

На практике этот механизм фильтрации основан на следующем принципе. Для переменного тока конденсатор действует как емкость, величина которой обратно пропорциональна частоте, т.е. Чем выше частота, тем меньше будет емкость в омах.

Поэтому, если через RC-цепь протекает переменный ток, то, подобно плечам делителя напряжения, через конденсатор будет падать напряжение, пропорциональное его емкости на частоте протекающего тока.

Если известны частота среза и амплитуда входного переменного сигнала, конструктору несложно подобрать конденсатор и резистор в RC-цепочке так, чтобы минимальное (частота среза – верхняя граница частоты) напряжение (для частоты среза) падало на конденсатор в виде реактивного сопротивления, включенного в делитель вместе с резистором.

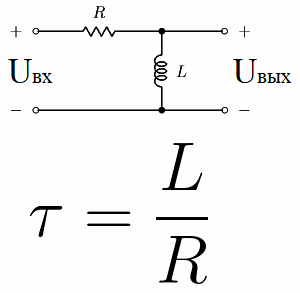
Теперь рассмотрим так называемую дифференциальную схему. Это цепь, состоящая из резистора и индуктора, соединенных последовательно, – цепь RL. Его постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.

Если к такой цепи приложить постоянное напряжение от источника, то через время tau напряжение на катушке уменьшится по отношению к Uin на 63,2%, что полностью соответствует постоянной времени этой цепи.

В цепях переменного тока (сигналах переменного тока) LR-контуры используются в качестве фильтров высоких частот, когда низкие частоты должны быть отсечены (подавлены), а частоты выше (выше частоты отсечки – нижняя частотная граница) должны быть пропущены. Чем выше частота, тем выше индуктивное сопротивление катушки.

Как и в случае с RC-цепью, рассмотренной выше, здесь используется принцип делителя напряжения. Ток более высокой частоты, протекающий через цепь RL, вызовет большее падение напряжения на индуктивности L, как индуктивном резисторе, который является частью делителя напряжения совместно с резистором. Задача конструктора – подобрать R и L таким образом, чтобы минимальное (отсекающее) напряжение на катушке было получено точно на частоте среза.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в своих социальных сетях. Это очень поможет в развитии нашего сайта!

Ниже приведена удобная таблица для оценки доли непостоянного значения напряжения конденсатора относительно конечного асимтотического значения (e -t/τ ) в моменты времени t от t=0.001τ до t=10τ экспоненциального процесса.

Term: постоянная времени RC-цепи

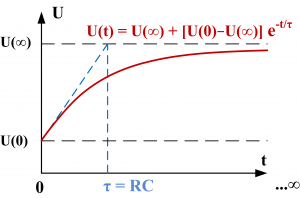
τ – постоянная времени RC-цепи. Это постоянная времени простой электрической цепи, в которой заряд конденсатора С изменяется за счет его разряда через сопротивление R. Постоянная времени рассчитывается как τ=R*C [Ф*Ом], что соответствует размерности “секунда” [c].

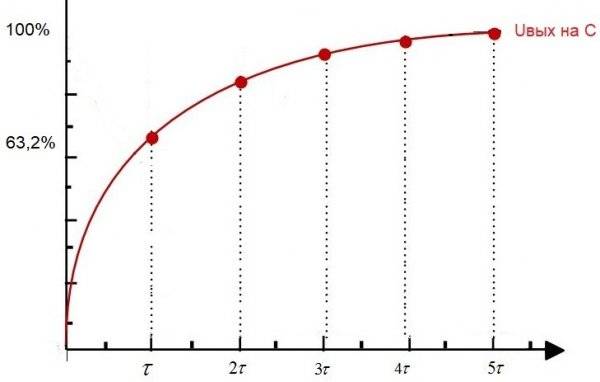
Как видно из рисунка, постоянная времени τ является частью аналитической функции, описывающей процесс изменения напряжения на конденсаторе U(t) при его зарядке от источника напряжения через сопротивление R. На рисунке U(0) – это начальное напряжение на конденсаторе (в момент времени t=0), а U(∞) – напряжение источника напряжения, к которому асимптотически переходит U(t).

За время, равное τ, напряжение на конденсаторе изменяется от U(0) до U(∞) + [U(0) – U(∞)]/e, где e=2,718. …

Экспоненциальный заряд конденсатора происходит для случая U(∞) > U(0), а экспоненциальный разряд – для случая U(∞) < U(0).

Геометрический смысл постоянной времени – это касательная к экспоненте (проекция на ось абсцисс отрезка касательной, проведенной между точкой касания и точкой пересечения с этой осью).

Ниже приведена удобная таблица для оценки доли непостоянного значения напряжения конденсатора относительно конечного асимптотического значения (значения e -t/τ ) в моменты времени t от t=0.001τ до t=10τ экспоненциального процесса.

Время процесса в единицах τ=RC	Доля непостоянного напряжения e -t/τ
Время процесса в единицах τ=RC	*100, %	10 6 , ppm*
0,001τ	≈99,9%	≈999000
0,01τ	≈99%	≈990000
0,1τ	≈90%	≈900000
0,5τ	≈61%	≈610000
τ	≈37%	≈370000
2τ	≈14%	≈140000
3τ	≈5,0%	≈50000
4τ	≈1,8%	≈1800
5τ	≈0,67%	≈6700
6τ	≈0,25%	≈2500
7τ	≈0,091%	≈910
8τ	≈0,034%	≈340
9τ	≈0,012%	≈120
10τ	≈0,0045%	≈45

Концепция постоянная времени RC-цепи помогает оценить продолжительность процесса при анализе эквивалентных схем, содержащих RC-цепи. Обратите внимание, что концепция постоянная времени не относится к специальному случаю зарядки-разрядки конденсатора постоянным током, когда закон изменения напряжения и заряда на конденсаторе линейный, а не экспоненциальный.

Постоянные времени RC-цепей (как величины с прозрачным физическим смыслом) участвуют в аналитических решениях дифференциальных уравнений, которые описывают не только экспоненциальные процессы в электрических цепях, содержащих RC-цепи (например, пассивные и активные RC-фильтры).

Если для конденсатора емкостью Cзаряженный до напряжения Uподключить параллельно резистор с сопротивлением Rто в цепи протекает разрядный ток.

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R быть подключен к источнику постоянного напряжения Uцепь будет проводить ток, который в любой момент времени t заряжает конденсатор до значения U_C и определяется выражением:

Тогда напряжение U_C на выводах конденсатора увеличится от нуля до значения U экспоненциально:

U_C = U(1 – e -t/RC )

Когда t = RCнапряжение на конденсаторе будет U_C = U(1 – e -1 ) = U(1 – 1/e) .
Время, численно равное произведению RCназывается постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

С течением времени τ конденсатор будет заряжен до (1 – 1/e)*100% ≈ 63,2% z U.
В момент времени 3τ напряжение составит (1 – 1/e 3 )*100% ≈ 95% от U.
На время 5τ напряжение увеличивается до (1 – 1/e 5 )*100% ≈ 99% от U.

Если конденсатор емкостью Cзаряженный до напряжения Uподключить параллельно резистор с сопротивлением Rто в цепи будет протекать ток разряда конденсатора.

Напряжение на конденсаторе во время разряда составит U_C = Ue -t/τ = U/e t/τ .

В это время τ напряжение на конденсаторе падает до П/экоторая будет равна 1/e*100% ≈ 36,8% от U.
В момент времени 3τ конденсатор разряжается до (1/e 3 )*100% ≈ 5% z U.
В момент времени 5τ к (1/e 5 )*100% ≈ 1% от U.

Параметр τ широко используется в расчетах RC-фильтры различных электронных схем и узлов.

Постоянная времени разряда – это время, необходимое для разряда конденсатора до 36, 8% от первоначального заряда.

14 Постоянная времени RC-цепи

После завершения этого эксперимента вы сможете продемонстрировать, как значения емкости и сопротивления контролируют время заряда и разряда конденсатора.

Необходимые принадлежности

* Цифровой мультиметр

* Источник постоянного напряжения

* секундомер или часы с секундной стрелкой

один электролитический конденсатор 22 мкФ, один электролитический конденсатор 100 мкФ, один резистор 33 кОм, 1/4 Вт,

* один резистор 100 кОм, 1/4 Вт, один резистор 220 кОм, 1/4 Вт, один резистор 1 MΩ, 1/4 Вт.

ВХОДНАЯ ЧАСТЬ

Конденсатор – это электрический компонент, который накапливает электрическую энергию в виде электрического поля. Когда к конденсатору прикладывается постоянное напряжение, электроны покидают одну грань конденсатора и накапливаются на другой грани благодаря

сила внешнего напряжения. В результате конденсатор заряжается до напряжения, равного приложенному напряжению.

Положительный заряд на одной грани конденсатора и отрицательный заряд на другой грани конденсатора создают сильное электрическое поле между гранями в диэлектрике. Этот заряд сохраняется даже при отключении источника напряжения. Конденсатор можно разрядить, соединив его клеммы вместе, чтобы нейтрализовать заряд на катушках.

Зарядка и разрядка конденсатора до определенного напряжения занимает определенное время (называемое постоянной времени); это время зависит в основном от емкости конденсатора и сопротивления, включенного в серию. Постоянная времени заряда – это время, необходимое для заряда конденсатора до 63, 2% от приложенного напряжения. Это время (T) в секундах выражается следующим образом:

Постоянная времени разряда – это время, необходимое для разряда конденсатора до 36, 8% от первоначальной платы.

Время, необходимое для полной зарядки конденсатора до приложенного напряжения или полной разрядки до нуля, приблизительно равно пятикратной постоянной времени, или 5T.

Аннотация

В основе многих электронных схем лежит идея использования постоянной времени для их работы. Такие схемы включают, например, схемы временной задержки, схемы формирования импульсов и сигналов и схемы осцилляторов. В этом эксперименте вы узнаете о постоянной времени зарядки и разрядки с использованием трех различных групп резисторов и конденсаторов.

Процесс зарядки

Резистор 100 кОм; конденсатор 100 мкФ

1 Соберите схему, показанную на рисунке 14-1. Соблюдайте полярность при подключении электролитического конденсатора. 2.

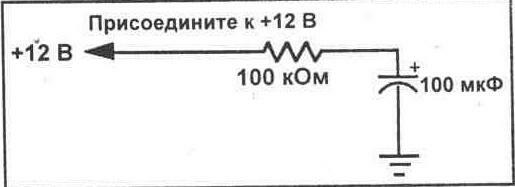
2. установите питание на 12 В.

3. Рассчитайте напряжение, которое появится на конденсаторе за одно фиксированное время.

Напряжение (T) = ______ V

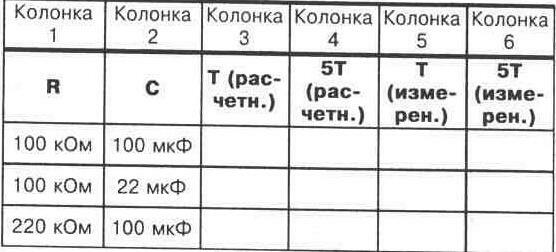
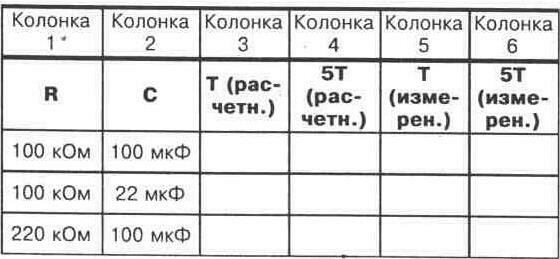
4 Рассчитайте постоянную времени, используя значения, показанные на рисунке 14-1. Запишите результат в столбец 3 рисунка 14-2. Также рассчитайте значение времени, необходимого для полной зарядки конденсатора (5T). Запишите свой результат в колонку 4 на рисунке 14-2.

5 Подключите тестовые провода мультиметра, соблюдая полярность, к выводам конденсатора. Мультиметр должен показывать 0 вольт. Если этого не происходит, значит, на клеммах конденсатора имеется остаточное напряжение. Устраните это, замкнув контакты конденсатора вместе на несколько секунд. Снова измерьте напряжение мультиметром, чтобы убедиться, что напряжение на конденсаторе равно нулю.

6. Оставьте выводы мультиметра на выводах конденсатора и подключите свободный конец резистора 100 кОм к контакту + источника питания 12 В. При подключении

Запустите секундомер или начните отсчет времени по секундной стрелке ваших часов. Когда напряжение на конденсаторе начнет расти, запишите его значение. Когда напряжение на конденсаторе достигнет значения, рассчитанного в шаге 2, засеките время с помощью секундомера или секундной стрелки. Запишите это значение в качестве измеренной постоянной времени в колонке 5 на рисунке 14-2.

ПРИМЕЧАНИЯ: Повторите этот шаг несколько раз, чтобы убедиться, что показания времени относительно точны. Наконец, вы пытаетесь наблюдать за показаниями как вольтметра, так и секундомера, чтобы определить время, необходимое для достижения определенного уровня напряжения. Это довольно громоздкая операция, поэтому повторите ее несколько раз, чтобы получить более точное измерение. ПРЕДУПРЕЖДЕНИЕ:

если необходимо повторить эксперимент, удалите резистор 10 кОм и полностью разрядите конденсатор 100 мкФ, прежде чем приступать к каждому последующему измерению. 7. Снова полностью разрядите конденсатор и снова подсоедините тестовые провода. Подключите свободный вывод резистора 100 кОм к клемме +12 В источника питания. На этот раз измерьте время, необходимое для полной зарядки конденсатора до напряжения, приложенного в шаге 1. Как и раньше, начинайте отсчитывать время с помощью секундомера или секундной стрелки часов по мере подачи напряжения на резистор. Запишите это измеренное время,

который необходим для полной зарядки конденсатора, в столбце 6 рисунка 14-2.

Резистор 11 к0м; конденсатор 22 мкф

(8) Повторите шаги с 4 по 7, используя конденсатор 22 мкф и резистор 100 к0м. Заполните поля в таблице на рисунке 14-2, как вы это делали ранее. С расчетными и измеренными значениями.

Резистор 220 к0м; конденсатор 100 мкФ.

9. повторите шаги с 4 по 7 еще раз, но на этот раз используйте конденсатор 100 мкФ и резистор 220 к0м. Запишите рассчитанные и измеренные значения в таблицу на рисунке 14-2.

Наблюдения

10. Изучив информацию на рисунке 14-2 и отметив различные значения времени, полученные при различных значениях сопротивления и емкости, сделайте собственный вывод о влиянии значений сопротивления и емкости на постоянную времени.

Процесс опорожнения

Резистор 100 к0м; конденсатор 100 мкФ

11 Соберите схему в соответствии со схемой, показанной на рис. 14-3. Соблюдайте полярность при подключении электролитического конденсатора. В этой части эксперимента мы продемонстрируем процесс разрядки конденсатора. Для этого подключите резистор параллельно конденсатору.

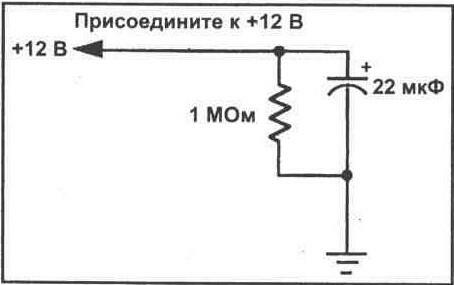
(12) Рассчитайте постоянную времени цепи и время, необходимое для полной разрядки конденсатора, и запишите свои данные в столбец 3 рисунка 14-4.

13. Далее определите величину напряжения, до которого конденсатор разрядится за одну постоянную времени. Используйте начальное напряжение

источника питания, который был измерен на этапе 1. Рассчитайте напряжение, которое будет присутствовать на конденсаторе после его разрядки в течение фиксированного времени.

Напряжение (t) = _______ V

Резистор 100 кОм; конденсатор 22 мкф

14 Подключите тестовые провода мультиметра к конденсатору емкостью 22 мкФ. В этот момент напряжение должно быть равно нулю, поскольку любой заряд на катушках конденсатора был устранен разрядкой конденсатора через резистор 1 МОм. Подключите схему к контакту +12 В + источника питания. Конденсатор заряжается сразу до напряжения питания; резистор последовательно с конденсатором не подключен.

15. Продолжайте подключать тестовые провода мультиметра параллельно выводам конденсатора. Отсоедините соединительный провод от + провода источника питания 12 В. Одновременно с удалением поводка начните отсчет времени с помощью секундомера или секундной стрелки часов. При этом следите за напряжением на клеммах конденсатора. Когда напряжение достигнет желаемого значения, засеките время. Запишите постоянную времени в столбец 5 таблицы на рисунке 14-4. как и раньше. Вы можете повторить шаги 13 и 14 несколько раз, чтобы повысить точность измерения. Поскольку вам приходится наблюдать две величины одновременно, измерение довольно сложно. Усреднив несколько показаний, вы добьетесь большей точности измерений.

Резистор 220 кОм; конденсатор 22 мкф

16 Повторите шаги с 12 по 15 еще раз, но на этот раз используйте конденсатор 22 мкФ и резистор 220 кОм. Снова рассчитайте значения времени разряда для одной постоянной времени и для пяти постоянных времени. Запишите все свои данные в таблицу на рисунке 14-4.

Наблюдение

17. Проанализировав информацию на рисунке 14-4 и отметив различные значения времени, полученные при разных значениях сопротивления и емкости, сделайте вывод о связи между временем разряда и значениями сопротивления и емкости.

18. На основе сравнения рассчитанных и измеренных значений объясните любые расхождения.

ОБЗОРНЫЕ ВОПРОСЫ

1 Для полной зарядки конденсатора требуется столько же времени, сколько и для его полной разрядки:

(a) утверждение истинно,

б) утверждение является ложным.

. 2 До какого напряжения будет заряжаться конденсатор 5 мкф резистором 10 кОм за одну постоянную времени при подключении к источнику питания 6 В?

3. сколько времени потребуется конденсатору из вопроса 2, чтобы полностью разрядиться?

4. конденсатору требуется 80 миллисекунд для полной зарядки. Поэтому постоянная времени равна:

5. Для заданного значения R (сопротивления) и C (емкости) емкость удваивается, а сопротивление уменьшается вдвое, с постоянной времени:

Номинальный f _{3 дБ} вытекает из выражения мощности в децибелах и наблюдения, что половина мощности соответствует уменьшению | V _∞ | на коэффициент 1 / √2 или 3 децибела.

Примеры

Постоянные времени в электрических цепях

В цепи RL, состоящей из резистора и индуктора, постоянная времени (в секундах) равна τ

Аналогично, в RC-цепи, состоящей из одного резистора и конденсатора, постоянная времени (в секундах) равна τ

τ знак равен p C

где R – сопротивление (в омах) и C – емкость (в фарадах).

Электрические цепи часто сложнее этих примеров и могут иметь несколько постоянных времени (см. некоторые примеры в разделах “Переходная характеристика” и “Разделение полюсов”). При наличии обратной связи в цепи могут наблюдаться неустойчивые нарастающие колебания. Кроме того, физические электрические цепи редко являются действительно линейными системами, за исключением очень низкоамплитудных возбуждений; тем не менее, приближение линейности широко используется.

В цифровых электронных схемах часто используется другая мера, FO4. Это можно перевести в единицы постоянной времени с помощью уравнения . 5 τ знак равен FO4 >>

Тепловая постоянная времени

Постоянная времени является характеристикой фокусированного системного анализа (метод фокусированного анализа мощности) для тепловых систем, который используется, когда объекты равномерно охлаждаются или нагреваются конвективным охлаждением или нагревом. В этом случае теплопередача от тела к окружающей среде в определенный момент времени пропорциональна разнице температур между телом и окружающей средой:

где h – коэффициент теплопередачи , A _s – поверхность T – температурная функция, т.е. T ( t ) – температура тела в момент времени t , а T _a – постоянная температура окружающей среды. Положительный знак указывает на то, что F положительна, если тепло уходит за пределами тело, потому что его температура выше температуры окружающей среды ( F – является исходящим потоком). Если тепло теряется в окружающую среду, его отдача вызывает снижение температуры тела, определяемое по формуле:

где ρ = плотность, с _р = удельная теплоемкость и V представляет собой объем тела. Отрицательный знак указывает на снижение температуры, когда радиатор переходит в состояние покоя. за пределами вдали от тела (т.е. когда F > 0). Уравнение этих двух выражений для теплопередачи,

Очевидно, что это LTI-система первого порядка, которую можно представить в виде:

Другими словами, постоянная времени указывает на то, что большие массы ρV и высокая теплоемкость c _p приводит к более медленному изменению температуры, в то время как большая площадь поверхности A _s и лучшая теплопередача h приводят к более быстрым изменениям температуры.

Сравнение с вводным дифференциальным уравнением предполагает возможное обобщение на изменяющуюся во времени температуру окружающей среды T _a . Однако, сохраняя простой пример постоянной среды, подставляя переменную Δ T ≡ ( T – T _a ), можно найти:

Системы, для которых охлаждение удовлетворяет приведенному выше экспоненциальному уравнению, считаются удовлетворяющими закону охлаждения Ньютона. Из решения этого уравнения следует, что в таких системах разница между температурой системы и ее окружения Δ T как функция времени t определяется выражением

где Δ T ₀ – начальная разность температур в момент времени t = 0. Другими словами, тело принимает ту же температуру, что и окружающая среда, с экспоненциально медленной скоростью, определяемой постоянной времени.

Постоянные времени в нейробиологии

В возбудимой клетке, такой как мышца или нейрон, постоянная времени мембранного потенциала равна τ

где r _m – сопротивление через мембрану, и c _m – производительность мембраны.

Сопротивление мембраны зависит от количества открытых ионных каналов, а емкость – от свойств липидного слоя.

Постоянная времени используется для описания нарастания и спада мембранного напряжения, где нарастание описывается выражением

а снижение описывается

где напряжение – в милливольтах, время – в секундах. τ

V _max определяется как максимальное изменение напряжения от потенциала покоя , где

где r _m – сопротивление через мембрану, I – ток, протекающий через мембрану.

Обстановка для t = для увеличения настройки V ( t ) равна 0,63 В _макс. . Это означает, что постоянная времени – это время, прошедшее после 63%. V _max была достигнута τ

Обстановка для t = для осенних наборов V ( t ) равна 0,37 В _{максимум. Это} означает, что постоянная времени – это время, прошедшее с момента падения до 37% от _{максимальный} напряжение . τ

Чем больше постоянная времени, тем медленнее повышается или понижается потенциал нейрона. Большая постоянная времени может привести к суммированию по времени или алгебраическому суммированию повторяющихся потенциалов. Короткая постоянная времени дает детектор совпадений из-за пространственного суммирования.

Экспоненциальный распад

При экспоненциальном распаде, например, радиоактивного изотопа, постоянную времени можно интерпретировать как среднее время жизни. Период полураспада Т _HL связана с экспоненциальной постоянной времени через τ

Обратная величина постоянной времени называется константой затухания и обозначается . Знак λ равен 1 / τ лямбда = 1 / тау

Метеорологические датчики

Постоянная времени – это время, необходимое метеорологическому датчику для реакции на быстрое изменение измеряемого значения до тех пор, пока он не измерит значение в пределах допуска точности, обычно ожидаемого для данного датчика.

Чаще всего это относится к измерениям температуры, температуры точки росы, влажности и давления воздуха. Радиозонды особенно страдают из-за быстрого увеличения высоты.

Читайте далее: