ПИД-регулятор

Компонент интеграции просто суммирует ту же ошибку, разницу между текущим значением и целевым значением, умноженную на период выборки системы, т.е. время, прошедшее с момента предыдущего расчета dt – на самом деле берется интеграл ошибки по времени.

Содержание

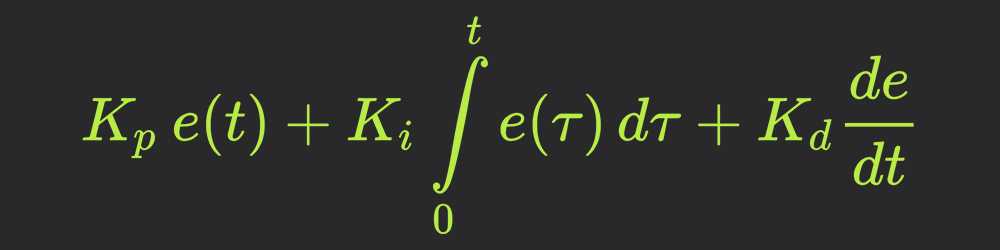
ПИД-регулятор является одним из самых популярных автоматических регуляторов. Он настолько универсален, что используется практически везде, где требуется автоматическое управление. Например, температура: специальные печи, кулеры, инкубаторы, паяльники, насадки и стол для 3D-принтеров, инфракрасные паяльные станции и т.д. Регулирование скорости вращения двигателя, например, в станках. Всевозможные балансирующие штуки, гироскопические скутеры, сегвеи, левитирующие магнитные платформы и, конечно, квадрокоптеры и самолеты с автопилотом. Это все ПИД-регулирование. Почему именно PID? Существуют и другие регуляторы, которые превосходят ПИД-регулятор по адаптивности и стабильности, например, линейно-квадратичные регуляторы. Однако для грамотного синтеза такого регулятора требуется гораздо больше, чем гаечный ключ в голове, а настройка ПИД-регулятора – это неприятная, но, по сути, очень простая операция, которую может выполнить каждый, а сам ПИД-регулятор универсален практически для любого процесса.

Смена этапа (t+1) = Функция

ПИД-регуляторы – для фиктивных практиков

Недавно я пообещал своему другу – хорошему электрику и тупице, практикующему в электронике – сделать небольшое устройство в автомобиле, которое будет поддерживать обороты на низком уровне путем регулировки дроссельной заслонки (все подробности о детали автомобиля будут позже). Я знаю, что мы называли эту штуку умным словом “регулятор холостого хода”). И эти обороты должны зависеть от текущей температуры двигателя. “Значит, тебе придется работать с ПИД-регулятором”, – сказал я ему. И ответом был туман в глазах, дым в ушах и дрожащий голос – “И это не имеет никакого отношения к СПИДу. “. В любом случае, вам придется объяснять ему детали, избегая при этом математики. В интернете есть море статей на эту тему (начните отсюда). Моя статья – это еще одна ложка в море информации. Если вы заинтересованы, пожалуйста, обратитесь к этой ссылке!

Что нам делать?

Поэтому мы делаем регулятор холостого хода.
В этом случае требуется система управления с обратной связью. В своей статье о датчиках и АЦП я рассказывал о системе управления с замкнутым контуром, подробности ищите там. Там также была красивая фотография на эту тему:

Что это будет в данном случае?
Мы хотим контролировать скорость двигателя на холостом ходу. Для этого у нас есть шаговый двигатель, который открывает/закрывает дроссель, регулирующий подачу воздуха. У нас также есть таблица, которая определяет желаемую скорость вращения двигателя в зависимости от текущей температуры. Здесь объект управляется шаговым двигателем. Состояние объекта определяется 1) скоростью вращения двигателя и 2) текущей температурой.
Для этого изображения мы получаем следующие данные:

Объект – двигатель автомобиля;
Измерение выполняется для 1) частоты вращения двигателя (в нашем случае это интервал времени между последовательными импульсами тахометра, которых два на оборот) и 2) температуры двигателя (сопротивление термистора);
Влияние направлена на обороты двигателя, для этого регулируется воздушная заслонка. Он регулируется шаговым двигателем. Таким образом, мы задаем степень смещения для шагового двигателя;
Расчет – Расчет необходимого смещения в зависимости от 1) скорости вращения двигателя, 2) температуры двигателя, 3) текущего состояния шагового двигателя;
Общение в данном случае отсутствует (однако я выведу COM-порт для конфигурации/диагностики устройства).

Что это за функция? Он дает нам текущее значение шага, которое зависит от всех вышеперечисленных факторов. Как это работает?
Вся собака зарыта в том, что мы хотели получить один оборот для данного шага, а на самом деле они совершенно разные! Поэтому нам нужно знать значение текущей ошибки (несоответствие), и его можно рассчитать как разницу между ожидаемым будущим оборотом и текущим оборотом:

Ошибка (t) = Обороты (t+1) — Обороты (т).

В случае, когда обороты четко соответствуют требуемому значению (к чему мы и стремимся), ошибка будет равна нулю. Эта ошибка показывает нам, насколько сильным должно быть воздействие.
Теперь формула для следующего шага может быть записана следующим образом:

Теперь вы можете вынести значение из предыдущего шага за скобки:

Шаг (t+1) = Шаг (t) + Функция

Это понятно? Нам нужно установить текущее положение шагового двигателя на каждом шаге контроллера. Это, понятно, зависит от предыдущего шага и от ошибки. Шаговый двигатель управляется смещением, поэтому нас не так сильно волнует текущий шаг (оставим в стороне тему превышения допустимого количества шагов – моему другу-электрику это знать не обязательно). Вывод таков: мы можем ввести такую запись:

ChangeStep (t+1). = Функция

усмотрениеtили размер шага. С какой частотой мы оказываем свое влияние? Я не знаю – я все еще разбираюсь в этом техническом чуде. Я думаю, что шага в 50 мс будет достаточно. В моей программе это будет конфигурируемый параметр из EEPROM. Но эту тему нельзя игнорировать, и мы к ней еще вернемся;
управление шаговым двигателем. Здесь есть много нюансов. Почитайте в интернете, погуглите – эта тема широко обсуждается;
Связь функции с ростом и скоростью .. Мы рассчитали ошибку, ее размерность совпадает с размерностью RPM (в моем случае это время, мсек). Как она преобразуется в размерность шага? Эту тему мы также пропустим, потому что … Это не имеет никакого отношения к теме самих ПИД-регуляторов. Для особо любознательных я возьму % максимально возможной ошибки (заданный максимальной/минимальной допустимой скоростью) и пропорционально преобразую его в % максимально возможного изменения одного шага (заданный полным диапазоном шагов двигателя).

Формула ПИД-регулятора

Как и было обещано, здесь не будет формул…. хорошо, почти Не многие. И этот раздел – как раз такая формула. Я обещаю, что формул больше не будет! Так что терпите!
Итак, формула для ПИД-регулятора:

(по материалам Википедии)
Здесь у нас есть следующие списки (пояснения чуть ниже):

u (t) – это наш функция;
P – пропорциональная составляющая;
I – неотъемлемый компонент;
D – дифференциальный компонент;
e (t) – это текущая ошибка;
Kp – коэффициент пропорциональности;
Ki – фактор целостности;
Kd – дифференциальный коэффициент;

u(t) = P (t) + I (t) + D (t);
P (t) = Kp * e (t);
I (t) = I (t — 1) + Ki * e (t);
D (t) = Kd * <e (t) — e (t — 1)>;

Теперь он выглядит гораздо более реалистичным и прозрачным! Мы рассчитываем сумму трех компонентов. Каждый из них определяется своими коэффициентами. Если коэффициент равен нулю, компонент не участвует в расчете. Это формула, с которой мы будем работать дальше, и это то, что я намерен реализовать.
Однако есть еще один, повторяемое выполнение:

u(t) = u(t — 1) + P (t) + I (t) + D (t);
P (t) = Kp * <e (t) — e (t — 1)>;
I (t) = I * e (t);
D (t) = Kd * <e (t) — 2 * e (t — 1) + e (t — 2)>;

Какой из них лучше/правильнее? Математика в основном та же самая. Так же как и коэффициенты. Говорят, что при внедрении существуют различные подводные камни.
Обратите внимание! Коэффициенты здесь обязательно являются дробными числами! В языке программирования C, по крайней мере floatили еще лучше двойной.
Магия ПИД-регуляторов заключается именно в этих коэффициентах. Как их выбирать, мы увидим в конце. А пока оставим математику и займемся изучением поведения этой формулы.
Все расчеты и моделирование модели я проводил в Excel. Файл прикреплен ниже, не стесняйтесь играть с ним. Модель предназначена только для ознакомления с идеей! То есть, не пытайтесь свести его к какому-то реальному процессу, искать в нем научный смысл и т.д. Все цифры немного “залежались”. Но файл прост и незатейлив. И он быстро моделируется. И это дает возможность понять суть работы ПИД-регулятора. Наконец, несколько слов о файле.

Пропорциональный компонент

Первый фактор – это пропорциональная составляющая. Она наиболее очевидна и понятна (кстати, я сам когда-то давно вывел формулу для ПИД-регулятора, показал ее кому-то, и он рассказал мне об этой теории; так что я начал вывод с пропорциональной формы).
Давайте посмотрим, как он – фактор пропорциональности – влияет на результат.

“Ожидаемое” – это то, что мы хотим получить. Сначала он равен некоторому низкому значению (в нашем примере это обороты двигателя, создаваемые стартером). Затем, в момент времени 3, он внезапно становится равным 2000 (запустите двигатель, и мы должны получить 2000 об/мин, исходя из текущей температуры).
(Небольшое примечание – в автомобилях частота измеряется в оборотах в минуту. в минуту!)
Давайте сделаем первый вариант: Kp = 2. Посмотрите на красную линию. Что мы видим? Со временем обороты начали увеличиваться – ошибка начала уменьшаться – значение коррекции постепенно увеличивается – красная линия поднимается вверх (обороты двигателя увеличиваются). В какой-то момент (13. по каким-то причинам) оборот достигает требуемого значения. Круто? Круто! Но это немного медленно…
Давайте попробуем другой коэффициент: Kp = 5. Что мы видим? Зеленая линия. Результат достигается быстро – на этапе 6. Отлично! Но здесь – ой! – через (научно сверхрегулирование). Но потом мы вернулись – все в порядке.
Но что если это соотношение еще выше? Kp = 20. Синяя линия – бух! За один шаг! Но – немедленное бегство. Затем падение вниз – ошибка стала отрицательной. Снова жесткий спуск! Поднимайся! Снова вниз! Что мы видим? Поехали. . Они, слава Богу, затухают.
Если мы увеличим коэффициент еще больше, то такие колебания могут стать незатухающими. Система начнет колебаться все сильнее и сильнее, пока . Ну, все зависит от конкретной системы.
Какова природа этих колебаний? Воздействующая система всегда (в действительности) инерциальна. Оборот увеличивается – коэффициент падает до нуля. А потом – попадает в нужную точку. Коэффициент ошибок (и корректировка) достиг нуля. Но процесс ускорения является инерционным! Двигатель запускается, обороты продолжают расти за счет инерции. Затем мы перемещаем амортизатор назад – на более низкие обороты. Мы снова достигаем нуля – скорость падает… и так далее до бесконечности.
Это особенно заметно в системах контроля температуры. Отопление должно быть отключено на нужную температуру – так, чтобы сам нагреватель перестал нагреваться и нагревать объект.
Для решения этой задачи используется следующее решение

Интегральный элемент.

Этот элемент накапливает ошибку (как и любой интегратор). Это означает, что ошибка будет постепенно накапливаться, интегратор будет “заполняться” и его влияние будет возрастать. Эффект от этого накопления не является немедленным – ведь ошибка должна быть накоплена, что требует определенного количества шагов алгоритма.
Рассмотрим случай, когда Kp = 5, а Ki изменится:

Вариант 1 (красный) – Ki = 0.
Вариант 2 (зеленый) – Ki = 0.2.
Вариант 3 (синий) – Ki = -0.3.
Использование положительного коэффициента (зеленая линия) в данном случае было бесполезным. Отрицательный коэффициент (синяя линия) очень помог нам! Но только линия вышла из строя, и тогда это приведет к качанию системы….. (но на практике системные колебания обычно не происходят, потому что…. будут постоянно вноситься коррективы в текущее состояние)
Таким образом, интегральная составляющая позволила нам сгладить резкий эффект пропорциональной составляющей. Это не плохо!
Но подождите – скоро он покажет нам всю свою мощь.

Дифференциальный компонент.

Этот компонент пропорционален на скорость изменений. Как было сказано в комментариях, он “придает ускорение”.
Как и прежде, Kp = 5, а Kd изменится:

Вариант 1 (красный) – Kd = 0.
Вариант 2 (зеленый) – Kd Kd = 0.2.
Вариант 3 (синий) – Kd Kd = -0.2.
Что вы чувствуете? И разглаживает, и предотвращает будущую качку!

Реакция на нарушение

Есть одна вещь, о которой мы не должны забывать – вмешательство. помехи. Они раскачают лодку нашей системы.
Вот картина, когда перед нами стоит задача поддерживать одно и то же значение RPM:

Влияние (случайного) шума одинаково для всех вариантов.
Вариант 1 (красный) – Kp = 10, Ki = 0, Kd = 10.
Вариант 2 (зеленый) – Kp = 10, Ki = 2, Kd = 0.
Вариант 3 (синий) – Kp = 10, Ki = 2, Kd = 6.
Как вы видите, стабильность увеличивается (незначительно) по мере добавления ингредиентов.

Настройка

Я думаю, вы уже имеете общее представление о формуле ПИД-регулирования. Его легко программировать, а результат получается прекрасным. И следующим вопросом будет “как получить коэффициенты”? И вот здесь становится неприятно…. Потому что если до сих пор была строгая математика, то дальше начинаются танцы с бубнами, шаманство и шаманизм. Нет, есть еще точные методы, но меня тошнит от мысли, что я должен это сделать для моего двигателя в машине!
В комментариях мой метод (и мое понимание) настройки был растоптан, похоронен и растоптан. И они посоветовали прочитать хорошую книгу “ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДЛЯ ДЕТЕЙ”. K.Y. Поляков (созвучное название, не находите?). Согласен, тема (настройки) сложная и для меня неоднозначная, поэтому я согласен с комментаторами – стоит прочитать эту книгу и углубиться в тему. Но. это не будет уровень для чайников, верно? В книге Полякова столько узоров, а это уже уровень электрочайника! Поэтому позвольте мне изложить свой подход. Он не идеален, но его достаточно, чтобы начать и изучить тему более подробно.

Во-первых, необходимо иметь четкое представление о вашей системе управления – насколько она инерционна? Какие возмущения могут повлиять на него? Какие воздействия (результаты функции ПИД) для него неприемлемы?
Другой вопрос, в какой степени система может двигаться вперед и назад? Все методы, которые я нашел, основаны на тестировании системы и анализе результатов. Нужно пробовать, пробовать, считать, считать, считать (или по-научному – строить модель)… Но температура двигателя повышается, и через полчаса работы результат будет не таким, как в начале. И как вы в тот же день проверьте работоспособность при температуре -30oC и +30oC.
Вот несколько полезных советов оттуда же:

увеличение коэффициента пропорциональности увеличивает время отклика и уменьшает запас устойчивости;
Уменьшение интеграла приводит к тому, что ошибка управления со временем уменьшается быстрее;
Уменьшение интегральной константы уменьшает запас устойчивости;
Увеличение дифференциальной составляющей увеличивает запас устойчивости и время отклика.

Частота допросов/действий

Существует очень важная рабочая точка при проектировании ПИД-регулятора: Действие должно быть строго периодическимт.е. через регулярные промежутки времени! Аналогично, ошибка также должна периодически вычисляться.
Каким должен быть период измерения/действия? Сначала определите время стабилизации системы – сколько времени требуется системе для достижения устойчивого состояния (для неработающего контроллера достаточно периода в 0,5 секунды). Затем разделите это время на 10 … 100 – и вы получите длительность шага (в моем случае достаточно 10 мс). В целом – чем выше частота, тем лучше! Помните, однако, что операции над дробными числами выполняются очень медленно. Фактически, они установят вам срок.
Давайте посмотрим, как период выборки (и влияние) влияет на качество результата:

PID-коэффициенты: -. Kp = 10, Ki = 0, Kd = 0.
Вариант 1 (красный) – период отбора проб 0,5 куб.м.
Вариант 2 (зеленый) – период отбора проб 0,35 куб. ярдов.
Вариант 3 (синий) – период опроса 0,15 у.е.
Как видите, в первом случае мы имеем дело с сильными выбросами. Во втором случае (70% от первого периода) они стали слабее, а в третьем случае (30%) трансформация была плавной! Это означает, что в первых двух случаях дополнительно требуется целочисленная или дифференциальная составляющая, а в последнем случае – только пропорциональная составляющая. Это существенная разница в расчетах!
Таким образом, вопрос о выборе периода должен быть приоритетным.
Итак, период выбран, все коэффициенты обнулены. Начните управлять системой.
В идеале, если вы можете собрать статистику – сохраните информацию о воздействии/результате/связанную информацию в текстовом файле. Затем вы можете открыть его в том же Excel и проанализировать.

Установите коэффициент пропорциональности Kp

Я начинаю с установки Kp до 1 и посмотрите, что произойдет. Он растет слишком медленно – я увеличиваю его. В какой-то момент он начнет проскакивать и колебаться. Так что это слишком много – бросайте. Ушел – немного увеличить. Начал – немного уменьшился. Исчезнуть – и так далее, пока не надоест. В результате получился довольно стабильный пропорциональный регулятор, который нуждается в небольшой настройке (так ли это? Если он работает вполне нормально, не заморачивайтесь и считайте, что все отрегулировано)

Настройка дифференциального коэффициента Kd

Медленное наращивание коэффициента Kd – 0.5, 1,… Колебания системы уменьшаются, все работает приятнее… Пока не произойдет обратное – не начнутся массовые выбросы. Вот так, перерегулировать, сократить.
Поэтому у нас есть шипы – меньшие, но все же. Правильно будет сгладить его, чтобы замедлить удар!

Установка коэффициента интегрирования Ki

Пойдем дальше. Попробуйте очень маленькое значение, для начала 0,1. Вы также можете попробовать небольшое отрицательное значение. Смотрите, пробуйте, крутите…
Этот процесс корректировки является итеративным. Стоит попробовать различные вариации, начиная с самого начала. Для меня это все еще неясно и подозрительно.

Дополнительные модули?

Вы строите его, вы создаете его, а потом видите, что все еще есть некоторые вибрации, нежелательные вибрации. Ну, а чего вы ожидали. Серьезный подход изобилует формулами, сложными расчетами!
И да пребудет с ними Бог – так я говорю! С тем же успехом можно добавить усреднение последних нескольких циклов на выходе – дешево (в плане вычислений) и серо (в плане стабильности эффектов). Вы также можете настроить другие фильтры.
Давайте не будем догматиками! Кто сказал, что нужно использовать только ПИД-регулятор?

Информация о модели

А теперь, как и было обещано, несколько слов о файле Excel. В нем реализована модель, аналогичная перемещению линии. Это не очень корректноМожет быть и так, но для начала этого достаточно (возможно, после обсуждения я сделаю более точную модель – например, возьму модель электродвигателя из статьи Полякова). Имеется предыдущее положение, скорость и ускорение. Скорость рассчитывается как разность предыдущих смещений. Ускорение определяется как P-I-D – удар, умноженный на усиление (в верхней части таблицы).
В таблице представлены 3 варианта. Они регулируются в верхней части:

Коэффициент усиления устанавливает множитель для ускорения. Меньше одного – воздействие “затормозится”, больше одного – пошатнет систему;
Начальное значение – Начальное значение вращения двигателя;
временной шаг используется в формуле для расчета новых значений. Увеличение его “ускоряет” моделирование (и все мелкие шаги исчезают);
шум – это диапазон изменения случайного числа. Если установить значение 0, его влияние на моделирование исчезнет;
Влияние – три коэффициента для расчета. Об изменениях см;
Колонка желаемый – это значение, на которое ориентируется ПИД-регулятор. Его можно изменить в каждой ячейке по высоте. В настоящее время существует несколько этапов

Наконец, что касается реализации

чтение текущего состояния (измерение ошибок) и действие должны быть перенесены в отдельный поток с максимально возможным приоритетом, поскольку периодичность чтения/действия очень критична. Эти потоки должны быть синхронными, но сдвинутыми по фазе (другими словами, потоки должны запускаться с одинаковой периодичностью, но в разные моменты времени).
Расчет воздействия осуществляется в потоке с относительно низкий приоритет. Ну, может быть, он и достаточно высок, но явно ниже, чем приоритет обработчиков прерываний и непосредственно связанных с ними функций – обработчиков прерываний.
Также имеет смысл сделать поток, рассчитывающий воздействие, “спящим” и разбудить его потоком, измеряющим ошибку (после ее расчета, конечно).
Возможно, что время воздействия наступило, но воздействие еще не подсчитано (потому что установлены другие приоритеты). Следовательно, влияющая переменная должна измениться атомарнои читайте также: 1) изменение только в конце только в конце расчет, 2) читать только в одной точке ударного потока. По крайней мере, старые эффекты будут повторяться. Это, конечно, немного испортит картину, но потом, я думаю, система придет в норму. И не забывайте, что в Си это атомарная операция float, в Ассемблере – совсем нет! Похоже, что без мер синхронизации/блокировки не обойтись.

Как видите – ничего революционного!
Во-первых, все самое интересное происходит в отдельной функции, которая вызывается циклически.
Первый вызов – это инициализация из EEPROM или откуда-то еще, мы сбрасываем переменные для рекурсивных вызовов. Затем мы начинаем шаг за шагом: 1) измерять, 2) вычислять, 3) влиять и так далее. Одновременно относится к реальному времени. Если текущее время меньше требуемого (функция TimeIsLower), действие не будет выполнено.
Комментаторы спрашивали, почему у нас такие сложности с государственной машиной. С недетерминированным алгоритмом? Я отвечу: при таком подходе я реализую простой “параллелизм”. Т.е. между этапами вычислений я выполняю какие-то другие действия (в моем случае, обмен данными по UART, который может быть довольно напряженным – когда я использую это устройство в качестве регистратора событий).
Вот и все… Все, что вы забыли, все, что перепутали – не стесняйтесь писать мне. Как всегда, комментарии о промахах и ошибках приветствуются!

Для успокоения этих колебаний имеется дифференциальный элемент, позволяющий роботу плавно войти в линию.

Доступный и простой ПИД-регулятор

Алексей Овсянников, методист Робототехнической олимпиады Университета Иннополис, рассказывает об алгоритмах управления. Освоив этот урок, вы научитесь программировать движение робота по тросу, удерживать ROV на заданной глубине, регулировать скорость каретки при подъеме и спуске, а также решать другие задачи.

Продолжение публикации материалов для стажеров Иннополис открыт для обучения робототехнике. Ранее я уже обсуждал подготовка моделей ManIRS для тренажера и о Отслеживание показаний энкодера в роботах на Arduino. Я обязательно продолжу эти темы, но немного позже. Сейчас я хотел бы немного перейти к алгоритмам. Мы уделяем им большое внимание во всех наших КПК – мы не знаем, на основе чего преподаватели-стажеры и их студенты будут писать свои программы в будущем, поэтому важно объяснить принципы, логику, лежащую в основе программ. В каждом курсе рассматриваются различные алгоритмы (фильтрация и нормализация показаний датчиков, алгоритмы поиска объектов на изображении, алгоритмы навигации и поиска пути в лабиринте), но почти во всех соревнованиях, во всех возрастах, используются регуляторы. В этой статье я хотел бы рассмотреть, что за зверь такой – контроллер? И я постараюсь объяснить это простым и понятным языком.

Так что же такое контроллер? В робототехнике и автоматизации это понятие относится к алгоритму, который поддерживает систему (или робота) в желаемом состоянии, чтобы датчики видели нужные показания. Чуть реже этот термин относится к устройству, реализующему такой алгоритм, но это редко встречается в DIY и образовательной робототехнике. Гораздо чаще контроллер пишется как программа или часть программы контроллера.

Давайте остановимся на этом моменте и перечитаем предыдущий абзац, что мы поняли? Что контроллер – это алгоритм, программа. Если вы собираете своего собственного робота из Lego или VEX, вы не найдете никакой специальной “детали регулятора”, вам придется описать ее в программе.

Второй важный момент заключается в том, что контроллер поддерживает и направляет системы таким образом, чтобы датчики видели заданное значение. Это означает, что контроллер всегда подстраивается под показания одного или нескольких датчиков. Они позволяют определить, находится ли система в состоянии уставки. Без датчиков контроллер не имеет смысла – вы не будете знать, что в данный момент происходит с роботом и как корректировать его поведение. Например, у нас есть коптер (робот-вертолет), и мы хотим, чтобы он пролетел 100 м. Датчик робота видит на расстоянии 95 м, поэтому ему нужно немного отойти. Если датчик видит 110 м, то коптер должен немного снизиться. Контроллер будет представлять собой программу, которая будет автоматически управлять взлетом и спуском робота. Если бы у робота не было датчика, он не знал бы, на какой высоте находится и нужно ли ему взлетать или спускаться.

Таких примеров можно привести множество, практически в каждом соревновании:

следование строго на север по датчику компаса и управление, если робот сбивается с курса;
поддерживать руку робота на нужной высоте, даже если нагрузка на робота увеличивается;
двигаться по границе черной линии на белом фоне и подруливать, если робот сильно отклоняется в сторону черного или белого цвета;
поддерживать одинаковую скорость, пока робот движется вверх и вниз по склону;
удерживать подводного робота на заданной глубине;
и т.д.

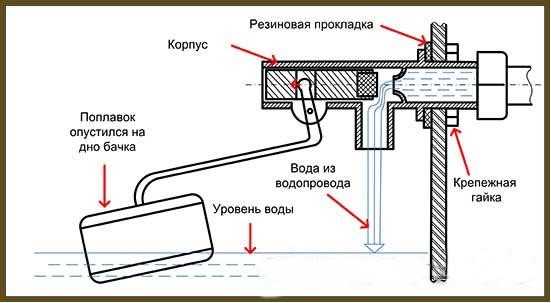
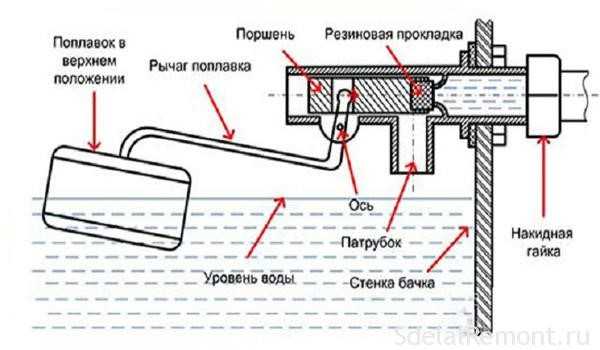
Алгоритм “удержания” желаемого состояния может быть реализован различными способами. Обычно принято выделять четыре. Самым простым из них является реле-регулятор. Это устройство, похожее на реле. Это переключатель, который может иметь только два состояния (посылать два типа сигналов). Наиболее распространенным из них является “вкл/выкл”. Классическим примером релейного переключателя является поплавковый клапан. Пока уровень воды низкий, клапан открыт, и вода продолжает поступать в резервуар. Как только воды становится достаточно и поплавок всплывает, он закрывает клапан, и вода перестает поступать:

Релейный контроллер буквально описан одним оператором с точки зрения программы:

Если температура в печи ниже заданной, отопительный прибор включается, в противном случае он выключается.

Такой алгоритм подходит для систем с медленной реакцией на управляющие воздействия. Эта же духовка медленно нагревается и долго остывает, поэтому подобный алгоритм будет для нее в самый раз. Но если мы хотим, чтобы робот проехал заданное расстояние и повернул двигатели вперед, если датчик видит меньше порогового значения, и назад, если мы проехали слишком далеко (датчик видит больше порогового значения):

В итоге мы получаем робота, который колеблется около желаемого значения тарифа. Он едет вперед, останавливает двигатели и за счет инерции проезжает еще немного. Слишком далеко в плане алгоритма. И он едет назад, после остановки робот проезжает еще немного. И все повторяется до бесконечности. Как бы выглядел такой коптер с аналогичным алгоритмом, который переходит от включения пропеллеров на максимум и взлета к их полному выключению и началу снижения? Для систем с быстрой реакцией на управляющие воздействия необходим более подходящий алгоритм, который плавно регулирует поведение.

Остальные три метода контроля как раз подходят для этой цели:

пропорциональный компонент;
неотъемлемый компонент;
дифференциальный компонент.

Комбинируя их, можно добиться различного поведения контроллера. Контроллеры обычно называются в зависимости от того, какие части они содержат: ПИД-регулятор имеет все три компонента, П-регулятор содержит только пропорциональный компонент, ПД-регулятор содержит как пропорциональный, так и дифференциальный компонент, и так далее.

Как правило, часть P выполняет большую часть работы контроллера, а части I и D улучшают его работу. Поэтому обычно используются P-, PI- и PD-регуляторы, и редко I- или ID-регуляторы. После рассмотрения всех компонентов я объясню, где их можно использовать.

Прежде чем мы перейдем к рассмотрению работы каждого компонента, я предлагаю ввести некоторые термины, которые используются при работе с контроллерами.

Уставка – Желаемое состояние системы (или робота), т.е. желаемые показания датчиков. Обычно он задается самим программистом и может быть сохранен в какой-то момент (когда система находится в нужном нам состоянии) и затем поддерживаться. Например, робот-футболист запоминает азимут ворот соперника и движется к ним с помощью датчика компаса.

Ошибка – это разница между показаниями датчика и заданным значением. Это не ошибка в программном обеспечении, а ошибка в поведении системы. Он должен быть на заданном значении, а датчик видит по-другому. Коптер должен лететь на высоте 100 м, а он летит на высоте 110 м, следовательно, ошибка равна 10. Обратите внимание, что если коптер летит на высоте 85 м, ошибка будет равна -15! Символ ошибки четко указывает, в какую сторону идет отклонение.

Вход управления – Сигнал от контроллера для воздействия на систему, возвращающий ее в заданное состояние. Он состоит из всех частей контроллера: пропорциональной, интегральной и дифференциальной.

Имея в виду эти понятия, давайте рассмотрим

Как работает пропорциональная часть контроллераПример: чем дальше система находится от заданного значения, тем больше она стремится достичь заданного значения. Вернемся к примеру с коптером – при ошибке -15 (робот летит на высоте 85 метров) он сильно взлетает. Чем ближе к требуемой высоте, тем слабее/медленнее он взлетает. Если мы рассмотрим модель подводной лодки или самолета, то на требуемой глубине/высоте ее рули расположены вертикально, и чем дальше модель удаляется от требуемой глубины/высоты, тем сильнее отклоняются ее рули:

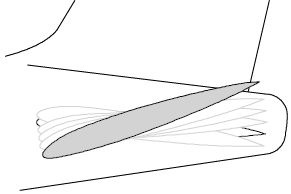
Теперь давайте “преобразуем” эти понятные слова в математику, чтобы сделать ее непонятной. Хорошо, позвольте мне объяснить. Рассмотрим пример робота, движущегося вдоль линии с одним датчиком:

S – показания датчика;

рот – уставка (требуемое показание датчика);

P – пропорциональная составляющая;

kp – коэффициент пропорциональности;

U – управляющее воздействие;

Vleft, Vright – скорости левого и правого двигателей робота;

Vbase – это опорная скорость, которую должны иметь двигатели, когда робот находится в заданном состоянии.

Эти команды (математические операции) должны выполняться в цикле, вычисляя ошибку и изменяя управляющее воздействие на каждом шаге цикла.

Давайте посмотрим, как это работает. Уставка задается программистом самостоятельно. Для робота, движущегося вдоль линии, заданное значение принимается за показания датчика на границе. Например, на черной стороне датчик видит 10, на белой – 80, а на границе среднее арифметическое этих чисел равно примерно:

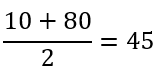
То есть, заданное значение равно 45. Форм-фактор – это просто число. Студенты и ученые рассчитывают его на основе математической модели робота, его физических параметров, электромеханических свойств двигателей и т.д. В проектах для детей его можно просто поднять. Например, предположим, что коэффициент равен 2. Пусть базовая скорость равна 50.

Предположим, что в момент старта датчик видит ровно 45, получаем:

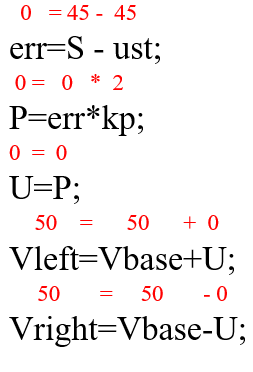
Робот находится в заданном состоянии, ошибка равна нулю, умножаем этот ноль на коэффициент пропорциональности и получаем один и тот же ноль в пропорциональной части и в управляющем воздействии. Оба двигателя вращаются с базовыми скоростями, и робот движется прямо вперед.

В какой-то момент линия начнет поворачивать, и робот поедет прямо вперед. Предположим, что линия идет вправо, и датчик робота начинает видеть 50:

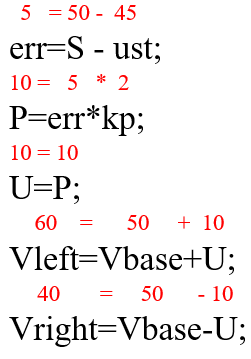
Получаем положительную ошибку 5. Умножаем ее на коэффициент пропорциональности и получаем 10 в пропорциональной части (а также в управляющем воздействии). Скорость левого двигателя увеличивается на 10, а скорость правого двигателя уменьшается на 10. В результате, поскольку левый двигатель вращается быстрее, робот начинает поворачивать вправо, к линии.

Предположим, что робот пропустил границу линии, и теперь датчик видит 40:

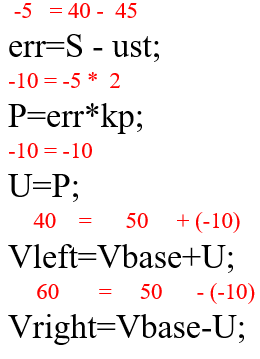
Мы получаем ошибку того же размера, но с другим знаком. В результате скорость вращения колес изменится, и робот начнет поворачивать влево.

Чем больше значение (модуль) ошибки, тем больше будет пропорциональная часть, тем сильнее она будет тянуть робота к линии.

Рассмотрим фактор пропорциональности. Как уже говорилось, это просто номер, и его можно просто взять. Это число не может быть отрицательным (иначе робот не вернется к заданному значению, а убежит от него), и оно не может быть целым числом. Выбор kp может быть сделан буквально “на глаз”. – если система слишком слабо реагирует на изменения состояния, то kp слишком мал и его следует увеличить. Если система быстро реагирует на изменения и колеблется, значит, kp слишком высок. Вы можете начать с числа 1 или 2 и регулировать коэффициент в течение нескольких итераций.

Даже при самом идеально подобранном kp система с P-контроллером неизбежно будет “колебаться” вокруг заданного состояния. На примере робота, движущегося вдоль линии, причина ясна: если робот немного отклоняется от своего пути, он находит заданное состояние, когда возвращается к границе. В этот момент он едет прямо, но где он находится относительно линии?

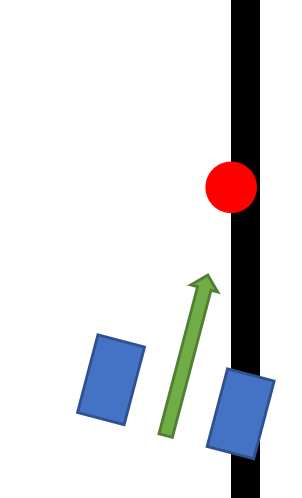
На рисунке датчик находится точно на границе черной линии, колеса вращаются вперед с одинаковой скоростью, робот неизбежно проскочит заданное состояние.

Дифференциальный компонент помогает приглушить эти колебания, позволяя роботу плавно двигаться к линии.

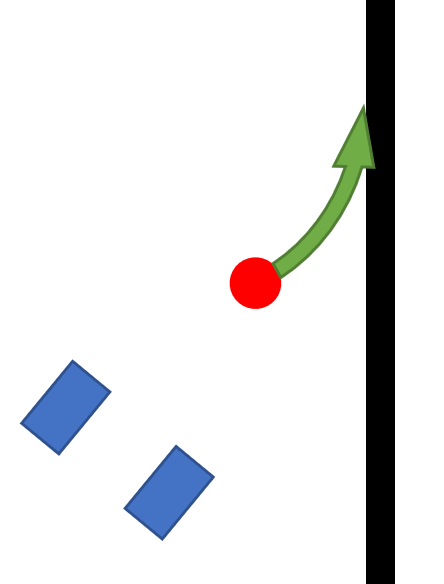
Принцип работы дифференциального компонентаЧем быстрее система удаляется от заданного состояния, тем ближе она к нему движется. Этот компонент отслеживает уже не величину ошибки, а скорость ее изменения. Компонент дифференциала позволяет роботу лучше управляться на резких поворотах. Чтобы математически или программно описать компонент D, нам нужно вспомнить значение ошибки из предыдущего шага:

D – дифференциальная составляющая;

kd – дифференциальный коэффициент;

errold – ошибка на предыдущем шаге.

Мой дифференциальный коэффициент обычно примерно в 10 раз меньше, чем kp. Найти его “на глаз” сложнее, лучше произвести специальные расчеты. Давайте оставим их за скобками, я буду говорить о них на PDA и в последующих статьях. Для упрощения расчетов будем считать, что kd равно единице.

Рассмотрим расчет в три этапа: начало движения и ошибка равна 0, затем резкий поворот и ошибка равна 15, затем робот начинает приближаться к линии и ошибка уменьшается до 10:

Обратите внимание, что на третьем шаге часть D поменяла знак. В первый момент, когда текущая ошибка стала больше, чем ошибка предыдущего шага, часть D имела тот же знак, что и часть P, и они работали вместе, чтобы вернуть робота на линию. В следующее мгновение ошибка начала уменьшаться, и часть D начала сопротивляться. Компонент P тянет робота к линии, компонент D препятствует этому. Именно эта помеха заставляет робота плавно приближаться к линии.

Еще одним очень важным моментом является то, что разница зависит от времени. Мы оцениваем скорость изменения ошибки, а скорость – это изменение чего-либо в единицу времени. Если итерации цикла выполняются с разной скоростью, разность (err-errold) будет принимать разные значения. И итерации будут разными по разным причинам: на некоторых этапах будут сложные последующие вычисления, на некоторых этапах будут долгие считывания с медленных датчиков, и многие другие. И после каждой длинной итерации робот будет немного (или много, в зависимости от порядка задержки) колебаться.

Этого можно избежать различными способами. Идеальным способом является расчет части D по следующей формуле:

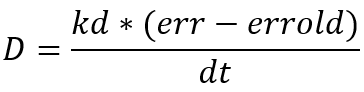
В нем dt – это период времени от предыдущего шага до текущего. Если это время во много раз больше, чем на других этапах, то часть d будет пропорционально меньше. Вопрос в том, как измерить это время на конкретной платформе.

В первом математическом описании дифференциала я сделал задержку в 5 миллисекунд с помощью команды pause(0.005). Это один из самых простых способов сделать это – я намеренно делаю паузу на каждой итерации. Это предполагает, что все вычисления выполняются за меньшее время, около 50 микросекунд. Я делаю паузу в 100 раз длиннее и получаю длительность одной итерации 50+5000=505050 микросекунд. Даже если шаг отсчитывается намного дольше обычного, 500 микросекунд, общая длина шага составит 500+5000=5500 микросекунд, что всего на 9% больше. И тогда я могу взять dt как константу и подобрать не kd, а kd/dt.

Другой способ, используемый на Arduino (с использованием регистров микроконтроллера ATMega) или STM, заключается в выполнении каждого нового вычисления контроллера через прерывания таймера. В этом случае временной интервал также строго определен и установлен в часах, ситуация аналогична предыдущему методу.

Теперь у нас остался только один интеграл регулятора, перейдем к нему.

Принцип работы неотъемлемой части регулятораЧем дольше система находится вне заданного состояния, тем больше она стремится его достичь. Этот элемент постепенно накапливает ошибку. Чем дольше оно накапливается, тем сильнее становится неотъемлемая часть Я. Этот элемент полезен, когда робот находится в тесном углу и не может приблизиться к линии. Или в роботе сегвей, где робот должен позиционировать себя вертикально.

Математически полный контроллер, содержащий все три элемента, включая часть AND, которая накапливает ошибки, выглядит следующим образом:

Я не буду анализировать значения шаг за шагом, интегральная составляющая просто плавно увеличивается на каждой итерации цикла.

Интегральный коэффициент ki должен быть на несколько порядков меньше, чем kp. Например, если ki в 100 раз меньше kp, то часть I станет такой же сильной, как часть P, только через 100 шагов (при указанном выше интервале – через 0,5 секунды).

Интегральная составляющая также зависит от времени. В идеале он должен быть рассчитан по следующей формуле:

Здесь используется тот же dt. И избавиться от него можно тем же способом (приостановив или запустив вычисление с помощью таймера).

Кроме того, можно проверить, равна ли ошибка нулю. Когда ошибка достигает нуля (система достигает заданного значения), часть AND может быть принудительно обнулена. Если этого не сделать, то в части AND останется некоторое накопленное значение, и оно продолжит тянуть систему в направлении, противоположном последней ошибке.

Иногда контроллеры строятся с использованием только части AND. Это тот случай, когда требуется плавное увеличение управляющей переменной. Например, робот вращается с помощью компаса. Азимут (заданное значение) быстро меняется, и возникает ошибка. Части P и D будут дергать робота, и его колеса начнут скользить, скользить. Если контроллер имеет только часть I, он будет плавно накапливать и постепенно увеличивать мощность двигателей, в результате чего робот будет двигаться плавно, без пробуксовки колес.

Я рассмотрел основные типы контроллеров и их компоненты. Для большинства применений достаточно P- или PD-контроллера или даже релейного контроллера. Не забывайте, что чем больше компонентов, тем больше коэффициентов вам нужно собрать.

Конечно, наши люди умны и придумали множество вариаций. Например, я сталкивался с накоплением I-частей с “забыванием” старых значений ошибок; в книге С.А. Филиппов”.Робототехника для детей и родителей” упоминает кубический регулятор; многие из них используют переменные коэффициенты, которые увеличиваются на резких поворотах и сглаживаются на прямых. Надеюсь, каждый из вас найдет свою собственную версию, адаптированную к вашему конкретному роботу. Начните с классического ПИД-регулятора и подойдите к делу творчески!

В следующих статьях я расскажу об использовании регуляторов в различных задачах. Хитрости выбора коэффициентов и многое другое будет объяснено в разделе Курсы повышения квалификации и Школьная олимпиада для Innopolis Open по робототехнике.

Простой ПИД-регулятор в системе с обратной связью не всегда может обеспечить требуемые характеристики скорости из-за наличия нежелательных колебаний или неприемлемо высокого перерегулирования. Для улучшения характеристик управления используются следующие методы замкнутый контур управления – управление в замкнутом и разомкнутом контуре для улучшения поведения системы управления. К управляющей переменной (выходу контроллера) добавляется сигнал опережающего действия, который не зависит от рассогласования и поэтому не может вызвать автоколебаний в системе.

Контроллеры процессов

Контроллеры процессов – это параметризованные цифровые контроллеры со встроенными стандартными функциями для управления переменными процесса (температура, давление и т.д.).

Опорными сигналами являются либо фиксированные уставки, либо внешние уставки.

Аналоговые входы используются для подключения датчиков обратной связи (термометры сопротивления, термопары, манометры и т.д.).

Дискретные входы используются для установки фиксированных уставок и переключения между режимами.

Дискретные выходы используются для сигнализации: режима ожидания, тревоги, состояния.

Релейные выходы используются для дискретного управления, а аналоговые выходы – для непрерывного управления.

Дискретное управление

Двухпозиционный контроллер использует только 2 состояния:
- включено (открыто)
- выключен (закрыт) Пример: Управление нагревом или охлаждением.
- отключен
- вращение по часовой стрелке
- вращение против часовой стрелки (инвертированное) Пример: управление реверсивным двигателем
- отключен
- первая скорость вращения по часовой стрелке
- Вторая скорость по часовой стрелке
- Первая скорость против часовой стрелки
- вторая скорость против часовой стрелки Пример: управление реверсивным двигателем с 2 скоростями.
Непрерывный контроль

ПИД-регуляторы используются для непрерывного управления. Возможна реализация каскадного управления (ведомый).

Управление в замкнутом контуре

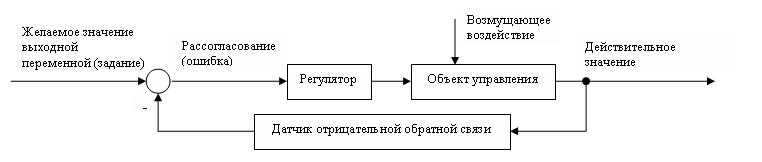
Переходный процесс

Переходный процесс – это реакция системы на внешнюю силу (задачу, возмущение).

Нестабильный (дивергентный) переходный процесс

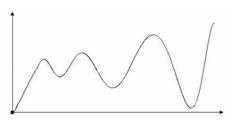
Стабильный (конвергентный) переходный процесс

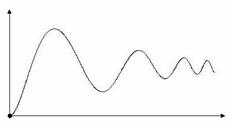
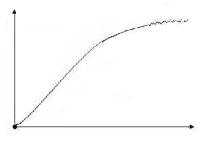
Колебания Апериодический Монотонный

ПИД-регулятор

Регулируя ПИД-регулятор, мы можем адаптировать переходный процесс к потребностям нашего приложения.

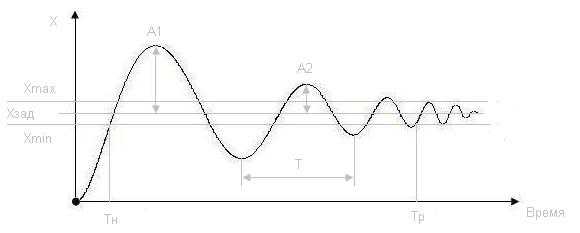
Х_назад – целевое (желаемое) значение выходной переменной
X_max – верхний предел выходной переменной
X_min – нижний допустимый предел выходной переменной
T – период колебаний
Т_н – время нарастания
Т_р – время перехода (последняя точка пересечения кривой с X_min или X_max)
А₁ – первый проскок
А₂ – второй избыток
d=A₁/A₂ – Степень (падение) демпфирования переходных процессов (отношение первого превышения к второму превышению)

Дивергенция, проскакивание, время нарастания, время перехода и степень демпфирования описывают контроль качества.

Пример

ПИД-регулятор открывает и закрывает регулирующий клапан на горячей трубе так, чтобы из крана текла вода температурой +40°C с погрешностью плюс-минус 2 градуса. Контроллер рассчитывает расхождение (ошибку) – отклонение фактической температуры (например, +20°C) от заданной температуры (+40°C) – и решает, когда и на сколько открыть клапан отопления, чтобы повысить температуру на 20°C. Контроллер узнает фактическую температуру от датчика температуры (обратная связь) и заданную температуру от оператора, например, путем ввода “40” на компьютере.

Для настройки ПИД-регулятора необходимо выбрать подходящую комбинацию из трех факторов:
- Пропорциональный – K_p
- Интеграл K_i
- Дифференциал – K_d
Также можно использовать простые P- и PI-регуляторы.

Формула для ПИД-регулятора выглядит следующим образом

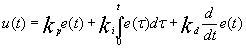
где e(t) – ошибка (рассогласование), u(t) – выход регулятора (управляющее воздействие).

Подробнее ПЧем выше коэффициент пропорциональности, тем быстрее работа, но тем меньше запас устойчивости. Но! Простой P-регулятор не может полностью справиться с рассогласованием, т.е. он всегда работает с ошибкой.

ПИ-регулятор позволяет избежать статической ошибки, но чем больше ИЧем больше коэффициент интегрирования, тем больше перерегулирование (динамическая ошибка).

ПИД-регулятор позволяет нам уменьшить перерегулирование, но чем больше Ддифференциального коэффициента, тем больше ошибка из-за влияния шума.

Если шум исходит из цепи обратной связи, мы можем отфильтровать его с помощью фильтра низких частот, но чем выше постоянная этого фильтра, тем медленнее контроллер будет реагировать на шум.

Настройка ПИД-регулятора по методу Циглера-Николса

Ziegler и Nicholls предложили свой вариант быстрой настройки ПИД-регулятора для периодического переходного процесса, когда демпфирование составляет около 4.
- Мы обнуляем K_i и K_d
- Постепенно увеличивайте Kp до критического значения K_cпри котором возникает автоколебание.
- Измерьте период настройки T
- Рассчитайте значение K_p, K_i и K_d используя различные формулы для разных регуляторов:
  - Для регулятора P: K_p=0,50*K_c
  - Для ПИ-регулятора: K_p=0,45*K_c, K_i=1,2*K_p/T
  - Для ПИД-регулятора: K_p=0,60*K_c, K_i=2,0*K_p/T, K_d=K_p*T/8
  Каскадный контроллер (ведомое управление)
  
  Продолжение примера
  
  Теперь мы хотим добавить комфорта и сделать так, чтобы заданное значение температуры воды менялось в зависимости от наружной температуры (на улице мороз – вода теплая, на улице жара – вода прохладная). Вы также можете установить контроллер комфортной температуры, который узнает текущую температуру наружного воздуха от термометра и решит, что комфортная температура воды должна быть, например, такой +40°C, тем самым давая команду регулятору температуры воды поддерживать температуру на уровне +40°C (см. пример выше). Здесь мы имеем дело с каскадным управлением: контур регулирования температуры воды подчиняется контуру регулирования комфортной температуры.
  
  С помощью контроллеров процессов мы можем реализовать и более сложные комбинации. Например, поддержание постоянного расхода и температуры воды независимо от давления и температуры в трубах горячей и холодной воды.
  
  Управление с опережением
  
  Простой ПИД-регулятор в системе с обратной связью не всегда может обеспечить требуемое время отклика из-за нежелательных колебаний или неприемлемо высокого перерегулирования. Для улучшения характеристик управления используется комбинированное управление комбинированный контроль – Для улучшения характеристик управления используются замкнутые и разомкнутые контуры. К управляющей переменной (выходу контроллера) добавляется сигнал опережающего действия, который не зависит от рассогласования и поэтому не может вызвать автоколебаний в системе.
  
  Продолжение примера
  
  Если нарушениевозмущения, можно предпринять упреждающее действие, которое может компенсировать влияние возмущения на процесс до того, как управляемая переменная начнет изменяться.
  
  Системы частотных преобразователей содержат контроллеры, которые могут обеспечить работу устройства в режиме ПИ или ПИД. Специализированные преобразователи частоты часто имеют предустановленные параметры, которые настраиваются после установки.
  
  Настройки ПИД
  
  Настройка ПИД-регулятора сводится к определению коэффициентов Kp, Ki, Kd. Компоненты определяются на основе формулы:
  
  Они используются для определения передаточной функции системы автоматического управления и расчета ее параметров:
  - Точность.
  - Скорость регулирования.
  - Форма графов переходов.
  - Инерция.
  - Другие значения и функции.
  Математическая модель системы автоматического управления не может дать полного представления о том, как работает система. Расчеты выполнены для “идеального регулятора”. Нелинейность контролируемых параметров, внешние возмущения, возмущения на объекте управления не позволяют использовать эти расчеты для построения системы автоматического управления на практике. В качестве вспомогательных данных используются результаты математических расчетов.
  
  При разработке ПИД- и СЗР-регуляторов используются устройства, имитирующие изменение управляемой характеристики, измерительные приборы и компьютеры. Эти устройства позволяют определить и проанализировать реакцию системы на взаимодействия и более точно подобрать коэффициенты.
  
  На практике используется подбор коэффициентов методом проб и ошибок. ПИД-регуляторы устанавливают на месте, вводят коэффициенты, полученные в результате расчетов или стендовых испытаний, и регулируют параметры на месте.
  
  Больший коэффициент усиления между входом и выходом означает меньшую статическую ошибку, но если коэффициент усиления (по сути, коэффициент пропорциональности) слишком высок, система вскоре начнет колебаться при наличии задержки (что часто неизбежно), а если коэффициент усиления увеличить еще больше, система просто станет нестабильной.
  
  Что такое ПИД-регулятор
  
  ПИД-регулятор (P-proportional, I-integral, D-derivative) – это устройство, используемое в контурах управления, оснащенных обратной связью. Эти регуляторы используются для формирования управляющего сигнала в автоматических системах, где необходимо обеспечить высокие требования к качеству и точности переходных процессов.
  
  Управляющий сигнал ПИД-регулятора получается в результате сложения трех составляющих: первая пропорциональна значению сигнала ошибки, вторая – интегралу сигнала ошибки и третья – его производной. Если какой-либо из этих трех компонентов не включен в процесс сложения, то регулятор уже не является ПИД-регулятором, а просто пропорциональным, пропорционально-дифференциальным или пропорционально-интегральным.
  
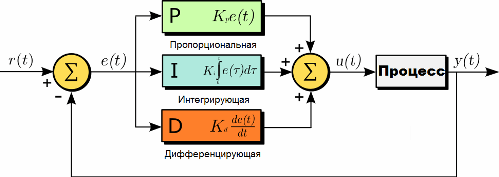
  Первый компонент пропорционален
  
  Выходной сигнал задается пропорциональной составляющей. Этот сигнал противодействует текущему отклонению регулируемой входной переменной от заданного значения. Чем больше отклонение, тем больше сигнал. Когда входное значение управляемой переменной равно уставке, выходной сигнал становится равным нулю.
  
  Если оставить и использовать только этот пропорциональный компонент, значение регулируемой величины никогда не стабилизируется на правильном значении. Всегда существует статическая ошибка, равная такому отклонению управляемой переменной, при котором выход стабилизируется на этом значении.
  
  Например, термостат управляет мощностью нагревательного устройства. Выходной сигнал уменьшается по мере приближения к желаемой температуре объекта, а управляющий сигнал стабилизирует выходной сигнал на уровне тепловых потерь. В конечном итоге температура никогда не достигает заданного значения, потому что нагреватель просто вынужден отключиться и начинает охлаждаться (мощность равна нулю).
  
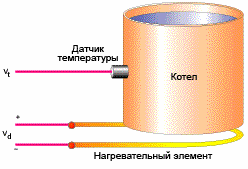
  Больший коэффициент усиления между входом и выходом означает меньшую статическую ошибку, но если коэффициент усиления (по сути, пропорциональный коэффициент усиления) слишком высок, система вскоре начнет колебаться при наличии задержки (что часто неизбежно), а увеличение коэффициента усиления еще больше сделает систему нестабильной.
  
  Или пример позиционирования двигателя с помощью редуктора. Если коэффициент низкий, желаемое рабочее положение достигается слишком медленно. Увеличьте коэффициент, и реакция будет быстрее. Если мы увеличим коэффициент еще больше, двигатель будет “лететь” в нужное положение, а система не будет быстро перемещаться в нужное положение, как можно было бы ожидать. Если теперь мы еще больше увеличим форм-фактор, начнутся колебания вокруг желаемой точки, и результат снова не будет достигнут.
  
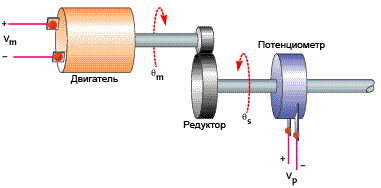
  Второй компонент – интегрирующий компонент
  
  Временной интеграл рассогласования является основной частью интегрирующей составляющей. Он пропорционален этому интегралу. Интегрирующий компонент служит именно для устранения статической ошибки, поскольку контроллер учитывает статическую ошибку во времени.
  
  При отсутствии внешних возмущений управляемая величина стабилизируется на правильном значении через некоторое время, когда пропорциональная составляющая равна нулю, а точность выхода полностью обеспечивается интегральной составляющей. Однако интегральная составляющая также может вызвать колебания вокруг точки позиционирования, если коэффициент выбран неправильно.
  
  Третий компонент – это дифференциальный компонент.
  
  Скорость изменения отклонения контролируемой величины пропорциональна третьей дифференциальной составляющей. Он необходим для противодействия отклонениям (вызванным внешними воздействиями или задержками) от правильного положения, прогнозируемого в будущем.
  
  Что такое ПИД в упрощенном виде на примере дрона:
  
  Теория работы ПИД-регулятора
  
  Как вы уже поняли, ПИД-регуляторы используются для поддержания заданного значения x0 некоторой величины путем изменения значения u другой величины. Имеется заданная точка или уставка x0, и имеется разница или рассогласование (несовпадение) e = x0. Если система линейна и стационарна (что маловероятно на практике), то для определения u применяются следующие формулы:
  
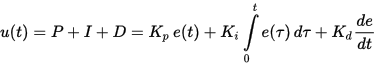
  Эта формула показывает коэффициенты пропорциональности для каждого из трех членов.
  
  На практике в ПИД-регуляторах используется другая формула настройки, где коэффициент усиления применяется сразу ко всем компонентам:
  
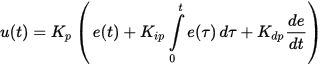
  Практическая сторона ПИД-регулирования
  
  На практике теоретический анализ систем с ПИД-регулятором используется редко. Сложность заключается в том, что характеристики объекта управления неизвестны, а система почти всегда является нестационарной и нелинейной.
  
  Реалистичные ПИД-регуляторы всегда имеют ограниченный диапазон работы снизу и сверху, что, по сути, объясняет их нелинейность. Поэтому управление почти всегда и везде осуществляется экспериментально, когда объект управления подключен к системе управления.
  
  Использование значения, генерируемого алгоритмом программного управления, имеет ряд специфических нюансов. Для регулирования температуры, например, часто требуется два устройства вместо одного: первое управляет нагревом, а второе – охлаждением. Первый обеспечивает нагревательную среду, второй – охлаждающую среду. Можно рассмотреть три практических решения.
  
  Первый вариант близок к теоретическому описанию, где выход является аналоговым и непрерывным значением. Второй выводится в виде набора импульсов, например, для управления шаговым двигателем. Третий способ – ШИМ-управление, при котором выход контроллера используется для установки ширины импульса.
  
  В настоящее время почти все системы автоматизации основаны на ПЛК, а ПИД-регуляторы представляют собой специальные модули, добавляемые к контроллеру, или обычно реализуются программно путем загрузки библиотек. Для того чтобы правильно установить коэффициент усиления в этих контроллерах, их разработчики предоставляют специальное программное обеспечение.
  
  Структурированный текст
  
  Добро пожаловать в книгу IEC 61131-3 Структурированный текст (ST). Автор – Сергей Романов
  
  Книга “Изучение структурированного текста МЭК 61131-3”: Ссылка на книгу
  
  Вы любите умные гаджеты и DIY? Станьте экспертом в области Интернета вещей и создайте сеть умных гаджетов!
  
  Запишитесь в онлайн-университет с GeekBrains:
  
  Изучите язык C, механизмы отладки и программирование микроконтроллеров;
  
  Приобрести опыт работы с реальными проектами, в команде и самостоятельно;
  
  Получите сертификат и свидетельство, подтверждающее приобретенные вами знания.
  
  Стартовая коробка для ваших первых экспериментов в подарок!
  
  По окончании курса в вашем портфолио будут представлены: игровые часы, распределенная сеть устройств, устройство контроля температуры (PID), устройство контроля влажности, интеллектуальная система полива растений, устройство контроля утечки воды.
  
  Вы получите диплом о переподготовке и электронный сертификат, который вы сможете добавить в свое портфолио и показать работодателю.