Почему пи равен 180 градусам

Но если вы абсолютно уверены в своих ответах и вас не интересуют простые и надежные способы работы с радианами – не утруждайте себя посещением 555. Я не настаиваю).

Содержание

На предыдущем уроке мы освоили подсчет углов на тригонометрической окружности. Мы научились считать положительные и отрицательные углы. Мы узнали, как нарисовать угол больше 360 градусов. Пришло время узнать о мере углов. Особенно с числом пи, которое трудно спутать, да.

Стандартные задачи по тригонометрии с pi решаются довольно хорошо. Визуальная память помогает. Но любое отклонение от формулы – это настоящий провал! Чтобы не упасть… вы должны понять вы должны понять. Что мы и собираемся сделать. Давайте понимать друг друга!

Так что.., что делать углы? В школьной тригонометрии есть две меры: мера градуса угла и радианная мера угла. Давайте рассмотрим эти меры. Он не встречается нигде в тригонометрии.

Мера градуса угла.

Степени – это то, к чему мы привыкли. Мы занимаемся геометрией уже некоторое время. И в жизни мы часто встречаем, например, термин “повернутый на 180 градусов”. Степень, короче говоря, – это простая вещь.

Правда? Так скажи мне, что такое ученая степень? Что, вы не можете сделать это правильно? Это правда.

Степени были изобретены в древнем Вавилоне. Это было очень давно. Около 40 веков назад. И это было просто. Они взяли круг и разделили его на 360 равных частей. Один градус – это 1/360 часть окружности. Вот и все. Вы можете разделить его на 100 частей. Или 1000. Но они разрезали его на 360. Почему 360, кстати? Чем 360 лучше 100? 100 кажется более ровным. Попробуйте ответить на этот вопрос. Или слабость против древнего Вавилона?

Примерно в то же время Древний Египет мучил другой вопрос. Во сколько раз длина окружности равна длине ее диаметра? Они измеряли его то так, то эдак. Получилось чуть больше трех. Но он был немного лохматый, неровный. Но это была не их вина, египтян. Затем последовали еще 35 веков агонии. Пока они наконец не доказали, что как бы тонко вы ни разрезали круг на ровные ломтики, эти ломтики образуют именно длина диаметра. На самом деле, вы не можете. Ну, сколько раз окружность была установлена как диаметр, конечно. Приблизительно. 3.1415926 раз.

Это число пи. Он лохматый, он лохматый. После запятой – бесконечное число цифр без порядка. Такие числа называются иррациональными. Что, кстати, означает, что из равных частей окружности диаметр именно …не могут быть сложены вместе. Когда-нибудь.

Для практических целей принято запоминать только две цифры после десятичной точки. Запомнил:

Теперь, когда мы поняли, что окружность круга равна “пи”, умноженному на диаметр, полезно запомнить формулу для окружности:

Где L – длина окружности, и d – диаметр круга.

Это пригодится в геометрии.

Для общего образования добавлю, что число пи встречается не только в геометрии. Во многих отраслях математики, и особенно в теории вероятностей, это число встречается постоянно! Один. За пределами наших желаний. Вот так.

Но вернемся к градусам. Узнали ли вы, почему древний Вавилон разделил круг на 360 равных частей? А не 100, например? Нет? Ну тогда. Позвольте мне дать вам теорию. Вы не можете спросить древних вавилонян. Для строительных или, скажем, астрономических целей круг удобно разделить на равные части. Теперь подумайте о всех числах, которые делят 100, и какое из них делит 360? И в каком варианте эти разводы…. это – …больше? Люди чувствуют себя очень комфортно в этом подразделении. Но.

Как мы узнали гораздо позже древнего Вавилона, не все любят градусы. Высшая математика их не любит. Высшая математика – серьезная дама, по законам природы. И эта женщина говорит: “Сегодня ты разбиваешь круг на 360 частей, завтра на 100, послезавтра на 245, а что мне делать? Нет, это не так. “Я должен был подчиниться. Вы не можете обмануть природу.

Мы должны были ввести угловую меру, не зависящую от человеческой изобретательности. Знакомьтесь: радиан!

Мера угла в радианах.

Что такое радиан? В основе определения радиана по-прежнему лежит окружность. Угол длиной 1 радиан – это угол, пересекающий дугу длиной (L) равна длине радиуса (R). Давайте посмотрим на фотографии.

Предположим, что этот малый угол имеет значение 1 степень:

Это небольшой угол, практически не существующий. Когда вы наводите курсор на фотографию (или касаетесь фотографии на планшете), вы видите около одного радиан. L = R

Один радиан во много раз больше одного градуса. И во сколько раз больше?

Давайте посмотрим на другую картину. В котором я нарисовал полукруг. Тупой угол – это, конечно же, 180°.

А теперь я разрежу этот полукруг в радианах! Наведите курсор на рисунок, и вы увидите, что в 180° 3 радиана.

Кто может догадаться, что означает этот хвост!

Да, этот хвост равен 0,1415926 Здравствуй, число Пи, мы еще не забыли о тебе!

На самом деле в 180° содержится 3,1415926 радиана. Как вы сами понимаете, неудобно все время писать 3,1415926, поэтому вместо этого бесконечного числа вы всегда пишете просто 3,1415926:

Но в Интернете число

неудобно писать. Поэтому в тексте я пишу его по имени – “Pi”. Вы не запутаетесь.

Теперь имеет смысл написать приближенное равенство:

Или точное равенство:

Давайте узнаем, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раза меньше градусов! То есть, мы делим первое уравнение (формула – это тоже уравнение!) на 3,14:

Это соотношение полезно запомнить В 1 радиане содержится около 60°. В тригонометрии очень часто приходится оценивать, судить о ситуации. Именно здесь эти знания очень помогают.

Но главный навык в этой теме это преобразование градусов в радианы и обратно.

Если угол задан в радианах с числом “Пи”, то все очень просто. Мы знаем, что радиан “Пи” = 180°. Поэтому мы заменяем 180° на пи для получения радиана. Вы получите значение угла в градусах. Сократите то, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусы в “пи”/2 радиан? Поэтому мы его записываем:

Или более экзотический термин:

Обратный перевод немного сложнее. Но не намного. Если угол задан в градусах, нужно выяснить, сколько один градус равен одному радиану, а затем умножить это число на количество градусов. Сколько составляет 1° в радианах?

Мы рассмотрели формулу и пришли к выводу, что если 180° = “Пи” радиан, то 1° в 180 раз меньше. Или, другими словами, разделите уравнение (формула – это тоже уравнение!) на 180. Нет необходимости представлять “Пи” как 3,14, оно всегда пишется как буква. Мы понимаем, что одна степень равна другой:

Вот и все. Умножив количество градусов на это значение, вы получите угол в радианах. Например:

Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радиан – это очень просто. И с переводом проблем нет. А P – вполне сносный. Так откуда же берется путаница?

Вот в чем загадка. Дело в том, что в тригонометрических функциях знак для градусов записывается. Всегда. Например, sin35°. Это синус 35. градусы. Значок радиана (rad) не написано! Это подразумевается. Либо лень математиков, либо что-то другое. Но они решили не писать его. Если внутри синуса-котангенса нет знаков, то угол равен в радианах! Например, cos3 – косинус трех. радианы.

Это приводит к путанице. Человек видит пи и думает, что это 180°. Всегда и везде. Кстати, это работает. При условии, что примеры стандартные. Но “Пи” – это число! Число равно 3,14, а не градусам! Это радиан “Пи” = 180°!

И снова “Пи” – это число! 3.14: Иррационально, но это число. Так же как и 5 или 8. Например, вы можете сделать примерно “Pi” шагов. Три шага, а потом еще несколько. Или купить “пи” килограммов конфет. Если продавец образован.

“Пи” – это число! Не надоела ли вам эта фраза? Вы уже разобрались с этим? Ну тогда. Давайте посмотрим. Скажите, какое число больше?

Это один из тех немного нестандартных вопросов, которые могут сбить с толку.

Если вы тоже запутались, вспомните заклинание: “Пи” – это число! 3,14. Уже в первом синусе ясно написано, что угол в градусах.! Поэтому нельзя заменить “Pi” на 180°! Число “пи” градусов составляет приблизительно 3,14°. Поэтому его можно записать:

Во втором синусе нет никаких обозначений. Таким образом, существуют радианы! Здесь преобразование “Pi” в 180° поможет решить эту проблему. Преобразуйте радианы в градусы, как написано выше, и вы получите:

Остается только сравнить два синуса. Что… ты забыл как? С помощью тригонометрического круга, конечно же! Начертите окружность, начертите приблизительные углы 60° и 1,05°. Давайте посмотрим, каковы синусы этих углов. В общем, все так, как описано в конце темы о тригонометрической окружности. На окружности (даже самой кривой!) будет ясно, что sin60° значительно больше, чем sin1.05°.

То же самое относится и к косинусам. На окружности мы рисуем углы приблизительно 4 градусы и 4 радианы (разве вы не забыли, сколько приблизительно составляет 1 радиан?). Колесо подскажет вам! Конечно, cos4 меньше cos4°.

Давайте потренируемся с мерами углов.

Переведите эти углы из градусной меры в радианную:

360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°

Вы должны получить эти значения в радианах (в разном порядке!)

Кстати, я специально выделил ответы в две строки. Давайте посмотрим, каковы углы в первом ряду? Хоть в градусах, хоть в радианах?

Да, это оси системы координат! Если посмотреть на тригонометрический круг, то подвижная сторона угла при этих значениях точно по осям….. Эти ценности должны быть известны с иронией. И не зря я отметил угол 0 градусов (0 радиан). Потому что некоторые люди не могут найти этот угол на диске. И, соответственно, они путаются в тригонометрических функциях нуля. Другое дело, что положение подвижной стороны при нуле градусов такое же, как и при 360°, поэтому конгруэнции на окружности есть везде.

Во второй линии углы также особенные. Это углы 30°, 45° и 60°. И что же в них такого особенного? Ничего особенного. Единственное отличие этих углов от всех остальных заключается в том, что это углы, которые вам необходимо знать . А также где они расположены и каковы тригонометрические функции этих углов. Предположим, что значение sin100° вам не нужно знать. А sin45° – если сможете! Это обязательные знания, без которых в тригонометрии делать нечего. Но об этом подробнее в следующем уроке.

А пока давайте продолжать тренироваться. Переведите эти углы из радиан в градусы:

Вы должны получить результаты, подобные приведенным ниже (в беспорядке):

210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.

Вы получили его? Тогда вы можете предположить, что преобразование градусов в радианы и обратно – больше не является вашей проблемой). Но преобразование углов – это первый шаг к пониманию тригонометрии. Вам нужно работать с синусами и косинусами. И касательные, и котангенсы тоже.

Вторым мощным шагом является это определение положения любого угла на тригонометрической окружности. Как в градусах, так и в радианах. На этот конкретный навык я буду занудно намекать на протяжении всей тригонометрии, да. ) Если вы знаете (или думаете, что знаете) все о тригонометрическом круге и подсчете углов на тригонометрическом круге, вы можете проверить это. Решите эти простые задачи:

1. в каком квадранте лежат углы:

45°, 175°, 355°, 91°, 355° ?

2. в каком квадранте лежат углы:

402°, 535°, 3000°, -45°, -325°, -3000°?

Тоже не проблема? Ну, посмотрите. )

3. Не могли бы вы поставить углы в четверти:

А вы могли бы? Вы, наверное, шутите

4. На какую ось падает угол:

5. В каком квартале расположены углы:

И это все!? Ну, я просто не знаю. )

6. определите, в каком четырехугольнике лежат углы:

1, 2, 3 и 20 радиан.

Позвольте мне просто дать вам ответ на последний вопрос (который является немного сложным) последнего задания. Угол величиной 20 радиан попадает в первый квадрант.

Остальную часть ответа я не дам, не из жадности). Дело в том, что если Я еще не решил. о чем-то, вы не уверены или если вы потратили более 10 секунд более 10 секунд, вы плохо понимаете, что такое круг. Это будет вашей проблемой на протяжении всей тригонометрии. Лучше сразу избавиться от нее (от проблемы, а не от тригонометрии!). Вы можете сделать это в теме: Практическая работа с тригонометрической окружностью в главе 555.

В ней вы узнаете, как просто и правильно решать подобные проблемы. Эти проблемы, конечно, решаемы. А четвертая проблема решается за 10 секунд. Она решена настолько хорошо, что это может сделать каждый!

Если вы полностью уверены в своих ответах и вас не интересуют простые и надежные способы работы с радианами, вам не нужно переходить на 555. Я не настаиваю).

Хорошее понимание – достаточная причина, чтобы двигаться дальше!)

Он обозначается следующим образом: 360 и значок градуса в верхней части.

Что такое радиан? И почему в круге 360 градусов?

Сегодня мы поговорим об измерении углов. Почему в круге 360 градусов? Что такое 1 радиан? А как связаны градусы и радианы?

Давайте начнем со степеней. Что это за странное число 360? Мы привыкли говорить, что в рубле 100 копеек, в метре – 100 сантиметров, а в килограмме – 1000 граммов. У нас десятичная система, потому что у нас 10 пальцев на ноге. Но почему в нашем языке есть такие странные слова, как дюжина или 12? Почему в часе 60 минут, а не 100? А в минуте есть 60 секунд. Также круг имеет 360 градусов, а не 1000. Дюжина – это 12 штук. 60 разделить на 12. Могли ли наши предки иметь 12 пальцев на каждой руке? Конечно, нет.

Оказывается, пальцами одной руки можно сосчитать не 5, а 12. Так делали разные народы: считали фаланги пальцев. Их всего 12.

Но почему число 12 лучше, чем 10? Возможно, потому что у 12 больше делителей. Посмотрите на делители числа 10 и делители числа 12 на экране. А число 360 имеет еще больше делителей, целых 24. Если в круге 360 градусов, то его легко разделить на много частей. И это еще не все.

В день равноденствия солнце восходит почти точно на востоке и заходит почти точно на западе и за день проходит по небу в 360 раз больше, чем диаметр солнца, видимый с Земли. Небесный полукруг делится на 180 градусов. Угловой диаметр Солнца составляет около 32 угловых минут, или чуть больше половины градуса. Она немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая. Утверждение, что в день равноденствия Солнце проходит по небу расстояние, равное 360 его “шагам”, или 360 видимым диаметрам Солнца, верно с определенной точностью.

– Замечательно! – говорили древние шумеры. – В небе есть подтверждение наших расчетов! А также яркая звезда Юпитер!

Оказывается, Юпитер совершает полный оборот вокруг Солнца за 12 лет. Конечно, не 12, а 11,86 земных лет, но астрономам очень хотелось округлить до своего любимого числа.

Давайте посмотрим на Луну. В отличие от Юпитера, любой может найти его на небе, когда он полон. Лунный месяц составляет около 29,5 земных суток. А если в году 12 месяцев, а в году 365 дней (точнее, конечно, 365,242 земных дня). Что-то близкое к числу 360. Астрономы подумали: “Может быть, Боги хотели, чтобы у нас был год из 360 дней и 12 месяцев по 30 дней каждый, но где-то, вероятно, они ошиблись в своих расчетах, или кто-то помешал им. Но нас никто не остановит, и мы разделим круг на 360 градусов”.

Он обозначен следующим образом: 360 и вверху есть символ градуса.

Так что же такое радианы? Что такое угол с мерой измерения 1 радиан? С радианами все гораздо проще.

1 радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности. 1 радиан равен приблизительно 57 градусам (изображение на экране, 5:20 мин).

Как перевести градусы в радианы? Мы уже говорили, что 1 окружность имеет 360 градусов. Но чему равна длина всей окружности радиуса r? Вспомните формулу (5:44). Появится число pi. Число пи известно людям с древних времен, потому что люди, увидев на небе круглые солнце и луну, захотели создать нечто подобное. Они плели круглые корзины и делали круглые тарелки. И они заметили, что отношение длины окружности к ее диаметру всегда одинаково. Это число немного больше 3, а точнее 3,1415926. С течением веков число Пи вычислялось все более точно. Отношение длины окружности к ее диаметру равно пи.

Полный круг – это 360 градусов. Длина окружности равна 2PiR (6:50).

Наш угол меры 1 радиан лежит на дуге окружности радиуса r. Получаем, что угол в один радиан соответствует дуге окружности радиуса, равного r – радиусу окружности. 360 градусов, полный круг, соответствует окружности круга, т.е. 2Pir. Во сколько раз полный круг больше 1 радиана? 2Pi раз, конечно. 360 градусов соответствует 2Pi радианам. 180 градусов – это Pi радиан, 90 градусов – Pi/2 радиан.

Теперь вы знаете, что такое тригонометрическая окружность, что такое радианы и почему в окружности 360 градусов.

Если у вас есть другие версии, почему именно 360, пишите в комментариях. Присылайте больше интересных вопросов и проблем!

Радиан – это единица измерения движения по окружности, характеристикой которой является радиус. Я думаю, что слово “радиан” иллюстрирует именно то, как оно соотносится с радиусом движения.

Математические расчеты в Sun выглядят довольно хорошо

360 – это идеальное количество дней в году. Но эта цифра выглядит довольно субъективной: на Марсе у нас было бы

680 градусов в окружности, потому что марсианский год длится дольше (и сам марсианский день тоже длится дольше, как вы понимаете). В некоторых европейских странах люди используют град, в котором круг должен быть разделен на 400 частей.

Многие из этих объяснений совпадают со следующими: “Ну, градусы – довольно субъективная мера, но мы должны были выбрать какое-то число”. Не сейчас: через мгновение мы увидим, что на самом деле скрывают градусы.

Пусть α = 3, 2 рад. Нам нужно найти меру градуса этого угла.

Формулы для преобразования радиан в градусы и наоборот

Из формулы, полученной выше, можно вывести другие формулы для преобразования углов из радианов в градусы и из градусов в радианы.

Выразим один радиан в градусах. Для этого разделите левую и правую части радианов на пи.

1 p a d = 180 π ° – мера градуса угла в 1 радиан равна 180 π .

Также можно выразить один градус в радианах.

1 ° = π 180 p a d

Можно производить приблизительные расчеты значений углов в радианах и наоборот. Для этого возьмите значения π с точностью до одного десятичного знака и подставьте их в полученные формулы.

1 п а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °.

Таким образом, в одном радиане около 57 градусов.

1° = π 180 r a d = 3 , 1416 180 r a d = 0 , 0175 r a d

Один градус содержит 0,0175 радиана.

Формула для преобразования радианов в градусы

x p a d = x – 180 π °

Чтобы перевести угол из радиан в градусы, угол в радианах нужно умножить на 180 и разделить на пи.

В 20 веке человечество уже смогло вычислить десятки триллионов десятичных чисел с помощью компьютеров, и, как и в древние времена, это имеет практическое значение – с помощью этих вычислений можно оценить производительность компьютерных систем.

Число “пи” не имеет точного значения. Это можно легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр, и вы получите десятичную дробь с большим количеством цифр после запятой. Математики называют такие числа иррациональными. В результате получится 3 целых числа и несколько десятичных, сотых, тысячных – и так далее, вплоть до дисплея калькулятора. Число pi имеет бесконечное количество цифр после запятой. Но округленные значения используются в расчетах для удобства.

Число π приблизительно равно 3,14, точнее, 3,1415926535 – это значение с десятью цифрами после запятой, которое обычно используется. Но все зависит от округления. Там, где не нужны самые точные расчеты, пи часто принимают за 3. Но для точных расчетов в науке ученые используют пи с 38 десятичными знаками (после запятой). Таким образом:

π = 3,14

π = 3,1415926535

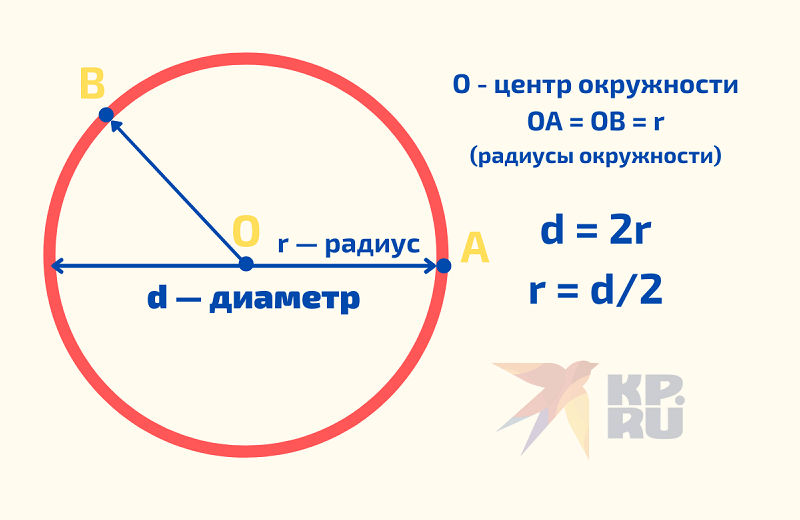
В школе нас учат использовать число “пи” для вычисления площади круга. Он рассчитывается по следующей формуле: S = πr²где S – площадь поверхности, π – пи, а r² – радиус в квадрате. Можно использовать следующую формулу S = πdгде d – диаметр. В конце концов, мы знаем, что диаметр равен радиусу, умноженному на два.

Зная число пи и диаметр, мы можем вычислить длину окружности. Для этого вспомним школьные уравнения. Если π = C/dзатем C (окружность) рассчитывается по формуле C = πd.

Но использование пи в науке гораздо шире. Он используется практически для всех расчетов в любой области, будь то архитектура, авиация или даже статистика. Например, число π необходимо для расчета времени полета самолета и расстояния, которое он должен преодолеть. В статистике pi используется для вычисления значения, находящегося ниже так называемой кривой нормального распределения. Идея заключается в том, чтобы выяснить, например, как распределились голоса респондентов в опросе.

Считается, что первым, кто обозначил пи буквой греческого алфавита π (пи), был британский математик Уильям Джонс в 1706 году, а популяризировал это обозначение его швейцарский коллега Леонгард Эйлер в 1737 году. Существует теория, что эта буква была выбрана не случайно, а в качестве инициала в греческом слове perijereia, что означает “окружность”, “периферия”.

Как и в случае со многими явлениями, известными современной науке, существование константы, которую можно использовать для вычисления площади круга, было отмечено уже в древнем мире. Однако ученые того времени имели разные мнения о значении этой константы: одни принимали значение 3,125, другие 3,16, третьи 3,139. Но всегда это было 3 и небольшое число.

Потребовались тысячи лет, чтобы вычислить точное число “пи”. Первым, кто определил более или менее приблизительное значение π, был древнегреческий ученый Архимед. Он рассчитал, что пи равно 3,142857142857143. Как мы уже знаем, только первые два числа после запятой были правильными.

Более точным был расчет китайского математика в 480 году нашей эры: 3.1415927. Именно это значение пи считалось наиболее правильным до 1420-х годов, когда ученые расширили число до 16 десятичных цифр, затем до 20, 32 и так далее.

В 20 веке, с появлением компьютерных систем и вычислительной техники, дело пошло быстрее: теперь машины вычисляли точное десятичное значение. Используя специальные алгоритмы, математики всего мира продолжают определять новые, более точные значения для числа пи, побивая рекорды по количеству цифр десятичного расширения (после запятой).

Чтобы не запоминать число pi с большим количеством знаков после запятой, принято округлять число pi. В математике все округления подчиняются строгим правилам. Для округления значения числа “пи” используется округление до ближайшего целого числа. Если округляемому числу предшествует 5 или более, оно будет округлено до старшего целого числа. Например, 12,5 → 13. Другой пример: 12,58 → 12,6 → 13.

Если перед округляемым числом стоит цифра меньше 5, то число округляется в меньшую сторону. Например: 12.4 → 12. Или: 12.34 → 12.3 → 12.

Предположим, что значение числа Пи равно 3,1415. Округление начинается с последнего значения, в данном случае это 5. Поэтому следующее за ним число округляется до двух: 3.1415 → 3.142. Последняя цифра 2 меньше пяти, поэтому следующая 4 остается без изменений: 3.142 → 3.14. Это приводит нас к общепринятому значению числа пи.

Следуя тому же принципу, продолжим округлять до целого числа: 3.14 → 3.2 → 3. И здесь мы имеем значение числа пи 3.

Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт региональной предметной комиссии ЕГЭ и ОГЭ по математике и информатике:

На практике мы часто используем округление числа pi до сотых – 3.14. Чуть реже нам требуется большая точность, и мы берем 3.14159. Чтобы запомнить дробную часть, можно использовать простой прием: выучить одно предложение: “Я знаю и помню это прекрасно”. Количество букв в словах соответствует первым цифрам числа пи: “это” – 3, “я” – 1, “я знаю” – 4 и так далее.

Для запоминания большего количества чисел существуют специальные линии, это называется мнемоническим запоминанием.

Ирина Ходакова, учитель математики:

Чтобы запомнить значение числа π, один из самых популярных способов – запомнить предложение, в котором количество букв в каждом слове соответствует цифрам числа π.

Например: “Что(3) я(4) знаю(1) о(1) круге(5)?

Для того чтобы запомнить больше цифр числа π, используются различные мнемонические техники (набор приемов, помогающих запомнить информацию). Например, есть стихотворение С. Боброва “Волшебный двурог”, чтобы запомнить число π, которое несложно выучить:

Чтобы мы не совершали ошибок”,
Мы должны прочитать его правильно:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

А остальное мы должны знать,
Если бы мы спросили вас.
Это пять, три, пять,
Восемь, девять, восемь”.

Вячеслав Смольняков:

В школе ученики впервые изучают pi в 6 классе, и я обычно привожу различные примеры его использования в жизни. Например, девочки на уроках технологии часто шьют круглые предметы, и пи может помочь им рассчитать, сколько пледа нужно для подшивания края круглой салфетки. Мальчики часто интересуются, как подсчитать расстояние, которое они преодолели на уроке физкультуры, бегая по спортзалу. И все любят подарки… Сколько оберточной бумаги нужно, чтобы завернуть подарок в цилиндрическую коробку? Чтобы сделать все это, необходимо знание числа “пи”. В старших классах мы используем знание числа “пи” для решения геометрических задач (но оно используется не только в геометрии).

В науке пи используется во многих геометрических формулах, в первую очередь для нахождения объемов тел, площадей фигур, содержащих круг. В тригонометрии это одно из основных чисел. Он также встречается при вычислении интегралов в высшей математике и в формулах математической статистики и физики.

Если говорить о том, где человечество заинтересовалось этой темой, то стоит вернуться в древность. Приобретение знаний в ту эпоху, как и сейчас, было практическим. Сколько каменных блоков нужно, чтобы построить круглую башню? Подобные вопросы интересовали Архимеда, а также древних правителей, которым приходилось рассчитывать ресурсы, необходимые для защиты своих территорий.

В 20 веке с помощью компьютеров человечество смогло вычислить несколько десятков триллионов знаков после запятой, и, как и в древние времена, это имеет практическое значение – с помощью этих вычислений можно оценить производительность компьютерных систем.

Ирина Ходакова:

Первоначально число π было необходимо для применения в строительстве. Иногда ошибка в значении π приводила к обрушению башен и разрушению целых дворцов. Сегодня π используется в самых разных областях нашей жизни.

Мы уже узнали, что π позволяет нам вычислять и создавать окружности. Если колеса вашего автомобиля немного отличаются, поездка будет, мягко говоря, некомфортной. Но использование π не ограничивается только этим. Например, без числа π телевизоры, радиоприемники и телефоны не могли бы хорошо работать, поскольку инженеры используют число π для расчета и оптимизации звуковых волн. Кроме того, π играет важную роль при расчете времени и расстояния полета аэроплана, поскольку аэропланы пролетают большие расстояния по дуге окружности. Не было бы даже таких игр, как футбол, баскетбол и теннис, потому что мячи должны быть идеально круглыми.

Оказалось, что вероятность того, что игла приземлится именно так, равна 2/Pi, или около 64%. Таким образом, число Пи теоретически можно вычислить с помощью этой техники, если только вы найдете человека, у которого хватит терпения провести этот кропотливый эксперимент. Обратите внимание, что схема никак не задействована.

Пи и квантовая механика

Пи тесно связана с теорией относительности Эйнштейна

Пи – это, несомненно, неизбежная и сложная основа нашего мира, но как насчет нашей бесконечной вселенной? Пи действует во всей Вселенной и принимает непосредственное участие в объяснении природы космоса. Фактом является то, что многие уравнения, используемые в квантовой механике, которые управляют миром атомов и ядер, содержат Pi.

Одними из самых известных уравнений в этой области являются уравнения гравитационного поля Эйнштейна (также известные просто как уравнения Эйнштейна). Это 10 уравнений, разработанных как часть теории относительности, которые описывают фундаментальное взаимодействие гравитации, возникающее в результате искривления пространства-времени массой и энергией. Сила тяжести, присутствующая в системе, пропорциональна количеству энергии и импульса, причем константа пропорциональности, связанная с G, является числовой постоянной.

Мы надеемся, что наша статья помогла вам лучше понять природу и назначение числа Пи. Кто бы мог подумать, что он является неотъемлемой частью нашей повседневной жизни и даже природные процессы происходят в соответствии с его значением.

Дорогие друзья, пожалуйста, ставьте лайк и подписывайтесь на страницу и делитесь своим мнением в комментариях!

Я также рекомендую прочитать :

Читайте далее: