Потенциал электростатического поля. Разница потенциалов - услуги электромонтажа, строительства и ремонта

Однако, это отношение потенциальной энергии приведенного в пример заряда в поле к величине этого заряда для данной точки поля:

Чтобы получить доступ к этому и другим видеоурокам из набора, необходимо добавить его в свой личный кабинет, купив его в каталоге.

Содержание

Получите удивительные возможности

Конспект урока “Потенциал электростатического поля. Разница потенциалов”.

В предыдущем уроке мы говорили о том, что на заряд, помещенный в электростатическое поле, действует сила, которая может перемещать заряд вдоль линии напряженности поля. Другими словами, электростатическое поле способно совершать работу, величина которого пропорциональна величине перенесенного заряда и зависит только от того, откуда и в какую точку поля переносится заряд:

В этом случае на замкнутой траектории работа сил электростатического поля равна нулю.

Напомним, что если работа силовое поле не зависит от формы траектории и равно нулю на замкнутой траектории, такое поле называется потенциальным. Следовательно, точечный заряд в любой точке электростатического поля имеет потенциальную энергию взаимодействия с полем, которая определяется относительно произвольной нулевой точки (обычно бесконечно удаленной точки поля). В нулевой точке потенциальная энергия заряда в поле принимается равной нулю. Затем Потенциальная энергия точечного заряда, взаимодействующего с электростатическим полем, равна работе, которую должны совершить силы поля, чтобы переместить заряд из данной точки поля в нулевую точку:

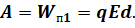
Из этого определения следует, что величина потенциальной энергии заряда в электростатическом поле пропорциональна величине этого заряда:

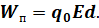
Другими словами, если в одну и ту же точку электростатического поля поместить пробные заряды, величины которых отличаются в два, три, четыре и т.д. раза, то потенциальные энергии этих зарядов будут отличаться на такой же коэффициент.

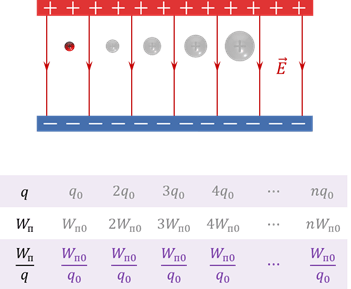
Однако, отношение потенциальной энергии пробного заряда в поле к величине этого заряда для данной точки поля остается неизменным:

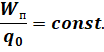
Отношение потенциальной энергии пробного заряда, помещенного в данную точку поля, к величине этого заряда называется потенциалом электростатического поля в данной точке пространства:

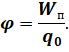
Мы будем обозначать этот потенциал греческой буквой “Phi” (φ).

Вы уже знаете, что характерной силой электрического поля является его напряженность. Потенциал описывает энергетическое состояние поля в данной точке пространства.

Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, это соотношение сохраняется и для потенциала. Если предположить, что на бесконечном расстоянии от источника поле отсутствует, то потенциал поля в данной точке численно равен работе, затраченной на перемещение заряда образца из этой точки поля в бесконечность (т.е. в ноль):

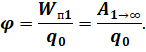
Найдем формулу, по которой можно вычислить потенциал электростатического поля, создаваемого точечным зарядом на некотором расстоянии от него. Для этого запишем формулу для работы электростатического поля:

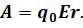
Здесь r – расстояние от образующей поля до точки исследуемого поля. А модуль напряженности поля прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, где определяется значение напряженности:

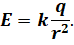
Перепишем формулу для потенциала поля с учетом наших рассуждений.

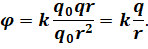
После упрощений мы получаем формулу, с помощью которой можно рассчитать потенциал электростатического поля точечного заряда на заданном расстоянии от него. Из формулы следует, что знак заряда источника определяет знак потенциала поля.

Та же формула может быть использована для расчета потенциала поля, создаваемого равномерно заряженной проводящей сферой в точках вне сферы. Однако, для точек на поверхности и внутри сферы, в знаменателе формулы “Er мало” заменяется на радиус сферы:

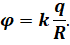
Если электростатическое поле создается системой зарядов, то действует принцип суперпозиции: потенциал такого поля в любой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым из зарядов системы:

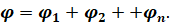
Зная потенциал поля в данной точке, мы можем вычислить потенциальную энергию заряда, помещенного в эту точку:

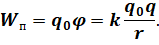
В прошлом уроке мы отметили, что Работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятой с противоположным знаком:

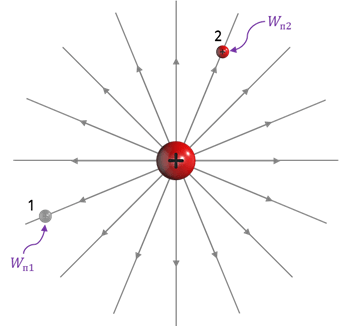
Выразите потенциальную энергию через потенциалы полей в соответствующих точках:

За основу значений потенциальных энергий возьмем формулу работы.

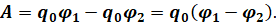
Как видно из формулы, работа поля по перемещению заряда из одной точки в другую пропорциональна величине перенесенного заряда и разности потенциалов между начальной и конечной точками.

Теперь разделите выражение работы на величину перенесенного заряда q₀:

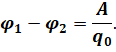
Скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между заданными точками поля к величине этого заряда, называется разностью потенциалов.

Например, изменение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.

Из определения следует, что единицей разности потенциалов в СИ является Дж/Кл. Эта единица называется вольт, в честь итальянского ученого Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.

1 В – это разность потенциалов между двумя такими точками в электростатическом поле, когда заряд 1 Кл перемещается между ними под действием сил поля, совершается работа 1 Дж.

Как вы уже догадались, разность потенциалов часто называют напряжение.

То есть, напряжение между двумя точками в поле определяется работой сил поля по перемещению заряда 1 Кл из одной точки в другую. В электростатическом поле напряжение в замкнутой цепи всегда равно нулю.

Чтобы закрепить новый материал, давайте вместе с вами решим несколько задач. Проблема 1. В центре проводящей сферы с равномерно распределенным положительным зарядом 45 нКл находится металлическая сфера с отрицательным зарядом, модуль которого равен 17 нКл. Найдите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии 30 м от ее центра.

Проблема 2. Электрон влетает в однородное электростатическое поле в направлении линии действия силы. Определите потенциал точки поля, в которой электрон изменит направление, если в точке поля с потенциалом 1 В его скорость была 300 км/с.

(Потенциальная функция) (от лат. ro-tentia – сила) – это характеристика векторных полей, к которым относятся многие силовые поля (электромагнитное гравитационное), а также поле скоростей в жидкости и др. Если P векторного поля является скалярной функцией, то поле X называется потенциальным полем (иногда P – функция). Потенциальное поле определяется в терминах константы. Для потенциального поля справедливо условие = 0 и наоборот, если для некоторого поля везде = 0, то оно потенциально, так как существует P.

ПОТЕНЦИАЛ

Энциклопедический словарь по физике. – М.: Советская энциклопедия. Главный редактор А. М. Прохоров . 1983 .

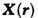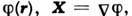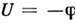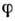(Потенциальная функция) (от лат. ro-tentia – сила) – характеристика векторных полей, к которым относятся многие силовые поля (электромагнитное гравитационное), а также поля скоростей в жидкостях и др. Если P. векторное поле является скалярной функцией является скалярной функцией тогда поле X называется потенциальным полем (иногда P называют структурой f). ). П.). П.определяется с точностью до постоянной величины. 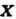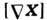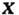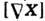Для потенциального поля действительна для действительна для = 0 и наоборот, если для некоторого поля везде везде = 0, тогда поле 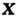– является потенциальным, для него существует P.

Если векторное поле 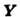является соленоидальным, т.е.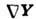является соленоидальным, т.е.= O, можно ввести векторный потенциал 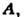такой, что 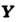такой, что =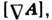поэтому предопределено 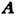поэтому предопределено относительно градиента любой функции ( градиентная инвариантность). В В общем случае каждое векторное поле представляется как сумма потенциального и соленоидного полей.

В классической и квантовой физике силовые характеристики полей – их интенсивности – измеряются экспериментально. На первый взгляд кажется, что потенциальные поля сами по себе не имеют физического смысла, а их введение в теорию – всего лишь удобный прием. Однако оказалось, что в квантовой механике существуют эффекты ( Квантование магнитного потока, Ааронов – Эффект Бома, эффект Джозефсона, эффект Казимира), при котором можно непосредственно воспринимать физическую природу P. Все эти эффекты имеют четкую геом. интерпретацию. Векторными потенциалами являются подключение в слоистой системе на основе соответствующего пространства (например, пространства Минковского M 4 ). В в квантовой теории поля Основной объект исследования – квантовые поля – аналогичны классическим П. П. в том смысле, что набор потенциальных функций является минимальным набором независимых динамических переменных, который полностью описывает систему. Например, в в квантовой электродинамике эти переменные являются квантовыми полями (потенциалами) 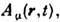где четырехкомпонентный вектор 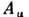где четырехкомпонентный вектор задается потенциалам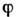и 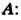и и

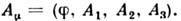
Лит: Tamm I. П., Основы теории электричества, десятое издание, М., 1989; Ландау Л. Д., Лифшиц Е. М., Теория поля, 7-е издание, М., 1988; A. A. Славное, Л. Д. Фаддеев, “Введение в квантовую теорию характеристических полей”, 2-е изд. М., 1988. Л. О. Чехов.

Энциклопедия физики. В 5 томах. – Москва: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Полезная страница

Смотреть что такое “ПОТЕНЦИАЛ” в других словарях:

ПОТЕНЦИАЛ – VOLUME. Количество любого вида энергии может быть выражено произведением двух различных величин, одна из которых характеризует “уровень энергии”, определяя направление, в котором должно происходить ее преобразование; так, например, тяжелое тело…..

потенциальный – ресурсы, заряд, запас, резерв, запас, (внутренние, жизненные) резервы, потенциал, биопотенциал Словарь синонимов русского языка. потенциал см. потенциал Словарь синонимов русского языка. Практический справочник. М.: Русский язык … Словарь синонимов

потенциальный – a, m. potentiel m. , немецкий. Потенциал <лат. potentia сила, мощь. 1. Величина, определяющая запас энергии тела в данной точке в поле (электрическом, магнитном). Водородный потенциал. Магнитный потенциал. Разность потенциалов…. … Исторический словарь галлицизмов русского языка

ПОТЕНЦИАЛ – (Phys.) в учении об электричестве, так называемое значение электрического состояния на поверхности проводника, которое очень похоже на то, что в учении о теплоте называется температурой, и которое измеряет электрическое напряжение на проводниках. Словарь … Словарь иностранных языков

потенциальный – Разность электрических потенциалов между данной точкой и другой произвольно выбранной точкой. [ГОСТ Р 52002 2003] потенциал Общий термин, обозначающий максимальную возможность или способность данной точки быть электрически … Справочник для технических переводчиков

ПОТЕНЦИАЛ – ПОТЕНЦИАЛ, потенция, человек. (от лат. potentia сила, возможность). 1. Физический термин, обозначающий значение потенциальной энергии в данной точке пространства (физика, техника). Потенциал притяжения. Разница потенциалов. ПОТЕНЦИАЛ … Словарь Ушакова

ПОТЕНЦИАЛ – (от лат. potentia сила), источники, возможности, средства, резервы, которые могут быть использованы для выполнения определенной задачи или цели; способность человека, общества или государства в определенной области … … Современная энциклопедия

ПОТЕНЦИАЛ – (потенциальная функция), термин, описывающий широкий класс физических силовых полей (электрическое, гравитационное и т.д.) и, в целом, поля физических величин, представленных векторами (поле скорости жидкости и т.д.). В общем случае, потенциал …. Большой энциклопедический словарь

ПОТЕНЦИАЛ – (от лат. potentia сила) источники, возможности, ресурсы, запасы, которые могут быть использованы для выполнения какой-либо задачи или цели; способность человека, общества или правительства в какой-либо области (например, … Большой энциклопедический словарь,…

потенциальный – (1) В физике – величина, характеризующая поле сил в данной точке – электрических, магнитных, гравитационных и т.д. В связи с этим различают электрический потенциал, магнитный потенциал и т.д. В физике величина, характеризующая поле сил в данной точке – электрических, магнитных, гравитационных и т.д. В связи с этим различают электрический потенциал, магнитный потенциал и др. … Большая энциклопедия психологии

Если W_p2 = 0, в любой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из этой точки в точку с нулевой энергией.

Т. Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система “заряд – электростатическое поле” обладает потенциальной энергией (энергией электростатического взаимодействия). Таким образом, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, затраченная на перемещение заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

Если W_p2 = 0, в любой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

Пусть в некоторой области пространства положительным зарядом создается электростатическое поле q (рис. 2).

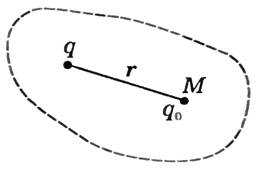
Давайте поместим в точку Μ этого поля различные примеры положительных зарядов q₀. Их потенциальная энергия различна, но соотношение (

Μ = оператор) для данной точки поля и служит характеристикой поля, называемой потенциальный φ в данной точке:

Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).

Потенциал электростатического поля в данной точке это скалярная физическая величина, характеризующая энергетическое состояние поля в данной точке пространства и численно равная отношению потенциальной энергии, которой обладает положительный заряд, помещенный в данную точку, к величине заряда.

Потенциал – это энергетическая характеристика поля, в отличие от напряженности поля, которая является силовой характеристикой поля.

Заметим, что потенциальная энергия заряда в данной точке поля, а значит и потенциал, зависит от выбора нулевой точки. Нулевая точка Эта точка называется нулевой точкой, потому что потенциальная энергия (соответственно потенциал) заряда, помещенного в эту точку поля, должна быть принята за нуль.

Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал может быть определен только до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.

В технике нулевой точкой считается любая точка, которая заземлена, т.е. соединена проводником с землей. В физике за начало потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если мы выберем нулевую точку, то потенциальная энергия (и, следовательно, потенциал в этой точке) заряда q₀ становится определенной величиной.

На расстоянии r от точечного заряда qкоторая генерирует поле, потенциал задается формулой

При указанном выше выборе нулевой точки, потенциал в любой точке поля, создаваемого положительным зарядом qположительное, а поле, создаваемое отрицательным зарядом, отрицательное:

если q > 0 тогда φ > 0; если q < 0, тогда φ < 0.

Из этой формулы мы можем рассчитать потенциальное поле, создаваемое равномерно заряженной проводящей сферой радиуса R в точках на поверхности сферы и за ее пределами. Внутри сферы потенциал такой же, как и на поверхности, т.е.

Если электростатическое поле создается системой зарядов принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым из зарядов в отдельности:

¯Warphi_p = ¯total_.^n )

Знание потенциала φ поля в этой точке можно вычислить потенциальную энергию заряда q₀ расположенных в этой точке: W_p1 = q₀φ. Если мы предположим, что W_p2 = 0, тогда из уравнения (1) имеем

Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q₀ от этой точки до нуля. Из последней формулы следует, что

Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из этой точки в ноль (в бесконечность).

Потенциальная энергия заряда q₀ помещенный в электростатическое поле точечного заряда q на расстояние r из него,

Если q и q₀ – имеют одинаковый заряд, тогда W_p > 0, если q и q₀ – имеют разный знак заряда, тогда W_p < 0.

Заметим еще раз, что эта формула может быть использована для вычисления потенциальной энергии взаимодействия двух точечных зарядов, если для нулевой точки W_p его значение выбирается в r = ∞.

Если электростатическое поле создается системой n точечных электрических зарядов, потенциальная энергия системы задается формулой

W = ¯frac 12 ¯sum_.^n q_i ¯varphi_i ¯)

где φ_i – потенциал поля, создаваемый всеми зарядами, кроме q_iв точке поля, где заряд q_i.

Возникает вопрос: в чем измеряется потенциал? Точнее было бы сказать, в чем обычно измеряется разность потенциалов, поскольку именно с величиной в виде напряжения имеют дело электрики. Для самого потенциала не существует определенной единицы измерения. В СИ принято измерять разницу в вольтах (В). Она равна одному вольту, если для переноса заряда массой один кулон из одной точки электрического поля в другую требуется работа в один джоуль.

Для чего электрику нужен потенциометр

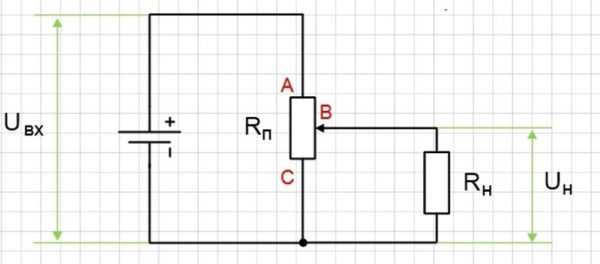
Это устройство широко используется на практике для модуляции напряжения. Дело в том, что многие источники (особенно те, которые предназначены для автономной работы: аккумуляторные батареи, солнечные панели и т.д.) имеют фиксированное напряжение, которое невозможно контролировать без специальных устройств, и это может вызвать проблемы. Для уменьшения опорного напряжения такой ячейки используются делители, оснащенные потенциометрами.

Как работает потенциометр? Он представляет собой резистор с парой выводов и подвижный ползунок со вторым выводом. Такой переменный резистор может быть подключен двумя способами:

Реостатного типа, с использованием скользящего провода и одного из пары других проводов. Сопротивление измеряется путем перемещения ползунка по корпусу резистора. Регулирование тока в цепи в этом случае возможно путем последовательного соединения такого реостата и источника напряжения.
Потенциометрический метод, используя каждый из выводов триплета, имеющихся на приборе. Два основных вывода подключены параллельно источнику, а поднапряжение берется с механизма ползунка и одного вывода. В этом случае через резистор протекает электрический ток, создавая падение напряжения между движком и боковыми выводами. В такой модели большой нагрузкой является источник питания, так как сопротивление резистора должно быть в несколько раз больше сопротивления нагрузки, чтобы регулирование было точным и не вышло из строя.

Поэтому понятие потенциала используется в различных областях физики: как в механике, так и при изучении электричества. В последнем случае она служит характеристикой поля. Эту величину нельзя измерить напрямую, но можно измерить разницу, в этом случае в качестве эталона берется один заряд.

Из механики мы знаем, что такое действие можно определить из произведения силы, действующей на заряд, и модуля смещения, умноженного на косинус угла между ними: A = F * S * cos (a). Поскольку заряд положительный, его направление будет совпадать с линиями электрического поля (напряженность E). Эта сила рассчитывается по формуле: F = q * E. Затем, подставив модуль этого вектора в выражение для работы, мы можем написать: A = q * E * S * cos (a).

Работа в электростатическом поле

Предположим, что в электрическом поле находится заряд. На него действует постоянная сила. Если носитель энергии перемещается из одной точки пространства в другую, мы говорим, что он совершает работу. В простейшем случае мы можем рассматривать однородное поле. В этом качестве можно использовать конденсатор. Пусть его правая пластина заряжена положительно, а левая – отрицательно.

Предполагается, что линии электрического поля будут направлены от плюса к минусу. В какой-то момент в этом однородном состоянии возникает заряд. Для краткости можно считать его положительным и обозначить буквой A. Под действием сил она перемещается в точку B. Задача состоит в том, чтобы найти работу, совершаемую полем для изменения положения заряженной частицы.

Из механики мы знаем, что эта работа может быть определена как произведение силы, действующей на заряд, и модуля смещения, умноженное на косинус угла между ними: A = F * S * cos (a). Поскольку заряд положительный, его направление будет совпадать с линиями электрического поля (напряженность E). Эта сила рассчитывается по формуле: F = q * E. Затем, подставив модуль этого вектора в выражение для работы, мы можем написать: A = q * E * S * cos (a).

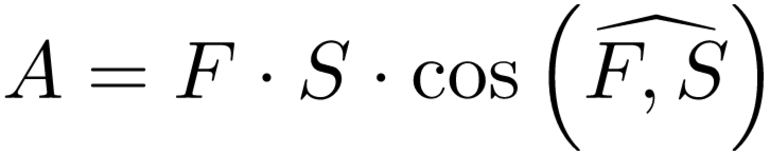
Произведение S * cos (a) – это проекция сегмента смещения на направление электрического поля. Его можно представить как перпендикуляр, опущенный на E. В результате получается правильный треугольник. Прилегающий катет (выступ) можно обозначить через d. В результате рабочая формула будет выглядеть следующим образом: A = q * E * d, где:

q – заряд;
E – стресс;
d – проекция смещения.

Пусть заряд движется по кривой. Например, он проходит путь A-C-B. В результате получатся два вектора S1 и S2. Тогда работа будет определяться как сумма A = Σ ΔAi. Это означает, что если поле однородное (электростатическое), то работа, необходимая для перемещения заряда, не зависит от траектории, а определяется только начальным и конечным положением носителя заряда.

Этим свойством обладают гравитационные и упругие силы. Они называются потенциальными силами. Следовательно, работа по перемещению электричества одинакова. Это происходит за счет потенциальной энергии заряда в поле. Поэтому работа эквивалентна снижению его стоимости. Произведенная работа пропорциональна заряду, т.е. соотношение: W / q. Эта величина называется “электрическим потенциалом”.

Потенциал поля точечного заряда

Потенциал. Разница потенциалов. Напряжение. Эквипотенциальные поверхности.

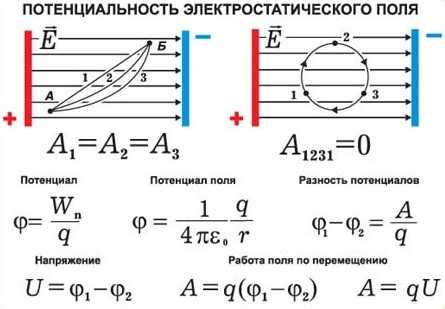
Потенциал. Разница потенциалов. Напряжение.

Потенциал электростатического поля – это скалярная величина, равная отношению потенциальной энергии заряда в поле к энергии этого заряда:

– это энергетическая характеристика поля в данной точке. Этот потенциал не зависит от величины заряда, помещенного в это поле.

Поскольку потенциальная энергия зависит от выбора системы координат, потенциал определяется как константа.

В зависимости от задачи в качестве точки отсчета потенциала выбирают: a) потенциал Земли, b) потенциал бесконечно удаленной точки поля, c) потенциал отрицательной пластины конденсатора.

– Следствие принципа суперпозиции полей (потенциалы складываются алгебраически).

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки в электрическом поле в бесконечность.

В системе СИ потенциал измеряется в вольтах:

Разница потенциалов

Напряжение – это разница между значениями потенциала в начальной и конечной точках траектории.

Напряжение численно равно работе электростатического поля по перемещению единичного положительного заряда вдоль линии поля.

Разность потенциалов (напряжение) не зависит от выбора

Единица измерения разности потенциалов

Напряжение равно 1 В, если поле совершает работу 1 Дж при перемещении положительного заряда массой 1 Кл вдоль линии действия силы.

Взаимосвязь между стресс и напряжение.

Из приведенного выше доказательства следует, что →

напряжение равно градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения следует, что:

Вектор напряжения направлен в сторону уменьшения потенциала.
Электрическое поле существует при наличии разности потенциалов.
Единица интенсивности: – Напряженность поля равна 1 В/м, если между двумя точками поля, расположенными на расстоянии 1 м друг от друга, существует разность потенциалов 1 В.

Эквипотенциальные поверхности.

Эквипотенциальные поверхности – это поверхности с одинаковым потенциалом.

– При движении заряда вдоль эквипотенциальной поверхности работа не совершается;

– вектор интенсивности перпендикулярен ЭПП в каждой точке.

Измерение электрического напряжения (разности потенциалов)

Между стержнем и телом существует электрическое поле. Измерение потенциала проводника Измерение напряжения в гальваническом элементе Электрометр обеспечивает большую точность, чем вольтметр.

Потенциальная энергия взаимодействия между зарядами

Потенциал поля точечного заряда

Потенциал заряженной сферы

a) Внутри сферы Е=0поэтому, потенциалы во всех точках внутри заряженной металлической сферы одинаковы (. ) и равен потенциалу на поверхности сферы.

b) За пределами сферы поле сферы уменьшается обратно пропорционально расстоянию от центра сферы, как в случае точечного заряда.

Перераспределение заряда при контакте заряженных проводников.

Перенос заряда происходит до тех пор, пока потенциалы соприкасающихся тел не сравняются.

Читайте далее: