Заданная плоскость и координатные плоскости образуют пирамиду с основанием .
Вычислим поток векторного поля через поверхность в нормальном направлении, спроецировав поверхность на одну координатную плоскость.
Спроецируем поверхность на плоскость в области .
Найдите поток по формуле ,
где – единичный вектор нормали на выбранной стороне.
По условию, нормаль направлена наружу пирамиды.
Нормальный вектор плоскости имеет координаты .
Поскольку третья координата вектора нормали положительна, вектор нормали образует острый угол с осью i .
Затем
Элемент площади .
Итак
Высшая математика и экономика
Решение
Преобразуем данное общее уравнение плоскости в уравнение плоскости на отрезках .
Из этого уравнения следует, что плоскость пересекает по осям отрезки , и , соответственно.
Эта плоскость и координатные плоскости образуют пирамиду с основанием .
Вычислим поток векторного поля через поверхность в нормальном направлении, спроецировав поверхность на одну координатную плоскость.
Спроецируем поверхность на плоскость в области .
Найдите поток по формуле ,
где – единичный вектор нормали на выбранной стороне.
По условию, нормаль направлена наружу пирамиды.
Нормальный вектор плоскости имеет координаты .
Поскольку третья координата вектора нормали положительна, вектор нормали образует острый угол с осью i .
Затем
Элемент площади .
Поэтому
Проблема 2.
Найдите поток векторного поля через поверхность , пересекаемую плоскостью (нормаль внешняя к замкнутой поверхности, образованной этими поверхностями).
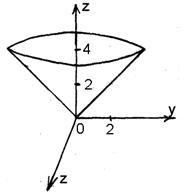
Проблема 3.
Найдите поток векторного поля a в части плоскости , лежащей в первом октанте (нормаль образует острый угол с осью).
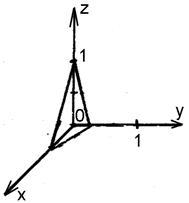
Проблема 4.
Найдите поток векторного поля через замкнутую поверхность (нормаль внешняя).
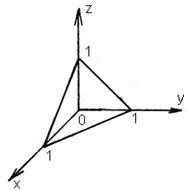
Задача 5. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)
Вариант 13         Вариант 14       Вариант 15         Вариант 16         Вариант 17     Вариант 18
Онлайн поток векторного поля
       Вариант 1      Вариант 2      Вариант 3      Вариант 4        Вариант 5      Вариант 6
Вариант 7         Вариант 8         Вариант 9             Вариант 10             Вариант 11             Вариант 12
Вариант 13       Вариант 14       Вариант 15       Вариант 16           Вариант 17       Вариант 18
Вариант 19     Вариант 20       Вариант 21       Вариант 22         Вариант 23       Вариант 24
Вариант 25     Вариант 26       Вариант 27   Вариант 28       Вариант 29       Вариант 30
            7.14 Нахождение потока векторного поля                         
.
Решение
Поверхность                       ограничена конусом радиуса, равного                         .
            Использование формулы Гаусса-Остроградского
. Здесь
– дивергенция векторного поля.
             Тогда флюс
              Где
– объем конуса.
            So
Ответ:         .
Решение. Площадь поверхности треугольника ABC показано на рисунке ниже.
Вычисление потока векторного поля: примеры
Пример 1. Вычислите поток векторного поля, проходящего через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решите проблему двумя способами: 1) поверхностным интегралом первого рода; 2) поверхностным интегралом второго рода.
1) По поверхности σ треугольник ABC и его проекция на ось xOy – треугольник AOB . .
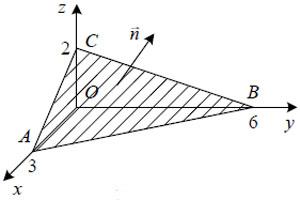
Координаты нормального вектора данной поверхности являются коэффициентами при переменных в уравнении плоскости:
Длина нормального вектора:
Единичный вектор нормали:
Из выражения для единичного нормального вектора следует, что косинус наводки равен . Затем
Теперь мы можем выразить поток векторного поля в виде поверхностного интеграла первого порядка и перейти к его решению:
Выразим переменную zet:
Далее мы вычисляем интеграл и, следовательно, поток векторного поля:
Получаем ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
Представим этот интеграл как сумму трех интегралов и вычислим каждый из них отдельно. Принимая во внимание, что проекция поверхности на yOz треугольник OCB которая ограничена линиями y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках области 2x = 6 − y – 3 , получаем первый интеграл и вычисляем его:
По проекции поверхности на ось xOz треугольник ОАК которая ограничена линиями x = 0 , z = 0 , 2x + 3z = 6 или . Используя эти данные, получаем второй интеграл, который решаем сразу:
Проецируя поверхность на ось xOy треугольник OAB которая ограничена линиями x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:
Остается только просуммировать все три интеграла:
Ответ заключается в том, что поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Пример 2. Вычислите поток векторного поля, проходящего через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решите проблему двумя способами: 1) поверхностным интегралом первого рода; 2) поверхностным интегралом второго рода.
Решение. Поверхность представляет собой треугольник ABC показано на рисунке ниже.
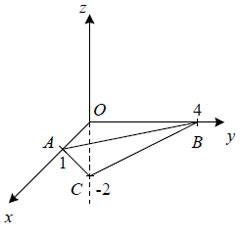
1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые следует брать с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, поэтому третья координата вектора нормали плоскости должна быть положительной). Поэтому нормальный вектор записывается в координатах следующим образом:
Длина этого вектора составляет:
Единичный вектор нормали (orth):
Скалярное произведение векторного поля и единичного нормального вектора:
Поэтому представим поток векторного поля в виде поверхностного интеграла первого рода
Давайте выражать zet и различать то, что уже можно различить:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
Первый и второй интегралы мы делаем со знаком минус, так как вектор нормали поверхности образует с осями Ox и Oy является тупым углом.
Вычислите первый интеграл:
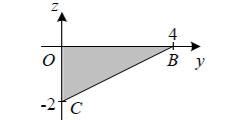
Вычислите второй интеграл:
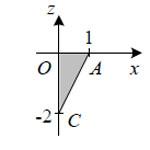
Вычислите третий интеграл:
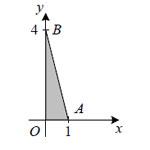
Сложите эти три интеграла и получите тот же результат:
Пример 3. Вычислите поток векторного поля, проходящего через внешнюю сторону параболоида в первом октанте, рассекаемом плоскостью z = 9 .
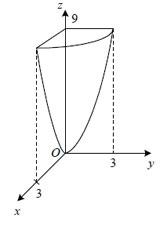
Представим поток векторного поля в виде поверхностного интеграла второго порядка:
Второй интеграл берем со знаком минус, так как вектор нормали поверхности образует с осью Oz является тупым углом. Вычислите первый интеграл:
a=(x-2z)i+(x+3y+z)j+(5x+y)k
Поток векторного поля в режиме реального времени
Пример 1. Вычислить поток вектора a=(2z-x)i+(x+2z)j+3zk
треугольником S, вырезанным из плоскости x+4y+z-4=0 через координатные плоскости в направлении нормали, образующей острый угол с осью OZ.
Решение. Мы рассмотрели два способа решения этой проблемы:
1) проецирование S на одну координатную плоскость,
2) проецирование S на три координатные плоскости.
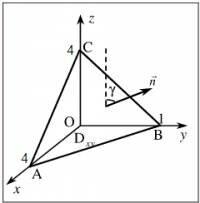
Пример 2. Найдите поток векторного поля
a=(x-2z)i+(x+3y+z)j+(5x+y)k
верхним краем части плоскости, заданной треугольником ABC с вершинами A(1,0,0), B(0,1,0), C(0,0,1)
Пример 3. Вычислите поток векторного поля a=xi+yj+√(x 2 +y 2 -1)k по всей поверхности z=√(x 2 +y 2 -1) ограниченный плоскостями z=0, z=√3
Пример 4. Вычислите поток векторного поля a=xzi над верхней гранью параболоида z=1-x 2 -y 2 ограниченный плоскостью z=0, (z ≥0).
Пример 5. Найдите поток векторного поля a=xi+yj+xzk через внешнюю часть цилиндрической поверхности x 2 +y 2 =9 ограниченный плоскостями z=2, x+z=4
Длина вектора / модуль вектора
Векторный калькулятор
Векторный калькулятор – это уникальный инструмент для решения задач и работы с векторами. Зная только начальную и конечную координату вектора, векторный калькулятор использует данные всех сегментов вектора не только для нахождения координат вектора, косинусов и результатов сложения, вычитания и умножения, но и для доказательства ортогональности, коллинеарности или компланарности двух или более векторов.
Здесь приведены основные формулы для расчетов по одному или двум векторам, ориентированным на плоскости или в пространстве. Другие векторные операции и отдельные калькуляторы можно найти в соответствующих разделах.
Координаты вектора по его начальной и конечной координатам.

Длина вектора / модуль вектора

Направленные косинусы вектора
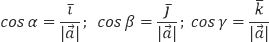
Скалярное произведение векторов. Проверка векторов на ортогональность.
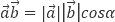
Векторное произведение векторов. Проверка векторов на коллинеарность.

.
Рис. 1. Поток векторного поля A через бесконечно малый элемент поверхности dS равно скалярному произведению .
Конев В.В. Скалярные и векторные поля
Поток векторного поля ,,где n – единичный вектор внешней нормали к поверхности S.
/> Используются и другие формы обозначений для выражения потока поля. Например, учитывая, что скалярное произведение A · n является проекцией An вектор A в направлении внешней нормали n на поверхности S.
/>Другой способ обозначения связан с введением вектора dS = n dSзначение которого равно поверхности элемента поверхности dSа направление определяется вектором n.
/>Со,..
Рис. 1. Поток векторного поля A через бесконечно малый элемент поверхности dS равно скалярному произведению . /> В координатной форме поток векторного поля записывается как.
где плоские поверхности являются проекциями поверхностей S на координатных плоскостях соответственно. Выражения получены из уравнения поверхность Sразрешением относительно соответствующих координат.
/>Для обозначения потока векторного поля через замкнутую поверхность используются выражения вида
- Векторное поле – это. Что такое векторное поле?.
- Поток и циркуляция векторных полей; Школа для инженеров-электриков: Электротехника и электроника.
- Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Векторное и скалярное управление преобразователями частоты – принцип работы, система управления.
- Скалярное произведение векторов. Формулы и определения.
- Звездные изображения.