Принцип работы колебательного контура - услуги электромонтажа, строительства и ремонта

Коэффициент качества рассчитывается по формуле:

Колебательный контур состоит из индуктора и конденсатора. Он может содержать резистор (элемент с переменным сопротивлением).

Катушка (или соленоид) – это стержень, на который намотано несколько слоев витков медной проволоки. Этот элемент создает колебания в колебательном контуре. Стержень в центре называется дросселем или сердечником.

Катушка колебательного контура вибрирует только до тех пор, пока в ней сохраняется заряд. Когда через него проходит ток, он накапливает заряд, который затем отдает обратно в цепь при падении напряжения.

Провода катушки обычно имеют очень малое сопротивление, которое всегда остается постоянным. В колебательном контуре очень часто происходит изменение напряжения и тока. Это изменение происходит по определенным математическим законам:

U = U0*cos(w*(t-t0) , где U – напряжение в момент времени t, U0 – напряжение в момент времени t0, w – частота электромагнитного колебания.

Другим неотъемлемым компонентом схемы является электрический конденсатор. Это элемент, состоящий из двух оболочек, которые отделены друг от друга диэлектриком. Толщина прослойки между вставками меньше их размеров. Такая конструкция позволяет диэлектрику накапливать электрический заряд, который затем может быть введен в цепь.

Разница между конденсатором и батареей заключается в том, что конденсатор не преобразует вещество с помощью электрического тока, а накапливает заряд непосредственно в электрическом поле. Поэтому конденсатор может накапливать достаточно большое количество заряда, который может быть высвобожден полностью. Таким образом, ток в цепи значительно увеличивается.

Колебательный контур также состоит из другого элемента – резистора. Этот элемент имеет сопротивление и используется для управления током и напряжением в цепи. Если мы увеличим сопротивление резистора при неизменном напряжении, ток будет уменьшаться в соответствии с законом Ома:

I = U/R , где I – ток, U – напряжение и R – сопротивление.

Эта ситуация эквивалентна механическим колебаниям, когда заряд отклоняется от своего равновесного положения в противоположном направлении, когда его кинетическая энергия полностью преобразуется в потенциальную.

Чтобы получить доступ к этому и другим видеоурокам из набора, вам необходимо добавить его в личный кабинет через покупку в каталоге.

Содержание

Получите удивительные возможности

Конспект урока “Колебательные контуры. Генерирование электромагнитных колебаний”.

После того как стало известно, что банка с воронкой испускает большой электрический заряд, начались исследования электрических разрядов в банке. В частности, путем короткого замыкания крышки банки с воронкой с катушкой со стальным сердечником было обнаружено, что последняя намагничивается. Конечно, это было неудивительно, поскольку мы знаем, что электрический ток создает магнитное поле, которое фактически намагничивает сердечник.

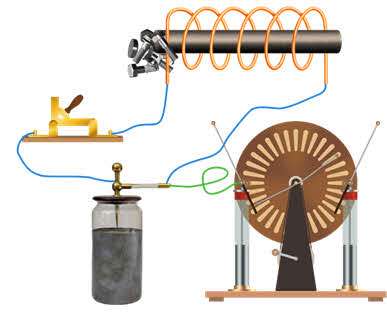
Удивительным было то, что никогда нельзя было точно предсказать, какой конец ядра будет северным полюсом, а какой – южным.

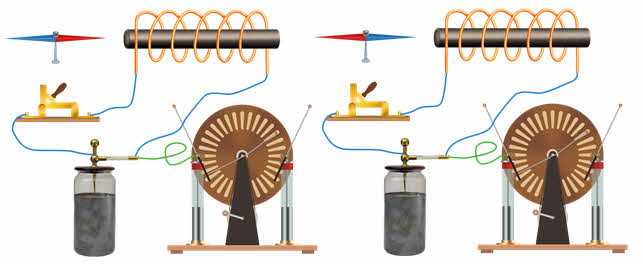
Теперь мы знаем, почему это произошло. Дело в том, что когда лейденская банка разряжается катушкой, в цепи возникают колебания. За время разрядки конденсатор успевает зарядиться несколько раз, поэтому ток в цепи также несколько раз меняет свое направление. Поэтому сердечник каждый раз намагничивался по-разному. А колебания в цепи были названы электромагнитный.

Вы знаете, что все колебания происходят в колебательной системе. Простейшей колебательной системой, в которой могут возникать свободные электромагнитные колебания, является Колебательный контур. Это электрическая цепь, состоящая из конденсатора и индукционной катушки (так называемый электромагнит)..

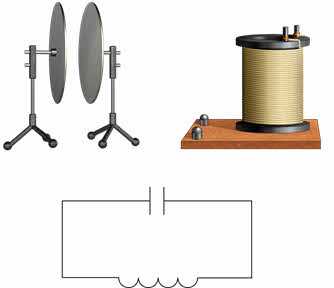
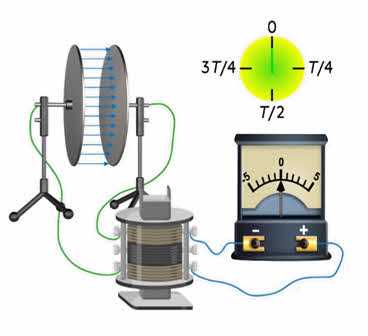
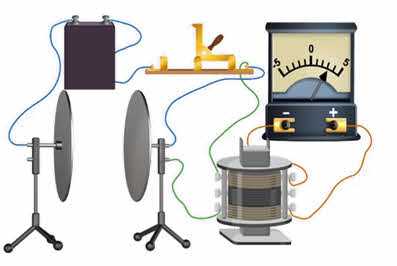
Давайте посмотрим, как создаются электромагнитные колебания в колебательном контуре. Для этого соберите схему, состоящую из источника постоянного тока, колебательного контура и переключателя. В качестве индуктора возьмем катушку с большим числом витков, на которую в середине, поверх первичной обмотки, намотана вторичная катушка с малым числом витков. Подключите вторичную обмотку катушки к гальванометру, который будет использоваться для регистрации возникновения колебаний в цепи.

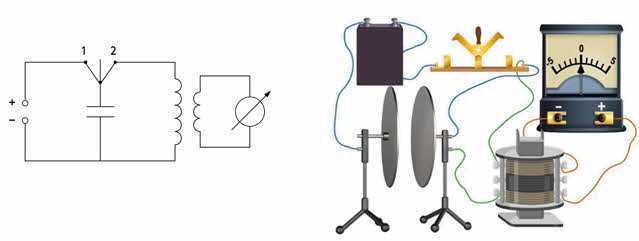
Используйте переключатель для зарядки конденсатора, замыкая его на источник тока. Теперь переведите переключатель во второе положение: стрелка гальванометра начнет вибрировать, указывая на наличие переменного тока в катушке.

– Почему стрелка гальванометра начинает колебаться?

Чтобы ответить на этот вопрос, давайте подробно рассмотрим разряд конденсатора.

Предположим, что в начальный момент времени наш конденсатор заряжен и между его катушками существует электрическое поле.

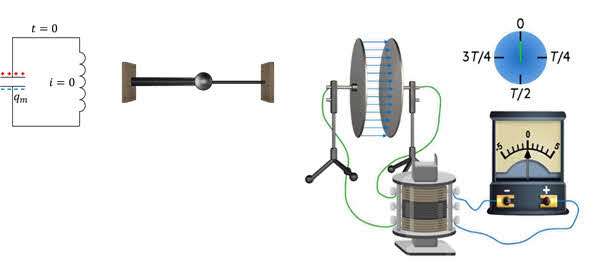
Эта ситуация эквивалентна механическому колебанию груза на пружине и соответствует положению, в котором груз был выведен из равновесия, что придало ему потенциальную энергию.

При замыкании цепи конденсатор начнет разряжаться, и под действием электрического поля заряды начнут двигаться в витках катушки, создавая в цепи ток, сила которого постепенно увеличивается.

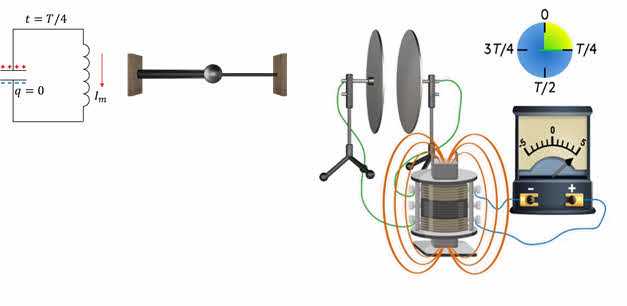
Результатом, как мы знаем, будет самоиндукция тока в катушке, противодействующая увеличению тока во внешней цепи. По мере разряда конденсатора электрическое поле в нем будет ослабевать, и в катушке будет создаваться магнитное поле. Когда конденсатор полностью разряжен, магнитное поле катушки будет самым сильным. Это означает, что энергия электрического поля конденсатора будет полностью преобразована в энергию магнитного поля катушки.

Эта ситуация эквивалентна механическим колебаниям гири при прохождении ею положения равновесия, когда ее потенциальная энергия полностью преобразуется в кинетическую.

Хотя в конденсаторе в этот момент нет электрического поля, заряды будут двигаться в цепи в одном направлении в течение некоторого времени по инерции. Ток в цепи начнет постепенно уменьшаться по мере реверсирования тока самоиндукции, поддерживая уменьшение тока в цепи.

В результате конденсатор снова зарядится, но только на катушке, где были положительные заряды, там будут отрицательные, а где были отрицательные, там будут положительные.

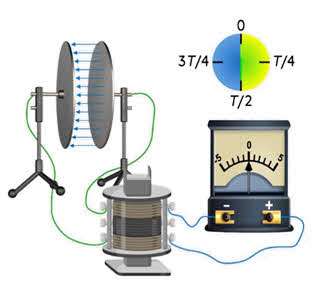
Другими словами, конденсатор зарядится, и ток на мгновение остановится. В этот момент вся энергия магнитного поля катушки будет преобразована обратно в энергию электрического поля конденсатора.

Эта ситуация эквивалентна механическому колебанию, когда груз отклоняется от положения равновесия в противоположном направлении, когда его кинетическая энергия полностью преобразуется в потенциальную.

Затем явление повторится в обратном порядке: конденсатор начнет разряжаться, энергия электрического поля будет преобразована в энергию магнитного поля. Однако в этом случае ток протекает через катушку в обратном направлении. Ток в катушке снова достигнет своего максимального значения, когда конденсатор будет полностью разряжен. Это означает, что вся электрическая энергия будет преобразована в энергию магнитного поля, подобно тому, как гиря на пружине возвращается в равновесное положение и ее потенциальная энергия полностью преобразуется в кинетическую.

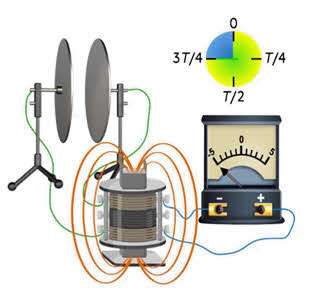
Затем ток начнет уменьшаться, и конденсатор будет заряжен. Когда ток в цепи прекратится, конденсатор будет заряжен так же, как и в начале. Теперь снова вся энергия колебательного контура заключена в его электрическом поле, второй заряд возвращает контур в исходное состояние. Эта ситуация похожа на возвращение груза на пружине в исходное положение, при этом его кинетическая энергия полностью преобразуется в потенциальную.

Таким образом, полное колебание в контуре завершается, и процесс повторяется в том порядке, который мы уже обсуждали.

Повторение процессов означает, что заряды в контуре будут колебаться, перемещаясь от одной обкладки конденсатора к другой.

Почему мы сравнили процессы, происходящие в колебательном контуре, с колебаниями пружинного маятника? Причина в том, что эти процессы описываются одними и теми же уравнениями, что позволяет переносить закономерности, полученные при изучении одного вида колебаний, на колебания другой природы.

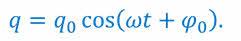
Если бы не было потерь энергии, колебания в контуре продолжались бы бесконечно, т.е. они были бы незатухающими. Такие колебательный контур называется идеальным колебательным контуром или контуром Томсона. Колебания, возникающие в идеальном колебательном контуре, являются свободнымипотому что они существуют благодаря первоначальному запасу энергии в конденсаторе.

Минимальный промежуток времени, после которого процесс в колебательном контуре полностью повторяется, называется периодом электромагнитного колебания.

Формула для определения периода свободных электромагнитных колебаний была выведена английским физиком Уильямом Томсоном в 1853 году и сегодня носит его имя.

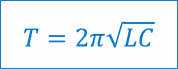
Из этой формулы следует, что период колебательного контура определяется параметрами его компонентов: индуктивностью катушки и емкостью конденсатора. Из формулы Томсона также следует, что, например, при уменьшении емкости или индуктивности период колебания должен уменьшаться, а его частота увеличиваться, и наоборот.

Это можно легко проверить экспериментально. Измените емкость конденсатора в нашей схеме. Разряжая конденсатор на катушке, мы видим, что колебания стрелки гальванометра становятся более частыми.

В заключение следует отметить еще одну важную особенность электромагнитных колебаний в контуре: если заряды на катушках конденсатора не пополняются извне, то колебания довольно быстро прекращаются. Причиной этого является сопротивление проводников: при протекании тока проводники нагреваются, что расходует энергию цепи. Для поддержания колебаний в контуре достаточно подключить его к источнику тока, напряжение которого периодически изменяется с определенной частотой, что будет вливать в контур новые порции энергии, не позволяя ей полностью расходоваться. В этом случае это будет вынужденные электромагнитные колебания происходящие с частотой, равной скорости изменения напряжения источника тока.

Когда частота переменного напряжения совпадает с частотой колебательного контура, будет резонанс. Это приводит к увеличению тока.

Электроны с нижней обкладки устремились по проводу катушки – к верхней обкладке конденсатора (можно сказать, что в то же время положительный заряд устремился к нижней обкладке), но они не могут устремиться туда сразу.

Колебательный контур

Колебательный контур – это замкнутый электрический контур, состоящий из катушки и конденсатора. Обозначьте индуктивность катушки буквой L, а емкость конденсатора – буквой C. Колебательный контур – это простейшая электрическая система, в которой могут возникать свободные гармонические электромагнитные колебания.

Конечно, реальный колебательный контур всегда содержит не только емкость C и индуктивность L, но и соединительные провода, которые, безусловно, имеют активное сопротивление R, но оставим сопротивление за рамками этой статьи, о нем вы можете узнать в главе о Q-факторе колебательной системы. Итак, давайте рассмотрим идеальный колебательный контур и начнем с конденсатора.

Предположим, что существует идеальный конденсатор. Зарядите его батареей до напряжения U0, т.е. создайте разность потенциалов U0 между клеммами, чтобы верхние клеммы стали “+”, а нижние “-“, как это принято называть.

Что это значит? Это означает, что мы перенесем часть отрицательного заряда Q0 (состоящего из электронов) с верхней обкладки конденсатора на его нижнюю обкладку. В результате на нижней обкладке конденсатора будет избыток отрицательного заряда и недостаток точно такого же количества отрицательного заряда на верхней обкладке, и, следовательно, избыток положительного заряда. В начале конденсатор не был заряжен, поэтому на обоих его витках было ровно столько же заряда одинакового знака.

То есть конденсатор заряжен, верхняя обкладка заряжена положительно (поскольку там нет электронов) по отношению к нижней обкладке, а нижняя обкладка заряжена отрицательно по отношению к верхней обкладке. В общем, для других объектов конденсатор электрически инертен, но внутри его диэлектрика существует электрическое поле, так что противоположные заряды на противоположных катушках взаимодействуют, то есть стремятся притянуть друг друга, но диэлектрик, по своей природе, не позволяет этого сделать. В этот момент энергия конденсатора максимальна и равна ECm.

Теперь возьмем идеальную индукционную катушку. Пусть он будет сделан из проводника, который не имеет электрического сопротивления, то есть обладает идеальной способностью пропускать через себя электрический заряд, не нарушая его. Подключим катушку параллельно с вновь заряженным конденсатором.

Что произойдет? Заряды на электродах конденсатора взаимодействуют, как и раньше, они стремятся притянуть друг друга – электроны из нижнего конца катушки стремятся вернуться в верхний конец, потому что они были насильно перетащены оттуда в нижний конец, когда конденсатор был заряжен. Система зарядов стремится вернуться к электрическому равновесию, и тогда присоединяется катушка – проводник, скрученный в спираль, которая обладает индуктивностью (способностью препятствовать изменению тока через магнитное поле по мере протекания этого тока)!

Электроны с нижней обкладки устремляются по проводу катушки – к верхней обкладке конденсатора (можно сказать, что одновременно положительный заряд устремляется к нижней обкладке), но они не могут устремиться туда немедленно.

Почему? Поскольку катушка обладает индуктивностью, а электроны, движущиеся по ней, уже являются током, а раз есть ток, то должно быть и магнитное поле вокруг нее. И поэтому, чем больше электронов попадает в катушку – тем больше будет их ток и тем больше магнитное поле вокруг катушки.

Когда все электроны с нижнего края конденсатора окажутся внутри катушки – ток в катушке будет максимальным Im, магнитное поле вокруг нее будет наибольшим, которое может создать данное количество движущегося заряда в ее проводе. В этот момент конденсатор полностью разряжен, энергия электрического поля в диэлектрике между его витками равна нулю EC0, но вся эта энергия теперь содержится в магнитном поле катушки ELm.

А дальше магнитное поле катушки начинает уменьшаться, потому что его нечему поддерживать, потому что нет других электронов, втекающих в катушку и вытекающих из нее, нет тока, и исчезающее магнитное поле вокруг катушки создает в ее проводе вихревое электрическое поле, которое толкает электроны дальше – к верхней обкладке конденсатора, куда они так стремились. Когда все электроны находились на верхней обкладке конденсатора, магнитное поле катушки было равно нулю EL0. Теперь конденсатор заряжен в направлении, противоположном тому, в котором он был заряжен в начале.

Теперь верхний лист конденсатора заряжен отрицательно, а нижний – положительно. Катушка все еще подключена, ее провод по-прежнему обеспечивает свободный путь для электронов, и между витками конденсатора снова возникает разность потенциалов, хотя и противоположного первоначальному знака.

И электроны снова устремляются в катушку, ток становится максимальным, но поскольку он теперь в противоположном направлении, создается магнитное поле в противоположном направлении, и когда все электроны снова оказываются в катушке (в своем нисходящем движении), магнитное поле больше не увеличивается, оно начинает уменьшаться, и электроны выталкиваются дальше – в нижнюю катушку конденсатора.

И в тот момент, когда магнитное поле катушки стало нулевым, оно полностью исчезло – верхняя обкладка конденсатора снова стала положительно заряженной по отношению к нижней. Состояние конденсатора стало таким же, как и в начале. Произошел полный цикл одного колебания. И так далее, и так далее. Период этих колебаний, который зависит от индуктивности катушки и емкости конденсатора, можно найти по формуле Томсона:

Процесс передачи энергии в колебательном контуре между электрическим полем конденсатора во время его разряда и магнитным полем, сосредоточенным в катушке, полностью аналогичен процессу преобразования потенциальной энергии растянутой пружины или поднятого груза математического маятника в кинетическую энергию при механических колебаниях последнего.

Свободные электромагнитные колебания в колебательном контуре.

Колебательный контур – электрическая цепь, содержащая индуктивность Lемкость С и устойчивость RВ которых могут быть вызваны электрические колебания.

Колебательный контур является одним из основных элементов радиотехнических систем. Различают линейный и нелинейный осциллирующий схемы. Параметры R, L и С линейного колебательного контура не зависит от интенсивности колебаний, а период колебаний не зависит от амплитуды.

Если нет потерь (R = 0) свободные гармонические колебания возникают в линейном колебательном контуре.

Чтобы вызвать колебания в этой цепи, конденсатор предварительно заряжается от аккумуляторной батареи путем подачи на него энергии W_pи установите переключатель в положение 2.

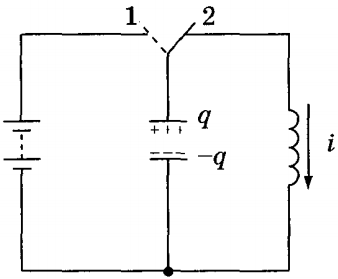
При замыкании цепи конденсатор начнет разряжаться через индуктор, теряя энергию. В цепи появится ток, вызывающий переменное магнитное поле. Переменное магнитное поле, с другой стороны, создает вихревое электрическое поле, которое препятствует протеканию тока, что приводит к постепенному изменению силы тока. При увеличении тока в катушке энергия магнитного поля увеличивается W_м. Общая энергия W электромагнитного поля контура остается постоянной (при отсутствии сопротивления) и равна сумме энергий магнитного и электрического полей. Полная энергия, по закону сохранения энергии, равна максимальной энергии электрического или магнитного поля:

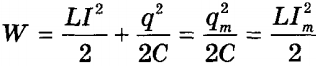
где L – индуктивность катушки, I и I_m – ток и его максимальное значение, q и q_m – это заряд конденсатора и его максимальное значение, С – емкость конденсатора.

Процесс передачи энергии в колебательном контуре между электрическим полем конденсатора при его разряде и магнитным полем, сосредоточенным в катушке, полностью аналогичен процессу преобразования потенциальной энергии растянутой пружины или поднятого груза математического маятника в кинетическую энергию при механических колебаниях последнего.

Взаимосвязь между механическими и электрическими величинами в колебательных процессах показана ниже.

Формула для расчета частоты колебаний выглядит следующим образом:

Электромагнитные колебания в колебательном контуре характеризуются определенной частотой. Эта величина называется резонансом.

Частота зависит от нескольких параметров колебательного контура:

емкость конденсатора (C) ;
индуктивность катушки ∆L ;
сопротивление резистора.

Формула для расчета частоты колебаний выглядит следующим образом:

Преобразование различных видов энергии с помощью колебательного контура нашло применение в различных областях электротехники и механики. Эти дисциплины изучаются студентами университетов и профессиональных училищ, а затем применяются в различных инженерных проектах. Быструю и квалифицированную помощь в процессе обучения можно получить на сайте Phoenix.Help.

Формула получена с использованием закона сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, в любой момент времени верно следующее

Колебательный контур и свободные электромагнитные колебания в контуре

Явление образования ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимается возникновение ЭДС в замкнутой, проводящей цепи, в результате изменения тока в самой цепи.

Правило Ленца: Индукционный ток в замкнутом проводящем контуре имеет направление, при котором магнитный поток, создаваемый им на поверхности, ограниченной контуром, стремится компенсировать изменение магнитного потока, вызвавшего ток.

Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора с электрической емкостью 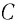и катушка (соленоид) с индуктивностью 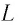(рис. 29, а), который называется идеальный колебательный контур или 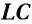-схема. Электрическое сопротивление идеальной цепи считается равным нулю. 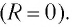Поэтому идеальный колебательный контур – это упрощенная модель реального колебательного контура.

Подключившись (с помощью ключа для зарядки конденсатора до напряжения 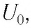зарядка 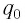(рис. 29, б). Поэтому в начальный момент времени 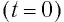конденсатор заряжен так, что на его катушке имеется заряд 1 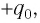и на депозите 2, заряд 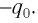Поэтому электростатическое поле, создаваемое зарядами электродов, имеет энергию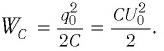

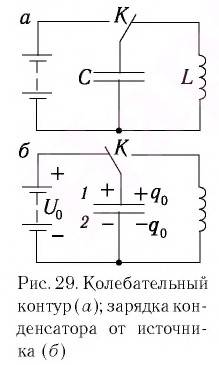
Рассмотрим процесс разрядки конденсатора в колебательном контуре. Когда заряженный конденсатор подключен к катушке (с помощью 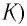(рис. 30) он начнет разряжаться, так как свободные электроны будут двигаться по цепи от отрицательно заряженной клеммы к положительно заряженной под действием электрического поля, создаваемого зарядами на клеммах конденсатора. Стрелка на рисунке 30 показывает начальное направление тока в цепи.

Таким образом, в цепи будет возникать электрический ток с возрастающим модулем, сила которого 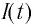будет меняться во времени (рис. 31, а). Но мгновенный разряд конденсатора невозможен, так как изменение магнитного поля катушки, создаваемое возрастающим по модулю током, создаст вихревое электрическое поле. Фактически, в индукционной катушке будет создан изменяющийся во времени магнитный поток, что приведет к возникновению ЭДС самоиндукции. Согласно принципу Ленца, самоиндуцированная ЭДС стремится противодействовать причине, которая ее вызвала, т.е. по модулю увеличения тока.

Следовательно, модуль тока в колебательном контуре с течением времени будет плавно увеличиваться от нуля до максимального значения 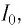определяется индуктивностью катушки и емкостью конденсатора (рис. 31, б).

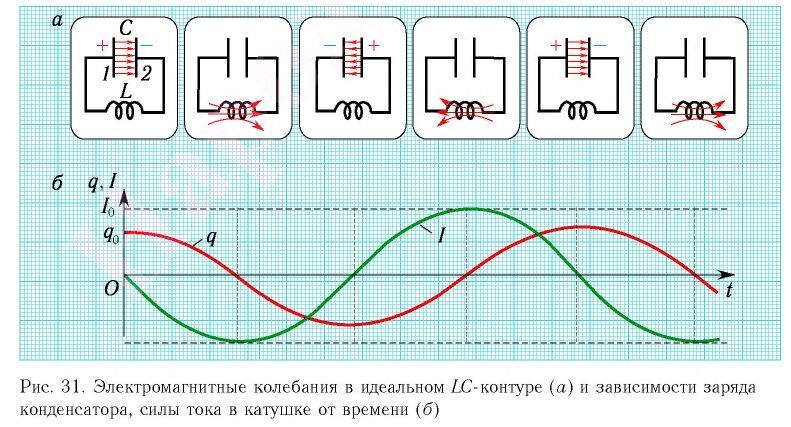
Когда конденсатор разряжается, энергия его электростатического поля преобразуется в энергию магнитного поля катушки с током. Согласно закону сохранения энергии, полная энергия идеального колебательного контура остается постоянной во времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):

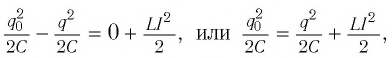
где 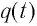– мгновенное значение заряда конденсатора i 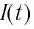– ток в катушке в определенный момент времени 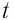после того, как конденсатор начнет разряжаться.

Когда конденсатор полностью разряжен 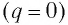ток в катушке 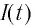достигнет своего максимального значения по модулю 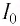(См. рис. 31, б). Согласно закону сохранения энергии, энергия электростатического поля, запасенная в конденсаторе, в этот момент преобразуется в энергию магнитного поля, запасенную в катушке:

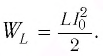
Когда конденсатор разряжается, ток в катушке начинает уменьшаться по модулю. Это тоже происходит не сразу, потому что вновь созданная самоиндуцированная ЭДС создает индукционный ток в соответствии с правилом Ленца. Он имеет то же направление, что и уменьшающийся ток в цепи, и поэтому “поддерживает” ее. Индукционный ток, создаваемый ЭДС самоиндукции катушки, заряжает конденсатор до начального напряжения 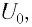но знак заряда на каждом витке оказывается противоположным знаку начального заряда. Поэтому к моменту исчезновения тока заряд конденсатора достиг своего максимального значения 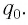В то же время его катушка, первоначально положительно заряженная, будет заряжена отрицательно. Затем процесс повторится, только электрический ток в цепи будет течь в противоположном направлении, как показано на рисунке 31, а.

Таким образом, в идеальном случае 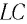-будут происходить периодические изменения тока и напряжения, при этом общая энергия цепи останется постоянной. В этом случае говорят, что в цепи свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре – это периодические изменения заряда на обмотках конденсатора, тока и напряжения в цепи, происходящие без добавления энергии от внешних источников.

Таким образом, существование свободных электромагнитных колебаний в цепи обусловлено зарядкой конденсатора, вызванной возникновением самоиндуцированной ЭДС в катушке. Отметим, что заряд конденсатора 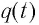конденсатора и ток 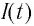в катушке достигают своих максимальных значений 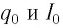в разные моменты времени (см. рис. 31 a, b).

Наименьший промежуток времени, за который LC-цепь вернется в исходное состояние (к начальным значениям зарядов на каждом полюсе), называется период свободных (собственных) электромагнитных колебаний в контуре.

Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 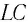-контур, который равен сумме энергии электростатического поля конденсатора и магнитного поля катушки, не сохраняется, поэтому во все моменты времени уравнение верно:

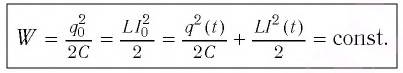
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:

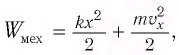
Где 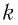– жесткость пружины, 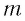– масса груза, 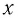– это проекция смещения тела из положения равновесия, 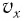– проекция его скорости на ось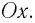

период его колебаний:

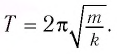
Давайте проанализируем соотношения (1) и (2). Можно отметить, что энергия электростатического поля конденсатора 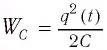аналогично потенциальной энергии упругой деформации пружины 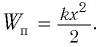Соответственно, энергия магнитного поля катушки 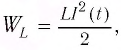которая обусловлена упорядоченным движением зарядов, аналогична кинетической энергии заряда 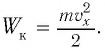Таким образом, аналог координаты 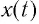пружинного маятника при колебаниях в электрических цепях является заряд конденсатора 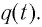Тогда, следовательно, аналогом проекции скорости заряда является ток в колебательном контуре, так как ток характеризует скорость изменения заряда конденсатора во времени.

По аналогии с уравнением для периода колебаний пружинного маятника, подставим массу 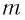индуктивностью 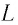и жёсткость 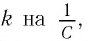для периода свободных колебаний в 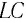-получаем формулу:

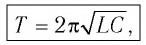
который называется Формула Томсона.

Дальнейшие простые рассуждения позволяют установить аналогии между физическими величинами в электромагнитных и механических колебаниях (табл. 4).

Для наблюдения и изучения электромагнитных колебаний используется электронный осциллограф, на экране которого получают временной ход колебания (рис. 32).

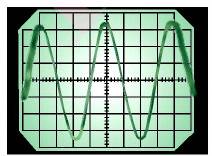
Временная зависимость заряда конденсатора имеет тот же вид, что и временная зависимость координаты (проекции смещения) тела, совершающего гармонические колебания:

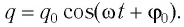
Ток (но с другой начальной фазой) в цепи и напряжение на конденсаторе также изменяются по гармоническому закону.

Для определения начальной фазы 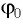и максимальный заряд 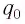необходимо знать заряд конденсатора и ток катушки в начальный момент времени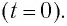

Обратите внимание, что колебательный контур, в котором только обмен энергией между конденсатором и катушкой называется замкнутым закрытый.

Полная энергия идеального колебательного контура 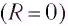сохраняется во времени, поскольку при протекании тока в нем не выделяется тепло. Реальный колебательный контур всегда имеет определенное электрическое сопротивление 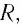которое возникает из-за сопротивления катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальной цепи исчезают со временем, тогда как в идеальной цепи они будут возникать столько, сколько нужно.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура – пружинный маятник с учетом трения.

Пример решения проблемы:

Идеальный колебательный контур состоит из конденсатора с емкостью 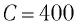пФ и катушка с индуктивностью 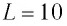м рт. ст. Найдите максимальное значение тока 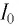в цепи, если максимальное значение напряжения на конденсаторе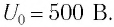
Дано:

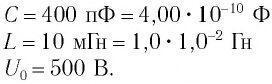
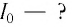
Решение

Максимальная энергия электростатического поля конденсатора:

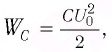
и максимальная энергия магнитного поля катушки:

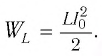
Поскольку схема является идеальной 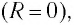его полная энергия сохраняется во времени. В соответствии с законом сохранения энергии 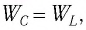это

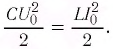
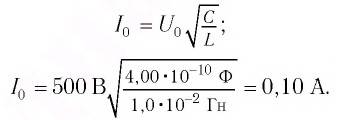
Ответ: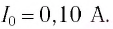

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан группой преподавателей на некоммерческой основе для дополнительного образования молодежи.

Сайт написан, поддерживается и управляется командой преподавателей

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.

Читайте далее: