Работа и мощность электричества - услуги электромонтажа, строительства и ремонта

Это соотношение выражает закон сохранения энергии в однородной системе.

Содержание

Что называется работой тока

Это соотношение выражает закон сохранения энергии в однородной системе.

Закон преобразования работы тока в теплоту был определен экспериментально независимо друг от друга Ж. Джоулем и Е. Ленца и называется законом Джоуля-Ленца.

Мощность электрического тока равна отношению работы, совершаемой током Δ, к отрезку времени Δ, за который эта работа совершается:

Работа электрического тока выражается в джоулях (Дж), а мощность – в ваттах (Вт).

Теперь рассмотрим полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением и внешней однородной цепи с сопротивлением . Закон Ома для полной цепи записывается в виде

( + ) = .

Умножив обе части этой формулы на Δ = Δ, мы получим коэффициент, выражающий закон сохранения энергии в полной цепи постоянного тока:

2 Δ + 2 Δ = Δ_св..

Первый член в левой части Δ = 2 Δ – это тепло, выделяемое во внешней части контура в момент времени Δ, второй член Δ_Δ = 2 Δ – тепло, выделяемое внутри источника за то же время.

Выражение Δ равно работе внешних сил Δ_св.действующие внутри источника.

Обратите внимание, что это соотношение не учитывает работу электрического поля. Когда ток течет в замкнутой цепи, электрическое поле не совершает никакой работы; поэтому тепло выделяется только под действием внешних сил, действующих внутри источника. Роль электрического поля сводится к перераспределению тепла между различными частями цепи.

Внешняя цепь может быть не только проводником с сопротивлением, но и энергопотребляющим устройством, таким как двигатель постоянного тока. В этом случае необходимо понимать эквивалентное сопротивление нагрузки. Энергия во внешней цепи может быть частично или полностью преобразована в другие формы энергии, напр. механическая работа, выполняемая электродвигателем в дополнение к теплу. Поэтому вопрос использования энергии от источника питания имеет большое практическое значение.

Полная мощность источника, т.е. работа, совершаемая внешними силами в единицу времени, равна
Мощность, выделяемая во внешней цепи, равна
Соотношение равно
называется КПД источника .

На рис. 1.11.1 графически показана зависимость мощности источника _istэффективная мощность, рассеиваемая во внешней цепи, и КПД η как функция тока в цепи для источника с электромагнитным полем и внутренним сопротивлением. Ток в цепи может изменяться от = 0 (при ) до (при = 0).

Из приведенных выше графиков следует, что максимальная мощность во внешней цепи _maxравен
достигается при = . В то же время ток в цепи
а эффективность источника составляет 50%. Максимальная эффективность источника достигается при , т.е. на В случае короткого замыкания полезная мощность = 0, и вся мощность высвобождается внутри источника, что может привести к его перегреву и разрушению. В этом случае эффективность источника равна нулю.

При хаотическом движении заряженных частиц в проводнике электрическое поле совершает работу, которую мы решили назвать работой тока. Определение работы тока таково: это работа электрического поля по перемещению зарядов в проводнике.

Любая физическая величина, которая может быть преобразована в энергию, измеряется в джоулях (Дж). 1 Джоуль равен работе, затраченной на перемещение точки, к которой приложена сила, равная 1 Ньютону, умноженная на расстояние 1 метр. Получается, что 1 J = 1 N – 1 m.

Единицей измерения мощности является ватт (Вт). Она равна работе 1 Дж в единицу времени 1 с. Поэтому 1 W = 1 J : 1 с.

Измерительная мощность

Величину электрического тока в проводнике можно определить с помощью амперметра и вольтметра. Но для измерения мощности можно также использовать специальный прибор, называемый ваттметром. Ваттметр. Это комбинация амперметра и вольтметра.

Что называется работой электричества

Работа и мощность электрического тока. Когда электрический ток проходит по цепи, он совершает различные действия: тепловые, механические, химические и магнитные. Таким образом, электрическое поле делает работа. Таким образом, электрическая энергия преобразуется в в другие формы энергиивнутренняя энергия, механическая энергия, магнитная энергия…

Как мы уже упоминали ранее, напряжение (U) в цепи равно отношению работы (F), осуществляемого перемещением электрического заряда (q) в этом участке цепи относительно заряда: U = A/q. Следовательно, A = qU .

Поскольку заряд равен произведению силы тока (I) и время (t) q = It, тогда A = IUt . Это означает, что работа, совершаемая электрическим током в цепи, равна произведению напряжения в этой цепи, силы тока и времени, в течение которого совершается работа.

Единица работы – это джоуль (1 J): [A] = 1 J = 1B – 1A – 1s.

Для измерения работы используются три измерительных прибора: амперметр, вольтметр и таймер. В действительности, однако, счетчики электроэнергии используются для измерения счётчики электроэнергии.

Если вы хотите найти работу тока, но не знаете силу тока или напряжение, вы можете воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: А = U 2 t/R или A = I 2 Rt .

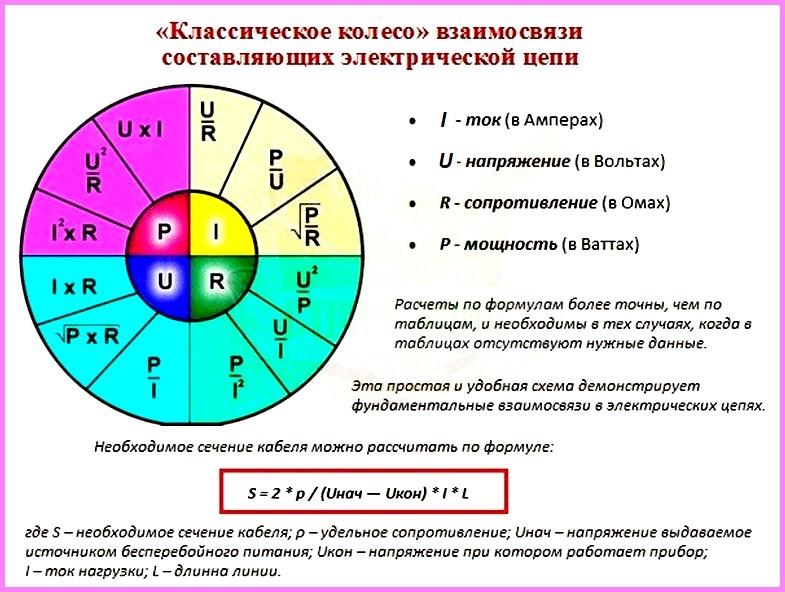
Мощность электрического тока

Мощность электрического тока равна отношению произведенной работы к времени P = A/t или P = IUt/t => P = IU . Другими словами сила электрического тока равна произведению напряжения и тока в цепи.

Единица мощности – это ватт (1W): [P] = 1A – 1B = 1W.

Используя закон Ома, можно вывести другие формулы для расчета мощности тока: Р = U 2 P/R = I 2 R .

Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра. Но для измерения мощности можно также использовать специальный прибор, называемый ваттметром. Ваттметр. Это комбинация амперметра и вольтметра.

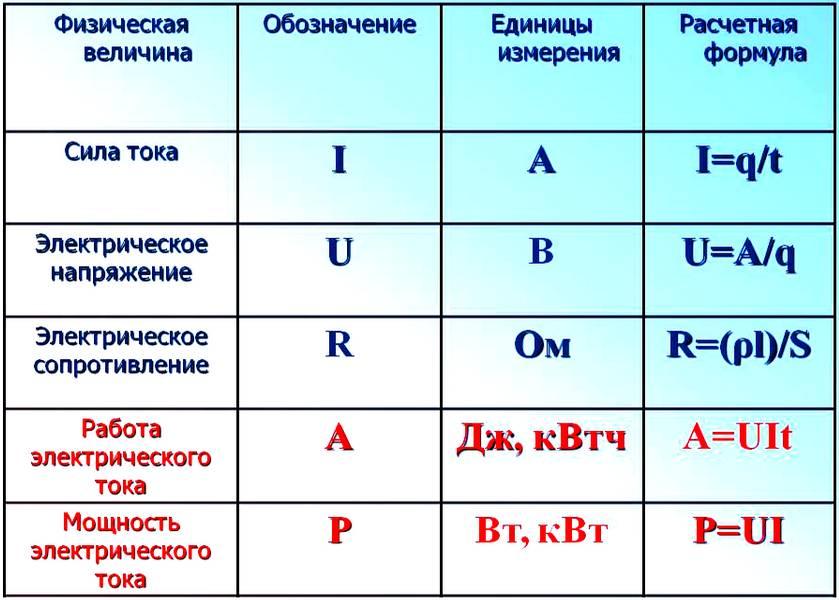
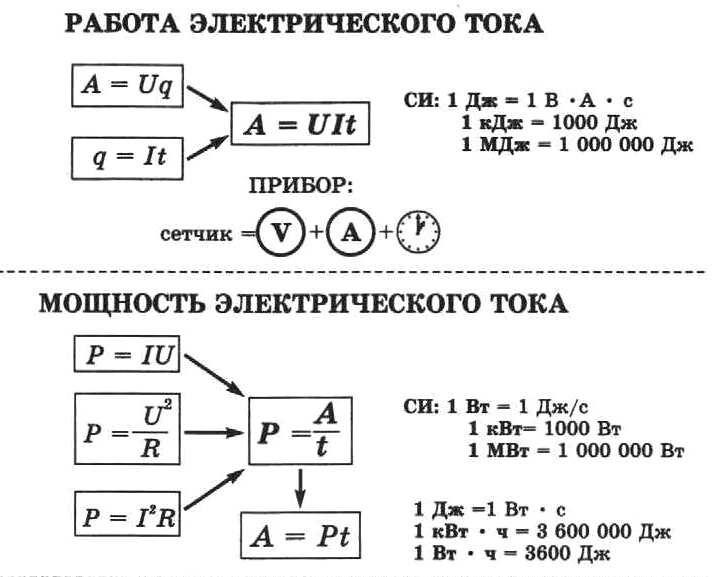
Конспект урока “Работа и мощность электрического тока”.

1 гВтч = 100 ватт = 360 000 Дж,

Работа электрического тока

Протекая по цепи, электрический ток совершает работу. Снова сравните течение электрического тока с течением воды в трубе. Если этот поток направляется, например, на лопасти генератора переменного тока, то поток совершает работу, вращая генератор. Точно так же электрический ток совершает работу, протекая по проводнику. И эта работа тем больше, чем больше ток и напряжение в цепи.

Таким образом, работа электрического токавыполняется на участке цепи прямо пропорциональна току в цепи, напряжению в цепи и длительности тока. Работа электрического тока обозначается латинской буквой A.

Формула для работы электрического тока выглядит следующим образом:

A = I*U*t

Произведение I*U есть не что иное, как мощность электрического тока.

Тогда формула для работы электрического тока выглядит следующим образом

A = P*t

Работа электрического тока измеряется в Ватт-секунды или, другими словами, в джоули.

Поэтому, если мы хотим узнать, сколько работы совершил ток, протекающий по цепи в течение нескольких секунд, нам нужно умножить мощность на это количество секунд.

Например, через реостат с сопротивлением 5 Ом протекает ток 0,5 А. Нам нужно определить, какую работу совершит ток за 4 часа (14 400 секунд). Так как работа тока за одну секунду составит:

P=I 2 R = 0,5 2 *5 = 0,25 *5 = 1,25 ДЮЙМА,

то в момент времени t=14400 сек она будет в 14,400 раз больше. Поэтому работа электрического тока A будет равна:

A = P*t= 1,25*14 400= 18 000 ватт-секунд.

Ватт-секунда (джоуль) – слишком маленькая единица для измерения работы электричества. Поэтому на практике единица, называемая ватт-час (ватт-час).

Один ватт-час равен 3600 джоулям, потому что в часе 3600 секунд.

В нашем последнем примере работа электричества, выраженная в ватт-часах, будет равна:

В электротехнике для измерения работы электричества используются еще более крупные единицы, называемые гектаватт-час (гВтч) и киловатт-час (кВтч):

1 кВтч = 10 гВтч =1000 вч = 3600000 Дж,

1 гВтч = 100 ватт-часов = 360 000 Дж

1 ватт-час = 3 600 джоулей.

ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

А3. На ножке лампы накаливания написано: 150 ВТ, 220 В. Определите силу тока в катушке, когда лампа подключена к сети с номинальным напряжением

§ 104 Работа и мощность постоянного тока

Рассмотрим любой участок цепи. Это может быть однородный проводник, например, нить лампы накаливания, обмотка электродвигателя и т.д. Пусть через поперечное сечение проводника протекает заряд Δq за время Δt. Электрическое поле совершит работу A = ΔqU (U – напряжение между концами участка проводника).

Поскольку в настоящее время 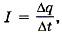работа тока равна:

Согласно закону сохранения энергии, эта работа должна быть равна изменению энергии на данном участке цепи. Поэтому

Если на данном участке цепи не совершается механическая работа и ток не вызывает никаких химических действий, то проводник просто нагревается, т.е. внутренняя энергия проводника увеличивается. Нагретый проводник отдает тепло окружающим телам.

Нагрев проводника происходит следующим образом. Электрическое поле ускоряет электроны. В результате столкновений с ионами кристаллической решетки они передают свою энергию ионам. Энергия неупорядоченного движения ионов вокруг равновесных положений увеличивается. Это представляет собой увеличение внутренней энергии. Поскольку температура является мерой кинетической энергии тела, температура проводника повышается, и он начинает передавать тепло окружающим телам. Через некоторое время после замыкания цепи этот процесс проходит, и температура проводника перестает меняться со временем. Благодаря работе электрического поля в проводнике постоянно выделяется энергия. Но его внутренняя энергия остается постоянной, потому что проводник передает окружающим телам количество тепла, равное работе тока. Таким образом, уравнение (15.12) для работы тока определяет количество тепла, передаваемое проводником другим телам.

Если выразить отношение напряжения к току или тока к напряжению в формуле (15.12), используя закон Ома для данного участка цепи, мы получим три эквивалентные формулы

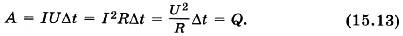
Формулу A = I 2 RΔt удобно использовать при последовательном соединении проводников, поскольку ток в этом случае одинаков во всех проводниках. В случае параллельного соединения формула 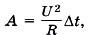потому что напряжение на всех проводниках одинаково.

Закон Джоуля-Ленца. Закон Джоуля-Ленца, определяющий количество тепла, которое проводник с током отдает окружающей среде, был впервые экспериментально установлен английским ученым Джоулем (1818-1889) и русским ученым Ленцем (1804-1885).

Закон Джоуля-Ленца
Количество тепла, выделяемого в проводнике с током, равно произведению квадрата силы тока, сопротивления проводника и времени, в течение которого протекает ток по проводнику:

Мы вывели этот закон путем рассуждений, основанных на законе сохранения энергии. Уравнение (15.14) позволяет рассчитать количество тепла, выделяемого на любом участке цепи, содержащем любой проводник.

Сила тока. Каждый электрический прибор (лампа, электродвигатель и т.д.) рассчитан на потребление определенного количества энергии в единицу времени. Поэтому термин “текущая мощность” также очень важен токовый выход.

Важно
Мощность тока равна отношению работы тока ко времени, протекающему через ток. Согласно этому определению, мощность тока

Электрическая мощность, как и механическая, выражается в Ватт (W).

Это выражение для мощности тока может быть переписано в нескольких эквивалентных формах с использованием закона Ома для данного участка цепи:

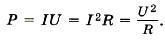
На большинстве электроприборов есть этикетка с указанием потребляемой мощности, предельного тока и предельного напряжения.

В бытовых условиях единицей расчета потребления электроэнергии часто является кВтч, 1 кВтч = 3,6 – 10 6Дж.

Подвопросы к параграфу

1. в чем заключается работа электричества?

2. В чем разница между понятием работы тока в электростатике и понятием работы в ® механике?

3. каков выходной ток?

4. в каких единицах выражается мощность электричества?

5. можно ли увеличить мощность электрического устройства, подав на него большее напряжение?

Примеры формул ЕГЭ

А1. Какую работу совершит электрический ток за 10 минут, если напряжение на концах провода 10 В, а сила тока 1,5 А?

1) 150 J 2) 900 J 3) 1500 J 4) 9000 J

А2. При протекании электрического тока по проводнику в течение 2 минут совершается работа, равная 96 кДж. Сила тока составляет 4 А. Каково сопротивление проводника?

1) 0,02 Ом 2) 50 Ом 3) 3 Ом 4) 15 Ом

А3. Она написана на цоколе электрической лампочки: 150 ВТ, 220 В. Определите ток катушки, когда лампа подключена к цепи с номинальным напряжением

1) 0,45 A 2) 0,68 A 3) 22 A 4) 220 000 A

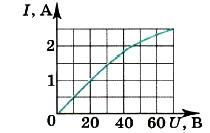
А4. На рисунке показан график тока в лампочке в зависимости от напряжения на ее клеммах. При напряжении 30 В ток в лампочке равен

1) 135 W 2) 67,5 W 3) 45 W 4) 20 W

А5. Как изменится мощность, потребляемая электрической лампой, если, не меняя ее электрического сопротивления, уменьшить напряжение лампы в 3 раза?

Член в подсопряженном выражении мал относительно сингулярности, и можно использовать приближенную формулу.

Что называется работой тока?

При протекании тока, который представляет собой упорядоченное движение носителей заряда в проводнике, действующее на них электрическое поле, определяемое напряжением, приложенным к концам проводника, совершает работу. Эту работу обычно называют работой электрического тока.

Работа сил электрического поля по перемещению носителей заряда равна произведению переносимого заряда на разность потенциалов между точками, в которых движется заряд:

При постоянном токе время, в течение которого происходит перенос заряда Поэтому работа, совершаемая постоянным током за время в цепи, на концах которой поддерживается напряжение, определяется соотношением

Мощность P электрического тока, определяемая работой, совершаемой в единицу времени, равна

Электрический ток, совершая работу, может зажигать нить электрической лампы, вращать якорь электродвигателя, плавить металлы, вызывать химические превращения, заряжать аккумулятор и т.д. Во всех этих случаях работа тока определяет меру преобразования электрической энергии в другие формы – внутреннюю энергию теплового движения, механическую энергию и т.д.

Работа электрического тока измеряется в тех же единицах, что и механическая работа. Это в GHSE и 1 Дж в

Мощность измеряется в ваттах: . Часто используются кратные (киловатты) (мегаватты) ватты. Для работы тока часто используется внесистемная единица (киловатт-час) – работа, выполненная за 1 час при развиваемой мощности

Закон Джоуля-Ленца. Прохождение электрического тока через проводник, обладающий сопротивлением, всегда сопровождается выделением тепла. Количество тепла, выделяемого с течением времени, определяется законом Джоуля-Ленца:

Для однородной цепи формулы (2) и (4) совпадают, т.е. количество выделяемого тепла равно работе тока, а работа тока может быть выражена одним из эквивалентных способов:

В однородной цепи, такой как резистор, работа тока сводится к выделению тепла.

В качестве примера рассмотрим электрический нагревательный прибор, который отдает тепло в окружающую среду. Скорость теплопередачи, которая представляет собой количество тепла, отдаваемое нагретым элементом в единицу времени, пропорциональна разнице температур между нагретым телом и окружающей средой:

Коэффициент k зависит от свойств тела (площади поверхности, размеров и формы). Мы будем считать, что его значение известно. Выделяемое тепло Джоуля может быть рассчитано по одной из формул (5). Поскольку нагреватель обычно подключается к сети с заданным напряжением, удобно использовать выражение

Сразу после включения выделяемое тепло Джоуля больше, чем тепло, отдаваемое окружающей среде, поскольку нагревается само устройство. В конце концов, его температура T фиксируется, при которой P и сравниваются, наступает устойчивое состояние, при котором разница температур между устройством и окружающей средой больше не меняется.

Если сопротивление элемента, нагреваемого током, не зависит от температуры, то, приравняв значения P и , мы сразу получим выражение для установившейся разности температур:

Однако в действительности, как правило, сопротивление зависит от температуры. Для металлической проволоки эту зависимость можно принять линейной (см. § 10):

где сопротивление при температуре окружающей среды может быть определено с высокой степенью точности. Если учесть температурную зависимость сопротивления, то, приравняв P и , получим квадратичное уравнение для

Физически значимый элемент этого уравнения может быть представлен в следующем виде:

В условиях, когда температура нагревательного элемента устройства мала, т.е. превышение температуры над окружающей средой невелико, второй

член в подкоренном выражении мал по сравнению с 1, и мы можем использовать приближенную формулу.

В других предельных больших случаях (например, лампочка с температурой нити накала в несколько тысяч градусов) можно, наоборот, опустить один перед другим членом в сопряженном выражении. В этом случае для аппроксимации мы имеем

– Разница температур теперь пропорциональна первой мощности приложенного напряжения, а не квадрату.

В неоднородных частях цепи, где ток определяется по формуле, выделяемое тепло не равно работе тока. Это означает, что протекание тока в таком участке сопровождается не только выделением тепла, но и другими процессами, связанными с преобразованием энергии.

Зарядка аккумулятора. Рассмотрим зарядку аккумулятора как пример преобразования энергии в неоднородной цепи. Не вдаваясь в подробности процессов, происходящих в аккумуляторе, а лишь учитывая, что во время зарядки все химические процессы в аккумуляторе происходят “в обратном направлении”, легко понять, что ток течет в обратном направлении, чем при разрядке, когда аккумулятор является источником питания для внешней цепи. Поэтому батарея включается в цепь, как на рис. 86, и ток в цепи течет в направлении, указанном стрелкой. Поскольку ЭДС батареи (сумма скачков потенциала в ней) понижает потенциал в цепи в направлении протекания тока, согласно закону Ома для неоднородного поперечного сечения ток в цепи равен

Рис. 86. Схема зарядки аккумулятора

В этой формуле присутствует внутреннее сопротивление батареи, а для регулирования зарядного тока в цепь включен резистор. Легко видеть, что ток будет положительным и, следовательно, будет течь только в указанном направлении, если приложенное напряжение больше электродвижущей силы батареи. Только при соблюдении этого условия можно заряжать аккумулятор.

Работа, совершаемая зарядной станцией (т.е. внешним источником напряжения в единицу времени, т.е. работа тока на всей рассматриваемой площади, равна при всех сопротивлениях,

С учетом внутреннего сопротивления батареи за единицу времени выделяется тепло в джоулях, равное . Кроме зарядки аккумулятора и выделения тепла, в этой цепи не происходит никаких других преобразований энергии. Таким образом, на основании закона сохранения энергии можно утверждать, что

где Pzar – мощность, затрачиваемая непосредственно на зарядку аккумулятора. Подставляя выражение для тока (6) в (7), получаем

Таким образом, во время зарядки аккумулятор накапливает энергию, равную 14 в единицу времени. Конечно, такого результата можно было ожидать, исходя из элементарных соображений: процессы в аккумуляторе считаются обратимыми, и при разряде аккумулятор развивает мощность

Заметим, что, учитывая известные выражения для полной работы тока, для джоулева тепла и для работы по зарядке аккумулятора, можно получить выражение (6) для тока в цепи на основе закона сохранения энергии. Это означает, что закон Ома для неоднородной цепи может быть выведен как следствие закона сохранения энергии.

Работа источника тока. Источник тока – это устройство, поддерживающее разность потенциалов на концах подключенной к нему электрической цепи. Это происходит под действием внешних сил, сил неэлектростатической природы. Какие энергетические преобразования происходят?

Как мы видели, ЭДС источника равна сумме напряжений во внешней и внутренней частях цепи:

Умножьте обе части этого уравнения на заряд, проходящий через цепь за определенное время. В левой части полученного уравнения находится сумма работ электрического тока во внешней и внутренней частях цепи. В правой части находится произведение

Электрический ток работает благодаря действию источника, или внешних сил. Закон сохранения энергии гласит, что работа, совершаемая током в цепи, равна работе, совершаемой внешней силой, действующей на источник тока в то же время.

Определение ЭМП. Поэтому работа источника тока по перемещению заряда в цепи равна электродвижущей силе источника, которую можно определить следующим образом: электродвижущая сила – это величина, равная отношению работы внешней силы Листора

движущегося заряда в цепи к этому заряду:

Поскольку работа источника тока равна, мощность, которую он производит, равна

Мощность и эффективность источника тока. Выясните, каким должно быть сопротивление нагрузки, чтобы получить максимальный ток в цепи, максимальную полезную мощность, максимальный КПД.

Ток в цепи (рис. 87) определяется законом Ома: Поэтому полная мощность P, развиваемая источником тока, равна . Полезная мощность, т.е. мощность, доступная для нагрузки, определяется по формуле

Коэффициент полезного действия источника в этой цепи, определяемый как отношение полезной мощности к кажущейся мощности, является функцией сопротивления нагрузки:

Давайте посмотрим на полученные выражения. Полная мощность P и ток в цепи I изменяются с постоянным коэффициентом, так что их отношение к сопротивлению нагрузки одинаково (кривая 1 на рис. 88).

Рисунок 87. Для проверки рабочих условий источника тока

Рис. 88. Зависимость мощности и КПД источника тока от сопротивления нагрузки

Максимальное значение этих величин будет иметь место при коротком замыкании источника. Как следует из уравнений (12) и (13), в этом случае полезная мощность и КПД равны нулю, кажущаяся мощность и ток равны половине максимального значения, КПД равен 0,5, а полезная мощность достигает максимального значения,

что составляет половину мощности P при данной нагрузке. Чтобы проверить, что полезная мощность достигает максимума, когда сопротивление нагрузки и внутреннее сопротивление источника тока равны, преобразуем правую часть выражения (12) следующим образом

Полезная мощность будет максимальной, когда знаменатель правой части выражения (14) будет минимальным. Преобразуйте знаменатель:

Функция (15) достигает минимума, когда выражение в скобках равно нулю, т.е. при Этот результат, конечно, можно получить, приравняв производную в знаменателе правой части выражения (14) к нулю.

При неограниченном увеличении сопротивления нагрузки полная и полезная мощность стремятся к нулю (кривая 2), а КПД – к единице (кривая 3).

На рисунке 87 показано, что требования к максимальному току цепи, максимальной полезной мощности и максимальной эффективности противоречат друг другу. Чтобы получить максимально возможный ток, сопротивление нагрузки должно быть небольшим по сравнению с внутренним сопротивлением источника, но полезная мощность и КПД должны быть близки к нулю: почти вся работа, совершаемая источником тока, посвящена выделению тепла на внутреннем сопротивлении. Значение максимальной полезной мощности, но КПД составляет всего 0,5.

Любая полезная мощность, меньшая максимальной, может быть получена, как видно из кривой 2 на рисунке 88, при двух значениях сопротивления нагрузки. На практике для получения заданной полезной мощности следует выбирать нагрузку с более высоким сопротивлением, поскольку ее КПД выше. Для получения КПД, близкого к единице, необходимо использовать нагрузку с сопротивлением, значительно превышающим внутреннее сопротивление источника тока, но при этом генерируемая мощность .

– О какой работе силы идет речь, когда мы говорим о работе, совершаемой электрическим током?

– В каких случаях работа электрического тока не равна работе Джоуля тепла, выделяемого в цепи?

– Чтобы зарядить батарею ЭДС, ее необходимо подключить к цепи постоянного напряжения Какая доля энергии, взятой из цепи, накапливается в батарее?

– Как работа внешних сил связана с ЭДС источника тока? Обоснуйте свой ответ.

– Какой должна быть нагрузка для источника тока, чтобы он развивал максимальную полезную мощность? Каков КПД источника тока?

– Почему условия получения максимальной полезной мощности и максимальной эффективности от источника тока противоречат друг другу?

– Покажите, что два значения сопротивления нагрузки i, при которых в нагрузке выделяется одинаковое количество Джоуля тепла, связаны соотношением где где – внутреннее сопротивление источника тока.

– Постройте график зависимости мощности источника тока, полезной мощности и КПД от силы тока I в цепи.

Внешнее силовое поле. Работа, совершаемая электрическим током при протекании заряда по цепи, равна работе внешних сил, действующих на источник. Поэтому ЭДС может быть выражена в терминах этих сил.

Введем новую величину Estor, которую назовем напряженностью внешнего силового поля. Это сила, действующая на единичный положительный заряд вследствие любой причины, кроме электростатического поля. Тогда полная сила, действующая на заряд, будет равна сумме электростатической силы и посторонней силы:

Рассмотрите замкнутый контур и рассчитайте общую работу, совершаемую всеми силами, действующими на заряд при его движении по контуру. Работа электростатических сил в замкнутой цепи равна нулю, потому что эти силы являются потенциальными силами. Поэтому общая работа, совершаемая в замкнутом контуре, равна работе, совершаемой только внешними силами. Именно эта работа определяет ЭДС источника тока.

Обратим внимание на кажущееся противоречие. Работа тока, по определению, является работой сил электрического поля. При этом, как мы видели, работа тока во всей цепи равна работе источника, т.е. работе внешних сил. Но, как мы только что узнали, работа электростатического поля равна нулю. Как нам примирить все это?

Дело в том, что когда мы говорили о работе электрического тока, мы имели в виду работу электрических сил не во всем замкнутом пути, а только в тех частях цепи, где заряды движутся под действием электрических сил. Мы не учли работу электрических сил в местах скачков потенциала (где действуют внешние силы), т.е.

внешние силы), т.е. там, где электрическое поле направлено противоположно движению положительных зарядов. Именно в этих точках внутри источника тока движение зарядов против сил электрического поля обусловлено действием внешних сил. Если мы включим работу электрических сил в этих точках, то их суммарная работа действительно будет равна нулю.

Здесь можно привести следующую механическую аналогию. Лыжник спускается с горы и, сделав круг, возвращается к подножию горы, а затем с помощью подъемника снова поднимается на вершину. Аналогом потенциального электростатического поля здесь является гравитационное поле. Роль внешних сил играют те силы, которые поднимают его в лифте. Конечно, общая работа силы тяжести на всем замкнутом пути равна нулю. Однако в данном случае это не имеет никакого значения. Единственная работа силы тяжести, которая имеет значение, – это работа силы тяжести, которая совершается, когда лыжник движется от вершины горы к ее основанию. Эта работа в точности равна работе “внешних” сил, действующих на лыжника в подъемнике.

Работа и теплота в произвольной цепи. В неоднородной цепи, содержащей источник с ЭДС и внутренним сопротивлением, когда для работы тока A, работы источника и выделяемого тепла имеем

Выделяемое тепло равно сумме работы тока и работы источника:

Мы подчеркиваем, что эти формулы применимы во всех случаях, независимо от того, протекает ли ток через источник в “естественном” направлении, когда он отдает энергию во внешнюю цепь, или в противоположном направлении, как при зарядке аккумулятора, когда он потребляет энергию (в этом случае I и H имеют противоположные знаки, и теплота Leaf будет положительной во всех случаях.

Как связаны работа внешних сил и работа сил электрического поля при переносе заряда по всей замкнутой цепи?

Объясните аналогию между работой электрических и внешних сил и работой силы тяжести и силы “подъема”, когда лыжник поднимается на подъемнике.

Читайте далее: