Расчет цепи постоянного тока с конденсаторами

Задание 5. Определите напряжение на выводах конденсаторов и их энергию после перевода переключателя из положения 1 в положение 2, показанное пунктирной линией на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ не заряжается.

Содержание

ε 0 = 1 4 π ⋅ s 2 ⋅ 10 – 7 ≈ 8,85418782 ⋅ 10 – 12 F m – электрическая постоянная.

3. на параллельное соединение конденсаторов С₁, С₂, …, С_n эквивалентная ёмкость равен

C = C 1 + C 2 + . + C n = ∑ k = 1 n C k .

4. на стороне при последовательном соединении конденсаторов эквивалентная емкость задается формулой

1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .

Для двух конденсаторов, соединенных последовательно, эквивалентная емкость это:

C = C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 = U ⋅ C 2 C 1 + C 2 ; U 2 = U ⋅ C 1 C 1 + C 2 .

5 Трансформация звезда мощности к эквиваленту треугольник ёмкостей или наоборот (рис. а и б)

осуществляется в соответствии с формулами:

6) энергия электростатического поля конденсатора:

W = C ⋅ U 2 2 = Q ⋅ U 2 = Q 2 2 C .

7. Расчет распределения заряда в сложных цепях, содержащих источники ЭДС и конденсаторырассчитывается путем составления уравнений в соответствии с двумя законами:

1) По закону сохранения электричества (закон сохранения электрического заряда): Алгебраическая сумма зарядов на катушках конденсаторов, подключенных к узлу и не подключенных к источнику энергии, равна алгебраической сумме зарядов на этих катушках до их подключения:

2) Согласно второму закону Кирхгофа: алгебраическая сумма э.д.с. в замкнутом контуре равно алгебраической сумме напряжений участков контура, включая конденсаторы в контуре:

∑ k = 1 n E k = ∑ k = 1 n U C k = ∑ k = 1 n Q k C k .

Для того чтобы перейти к решению задачи, необходимо определяется полярностью зарядов на обмотках конденсатора.

Решение задач по расчету электрической цепи постоянного тока с конденсаторами

Проблема. Докажите формулу для эквивалентной емкости в последовательного соединения конденсаторов (рис.1).

На рисунке 1 показано последовательное подключение трех конденсаторов. Если конденсаторная батарея подключена к источнику напряжения U₁₂а затем на левой пластине конденсатора С₁ будет нести заряд +qна правой пластине конденсатора C С₃ заряд –q.

Вследствие электризации за счет взаимодействия правой пластины конденсатора С₁ будет иметь заряд –qи поскольку пластины конденсатора С₁ и С₂ соединены и электрически нейтральны, то согласно закону сохранения заряда, заряд на левой пластине конденсатора C₂ будет равна +qи т.д. При таком соединении все пластины конденсатора будут иметь одинаковый заряд.

Нахождение эквивалентной емкости означает нахождение конденсатора такой емкости, который при той же разности потенциалов будет накапливать такой же заряд qкак батарея конденсаторов.

Разница потенциалов U₁₂ = φ₁ – φ₂ сумма разностей потенциалов между пластинами каждого конденсатора

U 12 = φ 1 – φ 2 = ( φ 1 – φ A ) + ( φ A – φ B ) + ( φ B – φ 2 ) = U 1 A + U A B + U B 2 .

Используя формулу для напряжения конденсатора

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная ёмкость из трёх последовательно соединенные конденсаторы

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная ёмкость на стороне последовательно соединенных конденсаторов

1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .

Проблема 1. Определите заряд и энергию каждого конденсатора на рис. 2, если система подключена к сети с напряжением U = 240 В.

Емкость конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Эквивалентная емкость конденсаторов C₁ и C₂соединённые параллельно

Эквивалентная емкость всей цепи равна

C = C 12 ⋅ C 3 C 12 + C 3 = 200 ⋅ 300 500 = 120 м F .

Заряд на эквивалентной емкости

равна величине заряда Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288 – 10 – 4 K; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288 ⋅ 10 – 4 300 ⋅ 10 – 6 = 96 V .

Напряжение на конденсаторах C₁ и C₂ равен

U₁ = U₂ = U – U₃ = 240 – 96 = 144 В.

Их заряды имеют следующие значения

Энергии электростатических полей конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72 ⋅ 10 – 4 ⋅ 144 2 ≈ 0,52 D g ; W 2 = Q 2 ⋅ U 2 2 = 216 ⋅ 10 – 4 ⋅ 144 2 ≈ 1,56 D g ; W 3 = Q 3 ⋅ U 3 2 = 288 ⋅ 10 – 4 ⋅ 96 2 ≈ 1,38 D g .

Проблема 2. Планарный слоевой конденсатор (рис. 3), площадь поверхности каждой пластины которого S = 12 см2 , имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщины d₁ = 0,3 мм и стекло (ε_r₂ = 7) толщины d₂ = 0,4 мм.

Силы разложения слюды и стекла составляют соответственно E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рассчитайте емкость конденсатора и предельное напряжение, при котором он может быть включен, предполагая вдвое большую диэлектрическую прочность более слабого слоя.

Эквивалентная емкость пленочного конденсатора будет определяться как емкость двух последовательно соединенных конденсаторов

C = C 1 ⋅ C 2 C 1 + C 2 = ε a 1 ⋅ S d 1 ⋅ ε a 2 ⋅ S d 2 ε a 1 ⋅ S d 1 + ε a 2 ⋅ S d 2 = ε a 1 ⋅ ε a 2 ⋅ S ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 .

Обозначим общее напряжение, подключенное к пленочному конденсатору, через U_апрельа заряд конденсатора будет равен

Напряжения в каждом слое будут

U 1 = Q C 1 = C ⋅ U n p ε a 1 ⋅ S d 1 = ε a 2 ⋅ d 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U n p ; U 2 = Q C 2 = C ⋅ U n p ε a 2 ⋅ S d 2 = ε a 1 ⋅ d 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U n p .

Напряженность электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U ′ n p ; E 2 = U 2 d 2 = ε a 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U″ n p .

Здесь U’_{например.} – общее напряжение, приложенное к конденсатору, при котором пробит первый слой, и U”_{например.} – общее напряжение, при котором пробивается второй слой.

Из последнего выражения следует, что

U ′ np = E 1 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 2 = 49,5 k V ; U ″ n p = E 2 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 1 = 27,0 k V .

Поэтому более слабым слоем является второй; по условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Проблема 3. Обкладки плоского конденсатора с воздушным диэлектриком удалены друг от друга на расстояние d₁ = 1 см друг от друга. Площадь поверхности покрытий S = 50 см2 . Конденсатор заряжается до напряжения U = 120 В и затем отключается от электросети.

Определите работу, которая будет совершена, если расстояние между пластинами увеличить до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, можно предположить, что емкость конденсатора обратно пропорциональна расстоянию между обкладками.

Энергия заряженного планарного конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅ S d 1 ⋅ U 2 2 ,

где С₁ – емкость до расстояния между обкладками.

Поскольку конденсатор отсоединен от источника, его заряд остается постоянным при изменении расстояния между обкладками. Поэтому из

где C₂ – является емкостью конденсатора после расстояния между обкладками, отсюда следует, что поскольку C₂ = ε₀·S/d₂ стала в 10 раз меньше (d₂ увеличивается в 10 раз), то напряжение на конденсаторе U₂ увеличилась в 10 раз, т.е. U₂ = 10U.

Таким образом, энергия конденсатора после его выключения и удаления обкладок на расстояние d₂ будет больше, чем начальная

W 2 = ε 0 ⋅ S d 2 ⋅ U 2 2 = ε 0 ⋅ S 10 d 1 ⋅ ( 10 U ) 2 2 = 10 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 10 ⋅ W 1 .

Увеличение энергии происходит за счет работы внешних сил, затраченной на разделение оболочек.

Следовательно, необходимо совершить работу, равную

W 2 – W 1 = 9 ⋅ W 1 = 9 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 2,86 ⋅ 10 – 7 D .

Проблема 4. Для системы (рис. 4) определите напряжение на каждом конденсаторе в двух случаях: при закрытом и открытом ключе К.

Дано: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Ключ К открыт. Конденсаторы соединены последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально их емкости

U 1 = C 2 C 1 + C 2 ⋅ U = 20 ⋅ 10 – 6 30 ⋅ 10 – 6 + 20 ⋅ 10 – 6 ⋅ 20 = 8V ; U 2 = U – U 1 = 20 – 8 = 12V .

Ключ К закрыта. Через сопротивления r₁ и r₂ ток протекает через

I = U r 1 + r 2 = 20 500 = 0,04 A ,

и через сопротивление r₃ ток не течет.

Поэтому точки c и d являются эквипотенциальными (φ_c = φ_d). Таким образом, напряжение между точками a и c (U_ac = φ_a – φ_c) равно напряжению между точками a и d (U_{реклама} = φ_a – φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

Аналогично, напряжение на втором конденсаторе равно

Проблема 5. Определите напряжение на зажимах конденсатора и его энергию после перемещения переключателя из положения 1 в положение 2, показанное пунктирной линией на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ не был предварительно заряжен.

Когда переключатель находится в положении 1, конденсатор C₁ заряжается до напряжения U и его заряд равен

Когда переключатель находится в положении 2, заряд Q распределяется между конденсаторами C₁ и C₂ (Рисунок 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения энергии мы имеем

Q = Q’₁ + Q’₂ = 125 10 -6 Кл. (1)

В соответствии со вторым законом Кирхгофа мы имеем

0 = U C 1 – U C 2 = Q ′ 1 C 1 – Q ′ 2 C 2 ,

Решая уравнения (1) и (2), получаем

Напряжение на зажимах конденсатора составит

U C 1 = Q ′ 1 C 1 = U C 2 = Q ′ 2 C 2 = 5 ⋅ 10 – 6 5 ⋅ 10 – 6 = 1 V .

Энергия обоих конденсаторов составит

W = C 1 ⋅ U C 1 2 2 + C 2 ⋅ U C 2 2 2 = 62,5 ⋅ 10 – 6 D g .

Рассчитайте энергию, запасенную в конденсаторе С₁когда он подключен к источнику электрической энергии

W n a h = C 1 ⋅ U 2 = 5 ⋅ 10 – 6 ⋅ 25 2 2 = 1562,5 ⋅ 10 – 6 J .

Как видно, существует большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5-10 -6 – 62,5-10 -6 = 1500-10 -6 Дж, расходуется на искрение при переключении резистора из положения 1 в положение 2 и на нагрев проводников при стекании заряда с конденсатора C₁ к конденсатору C C₂ после переключения миниатюрного переключателя в положение 2.

Задание 6. Рассчитайте напряжение, которое будет на каждом из конденсаторов в цепи (рис. 6) после переключения выключателя К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; Напряжение U = 30 В и ЭДС. E = 50 В.

Автоматический выключатель находится в положении 1. Заряд конденсатора C₁ равен

В данном положении переключателя конденсаторы C₂ и C₃ соединены последовательно, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 со знаками без кружков. В соответствии со вторым законом Кирхгофа мы имеем

E = U C 2 + U C 3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅ E = 30 ⋅ 10 – 6 ⋅ 60 ⋅ 10 – 6 90 ⋅ 10 – 6 ⋅ 50 = 1 ⋅ 10 – 3 K l .

Перемещение переключателя в положение 2 приведет к перераспределению нагрузки. Мы произвольно определяем новую полярность зарядов на электродах (отмечены кружками; предполагается, что она совпадает с предыдущей полярностью); соответствующие направления положительного напряжения на конденсаторах мы отмечаем стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения мы выведем уравнения, основанные на законе сохранения электрического заряда и втором законе Кирхгофа.

Для узла a

Для цикла 2ebda2

0 = U ′ C 1 – U ′ C 2 = Q ′ 1 C 1 – Q ′ 2 C 1 .

Для контура bcadb

E = U ′ C 2 – U ′ C 3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) – (3) после подстановки числовых значений будут иметь вид

Решая уравнения (4)-(6) вместе, получаем

Поскольку знаки всех зарядов были положительными, фактическая полярность облицовки была такой же, как и выбранная ранее.

Напряжения на конденсаторах после переключения выключателя будут равны

U C 1 = Q ′ 1 C 1 = 0,33 ⋅ 10 – 3 10 ⋅ 10 6 = 33V ; U C 2 = Q ′ 2 C 2 = 0,99 ⋅ 10 – 3 30 ⋅ 10 6 = 33V ; U C 3 = Q ′ 3 C 3 = 1,02 ⋅ 10 – 3 60 ⋅ 10 6 = 17V.

Проблема 7. Определите заряд и напряжение конденсаторов, соединенных, как показано на рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; источник а.д.с. E₁ = 20 В и E₂ = 5 В.

Выведем систему уравнений, основанную на законе сохранения энергии и втором законе Кирхгофа, сначала установив полярность обмоток конденсатора, обозначенных кружками

– Q 1 + Q 2 – Q 3 = 0 ; E 1 = U C 1 – U C 3 = Q 1 C 1 – Q 3 C 3 ; E 2 = – U C 2 – U C 3 = – Q 2 C 2 – Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получаем, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = -30 мкКл.

Поэтому реальная поляризация зарядов на катушках конденсатора C₁ и C₂ соответствует выбранной поляризации, а для конденсатора C₃ – противоположна выбранной.

Проблема 8. Пять конденсаторов соединены по схеме на рис. 3-22, а, емкость которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Определите эквивалентную емкость цепи и напряжение на каждом конденсаторе, если приложенное напряжение U = 10 В.

Метод 1. Звездная емкость C₁, C₂ и C₃ (Рис. 8, а) преобразуется в треугольник эквивалентной емкости (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 = 0,6 м до F ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 = 1,0 м до F ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 = 1,5 м до F .

Возможности C₁₂ и C₅ соединены параллельно друг с другом и с точками 1 и 2; их эквивалентные емкости

Схема имеет вид, показанный на рисунке 8, в. Емкость цепи между точками а и b равен

C a b = C 23 + C 6 ⋅ C 7 C 6 + C 7 = 2,7 m k F .

Рассчитайте напряжение на каждом конденсаторе.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅ U = 6 V .

Таким же является напряжение на конденсаторах C₄ и C₁₃

Напряжение на конденсаторе C₆ равен

Согласно закону сохранения электричества для узла 1 цепи 8, а и б у нас есть

и напряжение на конденсаторе, емкость C₁ это

U 1 = Q 1 C 1 = 1,8 V .

Далее мы находим напряжения и заряды на других конденсаторах

Поскольку знаки всех зарядов положительны, фактическая полярность зарядов на обкладках совпадает с выбранной ранее.

Метод 2. Выбирая положительные направления напряжений на конденсаторах (и, следовательно, знаки зарядов на каждом конденсаторе) с помощью формулы закон сохранения энергии (закон сохранения заряда) мы получаем два уравнения и по в соответствии со вторым законом Кирхгофа три уравнения (рис. 8, а)

для узла О

для цепи О13О

Q 1 C 1 – Q 4 C 4 + Q 3 C 3 = 0 ; ( 3 )

для цикла О12О

Q 1 C 1 + Q 5 C 5 – Q 2 C 2 = 0 ; ( 4 )

для петель a3О2b

Q 3 C 3 + Q 2 C 2 = U . ( 5 )

Система уравнений (1) – (5) – содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решая уравнения, мы находим желаемые заряды, а затем напряжения на конденсаторах. Во втором способе решения эквивалентной схемы емкость С_ab можно определить из соотношения

где Q = Q₃ + Q₄или Q = Q₂ + Q₅.

Проблема 9. На диаграмме с рис. 9 найдите распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

При выбранном распределении зарядов (в кружках), как на рисунке, система уравнений будет выглядеть следующим образом:

для узла а

для узла b

для узла c

для контура afcba

E 1 = U C 1 + U C 4 – U C 3 = Q 1 C 1 + Q 4 C 4 – Q 3 C 3 ;

для цикла gdbag

E 2 = U C 5 – U C 3 + U C 2 = Q 5 C 5 – Q 3 C 3 + Q 2 C 2 ;

для цикла cbdc

0 = U C 4 – U C 5 – U C 6 = Q 4 C 4 – Q 5 C 5 – Q 6 C 6 .

Подставив сюда численные значения и решив полученную систему из шести уравнений, находим требуемые заряды

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, реальные знаки заряда Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактические положения знаков заряда на конденсаторах не указаны в кружках.

Проблема 10. Определите заряд и энергию каждого конденсатора в цепи (рис. 10). Данные для схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Через резисторы протекает ток

I = U r 1 + r 2 = 0,05 A .

Учитывая полярность зарядов на катушках конденсатора, образуем систему уравнений:

– Q 1 + Q 2 + Q 3 = 0 ; U = U C 1 + U C 2 = Q 1 C 1 + Q 2 C 2 ; I ⋅ r 1 = U C 1 + U C 3 = Q 1 C 1 + Q 3 C 3 ,

Q 1 = Q 2 + Q 3 ; 45 = Q 1 6 ⋅ 10 – 6 + Q 2 ⋅ 10 – 6 ; 25 = Q 1 6 ⋅ 10 – 6 + Q 3 ⋅ 10 – 6 .

Решая эту систему уравнений, находим, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 µCL.

Параллельное соединение конденсаторов будет выглядеть следующим образом:

Схемы подключения конденсаторов – расчет емкости

В этой статье описаны различные соединения конденсаторов и формулы для их расчета с примером.

Последовательное подключение конденсаторов

Если условно разделить выводы каждого конденсатора на первый и второй, то конденсаторы соединяются последовательно следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора соединяется с первым выводом третьего конденсатора и так далее. Это дает нам группу (блок) конденсаторов, соединенных последовательно с двумя свободными проводами – первым проводом первого конденсатора в блоке и вторым проводом последнего конденсатора, через которые этот блок конденсаторов подключается в электрическую цепь.

Цепь конденсатора при последовательном соединении будет выглядеть следующим образом:

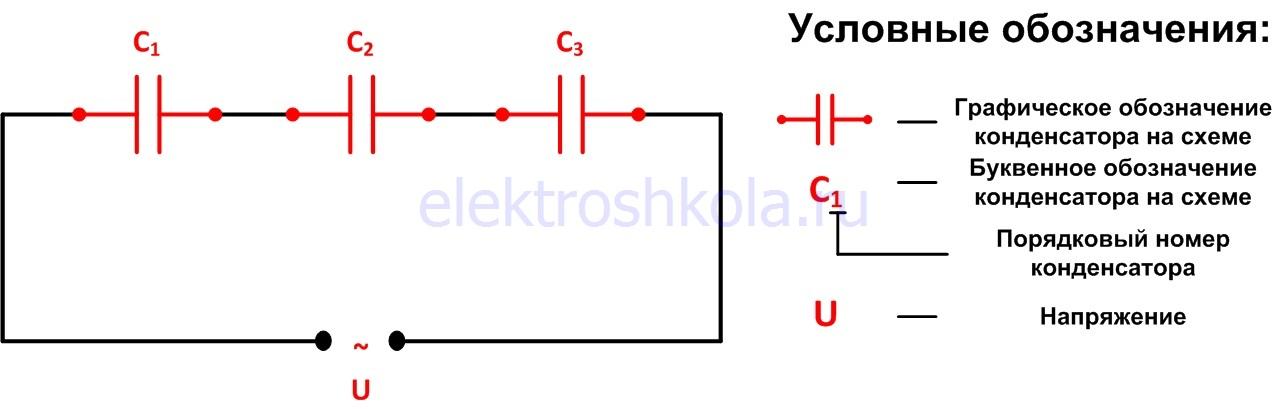
Фактически, последовательное соединение конденсаторов выглядит следующим образом:

При такой схеме подключения заряды на конденсаторах будут одинаковыми:

Где: Q₁, Q₂, Q₃ – соответственно заряд на первом, втором, третьем и т.д. конденсаторе

Напряжение на каждом конденсаторе в этой цепи зависит от его емкости:

U ₁, U₂, U₃ – соответственно напряжение на первом, втором, третьем конденсаторе
C ₁, C₂, C₃ – соответственно емкость первого, второго, третьего конденсатора

Тогда общее напряжение составит:

Для расчета общей емкости конденсаторов, соединенных последовательно, используйте следующие формулы:

Когда два конденсатора соединены последовательно:

Когда три или более конденсаторов соединены последовательно:

Параллельное соединение конденсаторов

Если условно разделить выводы каждого конденсатора на первый и второй, то параллельное соединение конденсаторов будет выглядеть следующим образом: Первые выводы всех конденсаторов подключены к одной общей точке (условно – точка № 1) Вторые выводы всех конденсаторов подключены к другой общей точке (условно – точка № 2). В результате получается группа (блок) конденсаторов, подключенных параллельно к электрической цепи через условные точки 1 и 2.

Схема параллельного соединения конденсаторов будет иметь следующий вид:

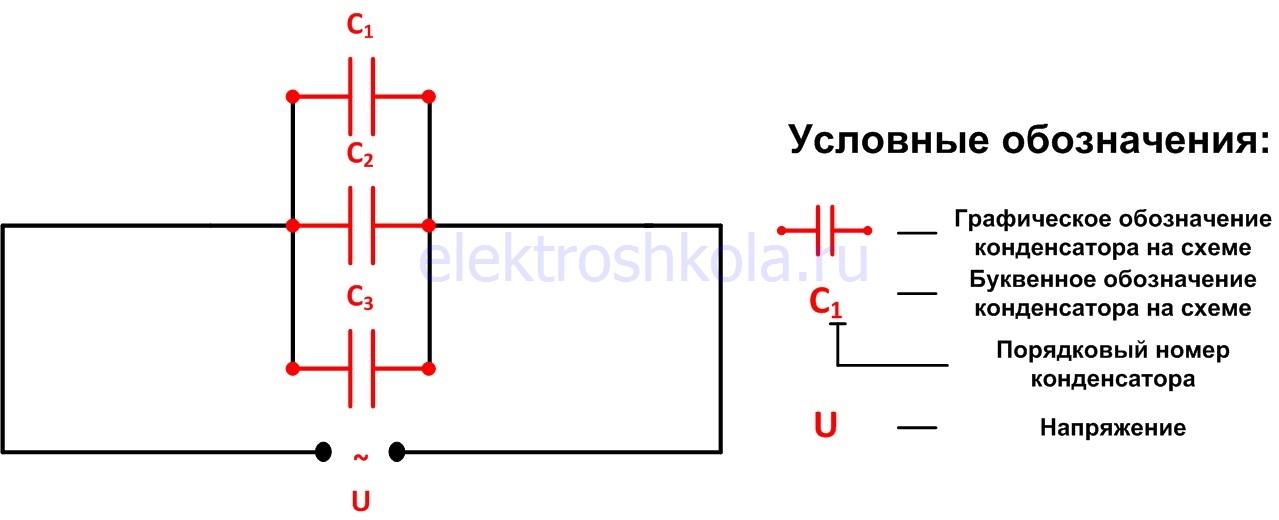
Таким образом, параллельное соединение конденсаторов будет иметь следующий вид:

В этой схеме напряжение на всех конденсаторах будет одинаковым:

Заряд на каждом конденсаторе зависит от его емкости:

Общий заряд цепи будет равен сумме зарядов всех конденсаторов, подключенных параллельно:

Для расчета общей емкости конденсаторов при параллельном соединении можно использовать следующую формулу:

Подключение смешанного конденсатора

Схема, в которой имеются две или более групп (блоков) конденсаторов с различными схемами подключения, называется смешанной схемой подключения конденсаторов.

Вот пример такой схемы:

Для расчетов такие цепи условно делятся на группы одинаково подключенных конденсаторов, а затем для каждой группы проводятся расчеты по формулам, приведенным выше.

Для наглядности приведем пример расчета общей емкости этой цепи.

Пример расчета

Разделив схему на группы, мы получаем следующие результаты:

Как видно из схемы на первом этапе, мы определили 3 группы (блока) конденсаторов, причем конденсаторы в первой и второй группах соединены последовательно, а конденсаторы в третьей группе соединены параллельно.

Давайте рассчитаем каждую из групп:

Группа 1 – три последовательно соединенных конденсатора:

Группа 2 – два последовательно соединенных конденсатора:

С_4,5 = C ₄* C ₅/ C ₄+ C ₅ = 20*30/20+30 = 600/50 = 12 мкФ

Группа 3 – параллельное соединение трех конденсаторов:

В результате расчетов схема упрощается:

Как вы видите, в упрощенной схеме есть еще одна группа из двух конденсаторов, соединенных параллельно, давайте рассчитаем ее емкость:

Группа 4 – параллельное соединение двух групп конденсаторов:

С_1,2,3,4,5 = C _1,2,3+ C_4,5 = 2,72+12 = 14.72 мкФ

В итоге получается простая схема из двух групп конденсаторов, соединенных последовательно:

Теперь можно определить общую емкость цепи:

С_всего = C _1,2,3,4,5* C _6,7,8/ C _1,2,3,4,5+ C _6,7,8 = 14,72*60/14,72+60 = 883,2/74,72 = 11.8 мкФ

Была ли эта статья полезной? А может быть, у вас У меня все еще есть вопросы? Пишите в комментариях!

Вы не нашли статью по интересующей вас теме тема, связанная с электротехникой? Пишите нам сюда. Мы свяжемся с вами.

Конденсаторы с емкостью ( = 5 мкФ и ( = 10 мкФ) конденсаторы заряжаются до напряжения ( = 60 В и = 100 V. Определите напряжения на катушках конденсатора при подключении к катушкам с одинаковым зарядом.

ОПРЕДЕЛЕНИЯ

характеристика проводника, количественная мера его способности удерживать электрический заряд

количественная характеристика, показывающая, в какой степени тело может участвовать в электромагнитных взаимодействиях

устройство, предназначенное для достижения требуемого значения электрической емкости и способное накапливать и отдавать (перераспределять) электрический заряд

разность потенциалов между двумя точками в электрической цепи; в цепи, не содержащей электродвижущей силы, она равна произведению силы тока и сопротивления цепи

Рисунок 2: Параллельное соединение конденсаторов.

Последовательное подключение конденсаторов.

Если, с другой стороны, конденсаторы соединены в цепь, и только пластины первого и последнего конденсатора непосредственно соединены с точками подключения в цепи, то подключение конденсатора называется последовательно (Рисунок 3).

Рисунок 2: Последовательное соединение конденсаторов.

При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, поскольку только крайние пластины (1 и 6) заряжаются непосредственно от источника тока, а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. Заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2, и так далее.

Напряжения на разных конденсаторах, в общем случае, будут разными, поскольку для зарядки одного и того же количества электричества на конденсаторах разной емкости всегда требуется разное напряжение. Чем меньше емкость конденсатора, тем выше напряжение, необходимое для зарядки конденсатора необходимым количеством электроэнергии, и наоборот.

Таким образом, когда заряжается группа последовательно соединенных конденсаторов, конденсаторы с низкой емкостью будут иметь более высокое напряжение, а конденсаторы с высокой емкостью – более низкое напряжение.

Как и в предыдущем случае, мы можем рассматривать всю группу последовательно соединенных конденсаторов как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, и заряд которого равен заряду любого конденсатора группы.

Возьмите самый маленький конденсатор в группе. На нем должно быть самое высокое напряжение. Но напряжение на этом конденсаторе – лишь часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше, чем напряжение на конденсаторе с наименьшей емкостью. Отсюда непосредственно следует, что общая емкость группы последовательно соединенных конденсаторов меньше емкости наименьшего конденсатора в группе.

Для расчета общей емкости конденсаторов, соединенных последовательно, удобнее всего использовать следующую формулу:

Для особого случая двух конденсаторов, соединенных последовательно, формула для расчета их общей емкости будет следующей:

q C = q C 1 + q C 2 + q C 3 .

характеристика проводника, количественная мера его способности удерживать электрический заряд

количественное свойство, показывающее, в какой степени тело может участвовать в электромагнитных взаимодействиях

устройство, предназначенное для создания необходимой емкости и способное накапливать и отдавать (перераспределять) электрический заряд

разность потенциалов между двумя точками в электрической цепи; в цепи, не содержащей электродвижущей силы, она равна произведению силы тока, умноженному на сопротивление участка.

Конденсаторы емкостью ( = 5) мкФ и ( = 10) мкФ заряжены до напряжений ( = 60) В и ( = 100) В, соответственно. Определите напряжения на катушках конденсаторов, когда они подключены к катушкам с одинаковым зарядом.

Eq – конечная энергия системы [J].

35 Электродинамика Читать 0 мин.

В системе отключенных конденсаторов заряд всегда остается постоянным. Напряжение и емкость могут изменяться.

Количество выделившегося тепла равно разности начальной и конечной энергии:

En – начальная энергия системы [Джоуль];

Ec – конечная энергия системы [J].

Начальная и конечная энергии определяются энергиями конденсаторов и индукторов, входящих в цепь.

После установления равновесия только те конденсаторы, которые не соединены параллельно с резисторами, имеют напряжение.

Конденсатор в цепи постоянного тока

Плоский конденсатор представляет собой пластину, на которой может накапливаться заряд. Между пластинами находится пространство, заполненное диэлектриком (или воздухом в качестве диэлектрика). Поскольку диэлектрики – это вещества, которые не проводят электричество, заряд не может перейти от одной пластины конденсатора через слой диэлектрика к другой пластине, что означает отсутствие тока, протекающего через конденсатор. Если на каком-то участке цепи имеется такой конденсатор, то этот участок “блокируется”, ток через него не течет.

Если в цепи есть конденсатор, который не заряжен или заряжен частично, и цепь подключена к источнику тока, заряд начинает накапливаться на катушках конденсатора. Это означает, что в той части цепи, которая находится перед конденсатором, есть ток – до тех пор, пока конденсатор не заряжен полностью.

Если цепь отключена от источника тока и в ней находится заряженный конденсатор – конденсатор начинает разряжаться. Заряды с одной катушки конденсатора пытаются переместиться на другую катушку по “длинному пути” – через всю цепь, создавая тем самым ток. Ток в такой цепи будет протекать до тех пор, пока конденсатор не разрядится.

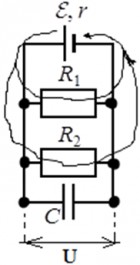
Пример: Предположим, что в цепи есть два резистора с сопротивлениями R1 и R2, источник электрического тока εи конденсатор с емкостью C:

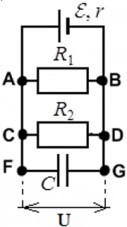
Конденсатор C полностью заряжен. В этом случае токи в цепи не протекают через FG – как если бы его не было в цепи, и не учитывается при расчете параметров цепи. Считается, что ток течет от положительно заряженной клеммы источника ЭДС (тонкая и длинная линия) к входящей отрицательно заряженной клемме (жирная короткая линия):

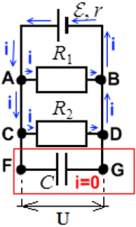
Конденсатор разряжен или заряжен не полностью. В этом случае конденсатор только заряжен, и ток в цепи течет через точку F – до катушки конденсатора – но дальше до точки G ток не течет.

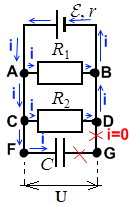
Конденсатор заряжен, но цепь отключена от источника ЭДС. В этом случае ток протекает по всей цепи – до тех пор, пока конденсатор может служить источником заряда и пока он не разряжен полностью. Когда конденсатор разряжается, ток в цепи прекращается.

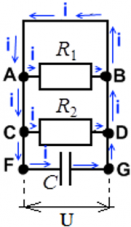
Напряжения на всех параллельных участках цепи равны – фундаментальное свойство параллельного соединения. Независимо от наличия резистора или конденсатора в ответвлении. Таким образом, во всех случаях для приведенного выше примера напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе RБлагодаря этому свойству, зная, например, энергию, запасенную в заряженном конденсаторе, или его заряд, можно рассчитать напряжение на резисторах.

Заряженный конденсатор, отключенный от цепи. Заряженный конденсатор имеет определенный заряд на своих катушках. Если конденсатор отключен от цепи, заряду некуда деваться, и он остается на конденсаторе неизменным. Если он заряжен не полностью, конденсатору также негде получить дополнительный заряд. Заряд конденсатора, отключенного от цепи, постоянен.

Емкость конденсатора – это его физическая и геометрическая характеристика, которая показывает, сколько заряда он может накопить. Емкость конденсатора не зависит от заряда на его выводах или напряжения в цепи.

Емкость конденсатора равна C = $frac = $fracгде

C – емкость конденсатора, [Ф];

(φ2 – φ1) – разность потенциалов между электродами конденсатора, [В];

U – напряжение на катушках конденсатора [В].

Емкость планарного конденсатора зависит от размера его пластин, расстояния между ними и типа диэлектрика, заполняющего пространство между пластинами.

Емкость планарного конденсатора равна C = $frac.$ , где

C – емкость конденсатора [Ф];

ε – диэлектрическая проницаемость;

ε0 – электрическая постоянная;

S – площадь поверхности обмоток конденсатора [м2];

d – расстояние между витками [м].

В электрической цепи тепло выделяется из-за сопротивления, преодолеваемого зарядами, проходящими через материал. Количество тепла, произведенного в контуре, равно разности между начальной и конечной энергией всей системы Q = En – Eqгде

En – начальная энергия системы [Джоули];

Eq – конечная энергия системы [J].

В цепи энергия накапливается в конденсаторах (энергия электрического поля) и катушках (энергия магнитного поля). Поэтому энергия электромагнитных сил в контуре в любой момент времени равна сумме энергий в конденсаторах и в катушках, входящих в контур.

Энергия электрического поля заряженного конденсатора равна Мой = $frac<cu^2> <2>= $frac <2>= frac<q^2><2C>$ , где

Мой – энергия электрического поля конденсатора, [J];

C – электрическая емкость конденсатора, [Ф];

U – напряжение на катушках конденсатора, [В];

q – заряд на катушках конденсатора, [kl].

Энергия магнитного поля в индукционной катушке равна E = $frac<li^2><2>$ , где

E – энергия магнитного поля катушки [J];

L – индуктивность катушки [Gn];

I – ток катушки [А].

Равновесное состояние и зарядка конденсаторов

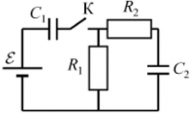
Пример 1: Цепь на рисунке имеет ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора имеют емкость C1 и C2 разряжены.

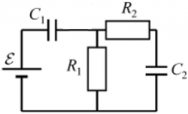
Ток, протекающий от источника ЭДС к конденсатору C1 будет протекать до тех пор, пока конденсатор C1 полностью заряжен. В то же время, из конденсатора C1 не проходит дальше – ни к резисторам R1 и R2, или к конденсаторуC2. как только конденсатор C1 полностью заряжен, в системе наступает состояние равновесия – напряжение на конденсаторе становится равным ЭДС, т.е. всему возможному заряду, который принял конденсатор. Поскольку ток не протекал через конденсатор до того, как C2 – этот конденсатор остается незаряженным. Напряжение только на конденсаторе C1 и конденсатор C2Напряжение равно нулю. Зарядка конденсатораC1:

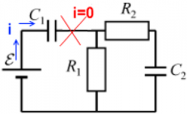
После конденсатора C1 заряжен, ток в цепи прекращается.

Пример 2: Цепь, показанная на рисунке, содержит ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора имеют емкость C1, C2 и C3 разряжены.

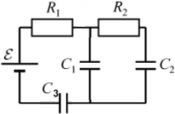
Ток, выходящий из источника ЭДС, разделяется на два тока – один питает зарядный конденсаторC1, а другой – к конденсаторуC2. состояние равновесия наступает, когда оба конденсатора полностью заряжены – ток в цепи больше не течет. Но поскольку вне конденсаторов ток не течет, конденсатор C3 не заряжается и остается разряженным. Напряжение на конденсаторе C3 – ноль.

Зарядка конденсаторов C1 иC2:

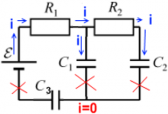
После конденсаторовC1 и C2 заряжены, ток в цепи завершен.

</li^2></q^2></cu^2>

Читайте далее: