Разветвленные цепи. Правило обхода цепи - Электричество и магнетизм - Киберфорум - услуги электромонтажа, строительства и ремонта

Добавлено спустя 28 секунд
Что вам может не понравиться в формулировке этого задания?

Содержание

Разветвленные цепи. Принцип шунтирования цепи

Помощь в написании контрольных работ, курсовых и дипломных работ здесь.

Поиск обхода цепи
Здравствуйте, задача состоит в том, чтобы найти направление контура. Контур – это n-ое число.

Математическое моделирование идеального контура. Определите фазовую траекторию контура
Постройте модель идеального контура. Определите фазовую траекторию контура для q(0)=10^-5 K.

Сообщение от Вейгон Сообщение от vetvet

Ребята! Кто может объяснить траекторию контура.

Добавлено спустя 28 секунд
Что может пойти не так с формулировкой этого произведения?

Добавлено через 5 минут

Сообщение от IGPIGP Сообщение от Вейгон Сообщение от СООБЩЕНИЕ IGPIGP Сообщение от Вейгон Сообщение от IGPIGP

Я запишу, а вы скажете мне, правильно это или нет, именно так это должно быть сделано для начала.
Допустим, это движение по часовой стрелке:
E₁=E₄+E₅

Сообщение от Вейгон

Запишите координаты контура в линейный динамический список. Вычислите площадь контура и его весовые координаты.
Запишите координаты контура в линейный динамический список. Вычислите площадь контура и его координаты.

Правило Сарриса (правило треугольника, метод звезды) Правило Паскаля
Привет всем активным пользователям форума. Я прошу помощи в написании программы на языке Pascal.

разветвлённые процессы
Доброе утро. Требуется выполнить программу в среде Dev-C++ для обработки данных.

Вам необходимо составить уравнения в соответствии с первым законом Кирхгофа для следующей цепи:

Задачи на правило Кирхгофа с решением

Как решать задачи, используя правило Кирхгофа? Обязательно изучите теорию, прежде чем приступать к решению задач. Мы также подготовили для вас универсальное руководство по решению задач по физике.

Задача 1 по эквивалентным преобразованиям соединений проводов.

Пререквизиты

Преобразование схемы с помощью эквивалентных преобразований.

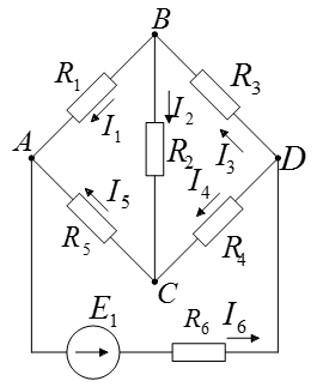
Решение

Помимо основных формул для последовательного и параллельного соединения проводников, существуют формулы для преобразования резистора звезды в эквивалентный резистор треугольника и наоборот. Дельта-резистор R2 R3 R4 можно преобразовать в эквивалентный звездообразный резистор RB RB RD, используя формулы:

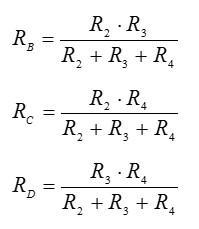
Преобразованная схема будет выглядеть следующим образом:

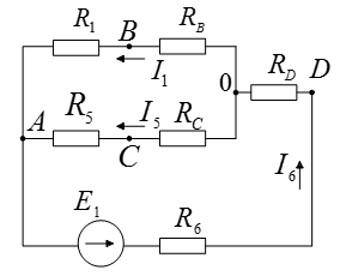
Ответ: см. выше.

Правила Кирхгофа применяются для сложных схем (например, схем с несколькими источниками питания), когда эквивалентные преобразования не работают.

Задача 2 по первому принципу (закону) Кирхгофа

Пререквизиты

Напишите уравнения первого закона Кирхгофа для приведенной ниже цепи:

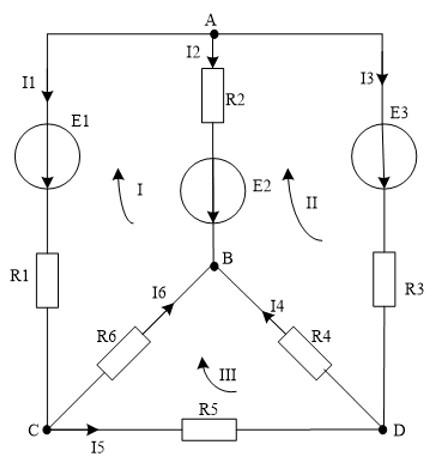
Решение

Схема имеет 4 узла. По первому закону напишите 3 уравнения (на 1 уравнение меньше, чем количество узлов):

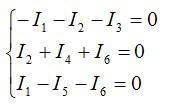
Ответ: см. выше.

Для решения задач, включающих принципы Кирхгофа, необходимо знать, как решать системы линейных уравнений. Для решения сложных систем удобно использовать специальные программы: MathCad, MatLab и т.д.

Затем, для наглядности, рассмотрим задачу с более простой схемой.

Задача 3 по правилам Кирхгофа

Состояние

Два источника питания E1=2В и E2=1В подключены в соответствии со схемой. Сопротивление R=5 Ом. Внутреннее сопротивление источников одинаково и составляет r1=r2=1 Ом. Определите силу тока, протекающего через сопротивление.

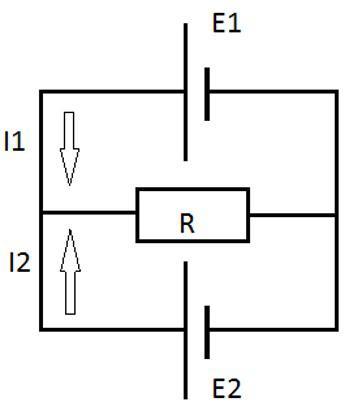
Решение

Согласно первому закону Кирхгофа, сумма токов, сходящихся в узле, равна нулю (обозначим токи произвольно):

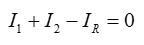
Давайте выберем направление против часовой стрелки, чтобы обойти верхний контур. Согласно второму закону Кирхгофа, сумма падений напряжения в цепи равна сумме электромагнитных полей:

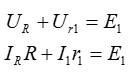
Напишем то же самое для второго контура, обведя его по часовой стрелке:

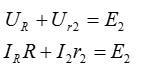
Объедините уравнения с неизвестными токами в цепь:

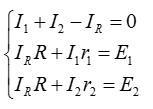
Чтобы решить систему, выразите ток I1 из второго уравнения и ток I2 из третьего уравнения:

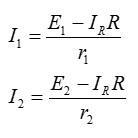
Теперь первое уравнение можно записать в виде:

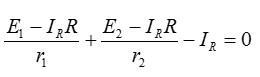
Выражая желаемый ток и подставляя значения из условия, получаем:

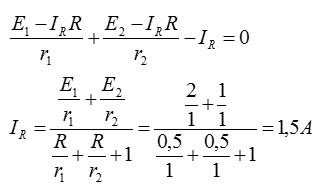
Ответ: 1,5 А.

Задача № 4 о правиле Кирхгофа

Состояние

Дана схема электрической цепи. Необходимо:

Обозначьте сопротивления, укажите над каждой ветвью различные источники тока и ЭДС;
Укажите направления токов и ЭДС на диаграмме;
Напишите уравнения в соответствии с первым и вторым законами Кирхгофа.

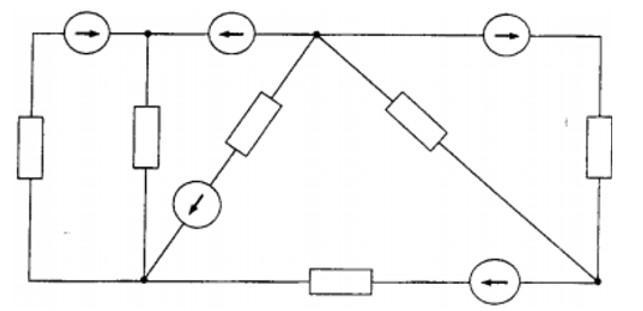
Решение

Составьте схему, обозначив сопротивления, ЭДС и токи:

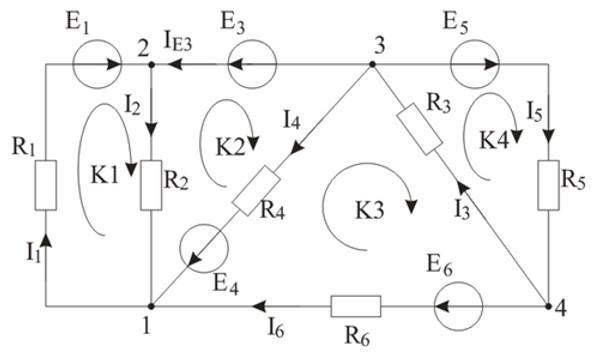
В цепи 7 токов и 4 узла. Необходимо привести 4 – 1 = 3 уравнения по первому закону Кирхгофа и 7 – 3 = 4 уравнения по второму закону Кирхгофа.

Первый закон Кирхгофа:

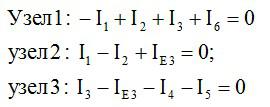
Второй закон Кирхгофа (на рисунке показаны выбранные цепи K1, K2, K3, K4):

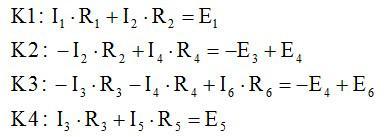
Ответ: см. выше.

Задача 5 по правилу Киршнова

Пререквизиты

Определите все токи ветвей, составив систему уравнений в соответствии с законами Кирхгофа.

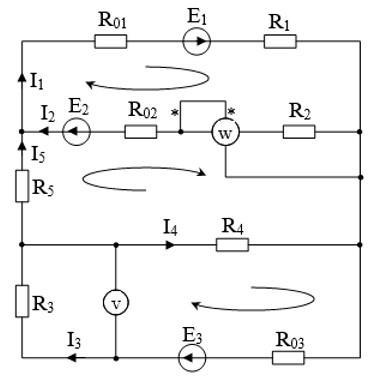
Параметры цепи: E1 = 40 В, E2 = 50 В, E3 = 60 В, R01 = 0,1 Ом, R02 = 0,3 Ом, R03 = 0,2 Ом, R1 = 4,4 Ом, R2 = 4,7 Ом, R3 = 4,6 Ом, R4 = 5,2 Ом, R5 = 7,6 Ом.

Решение

Направления токов в ветвях цепи и направления обхода контура показаны на схеме. Эта схема имеет 3 узла и 3 независимых контура. Поэтому для расчета токов ветвей необходимо написать два уравнения по первому закону Кирхгофа и три по второму закону:

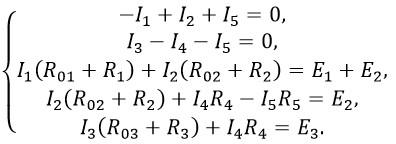
Подставьте числовые значения и решите систему уравнений:

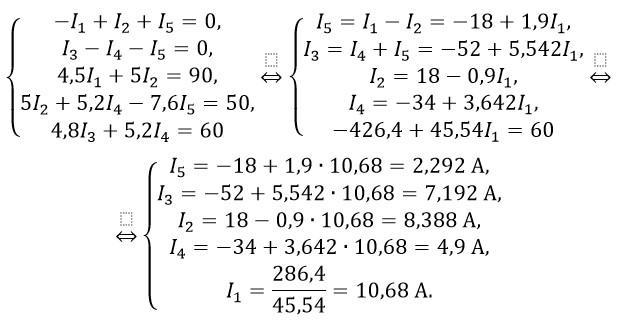
Ответ: I1=10,68 A; I2=8,388 A; I3=7,192 A; I4=4,9 A; I5=2,292 A.

Для внешней цепи:

Второй закон Кирхгофа.

Формула: Алгебраическая сумма ЭДС, действующих в замкнутой цепи, равна алгебраической сумме падений напряжения на всех резистивных элементах этой цепи.

Термин “алгебраическая сумма” означает, что и ЭДС, и падение напряжения на элементах могут быть “+” или “-“. Для определения знака можно использовать следующий алгоритм:

1. выберите направление контура (по часовой стрелке или против часовой стрелки).

2. произвольно выбрать направление токов, протекающих через элементы цепи.

3. нанести на элементы знаки ЭМП и падающих напряжений в соответствии с правилами:

– ЭМП, создающие в цепи ток, направление которого совпадает с направлением обхода цепи, регистрируются со знаком “+”, в противном случае ЭМП регистрируются со знаком “-“.

– Напряжения, падающие на элементы цепи, записываются со знаком “+”, если ток, протекающий через элементы, совпадает с направлением обхода цепи, в противном случае напряжения записываются со знаком “-“.

Например, рассмотрим схему, показанную на рисунке 3, и запишем выражение в соответствии со вторым законом Кирхгофа, обведя схему по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.

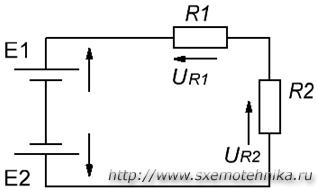
Рисунок 3: Электрическая цепь для объяснения второго закона Кирхгофа.

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхгофа (теория).

Это оказывается более чем просто для всех ветвей системы:

Метод контурного тока

Сегодня мы рассмотрим еще один важный (и втайне наш любимый) метод определения токов в цепях постоянного тока. Это метод контурного тока. На наш взгляд, она проще, чем уравнения Кирхгофа, хотя бы потому, что в схеме нужно решить ровно в два раза меньше уравнений. Итак, рассмотрим ту же электрическую цепь постоянного тока, которую мы рассчитали по методу Кирхгофа. Вспомните, как выглядит схема

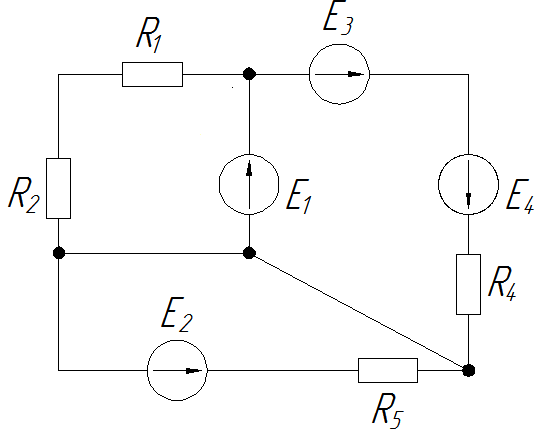
В этой диаграмме нас интересует количество независимых контуров, мы выбираем их, как и в прошлый раз. Здесь мы имеем дело с тремя независимыми схемами.

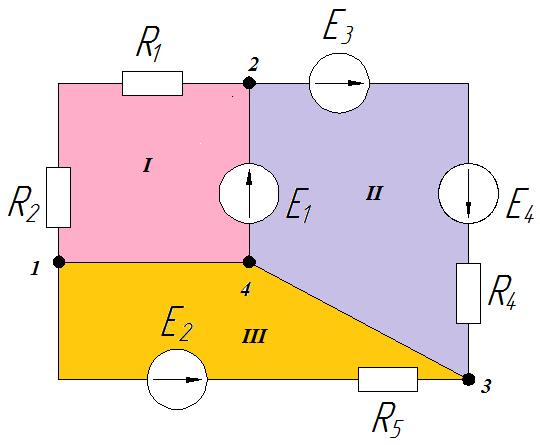
В каждой ветви цепи обозначим направления неизвестных токов стрелками, как и раньше (если мы уже рассчитали цепь другим методом, то должны сохранить направления и нумерацию токов, чтобы можно было сравнить результаты расчетов двумя методами). В методе Кирхгофа мы делали это так, давайте сделаем это снова.

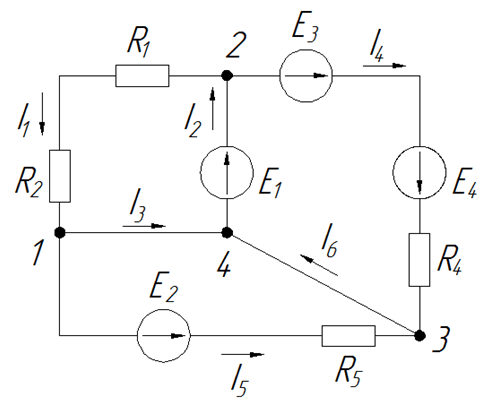
Последний штрих – в каждом контуре мы выбираем направление обхода и рисуем ток контура. Нам нравится брать те же направления, что и в методе Кирхгофа, хотя бы для того, чтобы не рисовать одно и то же дважды. Контурные токи обозначаются заглавной буквой I, с подстрочными индексами 11, 22, 33.

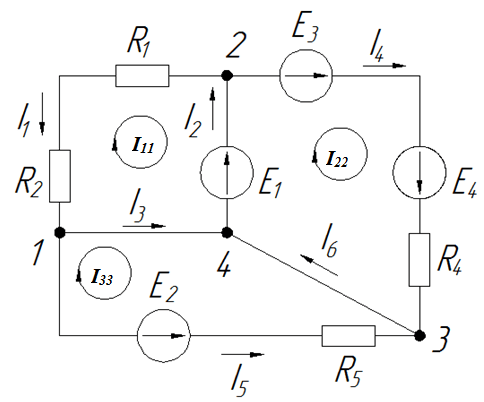
Подготовительная часть работы завершена, переходим непосредственно к определению течений. Записываются три уравнения (в зависимости от количества контурных токов). Фактически, каждое уравнение чем-то похоже на второй закон Кирхгофа, только для тока в контуре.

В общем случае система уравнений для трех контуров имеет вид

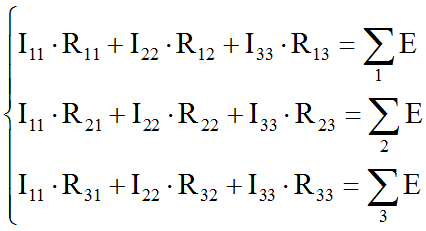
Токи контура, конечно, неизвестны и должны быть определены. Резисторы R11, R22, R33 – это суммарные сопротивления каждой цепи, взятые со знаком плюс. Это означает, что мы обходим каждую цепь и складываем все сопротивления в ней.

Для цепи 1 это резисторы 1 и 2, для цепи 2 – резистор 4, для цепи 3 – резистор 5.

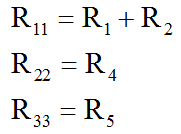
Резисторы типа Rij – это сопротивления ветвей, общих для контуров i и j. Таким образом, если мы хотим определить R12, мы находим ветвь, общую для контуров 1 и 2, и записываем ее сопротивление. Знак зависит от направления токов в цепях: если токи в двух цепях идут в одном направлении, сопротивление ветви берется с плюсом; если токи идут в противоположных направлениях, оно берется с минусом. На примере резистора R12: ветвь, общая для цепей 1 и 2, является ветвью между узлами 2 и 4 (ветвь 2 в соответствии с текущей нумерацией). На ней нет резисторов, поэтому сопротивление R12=0. Знак в данном случае, конечно, не имеет значения, но токи I11 и I22 в этой ветви противоположно направлены, поэтому если бы здесь было сопротивление, мы бы вписали его в цепь со знаком “минус”. Очевидно, что сопротивления с индексами ij и ji равны.

Для всех ветвей системы это оказывается более чем просто:

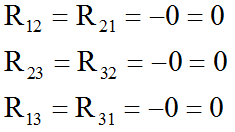
В правой части уравнения находятся суммы ЭДС источников напряжения. Принцип тот же, что и во втором законе Кирхгофа: сложите ЭДС, принимая во внимание знаки. Если направление ЭДС совпадает с направлением тока в цепи, запишите его со знаком плюс, если не совпадает – со знаком минус.

На примере схемы 1: в схеме 1 имеется только один источник напряжения E1, направление которого противоположно направлению тока в схеме. Таким образом,

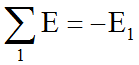
Для всех петель мы получаем

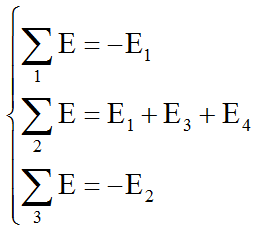
Теперь мы можем написать и решить полную систему уравнений для трех контурных токов. Получается следующее:

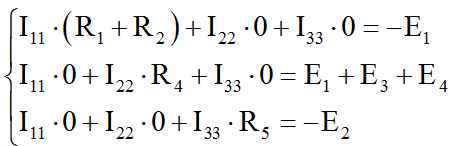
Упрощая и сокращая то, что упрощено и сокращено, получаем несложную систему уравнений с тремя неизвестными, из которой однозначно определяются контурные токи.

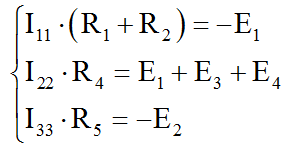
Определив контурные токи, нам остается определить токи ветвей. Это можно сделать довольно простым способом. Мы пройдем по ветвям нашей цепи по порядку и посмотрим, как складываются токи контуров в ветвях. Только один контурный ток, I11, участвует в токе на ветви 1, и он направлен в другую сторону. Так что

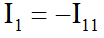
В ветви 2 ток I2 складывается из контурных токов I11 и I22, где I22 берется с “плюсом” (направления токов I2 и I22 совместимы), а I11 берется с “минусом” (направления токов I2 и I11 противоположны).

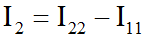
Для всех филиалов

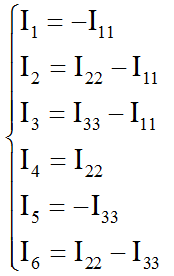
Вот и все, проблема решена. Остается только сравнить результаты с ответами, полученными другим методом, и убедиться, что все было сделано правильно.

Набор (система) уравнений для определения фактических токов ветвей в MCT строится следующим образом:

Оптимизированная процедура построения системы

В общем случае процедура построения системы уравнений состоит из следующих шагов:

1. для N-го контура в левой половине N-го уравнения записывается JN (значение КТ, умноженное на сумму всех импедансов данного контура):

Где JN – ток контура, RN1, RN2. RNn – сопротивления, присутствующие в данном контуре.

(2) Из левой половины уравнения вычтите оставшийся КТ, умноженный на сумму сопротивлений на пересечениях N-го контура:

. – JA (RNA1 + RNA2 + . . ) – JB (RNB1 + RNB2 + . . ) – .

где JA, JB – сечения, пересекающие контур N; RNA1, RNA2 – сопротивления сечений, входящих в контуры N и A.

3. правая половина уравнения – это сумма ЭДС источника данного контура:

С “плюсом”, когда обход контура и направление ЭДС совпадают, и с “минусом”, когда они ориентированы по-разному.

4 Также добавляем к правой половине произведения значений источников тока на сопротивление соответствующего участка цепи (знаки “плюс” или “минус” выбираются аналогично шагу 3):

Написав уравнения для всех независимых контуров, получаем требуемую систему (Np – Nu + 1) уравнений для нахождения такого же числа неизвестных контурных токов.

Формальный подход.

Система уравнений для MCT, записанная в матричном представлении, называется формальным подходом. Для расчета необходимы следующие матрицы:

C – состоит из i строк и j столбцов, где i – количество строк, j – количество столбцов;
Z – диагональная матрица сопротивления, количество строк и столбцов которой равно количеству ветвей;
C – транспонированная матрица C. В транспонированной матрице строки и столбцы меняются местами;
I – матрица CT (состоит из одного столбца);
J – матрица-столбец – источники тока;
E – матрица столбцов, содержащая электродвижущую силу источника с одним или другим знаком.

Окончательное уравнение для расчета в матричном представлении выглядит следующим образом:

C * Z * St * I = C * (E + Z * J)

Пример применения MCT

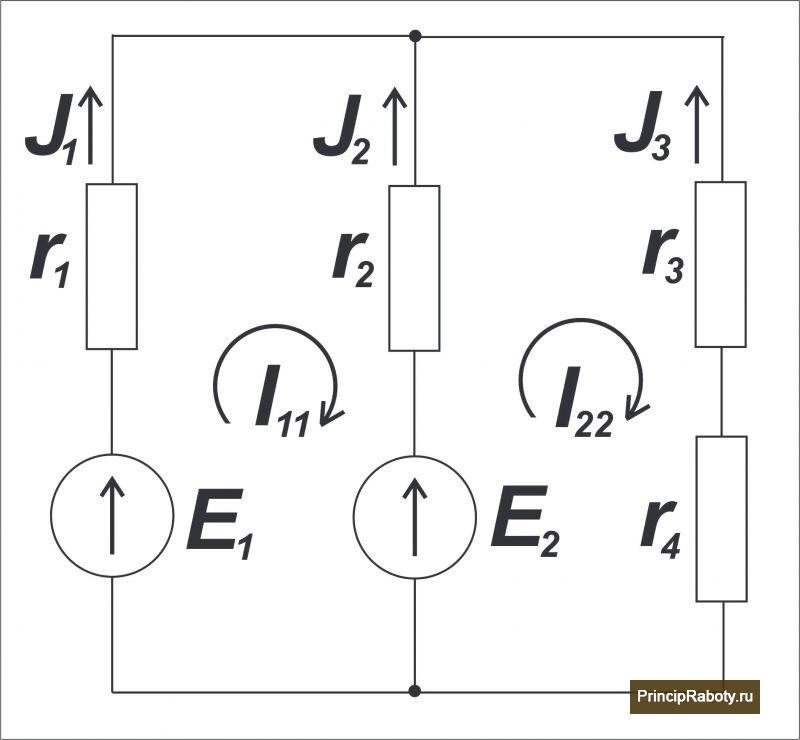
На рисунке 2 показана двухконтурная схема с четырьмя резисторами и двумя источниками напряжения. Применим МКТ для определения действительных токов J1, J2, J3. Пусть R1 = R2 = 4 Ом, R3 = 1 Ом, R4 = 3 Ом, E1 = 24 В, E2 = 12 В.

Следуя MCT, сформулируем два уравнения. Пусть циркулирующие токи I11 и I22 движутся по часовой стрелке, тогда:

I11 * (R1 + R2) – I22 * R2 = E1 – E2
– I11 * R2 + I22 * (R2 + R3 + R4) = E2

Подставляя численные значения резисторов и источников напряжения, получаем

I11 * 8 – I22 * 4 = 12
– I11 * 4 + I22 * 8 = 8

Тогда получаем: I11 = I22 = 3 A. На следующем этапе перейдем от токов КТ к реальным токам. В первой ветви течет только I11, который имеет то же направление, что и J1, из чего следует, что J1 = I11 = 3 A. Во второй ветви текущий ток состоит из I11 и I22.

Так как I22 находится в том же направлении, что и J2, а I11 противоположно J2, то: J2 = I22 – I11 = 3 A – 3 A = 0 A. Единственный ТТ I22 напротив проходит через третью ветвь, поэтому J3 = – I22 = – 3 A. Таким образом: J1 = 3 A, J2 = 0 A, J3 = – 3 A.

Решая полученную систему уравнений относительно контурных токов, получаем:

Метод контурного тока

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) приходится решать систему из большого числа уравнений, что значительно усложняет расчеты.

Например, для схемы на рис. 4.13 необходимо решить и рассчитать систему из 7 уравнений

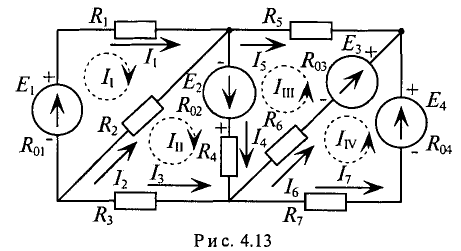
Эту же задачу можно решить, написав всего 4 уравнения по второму закону Кирхгофа, если использовать метод контурных токов.

Суть этого метода заключается в том, что в одной цепи выделяют t независимых контуров, в каждом из которых токи направлены произвольно (см. рис. 4.13). (пунктирные стрелки) контурные течения 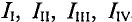. Ток цепи – это расчетная величина, которую нельзя измерить.

Как показано на рис. 4.13, отдельные ветви цепи являются частью двух соседних цепей. Фактический ток в такой ветви определяется алгебраической суммой контурных токов соседних цепей.

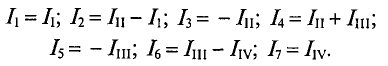
Для определения контурных токов составляются t-уравнения в соответствии со вторым законом Кирхгофа. Каждое уравнение содержит алгебраическую сумму ЭДС, содержащейся в данном контуре (по одну сторону от знака равенства) и общее падение напряжения в данном контуре, образованное током контура и токами соседних контуров (по другую сторону от знака равенства).

Для этой схемы (рис. 4.13) необходимо составить 4 уравнения. Со знаком “плюс” напишите ЭДС и падения напряжения, действующие в направлении контурного тока, со знаком “минус” – в направлении контурного тока. – те, которые направлены против контурного течения.

Система уравнений для схемы (рис. 4.13):

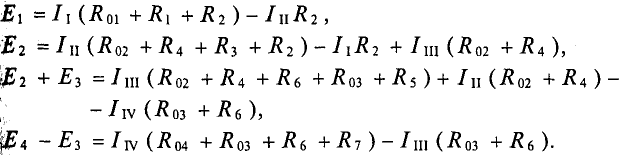
Решив систему уравнений, можно рассчитать токи контура, которые определяют реальные токи в каждой цепи (рис. 4.13).

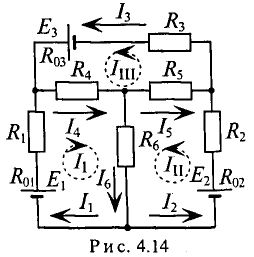
Пример 4.11

Определите токи во всех элементах сложной цепи (рис. 4.14), если: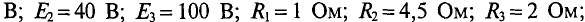

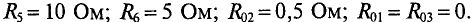
Решение

Для определения циркулирующих токов приведите 3 уравнения в соответствии со вторым законом 1 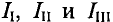(направление токов выбрано произвольно и обозначено пунктирными линиями).

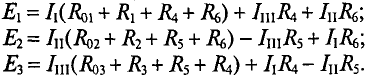
Подставьте числовые значения

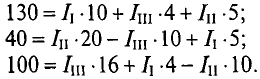
Из уравнения (2) определите силу тока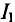

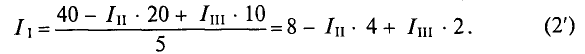
Текущее значение 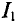(выражение (2′)) следует подставить в уравнение (1):

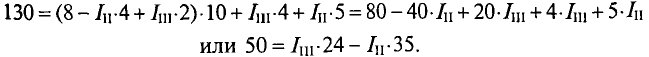
Одинаковая приведенная стоимость 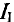подставляется в уравнение (3):

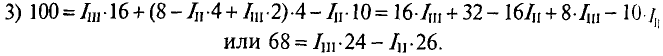
Полученное уравнение (3) вычитается из полученного уравнения (1). Результат был следующим

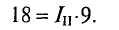
Откуда берется ток в петле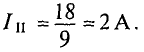

Из уравнения (3) следует, что ток контура составляет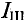

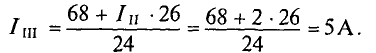
Из уравнения (2′) следует, что ток составляет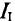

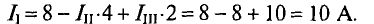
Рассчитываются фактические токи в цепи:

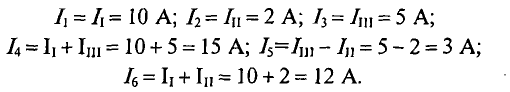
Проверяется правильность решения для первой цепи (рис. 4.14).

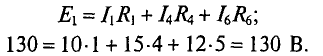
Такую же проверку можно выполнить и для других цепей (2. и 3.):

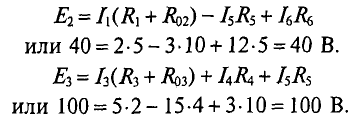
Проверка показывает, что решение правильное.

Определение метода контурного тока

Этот метод является базовым и может быть использован для расчета любой электрической цепи. Он основан на уравнениях, полученных из второго закона Кирхгофа. В схеме выделяются независимые контуры, направления контурных токов в каждом контуре выбираются произвольно, и составляются уравнения в соответствии со вторым законом Кирхгофа. Для схемы согласно рис. 3.1 имеем:

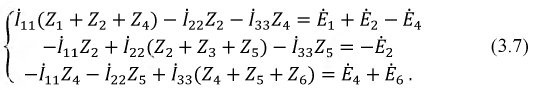
Введем в полученную систему уравнений обобщенные параметры:

внутреннее сопротивление цепи – сумма сопротивлений, включенных в цепь, например, для первой цепи:

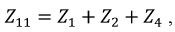
соседние сопротивления – сопротивления на границах контура, напр, 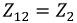сопротивление на границе первой и второй петли, суммарная ЭДС, например, для первой петли:

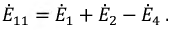
Тогда система уравнений будет иметь вид:

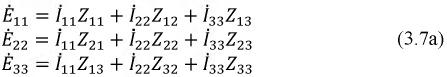
Используя матричный метод расчета, мы можем записать:

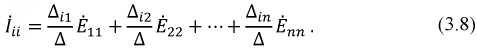
В уравнении (3.8) 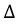– определитель системы (3.7a), и 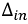– является алгебраическим дополнением для соответствующей ЭДС контура. В ветвях, не примыкающих к другим цепям, фактические токи будут:

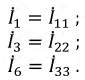
Токи ветвей на границах контуров:

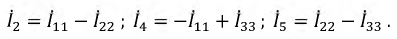
Исходный материал по методу контурного тока

Метод контурных токов является одним из основных методов расчета сложных электрических цепей и широко используется на практике. Этот метод заключается в определении на основе второго закона Кирхгофа вместо токов ветвей так называемых контурных токов, замыкающихся в контурах.

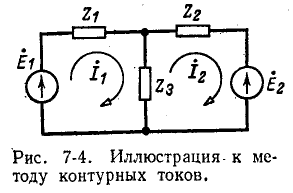
Рис. 7-4 в качестве примера показана двухконтурная электрическая цепь, в которой 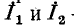– петлевые токи. Токи в сопротивлениях 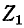и 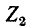равны соответствующим контурным токам; ток в сопротивлении 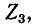который является общим для обоих контуров, равен разности токов контуров 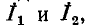поскольку эти токи текут в противоположных направлениях в ветви 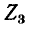в противоположных направлениях*. Если положительное направление искомого тока в ветви 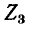предполагается совпадающим с направлением контурного тока 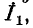тогда ток ветви будет равен 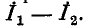В противном случае он будет равен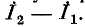

Число уравнений, которые необходимо записать для контурных токов согласно второму закону Кирхгофа, равно числу независимых контуров, т.е. для электрической цепи с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы уравнений p – q + I. Таким образом, в схеме рис. 7-4 q = 2, p = 3; следовательно, количество уравнений равно 3 – 2+1=2 (количество независимых контуров).

Обратите внимание, что если положительное направление одного из контурных токов 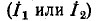меняется на противоположный, тогда ток ветви 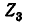будет равна сумме этих токов.

Назовем сумму комплексных сопротивлений, принадлежащих контурам, собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или более контурам, – общим сопротивлением этих контуров.

Положительные направления контурных токов определяются произвольно. Обычно предполагается, что направление шунта каждой цепи совпадает с выбранным положительным направлением тока контура; поэтому падение напряжения от данного тока контура на собственном сопротивлении цепи при составлении второго уравнения закона Кирхгофа берется со знаком плюс. Падение напряжения от соседнего контурного тока в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении имеют противоположные направления, как, например, в схеме рис. 7-4, где направление обоих токов – по часовой стрелке.

Для заданной электрической цепи с двумя независимыми контурами (рис.7-4), согласно второму закону Кирхгофа, можно записать два уравнения, а именно,

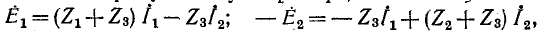
где 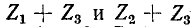– собственные сопротивления цепей 1 и 2; 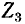– общее сопротивление цепей 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений токов в цепях).

Если заданная электрическая цепь состоит из n независимых контуров, мы получаем систему из n уравнений, основанных на втором законе Кирхгофа:

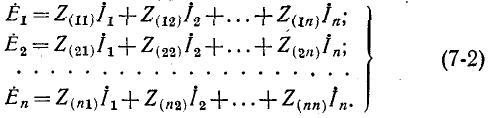
Здесь 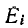– мощность контура 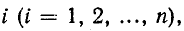это алгебраическая сумма значений э.ф., действующих в данном контуре; значения э.ф., соответствующие направлению обхода, берутся со знаком плюс, а противоположные – со знаком минус;

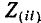– внутреннее сопротивление контура i;

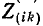– полное сопротивление контура 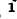i и k.

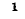Индексы собственного и полного сопротивлений контура заключены в скобки, чтобы отличать их от входных и передаточных сопротивлений, приведенных в последующих разделах книги.

Как было сказано ранее, собственные сопротивления 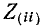положительны, так как предполагается, что шунт контура совпадает с положительным направлением тока контура 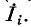Суммарные сопротивления 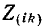будет входить со знаком минус, когда токи 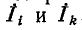в них перевернуты.

Решение уравнений (7-2) относительно искомых токов цепи может быть найдено с помощью определителей:

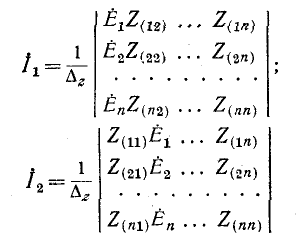
и т.д., где детерминант системы

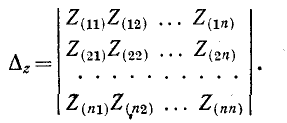
Согласно правилу разложения определителя по элементам столбца, определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений должно быть записано в виде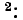

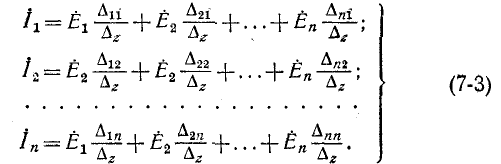
Определителю предшествует буква z, поскольку его элементы являются комплексными сопротивлениями.

На практике во многих случаях решение системы уравнений (7-2) может быть выполнено более просто путем последовательного исключения неизвестных,

Здесь Ditl – алгебраическое дополнение Z <lk) определителя=”” системы,=”” т.=”” е.=”” умноженный=”” на=”” (—1)‘+*=”” минор=””></lk)>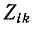(минор возникает из определителя системы путем исключения i-го порядка и 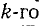колонна).

В краткой форме система уравнений (7-3) может быть записана как

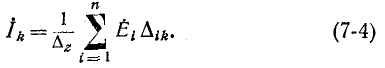
Первый индекс алгебраического дополнения i, обозначающий номер линии, которая будет построена в определителе системы, соответствует номеру контура, контурный вывод которого умножается на это алгебраическое дополнение. Второй подстрочный индекс 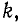обозначающий номер подчеркиваемого столбца в определителе системы, соответствует номеру цепи, для которой рассчитывается ток цепи.

Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источники электричества являются источниками напряженности электрического поля. Если в электрической цепи есть источники тока, их можно заменить эквивалентными источниками напряженности электрического поля.

Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве циркулирующих токов; тогда число неизвестных циркулирующих токов и число уравнений уменьшится на число заданных токов.

Если в электрической цепи есть параллельные ветви, то замена их эквивалентным комплексным сопротивлением уменьшает количество цепей (за счет тех, которые образованы параллельными ветвями).

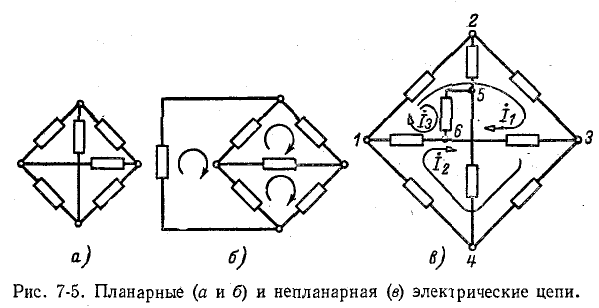
Электрические цепи могут быть планарными и непланарными.

Плоскую или планарную электрическую цепь можно нарисовать на плоскости в виде диаграммы с непересекающимися ветвями. В некоторых случаях пересечение ветвей в цепи, возникающее в результате принятого способа рисования схемы, устраняется при другом способе представления данной планарной схемы, как показано, например, на рис. 7-5. 7-5.

Электрическая цепь, показанная на рисунке 7-5, а, является планарной, поскольку существующее пересечение ветвей устранено в соответствии с рисунком 7-5, б.

Непланарная схема не может быть построена в виде диаграммы с непересекающимися ветвями. Примером такой схемы является схема, показанная на рис. 7-5, в непланарной схеме, в которой пересечение ветвей не может быть устранено.

Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например, совпадает с направлением часовой стрелки, то полные сопротивления соседних контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи соседних контуров

в общей обмотке направлены в противоположные стороны. Направление токов контура по часовой стрелке предполагается во всех контурах, за исключением внешнего контура, который охватывает весь контур. В последнем случае ток в контуре идет против часовой стрелки”. (см. пример 7-2). Однако это правило не является обязательным.

В случае непланарной цепи невозможно, чтобы были только различия в токах контуров в общих ветвях, как это видно, например, в цепи на рис. 7-5, в.

Пример 7-2.

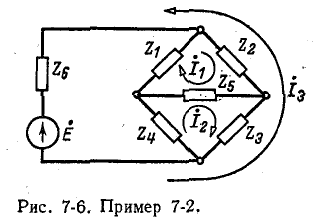
Используя метод контурного тока, определите ток в диагонали дуговой цепи с рисунка 7-6.

Выбранные положительные направления циркулирующих токов 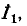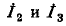обозначены стрелками на рисунке. Число уравнений, которые необходимо записать в соответствии со вторым законом Кирхгофа, равно трем (по числу независимых цепей):

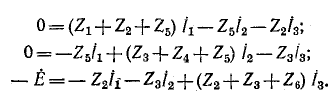
Решение полученной системы уравнений относительно циркулирующих токов 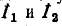урожайность:

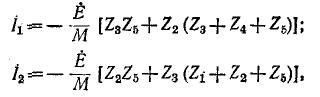
Где M имеет то же значение, что и в примере 7-1.

Искомый ток в диагонали мостовой схемы равен разности контурных токов:

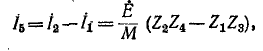
М, что совпадает с ответом, полученным в примере 7-1.

Обратите внимание, что если в данной цепи контуры выбраны таким образом, что ток только одного контура 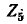через ветвь будет протекать только один контурный ток, то требуемый ток ветви 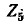будет точно таким же, как на рис. 7-6. Пример 7-2. к этому контурному току, т.е.

проблема будет сведена к поиску только одного циркулирующего тока (вместо двух).

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан командой педагогов на некоммерческой основе для дополнительного образования молодежи.

Сайт написан, поддерживается и управляется командой преподавателей.

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.

Читайте далее: