3) 1≤ a = 1 ≤ 2 = верно;
Таблицы истинности и булевы графы
Булева алгебра (алгебра логики алгебра логики) – одна из основных ветвей математической логики, в которой методы алгебры используются в логических преобразованиях.
Создателем алгебры логики был английский математик и логик Дж. Буль (1815-1864), который основывал свое учение о логике на аналогии между алгеброй и логикой. Он записывал любую теорему с помощью символов разработанного им языка и получал “уравнения”, истинность или ложность которых можно было доказать на основе определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и т.д.
Современный алгебра логики является ветвью математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истинно, ложно). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных пропорциях.
Логическое утверждение – это любое повествовательное предложение, для которого мы можем однозначно утверждать, что его содержание истинно или ложно.
Например, “3 умножить на 3 равно 9”, “Архангельск находится севернее Вологды” – истинные высказывания, а “Пять меньше трех”, “Марс – звезда” – ложные.
Конечно, не каждое тезисное утверждение может быть логическим утверждением, потому что не всегда можно сказать, что оно ложно или истинно. Например, утверждение “Информатика – интересный предмет” является расплывчатым и требует дополнительной информации, а утверждение “Информатика – интересный предмет для ученика 10 класса, А.А. Иванов” может иметь значение “истинный” или “ложный”, в зависимости от интересов Иванова.
В дополнение к бивалентная алгебра теоремкоторый принимает только два значения – “истина” и “ложь”, существует Алгебра многозначных утверждений. В такой алгебре, помимо “истинно” и “ложно”, используются такие истинностные значения, как “вероятно”, “возможно”, “невозможно” и т.д.
В алгебре логики различают простой (элементарно) заявленияобозначаемые латинскими буквами (A, B, C, D, …), и комплекс составные (сложные) предложения, которые состоят из нескольких простых предложений с использованием логических соединителей, напр. “Не”, “и”, “или”, “тогда и только тогда”, “если .. Истинность или ложность таких составных высказываний определяется значением простых высказываний.
Обозначим через А утверждение “Алгебра логики успешно используется в теории электрических цепей”, и по В – “Применение алгебры логики в синтезе релейно-контактных схем”.
Тогда составное утверждение “Булева алгебра успешно используется в теории электрических цепей и при синтезе лестничных и контакторных схем” можно записать как A и B; здесь “и” – это логическая связка. Очевидно, что поскольку элементарные утверждения A и B истинны, то составное высказывание A и B.
Каждая логическая связка рассматривается как операция над логическими выражениями и имеет собственное имя и обозначение.
Есть только два логических значения: True (TRUE) и false (ЛОЖЬ).. Это соответствует числовому представлению – 1 и 0. Результаты каждой логической операции можно хранить в таблице. Такие таблицы называются таблицами истинности.
Основные операции булевой алгебры
1 Логическое отрицание, инверсия (лат. инверсия – это логическая операция, в результате которой из данного высказывания (например, A) мы получаем новое высказывание (не A), который называется отрицание первоначального утвержденияСимволически это обозначается чертой сверху ($A<->$) или условными обозначениями, например. ¬, “нети гласит: “не А”, “А ложно”, “неверно, что А”, “отрицание А”.. Например: “Марс – это планета в Солнечной системе”. (утверждение А); “Марс не является планетой Солнечной системы”. ($A<->$); утверждение “10 – простое число” (утверждение B) ложно; утверждение “10 не является простым числом” (утверждение B ) истинно.
Операция, применяемая к одной величине, называется унарный. Массив значений данной операции выглядит следующим образом
| A | ¬A |
| правда | ложный |
| ложный | правда |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A<->$ ложно, когда A истинно, и истинно, когда A ложно.
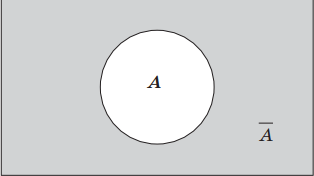
Геометрически отрицание можно представить следующим образом: если A – это некоторое множество точек, то $A<->$ – это дополнение множества A, то есть все точки, которые не принадлежат множеству A.
2. Конъюнктура (лат. conjunctio – конъюнкция) – это логическое умножение, операция, требующая по крайней мере двух логических значений (операндов) и объединяющая два или более высказываний путем “и” (например, “А и Б”), которую мы символически обозначим через ∧ (A ∧ B) и прочитаем: “А и Б”. Следующие символы также используются для обозначения конъюнкции: A ∙ B; A & B, A и BИногда между высказываниями нет знака: AB. Пример логической связки: “Этот треугольник равнобедренный и прямоугольный”. Высказывание может быть истинным только при выполнении обоих условий, в противном случае высказывание ложно.
Таблица истинности для этой операции
| A | B | A ∧ B |
| правда | ложный | ложь |
| ложь | правда | ложь |
| ложь | ложь | ложь |
| правда | правда | правда |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Предложение А ∧ В истинно только в том случае, если оба утверждения А и В оба верны.
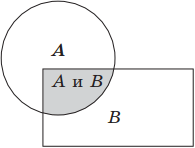
Геометрически конъюнкция может быть представлена следующим образом: если A, B А ∧ В является пересечением множеств А и В.
3. Дисъюнкция (лат. дизъюнкция – деление) – это логическое дополнение, операция, соединяющая два или более высказываний посредством “или” (например, “А или Б”), который символически обозначается ∨. (А ∨ В) и гласит: “А или Б”.. Следующие символы также используются для обозначения дизъюнкции: A + B; A или B; A | B. Пример логического сложения: “Число x делится на 3 или на 5”. Это утверждение будет истинным, если выполнены оба или хотя бы одно из условий.
Таблица истинности этой операции выглядит следующим образом
| A | B | A ∨ B |
| правда | ложный | правда |
| ложь | правда | правда |
| ложь | ложь | ложь |
| правда | правда | правда |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Заявление А ∨ В ложно только в том случае, если оба утверждения А и В оба ложны.
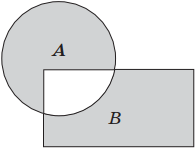
Геометрически логическое сложение можно представить следующим образом: если A, B А ∨ В – является объединением множеств А и Вт.е. фигура, сочетающая в себе и квадрат, и круг.
4. Строго разделимая дизъюнкция, по модулю два дополнения – это логическая операция, которая объединяет два выражения, используя “или”используется в исключительном смысле, символически обозначается ∨ ∨ или ⊕ (А ∨ ∨ B, A ⊕ В) и читайте: “либо А, либо Б”.. Примером сложения по модулю два является утверждение “Этот треугольник раздвоенный или остроугольный”. Утверждение истинно, если выполняется одно из условий.
Таблица истинности этой операции выглядит следующим образом
| А | В | А ⊕ B |
| правда | ложный | правда |
| ложь | правда | правда |
| ложь | ложь | ложь |
| правда | правда | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Утверждение A ⊕ B истинно только в том случае, если утверждения A и B имеют разные значения.
5. Импликация (лат. implisito – (лат. implisito) – это логическая операция, соединяющая два высказывания с помощью связки “если. то” в составное предложение, которое символически обозначается → (А → В), и мы читаем: “если А, то В”, “А влечет за собой В”, “из А следует В”, “А подразумевает В”.. Для обозначения импликации также используется символ ⊃ (A ⊃ B). Примером импликации является: “Если полученный четырехугольник является квадратом, то вокруг него можно нарисовать круг”. Эта операция объединяет два простых логических выражения, первое из которых является условием, а второе – следствием. Результат операции ложен только в том случае, если посылка истинна, а следствие ложно. Например, “Если 3 * 3 = 9 (A), то Солнце – планета (B)”, результат импликации A → B является ложным.
Таблица истинности для этой операции
| А | В | А → В |
| правда | ложь | ложь |
| ложь | правда | правда |
| ложь | ложь | правда |
| правда | правда | правда |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации верно, что из лжи может следовать что угодно, но из истины может следовать только истина.
6. Эквивалентность, двойная импликация, эквивалентность (лат. aequalis – равный и валентис – действительный) – это логическая операция, которая позволяет вывести два утверждения А и В для получения новой выписки A ≡ B, который гласит следующее: “A эквивалентно B”.. Для обозначения эквивалентности также используются следующие знаки: ⇔, ∼. Эта операция может быть выражена конъюнкцией “тогда и только тогда”, “необходимый и достаточный”, “эквивалентный” .. Примером эквивалентности является утверждение: “Треугольник является правильным тогда и только тогда, когда один из его углов равен 90 градусам.
Таблица законов эквивалентности выглядит следующим образом
| А | В | А ∼ В |
| правда | ложь | ложь |
| ложь | правда | ложь |
| ложь | ложь | правда |
| правда | правда | правда |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат “истина” тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, мы можем использовать таблицы истинности для определения значений сложных высказываний. Важно знать, что для представления любой функции в булевой алгебре достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | A ⊕ B | $(A <->∧B) ∧ (A ∧ B<->)$ |
| Импликация | A → B | $A <->∨ B$ |
| Эквивалентность | A ∼ B | $(A <->∧ B<->) ∨ (A ∧ B)$ |
Приоритет логических операций следующий: отрицание (“нет”) имеет наивысший приоритет, за ним следует конъюнкция (“и”), после конъюнкции – дизъюнкция (“или”).
С помощью логических переменных и логических операций любое логическое высказывание может быть формализовано, то есть заменено логической формулой. Таким образом, элементарные высказывания, составляющие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определить истинность или ложность составного высказывания. Например, утверждение “Если пять больше двух (А), вторник всегда следует за понедельником (В)” – эффект А → Ви результатом операции в данном случае будет ‘true’. В логических операциях смысл высказываний не рассматривается, только их истинность или ложность.
Рассмотрим, например, построение высказывания, состоящего из утверждений А и Вкоторое будет ложным тогда и только тогда, когда оба утверждения истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А утверждение может быть, например, таким: “Этот шар полностью красный или полностью синий”. Следовательно, если утверждение А “Этот шар полностью красный” – истинно, а утверждение В “Этот шар полностью синий” истинно, тогда составное высказывание ложно, потому что шар не может быть одновременно красным и синим.
Примеры решений
Пример 1. Найдите для заданных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Порядок операций следующий: сначала выполняется операция парентетического сравнения, затем операция дизъюнкции и, наконец, операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации такова
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
((1 > 3) ∨ (1 < 3)) → (1 < 4) = false ∨ true → true
((12 > 3) ∨ (12 < 3) → (12 < 4) = true ∨ false → true → false = false;
((3 > 3) ∨ (3 < 3)) → (3<4) = false ∨ false → true → false = true.
Пример 2. Найдите множество целых значений X, для которых верно выражение ¬((X > 2) → (X > 5)).
Решение. Операция отрицания применяется ко всему выражению ((X > 2) → (X > 5)) Поэтому, когда ¬((X > 2) → (X > 5)) истинно, то выражение ((X > 2) → (X > 5)) ложно. Поэтому мы должны определить, для каких значений X выражение ((X > 2) → (X > 5)) является ложным. Операция импликации принимает значение “false” только в одном случае: когда за истиной следует ложь. И это верно только для X = 3; X = 4; X = 5.
Пример 3. Для какого из приведенных слов утверждение ¬(гласная первая буква ∧ гласная третья буква) ⇔ строка из 4 символов является ложным? 1) assa; 2) cucu; 3) corn; 4) error; 5) strongman.
Решение. Рассмотрите все предложенные слова по очереди:
1) для слова assa мы получаем: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 – высказывание истинно;
2) для слова кукушка мы получаем: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 – утверждение истинно;
3) для слова кукуруза мы получаем: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 – утверждение ложно;
4) для слова ошибка получаем ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 – утверждение истинно;
5) для слова strongman получаем: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 – утверждение ложно.
Булевы выражения и их преобразования
На сайте Булево выражение это обозначение, которое может принимать логическое значение “true” или “false”. В этом определении следует различать логические выражения:
- выражения, которые используют операции сравнения (“больше”, “меньше”, “равно”, “не равно” и т.д.) и принимают логические значения (например, выражение a > b , где a = 5 и b = 7, равно значению “false”);
- прямые логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ B ∧ C, где A = true, B = false и C = true).
Булевы выражения могут содержать функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения операций следующий:
- вычисление существующих функциональных связей;
- выполнение алгебраических операций (сначала умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в любом порядке);
- Выполнение логических операций (сначала операции отрицания, затем логическое умножение, логическое сложение, а затем операции импликации и эквивалентности).
Круглые скобки можно использовать в логическом выражении, чтобы изменить порядок выполнения операций.
Пример. Найдите значение этого выражения:
$1 ≤ a ∨ A ∨ sin(π/a – π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для a = 2, b = 3, A = true, B = false.
Решение. Порядок подсчета значений следующий:
1) b a + a b > a + b, после подстановки получаем: 3 2 + 2 3 > 2 + 3, т.е. 17 > 2 + 3 = верно;
2) A ∧ B = true ∧ false = false.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = true ∨ false = true;
3) 1≤ a = 1 ≤ 2 = верно;
4) sin(π/a – π/b) < 1 = sin(π/2 – π/3) < 1 = верно.
После этих вычислений мы получаем: true ∨ A ∧ true ∧ ¬B ∧ ∧ true.
Теперь выполните операции отрицания, а затем логического умножения и сложения:
5) ¬B = ¬false = true; ¬truth = false;
6) A ∧ true ∧ true ∧ false ∧ false = true ∧ true ∧ true ∧ true ∧ false = false;
7) true ∨ false = true.
Таким образом, результатом булева выражения с заданными значениями является “true”.
Примечание. Учитывая, что выходное выражение в итоге является суммой двух слагаемых, а значение одного из них 1 ≤ a = 1 ≤ 2 = true, без дальнейших вычислений можно сказать, что результат для всего выражения также “true”.
Идентичные преобразования логических выражений
В алгебре логики выполняются основные законы, допускающие тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| пермутативный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Комбинаторика | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | $<->$ = $A <->∧ B<->$ | $<->$ = $A <->∨ B<->$ |
| Идемпотентность | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Связывание | (A ∧ B) ∨ (A <->∧ B) = B | (A ∨ B) ∧ (A <->∨ B) = B |
| Переменный режим работы с его реверсированием | $A ∨ A<->$ = 1 | $A ∧ A<->$ = 0 |
| Операции с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойное отрицание | $A<=>$ = A | |
Доказательства этих теорем проводятся путем построения таблиц истинности для соответствующих записей.
Эквивалентные преобразования логических формул имеют ту же цель, что и преобразования формул в обычной алгебре. Они используются для упрощения формул или приведения их к определенной форме с помощью основных законов булевой алгебры. На сайте упрощение формулыкоторая не содержит операций импликации и эквивалентности, является эквивалентным преобразованием, приводящим к формуле, которая содержит либо меньше операций по сравнению с исходной формулой, либо меньше переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование перестановок и законов комбинаторики и т.д.), другие основаны на свойствах, которыми не обладают операции в обычной алгебре (использование закона делимости для конъюнкции, закона поглощения, склеивания, де Моргана и т.д.).
Рассмотрим в качестве примеров некоторые приемы и методы, используемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Здесь для преобразований можно использовать закон идемпотентности, закон делимости, операцию переменной с инверсией и операцию константы.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для простоты используется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
Преобразования используют правило Де Моргана, операцию над переменной с ее инверсией, операцию над константой
Примеры решений
Пример 1. Найдите логическое выражение, которое равно A ∧ ¬(¬B ∨ C) .
Решение. Примените правило де Моргана для B и C: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равное исходному выражению: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Пример 2. Напишите значения логических переменных A, B, C, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в том случае, если истинная посылка ложна. Следовательно, для данного выражения посылка A ∨ B должна быть истинной, а следствие, то есть выражение B ∨ ¬C ∨ B, должно быть ложным.
1) A ∨ B – результат дизъюнкции является “истинным”, если хотя бы один из операндов является “истинным”;
2) B ∨ ¬C ∨ B – выражение ложно, если все слагаемые ложны, т.е. B – ‘false’; ¬C – ‘false’, и поэтому переменная C имеет значение ‘true’;
3) если мы рассмотрим посылку и обнаружим, что B “ложно”, то получим, что значение A “истинно”.
Ответ: A – истинно, B – ложно, C – истинно.
Пример 3. Каково наибольшее целое число X, при котором справедлива теорема (35)?
Поскольку каждая логическая операция может быть представлена как комбинация трех базовых операций, любое компьютерное устройство, обрабатывающее или хранящее информацию, может быть собрано из базовых логических элементов, как из “строительных блоков”.
Лекция на тему “Построение логических схем с использованием базовых логических элементов” в рамках дисциплины “Основы математической логики”.
Логический элемент Как дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций.
Поскольку каждая логическая операция может быть представлена как комбинация трех базовых операций, любое компьютерное устройство, обрабатывающее или хранящее информацию, может быть собрано из базовых логических элементов в виде “кирпичиков”.
Логические элементы компьютера работают на основе сигналов, или электрических импульсов. Есть импульс – логическое значение сигнала равно 1, отсутствие импульса – 0. Входами логического элемента являются сигналы-значения аргументов, выходом – сигнал-значение функции.
Преобразование сигнала логическим элементом определяется таблицей состояний, которая на самом деле является таблицей истинности, соответствующей логической функции.
Рассмотрим символы (массивы) основных логических элементов, реализующих логическое умножение (конъюнкция), логическое сложение (дизъюнкция) и отрицание (инвертор).
Логический элемент ИЛИ:
Например,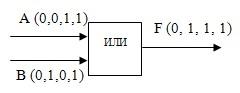 
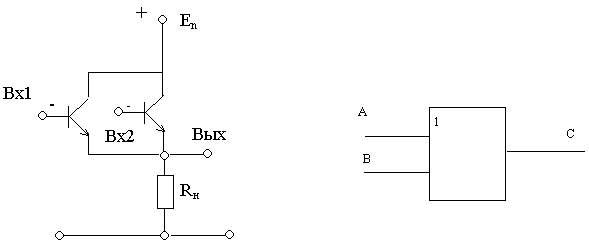
НЕ логический элемент:
Ex,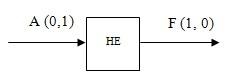 
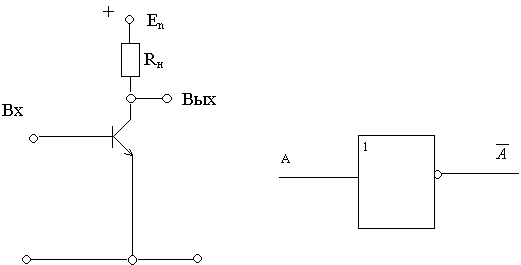
Булевский элемент “AND”:
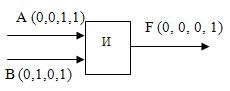
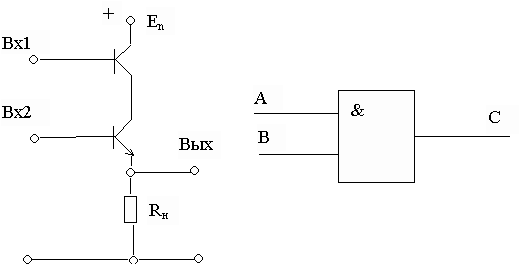
ИЛИ ДРУГОЙ ТИП ЛОГИЧЕСКОГО ЭЛЕМЕНТА
Компьютерные устройства (сумматоры в процессоре, ячейки памяти в ОЗУ и т.д.) основаны на базовых логических элементах.
Если элемент имеет входное напряжение от 0 до 0,4 В, он рассматривается как логический 0, если напряжение находится в диапазоне от 0,7 до 1,5 В, он рассматривается как 1. Выходное напряжение имеет более или менее такие же характеристики.
Конструкция цепи 
Пример 1. Составьте схему
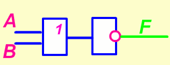
Пример 2. Составьте схему
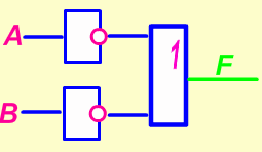
Пример 3. Составьте диаграмму 
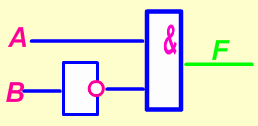
Пример 4. Составьте диаграмму 
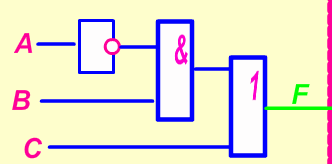
Пример 5. Составьте диаграмму 
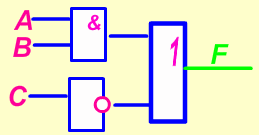
Пример 6. Составьте диаграмму
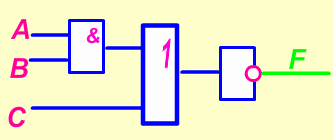
Пример 7. Составьте диаграмму. 
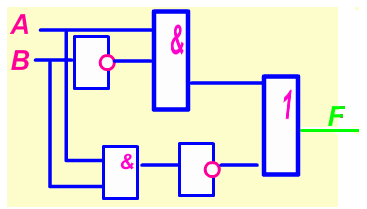
II. Выполните обратное задание. Создайте логическое выражение в соответствии с заданной логической схемой:
Данное логическое выражение может быть упрощено.
AND – логическое умножение, OR – сложение. Запишите выражение, заменив знаки & и U на знаки * и + соответственно.
Упростите , затем напишите
и тогда логическая диаграмма будет выглядеть следующим образом:
Выводы: Логические схемы, содержащие минимальное количество элементов, обеспечивают более высокую скорость работы и повышают надежность устройства.
Алгебра логики дала разработчикам мощный инструмент для проектирования, анализа и улучшения логических схем. Проще и быстрее изучить свойства и доказать правильность схемы с помощью выражающей ее формулы, чем проектировать реальное техническое устройство.
В соответствии с заданной логической функцией 
для построения логической схемы.
Мы начнем построение схемы с логической операции, которая должна выполняться в последнюю очередь. В нашем случае такой операцией является логическое сложение, поэтому на выходе логической схемы должен быть дизъюнктор. На него будут подаваться сигналы от двух конъюнкторов, на которые, в свою очередь, будет подаваться один нормальный и один инвертированный (от инверторов) входной сигнал.
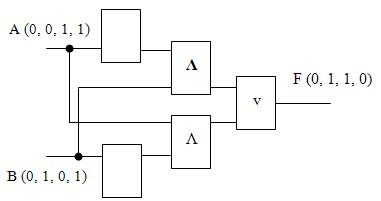
Пример 2. Выпишите соответствующую логическую формулу из логической диаграммы:
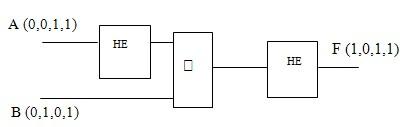
Построение логических схем.
Используя заданную логическую функцию 
Постройте логическую схему и таблицу истинности.
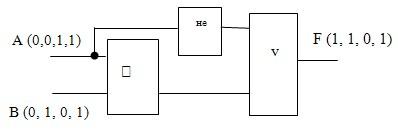
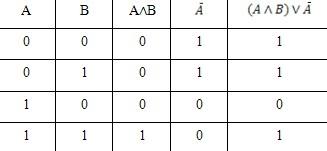
2. выпишите соответствующую логическую формулу из логической диаграммы:
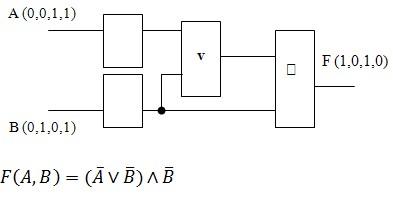
1. в соответствии с заданной логической функцией 
построить логическую схему и таблицу истинности.
Решение:
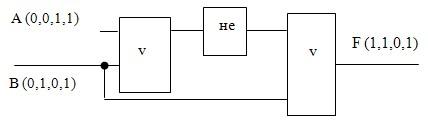
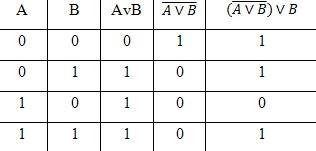
2. выпишите соответствующую логическую формулу из логической диаграммы:
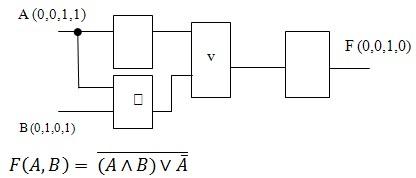
Дана логическая функция 
Постройте логическую схему и таблицу истинности.
Перечислите основные логические операции.
Что такое логическое умножение?
Что такое логическое сложение?
Что такое инверсия?
Что такое таблица истинности?
Что такое сумматор?
Что такое полусумматор?
Компьютерные науки и информационные технологии. Учебник для 10-11 классов, Н. Д. Угринович – 2007;
2 Практика в области компьютерных наук и информационных технологий. Учебник для общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова – 2007.
Задача анализа состоит в том, чтобы определить функцию f реализуемых данной логической схемой. При решении такой задачи удобно использовать следующий порядок действий.
Пример 4. Найдите булеву функцию логической схемы и создайте таблицу истинности для этой схемы.
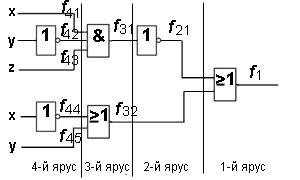
Решение. Разделите логическую диаграмму на уровни. Выпишите все функции, начиная с уровня 1:
Теперь напишите все функции, подставляя входные переменные x, y, z :
Результатом является функция, которую логическая схема реализует на выходе:
Таблица истинности для этой логической схемы:
| x | y | z | f | ||
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 |
Пример 5. Найдите булеву функцию логической системы и создайте таблицу истинности для этой системы.
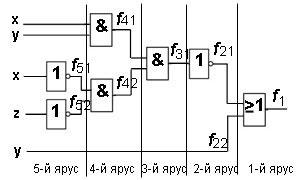
Решение. Разделите логическую схему на уровни. Структура этой логической схемы, в отличие от предыдущих примеров, имеет 5 уровней вместо 4. Но одна входная переменная – самая нижняя – проходит через все уровни и непосредственно входит в логический элемент на первом уровне. Выпишем все функции, начиная с уровня 1:
Давайте теперь выпишем все функции путем подстановки входных переменных x, y, z :
Результатом является функция, которую логическая схема реализует на выходе:
Таблица истинности для этой логической схемы:
| x | y | z | f | ||
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 |
Шаг 1. Давайте составим таблицу истинности
КОМБИНАТОРНАЯ ЛОГИКА
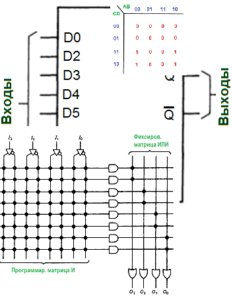
Любое обсуждение комбинаторной логики было бы неполным без рассмотрения логических тождеств, представленных ниже:
Логические тождества
AVC = (AV) C = A(OS)
AB = BA
AA = A
A1 = A
А0 = 0
A(B + C) = AV + AS
A + AB = A
A + C = (A + B)(A + C)
A + C + C = (A + C)
A + B = B + A
A + A = A
А + 1 = 1
A + 0 = A
1′ = 0
0′ = 1
A + A’ = 1
A’ = 0
(A’)” = A
A + A’IN = A + C
(A + C)” = A’ C’
(A’)” = A’ + B’
Большинство взаимосвязей очевидны. Последние две теоремы составляют теорему Моргана, наиболее важную для проектирования схем. Вы не можете использовать затворы (или другие схемы) с активным выходом для возбуждения шины. Это происходит потому, что они не могут быть отключены от общих линий данных.
Пример: исключающее ИЛИ. Следующий пример иллюстрирует использование логических тождеств. Мы построим схему исключающего ИЛИ с использованием обычных затворов. Таблица истинности для исключающего ИЛИ показана на рисунке ниже.
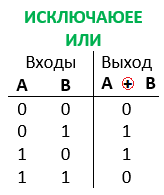
Проанализировав это и поняв, что “1” на выходе существует только тогда, когда (A, B) = (0,1) или (1,0), мы можем написать
Соответствующая схема реализации показана на рисунке
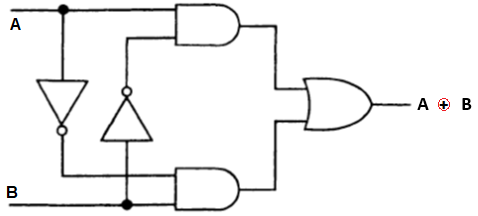
Внедрение клапана исключения операционной.
Однако эта реализация не является единственной. Используя логические тождества, находим, что
(На первом этапе мы добавили два значения, равные нулю, а на третьем применили теорему Моргана). Схематическая реализация для этого случая показана на рисунке
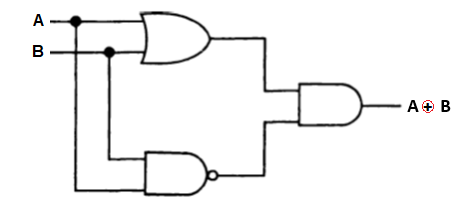
Еще одна реализация вентилятора “Исключающее ИЛИ”.
Однако эта реализация не является единственной. Используя логические тождества, находим, что
Минимизация и карты Карно
Поскольку логическая функция, даже такая простая, как исключительное ИЛИПоскольку логическая функция, даже простая, может быть реализована различными способами, часто необходимо найти самое простое решение, возможно, наиболее удобное схемное решение. Над этой проблемой бились многие просвещенные умы. В настоящее время существует несколько способов ее решения, в том числе алгебраические методы, реализуемые с помощью компьютера. Если количество входов не превышает четырех, лучшим методом является карта Карно. Этот метод также находит логическое выражение из таблицы истинности.
Проиллюстрируем этот метод на примере. Предположим, мы хотим построить мажоритарную схему подсчета голосов. Мы будем считать, что есть три входа, работающих в положительной логике, и выход (0 или 1). Каждый из входов может быть либо 1, либо 0. Выход равен 1, если 1 присутствует как минимум на двух входах.
Шаг 1. Составьте таблицу истинности
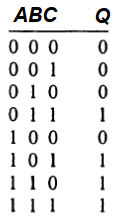
Это должно показать все возможные комбинации и соответствующие им состояния выхода (или выхода). В случае, когда состояние входа не влияет на выход, положите X (любое значение).
Шаг 2. Давайте создадим карту Карно. Это нечто очень похожее на таблицу истинности, но содержит переменные, расположенные вдоль двух осей. Переменные должны быть расположены таким образом, чтобы при переходе от каждого квадрата к соседнему изменялось состояние только одного входа.
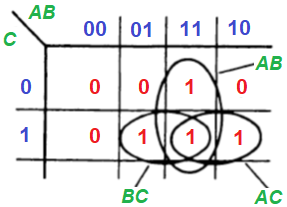
Шаг 3. Отметьте на карте группы, в которых находятся подразделения. Также можно использовать группы, содержащие нули. Три овала на рисунке определяют логические выражения AB, AC и БК. Тогда мы получаем требуемую функцию
Его схематическая реализация показана на рисунке:
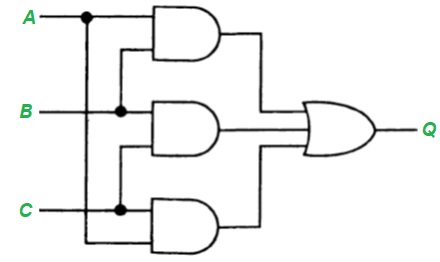
Этот результат кажется очевидным, когда он получен. Мы можем составить выражение для нулей и получить вместо этого
Q’ = A’B’ + A’C’ + B’C’
Это выражение может быть полезно, если в любых точках графика есть дополнения A’, B’ и С’.
Комментарии к картам Карно.
- Ищите группы, содержащие 2, 4, 8 и т.д. квадратов. Имеют простые логические выражения.
- Чем проще логика, тем больше будет описанный вами блок.
- Соедините края карты Карно. Например, карта на рисунке ниже описывается выражением Q=B’C.
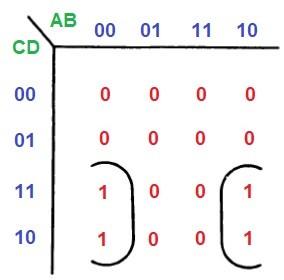
4 Блок “единиц”, содержащий один или два “нуля”, лучше всего описывается группировкой:
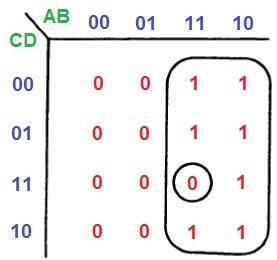
Этот блок соответствует логическому выражению Q = A (BCD)’.
5. места, содержащие X (любой стоимости) имеют “карт-бланш”. Поставьте в них “нули” или “единицы” так, чтобы получилась простейшая логика.
- Карта Карно может не привести к лучшему решению. Иногда более сложное логическое выражение имеет более простую реализацию в схеме. Например, когда некоторые члены выражения уже сформированы схемой в виде логических сигналов, которые могут быть использованы в качестве входов. Кроме того, реализация “Эксклюзивное ИЛИ” не следует однозначно из карты Карно. Наконец, ограничения на проектирование микросхем играют определенную роль в выборе структуры логической схемы. Например, когда в одном шасси установлено четыре 2-входных клапана. Когда программируемые логические устройства, такие как PML, используются для проектирования логических функций, их внутренняя структура ограничивает полную реализацию.
Комбинационные функциональные схемы, реализованные на стандартных ИС
Карты Карно можно использовать для построения логических схем, выполняющих достаточно сложные функции. Например, двоичное сложение и сравнение значений, контроль четности, мультиплексирование (выбор одного из нескольких входов, заданных двоичным адресом) и т.д. Фактически, наиболее часто используемые сложные функции реализуются в виде функциональных ИС со средней степенью интеграции (до 100 вентилей в корпусе). Хотя многие из этих ИС содержат триггеры, большинство из них имеют чисто комбинационные функции и состоят исключительно из вентилей.
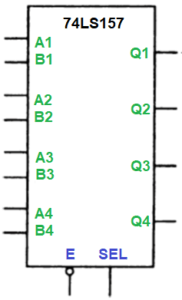2-входной квадратурный селектор
Когда на входе SEL (SEL на рисунке) низкий уровень, сигналы на выходы Q поступают с соответствующих входов A. Когда на входе SEL высокий уровень, они поступают со входа B. Когда на входе ENABLE (ENABLE- E на рисунке) высокий уровень, на всех выходах устройства принудительно устанавливается низкий уровень. Здесь просто таблица истинности, где X означает, что состояние данного входа не имеет значения, B-высокое, H-низкое.
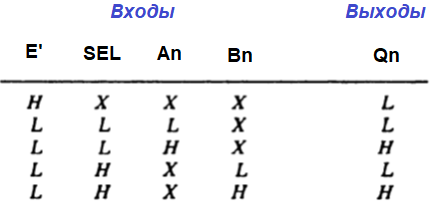
Таблица истинности селектора
Хотя в некоторых случаях функцию селектора может выполнять механический переключатель, затворы предпочтительнее по многим причинам. Клапанная схема имеет следующие преимущества:
(a) это менее затратно;
(b) он быстро и одновременно переключает все каналы;
c) Благодаря логическим сигналам, генерируемым в устройстве, переключение может происходить практически мгновенно;
d) Чтобы избежать помех и снижения уровня из-за емкости, лучше не передавать логические сигналы через кабели и переключатели. Поскольку переключающий клапан разблокирован уровнем напряжения постоянного тока, логические сигналы управления могут быть взяты с той же платы, на которой он расположен. Это уменьшает количество внешних соединений. Все, что необходимо, – это одна линия с нагрузкой, переключенная на землю с помощью однополюсного переключателя.
Этот метод управления логической схемой с помощью внешних уровней постоянного напряжения известен как “холодное переключение”.. Предпочтительнее прямое управление сигналами от переключателей, потенциометров и т.д. Помимо прочих преимуществ, холодное переключение позволяет шунтировать линии управления через конденсаторы. Это подавляет взаимные помехи, тогда как сигнальные линии обычно не могут быть зашунтированы конденсаторами.
Ворота передатчика. Из КМОП-элементов можно сконструировать “передающий клапан”. Это два комплементарных переключателя на MOSFET-транзисторах, соединенных параллельно. Через эти транзисторы подается входной (аналоговый) сигнал в диапазоне от 0 до Ucc, может либо подаваться непосредственно на выход через небольшое сопротивление (несколько сотен Ом), либо отсекаться (выходное сопротивление фактически бесконечно). Такие устройства являются двунаправленными. Для них нет разницы, какой выход используется как вход, а какой как выход. Передаточные затворы хорошо работают с цифровыми уровнями КМОП и широко используются в КМОП-схемах. На рисунке показана принципиальная схема четырехполюсного КМОП-ключа типа 4066.
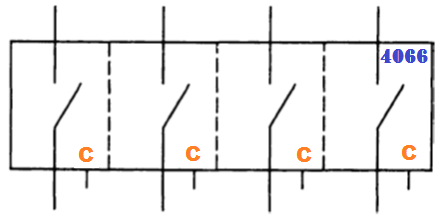
Двухсторонний квадрупольный ключ с двухсторонним квадрупольным ключом с двухсторонним квадрупольным ключом с двухсторонним квадрупольным ключом
Каждая клавиша имеет индивидуальный вход управления. Высокий уровень закрывает ключ, а низкий уровень открывает ключ. Затворы передатчика являются просто ключами, и поэтому не имеют возможности разветвления на выход. Они просто передают на вход логический уровень. Они не обеспечивают дополнительную несущую способность с возможностью усиления.
Эмиттерные затворы могут быть использованы для построения схем выборки 2 и более входов для цифровых уровней КМОП и аналоговых сигналов. Пучок эмиттерных затворов можно использовать для выбора одного из нескольких входов. Это делается путем генерирования управляющих сигналов с помощью декодера. Эта логическая функция используется настолько широко, что официально называется “мультиплексор”.
В начале каждого модуля есть карты маршрутов, В них указывается последовательность самостоятельного изучения теоретического материала, сроки выполнения практических и индивидуальных заданий, а также сроки промежуточных и итоговых тестов.
Руководство по изучению курса для студентов
В Модуль 1 Представлены основы булевой алгебры, принципы работы логического и арифметического устройств компьютеров, системы счисления и принципы перевода чисел из одной системы счисления в другую.
В Модуль 2 Модуль содержит материал по теме “Алгоритмические языки и программирование”, теоретические сведения, примеры программирования и варианты индивидуальных заданий.
В начале каждого модуля вы найдете карты маршрутов, Маршрутные карты определяют порядок самостоятельного изучения теоретического материала, сроки выполнения практических и индивидуальных заданий, сроки промежуточных и итоговых тестов.
Для независимой проверки своих знаний вам необходимо использовать интерактивное обучение.
Адрес электронной почты учебного сайта департамента:
http :// инф . tltsu . ru / рец. строгов /
Реализовано с помощью булевой функции .
Тема 5 Контактные и логические схемы
В начале прошлого века известный физик П. Эренфест впервые обратил внимание на возможность использования аппарата алгебры логики в технике. Эта идея была воплощена в работах советского физика В.И. Шестакова, американского математика С. Шеннон и японский инженер А. Какашима. Первыми приложениями булевой алгебры к техническим проблемам были контактные цепи. Под контактными цепями подразумеваются электрические цепи, содержащие только контакты. Каждый контакт может находиться в двух состояниях – разомкнутом (0) и замкнутом (1). Изобразим такие цепи схемой, на которой напишем или . Причем значение 1 этих переменных соответствует прохождению контакта, а значение 0 – нет.
Если контакт X и y соединены последовательно, цепь замкнута, когда оба контакта замкнуты, и разомкнута, когда хотя бы один из них разомкнут. Очевидно, что такая схема
соответствует булевой функции .
Если контакты X и y соединены параллельно, то цепь замкнута, когда хотя бы один контакт замкнут, и разомкнута, когда оба контакта разомкнуты. Очевидно, что в такой схеме.
соответствует булевой функции .
Это соответствие позволяет представить любую булеву функцию в виде контактной цепи. С другой стороны, любая контактная цепь с последовательно или параллельно соединенными контактами реализуется булевой функцией. Задача анализа контактной диаграммы заключается в построении соответствующей булевой функции.
Например, контактная цепь
реализуется булевой функцией .
Однако, поскольку одна и та же булева функция может быть выражена разными формулами, ее реализация контактными схемами неоднозначна. Всегда можно построить множество различных контактных схем, соответствующих заданной функции. Такие схемы называются эквивалентными схемами. Задача проектирования контактных цепей заключается в построении контактной цепи в соответствии с заданной булевой функцией, которая может быть задана либо формулой, либо таблицей. В обоих случаях необходимо выразить функцию с помощью операций конъюнкции, дизъюнкции и отрицания. Каждая операция соединения соответствует последовательному соединению контактов. Параллельное соединение приводит к возникновению контактной цепи. Из набора эквивалентных схем, упрощая формулы, выбирается самая простая схема. Центральной проблемой в синтезе контактных схем является построение более простой схемы для заданной булевой функции. Эта задача часто сводится к минимизации булевых функций, то есть к такому представлению, при котором соответствующие формулы содержат минимальное количество вхождений переменных.
Эта схема реализуется по следующей формуле:
Давайте упростим эту формулу. Используя закон делимости, получаем:
Следовательно, эту схему можно упростить, заменив ее следующей эквивалентной схемой:
Теперь давайте решим следующую задачу: составьте из контактов как можно более простую цепь, чтобы она замыкалась тогда и только тогда, когда хотя бы два контакта закорочены.
Составьте таблицу истинности для булевой функции, которая соответствует требуемой контактной схеме
Читайте далее: