Топология электрической цепи (Лекция N 2) - услуги электромонтажа, строительства и ремонта

Для определения матрицы В из известной матрицы А=А Д А С, где А Д – подматрица, соответствующая ветвям определенного дерева, А С – подматрица, соответствующая ветвям связи, отношение В= (-А T C А -1T D 1).

Содержание

Как определить количество ветвей в цепи?

Электрическая цепь характеризуется комбинацией элементов, из которых она состоит, и способом их соединения. Сочетание элементов в электрической цепи наглядно представлено схемой. Возьмем две электрические цепи (рис. 1 и 2), введем понятие ветви и узла.

Ветка это участок цепи, который питается одним и тем же током.
Узел – Перекресток, где соединяются три или более ветвей.

Показанные схемы различаются как по форме, так и по назначению, но каждая схема содержит 6 ветвей и 4 узла, соединенных одинаковым образом. Поэтому с точки зрения геометрии (топологии) соединений ветвей эти схемы идентичны.

Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, составляющих ветвь. Поэтому полезно представлять каждую ветвь схемы в виде отрезка линии. Если заменить каждую ветвь на рисунках 1 и 2 отрезком прямой, то получится геометрическая фигура, показанная на рисунке 3. 3.

Фиктивное изображение цепи, в котором каждая ветвь заменена отрезком линии, называется схема электрической цепи. Обратите внимание, что ветви могут состоять из нескольких элементов, которые, в свою очередь, связаны друг с другом различными способами.

Отрезок прямой, соответствующий ветви цепи, называется ветвь графа. Точки границ ветвей графа называются узлы графа. Ветвям графа можно придать определенную ориентацию, обозначаемую стрелкой. Граф, в котором все ветви ориентированы, называется целевой.

Подграф графа – это часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, или любое множество ветвей и узлов, содержащихся в графе.

В теории электрических цепей важны следующие подграфы:

1. путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, и каждая ветвь и узел встречаются только один раз на этом пути. Например, в диаграмме на рисунке 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3 . Таким образом, путь – это совокупность ветвей, проходящих непрерывно.

2 Контур – это замкнутый путь, в котором один из узлов является начальным узлом и конечным узлом пути. Например, для графа на рисунке 3 мы можем определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4 . Если между любой парой узлов графа существует связь, мы называем граф связным.

3 Дерево – это связный подграф, содержащий все узлы графа, но без контуров. Примерами деревьев для графа на рисунке 3 могут быть фигуры на рисунке 4.

Соединение ветвей (дополнения к дереву) – это ветви графа, которые завершают дерево до исходного графа.

Если граф содержит m узлов и n ветвей, то число ветвей любого дерева равно , а число соединительных ветвей графа равно .

5 Перекрестный график – это множество ветвей, удаление которых разбивает граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.

Поперечное сечение можно представить визуально как след некоторой замкнутой поверхности, пересекающей соответствующие ветви. Примерами таких поверхностей являются, для нашего графика на рис. 3 S 1 и S 2 . Здесь мы имеем, соответственно, сечения, образованные ветвями 6-4-5 и 6-2-1-5 .

С понятием дерева связаны понятия основных контуров и ветвей:

основной контур – Контур, состоящий из ветвей дерева и только одной соединительной ветви;
основной раздел – участок, состоящий из соединительных ветвей и только одной ветви дерева.

Топологические матрицы

Трудно дать компьютеру изображение топологии схемы, поскольку не существует эффективных программ распознавания изображений. Поэтому топология схемы вводится в компьютер в виде матриц, называемых топологические матрицы. Существует три таких матрицы: матрица узлов, матрица контуров и матрица сечений.

1. матрица узлов (матрица связей) – это массив коэффициентов уравнений, основанных на первом законе Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.

Для схемы на рис. 3 имеем число узлов m =4 и число ветвей n =6. Тогда запишем матрицу A H Предположим, что элемент матрицы (i – номер строки; j – номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если она ориентирована на него, и 0, если ветвь j не соединена с узлом i. Ориентируя ветви графа на рис. 3, получаем

Эта матрица A H записывается для всех четырех узлов и называется неопределенным. Следует отметить, что сумма элементов столбцов матрицы A H всегда равен нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные – нули.

Обычно один (любой) обосновывается в расчете. Затем мы приходим к матрице узлов А (сокращенная матрица), которая может быть получена из матрицы A H вычеркнув любой из его рядов. Например, если мы вычеркнем строку “4”, то получим

Количество строк матрицы А равно числу независимых уравнений для узлов , то есть числу уравнений, которые необходимо записать для электрической цепи в соответствии с первым законом Кирхгофа. Таким образом, вводится понятие матрицы узлов А мы приходим к первому закону Кирхгофа.

Первый закон Кирхгофа

Первый закон Кирхгофа обычно пишут для узлов цепи, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. соотношение

где – вектор плотности тока; – нормаль к сегменту dS замкнутой поверхности S .

Первый закон Кирхгофа также справедлив для любого сечения. В частности, для участка S 2 графа на рис. 3, предполагая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, мы можем написать

Поскольку в этом случае ветви поперечного сечения сходятся к узлу, первый закон Кирхгофа справедлив и для него. Пока что мы будем применять первый закон Кирхгофа для узлов, который математически можно записать как

т.е. алгебраическая сумма токов ветвей, подключенных к узлу, равна нулю.

Следовательно, в расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов, один (любой) из них будет линейно зависим от остальных, т.е. не дает никакой дополнительной информации.

Введем столбцовую матрицу токов ветвей

Тогда первый закон Кирхгофа в матричной нотации имеет вид

– где O – матрица с нулевым столбцом. Как мы видим, матрица, взятая в качестве узла, имеет вид А, вместо A H так как, следовательно, уравнения по первому закону Кирхгофа записаны для (m-1) узлов.

В качестве примера, для схемы на рис. 3

Следовательно, для первого узла мы получаем

которая должна выдержать.

Контурная матрица (контурная матрица) – это массив коэффициентов комплексных уравнений в соответствии со вторым законом Кирхгофа. Строки контурной матрицы B соответствуют контурам, а столбцы – ветвям схемы.

Элемент b ij матрицы В равен 1, если ветвь j входит в контур i и ее ориентация соответствует направлению контура, -1, если она не соответствует направлению контура, и 0, если ветвь j не входит в контур i.

Матрица Внаписанный для основных контуров, называется матрица основных контуров. В этом случае направление ветви связи этого контура принимается за направление обхода контура. В нашем примере (см. рисунок 5) дерево, образованное ветвями 2-1-4 запишем коэффициенты для матрицы В .

Теперь перейдем ко второму закону Кирхгофа.

Напряжение в определенной части электрической цепи – это разность потенциалов между конечными точками этой части, т.е.

Просуммируем напряжения на ветвях цепи:

Поскольку потенциал каждой точки и цепи встречается дважды, один раз с “+”, а второй раз с “-“, общая сумма равна нулю.

Поэтому второй закон Кирхгофа математически записывается как:

– и имеет следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) цепи равна нулю. При расчете цепей по законам Кирхгофа независимые уравнения записываются в соответствии со вторым законом Кирхгофа, т.е. уравнения записываются для цепей, каждая из которых отличается от других хотя бы одной ветвью. Значение топологического термина “дерево”: дерево позволяет создавать независимые цепи и ветви, и, таким образом, создавать независимые уравнения по законам Кирхгофа. Таким образом, задав (m-1) уравнений, заданных по первому закону Кирхгофа, мы получаем систему уравнений, равную числу ветвей цепи, а значит, токи, протекающие в них, находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

Тогда второй закон Кирхгофа в матричной нотации выглядит следующим образом

В качестве примера для схемы на рис. 5 имеем

где, например, для первой цепи мы имеем

как и должно быть.

Если мы введем столбцовую матрицу потенциалов узлов

и потенциал последнего узла, матрица напряжений ветвей и потенциалов узлов связана соотношением

где A T – матрица транспонирования узлов.

Для определения матрицы В по известной матрице А=А Д А С, где А Д – подматрица, соответствующая ветвям определенного дерева, A C – подматрица, соответствующая ветвям связей, отношение В= (-А T C А -1T D 1).

3 Матрица сечений – массив коэффициентов комплексных уравнений по первому закону Кирхгофа для сечений. Его строки соответствуют разделам, а столбцы – ветвям графа.

Матрица Q которая рассчитывается для главных сечений, называется матрица главных сечений. Количество строк матрицы Q равно числу независимых сечений.

Элемент q ij матрицы Q равен 1, если ветвь входит в i-й сегмент и ориентирована в соответствии с направлением этого сегмента (положительное направление сегмента – это направление входящей в него ветви дерева), -1, если она ориентирована противоположно направлению сегмента, и 0, если ветвь j не входит в i-й сегмент.

В качестве примера рассмотрим матрицу Q главных отрезков для схемы на рис. 5. Для ориентации ветвей, указанных на рис. 5, имеем

В заключение следует отметить, что для топологических матриц А, В и Q Следующие соотношения применимы к матрицам для одного и того же графа

которые, в частности, могут быть использованы для проверки корректности этих матриц. Здесь 0 – является нулевой матрицей порядка .

Приведенные выше уравнения позволяют сделать важный вывод: зная одну из топологических матриц, мы можем восстановить остальные по ее структуре.

1. Теоретический Основы электротехники. Том 1. Основы теории линейных цепей / под редакцией P.A. Ионкин. Пособие для институтов электротехники. Издание 2-е, переработанное и дополненное (на русском языке) – М.: Высшая школа, 1976.

2. Матханов Х.Н.. Основы анализа электрических цепей. Линейные цепи: Учебник для специальности “Электро- и радиотехника”. Анализ электрических и электронных цепей: учебник для специальностей электро- и радиотехники, 1990 г. -400с.

3. Основы Основы теории цепей: учебник для средних школ / Г.В. Зивеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. -Пятое издание, пересмотренное. -М.: Энергоатомиздат, 1989. -528с.

Контрольные списки и задания.

Сформулировать основные топологические понятия электрических цепей.
Что такое контурная матрица?
Что такое контурная матрица?
Что такое матрица сечений?
Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:

Реконструируя граф схемы, составьте матрицы главных контуров и сечений, предполагая, что ветвям дерева присвоены простые номера.

Эта энергия не может быть преобразована в тепловую энергию, но существует в контуре как своего рода резерв. Если между проводами нет напряжения, то в цепи нет запаса энергии электрического поля.
Значение емкости С определяется как отношение электрического заряда q одного из проводников к напряжению u между ними и измеряется в фарадах (F):

Графическое представление электрической цепи и ее компонентов

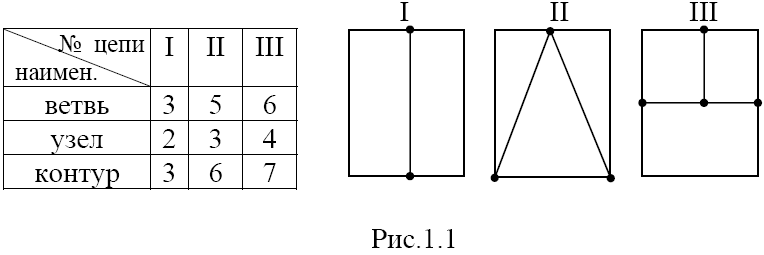
Графическое представление электрической цепи называется принципиальная схема .. Цепь состоит из ветвей, узлов и контуров. Ветка – является частью цепи, состоящей только из источников и потребителей, соединенных последовательно. Узел – Точка в цепи, в которой сходятся не менее трех ветвей (ветви начинаются и заканчиваются в узлах цепи). Контур – Часть схемы, образованная ветвями; количество петель определяется количеством изменений в ветвях схемы. На рисунке 1.1 показаны структурные схемы трех электрических цепей и указано количество узловых ветвей и контуров в каждой цепи.

Схемы основных элементов схемы, принятые в данном учебнике, показаны на рисунке 1.2.

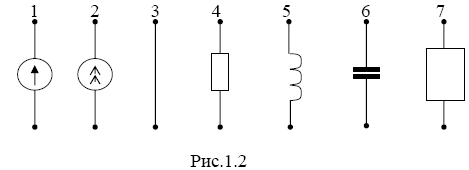
На рис: 1 – источник ЭДС; 2 – источник тока; 3 – соединительный провод; 4 – сопротивление R цепи; 5 – индуктивность L цепи; 6 – емкость C цепи; 7 – двухполюсник (цепь неизвестной структуры, имеющая две входные клеммы).

В цепях постоянного тока (рис. 1.3, а) направление ЭДС источника обычно задается в направлении клеммы, на которой генерируются положительные заряды. Направление тока во внешней цепи обычно указывается от положительно заряженного полюса (клеммы) источника к отрицательно заряженному полюсу. Направление напряжения на приемнике всегда указывает в ту же сторону, что и направление тока.
В цепях синусоидального тока (рис. 1.3,б) принято обозначать направления тока и напряжения ЭДС с помощью положительного полупериода тока, при котором ток не меняет своего направления. Схема этих направлений похожа на схему постоянного тока.

Законы электрических цепей

Суть расчета, как правило, заключается в определении токов во всех ветвях и напряжений через все элементы (резисторы) цепи на основе известных значений всех сопротивлений цепи и параметров источника (ЭДС или тока).

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Суть расчета обычно сводится к определению токов во всех ветвях и напряжений через все элементы (резисторы) цепи по известным значениям всех сопротивлений цепи и параметров источника (ЭДС или тока).

Для расчета электрических цепей постоянного тока можно использовать различные методы. Основными из них являются :

– Метод, основанный на уравнениях Кирхгофа;

– Метод эквивалентного преобразования;

– Метод контурного тока;

– Метод узловых потенциалов;

– Метод эквивалентного источника;

Метод, основанный на методе уравнений Кирхгофа, является универсальным и может быть применен как к одноконтурным, так и к многоконтурным схемам. В этом случае число комплексных уравнений согласно второму закону Кирхгофа должно быть равно числу внутренних контуров схемы.

Число уравнений по первому закону Кирхгофа должно быть на единицу меньше, чем число узлов в цепи.

Например, для данной цепи

2 уравнения по 1-му закону Кирхгофа и 3 уравнения по 2-му закону Кирхгофа.

Рассмотрите другие методы расчета электрических цепей:

Метод эквивалентных преобразований используется для упрощения схем и расчета электрических цепей. Под эквивалентным преобразованием понимается такая замена одной цепи на другую, при которой электрические величины цепи в целом не изменяются (напряжение, ток, потребляемая мощность остаются неизменными).

Давайте рассмотрим некоторые виды преобразования эквивалентных схем.

a). последовательное соединение элементов

Общее сопротивление последовательно соединенных элементов равно сумме их сопротивлений.

b). Параллельное соединение элементов.

Рассмотрим два параллельно соединенных элемента R1 и R₂ . Напряжения на этих элементах равны, поскольку они подключены к одним и тем же узлам a и b.

Используя закон Ома, получаем

Применим первый закон Кирхгофа к переходу (a)

Выразите токи I₁ и я₂ по напряжениям получаем

В соответствии с законом Ома имеем I=U_AB / R_Э где R_Э – эквивалентное сопротивление

Исходя из этого, мы можем написать

Введем следующие обозначения: 1/R_Э=G_Э – эквивалентная проводимость

Запишем уравнение (6) в следующей форме

Из этого выражения следует, что эквивалентная проводимость параллельно соединенных элементов равна сумме проводимостей элементов.

Исходя из (3.13), получаем эквивалентное сопротивление

в). Преобразование сопротивления треугольника в эквивалент звезды и обратное преобразование.

Подключение трех элементов цепи R₁ , R₂ , R₃ в виде трехлучевой звезды с общей точкой (узлом) называется звездным соединением, а соединение тех же элементов, когда они образуют стороны замкнутой дельты, называется дельта-соединением.

соединение звездой ( ) соединение треугольником ( )

Преобразование треугольника импеданса в эквивалентную звезду происходит по следующему правилу и с помощью следующих коэффициентов:

Сопротивление эквивалентного пучка звезды равно произведению сопротивлений двух соседних сторон треугольника, деленному на сумму всех трех сопротивлений треугольника.

(3.15)

Преобразование сопротивления звезды в эквивалентный треугольник производится по следующему правилу и коэффициентам:

Сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух соседних лучей звезды плюс произведение этих двух сопротивлений, деленное на сопротивление третьего луча:

(3.16)

г). Преобразование источника тока в эквивалентный источник ЭДС При наличии в цепи одного или нескольких источников тока часто необходимо заменить источники тока на источники ЭДС для упрощения расчетов

Пусть источник тока имеет параметры I_К и G_HV .

Е_Э

Параметры эквивалентного источника ЭДС могут быть определены из следующего соотношения

При замене источника ЭДС на эквивалентный источник тока должны использоваться следующие зависимости

Метод контурного тока.

Этот метод обычно используется при расчете многоконтурных схем, когда число комплексных уравнений по I и II законам Кирхгофа равно шести и более.

Для схемного метода внутренние цепи сложной схемы определяются и нумеруются. В каждой цепи случайным образом выбирается направление контурного тока, т.е. тока, который замыкается только в этой цепи.

Затем для каждой цепи составляется уравнение в соответствии со 2-м законом Кирхгофа. В этом случае, если сопротивление принадлежит одновременно двум соседним цепям, напряжение на нем определяется как алгебраическая сумма напряжений, создаваемых токами каждой из этих двух цепей.

Если число схем равно n , то уравнений будет n. Решая эти уравнения (путем подстановки или определения), получают значения циркулирующих токов. Затем, используя уравнения, записанные в соответствии с 1-м законом Кирхгофа, найдите токи в каждой ветви цепи.

Запишем уравнения контура для этой цепи.

Для первого круга:

Для 2-го контура

Для 3-го округа

Используя преобразование, запишем систему уравнений в виде

Решая эту систему уравнений, мы определяем неизвестные I₁ , I₂ , I₃. Токи ветвей определяются с помощью уравнений

Этот метод основан на принципе суперпозиции и используется для схем с несколькими источниками электрической энергии. Согласно этому методу, при расчете цепи, содержащей несколько источников электроэнергии, все ЭМП поочередно принимаются равными нулю. В свою очередь, все ЭМП, кроме одного, принимаются равными нулю. Рассчитываются токи в цепи, создаваемые этой ЭДС. Расчет выполняется отдельно для каждой ЭДС, содержащейся в цепи. Фактические токи в отдельных линиях цепи определяются как алгебраическая сумма токов, генерируемых независимым действием каждой ЭДС.

Пример:

На рис. 3.19 исходная схема, а на рис.3.20 и рис.3.21 схема заменена одним источником в каждой.

Токи в ветвях исходной цепи задаются формулами;

Метод узловых потенциалов

Метод узловых потенциалов позволяет сократить число уравнений с общим решением до U – 1, где U – число узлов в схеме замещения. Он основан на первом законе Кирхгофа:

(1) Предполагается, что один узел в цепи является базой с нулевым потенциалом. Это предположение не изменяет значения токов ветвей, поскольку – ток в каждой ветви зависит только от разности потенциалов узлов, а не от фактических значений потенциалов;

(2) Для оставшихся U – 1 узлов мы строим уравнения в соответствии с первым законом Кирхгофа, выражая токи ветвей через потенциалы узлов.

В этом случае коэффициент в левой части уравнений при потенциале рассматриваемого узла положителен и равен сумме проводимостей сходящихся к нему ветвей.

Коэффициенты при потенциалах узлов, соединенных ветвями с рассматриваемым узлом, отрицательны и равны проводимостям соответствующих ветвей. Правая часть уравнений содержит алгебраическую сумму токов ветвей с источниками тока и токов короткого замыкания ветвей с источниками ЭДС, сходящихся к рассматриваемому узлу. Суммы берутся со знаком плюс (минус), если источник тока и ЭДС направлены к рассматриваемому узлу (от узла).

Решая систему уравнений, мы определяем потенциалы U-1 относительно фундаментальных узлов, а затем токи ветвей, используя обобщенный закон Ома.

Рассмотрим применение этого метода на примере расчета схемы согласно рис. 3.22.

Для решения методом узловых потенциалов мы предполагаем, что .

Система узловых уравнений: количество уравнений N = N_y – N_B -1,

где: N_y = 4 – количество узлов

N_B = 1 – число вырожденных ветвей (ветви с 1 источником ЭМП),

Т.е. для этой схемы: N = 4-1-1-1=2.

Для узлов (2) и (3) составляем уравнения в соответствии с первым законом Кирхгофа;

I2 – I4 – I5 – J5=0; I4 + I6 -J3 =0;

Представим токи ветвей по закону Ома через узловые потенциалы:

I2 = (φ2 – φ1) / R2 ; I4 = (φ2 +E4 – φ3) / R4

I5 = (φ2 – φ4) / R5 ; I6 = (φ3 – E6 – φ4) / R6;

Где,

Подставляя эти выражения в уравнения узловых токов, получаем систему;

где ,

Решая систему уравнений численно методом подстановки или разложения, мы находим потенциалы узлов, а из них получаем напряжения и токи ветвей.

Метод эквивалентного источника (активный биполярный)

Биполярная цепь – это цепь, которая подключена к внешнему компоненту через две точки, полюса. Различают активные и пассивные биполярные устройства.

Активная биполярная цепь содержит источники электричества, пассивная биполярная цепь – нет. Биполярные символы представлены прямоугольником, в котором A обозначает активный, а P – пассивный (Рисунок 3.23).

Для расчета схем с двухполюсниками последние представляются эквивалентной схемой. Эквивалентная схема линейного двухполюсника определяется его вольт-амперной или внешней характеристикой V (I ). Вольт-амперная характеристика пассивного двухполюсника представляет собой прямую линию. Поэтому его эквивалентная электрическая схема представлена резистивным элементом с сопротивлением:

Где: U – напряжение между клеммами, I – ток, а rvx – входное сопротивление.

Вольт-амперная характеристика активного двухполюсника (рис. 3.23, б) может быть определена в двух точках, соответствующих состоянию холостого хода, т.е. при r_н = °, U = U_хI = 0, и короткое замыкание, т.е. при d_н =0, U = 0, I = Ic. Эта характеристика и ее уравнение выглядят следующим образом:

где: r_eq – эквивалентный или выходной импеданс двухполюсника, совпадающий с характеристикой

Одновибрационные характеристики и уравнение источника питания показаны на эквивалентных диаграммах на рис. 3.23.

Таким образом, активный двухполюсник представлен эквивалентным источником с ЭДС – E_eq = U_х и внутреннее сопротивление – r_ek = г_{за пределами} (Рис. 3.23, a) Пример активного двухполюсника. Если ток изменяется в диапазоне 0<><>_к активный двухполюсник отдает энергию во внешнюю цепь. При токе 1<0 он получает энергию от внешней цепи. Это возможно, если участок внешней цепи, содержащий необходимые источники энергии, подключен к клеммам a-b двухполюсника. При U<0 резисторы активного двухполюсника получают питание от внешней цепи и самого активного двухполюсника.

Если нагрузка с сопротивлением нагрузки r_н подключен к активному двухполюснику, его ток определяется методом эквивалентного источника:

В качестве примера рассмотрим расчет тока I в цепи на рисунке 3.24, используя метод эквивалентного источника. Для расчета напряжения холостого хода U_х Разомкните ветвь между клеммами а и Ъ активной двухполюсной цепи с резистивным элементом d_н (рис. 3.24, б).

Применяя метод суперпозиции и учитывая симметрию диаграммы, получаем

U_х =J r / 2 + E / 2

Заменив источники энергии (в данном примере источники ЭДС и тока) активного биполя резистивными элементами с сопротивлениями, равными внутренним сопротивлениям соответствующих источников (в данном примере нулевое сопротивление для источника ЭДС и бесконечное сопротивление для источника тока), получим выходное сопротивление (сопротивление, измеренное на контактах a и b) r_{за пределами} = r/2 (рис.3.24, в). Согласно (3.21) требуемый ток:

I = (J d / 2 + E / 2) / (d_н + r / 2) .

Определение максимальной передачи энергии приемнику

В устройствах связи, электронике, автоматизации и т.д. Часто желательно передать как можно больше энергии от источника к приемнику (приводу), при этом эффективность передачи имеет второстепенное значение из-за малого количества энергии. Рассмотрим общий случай питания приемника от активного двухполюсника, на рис. 3.25 последний представлен эквивалентным источником с ЭДС E_eq и внутреннее сопротивление d _{eq .}.

Определим мощность Pn и PE и энергоэффективность:

Для двух предельных значений сопротивления r_н = 0 и r_н = °° мощность приемника равна нулю, так как в первом случае напряжение между клеммами приемника равно нулю, а во втором случае ток в цепи равен нулю. Отсюда следует, что для данного значения rn_н является максимально возможным (с учетом e_eq и г_ek) мощности приемника. Чтобы определить это значение сопротивления, приравняем первую производную от мощности p_н при р_н и получаем:

из чего следует, что при условии

мощность приемника будет максимальной:

Уравнение (1.38) называется условием максимальной мощности приемника, т.е. максимальной передачи энергии.

Рис. 3.26 Соотношения Pn,PE, U_н и η в зависимости от силы тока I.

ТЕМА 4: ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Переменный ток – это электрический ток, направление и амплитуда которого периодически меняются. Если переменный ток изменяется синусоидально, он называется синусоидальным, если нет – несинусоидальным. Электрическая цепь, в которой протекает такой ток, называется цепью переменного (синусоидального или несинусоидального) тока.

Электрооборудование переменного тока широко используется в различных отраслях экономики, таких как производство, передача и преобразование электроэнергии, электроприводы, бытовая техника, промышленная электроника, радиотехника и т.д.

Существует множество причин, по которым устройства, использующие синусоидальный ток, получили такое широкое распространение в электротехнике.

Современное производство энергии основано на передаче энергии на большие расстояния с помощью электрического тока. Одним из необходимых условий является то, что ток может быть легко преобразован с незначительными потерями энергии. Этого можно достичь только с помощью электрических устройств переменного тока – трансформаторов. В настоящее время синусоидальный ток является основным источником тока, используемым в электротехнической промышленности, благодаря большим преимуществам преобразования энергии.

Основным стимулом для развития технологии синусоидального тока является возможность генерировать высокие уровни электрической мощности. Современные турбогенераторы на тепловых электростанциях имеют мощность от 100 до 1500 МВт на единицу, а генераторы на гидроэлектростанциях обладают высокой производительностью.

Самыми простыми и дешевыми электродвигателями являются асинхронные синусоидальные двигатели переменного тока, которые не имеют подвижных электрических контактов. Стандартная частота 50 Гц (60 Гц в США) принята в электроэнергетических установках (особенно на всех электростанциях) в России и в большинстве мест в мире. Причины такого выбора просты: более низкая частота неприемлема, поскольку даже при 40 Гц лампочки заметно мигают на глаз; более высокая частота нежелательна, поскольку пропорционально частоте увеличивается индукция ЭМП, что отрицательно сказывается на передаче энергии” и работе многих электроприборов. Однако эти соображения не ограничивают использование переменного тока на других частотах для различных технических и научных применений. Например, частота синусоидально переменного тока в электропечах для плавки тугоплавких металлов достигает 500 Гц.

Высокочастотные (мегагерцовые) устройства используются в радиоэлектронике, поскольку на этих частотах увеличивается излучение электромагнитных волн.

В зависимости от количества фаз цепи переменного тока делятся на однофазные и трехфазные.

В этом методе в каждую независимую цепь вместо реальных токов ветвей вводится ток обычной цепи. Фактический ток в любой ветви, принадлежащей одной цепи, численно равен току цепи. Фактический ток в любой ветви, принадлежащей нескольким цепям, равен алгебраической сумме токов цепей, проходящих через эту ветвь.

Методы расчета сложных электрических цепей

Сложная цепь – это цепь с несколькими источниками электрической энергии. Применение метода эквивалентного преобразования к таким схемам обычно неэффективно, поскольку не позволяет упростить их до одно- или двухузловой системы. Для расчета этих цепей используются более общие методы.

Прямое применение законов Кирхгофа

Этот метод предполагает выведение системы уравнений, применяющих первый и второй законы Кирхгофа к заданной электрической цене, решение которых позволяет определить токи ветвей цепи.

Как и любой другой метод расчета сложной электрической цены, этот метод начинается с первоначального анализа схемы цепи для определения количества узлов. 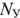количество филиалов 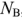количество независимых контуров 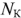количество филиалов 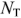источники тока, и посмотрите, можно ли упростить схему.

Сначала определяется количество неизвестных токов, которое равно 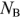— 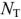. Для каждой ветви указано положительное направление тока.

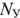
Тогда в соответствии с первым законом Кирхгофа они образуют – 1 независимых уравнений.

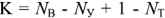
Тогда по второму закону получаются уравнения. Выберите независимые цепи, не содержащие источников тока.

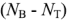
Общее число, образуемое первым и вторым законами Кирхгофа, должно быть равно числу неизвестных токов.

Рассмотрим применение законов Кирхгофа для определения токов в ветвях цепи, показанной на рисунке 1.25. Пусть ЭДС идеальных источников напряжения 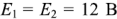, сопротивления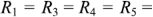 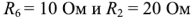. Все токи в цепи должны быть определены путем прямого применения законов Кирхгофа.

Схема содержит 6 ветвей с неизвестными токами и четыре узла. Узлы обозначены арабскими цифрами, предполагаемые направления токов и направления обхода контуров A, B и C показаны на схеме.

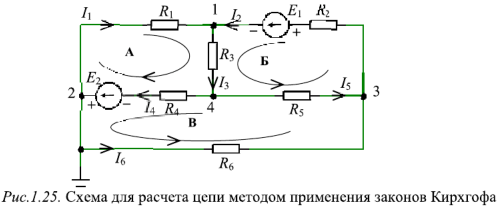
Составим систему из 6 уравнений. Напишите уравнения по первому закону Кирхгофа для узлов 1, 2, 3 и уравнения по второму закону Кирхгофа для контуров A, B, C:

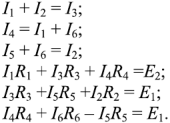
Решив эту систему уравнений, получим 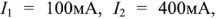. Отрицательное значение тока 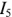указывая на то, что выбранное в уравнениях направление этого тока не соответствует действительности. Правильное направление – от узла 3 к узлу 4.

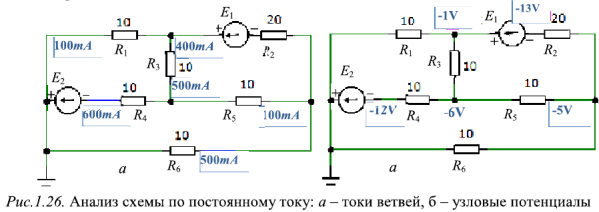
Для проверки расчетов был проведен анализ цепи постоянного тока, показанной на рис. 1.25, с помощью программы моделирования цепей Micro Sar. Токи ветвей (в мА), показанные на рис. 1.26,а, подтверждают правильность наших расчетов. Единичные потенциалы цепи (в В), показанные на рис.1.26,б, позволяют определить направление токов ветвей.

Метод контурного тока

Метод контурных токов наиболее часто используется на практике для расчета сложных цепей, так как он позволяет найти все неизвестные, когда число уравнений меньше числа неизвестных.

В этом методе в каждую независимую цепь вводится условный контурный ток вместо реальных токов в ветвях. Реальный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току. Фактический ток в любой ветви, принадлежащей более чем одной цепи, равен алгебраической сумме токов цепей, проходящих через эту ветвь.

Уравнения для расчета токов контура разработаны в соответствии со вторым законом Кирхгофа. Все пассивные элементы цепи подвержены напряжению от собственных токов цепи, а в соседних элементах – от токов соседних цепей. Направление тока в независимой петле выбирается произвольно. Направление шунта обычно выбирается так, чтобы оно совпадало с направлением тока в контуре.

Падение напряжения на токе соседнего контура в элементе считается положительным, если направление тока соседнего контура совпадает с направлением шунта. Если направление тока соседнего контура не совпадает с направлением шунта, то падение напряжения принимается отрицательным. Значение ЭДС берется со знаком плюс, если направление обхода цепи совпадает с положительным направлением ЭДС, и со знаком минус, если оно не совпадает с положительным направлением ЭДС.

Метод контурного тока Рассмотрим пример схемы, показанной на рис. 1.27. Эта схема состоит из трех независимых контуров: A, B, C. Каждое сопротивление цепи имеет свой контурный ток 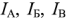. Направление каждой петли совпадает с направлением тока этой петли. ЭДС идеального источника напряжения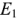 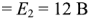, сопротивления 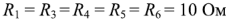и .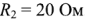

Уравнения, полученные из второго закона Кирхгофа для цепей A, B и C:

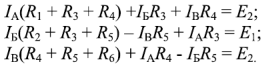
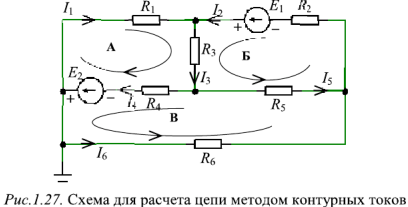
Подставляя численные значения ЭДС источников и сопротивлений в эту систему уравнений и решая ее, получаем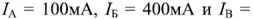

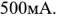
Эффективные токи ветвей цепи:

Полученные значения находятся в полном согласии с результатами более раннего расчета этой же величины методом прямого применения законов Кирхгофа.

Метод узловых потенциалов

Потенциал любой точки электрической цепи определяется напряжением между этой точкой и точкой цепи с потенциалом, равным нулю.

Метод узловых потенциалов заключается в том, чтобы сначала принять потенциал некоторого фундаментального узла равным нулю, а затем составить уравнения для остальных ( -1) узлов в соответствии с первым законом Кирхгофа: алгебраическая сумма токов всех ветвей, подключенных к рассматриваемому узлу, равна нулю. В этом случае токи ветвей, соединяющих узлы, определяются обобщенным законом Ома. Решая полученную таким образом систему уравнений, определяются потенциалы узлов.

Затем, применяя обобщенный закон Ома к ветвям, определяются необходимые токи.

Рассмотрим метод узловых потенциалов на примере цепи, показанной на рис. 1.28 (i). В этой цепи ЭДС идеальных источников напряжения 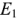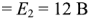, сопротивления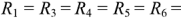 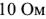и .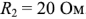

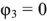
Схема имеет четыре узла. Предположим, что потенциал узла равен 3. Уравнения выполняются с использованием метода узловых потенциалов. Сумма токов узла 1 равна нулю. Ток каждой ветви, подключенной к узлу 1, записывается в соответствии с обобщенным законом Ома

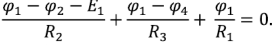
Аналогично для узла 2

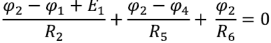
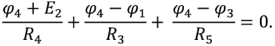
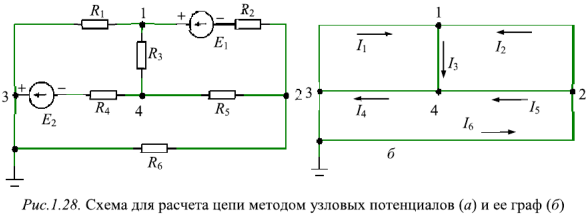
Подставляя численные значения ЭДС источников и сопротивлений в полученную систему уравнений и решая ее, получаем 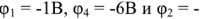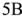. Результаты такие же, как на рис.1.26,6^, полученные программой Micro-Sar для анализа постоянного тока цепи, показанной на рис.1.28 а.

Применяя обобщенный закон Ома для каждой ветви цепи, мы получим искомые токи:

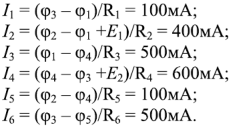
Полученные значения токов совпадают с результатами расчетов этой цепи методом прямого применения законов Кирхгофа и методом контурных токов.

Направления найденных токов отмечены на схеме на рисунке 1.28,6. Принципиальная электрическая схема – это представление электрической схемы, в которой все ветви заменены линиями, источники напряжения закорочены, а источники тока разомкнуты. Все ветви и все узлы поддерживаются.

Метод узловых потенциалов имеет преимущество перед методом циркулирующего тока, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа.

Метод двух узлов является специальной вариацией метода узловых потенциалов. Он применяется, когда анализируемая схема содержит только два узла (для определенности узлы 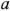и 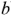) и большое количество параллельных ветвей с источниками ЭМП и без них. В соответствии с двухузловым методом, межузловое напряжение

где 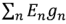– алгебраическая сумма произведений ветвей ЭДС (ЭДС считается положительной, если она направлена к узлу 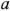и отрицательные, если они направлены от узла 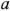к узлу 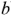) на проводимости этих ветвей; 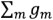– это сумма проводимостей всех ветвей, соединяющих узлы 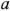и .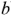

Эта теория взята со страницы помощи в решении задач по электротехнике:

Вы можете найти эти страницы полезными:

Образовательная страница для студентов и школьников

Копирование материалов возможно только после указания активной ссылки “www.lfirmal.com” в качестве источника.

Найти узлы, циклы и ветви
Задача состоит в том, чтобы найти количество узлов, ветвей и циклов в заданной схеме. Я насчитал 6 веток, 3 петли и.

Количество узлов в цепи

Просто из любопытства! Есть цепь (см. приложение), на практике в универе говорили, что количество узлов в данной цепи равно 2. Но, судя по определению узла (место соединения трех или более ветвей), узлов не 2, а 4! Где правда?

Сколько узлов и ветвей в цепи
Сколько узлов и ветвей в цепи?

Найти количество узлов, цепей и ветвей
Задача состоит в том, чтобы найти количество узлов, ветвей и циклов в цепи. Я насчитал 6 веток, 3 петли и.

Определите токи в цепи. Метод двух узлов. Поиск ошибки
Я провел много часов, пытаясь решить эту проблему. Используя метод двух узлов (решенная система линейных уравнений) и.

Сообщение от AK3RN.

Из ваших четырех “узлов” два являются виртуальными, поскольку они соединены ветвями с единичной проводимостью (нулевым сопротивлением). Другими словами, на них нет падения напряжения, они не отдают ток, в смысле потока энергии они физически не существуют (в оптической аналогии они полностью прозрачны).

(1) Узел, в котором сходятся две ветви, называется уникальным узлом, т.е. топологически это не узел.
2. ТопологическийНастоящий узел или нередуцируемый узел – это узел с тремя или более соединенными ветвями.
или несколько ветвей соединены.
Речь идет прежде всего о “топологически”, то есть схематически.
Но почему-то об узлах принято говорить спокойно,
между которыми нужно определить напряжение, в последовательной цепи.
Это не узлы – это точкино обладающий свойствами узла Кирхгофа.
Токи, втекающие и вытекающие из точки, равны, для всех намерений и целей.
Хотя это звучит банально, если не сказать безумно.
3 Обычная техника в электротехнике и электронике – “растянуть” узел так, чтобы на листе бумаги или в печатном виде схема “выглядела как”,
чтобы при печати или на листе бумаги диаграмма выглядела и печаталась хорошо и была читабельный.
Хотя даже со стороны это выглядит так, как будто третий узел “зажат” между двумя узлами.
4. В учебниках, в самом начале, говорится, что если между двумя точками или узлами нет сопротивления, источника или любого другого электрического элемента.
Сопротивление, источник или любой другой электрический элемент – это один узел или одна точка.
Это только для удобство в связи с R=0.

Таким образом, у вас есть два узла, и вы не сходите с ума, AK3RN вы не захотите об этом думать.

Количество узлов
Я не могу определить количество ветвей и узлов на диаграмме. Я знаю, что узлы являются пересечением трех “i”.

Количество ветвей и узлов
Утро. Люди, скажите, пожалуйста, сколько здесь ветвей и узлов.

Количество ветвей и узлов
Привет всем. В нем указано количество ветвей и узлов, но я сомневаюсь, что это правильно. Если вы ошиблись, пожалуйста, спросите.

Количество узлов и цепей
Добрый вечер, подскажите, пожалуйста, правильное ли у меня количество ветвей, 10 узлов, 4.

У вас наверняка возник вопрос: зачем мы проделали все эти манипуляции с исходной формой уравнения (-28 + E_R2 + E_R1)? Какая разница, выражено ли уравнение через напряжение или через ток (умноженный на сопротивление), ведь в обоих случаях последние два члена все равно неизвестны? Ответ на эти вопросы прост. Цель всех вышеперечисленных преобразований – получить второе уравнение закона Кирхгофа, используя те же неизвестные переменные, что и в первом уравнении закона Кирхгофа, поскольку это необходимое условие для решения любой системы уравнений. Чтобы найти значения трех неизвестных токов (I₁, I₂ и я₃) мы должны иметь три уравнения, соединяющие их вместе.

Как определить количество ветвей в цепи?

Метод токов ветвей

Первый и самый простой метод анализа цепей постоянного тока называется методом токов ветвей. В этом методе мы должны сначала определить направления токов в цепи, а затем написать уравнения, описывающие их взаимосвязь друг с другом, используя законы Кирхгофа и Ома. Получив уравнения для каждого из неизвестных токов, мы можем решить систему уравнений, вычислив таким образом все токи, а затем все напряжения в цепи.

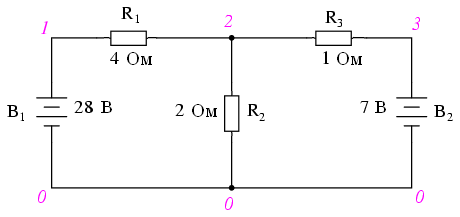
Для рассмотрения этого метода мы воспользуемся следующей схемой:

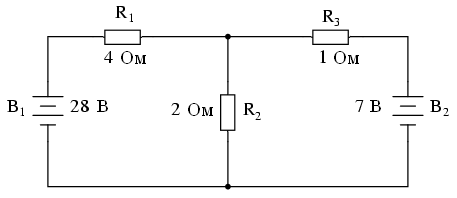
Первое, что нам нужно сделать, это выбрать узел в цепи (место соединения проводов), чтобы использовать его в качестве эталона для нахождения неизвестных токов. Выберем узел, соединяющий резистор R₁ справа, R₂ ниже и R₃ слева.

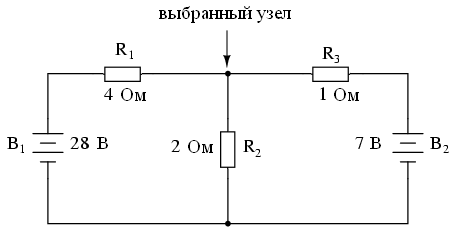
Теперь определите направления токов в проводах, прилегающих к этому узлу, обозначив их I₁, I₂ и я₃ соответственно. Обратите внимание, что эти направления будут только предполагаться. Если окажется, что наши предположения неверны, мы увидим это в математических расчетах (любые “неправильные” направления токов будут отображаться в виде отрицательных чисел).

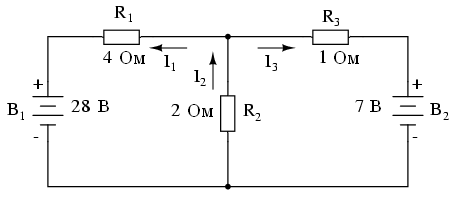
Согласно первому закону Кирхгофа, алгебраическая сумма токов, втекающих и вытекающих из узла, должна быть равна нулю, поэтому мы можем связать все токи нашей цепи (I₁, I₂ и я₃) друг с другом с помощью одного уравнения. Мы будем обозначать все токи, входящие в узел, знаком плюс, а все токи, вытекающие из узла, знаком минус:

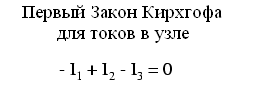
На следующем этапе обозначьте полюса напряжения на всех резисторах в соответствии с предполагаемыми направлениями токов. Конец резистора, куда втекает ток, будет отрицательным, а конец, куда он вытекает, будет положительным (электрон заряжен отрицательно и течет от минуса к плюсу):

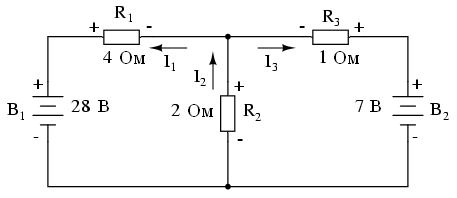
Полярность батареи обозначена в соответствии со стандартом (короткий конец отрицательный, длинный конец положительный). В некоторых случаях вы можете обнаружить, что полярность резисторов не совпадает с полярностью батареи, и ток течет обратно через батарею. Никакого вреда, это просто принятое направление тока. При этом помните, что установка полярности напряжений на резисторах и последующие расчеты должны производиться в соответствии с первоначально предполагаемыми направлениями тока. Как упоминалось ранее, если ваши предположения окажутся неверными, вы увидите это в окончательных результатах расчета (они будут отрицательными). Полученные значения все равно будут правильными.

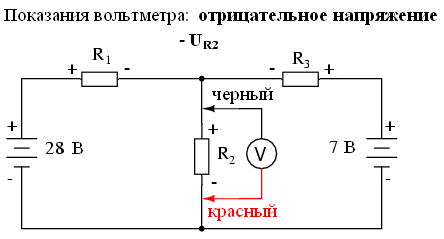
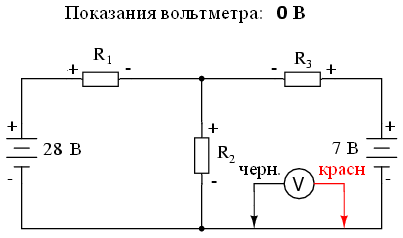
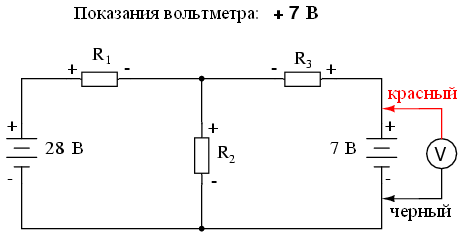
Согласно второму закону Кирхгофа, алгебраическая сумма всех напряжений в цепи должна быть равна нулю. Исходя из этого, мы можем составить некоторые уравнения для нашей системы, подставив неизвестные токи (I₁, I₂ и я₃). Чтобы вывести уравнения второго закона Кирхгофа, нам необходимо знать число и полярность напряжений в каждой ветви цепи. Чтобы облегчить эту задачу, представим, что мы измерили все напряжения настоящим вольтметром, обозначив неизвестные значения как положительные или отрицательные. Сначала составим уравнение для левой части схемы, начиная с левого верхнего угла и двигаясь против часовой стрелки (выбор начальной точки и направления произвольный). Результат будет выглядеть следующим образом:

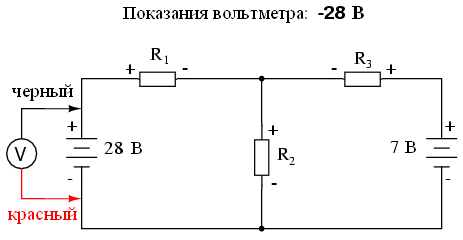
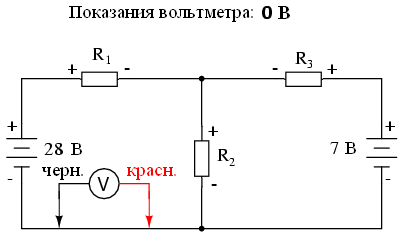
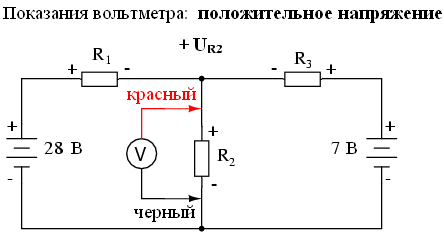
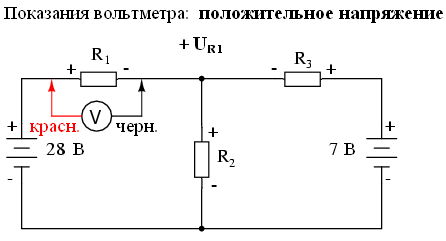
Когда мы закончим тестирование левой ветви цепи, мы можем применить второй закон Кирхгофа к полученным значениям (сумма всех напряжений цепи равна нулю):

Мы еще не знаем значения напряжений на резисторах R₁ и Р₂поэтому мы не можем ввести их в уравнение в виде числовых значений. Однако мы знаем, что сумма этих трех напряжений равна нулю, поэтому уравнение верно. Пойдем дальше и выразим неизвестные напряжения как произведение неизвестных токов и соответствующих сопротивлений (используя закон Ома: U = IR) и удалим все нулевые значения из левой части уравнения:

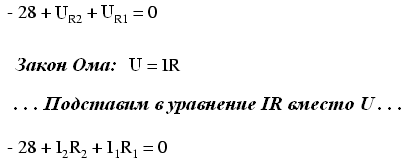
Поскольку мы знаем сопротивления всех резисторов, подставим конкретные числовые значения в уравнение:

Вам может быть интересно, почему мы проделали все эти манипуляции с исходной формой уравнения (-28 + E_R2 + E_R1)? Какая разница, выражено ли уравнение через напряжение или ток (умноженный на сопротивление), ведь в обоих случаях последние два члена все равно неизвестны? Ответ на эти вопросы прост. Цель всех вышеперечисленных преобразований – получить второе уравнение закона Кирхгофа, используя те же неизвестные переменные, что и в первом уравнении закона Кирхгофа, поскольку это необходимое условие для решения любой системы уравнений. Чтобы найти значения трех неизвестных токов (I₁, I₂ и я₃), мы должны иметь три уравнения, соединяющие их вместе.

Применив те же действия к правой ветви цепи (начиная с выбранного узла и двигаясь против часовой стрелки), мы получим еще одно уравнение второго закона Кирхгофа:

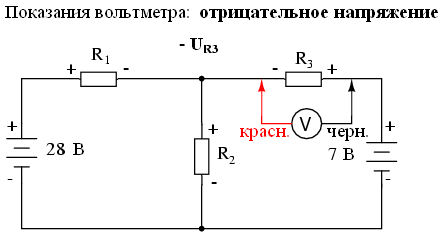
Зная, что напряжение на каждом резисторе может и должно быть выражено как произведение соответствующих токов и сопротивлений (величины которых известны), мы можем записать это уравнение следующим образом:

Теперь у нас есть система из трех уравнений (одно уравнение из первого закона Кирхгофа и два уравнения из второго закона Кирхгофа) с тремя неизвестными:

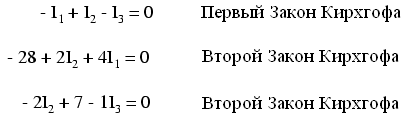
Затем мы должны перенести все известные величины в правые части уравнений, а неизвестные оставить в левой части, дополнив их недостающими нулевыми значениями:

Решив эту систему уравнений, мы получим следующий результат:

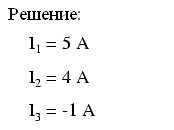
Таким образом, ток I₁ равен 5 амперам, ток I₂ равен 4 амперам, а ток I₃ равна минус 1 амперу. Отрицательное значение тока I₃ означает, что наше предположение о его направлении неверно. Вернемся к исходной схеме и перерисуем стрелку этого тока в обратном направлении (соответственно, корректируя полярность напряжения на резисторе R).₃):

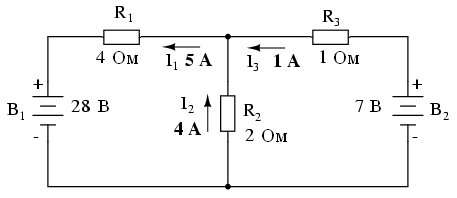
Обратите внимание, что в правой ветви цепи ток течет обратно через батарею 2. Это связано с более высоким напряжением батареи 1 (где ток течет “нормально” – через цепь минус – плюс). Означает ли это, что “более мощная” батарея всегда будет “побеждать” более слабую. Вовсе нет! Это соотношение зависит как от относительных напряжений батарей, так и от сопротивления резисторов цепи. Единственный способ выяснить, что происходит в цепи, – это математический анализ.

Таким образом, мы знаем величины всех токов в данной цепи. Теперь, используя закон Ома (U = IR), мы можем рассчитать напряжения на всех резисторах:

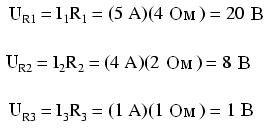
Давайте теперь проанализируем эту схему с помощью PSPICE, тем самым проверив результаты, полученные для напряжений. Программа, конечно, сможет рассчитать токи, но тогда нам придется учитывать дополнительные элементы в цепи. Учитывая этот факт, мы выберем путь наименьшего сопротивления (если напряжения, выданные программой, совпадают с нашими расчетами, значит, мы правильно рассчитали токи). Диаграмма с номерами узлов для программы показана ниже:

Как видите, результаты работы программы совпадают с нашими расчетами: 20 В в резисторе R₁ (узлы 1 и 2), 8 В на резисторе R₂ (узлы 2 и 0) и 1 вольт на резисторе R₃ (узлы 2 и 3). Обратите внимание на знаки всех этих напряжений: они имеют положительные значения! PSPICE основывает свою полярность на порядке перечисления узлов: первый узел должен быть положительным, а второй – отрицательным. Например, положительный (+) 20 В между узлами 1 и 2 означает, что узел 1 является положительным по отношению к узлу 2. Если это число окажется отрицательным, то ошибку будут искать в том порядке, в котором перечислены узлы.

Читайте далее: