Трехфазные цепи (общая информация) - услуги электромонтажа, строительства и ремонта

Давайте рассмотрим схему соединения звездой

Содержание

Трехфазные цепи

При изучении электродинамики мы рассматривали только двухпроводные цепи постоянного и переменного тока. Однако из-за многочисленных преимуществ на практике стали широко применяться схемы, в которых переменный ток протекает по нескольким проводникам одновременно, но со сдвигом фаз.

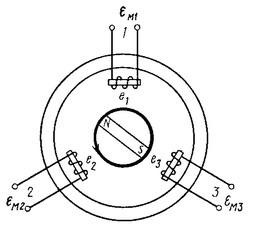Если в линии передачи одновременно действуют три переменных тока, колебания которых смещены на 120°, то такую линию передачи называют трехфазной, а электрический ток – трехфазным.

Для получения трехфазного тока в синхронном генераторе размещают три обмотки 1, 2 и 3, плоскости которых повернуты на 120° относительно друг друга. Согласно закону электромагнитной индукции Фарадея, при вращении ротора в обмотках наводится переменный электрический ток. с одинаковыми частотами, но их фазы сдвинуты на 120°.

В электротехнике термин “фаза” имеет два значения: фаза в периодическом процессе и однофазная цепь, образующая многофазную систему.

В трехфазных системах токи (напряжения) фаз сдвинуты на одну треть периода, или на 120°.

Когда магнит вращается, в обмотках наводится ЭДС, сдвинутая на 120°.

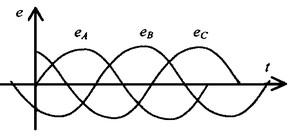
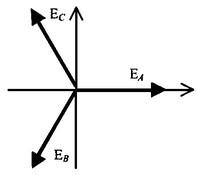
Выражения для ЭДС фаз A, B, C и их векторные диаграммы приведены ниже:

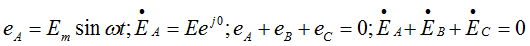
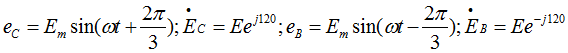
1. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

Общие требования к лабораторным работам

В соответствии с методическими указаниями и конспектом лекций изучите теоретические вопросы, связанные с темой будущей работы. Ознакомьтесь с содержанием работы и последовательностью ее выполнения.

В тетради для лабораторных работ запишите номер, название и цель работы, начертите принципиальную схему и таблицу для записи результатов экспериментов и расчетов.

Соберите цепь в соответствии с приведенной схемой. Рекомендуется сначала подключить все последовательно соединенные компоненты, а затем параллельно соединенные. Проверьте правильность подключения цепи.

Общая маркировка фазных проводников:

Преимущества

Экономическая эффективность.
- Экономичная передача энергии на большие расстояния.
- Снижение расхода материалов в 3-фазных трансформаторах.
- Более низкий расход материалов в силовых кабелях, поскольку токи в фазах меньше (по сравнению с однофазными цепями) при одинаковой потребляемой мощности.
Благодаря этим преимуществам трехфазные системы являются наиболее распространенными в современной электроэнергетике.

– Способность генерировать вращающееся магнитное поле с помощью неподвижных обмоток, на которой основаны синхронные и асинхронные двигатели и ряд другого электрооборудования;

Какая нагрузка называется симметричной?

Трехфазная цепь является частным случаем многофазных электрических систем, которые представляют собой совокупность электрических цепей, в которых ЭДС одинаковой частоты действуют под определенным углом в фазе друг к другу. Обратите внимание, что эти ЭДС обычно синусоидальны, в основном в энергетике. Однако в современных электромеханических системах, где для управления исполнительными двигателями используются инверторы, система напряжения обычно несинусоидальна. Каждая часть многофазной системы, характеризующаяся одним и тем же током, называется фаза, Т.е. фаза – это часть цепи, относящаяся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.

Поэтому термин фаза имеет два различных значения в электротехнике:
- Фаза как аргумент синусоидально изменяющейся величины;
- Фаза как элемент многофазной электрической системы.
Развитие многофазных систем было обусловлено историей. Исследования в этой области были обусловлены потребностями развивающегося производства, а прогрессу в разработке многофазных систем способствовали открытия в области физики электрических и магнитных явлений.

Открытие вращающегося магнитного поля (Г. Феррарис и Н. Тесла, 1888) стало важнейшей предпосылкой для разработки многофазных электрических систем. Первые электродвигатели были двухфазными, но они были не очень эффективными. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Выдающийся русский электротехник М.О.Доливо-Добровольский, разработавший трехфазные асинхронные двигатели, трансформаторы и предложивший трех- и четырехпроводные схемы, внес большой вклад в развитие трехфазных систем и поэтому по праву считается основателем трехфазных систем.

Трехфазный источник напряжения представляет собой трехфазный генератор переменного тока с трехфазной обмоткой в статоре (см. рис. 1). Фазы этой обмотки расположены так, что их магнитные оси смещены в пространстве относительно друг друга на радиан. На рис. 1 каждая фаза статора условно представлена в виде одной катушки. Обмотки начинаются с заглавных букв A, B и C и заканчиваются заглавными буквами x, y и z. ЭДС в неподвижной обмотке статора индуцируется магнитным полем, создаваемым током возбуждения во вращающемся роторе (на рисунке 1 ротор представлен в виде постоянного магнита, который используется на практике для относительно небольших мощностей). При вращении ротора с равномерной скоростью в фазных обмотках статора наводятся периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся по фазе из-за пространственного сдвига относительно друг друга на рад. (см. рис. 2).

В настоящее время наиболее распространены трехфазные системы. Все крупные электростанции и потребители работают на трехфазном токе, благодаря многочисленным преимуществам трехфазных цепей перед однофазными, наиболее важными из которых являются:

– Экономичная передача электроэнергии на большие расстояния;

– Наиболее надежным и экономичным асинхронным двигателем, отвечающим требованиям промышленных электроприводов, является двигатель с короткозамкнутым ротором;

– Возможность получения при неподвижных обмотках вращающегося магнитного поля, на котором основана работа синхронных и асинхронных двигателей, а также ряда других электрических устройств;

– баланс симметричных трехфазных систем.

Для того чтобы учесть наиболее важные свойство равновесия трехфазной системы, что будет доказано ниже, мы вводим понятие симметрии многофазной системы.

Система ЭМП (напряжения, токи и т.д.) называется симметричный если он состоит из m векторов равных по модулю ЭДС (напряжений, токов и т.д.), сдвинутых по фазе относительно друг друга на одинаковый угол . В частности, векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной синусоидальной системе рис.2, показана на рис.3.

Рис.3 Рис.4

Среди асимметричных систем наибольший практический интерес представляет двухфазная система со сдвигом фаз на 90 градусов (см. рис. 4).

Все симметричные трехфазные (m>3) и двухфазные системы являются сбалансированный. Это означает, что, несмотря на пульсацию мгновенной мощности в отдельных фазах (см. рис. 5.a), меняющуюся не только по величине, но обычно и по знаку в течение периода, общая мгновенная мощность всех фаз остается постоянной в течение всего периода синусоидального ЭДС (см. рис. 5.b).

Баланс имеет большое практическое значение. Если бы полная мгновенная мощность пульсировала, то на валу между турбиной и генератором возникал бы пульсирующий момент. Такая переменная механическая нагрузка будет вредна для генераторной установки, сокращая срок ее службы. Те же соображения относятся и к многофазным двигателям.

Если симметрия нарушена (двухфазная система Теслы не рассматривается из-за ее специфики), то нарушается и баланс. По этой причине энергетики уделяют большое внимание тому, чтобы нагрузка генератора была симметричной.

Схемы подключения для трехфазных систем

Трехфазный генератор (трансформатор) имеет три выходные обмотки, которые имеют одинаковое число витков, но создают ЭДС, сдвинутую по фазе на 120°. Можно использовать систему, в которой обмотки генератора не соединены гальванически друг с другом. Это так называемая “развязанная система”. Это известно как незамкнутая система. В этом случае каждая фаза генератора должна быть подключена к нагрузке двумя проводами, т.е. это будет шестипроводная линия, что неэкономично. По этой причине такие системы не нашли широкого применения на практике.

Чтобы уменьшить количество проводов в линии, фазы генератора соединены гальванически. Различают два типа соединения: звезда и дельта-соединение. В звездообразном соединении система может быть три и четырехпроводное соединение.

Звездное соединение

На рисунке 6 показана трехфазная система с генератором и нагрузкой, соединенными в звезду. На рисунке 6 показана трехфазная система, в которой фазы генератора и нагрузки соединены звездой. Здесь AA’, BB’ и CC’ – линейные проводники.

Линейный это провод, соединяющий фазные концы обмоток генератора и нагрузки. Точка, где концы фаз соединяются в общий переход, называется нейтральный (На рис. 6 N и N’ – нейтральные точки генератора и нагрузки соответственно).

Провод, соединяющий нейтральные точки генератора и нагрузки, называется нейтральный (отмечено пунктирной линией на рис. 6). Трехфазная система в соединении звездой без нейтрального провода называется трехпроводной С нейтральным проводом называется четырехпроводной системой как четырехпроводная система.

Все величины, связанные с фазами, называются фазовые переменные, для линии линия. Как видно из схемы на рисунке 6, в соединении звездой линейные токи и равны соответствующим фазным токам. При наличии нейтрального проводника ток в нейтральном проводнике равен . Если система фазных токов симметрична, то . Следовательно, если бы симметрия тока была гарантирована, нейтральный проводник был бы не нужен. Как будет показано ниже, нейтральный провод обеспечивает сохранение симметричности напряжения нагрузки при несимметричности самой нагрузки.

Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек A,B и C до нейтрали N; – фазные напряжения нагрузки.

Напряжение в линии действует между проводниками линии. В соответствии со вторым законом Кирхгофа для линейных напряжений мы можем написать

; (1)

; (2)

. (3)

Обратите внимание, что это всегда сумма напряжений замкнутой цепи.

Векторная диаграмма для симметричной системы напряжений показана на рис.7. Как следует из ее анализа (радиусы фазных напряжений образуют стороны равнобедренного треугольника с углом при основании равным 300), в данном случае

В расчетах обычно предполагается, что . Тогда в случае прямая последовательность фаз , (в случае обратная фазовая последовательность фазовые сдвиги y и чередуются). С учетом этого, комплексы линейных напряжений могут быть определены из соотношений (1) …(3). Однако, учитывая симметрию напряжений, эти величины легко определить непосредственно из векторной диаграммы на рис. 7. Ориентируя вещественную ось системы координат вдоль вектора (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений относительно этой оси и определяем их модули согласно (4). Таким образом, для линейных напряжений и получаем: ; .

Треугольное соединение

В связи с тем, что значительная часть нагрузок в трехфазных цепях несимметрична, на практике, например, в цепях освещения, важно, чтобы работа отдельных фаз была независимой. В дополнение к четырехпроводным цепям, трехпроводные цепи также обладают подобными свойствами, когда фазы нагрузки соединены в треугольник. Однако можно также соединить фазы генератора в треугольник (см. рис. 8).

Для симметричной цепи с ЭДС имеем

Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рисунке 8 токи будут равны нулю. Однако если поменять местами начало и конец любой из фаз, в треугольнике также будет протекать ток короткого замыкания. Поэтому в случае соединения треугольником необходимо строго соблюдать порядок чередования фаз: начало одной фазы соединяется с концом другой.

Схема соединения фаз генератора и нагрузки в треугольник показана на рисунке 9.

Очевидно, что при соединении треугольником линейные напряжения равны соответствующим фазным напряжениям. Из первого закона Кирхгофа следует, что связь между током линии и фазным током приемника определяется следующим соотношением

Аналогичным образом мы можем выразить токи линии через фазные токи генератора.

Рисунок 10 представляет собой векторную диаграмму симметричной системы линейных и фазных токов. Из анализа этой диаграммы следует, что когда токи симметричны

Наконец, помимо рассмотренных выше соединений звезда – звезда и треугольник – треугольник, на практике также используются схемы звезда – треугольник и треугольник – звезда.

Суммарная мощность отдельных фаз

Напряжения будут равны U_a = U_A; U_b = U_B; U_c = U_C, U_Ф = U_Л / за счет нейтрального проводника на Z_N = 0.

Поэтому нейтральный провод обеспечивает симметрию фазных напряжений потребителя при несимметричной нагрузке.

По этой причине однофазные несимметричные нагрузки, такие как лампы накаливания, подключаются к четырехпроводной сети. Режим работы каждой фазы нагрузки, находящейся под постоянным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

Векторная диаграмма для несбалансированной нагрузки показана на рисунке 3.9. 3.9

Трехпроводная электрическая цепь

Соединение источника и нагрузки звездой без нейтрального проводника показано на рисунке 3.10.

Когда нагрузка симметрична, когда Z _a = Z _b = Z _c = Z_φНапряжение между нейтральной точкой источника N и нейтральной точкой нагрузки n равно нулю, U_nN = 0.

Отношение фазного и линейного напряжений приемника также является т.е. U_Ф = U_Л / и фазные токи определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением составляет φ = arctg (X / R).

В случае несимметричной нагрузки Z _a ≠ Z _b ≠ Z _c Между нейтральной точкой потребителя и источником питания напряжение смещения нейтральной точки U_nN.

Для определения реактивного напряжения нейтрали можно использовать формулу для межузлового напряжения, поскольку схема на рис. 3.10 является двухузловой,

,

где: Y _a = 1 / Z _a; Y _b = 1 / Z _b; Y _c = 1 / Z _c – комплексы с зарядовой фазовой проводимостью.

Очевидно, что теперь напряжения на фазах потребителей будут отличаться друг от друга. Из второго закона Кирхгофа следует, что

Зная фазные напряжения нагрузки, мы можем определить фазные токи:

Рассмотрим расчет мощности, когда приемники соединены в четырехпроводную звезду, и мы предполагаем, что нагрузка не сбалансирована. Учитывая, что сопротивление нейтрального проводника ненулевое и активное, имеем:

Определение трехфазных цепей

Кроме однофазных источников, существуют источники с двумя, тремя, четырьмя и т.д. фазами, характеризующиеся тем, что их ЭДС, хотя и имеют одинаковую частоту, смещены друг относительно друга на некоторый угол. Такие генераторы называются многофазными, а электрические цепи с такими источниками – многофазными.

Трехфазный генератор

Трехфазные цепи наиболее часто используются на практике. По этой причине основное изучение многофазных цепей будет проводиться на примере трехфазных цепей. Рассмотрим реализацию трехфазного источника, который представляет собой трехфазный генератор (рис. 4.1).

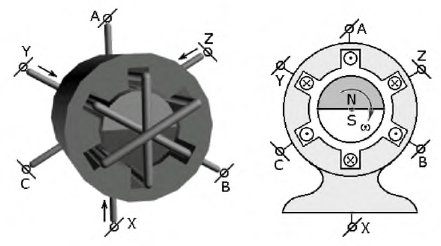
Рисунок 4.1 Трехфазный генератор

Для упрощения понимания принципа работы генератора обмотки (фазы) представлены одной обмоткой. В качестве ротора генератора переменного тока выбран постоянный магнит. Каждая из обмоток имеет начало – клеммы 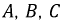и в конце – терминалы. 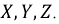Обмотки смещены друг относительно друга на 120°, что означает, что максимумы ЭДС в них достигаются в разное время, с разницей в одну треть времени.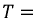 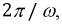где 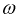– угловая частота ротора.

Порядок, в котором ЭДС достигают пика в соответствующих фазах, называется последовательностью фаз. Прямая фазовая последовательность – это последовательность 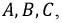в котором фаза 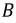фаза отстает от фазы 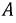по 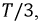и фаза 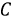задерживается по отношению к фазе 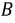через 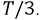На рис. 4.2 показаны мгновенные значения ЭДС для прямой последовательности фаз. Изменение направления вращения трехфазного генератора меняет эту последовательность фаз на противоположную и сужает ее.

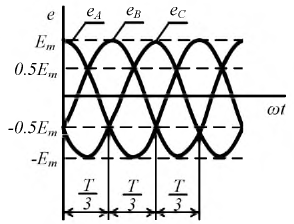
Рисунок 4.2: Графики мгновенных значений фазовой ЭДС

Зафиксируем мгновенные значения ЭДС, наведенных в фазах во время вращения ротора генератора:

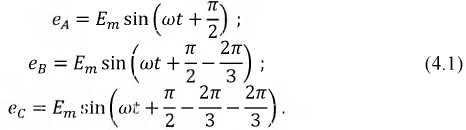
Поскольку ЭДС каждой фазы генератора синусоидальны, они могут быть представлены в комплексной плоскости в виде векторов соответствующих фазных ЭДС: 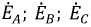(Рисунок 4.3).

Рисунок 4.3: Векторная диаграмма фазовой ЭДС

Важным обстоятельством является то, что система векторов фазовой ЭДС генератора на комплексной плоскости образует симметричную трехлучевую звезду, а сумма этих векторов в каждый момент времени равна нулю.

При подключении нагрузки к каждой фазе генератора через нее протекает ток. Таким образом, реализуется трехфазная система.

Методы совмещения фаз генератора и нагрузки

Соединение фаз генератора и нагрузки в системе с четырехпроводной звездой:

Когда фазы генератора соединены звездой, все концы или начала подключены к одной общей точке. На рисунке 4.4.a показана неподключенная трехфазная система, в которой каждая фаза генератора и нагрузки образует отдельную электрическую цепь, поэтому для подключения генератора и нагрузки требуется 6 проводов.

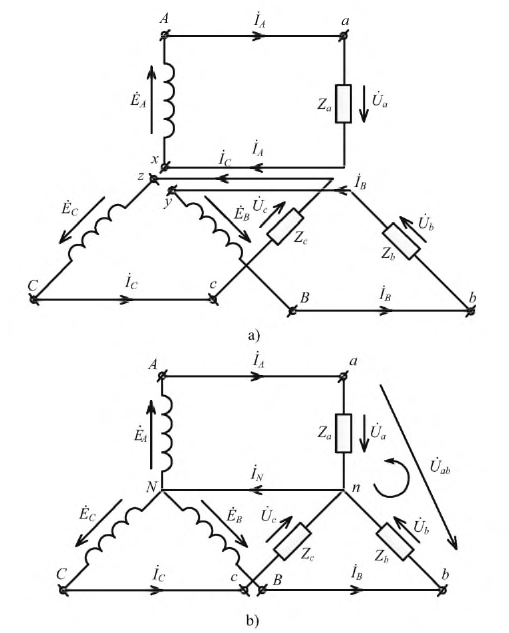
Рисунок 4.4: Соединение звездой (a) неподключенная трехфазная система, (b) четырехпроводное соединение звездой

При соединении звездой количество проводов сокращается до 4. Провод, соединяющий общие точки (нейтраль или нейтраль/земля) фаз генератора или нагрузки, называется нейтральным или нейтральным/земляным проводом. 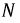и нагрузкой называется нейтральным или нейтрально-земным проводом. Другие провода, соединяющие фазы генератора и нагрузки, называются линейными проводами.

Токи, протекающие по фазам генератора или нагрузки, называются фазными токами, токи, протекающие по проводам, соединяющим фазы генератора и нагрузки, называются линейными токами, а ток, протекающий по нейтральному проводу, называется нейтральным током.

Напряжение между началом и концом фазы генератора или нагрузки называется фазным напряжением, напряжение между двумя фазами или линиями называется линейным напряжением.

При таком способе подключения между линейными и фазными параметрами цепи существуют следующие соотношения:

Установим взаимосвязь между наборами линейных и фазных напряжений источника (рис. 4.5).

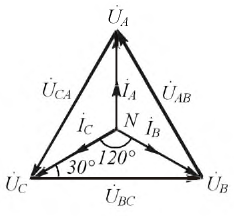
Рисунок 4.5: Векторная диаграмма трехфазной цепи с нагрузками, соединенными звездой, и симметричной активной нагрузкой

В последующем обсуждении мы заменим фазовые ЭДС напряжениями на фазах источника:

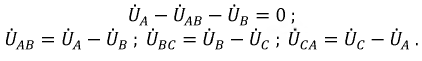
Выберем любой равнобедренный треугольник, образованный двумя фазными и линейными напряжениями, и проведем перпендикуляр из вершины 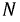на базе. Перпендикуляр – это средняя точка и биссектриса.

Из любого правильного треугольника получаем:

Это второе важное отношение для звездного соединения.

Частным случаем такого соединения является соединение “звезда” без соединение звездой без нейтрального проводника.

Соединение фаз генератора и нагрузки треугольником

Вторым основным способом соединения фаз генератора и нагрузки является соединение треугольником (Рисунок 4.6).

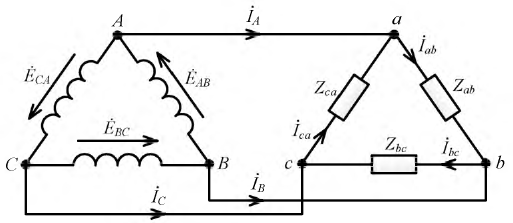
Рисунок 4.6: Дельта-соединение

Для дельта-соединения мы имеем следующее соотношение:

Установите взаимосвязь между фазными и линейными токами:

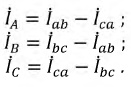
Построим векторную диаграмму токов и напряжений для этого способа подключения (Рисунок 4.7).

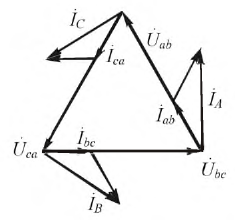
Рис. 4.7 Векторная диаграмма трехфазной цепи с подключением

Исследуя любую форму тока в треугольнике, можно сделать те же выводы, что и для напряжений в цепи, соединенной звездой (только для симметричных нагрузок):

Помимо вышеперечисленных режимов соединения, существуют также комбинированные режимы соединения: звезда-треугольник, дельта-звезда.

Режимы работы трехфазных цепей

Проводится различие между симметричной и несимметричной работой в трехфазных цепях. Z. В симметричном режиме сопротивления трех фаз одинаковы, и электромагнитные поля образуют трехфазную симметричную систему. В этом случае фазные токи a, b, c будут одинаковой величины и будут смещены на 120 градусов.

Соединение звездой с нейтральным проводником и без него

Поскольку трехфазные цепи представляют собой сумму однофазных цепей, для их расчета используются все специальные методы, рассмотренные ранее, включая метод комплексного расчета. Поэтому расчет трехфазных цепей может быть проиллюстрирован построением векторных диаграмм тока нагрузки и топографических диаграмм напряжения.

Метод двух узлов можно считать наиболее разумным для расчета такой цепи. Для выбранных положительных направлений напряжений и токов в цепи (рис. 4.8) составим систему уравнений для расчета токов.

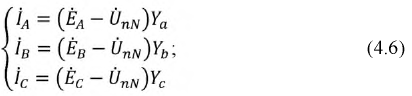
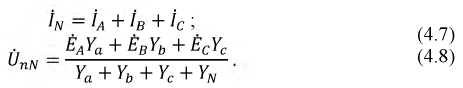
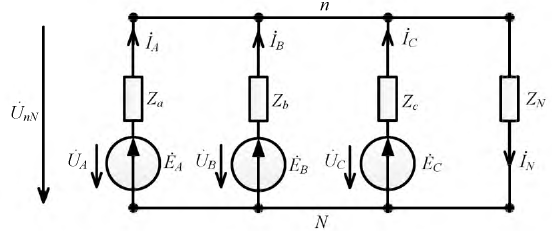
Рисунок 4.8: Подключение фаз генератора и нагрузки в системе четырехпроводной звезды

Симметричная нагрузка.

Нагрузка считается симметричной, если комплексные сопротивления ее фаз равны:

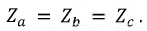
Для простоты будем считать, что приемниками фаз нагрузки являются резисторы 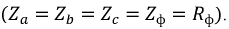Существование нейтрального провода означает, что потенциалы узлов 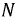и 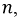если сопротивлением нейтрального проводника можно пренебречь 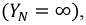затем 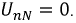В этом случае фазные токи равны, и фазные напряжения на нагрузке будут точно такими же, как фазные напряжения генератора. Для фазы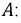

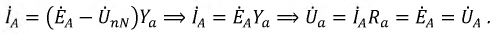
В равной степени для фаз 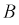и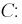

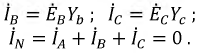
На основании приведенных выше данных постройте фазные напряжения и векторную диаграмму тока (рис. 4.9).

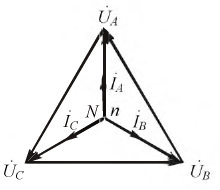
Рисунок 4.9: Векторная диаграмма для симметричной нагрузки в трех- и четырехпроводных системах

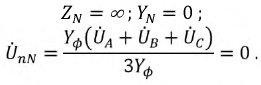
В случае симметричной нагрузки, как в четырехпроводной схеме, фазы нагрузки работают независимо друг от друга, и нейтральный провод не нужен. Схема в этом случае будет точно такой же, как и для четырехпроводной звезды.

2 – Несбалансированная нагрузка.

Пусть

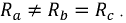
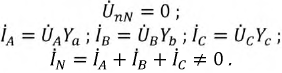
Векторная диаграмма токов и напряжений (рис. 4.10) показывает суммирование фазных токов.

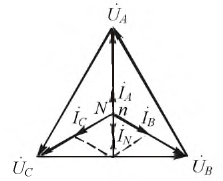
Рисунок 4.10: Векторная диаграмма для несбалансированной нагрузки

Пусть 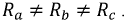Из-за неодинаковой проводимости ветвей 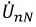не равна нулю, т.е. между точкам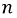и и 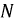существует разность потенциалов, нейтральный сдвиг. В этом случае фазные напряжения на нагрузках больше не будут повторять систему фазных напряжений генератора. Затем задача сводится к вычислению положения точки 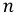в комплексной плоскости по отношению к 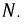Оно может быть определено по формуле узлового напряжения и рассчитано теоретически. Однако это можно сделать на основе экспериментальных данных, суть которых заключается в следующем: измерить напряжения на фазах нагрузки; по шкале, выбранной для напряжений, построить дуги окружностей с радиусами, равными измеренным фазным напряжениям, из точек 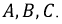Точка пересечения этих трех дуг даст искомое положение точки 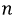в треугольнике, ограниченном линейными напряжениями (рис. 4.11).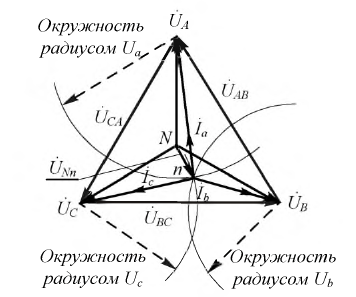

Рисунок 4.11: Определение смещения нулевой точки

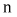
Соединение точек 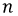и 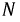отрезком прямой, мы получаем нейтральный сдвиг. Используя найденные межфазные напряжения, определите векторы тока. Равенство должно быть соблюдено: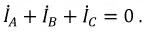

Главный вывод, который можно сделать: если известно, что нагрузка несимметрична или может стать таковой, следует использовать четырехпроводную схему.

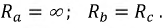
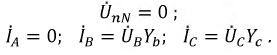
Векторная диаграмма (рис. 4.12) иллюстрирует работу четырехпроводной системы.

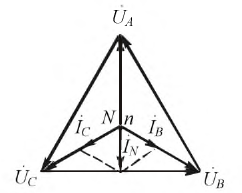
Рисунок 4.12: Векторная диаграмма для потери фазы в четырехпроводной системе

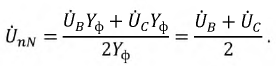
Напряжение сдвига 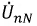можно также определить методом надреза, как показано на рисунке 4.13.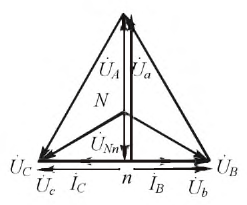

Рисунок 4.13: Векторная диаграмма для потери фазы в трехпроводной системе

Согласно первому закону Кирхгофа:

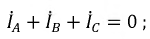
С сайта 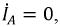затем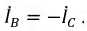

Токи в фазах 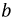и 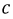должны быть в противофазе.

4 Фазное короткое замыкание.

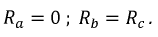
В четырехпроводной системе короткое замыкание фазы приемника вызывает короткое замыкание фазы источника.

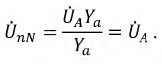
Фазные напряжения приемника:

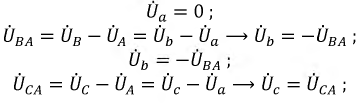
т.е. фазные напряжения выросли до линейных напряжений, а следовательно, и фазные токи:

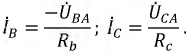
увеличились в разы 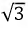времена. Ток в закороченной фазе будет определяться по первому закону Кирхгофа: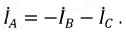

Построение векторной диаграммы для короткого замыкания показано на рис. 4.14.

Неравномерная нагрузка.

Общий принцип построения топографических диаграмм вектора тока и напряжения остается прежним. Единственным отличием будет появление фазовых сдвигов между токами и напряжениями на фазах нагрузки, в зависимости от характера нагрузки.

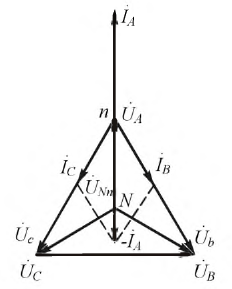
Рисунок 4.14: Векторная диаграмма для фазового короткого замыкания в трехпроводной системе

Трехпроводные схемы соединения “звезда” применяются к трехфазным симметричным потребителям, таким как трехфазные асинхронные и синхронные двигатели.

Подключение потребителей в дельта-соединении

Давайте рассмотрим различные режимы работы потребителя, соединенного треугольником (рис. 4.15).

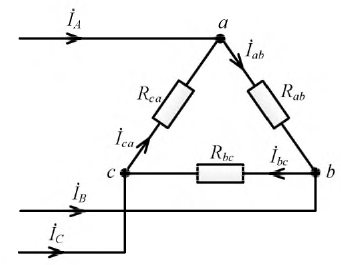
Рис. 4.15: Соединение фаз потребителя в треугольник

Опять же, мы будем считать, что активные резисторы включены в фазы как приемники (для простоты).

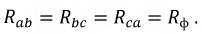
На рис. 4.7 представлена векторная диаграмма для симметричной нагрузки с фазами приемника, соединенными в треугольник.

Токи равны по модулю и отличаются только по фазе:

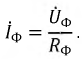
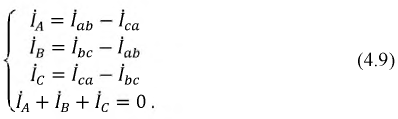
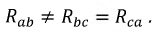
Фазы по-прежнему действуют независимо друг от друга, поэтому токи будут разными:

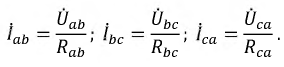
Токи линий определяются из уравнений (4.9) соответственно. Векторная диаграмма показана на рисунке 4.16.

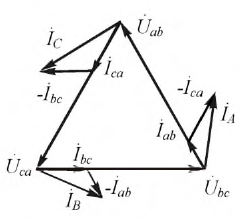
Рисунок 4.16: Векторная диаграмма для несимметричной нагрузки приемников, соединенных треугольником

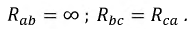
Рисунок 4.17: Векторная диаграмма для соединения приемников треугольником при обрыве фазы.

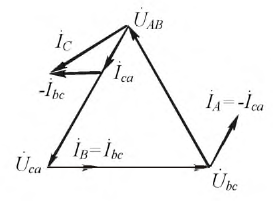
Рис. 4.17: Векторная диаграмма для обрыва фазы при соединении приемников треугольником

Отношения для токов:

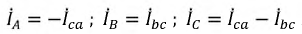
Для неравномерных нагрузок методика расчета не меняется.

Расчет мощности в трехфазных цепях

Рассмотрим расчет мощности, когда нагрузки соединены в четырехпроводную звездообразную систему и предположим, что нагрузка несимметрична. Учитывая, что сопротивление нейтрального проводника ненулевое и активное, имеем:

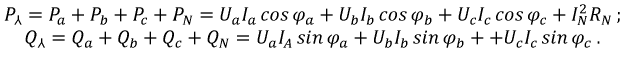
При симметричной нагрузке для трехпроводной и четырехпроводной системы получаем:

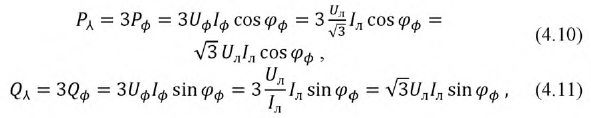
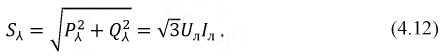
При соединении фаз приемника треугольником и несимметричной нагрузке имеем:

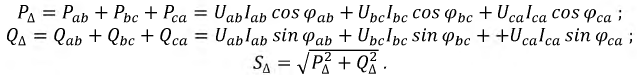
При симметричной нагрузке:

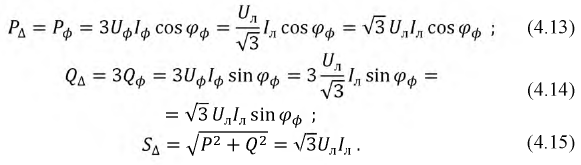
Обратите внимание, однако, что одинаковые формулы для расчета мощности при различных методах комбинирования (4.10 – 4.12) и (4.13 – 4.15) не означают одинаковых числовых значений.

Пример. Предположим, что трехфазная нагрузка с сопротивлением фаз 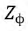. соединен звездой, то активная мощность будет :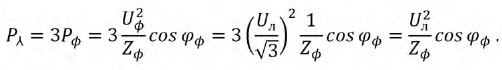

Теперь соедините фазы того же потребителя “в треугольник” и подключите к тому же трехфазному источнику:

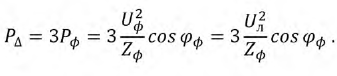
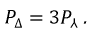
Измерение мощности в трехфазных цепях

Для измерения активной мощности в симметричной трехфазной цепи нужен только один ваттметр, подключенный для измерения мощности одной из фаз.

Подключение потребителей в четырехпроводной звездообразной системе

В схеме (рис. 4.18) в каждой фазе подключены однофазные ваттметры, через токовые катушки которых протекают токи линии, а катушки напряжения ваттметров подключены между нейтральным проводником и соответствующими проводниками линии.

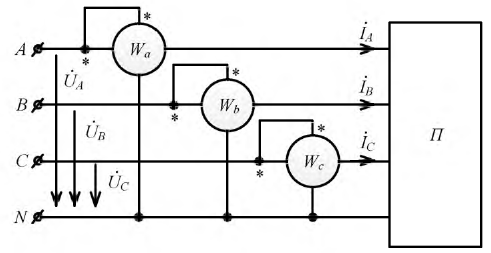
Схема подключения ваттметра для измерения мощности в четырехпроводной цепи

Поскольку активная мощность – это реальная часть полной мощности:

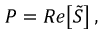
Суммарная мощность трех ваттметров может быть представлена выражением:

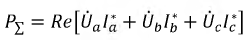
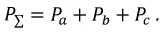
Для симметричной нагрузки достаточно использовать один ваттметр для измерения мощности, потребляемой нагрузкой, показания которого должны быть утроены.

Подключение нагрузок в трехпроводном соединении “звезда” или “треугольник

В этом случае мощность трехфазной нагрузки можно измерить с помощью двух ваттметров (рис. 4.19).

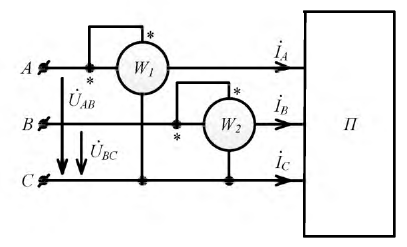
Рисунок 4.19: Схема измерения активной мощности с помощью двух ваттметров

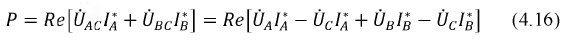
Учитывая это:

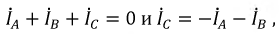
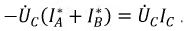
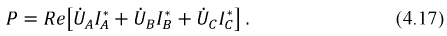
Оба ваттметра выполнены в одном корпусе, а прибор имеет две пары проводов для катушек тока и две пары проводов для катушек напряжения. Трехфазный ваттметр может быть подключен, как показано на рис. 4.19, или по любой схеме с циклическим чередованием фаз.

Метод симметричных компонентов

Любая несимметричная трехфазная система может быть разложена на три симметричные трехфазные системы: с прямой, обратной и нулевой последовательностью. Это разложение широко используется при анализе трехфазных машин и, в частности, при расчете токов короткого замыкания в трехфазных системах.

Предположим, что несимметричная трехфазная векторная система 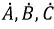(рис. 4.20).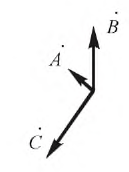

Рисунок 4.20: Несбалансированная трехфазная векторная система

Каждый вектор этой системы может быть представлен как сумма трех компонентов:

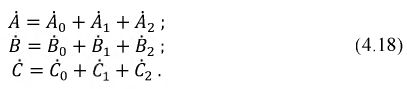
На рис. 4.21 показано расположение вышеуказанных последовательностей.

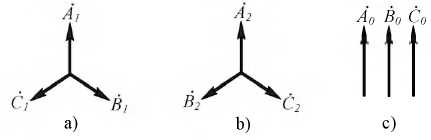
Рис. 4.21: Симметричные расположения векторов прямой (a), обратной (b) и нулевой (c) последовательности

Векторы простой, обратной и нулевой последовательностей удовлетворяют следующим соотношениям:

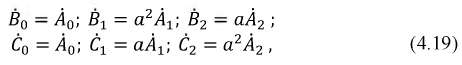
где

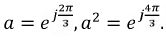
Коэффициент 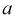называется коэффициентом поворота

Положим в основу соотношений (4.19) систему уравнений (4.18). Тогда получаем:

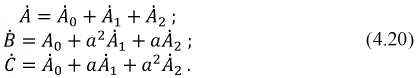
Решая систему уравнений (4.20) относительно 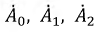дает: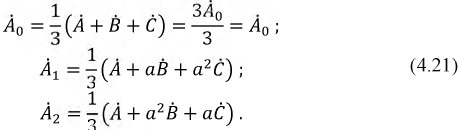

Симметричные компоненты можно определить графически, построив векторную диаграмму несимметричной системы векторов в соответствии с системой уравнений (4.21).

Симметричные компонентные фильтры

Симметричные компоненты асимметричных систем могут быть обнаружены не только аналитически или графически, но и с помощью электрических цепей, называемых фильтрами симметричных компонентов.

Эти фильтры используются в цепях защиты электроустановок. Степень асимметрии системы тока и напряжения не должна превышать известных пределов, т.е. нулевая и отрицательная составляющие последовательностей напряжения и тока в нормальных условиях должны быть меньше определенных заранее установленных значений, задаваемых индивидуально для каждой установки.

Возможность изолировать с помощью диаграмм отдельные симметричные компоненты позволяет воздействовать с помощью любого из них на защитные устройства установки, которые, соответствующим образом отрегулированные, отключат всю установку или ее часть, как только значение данного компонента превысит допустимый предел.

В качестве примера на рис. 4.22 показаны диаграммы фильтров нулевой последовательности для линейного тока и фазного напряжения.

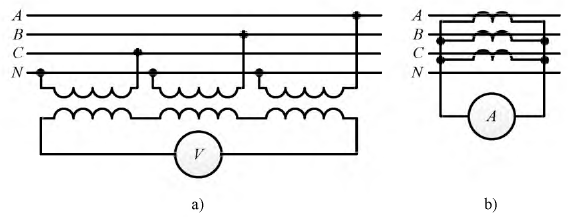
Рис. 4.22. Схемы фильтров нулевой последовательности

В схеме (рис. 4.22,а) вторичные обмотки трансформаторов напряжения соединены последовательно, поэтому вольтметр определяет сумму фазных напряжений, т.е. тройную составляющую нулевой последовательности системы фазных напряжений.

В схеме (рис. 4.22,б) вторичные обмотки трансформаторов тока соединены параллельно, поэтому амперметр измеряет сумму токов линии, т.е. нулевую тройную составляющую последовательности токов линии.

При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан педагогами на некоммерческой основе для дополнительного образования молодежи.

Сайт написан, поддерживается и управляется командой учителей

Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.

Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.