Как видно из рисунка, для трехмерного случая возможны более сложные конфигурации терминов. Например, четыре термина, принадлежащие одной стенке куба, объединяются в один термин с поглощением двух переменных:
В общем случае можно сказать, что 2K членов, принадлежащих одной стенке K-мерного гиперкуба, склеиваются в один член с K поглощенными переменными.
Схемы. Минимизация логических функций
Минимизация логических функций является одной из типичных задач при изучении схем. Именно поэтому я считаю, что эта статья имеет свое место, надеюсь, она вам понравится. 
Зачем он нужен?
Сложность логической функции, а значит, сложность и стоимость схемы, которая ее реализует, пропорциональна количеству логических операций и количеству вхождений переменных или их отрицаний. В принципе, любую булеву функцию можно упростить непосредственно с помощью аксиом и логических теорем, но такие преобразования обычно требуют громоздких вычислений.
Более того, процесс упрощения булевых выражений не является алгоритмическим. Поэтому целесообразнее использовать специальные алгоритмические методы минимизации, которые позволяют упростить функции более простым, быстрым и безошибочным способом. К таким методам относятся, например, метод Квайна, метод карт Карно, метод импликантного теста, метод импликантной матрицы, метод Квайна-МакКласки и др. Эти методы наиболее подходят для рутинной практики, особенно для минимизации логической функции с помощью карт Карно. Метод карт Карно сохраняет ясность, когда число переменных не превышает шести. Если число аргументов больше шести, обычно используется метод Квейна-Маккласки.
В процессе минимизации заданной логической функции обычно рассматривается, на каком основании будет эффективнее реализовать ее минимальную форму с помощью электронных схем.
Минимизация булевых функций с помощью карт Карно
Карта Карно – это графический метод минимизации коммутативных (булевых) функций, обеспечивающий относительную простоту в работе с большими выражениями и устраняющий потенциальные гонки. Он представляет собой парные операции неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестановка таблицы истинности функции соответствующим образом. Карты Карно можно рассматривать как некоторую плоскую перестройку n-мерного булева куба.
Карты Карно, изобретенные в 1952 году Эдвардом В. Вейчем и усовершенствованные в 1953 году Морисом Карно, физиком из Bell Labs, были разработаны для упрощения цифровых электронных схем.
В карте Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое последующее число отличается от предыдущего только одной цифрой.
Основным методом минимизации булевых функций, представленных в терминах СПНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания выполняется между двумя терминами, содержащими одинаковые переменные, вхождения которых (прямое и обратное) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, могут быть удалены из скобок, а оставшиеся заключенные в скобки прямые и обратные вхождения одной и той же переменной могут быть подвергнуты склеиванию. Например:
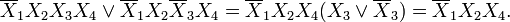
Возможность поглощения следует из очевидного равенства
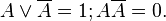
Таким образом, основной задачей минимизации NDFs и SCNFs является поиск терминов, подходящих для связывания и последующего поглощения, что может быть довольно сложным в больших формах. Карты Карно являются наглядным способом поиска таких терминов.
Как известно, булевы функции с N переменными, представленные в виде NDF или SCNF, могут иметь 2N различных членов в своем составе. Все эти термины образуют определенную структуру, топологически эквивалентную N-мерному кубу, и любые два термина, соединенные ребром, пригодны для склеивания и поглощения.
На рисунке показана простая таблица истинности для функций двух переменных, двумерный куб (квадрат), соответствующий этой таблице, и двумерный куб с SDNF-нотацией терминов и эквивалентной таблицей для группировки терминов:
Для функций трех переменных мы имеем дело с трехмерным кубом. Это более сложный и менее очевидный вариант, но технически возможный. На рисунке показан пример таблицы истинности для булевой функции трех переменных и соответствующий куб.
Как видно из рисунка, для случая с тремя переменными возможны более сложные конфигурации терминов. Например, четыре терма, принадлежащие одной стенке куба, объединяются в один терм с поглощением двух переменных: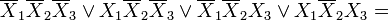 
В общем случае можно сказать, что 2K членов, принадлежащих одной стенке K-мерного гиперкуба, склеиваются в один член с K поглощенными переменными.
Чтобы упростить работу с булевыми функциями с большим числом переменных, была предложена следующая удобная техника. Куб, представляющий структуру терминов, разложен на плоскости, как показано на рисунке. Таким образом, можно представить булевы функции с более чем двумя переменными в виде плоского массива. Помните, что порядок кодов понятий в таблице (00 01 11 10) не соответствует порядку двоичных чисел, и что ячейки в крайних столбцах таблицы находятся рядом друг с другом.
Функции с четырьмя, пятью и более переменными могут быть обработаны аналогичным образом. Примеры таблиц для N=4 и N=5 показаны на рисунке. Для этих таблиц обратите внимание, что соседние ячейки – это ячейки в соответствующих ячейках крайних столбцов и соответствующих ячейках верхней и нижней строк. Для таблиц с 5 и более переменными также учитывайте, что квадраты 4×4 лежат практически один на другом в третьем измерении, поэтому соответствующие квадраты двух соседних квадратов 4×4 являются соседними, и соответствующие выражения можно склеить.
Карта Карно может быть составлена для любого количества переменных, но удобно работать не более чем с пятью переменными. По сути, карта Карно – это двумерная таблица истинности. Используя код Грея, верхняя строка примыкает к нижней строке, а правый столбец примыкает к левому столбцу, поэтому вся Карта сворачивается в форму тора (бублика). На пересечении строки и столбца записывается соответствующее значение из таблицы истинности. После того как карта составлена, можно приступать к минимизации.
Если нужна минимальная ДНФ, мы рассматриваем только те клетки, которые содержат единицы, если нужна КНФ, мы рассматриваем те клетки, которые содержат нули. Сама минимизация осуществляется по следующим правилам (на примере ДНФ):
- Мы объединяем соседние квадраты с единицами в область, так что одна область содержит 2 n (n integer = 0…
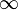) ячеек (помните, что крайние строки и столбцы являются смежными), область не должна содержать нулей; - Область должна быть симметричной относительно осей (оси располагаются через каждые четыре клетки);
- Области, не симметрично прилегающие к оси (осям), могут быть соединены вместе, чтобы образовать одну;
- Площадь должна быть как можно больше, а количество участков – как можно меньше;
- Области могут пересекаться;
- Возможны различные варианты перекрытия.
Затем возьмите первую область и посмотрите, какие переменные не изменяются в этой области, напишите конъюнкцию этих переменных, если переменная, которая не изменяется, равна нулю, поставьте над ней инверсию. Возьмите следующий регион и сделайте то же самое для первого региона, и так далее для всех регионов. Конъюнктуры регионов соединены конъюнктурой.
Например (для карты на 2 переменные):
Понятно, что при проектировании логических схем немаловажным является минимизация количества используемых элементов (другими словами, логических операций).
Минимизация карты Карно
Графический способ минимизации булевых функций. Представляет парные операции неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как правильно построенная таблица истинности функций.
Карты Карно можно рассматривать как некоторое плоское сечение n-мерного булева куба.
Изобретенные в 1952 году Эдвардом В. Вейчем и усовершенствованные в 1953 году Морисом Карно, физиком из Bell Labs, карты Карно были разработаны для упрощения цифровых электронных схем.
В карте Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое последующее число отличается от предыдущего только одной цифрой.
Булевы функции с ∗ переменными, представленные в виде SPNF или SCNF, могут иметь ∗ различных элементарных выражений.
Элементарные термины ФОС или СКНФ образуют структуру, топологически эквивалентную кубу размерности ∗. Действительно, если рассматривать множество значений функции ¯(x_1,¯,¯,x_N) как вектор из ¯(N) -мерных
Карно, Морис – Морис Карно (родился 4 октября 1924 года, Нью-Йорк) был американским физиком и изобретателем метода минимизации булевых функций, известного как “карта Карно”. Он изучал математику и физику в Городском колледже в Нью-Йорке с 1944 по 1948……..Wikipedia
Как работать с картой Карно
Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, давая ее значения при всех возможных 2 N наборы входных переменных X1 . XN. Карта Карно также содержит 2 N ячеек, каждая из которых связана с уникальным набором входных переменных X1 . XN. Таким образом, между таблицей истинности и картой Карно существует соответствие один-к-одному, и карту Карно можно рассматривать как соответствующим образом оформленную таблицу истинности.
В этом разделе мы будем использовать пример квадратичной функции, определяемой таблицей истинности, показанной на рис. 2a. Карта Карно для той же функции показана на рис. 2b.
Правила связывания
- Клетки карты Карно могут быть склеены единицами (если нам нужна ДНФ) или нулями (если нам нужна КНФ).
- Только прямоугольные области с количеством единиц (нулей) 2 n где n – является целым числом. Для карт Карно с более чем четырьмя переменными можно получить более сложные области, о чем будет рассказано в последующих главах.
- Склеенная область должна содержать только единицы (нули).
- Крайние клетки каждого уровня и каждой вертикали также граничат друг с другом (топологически карта Карно для четырех переменных является тором) и могут быть соединены в прямоугольники. Следствием этого правила является то, что все четыре угловые клетки карты Карно для N=4. Если все четыре угловые клетки имеют единицы (нули), их можно разделить на квадраты, как показано на рисунке 2c.
- Все единицы (нули) должны поместиться в некоторую область.
- С точки зрения минимальной ДНФ, количество областей должно быть как можно меньше (каждая область представляет собой терм), а количество ячеек в области как можно больше (чем больше ячеек в области, тем меньше переменных содержит терм). Термин размера 2 n клетки содержат N–n переменные).
- Одна ячейка карты Карно может принадлежать одновременно к нескольким областям. Это связано с очевидным свойством булевых функций: повторение уже существующей суммы (фактора) не влияет на функцию:
- В отличие от ДНФ (СКНФ), ДНФ (КНФ) не является уникальной. Возможны несколько эквивалентных ДНФ, которые соответствуют различным способам покрытия карты Карно прямоугольными областями.
Затем записываются алгебраические выражения логических функций для схем всех выходных и промежуточных элементов. Это самый критический момент при разработке бесконтактной системы автоматического управления. Составлены функции алгебры логики для всех реле, контакторов, соленоидов, сигнализаторов, которые включены в релейно-контакторную схему управления.
Минимизация комбинационных схем, карты Карно, синтез схем
В инженерной практике под логическим синтезом понимается процесс составления собственных функций конечного автомата, работающего по заданному алгоритму. Результатом этой работы должны стать алгебраические выражения для выходных и промежуточных переменных, на основе которых можно построить схемы, содержащие минимальное количество элементов. В результате такого синтеза можно получить несколько эквивалентных версий логических функций, алгебраические выражения которых удовлетворяют принципу минимальности элементов.
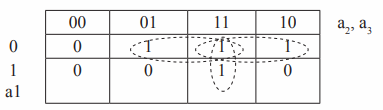Рисунок 1: Карта Карна
Процесс синтеза схемы заключается в основном в составлении таблиц истинности или карт Карно в соответствии с заданными условиями появления и затухания выходных сигналов. Метод определения логической функции с помощью таблиц истинности неудобен при большом количестве переменных. Гораздо проще определить логические функции с помощью карт Карно.
Карта Карно – это четырехугольник, разделенный на элементарные квадраты, каждый из которых соответствует различной комбинации значений всех входных переменных. Количество ячеек равно количеству всех наборов входных переменных – 2n, где n – количество входных переменных.
Обозначения входных переменных написаны сбоку и сверху карты, а значения переменных записаны в виде строки (или столбца) двоичных чисел в верхней части каждого столбца карты (или сбоку перед каждой строкой карты) и относятся ко всей строке или столбцу (см. рис. 1). Серия двоичных чисел записана таким образом, что соседние значения отличаются только для одной переменной.
Например, для одной переменной – 0.1. Для двух переменных – 00, 01, 11, 10. Для трех переменных – 000, 001, 011, 010, 110, 111, 101, 100. Для четырех переменных – 0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001, 1000. В каждой клетке записывается значение выходной переменной, соответствующей комбинации входных переменных для данной клетки.
Карта Карно может быть построена из словесного описания алгоритма, из графовой диаграммы алгоритма, а также непосредственно из логических выражений функций. В этом случае данное логическое выражение должно быть сведено к идеальной дизъюнктивной нормальной форме, под которой понимается дизъюнктивная форма логического выражения элементарных конъюнкций, имеющая полный набор входных переменных.
Логическое выражение содержит только конъюнкцию единичных компонентов, поэтому каждому набору переменных в конъюнкции должна быть присвоена единица в соответствующей ячейке карты Карно, а остальным ячейкам – ноль.
В качестве примера минимизации и синтеза комбинаторной схемы рассмотрим работу упрощенной транспортной системы. На рис. 2 показана система бункерного конвейера, состоящая из конвейера 1 с датчиком скольжения (SPS), расходного бункера 4 с датчиком верхнего уровня (ULS), затвора 3 и реверсивного конвейера 2 с датчиками наличия ленты (DNM1 и DNM2).
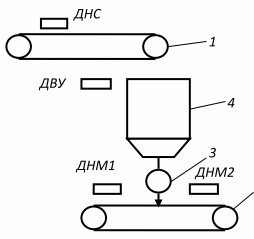
Рисунок 2: Транспортная система
Составим структурную формулу для включения аварийного реле в случае:
1) проскальзывание конвейера 1 (сигнал от датчика DNS);
2) переполнение бункера 4 (сигнал от датчика ДВУ);
3) отсутствие материала на ленте реверсивного конвейера при активации затвора (нет сигналов от датчиков наличия материала (DNM1 и DNM2).
Обозначим элементы входных переменных буквами:
Сигнал концевого выключателя затвора – a3.
Сигнал DNM1 – a4.
Сигнал DNM2 – a5.
Итак, у нас есть пять входных переменных и одна выходная функция P. Карта Карно будет иметь 32 ячейки. Ячейки заполняются в зависимости от условий работы реле сигнализации. Те ячейки, в которых значения переменных a1 и a2 условно равны единице, заполняются единицами, так как сигнал от этих датчиков должен активировать реле тревоги. Блоки также помещаются в ячейки при выполнении третьего условия, т.е. когда ворота открыты и на реверсивном конвейере нет материала.
Чтобы минимизировать функцию в соответствии с ранее упомянутыми свойствами карт Карно, мы разграничиваем контурами ряд единиц, которые по определению являются соседними клетками. В контуре, охватывающем вторую и третью линии карты, все переменные, кроме a1, меняют свои значения. Поэтому функция этого контура будет состоять только из одной переменной a1.
Аналогично, функция второго контура, охватывающего третью и четвертую линии, будет состоять только из переменной a2. Функция третьего контура, охватывающего последний столбец карты, будет состоять из переменных a3, a4 и a5, так как переменные a1 и a2 изменяют свои значения в этом контуре. Таким образом, функции булевой алгебры этой системы имеют следующий вид:
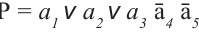
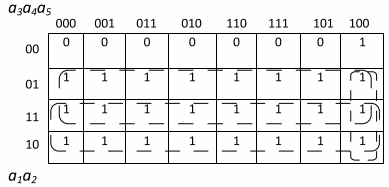
Рисунок 3: Карта Карно для транспортной цепи
На рисунке 3 показаны схемы реализации этого FAL на релейно-контактных элементах и на логических элементах.
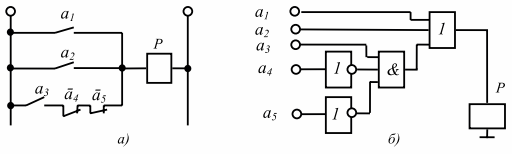
Рисунок 4: Схема управления аварийным реле транспортной системы: a – схема контактного реле; b – логические элементы
Помимо карты Карно, существуют и другие методы минимизации функций алгебры логики. В частности, существует метод прямого аналитического упрощения выражения функции, заданной в SDNF.
В этой форме можно найти компоненты, которые отличаются значением одной переменной. Такие пары компонент также называются аддитивными, и в них, как и в карте Карно, функция не зависит от переменной, которая изменяет ее значение. Поэтому, применяя закон конкатенации, можно сократить выражение на одну конъюнкцию.
Проделав это со всеми соседними парами, можно избавиться от повторяющихся конъюнкций, применив закон идемпотентности. Полученное таким образом выражение называется сокращенной нормальной формой (СНФ), а конъюнкции, входящие в СНФ, называются импликантами. Если к функции можно применить закон обобщенного склеивания, то функция будет еще меньше. После всех вышеперечисленных преобразований функция называется мертвой.
Синтез логических структурных схем
В инженерной практике часто возникает необходимость перехода от релейно-контактных схем к бесконтактным схемам на основе логических элементов, оптопар и тиристоров с целью усовершенствования аппаратуры. Чтобы осуществить этот переход, можно использовать следующую методологию.
После изучения лестничной диаграммы все сигналы, действующие в схеме, делятся на входные, выходные и промежуточные, а затем им присваиваются буквы. Входные сигналы включают в себя сигналы состояния концевых и шаговых выключателей, кнопок управления, универсальных переключателей (кулачковых контроллеров), датчиков, контролирующих технические параметры, и т.д.
Выходные сигналы управляют исполнительными механизмами (магнитные пускатели, электромагниты, сигнальные устройства). Промежуточные сигналы возникают при активации промежуточных элементов. Существуют реле для различных применений, например, реле времени, реле отключения механизмов, реле сигнализации, реле выбора режима и т.д. Контакты этих реле обычно включаются в цепи выходов или других промежуточных элементов. Промежуточные элементы делятся на сигналы без обратной связи и сигналы с обратной связью. Первые имеют в своих схемах только входные переменные, вторые – переменные входные, промежуточные и выходные сигналы.
Затем записываются алгебраические выражения логических функций для всех выходных и промежуточных схем. Это самый важный момент при проектировании бесконтактной системы управления. Алгебраические логические функции разрабатываются для всех реле, контакторов, соленоидов, сигнальных устройств, входящих в релейно-контакторную схему управления.
Релейные и контакторные устройства в силовой цепи устройства (тепловые реле, реле сверхтока, автоматические выключатели и т.д.) не описываются логическими функциями, поскольку эти элементы не могут быть заменены логическими элементами в соответствии с их функциями. Если имеются бесконтактные версии этих элементов, они могут быть включены в логику управления вместе с их выходными сигналами, которые должны быть учтены алгоритмом управления.
Полученные таким образом структурные формулы могут быть использованы для построения блок-схемы логических элементов нормальной формы на основе булевых формул (AND, OR, NOT). Следует придерживаться принципа минимального количества элементов и корпусов логических элементов. Для этого необходимо подобрать ряд логических элементов таким образом, чтобы он полностью реализовывал все структурные функции алгебры логики в минимальном диапазоне. Часто для этой цели подходят логические элементы “ВЗАИМОДЕЙСТВИЕ” и “ВЗАИМОДЕЙСТВИЕ”.
При конструировании логических устройств не принято использовать функционально полную систему логических элементов, реализующую все основные логические операции. На практике для ограничения номенклатуры элементов используется расположение элементов, включающее только два элемента, реализующих операции И-НЕ (полоса Шеффера) и ИЛИ-НЕ (стрелка Пирса) или даже только один из этих элементов. И обычно определяется количество входов этих элементов. Поэтому вопросы синтеза логических устройств в заданной базе логических элементов имеют большое практическое значение.
Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!
Хотя карты Карно представлены на плоскости, смежность квадратов определяется на поверхности тора. Верхняя и нижняя границы карты склеены вместе, как будто они образуют поверхность цилиндра. Склеивание боковых границ образует поверхность тора.
Метод минимизации карт Карно
Карты Карно – это графическое представление таблиц истинности логических функций. Они содержат по 2 n ячеек, где n – количество логических переменных. Например, график Карно для функции трех переменных содержит 2 n =2 3 =8 клеток, а для четырех переменных – 2 4 =16 клеток.
Система координат, соответствующая значениям входных переменных, нанесена на карту. Обратите особое внимание, что координаты столбцов (а также координаты строк, если n>3) следуют не в естественном порядке возрастания двоичных кодов, а в следующем: 00 01 11 10. Это делается для того, чтобы соседние наборы (включая столбцы 1 и 4) отличались только одной цифрой в любом разряде.
Процесс минимизации заключается в формировании правильных прямоугольников, содержащих по 2 k клеток, где k – целое число. Прямоугольники соединяют соседние ячейки, которые соответствуют соседним элементам (т.е. отличаются только одной цифрой).
Хотя карты Карно изображаются на плоскости, соседи квадратов фиксируются на поверхности тора. Верхняя и нижняя границы карты склеены вместе, как если бы они образовывали поверхность цилиндра. Склеивание боковых границ образует поверхность тора.
Пример: Минимизируйте функцию трех переменных, заданную таблицей истинности (таблица 6).
Таблица 6 Таблица истинности для функции трех переменных
| X1 | X2 | X3 | Y |
Нарисуйте карту Карно и отметьте ее стороны:
Рисунок 8 Карта Карно для функций 3 переменных.
Мы создаем два прямоугольника на карте Карнота. Первая соединяет (так сказать, в скобках) первые два минтерма (члена), а вторая соединяет первый и третий члены SPNF минимизирующей функции выше. Минтермы, заключенные в скобки, отличаются только одной цифрой. Их инвариант, выведенный за скобки методом вычислительной минимизации, является минимальным значением функции:
Таким образом, карта Карно позволяет размещать соседние элементарные продукты, отличающиеся только одним фактором, в соседних клетках.
Порядок операций при минимизации:
1 Показана карта Карно и отмечены ее стороны.
2 Клетки карты Карно, соответствующие наборам переменных, преобразующих функцию в “1”, заполнены единицами, остальные – нулями.
3 Выбирается наилучшее покрытие карты прямоугольниками. Наилучшим покрытием считается то, которое образовано минимальным количеством прямоугольников, а если таких вариантов несколько, то выбирается тот, который дает максимальную площадь прямоугольников.
Пример: Минимизируйте функцию четырех переменных, представленную картой Карно: (Рисунок 9).
Крайние клетки, соответствующие комбинациям 00 и 10, являются соседними и отличаются на одну переменную а.
Метод карты Карно
Карта Карно (карта минимизации) – это преобразование некоторой трехмерной фигуры в плоскость. Карта Карно состоит из клеток, число которых равно числу наборов переменных функции. Каждая ячейка соответствует четко определенному набору.
Например, карта Карно для одной переменной (рис. 1.14): п = 1, количество наборов N = 2″ = 2.
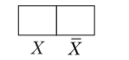
Рисунок 1.14. Карта Карно для одной переменной
Карта Карно для двух переменных (рисунок 1.15): п = 2, количество комплектов N=2 2 – 4.
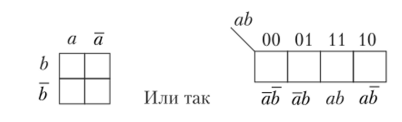
Рисунок 1.1 5. Карта Карно для двух переменных
Крайние клетки, соответствующие комбинациям 00 и 10, являются соседними и отличаются на одну переменную а.
Переменные в карте могут быть расположены произвольно, но Ячейки, соседние по вертикали и горизонтали, могут отличаться не более чем на одну переменную.
Карта Карно для трех переменных (рисунок 1.16): п = 3, количество наборов L = 2 3 = 8.
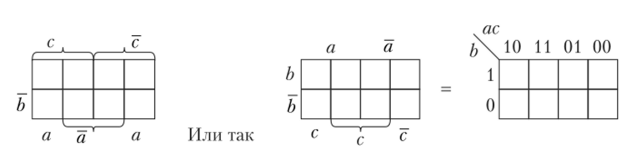
Рисунок 1.16. Карта Карно для трех переменных
Если существует функция от трех переменных, приведенных в таблице истинности ниже, то соответствующая карта Карно выглядит как на рисунке 1.17.
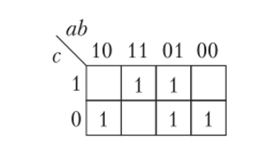
Рисунок 1.17. Карта Карно функции
Обычно нули в карту не вносятся, только единицы. Карта Карно для четырех переменных (рисунок 1.18): I = 4, JV = 16.
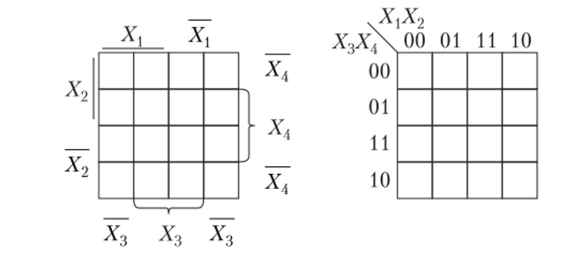
Рисунок 1.18. Карта Карно для функций четырех переменных
В этих картах переменные расположены по-разному, но обе карты верны, поскольку горизонтально или вертикально соседние клетки отличаются только по одной из переменных. Ячейки в верхней строке соседствуют с ячейками в нижней строке, а ячейки в крайнем правом столбце соседствуют с ячейками в крайнем левом столбце.
Карта Карно для пяти переменных (рисунок 1.19): п = 5, N=32. Это две 16-клеточные карты, отличающиеся только одной (пятой) переменной.
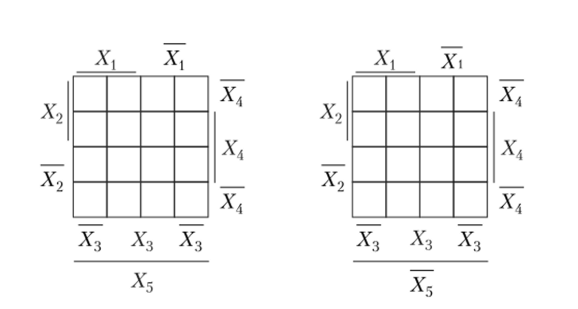
Рисунок 1.19. Карта Карно для функций пяти переменных
Карта Карно для шести переменных (рисунок 1.20): п = 6, N = 64. Это четыре 16-клеточные карты.
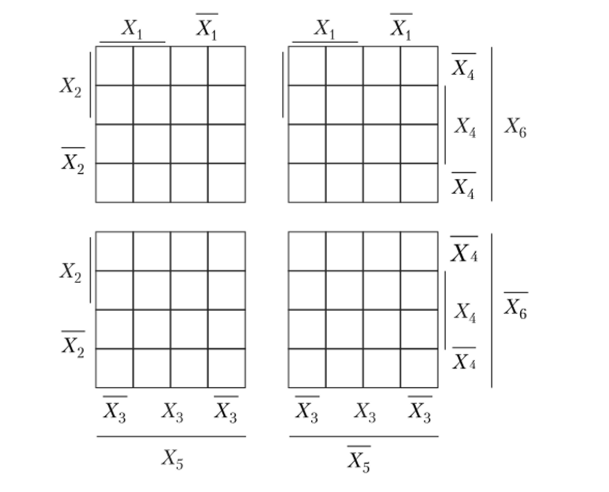
Рисунок 1.20. Карта Карно для функций шести переменных
Здесь любые ячейки являются смежными, если они отличаются только одной переменной.
Заполнив карту единицами из таблицы истинности, мы переходим к минимизации. Суть минимизации: Покройте все единицы карты Карно наименьшим количеством кубиков самого высокого ранга. Из каждого куба выписываются минимальные значения общих переменных. Минтермы дизъюнктивно связаны.
Куб это прямоугольный или квадратный контур, содержащий клетки с единицами:
- – единица является кубом с рангом “0”, так как 2°=1;
- – две единицы – куб ранга “1”, так как 2 1 = 2;
- – четыре единицы – куб ранга “2”, так как 2 2 = 4;
- – восемь единиц – куб ранга “3”, так как 2 3 = 8;
- – 16 единиц – куб “ранга 4”, так как 2 4 = 16 и т.д.
Куб не может содержать любое другое количество единиц и клеток с нулями. Одна и та же единица может одновременно принадлежать нескольким кубам, так чтобы ранг куба был наивысшим. Тогда форма будет в точности минимальной.
Требуется найти МДНФ такой функции: F (a, b, c) = v(l, 3, 6, 7). Составьте его таблицу истинности:
Читайте далее: