Цепи переменного тока с конденсатором

Используя треугольники токов и проводимостей, определите значения

Цепь переменного тока с конденсатором

Когда переменное напряжение прикладывается к реальному конденсатору, небольшие токи проводимости возникают через толщу диэлектрика (объемный ток) и на поверхности (поверхностный ток). Токи проводимости и поляризация диэлектрика сопровождаются потерями энергии.

Таким образом, в реальном конденсаторе, помимо изменения энергии электрического поля (характеризуемого реактивная мощность Qиз-за несовершенства диэлектрика происходит необратимый процесс преобразования электрической энергии в тепловую, скорость которого выражается через активная мощность P. Поэтому реальный конденсатор должен быть представлен на схеме активным и реактивным элементом.

Разделение реального конденсатора на два элемента является расчетным методом, поскольку конструктивно разделить их невозможно. Однако реальная цепь с двумя элементами, один из которых характеризуется только активной мощностью P (Q = 0), а другой – реактивной (емкостной) мощностью Q(P = 0), имеет такую же схему.

В реальном конденсаторе при изменении энергии электрического поля (это характеризует реактивную мощность) происходит необратимый процесс преобразования электрической энергии в тепловую, вызванный несовершенством диэлектрика, скорость которого выражается активной мощностью. Поэтому реальный конденсатор должен быть представлен на схеме активным и реактивным элементом.

Эквивалентная схема конденсатора с параллельным соединением элементов

В реальном конденсаторе, помимо изменения энергии электрического поля (характеризуемого реактивной мощностью 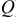) из-за несовершенства диэлектрического материала происходит необратимый процесс преобразования электрической энергии в тепловую, скорость которого выражается активной мощностью 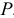. Поэтому реальный конденсатор должен быть представлен активным и реактивным элементом в эквивалентной схеме.

Реальный конденсатор (с потерями) может быть представлен эквивалентной схемой параллельного активного 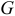и ёмкостный проводимость (рис. 9.13), где активная проводимость определяется емкостью конденсатора с потерями 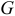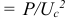а емкость определяется структурой конденсатора.

Предположим, что проводимост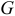и и для такой цепи известны, а напряжение имеет уравнение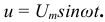

Требуется определить токи в цепи и мощность.

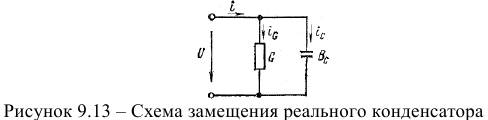
Изучение цепи с активным сопротивлением и цепи с емкостью показало, что когда напряжение синусоидально, токи в них также синусоидальны. При параллельном соединении ветве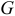й и согласно первому закону Кирхгофа, полный ток 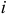это сумма токов в активной и емкостной ветвях: .

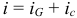Для определения среднеквадратичного значения полного тока Используя метод сложения векторов, построим векторную диаграмму в соответствии с уравнением: 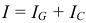Эффективные величины компонентов тока: .

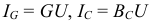Первый вектор в векторной диаграмме – это вектор напряжения (рис. 9.14 а), его направление совпадает с положительным направлением оси, с которой отсчитываются фазовые углы (начальная фаза напряжения ).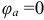

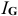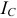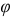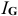вектор совпадает по направлению с вектором и вектор перпендикулярна вектору с положительным углом. Из векторной диаграммы следует, что вектор полного напряжения заторможен по отношению к вектору полного тока на угол значение которого больше нуля, но меньше 90°. вектор гипотенуза прямоугольного треугольника, катетами которого являются составляющие его векторы и :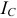

При напряжении 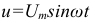в соответствии с векторной диаграммой уравнение тока .

Стороны треугольников тока, выраженные в единицах тока, деленного на напряжение 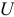. Аналогичный треугольник проводимости (рис. 9.14 6) получается при активном 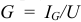и емкость 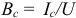проводимость, а гипотензия – общая проводимость цепи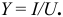

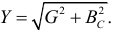
Из треугольника проводимости:

Эта страница относится к странице лекций по Теоретическим основам электротехники (ТЭ):

Вы можете найти эти страницы полезными:

Образовательная страница для школьников и студентов

Эта страница не может быть скопирована без активной ссылки “www.lfirmal.com”.

© Людмила Анатольевна Фирмаль – Официальный сайт Дальневосточного государственного физико-технического института, факультет математики

Довольно сложным и в основном неизученным аспектом предмета AC является построение векторных диаграмм. При анализе вынужденных электромагнитных колебаний мы уже обсуждали смещение тока и напряжения на реактивных сопротивлениях (катушке и конденсаторе) относительно активного сопротивления (резистора). Тогда одним из вопросов, задаваемых в задаче, является направление общего тока или напряжения в данный момент времени. Для ответа на этот вопрос используется метод векторной диаграммы.

Построение векторных диаграмм

Довольно сложным и в основном неизученным аспектом переменного тока является метод векторных диаграмм. При анализе вынужденных электромагнитных колебаний мы уже обсуждали смещение тока и напряжения на пассивных сопротивлениях (катушке и конденсаторе) по отношению к активному сопротивлению (резистору). Поэтому одним из вопросов, задаваемых в этой задаче, является направление общего тока или напряжения в данный момент времени. Для ответа на этот вопрос используется метод векторной диаграммы.

Векторная диаграмма – это представление гармонически изменяющихся величин (тока и напряжения) в виде векторов на плоскости.

Рисунок 1: Векторная диаграмма

Векторные диаграммы строятся в прямоугольной декартовой системе координат. Мы начинаем построение с рисования вектора, численно равного значению амплитуды тока в цепи. Этот вектор соосен с осью OX (рис. 1.1).

Поскольку напряжение на активном резисторе находится в той же фазе, что и ток, вектор амплитуды напряжения соосен с вектором тока (рис. 1.2. красный).

На катушке напряжение опережает ток, поэтому наклоним вектор амплитуды напряжения на катушке () вверх относительно вектора тока (рис. 1.2. синий).

Напряжение на конденсаторе отстает от тока, поэтому наклоним вектор амплитуды напряжения на конденсаторе () вниз относительно вектора тока (рис. 1.2, зеленый).

Угол , используемый в строительной логике, применяется, когда цепь и катушка идеальны.

Чтобы построить общий вектор напряжения, просто сложите напряжения векторно:

Проще всего сначала найти вектор суммы (так как они расположены вдоль одной прямой). В нашем случае эти векторы направлены по-разному, найдем (рис. 1.3 желтый).

Наконец, остается сложить полученные вектора, чтобы получить значение общего напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора мы воспользуемся теоремой Пифагора, так как векторы находятся под прямым углом. Тогда:

• где
  • – общее напряжение в цепи,
  • – напряжение на конденсаторе,
  • – напряжение на индукторе,
  • – напряжение на активном резисторе.

  Угол между вектором тока и вектором полного напряжения называется сдвиг фаз между переменным током и напряжением. Этот параметр также можно найти в параметрах системы:

  • где
    • – активное сопротивление,
    • – импеданс цепи.

    ЗаключениеСледующие задачи касаются нахождения сдвига фаз между колебаниями тока и напряжения по графику (рис. 1.4) или через соотношение (3), а также поиска полного напряжения цепи также по графику (рис. 1.4) или через соотношение (2).

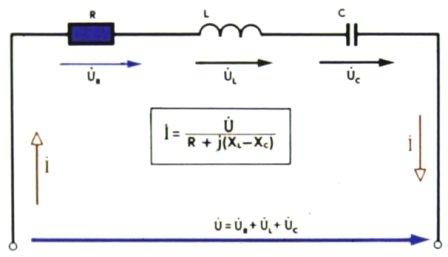
    Электрическая цепь с последовательно соединенными элементами R и L:

    Однофазные цепи переменного тока. Векторные диаграммы

    Последовательная цепь с резистивным, индуктивным и емкостным элементом:

    

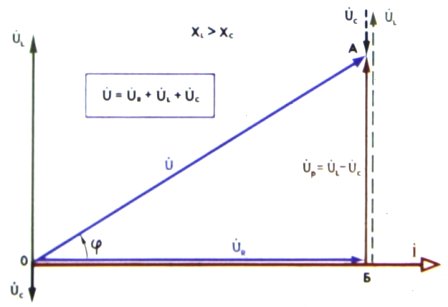
    Треугольники напряжений для последовательного соединения R, L и C:

    

    Треугольники напряжения и сопротивления с последовательно соединенными R, L и C:

    

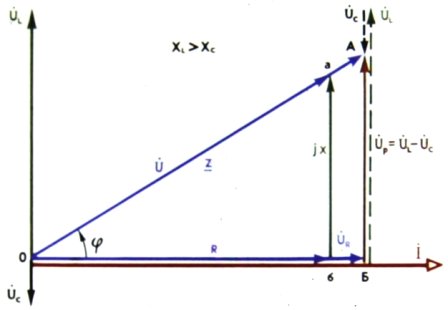
    Треугольники напряжения, сопротивления и емкости при последовательном соединении R, L и C:

    

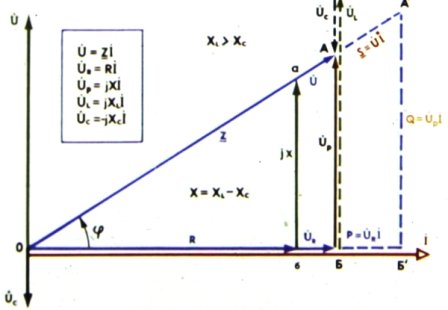
    Треугольники напряжения, сопротивления и емкости:

    

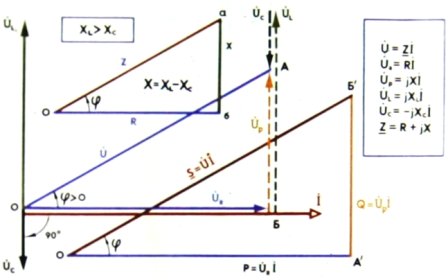
    Цепь с R, L и C соединена параллельно:

    

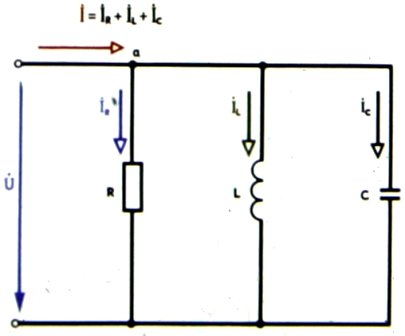
    Треугольники токов при параллельном соединении R, L и C:

    

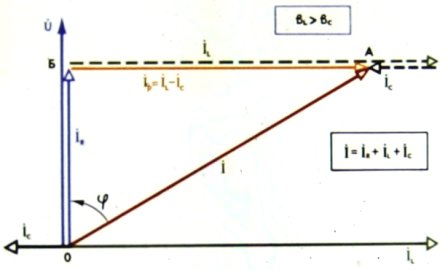
    Треугольники токов и проводимости при параллельном соединении R, L и C:

    

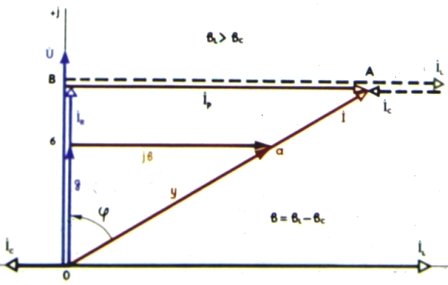
    Треугольники токов, проводимости и емкости при параллельном соединении R, L и C:

    

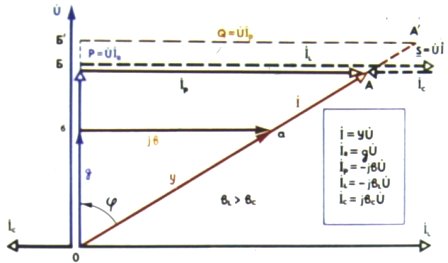
    Треугольники токов и проводимости:

    

    

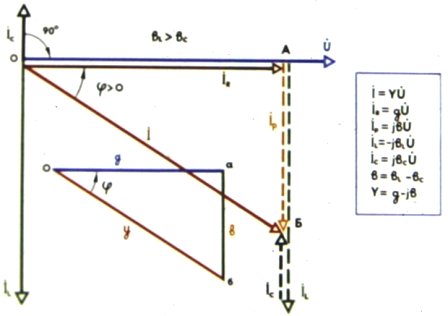
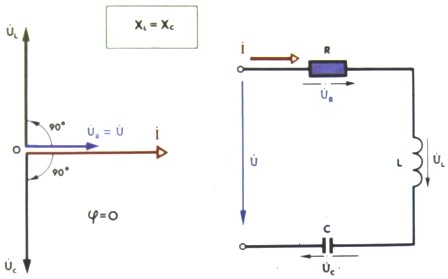
    График мгновенных значений u, i и p при резонансе напряжений:

    

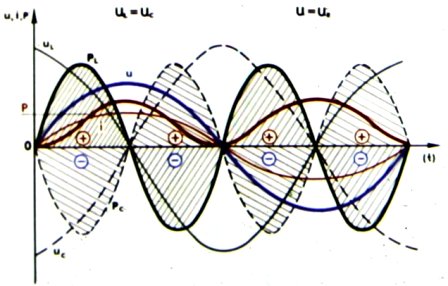
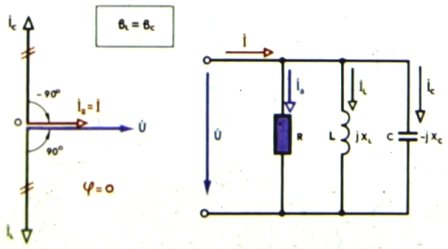
    Схема параллельного контура из R , L и C при резонансе токов:

    

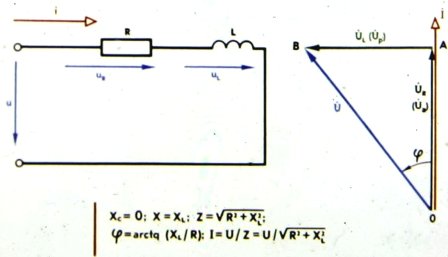
    Электрическая цепь, в которой элементы R и L соединены последовательно:

    

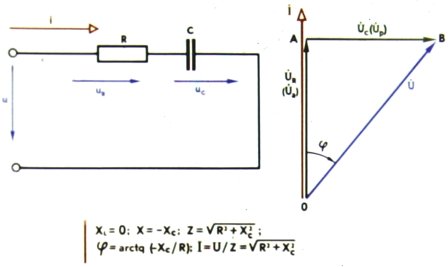
    Электрическая цепь, в которой элементы R и C соединены последовательно:

    

    Увеличение cos φ с помощью конденсаторов:

    

    Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

    Суммирование векторов происходит по правилу многоугольника (который вырождается в прямую линию и соединяется с мнимой осью). Напряжение на резисторе имеет тот же аргумент, что и входной ток, векторы и коллинеарны. Входное напряжение определяется вторым законом Кирхгофа

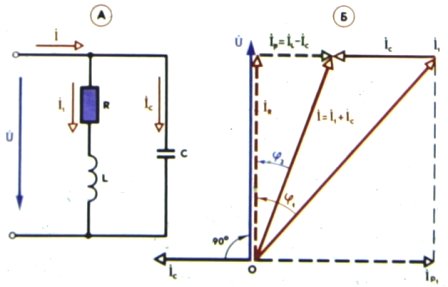
    Векторная диаграмма цепи с параллельным соединением

    Начнем построение схемы цепи с вектора напряжения, который одинаков для всех элементов цепи и определяет их токи, предположим 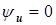. Ток резистора также имеет нулевую начальную фазу, векторы 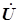и 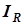коллинеарны (рисунок 4.14).

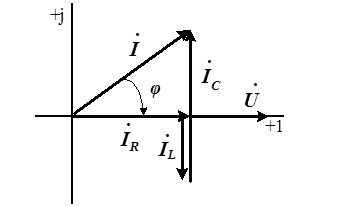
    Рисунок 4.14: Векторная диаграмма токов и напряжений для параллельной цепи

    соединение элементов ( )

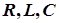    Векторы тока в реактивных элементах 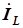и 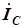перпендикулярны вектору напряжения. вектор 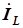заторможен по отношению к вектору 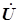по . вектор 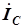опережает вектор напряжения на . 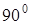. Векторы тока 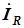, 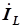и 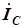построены в порядке, соответствующем отдельным элементам схемы. Начало каждого последующего вектора выравнивается с концом предыдущего для упрощения суммирования трех текущих векторов.

    Согласно первому закону Кирхгофа

    ,

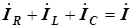    где 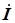– входной комплексный ток. Векторы тока в элементах цепи суммируются в схеме по правилу многоугольника. Фазовый угол между напряжением и током в этом случае отрицательный, а рассматриваемая цепь является емкостной (в параллельных ветвях сети). 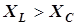и соответственно ).

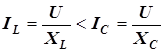    Векторная диаграмма смешанной цепи

    Элементы

    Векторную диаграмму токов и напряжений для цепи, показанной на рис. 4.15, начнем с вектора напряжений на параллельных элементах, которому присвоена нулевая начальная фаза ( , ).

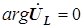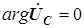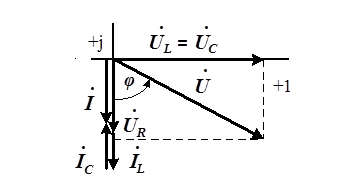
    Рис. 4.15. векторная диаграмма напряжений и токов в смешанном соединении

    элементы . ( )

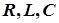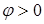    Векторы тока в реактивных элементах перпендикулярны вектору напряжения 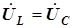. вектор 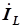заторможен по отношению к вектору по . Вектор 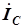обгоняет вектор 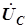по 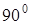. Входной ток определяется первым законом Кирхгофа

    ;

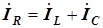    Суммирование векторов производится по правилу многоугольника (который вырождается в прямую линию и соединяется с мнимой осью). Напряжение на резисторе 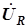имеет тот же аргумент, что и входной ток 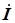векторы 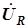и коллинеарны. Входное напряжение определяется вторым законом Кирхгофа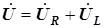

    ;

    Сложение векторов выполняется по правилу параллелограмма. Угол между входным напряжением и током положительный. Рассматриваемая цепь является индуктивной ( 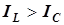, 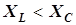в параллельных ветвях).

    Если комплексные напряжения и 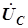, с которого начинается диаграмма, не имеет нулевых аргументов, а принимает то есть прямые векторы и 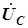вдоль мнимой оси, векторная диаграмма на рис. 4.15 переходит из четвертого квадранта комплексной плоскости в первый квадрант. Все векторы после и 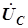будет повернута против часовой стрелки на .

    Если источник переменного тока подключен к резистору, ток и напряжение пропорциональны. Это означает, что их пик приходится на одно и то же время. Если конденсатор подключен к переменному напряжению, максимальный ток и напряжение пропорциональны. Ток достигает максимума в точке ¼ цикла пикового напряжения (приводит к 90°).

    Формулы для измерения напряжения конденсатора

    Численное значение напряжения равно электродвижущей силе. Она также определяется как емкость, деленная на величину заряда, исходя из формулы для определения его величины. Согласно другому правилу, напряжение равно току утечки, деленному на сопротивление изоляции.

    Может быть интересно определить ток короткого замыкания

    
    Основные формулы для расчетов

    В общем, конденсатор – это накопитель электрического заряда, состоящий из нескольких пластинчатых электродов, разделенных диэлектриком. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, значения которого можно рассчитать по формулам, описанным выше.

• Полное сопротивление цепи переменного тока – Основы электроники.
• Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.
• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• Векторная диаграмма трансформатора.
• Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.