Тяговое усилие следует рассматривать как сумму двух сил:
Тяговое усилие
Тяговая сила – это сила, приложенная к телу для поддержания его в непрерывном движении.
Потеря силы тяги вызывает пробуксовку из-за трения, вязкости среды и других сил, противодействующих движению.
Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называется состоянием инерции. Чтобы вывести тело из этого состояния, к нему необходимо приложить силу. Скорость тела при этом изменится, т.е. оно приобретет ускорение (или замедление, которое можно рассматривать как отрицательное ускорение).
Величина ускорения обратно пропорциональна массе тела (чем оно массивнее, тем труднее вывести его из состояния инерции) и прямо пропорциональна интенсивности приложенной силы. Таким образом:
- $F$ – это сила,
- $m$ – это масса,
- $a$ – ускорение.
Эта формула отражает второй закон Ньютона.
Переведем тонны в килограммы и килоньютоны в ньютоны:
Тяжелее Легче
Вес тела $<duże p=””>$ выражается произведением его массы $<duże m=””>$ и гравитационное ускорение $<duże g=””>$.
Когда тело легче лежит на земле (давление веса меньше), это приводит к уменьшению масса. На Луне это не так, уменьшение массы связано с изменением другого множителя, $<duże g=””>$, потому что гравитационное ускорение на поверхности Луны в шесть раз меньше, чем на Земле.
Ускорение силы тяжести Земли = $$ 9,81 м / c^2 >$
Гравитационное ускорение на Луне = $<<dużo 1,62=”” m=”” c^2=””>$
В результате продукт $<dużo m=””>$$, а значит и вес, уменьшается в 6 раз.
Но оба явления не могут быть описаны одним и тем же выражением “сделать легче”. На Луне тела не становятся легче, а только “меньше падают”).
$F_-F_-m g sin ≥alpha=m a(3)$
Основной единицей силы в СИ является [FT]=Н
Задание. На автомобиль массой 1 тонна, движущийся по горизонтальной поверхности, действует сила трения, равная $mu$=0,1 силы тяжести. Какова будет сила сопротивления, если автомобиль движется с ускорением 2 м/с?
Решение. Сделайте рисунок.
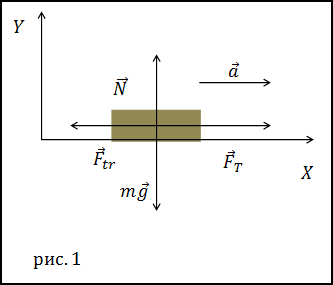
Используйте второй закон движения Ньютона в качестве основы для решения задачи:
Нанесите уравнение (1.1) на оси X и Y:
По постановке проблемы:
Подставляя правую часть выражения (1.4) вместо силы трения в (1.2), получаем
$F_=m a+ =m a+mu m g$
Переведите массу в СИ m=1t=10 3 кг, выполните расчет:
Ответ. FT=2,98 кН
Формула для силы тяги вам не по зубам? Эксперт расскажет вам за 10 минут!
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске лежит тело массой m. Коэффициент трения тела о доску равен $mu$ . К доске прикладывается горизонтальное тяговое усилие, которое зависит от времени как: F=At (где A=const). В какой момент планка начнет уходить из-под тела?
Решение. Давайте прикинем.
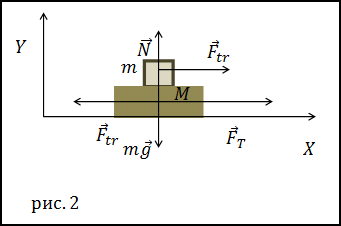
Для решения задачи нам нужны проекции сил на оси X и Y, которые ненулевые. Для тела массой m:
$ старт X: m a_<1>=F_(2.1) Y: m g=N (2.2) F_= = =mu N=mu m g rightarrow m a_<1>=mu m g rightarrow a_<1>=mu g (2.3) end $
Для тела массой M:
$M a_<2>=F-F_ Правая стрелка M a_<2>=A t-F_. стрелка вправо a_<2>= F-F_.>(2.2)$
Обозначает момент времени, в который доска начинает уходить из-под тела t0тогда
В современной физике эта формулировка была уточнена:
Формулы для определения тягового усилия
Согласно второму закону Ньютона, сумма сил, действующих на движущееся тело, равна его массе, умноженной на его ускорение. Не существует универсальной формулы для любой комбинации сил. Сила погружения чаще всего определяется по общей формуле ( F_t-; F_<с>=m), где F_t – сила сопротивления, F_<с> представляют собой силы сопротивления.
При решении конкретной задачи силы, действующие на тело, представляются схематично в виде векторов. В программе:
- гравитационная сила мг;
- Сила реакции опоры ∙ (Н) ;
- сила трения ∙ (F_)<тр>) ;</тр>
- тяговое усилие ∙(F) .
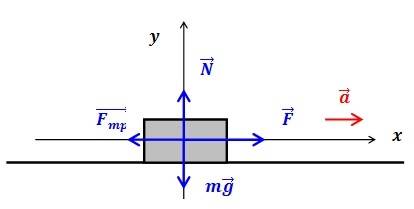
Когда тело находится на горизонтальной поверхности, сила тяжести и сила реакции опоры уравновешивают друг друга. Однако, если автомобиль движется в гору или под уклон, необходимо учитывать влияние уклона. Таким образом, формула может выглядеть следующим образом: (F_т-;F_с-;mg;times;sinalpha=m;times;a.)
Работа A, которую совершит сила тяги, перемещающая тело, связана с ней соотношением ¯(A = F = F = ¯) . ¯ – это расстояние, на которое переместилось тело.
Какое условие должно быть выполнено
Сила контакта всегда должна быть больше противодействующей силы.
Формула мощности
Полезная механическая мощность (N) может быть рассчитана по формуле (N=F_t;v), где (v) – скорость. Чтобы определить тягу, разделите мощность на скорость: (F_t;= frac N v.)
F_n), действующего на стенку обсадной трубы; следовательно,
Квант. Тяговое усилие
В заданиях по механике, особенно по Механической силе, часто встречается величина, называемая тяговой силой – поезда, автомобиля, самолета, велосипеда и т.д. Что это за сила? Какова его природа?
Иногда можно услышать ответ, что поскольку, например, автомобиль приводится в движение двигателем, сила тяги действует со стороны двигателя. Очевидно, что это не так. Внутренние силы, действующие от одной части системы к другой, не могут изменить скорость системы в целом – это противоречило бы закону сохранения импульса. Тогда становится ясно, что нам необходимо рассмотреть силы, действующие на автомобиль извне, из внешнего мира. Так, в случае автомобиля или поезда сила тяги – это сила трения покоя, действующая на ведущие колеса со стороны дороги; в случае аэроплана – это сила реакции воздуха, отбрасываемого назад. Правильно, для того чтобы сила трения покоя была направлена вперед, двигатель должен вращать колеса в нужном направлении, заставляя их как бы прилипать к дороге и создавать силу тяги. Так что без двигателя далеко не уедешь.
Зачем же вводить какую-то силу тяги, вместо того, чтобы написать просто “сила трения покоя” или “сила реакции воздуха”? Оказывается, все силы, действующие на автомобиль со стороны окружающих тел, удобно разделить на две части: одна часть называется силой тяги FTа другая – сила сопротивления FC. В этом случае, во-первых, уравнения движения принимают универсальную форму. Таким образом, для автомобиля, движущегося в гору с наклоном αмы пишем
F_T – F_C – mg ¯sin ¯alpha = ma¯. (1)
Во-вторых, механическая мощность, которую необходимо передать, очень просто выражается в виде тяги:
P_0 = F_T n n n n; (2)
где υ – скорость транспортного средства. (Как мы увидим, эту формулу можно рассматривать как своего рода определение полезной мощности автомобиля). Формулы (1) и (2) позволяют понять многие процессы, связанные с ускорением или движением автомобиля.
Водители знают, например, что при разгоне автомобиля на ровной дороге невыгодно включать большую мощность на низких скоростях. Действительно, когда сила тяги равна (
Frac<) достигает максимальной силы трения покоя μNколеса начинают вращаться, что крайне нежелательно. А максимальная мощность Pmax можно использовать только в том случае, если скорость (
■upsilon_0 = ■frac<>><), а до этого нужно плавно наращивать мощность. Большинство из вас, вероятно, прекрасно знают об этом, но меня побудило написать этот пост нечто другое. Дело в том, что формула для полезной мощности (2), внешне соответствующая определению механической мощности и поэтому не привлекающая особого внимания, содержит неожиданный парадокс. Должен признаться, что долгое время я не обращал на это внимания. Из чего она состоит?
Как уже упоминалось, сила тяги автомобиля, например, есть не что иное, как сила трения покоя, приложенная со стороны дороги к нижним точкам ведущих колес. Но эти точки (если, конечно, колеса не проскальзывают) касаются дороги, т.е. имеют нулевую скорость. Таким образом, работа силы трения покоя, а значит и работа силы тяги, равна нулю!
В первый момент, когда я осознал это, я почувствовал легкий страх. Нет, меня не испугал закон сохранения энергии – энергия не обязательно должна поступать в систему извне. Хотя внутренние силы, создаваемые двигателем, не могут изменить импульс системы, они могут изменить ее энергию. Например, если двигатель использует энергию от сгорания топлива, часть этой энергии будет потеряна во время работы двигателя, а часть будет преобразована в полезную механическую энергию. Однако, если в системе нет двигателя, обеспечивающего необходимую энергию, внешняя тяга должна быть “организована” для выполнения работы самостоятельно. (Пример: При буксировке автомобиля с выключенным двигателем тяговое усилие – это тяговое усилие тросов).
Проблема заключалась в том, что универсальная формула (2) потеряла свою очевидность. Стало неясно, можно ли использовать его в такой простой форме для решения различных задач, или же придется каждый раз рассчитывать полезную мощность на основе конкретной конструкции двигателя.
Рассмотрим, например, игрушечный автомобиль, в котором источником энергии является энергия упругой деформации пружины. Для простоты мы будем пренебрегать массой колес и пружины. Полезной работой в данном случае является сила, приложенная к телу, которая равна сумме силы (
■, действующая на ось колеса, и сила натяжения ≥ (
F_n), действующего на стенку тела; следовательно,
P_0 = (F_0 – F_n) .
Поскольку масса колеса равна нулю, сумма всех сил, действующих на колесо, равна нулю, т.е.
Поэтому, P0как в (2), равна произведению FTυ. В чем проблема? Мог ли это быть несчастный случай?
Чтобы понять причину этого совпадения, рассмотрим то, что в общем случае мы называем полезной механической работой, связанной с перемещением транспортного средства любого характера. Во-первых, это работа против сил сопротивления (
A_1 = F_C ), во-вторых, работа по увеличению кинетической энергии поступательного движения (
A_2 = Frac <2>- frac<2>) и, в-третьих, работа по изменению потенциальной энергии (
A_3 = mg delta h). Потерянная энергия – это потери тепла в механизме, кинетическая энергия вращения колес, движения шатунов, поршней и т.д., другими словами, все то, что не входит в энергию поступательного движения автомобиля в целом.
А теперь немного математики. Умножьте обе части формулы (1) на Δl. Принимая во внимание, что (
mg ΔDelta l ¯ þalpha = mg ΔDelta h ¯), мы пишем
F_T Delta l = F_C Delta l + left(frac <2>- figure. <2>{истина) + mg delta h) .
Получается, что величина, формально составленная как работа силы тяги FT на пути Δl (в действительности сила тяги не совершает никакой работы), в точности равна полезной работе A1 + A2 + A3. Поэтому полезную мощность можно смело рассчитывать по уравнению (2)!
Таким образом, мы видим, что сила тяги, определяемая как внешняя сила, входящая в уравнение движения (1), не совершает никакой работы, поскольку она приложена к неподвижной точке колеса. Более того, та часть работы двигателя, которая называется полезной работой, равна работе силы тяги, как если бы она была приложена не к неподвижной точке, а к движущемуся кузову автомобиля. Но самое главное – мы еще раз убедились, что за обычными и средними, на первый взгляд, понятиями скрываются зачастую неожиданные вопросы и парадоксы, над которыми стоит и стоит задуматься.
A – механическая работа [Дж]
Примеры решения проблем
Проблема 1
Ложка медленно погружается в большую банку с медом. На него действуют сила тяжести, вязкое трение и выталкивающая сила. Какая из этих сил совершает положительную работу при движении тела? Выберите правильный ответ:
- Толкающее усилие.
- Сила вязкого трения.
- Сила тяжести.
- Ни одна из вышеперечисленных сил.
Решение
Поскольку ведро падает вниз, смещение направлено вниз. Только сила тяжести направлена в ту же сторону, что и смещение. Это означает, что он выполняет положительную работу.
Ответ: 3.
Проблема 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной скоростью по модулю. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Какова работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая была затрачена на работу трения, должна быть передана системе за счет работы силы тяги. Отсюда получаем работу тягового усилия на оборот:
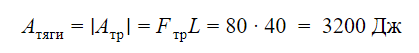
Ответ: 3200 J.
Проблема 3
Тело массой 2 кг под действием силы F движется вверх по наклонной плоскости на расстояние l = 5 м. Таким образом, расстояние тела от поверхности Земли увеличивается на 3 метра. Вектор силы F параллельна наклонной плоскости, модуль силы F составляет 30 Н. Какая работа была совершена при этом перемещении в системе отсчета, связанной с наклонной плоскостью, силой F?
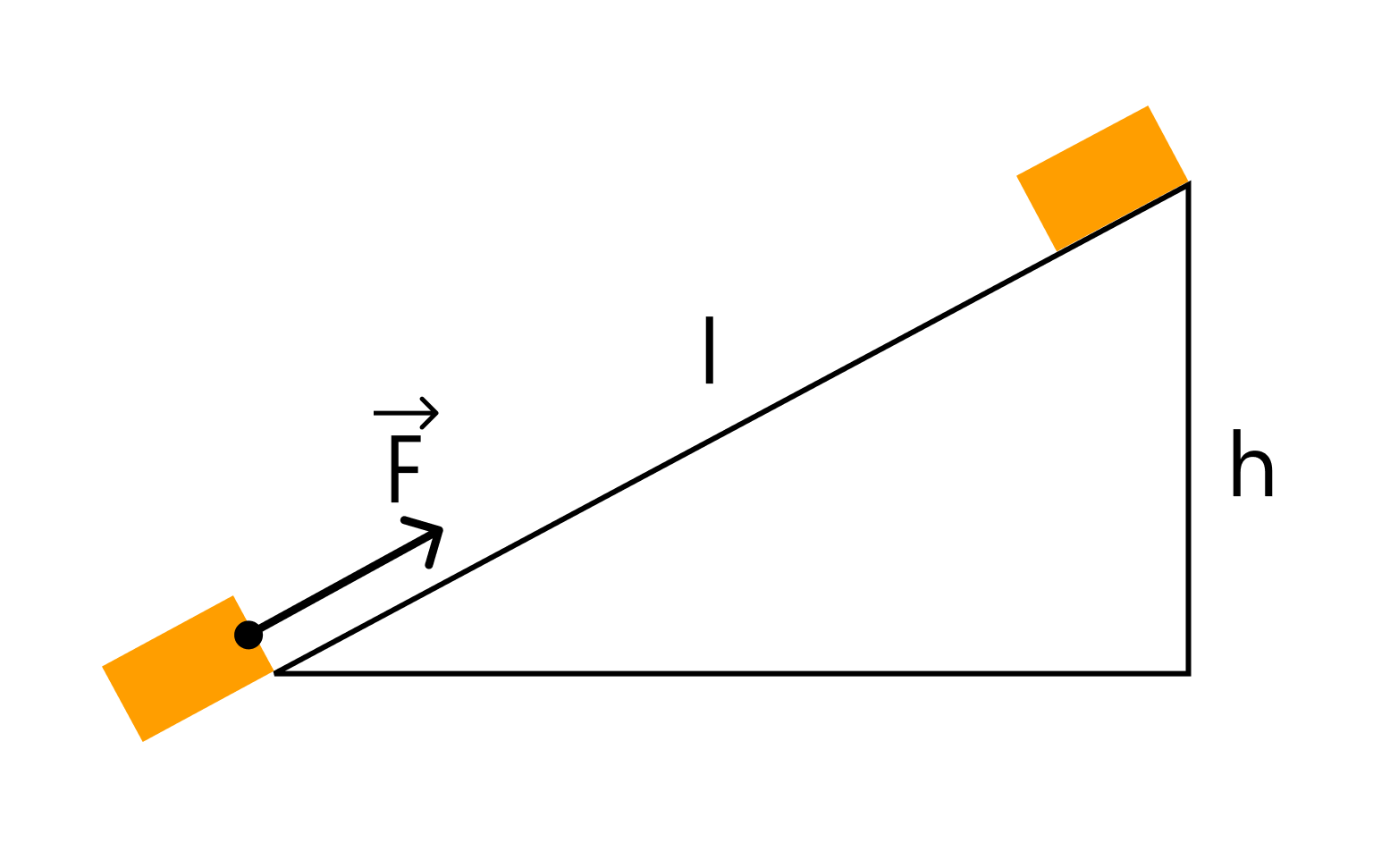
Решение
В данном случае нас просят найти работу силы Fпроведенный по движению тела по наклонной плоскости. Это означает, что нас интересует сила F и пройденное расстояние. Если бы нас спросили о работе силы тяжести, мы бы считали в терминах силы тяжести и высоты.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 J.
Проблема 4
Тело движется вдоль оси OX под действием силы F = 2 Н, направленная вдоль этой оси. Диаграмма на рисунке показывает проекцию скорости v x тела на этой оси как функция времени t. Какова мощность, развиваемая этой силой в момент времени t = 3 с?
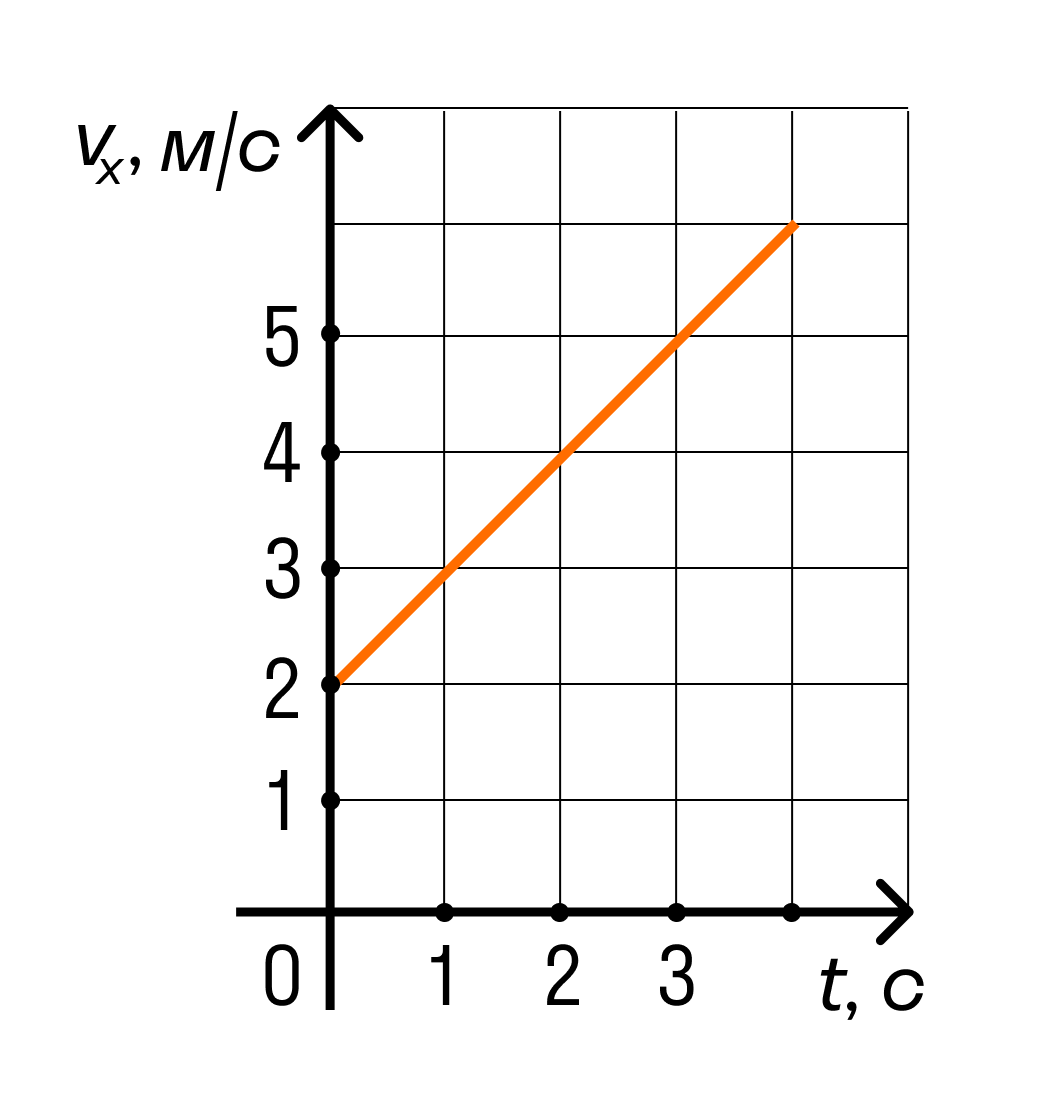
Решение
Из графика следует, что проекция скорости тела в 3 секунды равна 5 м/с.
Мощность можно рассчитать по формуле N = Fv.
N = Fv = 2×5 = 10 Вт
Ответ: 10 W.


Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Зарегистрироваться для участия в марафоне
- 0
- 0
- 0
- 0
- 0
- 0
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
</с></с></dużo></dużo></duże></duże></duże></duże>
Читайте далее:- Шаговые двигатели: свойства и практические схемы управления. Часть 2.
- Затухающие колебания – это. Что такое затухающие колебания?.
- Силы в физике.
- Перемещение и пройденное расстояние. Скорость ППД.
- Ответы: Какая величина: масса или сила – является вектором.
- Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.