УКВ – это. Что такое ГФЧ?

Фильтр В электронике – устройство для выделения желаемых компонентов спектра электрического сигнала и/или подавления нежелательных компонентов.

На странице пассивные аналоговые фильтры Используются реактивные элементы, такие как индукторы и конденсаторы. Сопротивление реактивного сопротивления зависит от частоты сигнала, поэтому, комбинируя эти элементы, можно усиливать или ослаблять гармоники на нужных частотах.

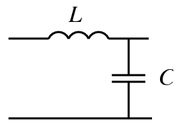
LC-фильтр

На рисунке показан пример простейшего LCФильтр низких частот: Когда сигнал определенной частоты подается на вход фильтра (слева), напряжение на выходе фильтра (справа) определяется отношением реактивных сопротивлений индуктора ( X_L = ωL ) и конденсатор (ω X_C = 1 / ωC ).

Коэффициент усиления УНЧ можно рассчитать, рассматривая делитель напряжения, сформированный из резисторов, зависящих от частоты. Комплексное сопротивление (с учетом сдвига фаз между напряжением и током) катушки индуктивности равно Z_L = jωL = jX_L конденсатор i Z_C = 1 / (jωC) = − jX_C где 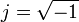поэтому для разгруженный LC-фильтр

.

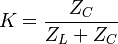Подставив значения сопротивлений, мы получим коэффициент усиления в зависимости от частоты:

.

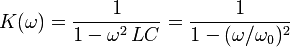Как видно, коэффициент усиления ненагруженного идеального LPF неограниченно возрастает по мере приближения к частоте 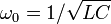а затем уменьшается. На очень низких частотах коэффициент усиления LPF близок к единице, а на очень высоких частотах он равен нулю. В общем случае, частотная зависимость модуля комплексного коэффициента передачи фильтра называется амплитудно-частотная характеристика (АФК) и фазовая зависимость частотно-фазовая характеристика (FFC).

В реальных системах к выходу фильтра подключается активная нагрузка, которая снижает добротность фильтра и предотвращает резкий резонанс АЧХ вблизи частоты ω₀ . Значение 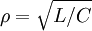называется . характеристический импеданс фильтра. LPF, нагруженный импедансом, равным характеристическому импедансу, имеет нерезонансную частотную характеристику, которая приблизительно постоянна на частотах ω < ω₀ и уменьшается как 1 / ω 2 на частотах выше ω₀ . Поэтому частота ω₀ называется частота среза.

Аналогичным образом LC-Фильтр высоких частот строится аналогичным образом. Индуктор и конденсатор меняются местами в схеме HPF. Разгруженный LPF имеет следующий коэффициент усиления:

.

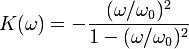На очень низких частотах модуль усиления THF близок к нулю. На очень высоких частотах он близок к единице.

Фильтры высоких частот

Как работает UFV

Фильтры высоких частот

Фильтры высоких частот работают прямо противоположно фильтрам низких частот: они эффективно пропускают частотный спектр выше определенной частоты (частоты среза) и ослабляют (затухают) частоты ниже этой частоты. Исходя из вышеизложенного, можно сделать вывод, что конструкции индуктивных и емкостных фильтров высоких частот противоположны соответствующим конструкциям фильтров низких частот:

” width=”347″ height=”179″>

Емкостной фильтр высоких частот

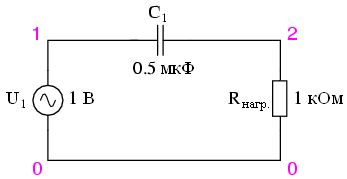
С уменьшением частоты импеданс конденсатора увеличивается. Этот высокий импеданс при последовательном соединении блокирует сигналы низких частот от попадания в нагрузку. Этот вывод можно проверить с помощью анализа SPICE:

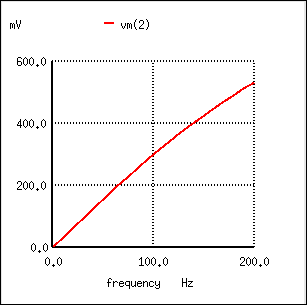!” width=”307″ height=”305″>

<1-omega^2,LC>=frac<1><1-(omega/omega_0)^2>,!” width=”344″ height=”174″>

Индуктивный фильтр высоких частот

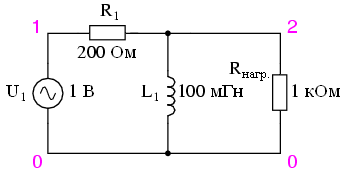
С уменьшением частоты импеданс индуктора уменьшается. Этот низкий импеданс при подключении параллельно сопротивлению нагрузки имеет тенденцию к “короткому замыканию” низкочастотных сигналов, пропуская большую часть напряжения через последовательный резистор R₁.

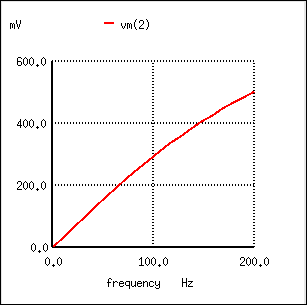” width=”307″ height=”305″>

На этот раз конструкция емкостного фильтра высоких частот является самой простой, требующей только одного компонента – конденсатора. Опять же, конденсаторы являются более “чистыми” реактивными элементами, чем индукторы, поэтому их использование в конструкции фильтров предпочтительнее. Использование индуктивных фильтров высоких частот может создать дополнительные проблемы, поскольку высокие частоты иногда способствуют неправильному поведению индукторов (из-за скин-эффекта и электромагнитных потерь в сердечнике).

Фильтры высоких частот, как и фильтры низких частот, имеют номинальную частоту среза, выше которой выходное напряжение поднимается выше 70,7% от входного напряжения. Частота среза простого емкостного фильтра высоких частот может быть рассчитана по той же формуле, что и расчет частоты среза простого емкостного фильтра низких частот:

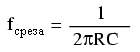
В схеме примера нет никакого сопротивления, кроме сопротивления нагрузки. Именно это сопротивление мы подставим в формулу вместо значения R.

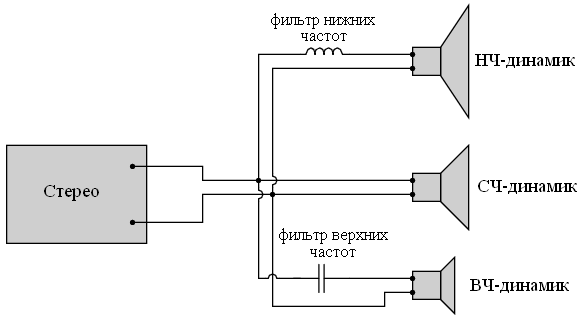
В качестве примера рассмотрим стереосистему. В этой системе конденсатор, подключенный последовательно с высокочастотным (высокочастотным) динамиком, действует как фильтр высоких частот, накладывая высокий импеданс на низкочастотные (басовые) сигналы, тем самым не позволяя им достичь динамика, который неэффективен для воспроизведения таких звуков. Индуктор, подключенный последовательно с низкочастотным динамиком, будет действовать как фильтр низких частот, не позволяя высоким частотам достигать этого динамика. Среднечастотный динамик воспринимает весь диапазон частот, воспроизводимых стереосистемой. В реальном оборудовании могут использоваться более сложные схемы фильтров, но этого должно быть достаточно для ознакомительных целей. Обратите также внимание, что мы показали только один стереоканал (левый или правый). Настоящая стереосистема содержит 6 динамиков: 2 низкочастотных динамика, 2 среднечастотных динамика и 2 высокочастотных динамика.

<1-(™omega/ ™omega_0)^2>.” width=”587″ height=”320″>

Для улучшения характеристик хорошо бы иметь фильтр, способный пропускать все частоты, кроме высоких и низких, к среднечастотному динамику. Такой фильтр называется полосовым фильтром, и мы рассмотрим его в следующей статье.

6. используя входное значение на шаге 3, рассчитайте выходное напряжение на частоте среза.

8. фильтры низких и высоких частот

После завершения этого эксперимента вы сможете рассчитать частоту среза резистивно-емкостных фильтров низких и высоких частот, а также узнать о влиянии изменения частоты на выходное напряжение.

Необходимые принадлежности

* Цифровой мультиметр

Один конденсатор 0,01 мкФ, один резистор 15 кОм

ВВЕДЕНИЕ

Фильтр – это частотно-чувствительная схема, амплитуда выходного сигнала которой изменяется в зависимости от частоты на входе.

Фильтр низких частот – это фильтр, который пропускает частоты меньше заданной частоты среза (fco), но ослабляет частоты, превышающие частоту среза. Фильтр высоких частот это фильтр, который пропускает частоты, превышающие определенную частоту среза, но ослабляет частоты, меньшие, чем частота среза.

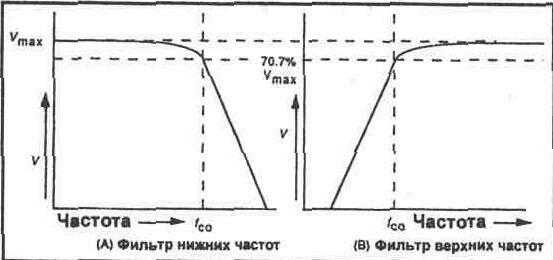
Частоты, которые ниже частоты среза. На рисунке 23-1 показаны выходные характеристики фильтров низких и высоких частот.

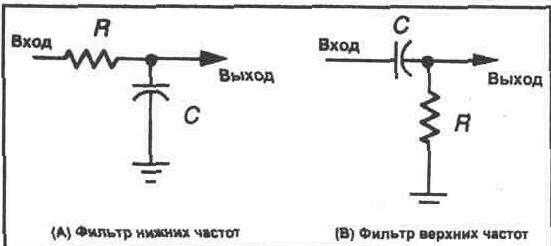
Фильтры низких и высоких частот могут быть реализованы различными способами. Простейший фильтр представляет собой резистор и конденсатор, соединенные вместе, как показано на рисунке 23-2.

Характеристики фильтра

Ключевой характеристикой фильтра низких или высоких частот является его частота среза (fco). Как показано на рисунке 23-1, частота среза – это частота, при которой выходное напряжение фильтра падает до 70,7% от максимально возможного выходного напряжения. В фильтре низких частот выходное напряжение остается относительно постоянным при увеличении частоты входного сигнала. По мере приближения к частоте среза выходное напряжение начинает уменьшаться. При достижении частоты отсечки выходное напряжение падает до 70,7% от максимально возможного значения. Выходное напряжение уменьшается при увеличении частоты.

В фильтре высоких частот выходное напряжение достигает максимального значения, когда частота входного сигнала превышает частоту среза на некоторое расстояние. При постепенном снижении входной частоты выходное напряжение уменьшается по мере приближения к частоте среза. При достижении частоты отсечки выходное напряжение падает до 70,7% от максимально возможного значения. Выходное напряжение продолжает уменьшаться при дальнейшем снижении частоты входного сигнала.

В фильтре низких частот сигналы с частотами

ниже fco проходят с небольшим затуханием или вообще без него; сигналы с частотами выше fco быстро затухают. В фильтре высоких частот сигналы ниже fco значительно ослабляются, а сигналы выше fco проходят через него практически без ослабления.

выше fco, проходят с минимальным противодействием. Снова обратитесь к рисунку 23-1.

Частота среза простого резисторно-конденсаторного фильтра, такого как показан на рисунке 23-2, рассчитывается по следующей формуле:

Пример: Если R = 3,3 кΩ и C = 0,15 мкФ, то частота среза составляет

fco = 1/6.28(3300)(0.15 x 10^-6)

Резюме

В этом эксперименте вы узнаете о работе резистивно-емкостных фильтров высоких и низких частот. Поскольку в настоящее время у нас нет средств для точного измерения частот, можно получить лишь общее представление о работе фильтра. Однако можно четко показать, что эти фильтры пропускают некоторые частоты с минимальным ослаблением, в то время как другие сильно ослаблены.

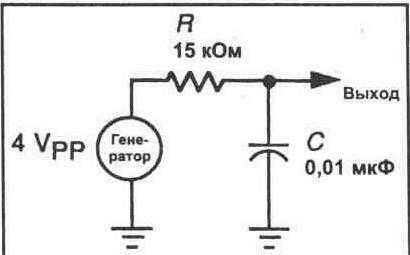
1 Рассчитайте частоту среза фильтра низких частот, показанного на рисунке 23-3.

fco______Hz

2. Соберите схему, показанную на рисунке 23-3,

Используйте разделочную доску. Подключите резистивно-емкостной фильтр к входу функционального генератора.

3. Установите регулятор частоты функционального генератора на 10 Гц. Затем поверните ручку регулятора амплитуды, чтобы подать на схему пиковое напряжение 4 В.

4. затем измерьте выходное напряжение фильтра на конденсаторе. Запишите полученное значение.

Выходное напряжение фильтра = ___ В

5. подключите осциллограф к конденсатору фильтра. Наблюдая за выходным напряжением, поверните ручку регулировки частоты, чтобы увеличить частоту до 1000 Гц. Увеличивается или уменьшается выходное напряжение?

________ увеличивается

_________ уменьшается

(6) На основе входного значения, полученного на шаге 3, рассчитайте выходное напряжение на частоте среза.

Напряжение на частоте среза

Частота среза = ________ V

7. Используя функциональный генератор, подайте в схему синусоидальный сигнал на каждой из частот, указанных в таблице ниже. Во время изменения частоты

Снова проверьте входное напряжение и убедитесь, что оно по-прежнему составляет 4 вольта от пика до пика. Измерьте выходное напряжение фильтра на каждой частоте и запишите результаты в таблицу ниже.

Произведение сопротивления и емкости ( R × C ) – постоянная времени (τ); она обратно пропорциональна частоте среза f _c то есть

Дискретно-временная реализация.

Также могут быть разработаны фильтры высоких частот дискретного времени. Разработка фильтра дискретного времени выходит за рамки данной статьи, но простым примером является преобразование фильтра высоких частот непрерывного времени, описанного выше, в дискретную реализацию. Это означает, что поведение в непрерывном времени может быть дискретизировано.

Из приведенной схемы на рисунке 1 следует, что согласно законам Кирхгофа и определению емкости :

Где – заряд, накопленный в конденсаторе в момент времени . Подставляя уравнение (Q) в уравнение (I), а затем уравнение (I) в уравнение (V), получаем: Q c ( t ) < Displaystyle Q_ (t ) > t

Это уравнение может быть дискретизировано. Для простоты предположим, что входные и выходные данные отбираются через равные промежутки времени. Пусть образцы представлены последовательностью , и пусть образцы представлены последовательностью, соответствующей тем же моментам времени. Выполнив эти замены: Δ T < displaystyle Delta _ > V w < displaystyle V _ < text >> ( X 1 , X 2 , … , X p ) < displaystyle (x_ <1>, x_ <2>, ldots, x_ )> V вне < displaystyle V _ < text >> ( y 1 , y 2 , … , y p ) < displaystyle (y_ <1>, y_ <2>, ldots, y_ )>

Это означает, что дискретная реализация простого RC-фильтра высоких частот с непрерывным временем является

Алгоритмическая реализация

Отношение повторения фильтра обеспечивает способ определения выходных выборок в терминах входных выборок и предшествующих выходных данных. Следующий псевдокод моделирует влияние восходящего фильтра на серию цифровых выборок, предполагая, что выборки расположены с одинаковым интервалом:

Цикл , который вычисляет каждый выход, может быть преобразован в эквивалент: n

Однако в более ранней форме было показано, как параметр α изменяет влияние предыдущего выхода y [i-1] и текущий изменить на входе (x [i] - x [i-1]) . В частности,

• Большое значение α означает, что выходной сигнал будет затухать очень медленно, но при этом будет сильно зависеть даже от небольших изменений входного сигнала. Согласно приведенной выше зависимости между α и постоянной времени, большое значение α соответствует большой и, следовательно, низкой угловой частоте фильтра. Следовательно, этот случай соответствует фильтру высоких частот с очень узкой полосой пропускания. Поскольку он возбуждается при небольших изменениях и имеет тенденцию сохранять свои предыдущие выходные значения в течение длительного времени, он может передавать относительно низкие частоты. Однако, фиксированный вход (т.е. вход z (x [i] - x [i-1]) = 0 ) всегда будет уменьшаться до нуля, как и следовало ожидать от фильтра высоких частот с большим . p C < displaystyle RC>p C < displaystyle RC>p C
• Малое значение α означает, что выход быстро затухает и требует больших изменений на входе (т.е. (X [i] - x [i-1]) является большим) для того, чтобы выход существенно изменился. Согласно взаимосвязи между параметром α и постоянной времени, упомянутой выше, малое значение α соответствует малой и, следовательно, высокой угловой частоте фильтра. Следовательно, этот случай соответствует фильтру высоких частот с очень широкой полосой пропускания. Поскольку это требует больших (т.е. быстро) меняется и имеет тенденцию быстро забывать предыдущие выходные значения, он может пропускать только относительно высокие частоты, как и следовало ожидать от фильтра высоких частот с низким . p C < displaystyle RC>p C < displaystyle RC>p C < displaystyle RC>p C

Следовательно, значение конденсатора равно 0,1 мкФ.

Фильтр высоких (HPF) и фильтр низких частот (LPF/LPF) в ламповом усилителе

Мне хотелось углубиться в тему ламповых усилителей, их простых и увлекательных схем, особенностей среды, в которой они работают и прочего, но я понял, что если начать рассказ сразу с какого-то интересного, но произвольного момента, без определенных теоретических знаний, то читатель может не набраться грамотности и будет продолжать тыкать дохлую белку палкой (заменять конденсаторы и резисторы, тыкая), надеясь, что белка оживет.

Если посмотреть на многие схемы ламповых усилителей, то глаз легко заметит цепочки фильтров. Они могут возникнуть там, где начинающий дизайнер никогда бы о них не подумал, то же самое касается и местных отзывов.

Итак, сегодня генеральная репетиция перед основным введением в ламповое усиление – будем разбираться с фильтрами.

При разработке схем обычно используют фильтр низких частот и фильтр высоких частот. Эта тема уже разбиралась в материалах ЦАПа на сайте, но имела свою специфику.

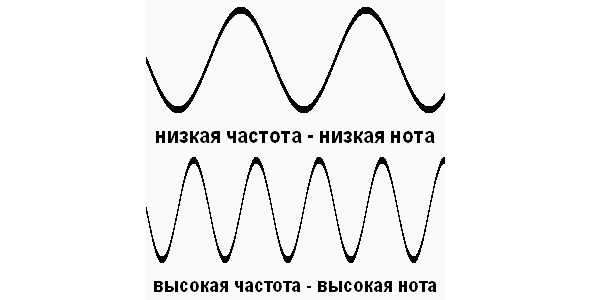
Во-первых, название фильтра – это не то, чем он кажется.

Например, фильтр низких частот предназначен для… отсекают высокие частоты.

Другими словами, он пропускает низкие частоты до определенной частоты, выше которой – все, проход закрыт. Английское название этого фильтра более понятно – LPF – Low Pass Filter.

Так, если вы хотите отсечь диапазон частот, скажем, от 0 до 35000 Гц, вам нужен фильтр низких частот (ФНЧ), который вы устанавливаете на верхнюю частоту среза 35000 Гц.

Другая ситуация – если вы хотите отсечь низкие частоты, в этом случае вам нужен фильтр высоких частот (HPF).

HPF пропускает все частоты от самого низкого значения частоты вверх.

Например, вы хотите, чтобы частотный диапазон вашего устройства начинался от 20 Гц и выше.

Вам нужен фильтр HPF, который будет отсекать все нижние частоты от 0 до Гц и пропускать все, что выше 20 Гц.

Фильтры высоких и низких частот создаются на схеме из набора резисторов и конденсаторов из-за того, как эти элементы реагируют на определенные частоты.

В фильтре высоких частот сначала стоит конденсатор, а затем резистор, см. рисунок.

напоминание, в VFD для отсечения всего, что ниже определенной частоты среза. Например, 20 Гц, и все, что ниже этого значения, не пройдет, а все, что выше 20 Гц, пройдет. То есть, мы отсекаем “низы” с помощью фильтра высоких частот.

Фильтр низких частот (ФНЧ) также состоит из резистора и конденсатора, но они меняются местами, см. рисунок ниже:

И вы устанавливаете верхний предел соответствующим образом, то есть отсекаете “пики”, а все, что ниже, остается. Например, вы установили его на 35 кГц, и все, что выше этой частоты, не пройдет, а все, что ниже, останется.

Таким образом, по логике вещей, чтобы ограничить диапазон устройства 20 Гц – 20 кГц, необходимо использовать оба фильтра, отсекая частоты выше (LPF) и ниже (HPF).

Чтобы было легче запомнить – LPF срезает верхние части, LFF – нижние.

Такая перевернутая логика.

Теперь с помощью небольшой математики рассчитайте, какие значения резистора и конденсатора необходимы для достижения желаемой частоты среза.

Поскольку фильтры высоких частот мы чаще всего видим в ламповых усилителях, давайте рассмотрим какую-нибудь похожую схему и определим, на какой частоте неизвестный автор схемы устанавливает срез (схема взята из Интернета).

Честно говоря, мне потребовалось время, чтобы найти схему для демонстрации примера, потому что в 9 из 10 случаев я понял, что авторы схем вообще не понимали значения используемых номиналов, а значения фильтров были просто maybes.

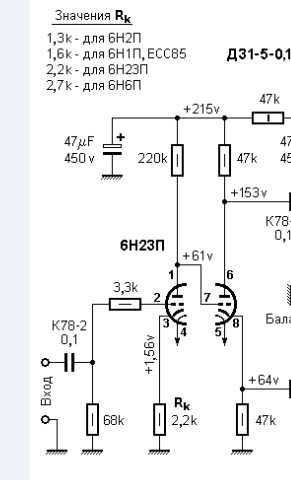
Внимательно посмотрите на раздел схемы, видите ли вы фильтр УКВ? Если вы еще не определили его, я выделил FFF ниже, заключив его в красный квадрат.

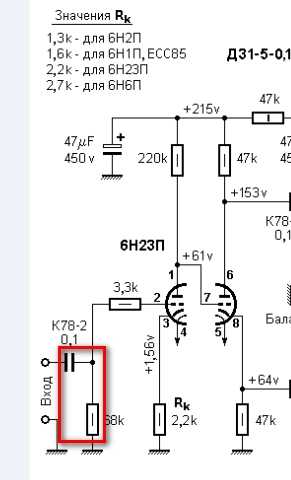
Давайте определим, какие частоты обрезает этот фильтр. Поскольку это HPF (фильтр высоких частот), он отсекает “низкие тона”. Следовательно, это должно быть какое-то небольшое значение в герцах, вплоть до 20-30.

Все формулы рассчитываются в основных величинах, т.е. в Омах, Фарадах, Герцах, а не в мега, кило, микро и т.д.

Итак, для начала нам нужно знать, как преобразовать микро/пико/нано/килограмм, мега в соответствующие значения для расчетов.

1 пикофарад = 0,0000000001 F или 1 * 10 до -12-й силы

1 нанофарад = 0,000000001 F или 1 * 10 до -9-й силы

1 микрофарад = 0,000001 F или 1 * 10 до -6-й силы

1 мегаом = 1000000 Ом

Например, давайте переведем 100 микрофарад в фарады.

1 фарад равен 10 в степени -6.

Вы можете сделать это более простым или более сложным способом. Проще говоря, 100 – это два нуля, или +2 градуса, а фарад – это -6 градусов, так что +2-6=4 градуса. Таким образом, наше число будет иметь 4 знака после запятой.

100 мкф преобразуется в 0,0001(00) Ф.

Посчитайте, сколько цифр после запятой – 4.

В противном случае умножьте 100 мкФ на число с 6 десятичными цифрами, последняя из которых не равна нулю:

100 * 0,000001= 0,0001 Ф

Хорошо, давайте немного углубимся в основы дворовой математики.

Формула, по которой рассчитывается частота среза, выглядит следующим образом:

Fчастота среза = 1/ 2Pi * R * C

R – номинальный резистор фильтра

C – номинал конденсатора фильтра

Pi равно 3,14, поэтому 2Pi = 2*3,14 = 6,28.

Давайте посмотрим на схему, выполненную в аудиофильском красном квадрате.

Значение конденсатора составляет 0,1.

В схемах (в отличие от формул) принято приводить значения в микрофарадах, если нет пояснений.

Следовательно, значение конденсатора равно 0,1 мкФ.

Резистор установлен на номинальное значение 68K.

Переведите значения для расчетов.

0,1 мкФ = -1 градус + -6 градусов = -7 градусов = запись 7 знаков после запятой = 0,0000001 F

68K равно 68 кОм.

1 кОм = 1000 Ом, поэтому

68 кОм = 68*1000 = 68000 Ом.

Теперь рассчитайте частоту среза.

Fчастота сдвига = 1/ 2Pi * R * C

Fчастота среза = 1 / 6,28 * 68000 * 0,0000001 = 23 Гц

Итак, разработчик схемы установил частоту среза фильтра HPF на 23 Гц.

Это означает, что все частоты ниже 23 Гц будут отсечены, а все частоты выше 23 Гц будут переданы.

Давайте также рассмотрим промышленную схему, как я ее понимаю.

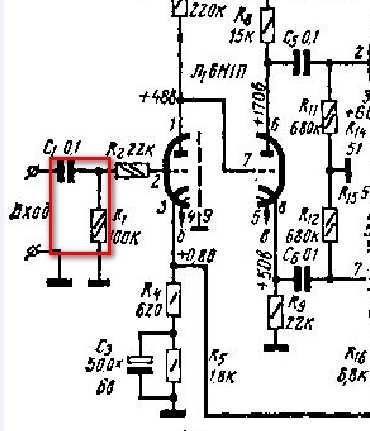
В нем значение конденсатора такое же, но значение резистора больше = 100k.

Давайте рассчитаем, на какую частоту среза настроен этот ЧРП.

Fчастота среза = 1/ 2Pi * R * C

Fчастота среза = 1/6,28 * 100000 * 0,0000001 = 16 Гц

Наконец, рассмотрим еще одну схему лампового усилителя для используемого фильтра высоких частот.

См. схему ниже.

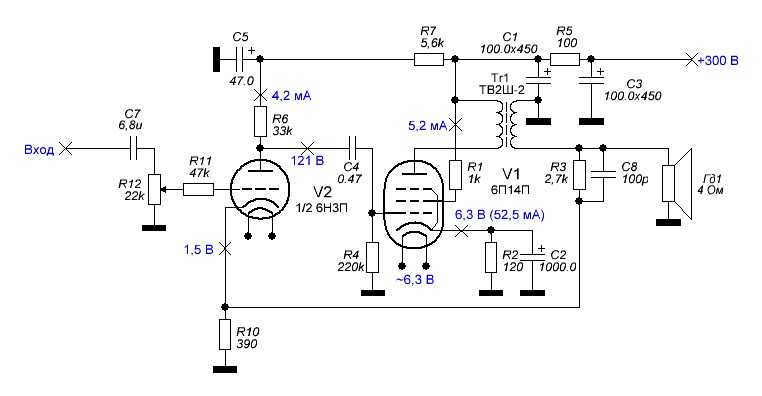
Это схема усилителя с использованием популярных ламп 6н3п + 6п14п.

Давайте рассмотрим схемы фильтров.

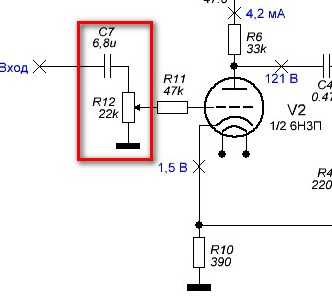
Один фильтр формируется на входе из комбинации входного конденсатора C7 (6.8mF), отсекающего постоянный ток, чтобы он не достиг сетки лампы, и регулятора громкости R12 (22K).

Очевидно, что изменение сопротивления переменного резистора R12 также изменит частоту среза – мы исследуем это ниже.

Второй фильтр VFD установлен на входе во вторую ступень на 6P14P.

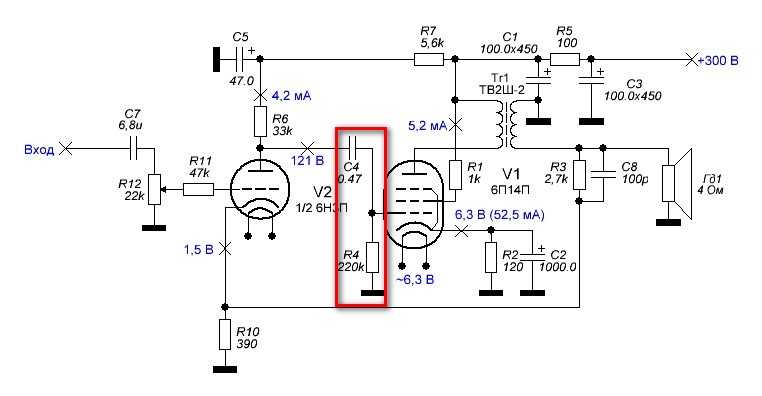
Давайте начнем с этого фильтра.

Конденсатор рассчитан на 0,47 мкФ, или -2 ступени (два знака после запятой). Пересчитывая в Фарады, которые являются -6-й силой, получаем -8-ю силу, поэтому 8 знаков после запятой = 0,00000047F

Резистор 220К = 220000 Ом

Fпредел отсечки = 1Очевидно, что изменение сопротивления переменного резистора R12 также изменит частоту отсечки – мы исследуем это ниже.

Второй фильтр VFD установлен на входе во второй каскад на 6P14P.Давайте начнем с этого фильтра.

Конденсатор рассчитан на 0,47 мкФ, что составляет -2 градуса (два знака после запятой). Пересчитывая в Фарады, которые являются -6-й силой, получаем -8-ю силу, поэтому 8 знаков после запятой = 0,00000047F

Резистор 220К = 220000 Ом

F

предел отключения = 1/ 2Pi * R * C

F

отсечка = 1/ 2Pi *220000 * 0.00000047 = 1/6.28*220000*0.00000047 = 1.5 Гц

Это означает, что вход лампы 6p14p будет обрезать низкие частоты от 1,5 Гц и выше.

Это кажется мне немного странным, но я не эксперт в ламповых схемах.

Хорошо, давайте посмотрим, что происходит на входе усилителя, где звуковой диапазон также обрезан.

C = 6,8 мкФ в микрофарадах получаем

MF = -6 градусов Фарадт.е. 6 десятичных знаков для целого числа (6,8 = 6 целых, 8 дробных) + еще одна дробь.

Итого 6,8 мкФ = 0,0000068или, если кому-то проще, для перевода из мкФ в Ф, умножьте микрофарады на 0,000001 (6 знаков после запятой).

6,8 мкФ = 6,8*0,000001 = 0,0000068 Ф

Резистор 22К = 22000 Ом

Fпредел отключения = 1/ 2Pi * R * C

F

отсечка = 1/ 2Pi * 22000 * 0.0000068 F = 1/6.28*22000*0.0000068 = 1 ГцOK, переменный регулятор со значением сопротивления 22K, устанавливает фильтр на 1 Гц.

А если мы повернем ручку громкости на 50%, сделав сопротивление меньше – 11 кОм, что произойдет с фильтром?

F

отсечка = 1/ 2Pi * 11000 * 0.0000068 = 1/6.28*11000*0.0000068 = 2 Гц

А если мы повернем ручку громкости до упора вниз, то сопротивление, пусть 1кОм = 1000 Ом.

F

отсечка = 1/ 2Pi * 1000 * 0.0000068 = 1/6.28*11000*0.0000068 = 23 Гц

Таким образом, мы видим картину, когда на входе фильтр плавает в диапазоне 1-23 Гц, а на входе второй трубки пытается ограничить себя на 1,5 Гц и ниже. Чтобы понять логику, стоящую за этим, вам, вероятно, придется углубиться в схему, а пока мы просто исследуем фильтры.

Ответ на ограничение диапазона заключается в том, что трансформаторы не являются бесконечно изменяемыми, и зная, что выходной трансформатор может работать, например, только от 30 Гц и выше, нет смысла запускать схему на частотах, которые усилитель не сможет воспроизвести.
Таким образом, исходя из характеристик трансформатора, вы ограничиваете диапазон тем, что он может выдержать. В приведенной выше схеме я не понял логику работы такого LPF. Если среди читающих этот материал есть люди, знакомые с ламповыми усилителями, пожалуйста, присоединяйтесь к обсуждению и поделитесь своими знаниями.

После этого материала вам, вероятно, не составит труда самостоятельно выяснить, используется ли в схеме частотный фильтр и на какую срезку он рассчитан.

И если да, то после изучения обзорного материала пора переходить к теме ламповых схем и самостоятельному проектированию схемы лампового усилителя.

Увидимся там.

20 Примечания

Теперь пришло время поговорить о фильтрах в усилителях… ламповый или транзисторный, не имеет значения. Прежде всего, любой фильтр плох и не имеет места в аудиотехнике, если вы можете конструктивно обойтись без него. Усилитель должен быть способен воспроизводить сигналы качества несущей вплоть до многих мегагерц, иначе аудиосистема может потерять свои константы и компоненты звукового диапазона могут быть искажены. Эта тема заслуживает особого внимания. Я боюсь, что возникнет борьба за якобы рекомендуемый диапазон 20-20000 Гц….. Приглашаю вас на форум, будем обсуждать.

Так вот, СССР за 70 лет не выпустил ни одного лампового усилителя, я имею ввиду для дома…а здесь каждый найдет ответ на раз….

В данной схеме он не имеет значения в качестве фильтра, поскольку низкие частоты все равно не проходят через трансформаторы.

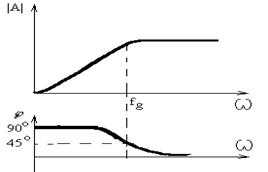
Если низкие частоты не проходят через трансформаторы, как вы объясните этот график?:
Странно, удивительно для меня, я попытаюсь выяснить, какие условия могут привести к такому чудесному графику.

электрический0 Цитата:Странно, удивительно для меня, я попытаюсь выяснить, при каких условиях можно получить такой чудесный график.Здесь нет ничего удивительного. Посмотрите на диаграмму на стр. 36:https://docviewer.yandex.ru/view/138446819/. Ознакомьтесь с технологией изготовления трансформатора. Однажды я ремонтировал магнитофон Kenwood, и они принесли мне усилитель Akai, что интересно, со схемой. Аналогичная трансформаторная схема.

@ SenyaG

Что-то не сработало при загрузке. В общем, это из журнала “Радио”, 1981, №1, с.36.

= .

То же, что и для LPF, постоянная времени для VFD =RC.

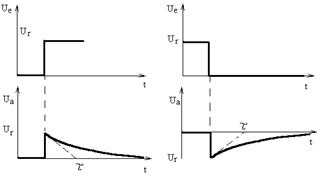Фильтр высоких частот:

HPF – это схема, которая пропускает неизмененные высокочастотные сигналы, а на низких частотах обеспечивает ослабление сигналов и их продвижение по фазе с входными сигналами. Амплитудно-частотные и фазо-частотные характеристики снова получаются из соотношения:₀Выражение для частоты среза f

g

Фазовый сдвиг на этой частоте составляет +45 0 .

Как и в случае с ФНЧ, постоянная времени ФВЧ =RC.

 

Читайте далее:

• Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.
• Компьютерная обработка изображений.
• Что такое электрическое сопротивление; Школа для электриков: электротехника и электроника.
• Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
• Шаговые двигатели: свойства и практические схемы управления. Часть 2.
• Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
• Расчет понижающего конденсатора.