2. Конденсатор с электрической емкостью 20 мкФ имеет заряд 4 мкКл. Какова энергия заряженного конденсатора?
Урок 28 Электрическая емкость. Конденсатор
Конденсатор – это устройство, используемое для хранения электрического заряда.
Емкость конденсатора равна это физическая величина, численно равная отношению заряда одного из проводников конденсатора к разности потенциалов между его выводами.
На сайте заряд конденсатора модуль заряда одной из его граней.
Серийное соединение – это электрическая цепь, не имеющая разветвлений. Все элементы в цепи соединены один за другим. При параллельном соединении концы каждого элемента соединяются с одной и той же парой точек.
Смешанное соединение это соединение, при котором цепь содержит как последовательные, так и параллельные соединения.
Энергия конденсатора прямо пропорциональна квадрату напряженности электрического поля внутри него: 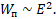
Для любого конденсатора энергия равна половине произведения электрической емкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Г. Мякишев. Ю., Буховцев Б., Харугин В. М. Физика. 10 класс Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2 Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа, 2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор с латинского означает “сгущает, уплотняет”, устройство для сбора зарядов энергии в электрическом поле. Конденсатор состоит из двух одинаковых параллельных пластин, расположенных на небольшом расстоянии друг от друга. Главной особенностью этого устройства, является его электрическая емкость, которая зависит от площади поверхности его пластин, расстояния между ними и свойств диэлектрика.
Заряд конденсатора определяется – модулем заряда на любой из его клемм. Заряд конденсатора прямо пропорционален напряжению между его клеммами. Коэффициент пропорциональности C называется емкостью, электрической емкостью или просто емкостью конденсатора.
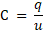
Емкость конденсатора – это физическая величина, численно равная отношению заряда одного из проводников конденсатора к разности потенциалов между его выводами.
Чем больше площадь поверхности проводников и чем меньше диэлектрическое пространство, тем больше емкость катушек конденсатора.
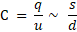
Электрическая емкость измеряется в системе СИ в фарадах. Этот блок назван в честь английского физика и экспериментатора Майкла Фарадея, который внес большой вклад в теорию электромагнетизма. Один фарад равен емкости конденсатора, который создает напряжение в один вольт между пластинами при приложении заряда в один кулон.
Емкость конденсаторов зависит от их конструкции, из которых плоские конденсаторы являются самыми простыми.
Чем больше перекрытие между обкладками и чем меньше расстояние между ними, тем больше увеличится емкость обкладок конденсатора. Когда в пространство между электродами вставляется стеклянная пластина, емкость конденсатора значительно увеличивается, как выяснилось, в зависимости от свойств используемого диэлектрика.
Емкость планарного конденсатора зависит от площади поверхности его граней, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между гранями, и определяется по формуле
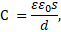 где
где 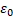 – электрическая постоянная.
– электрическая постоянная.
Для получения необходимой емкости берут несколько конденсаторов и объединяют их в батарею в параллельном, последовательном или смешанном соединении.
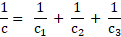
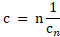
Энергия конденсатора равна половине произведения заряда конденсатора, напряженности поля и расстояния между пластинами конденсатора: u = Ed
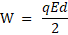
Эта энергия равна работе, которую совершит электрическое поле, когда пластины будут двигаться навстречу друг другу, поле совершит положительную работу. В то же время энергия электрического поля уменьшается:
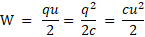
Для любого конденсатора энергия равна половине произведения электрической емкости и квадрата напряжения:
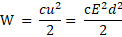
Примеры и конкретные примеры:
1. Плоский конденсатор, расстояние между пластинами которого составляет 3 мм, заряжен до 150 В и отключен от источника питания. Разность потенциалов между пластинами увеличилась до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Каким было расстояние между пластинами конденсатора, когда они были раздвинуты?
- Во сколько раз изменилось расстояние между тарелками.
Емкость конденсатора определяется по формуле:
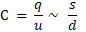
1.По условию разность потенциалов увеличилась в два раза. U1 = 150 В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилась в два раза, то по формуле расстояние между пластинами соответственно удвоилось и d = 2-3 мм = 6 мм.
3.Расстояние между пластинами увеличилось в два раза.
2. Конденсатор с электрической емкостью 20 мкФ имеет заряд 4 мкКл. Какова энергия заряженного конденсатора?
Данные: C = 20 μF = 20 – 10 -6 F, q = 4 μCL = 4-10 -6 Cl.
Энергия заряженного конденсатора W зарядом q и емкостью C определяется по формуле:
4. Докажите, что энергия поля Eel плоского конденсатора может быть определена из формулы Eel= CU2/2 .
§ 54 Конденсатор. –
Конденсатор предназначен для хранения заряда и энергии электрического поля.
2 – Что такое простейший конденсатор? Как он обозначен на схемах?
Простейший конденсатор представляет собой две одинаковые круглые металлические пластины, расположенные параллельно друг другу, разделенные диэлектриком (воздухом) и установленные на изолирующих основаниях. На схемах конденсатор обозначается символом
3 Что такое заряд конденсатора?
Заряд конденсатора – это модуль заряда q одной из его клемм.
4 От чего зависит емкость конденсатора и как он работает?
5 Какая формула используется для определения энергии заряженного конденсатора?
6 Как был проведен эксперимент, показанный на рисунке 149? Что это доказывает?
Соберите цепь, состоящую из источника тока, конденсатора, выключателя и лампы (рис. 149).
Зарядите конденсатор, переключив переключатель в положение 1. Через мгновение переключите в положение 2. В результате вы увидите короткую вспышку лампы. Этот эксперимент показывает, что конденсатор обладает накопленной энергией, которая высвобождается при заряде конденсатора в виде света и тепла.
7 Расскажите об устройстве и работе переменного конденсатора. Где он нашел свое самое широкое применение?
Переменный конденсатор представляет собой комбинацию неподвижных пластин 1 (статор) и подвижных пластин 2 (ротор), которые подогнаны друг к другу. Изменение емкости такого конденсатора достигается за счет изменения поверхности перекрытия. Переменные конденсаторы широко используются в радиоаппаратуре – например, в радиоприемниках, высокочастотных генераторах и антенном оборудовании.
Упражнения.
1. за какой период времени каждый радиосигнал радиограммы, переданной А. С. Попов достиг приемного устройства?
2. конденсатор емкостью 1 мкФ был заряжен до напряжения 100 В. Определите заряд конденсатора.
3. Как изменится емкость планарного конденсатора при уменьшении расстояния между обкладками вдвое?
4 Докажите, что энергия поля Eel планарного конденсатора может быть определена из формулы Eel= CU2/2 .
5. три конденсатора соединены параллельно. Емкость одного из них составляет 15 мкФ, второго – 10 мкФ и третьего – 25 мкФ. Определите емкость конденсаторной батареи.
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкостью , заряжается током, равным , то энергия этого конденсатора (можно сказать, энергия электрического поля конденсатора) равна
Глава 20 Конденсаторы
Устройство, называемое конденсатором, используется для хранения различных электрических зарядов. Конденсатор – это соединение двух изолированных проводников (часто называемых катушками конденсатора), один из которых заряжен положительно, а другой – с таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластины, расположенные на небольшом расстоянии друг от друга, конденсатор называется плоским.
Чтобы описать способность конденсатора накапливать заряд, вводится понятие электрической емкости (часто называемой просто емкостью). Емкость конденсатора 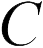 это отношение заряда конденсатора
это отношение заряда конденсатора 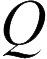 по отношению к разности потенциалов
по отношению к разности потенциалов  которая возникает между терминалами, когда они заряжены
которая возникает между терминалами, когда они заряжены 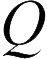 и
и  (эту разность потенциалов между проводниками часто называют электрическим напряжением между катушками и обозначают буквой
(эту разность потенциалов между проводниками часто называют электрическим напряжением между катушками и обозначают буквой 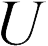 ):
):
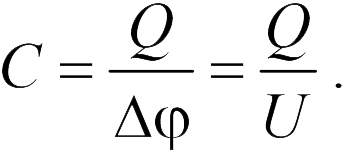
Поскольку значения 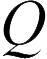 и
и  (или
(или  ) в уравнении (20.1) являются зависимыми, емкость (20.1) не зависит от
) в уравнении (20.1) являются зависимыми, емкость (20.1) не зависит от 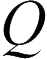 и
и  но является характеристикой геометрии системы проводников. Действительно, при передаче заряда проводникам
но является характеристикой геометрии системы проводников. Действительно, при передаче заряда проводникам 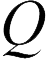 и
и  проводники достигнут потенциалов, разность которых будет пропорциональна заряду
проводники достигнут потенциалов, разность которых будет пропорциональна заряду 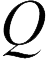 . Поэтому в соотношении (20.1) заряд уменьшается.
. Поэтому в соотношении (20.1) заряд уменьшается.
Выведем формулу для емкости плоского конденсатора (эта формула входит в школьный курс физики). Когда параллельные пластины, расположенные на небольшом расстоянии друг от друга, заряжаются зарядом 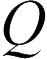 и
и  В пространстве между ними создается однородное электрическое поле с напряженностью (см. главу 18):
В пространстве между ними создается однородное электрическое поле с напряженностью (см. главу 18):
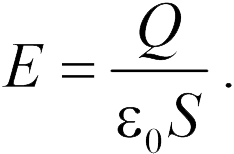
Разность потенциалов между пластинами составляет
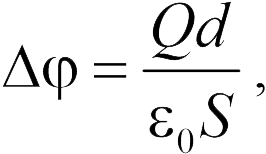
где 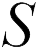 – площадь поверхности пластин,
– площадь поверхности пластин, 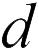 – расстояние между ними. Следовательно, вычислив отношение заряда к разности потенциалов (20.3), получим емкость плоского конденсатора
– расстояние между ними. Следовательно, вычислив отношение заряда к разности потенциалов (20.3), получим емкость плоского конденсатора
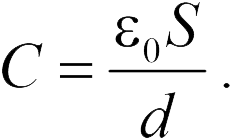
Если все пространство между катушками заполнено диэлектриком с проницаемостью 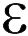 поле (20.2) и разность потенциалов (20.3) уменьшаются на
поле (20.2) и разность потенциалов (20.3) уменьшаются на 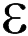 раз, а емкость конденсатора на
раз, а емкость конденсатора на 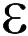 увеличивается в несколько раз.
увеличивается в несколько раз.
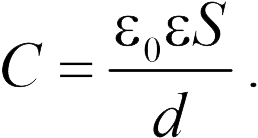
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости – это емкость одного конденсатора, который при заряде, равном заряду батареи, дает ту же разность потенциалов, что и батарея конденсаторов. Здесь приведены формулы для эквивалентной емкости, а также электрического заряда и напряжения на каждом конденсаторе при последовательном и параллельном соединении.
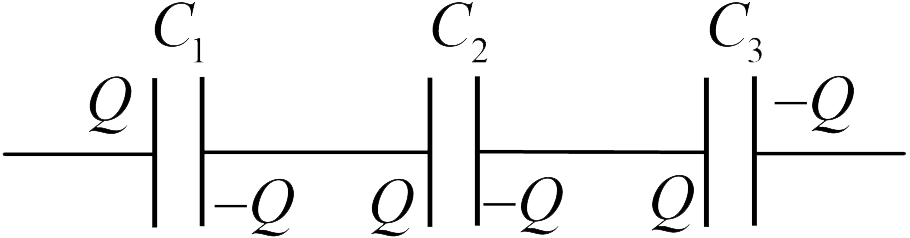
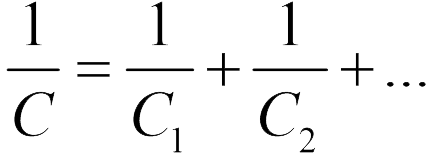
Последовательное подключение (см. рисунок). Последовательно заряжая левую пластину левого конденсатора и правую пластину правого конденсатора 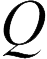 а на правой пластине правого конденсатора заряд
а на правой пластине правого конденсатора заряд  В результате поляризации на внутренних пластинах индуцируются заряды (см. рисунок, значения индуцированных зарядов указаны под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен одинаковыми зарядами
В результате поляризации на внутренних пластинах индуцируются заряды (см. рисунок, значения индуцированных зарядов указаны под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен одинаковыми зарядами 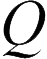 и
и  заряды крайних пластин равны сумме напряжений всех конденсаторов, а обратная величина емкости эквивалентной батареи равна сумме обратных величин емкостей всех конденсаторов
заряды крайних пластин равны сумме напряжений всех конденсаторов, а обратная величина емкости эквивалентной батареи равна сумме обратных величин емкостей всех конденсаторов
Параллельное подключение (см. рисунок). В этом случае, если мы подадим заряд в левый проводник 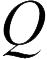 в правом проводнике дает заряд
в правом проводнике дает заряд  заряд будет распределен между конденсаторами, вообще говоря, не поровну, а в соответствии с законом сохранения заряда
заряд будет распределен между конденсаторами, вообще говоря, не поровну, а в соответствии с законом сохранения заряда  .
.
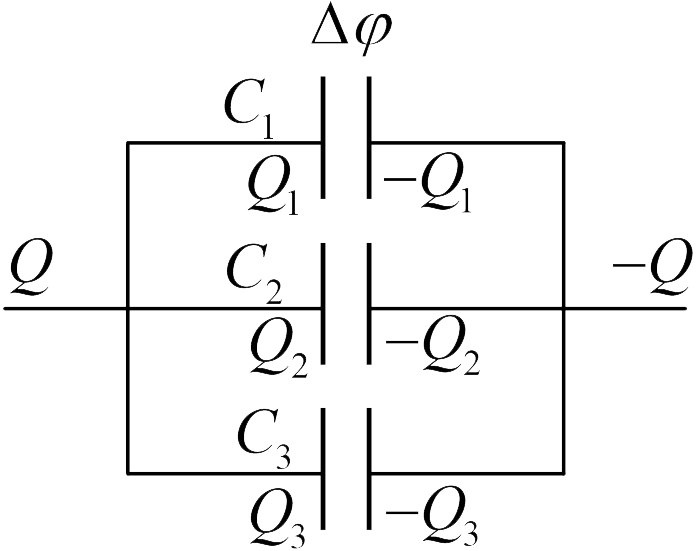
Поскольку правые пластины всех конденсаторов соединены друг с другом, левые пластины также соединены друг с другом, они являются одним проводником, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинаковой: 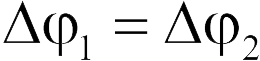 . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
. Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
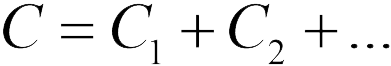
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкостью 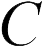 обвиняется в
обвиняется в 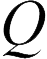 тогда энергия этого конденсатора
тогда энергия этого конденсатора 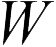 (можно сказать, что энергия электрического поля конденсатора) равна
(можно сказать, что энергия электрического поля конденсатора) равна
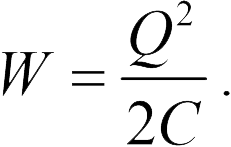
Используя определение электрической емкости (20.1), уравнение (20.8) можно записать в двух других формах:
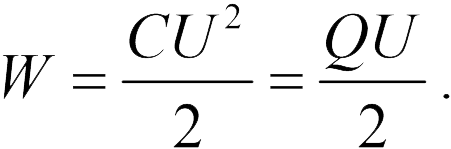
Рассмотрим в рамках этих минимальных знаний о конденсаторах типовые задачи Единого государственного экзамена (ЕГЭ) по физике, которые были предложены в первой части книги.
Емкость конденсатора – это его геометрическое свойство, которое не зависит от заряда конденсатора, если его геометрия остается неизменной (задание 20.1.1. – ответ 3). Аналогично, емкость конденсатора не изменяется при увеличении напряжения на нем (проблема 20.1.2. – ответ 3).
Связь между единицами измерения (проблема 20.1.3) следует из определения емкости (20.1). Единицей электрической емкости в Международной системе единиц СИ является фарада. 1 Фарада – это емкость конденсатора с напряжением 1 В между его пластинами для зарядов пластин 1 Кл и -1 Кл (ответ 4).
Поскольку электрическое поле в планарном конденсаторе однородно, напряженность поля конденсатора 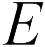 и напряжение между пластинами
и напряжение между пластинами  связаны между собой соотношением (см. формулу (18.9))
связаны между собой соотношением (см. формулу (18.9)) 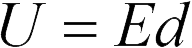 где
где 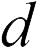 – расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в Проблема 20.1.4
– расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в Проблема 20.1.4
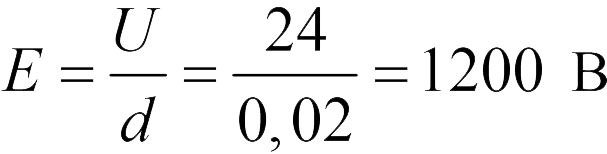
Согласно определению электрической емкости, мы имеем w в задаче 20.1.5
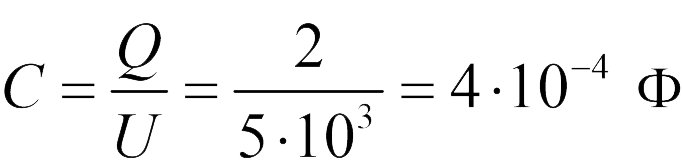
Из уравнения (20.4) для емкости плоского конденсатора следует, что если площадь его пластин увеличится в 3 раза (проблема 20.1.6) его емкость увеличивается в 3 раза (ответ 1).
Для коэффициента 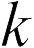 раз больше расстояния между пластинами, емкость планарного конденсатора увеличится на
раз больше расстояния между пластинами, емкость планарного конденсатора увеличится на 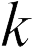 времена. Таким образом, новое напряжение на конденсаторе
времена. Таким образом, новое напряжение на конденсаторе 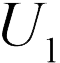 (проблема 20.1.7) может быть получена из следующей последовательности формул
(проблема 20.1.7) может быть получена из следующей последовательности формул

где 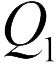 и
и 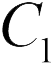 – это новый заряд конденсатора (ответ 3).
– это новый заряд конденсатора (ответ 3).
Поскольку конденсатор w в задаче 20.1.8. подключен к источнику, между его пластинами поддерживается постоянное напряжение  независимо от расстояния между ними. Следовательно, заряд конденсатора
независимо от расстояния между ними. Следовательно, заряд конденсатора 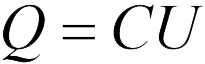 изменяется при удалении пластин друг от друга так же, как изменяется его емкость. А поскольку удвоение расстояния между пластинами вдвое уменьшает емкость конденсатора (см. формулу (20.4)), заряд конденсатора также уменьшается вдвое (ответ 2).
изменяется при удалении пластин друг от друга так же, как изменяется его емкость. А поскольку удвоение расстояния между пластинами вдвое уменьшает емкость конденсатора (см. формулу (20.4)), заряд конденсатора также уменьшается вдвое (ответ 2).
В проблемы 20.1.9 конденсатор отключается от источника во время сближения пластин. Поэтому его заряд не изменяется. А поскольку напряженность электрического поля между пластинами задается соотношением (20.2)
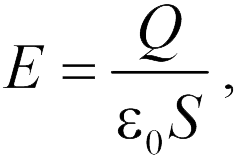
то напряженность электрического поля между пластинами также не изменится (ответ 3). Тот же результат можно получить, определив емкость 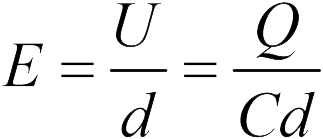 принимая во внимание, что
принимая во внимание, что
продукт 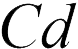 не зависит от расстояния между пластинами (см. формулу (20.4)).
не зависит от расстояния между пластинами (см. формулу (20.4)).
Из уравнений (20.8), (20.9) видно, что только один из ответов к проблеме 20.1.10 отношения (а именно – 2) определяет энергию конденсатора.
Когда конденсаторы соединены последовательно (проблема 20.2.1) их заряды одинаковы независимо от величины их электрических емкостей (ответ 2). Если конденсаторы соединены параллельно (задание 20.2.2) напряжения на каждом из них будут одинаковыми (ответ 3).
Поскольку конденсатор в в задаче 20.2.3 отсоединен от источника напряжения, его заряд не меняется по мере удаления пластин друг от друга. Поэтому удобно использовать уравнение (20.8) для исследования изменения энергии конденсатора
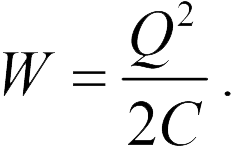
Поскольку при увеличении расстояния между пластинами на 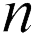 раз, емкость конденсатора уменьшается на
раз, емкость конденсатора уменьшается на 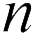 раз, то, согласно уравнению (1), энергия конденсатора увеличится на
раз, то, согласно уравнению (1), энергия конденсатора увеличится на 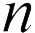 раз (Ответ 1).
раз (Ответ 1).
В (Ответ на задачу 20.2.4) напряжение на конденсаторе не изменяется. Поэтому используем первую формулу (20.9)
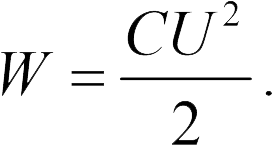
Из этой формулы мы делаем вывод, что при увеличении 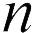 раз больше расстояния между пластинами, энергия конденсатора уменьшится на
раз больше расстояния между пластинами, энергия конденсатора уменьшится на 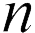 раз – ответ 2. (Отличие от предыдущей задачи в том, что здесь, помимо внешних сил, которые совершают работу при удалении пластин друг от друга, работу совершает источник напряжения).
раз – ответ 2. (Отличие от предыдущей задачи в том, что здесь, помимо внешних сил, которые совершают работу при удалении пластин друг от друга, работу совершает источник напряжения).
В Проблема 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно использовать формулу (20.8)
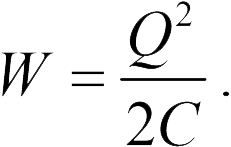
Из этой формулы следует, что если расстояние между пластинами увеличится в 2 раза, а заряд конденсатора увеличится в 2 раза, то его энергия увеличится в 8 раз (ответ 4).
Поскольку w Проблема 20.2.6 конденсаторы соединены последовательно, емкость конденсаторной батареи можно найти по уравнению (20.6), из которого следует, что емкость конденсаторной батареи 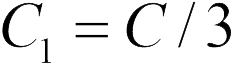 (ответ 2).
(ответ 2).
В (Ответ на задачу 20.2.7) конденсаторы соединены параллельно, поэтому емкость конденсаторной батареи можно найти по формуле (20.7): 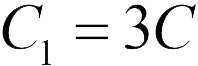 (ответ 2).
(ответ 2).
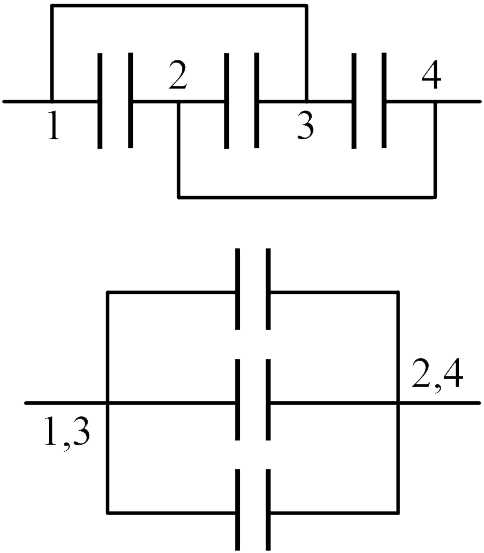
Главный вопрос, на который необходимо ответить в (Ответ) Основной вопрос, на который необходимо ответить в задаче 20.2.8как подключены конденсаторы? Последовательно, параллельно, каким-то другим способом? Давайте попробуем по-разному расположить их в пространстве и изменить длину соединительных проводов, чтобы сделать схему более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 (“укорачивая” длину проводов 1-3), а также вершины 2 и 4. Средний конденсатор расширяется в пространстве, и схема принимает вид, показанный на рисунке, из которого видно, что конденсаторы соединены параллельно. Поэтому, 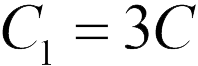 (Ответ 1).
(Ответ 1).
Когда металлическая пластина помещается в заряженный планарный конденсатор (проблема 20.2.9) параллельно электродам конденсатора, напряженность электрического поля внутри пластины становится равной нулю, вне пластины между электродами конденсатора остается такой же, как и при отсутствии пластины 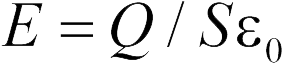 где
где 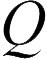 – заряд конденсатора,
– заряд конденсатора, 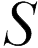 – площадь поверхности его пластин. Поэтому напряжение между пластинами конденсатора
– площадь поверхности его пластин. Поэтому напряжение между пластинами конденсатора 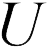 определяется соотношением:
определяется соотношением:
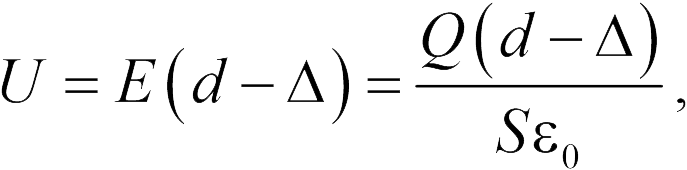
где 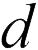 – расстояние между электродами конденсатора,
– расстояние между электродами конденсатора,  – толщина пластины. Отсюда находим емкость рассматриваемого конденсатора
– толщина пластины. Отсюда находим емкость рассматриваемого конденсатора
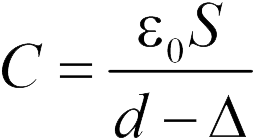
Чтобы найти емкость сферического конденсатора (проблема 20.2.10) назовем его вычисление  и
и  , найдите напряжение между клеммами и рассчитайте отношение заряда к напряжению. Разность потенциалов между двумя концентрическими сферами, заряженными
, найдите напряжение между клеммами и рассчитайте отношение заряда к напряжению. Разность потенциалов между двумя концентрическими сферами, заряженными  и
и  (напряжение между обкладками сферического конденсатора) определено в задаче 19.2.5. Как узнать емкость сферического конденсатора (ответ 3):
(напряжение между обкладками сферического конденсатора) определено в задаче 19.2.5. Как узнать емкость сферического конденсатора (ответ 3):
Емкость измеряется в фарадах: конденсатор с емкостью в один фарад производит напряжение в один вольт, если он содержит заряд в один кулон. Как и многие другие единицы СИ, он имеет непрактичный размер, поэтому, если вы не считаете суперконденсаторы, которые мы не будем здесь обсуждать, вы, скорее всего, встретите микро-, нано- и пикоконденсаторы. Емкость любого конденсатора может быть выведена из его размеров и диэлектрических свойств – если вам интересно, формулу для этого можно найти в Википедии. Его не нужно запоминать, если вы не готовитесь к экзамену, но он содержит один полезный факт. Емкость пропорциональна диэлектрической проницаемости εr В качестве диэлектрика используется конденсатор, что привело к появлению множества конденсаторов с использованием различных диэлектрических материалов для достижения большей емкости или улучшения характеристик напряжения.
Конденсаторы для посвященных

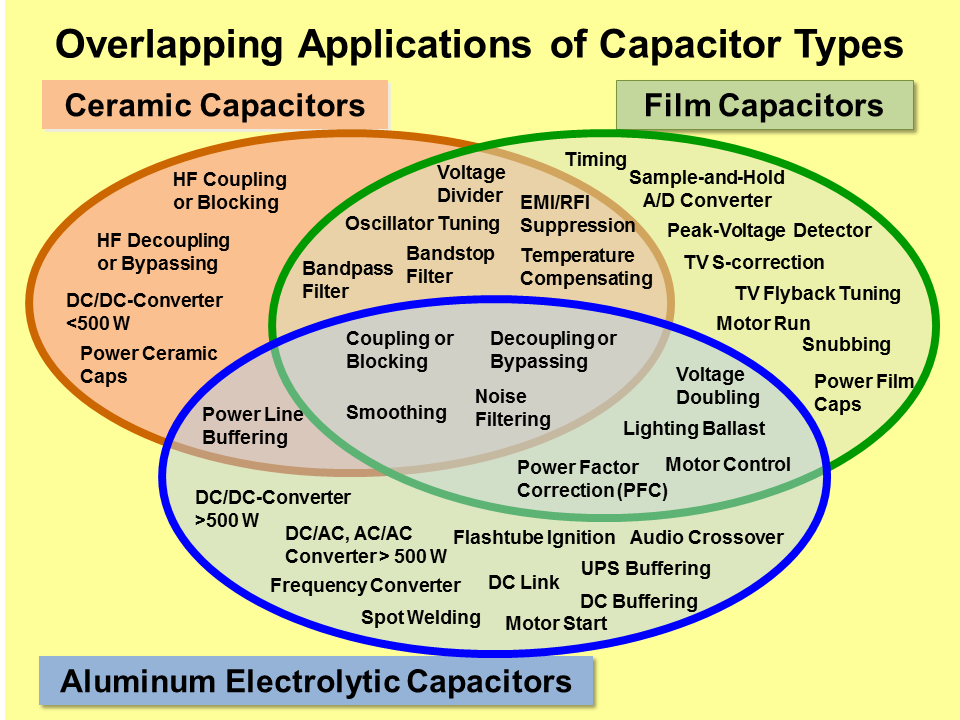
Если вы регулярно собираете электрические цепи, вы наверняка использовали конденсаторы. Они являются стандартной частью схем, так же как и резистор, который мы просто берем с полки, не задумываясь. Мы используем конденсаторы для сглаживания пульсаций напряжения/тока, для согласования нагрузки, в качестве источника питания для маломощных устройств и в других приложениях.
Но конденсатор – это не просто пузырек с двумя проводами и несколькими параметрами – рабочим напряжением и емкостью. Существует широкий спектр технологий и материалов с различными свойствами, которые используются для создания конденсаторов. И хотя в большинстве случаев практически любой конденсатор с нужной емкостью подойдет для любого применения, хорошее понимание того, как работают эти устройства, поможет вам выбрать не просто что-то подходящее, а самое подходящее. Если вы когда-либо сталкивались с проблемой стабильности температуры или проблемой поиска источника лишнего шума, вы оцените информацию в этой статье.
Давайте начнем с простого
Лучше всего начать с простого и описать основы работы конденсаторов, прежде чем переходить к конкретике. Идеальный конденсатор состоит из двух проводящих пластин, разделенных диэлектриком. Заряды накапливаются на пластинах, но не могут протекать между ними – диэлектрик обладает изолирующими свойствами. Именно так конденсатор накапливает заряд.
Емкость измеряется в фарадах: конденсатор емкостью в один фарад создает напряжение в один вольт, если его заряд равен одному кулону. Как и многие другие единицы СИ, он имеет непрактичный размер, поэтому, если вы не считаете суперконденсаторы, которые мы не будем здесь обсуждать, вы, скорее всего, встретите микро-, нано- и пикофарады. Емкость любого конденсатора может быть выведена из его размеров и диэлектрических свойств – если вам интересно, формулу для этого можно найти в Википедии. Вам не нужно запоминать его, если только вы не готовитесь к экзамену, но в нем содержится один полезный факт. Емкость пропорциональна диэлектрической проницаемости εr используемого диэлектрика, что привело к продаже различных конденсаторов, в которых используются различные диэлектрические материалы для достижения большей емкости или улучшенных характеристик напряжения.
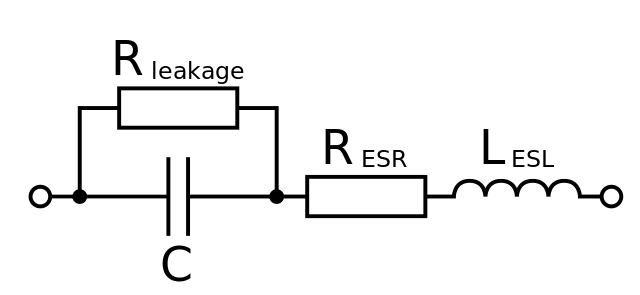
Паразитная индуктивность и сопротивление реального конденсатора
Существует одна проблема с использованием диэлектриков в конденсаторах, помимо того, что диэлектрик с нужными характеристиками имеет неприятные побочные эффекты. Все конденсаторы имеют небольшое паразитное сопротивление и индуктивность, которые иногда могут влиять на их работу. Электрические константы изменяются от температуры и напряжения, пьезоэлектричества или шума. Некоторые конденсаторы имеют завышенную цену, а некоторые – состояние отказа. И вот мы подошли к основной части статьи, где обсудим различные типы конденсаторов и их свойства, полезные и вредные. Мы не будем обсуждать все возможные технологии, но опишем большинство из них.
Алюминиевые электролитические конденсаторы

В алюминиевых электролитических конденсаторах в качестве одной диэлектрической пластины используется анодный окисленный слой на алюминиевом листе, а в качестве другой пластины – электролит из электрохимической ячейки. Наличие электрохимической ячейки делает их полярными, т.е. постоянное напряжение должно быть приложено в одном направлении, а анодированная пластина должна быть анодом, или плюсом.
На практике их пластины изготавливаются в виде сэндвича из алюминиевой фольги, завернутой в цилиндр и помещенной в алюминиевую банку. Рабочее напряжение зависит от глубины анодированного слоя.
Электролитические конденсаторы имеют самую высокую емкость среди наиболее часто используемых конденсаторов – от 0,1 мкФ до тысяч мкФ. Из-за плотной упаковки электрохимической ячейки они имеют высокую эквивалентную последовательную индуктивность (ESI или эффективную индуктивность), поэтому не могут использоваться на высоких частотах. Они обычно используются для сглаживания мощности, развязки и соединения на звуковых частотах.
Тантал электролитический

Танталовый конденсатор для поверхностного монтажа
Танталовые электролитические конденсаторы изготавливаются в виде спеченных танталовых анодов с большой площадью поверхности, на которой нарастает толстый оксидный слой, а затем в качестве катода помещается электролит из диоксида марганца. Сочетание большой площади поверхности и диэлектрических свойств оксида тантала дает высокую емкость на объем. В результате такие конденсаторы намного меньше алюминиевых конденсаторов сопоставимой емкости. Как и последние, танталовые конденсаторы поляризованы, поэтому постоянный ток должен течь строго в одном направлении.
Их доступные емкости варьируются от 0,1 до нескольких сотен мкФ. Они имеют гораздо меньшее сопротивление утечки и эквивалентное последовательное сопротивление (ESR), поэтому их используют в испытательном, измерительном оборудовании и высококачественной аудиоаппаратуре – везде, где эти свойства полезны.
Особую осторожность следует соблюдать с танталовыми конденсаторами – существует вероятность их возгорания. Аморфный оксид тантала является хорошим диэлектриком, а в кристаллической форме он становится хорошим проводником. Неправильное использование танталового конденсатора – например, подача слишком большого пускового тока может изменить форму диэлектрика, увеличив протекающий через него ток. Действительно, репутация воспламеняемости восходит к предыдущим поколениям танталовых конденсаторов, а усовершенствованные технологии производства привели к созданию более надежных изделий.
Полимерные пленки
В целом семействе конденсаторов в качестве диэлектрика используются полимерные пленки, причем пленка находится между скрученными или чередующимися слоями металлической фольги или имеет металлизированный слой на поверхности. Их рабочее напряжение может достигать 1000 В, но они не имеют большой емкости – обычно от 100 пФ до единиц мкФ. Каждый тип пленки имеет свои преимущества и недостатки, но в целом все семейство имеет более низкую емкость и индуктивность, чем электролитические. Поэтому они используются в высокочастотных приложениях и для развязки в системах с высоким уровнем электрического шума, а также в приложениях общего назначения.
Полипропиленовые конденсаторы используются в схемах, требующих хорошей термической и частотной стабильности. Они также используются в силовых системах, для подавления ЭМИ, в системах, использующих переменные токи высокого напряжения.
Полиэфирные конденсаторы, хотя и не обладают такими же тепловыми и частотными характеристиками, недороги и могут выдерживать высокие температуры пайки при поверхностном монтаже. Поэтому они используются в схемах, предназначенных для использования в некритичных приложениях.
Полиэтилен-нафталатные конденсаторы. Они не имеют стабильных температурных и частотных характеристик, но могут выдерживать гораздо более высокие температуры и напряжения, чем полиэфирные конденсаторы.
Полиэтиленсульфидные конденсаторы имеют температурные и частотные характеристики полипропиленовых конденсаторов и, кроме того, могут выдерживать высокие температуры.
Поликарбонатные и полистирольные конденсаторы можно найти в старом оборудовании, но они больше не используются.
Керамика
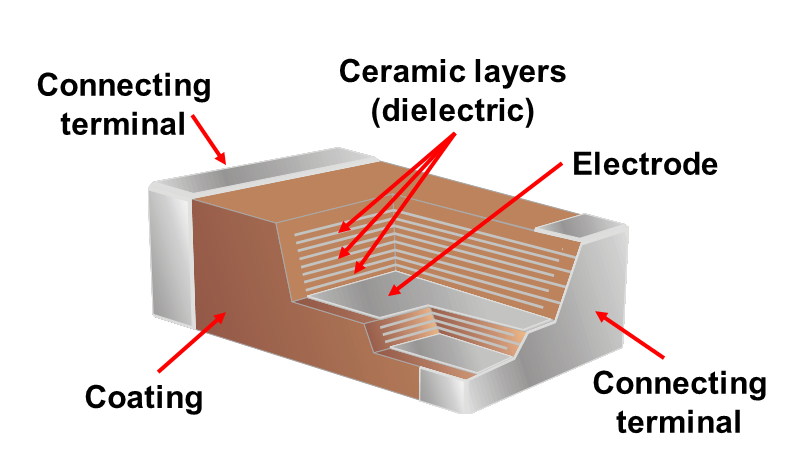
История керамических конденсаторов довольно длинная – они используются с первых десятилетий прошлого века до наших дней. Ранние конденсаторы состояли из одного слоя керамики, которая была металлизирована с обеих сторон. Более поздние конденсаторы также могут быть многослойными, где металлизированные пластины и керамика чередуются. В зависимости от диэлектрика их емкость варьируется от 1 пФ до десятков мкФ, а напряжение – до киловольт. Во всех областях электроники, где требуется низкая емкость, можно найти как однослойные керамические диски, так и многослойные конденсаторы для поверхностного монтажа.
Самый простой способ классификации керамических конденсаторов – по диэлектрику, поскольку именно диэлектрик придает конденсатору все его свойства. Диэлектрики классифицируются трехбуквенным кодом, в котором закодированы их рабочая температура и стабильность.
C0G имеет наилучшую стабильность емкости по отношению к температуре, частоте и напряжению. Используется в высокочастотных и других высокоскоростных цепях.
X7R не обладает такой хорошей устойчивостью к перепадам температур и напряжений, поэтому используется в менее ответственных приложениях. Как правило, это приложения для развязки и различные приложения общего назначения.
Y5V имеет гораздо более высокую емкость, но еще более низкую термостойкость и сопротивление напряжению. Также используется для развязки и различных применений общего назначения.
Поскольку керамика часто обладает также пьезоэлектрическими свойствами, некоторые керамические конденсаторы также проявляют микрофонный эффект. Если вы работали с высокими напряжениями и частотами в области аудио, например, с ламповыми усилителями или электростатикой, вы могли слышать, как конденсаторы “поют”. Если вы используете пьезоэлектрический конденсатор для обеспечения стабилизации частоты, вы можете обнаружить, что его звук модулируется вибрациями окружающей среды.
Как мы уже упоминали, эта статья не ставит своей целью охватить все конденсаторные технологии. Заглянув в каталог электроники, можно обнаружить, что некоторые из доступных технологий здесь не рассматриваются. Некоторые каталожные списки уже устарели или настолько нишевые, что их не часто можно найти. Мы просто надеялись развеять некоторые тайны о популярных моделях конденсаторов и помочь вам выбрать правильные компоненты при проектировании собственных устройств. Если мы разбудили ваш аппетит, вы можете ознакомиться с нашей статьей об индукторах.
Если вы обнаружили какие-либо неточности или ошибки, пожалуйста, напишите нам через личные сообщения на сайте. Спасибо.
Отключим заряженный конденсатор от генератора и подключим к его катушкам резистор.
Зарядка и разрядка конденсатора
Чтобы зарядить конденсатор, необходимо подключить его к цепи постоянного тока. На рисунке 1 показана схема цепи зарядки конденсатора. Конденсатор C подключен к клеммам генератора. Ключ можно использовать для размыкания или замыкания цепи. Давайте подробнее рассмотрим процесс зарядки конденсатора.
Осциллятор имеет внутреннее сопротивление. Когда ключ закрыт, конденсатор заряжается до напряжения между клеммами, равного пусковому току генератора: Uc = E. В этом случае клемма, подключенная к положительному полюсу генератора, получает положительный заряд (+ q), а другая клемма получает такой же отрицательный заряд (-q). Величина заряда q прямо пропорциональна емкости конденсатора C и напряжению на его витках: q = CUc
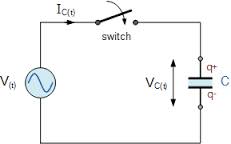
P isc. 1 . Диаграмма для зарядки конденсатора
Чтобы зарядить катушки конденсатора, необходимо, чтобы одна из них набирала, а другая теряла электроны. Перенос электронов с одной обкладки на другую осуществляется под действием электродвижущей силы генератора, а процесс переноса заряда в цепи есть не что иное, как электрический ток, называемый зарядовым емкостным током I зар.
Ток заряда в конденсаторе обычно длится тысячные доли секунды, пока напряжение на конденсаторе не достигнет значения, равного э.д.с. генератора. График нарастания напряжения на катушках конденсатора в процессе зарядки показан на рис. 2,а, из которого видно, что напряжение Uc нарастает плавно, сначала быстро, а затем все медленнее и медленнее, пока не сравняется с напряжением генератора E. После этого напряжение на конденсаторе остается неизменным.
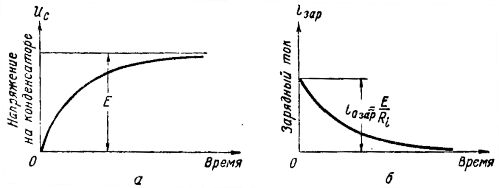
Рисунок 2: Диаграммы напряжения и тока для зарядки конденсатора
При зарядке конденсатора через цепь протекает зарядный ток. График зарядного тока показан на рисунке 2,b. В начальный момент зарядный ток наибольший, так как напряжение на конденсаторе еще равно нулю и по закону Ома io zar = E/ R i , потому что вся электрическая мощность генератора приложена к сопротивлению R i.
Поскольку конденсатор заряжается, т.е. напряжение на нем увеличивается, а зарядный ток уменьшается. Как только на конденсаторе появится напряжение, падение напряжения на сопротивлении будет равно разности между э.д.с. генератора и напряжением на конденсаторе, т.е. равно E – U c. Следовательно, i rar = (E-Uc)/R i
Отсюда следует, что с увеличением Uc, i-car уменьшается, и при Uc = E зарядный ток становится равным нулю.
Более подробную информацию о законе Ома можно найти здесь: Закон Ома для поперечного сечения цепи.
Продолжительность процесса зарядки конденсатора зависит от двух факторов:
1) внутреннее сопротивление осциллятора R i ,
2) емкость конденсатора C.
На рис. 2 показаны графики зарядных токов для конденсатора емкостью 10 мкФ: кривая 1 соответствует процессу зарядки от генератора с ee = 100 В и внутренним сопротивлением R i = 10 Ом, кривая 2 соответствует процессу зарядки от генератора с той же ee, но меньшим внутренним сопротивлением: R i = 5 Ом.
Сравнение этих кривых показывает, что при меньшем внутреннем сопротивлении генератора зарядный ток в начальный момент выше и, следовательно, процесс зарядки происходит быстрее.
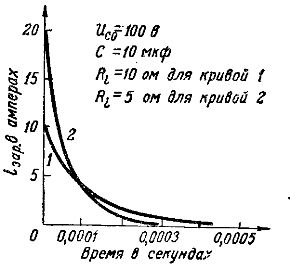
Рис. 2. Кривые тока зарядки для различных сопротивлений
На рис. 3 показано сравнение кривых зарядного тока при зарядке от одного и того же генератора с напряжением E = 100 В и внутренним сопротивлением R i = 10 Ом двух конденсаторов с разными емкостями: 10 мкф (кривая 1) и 20 мкф (кривая 2).
Значение начального зарядного тока io zar = E/ Ri = 100/10 = 10 A одинаково для обоих конденсаторов, но поскольку конденсатор с большей емкостью накапливает больше электроэнергии, его зарядный ток должен протекать дольше, и процесс зарядки длится дольше.
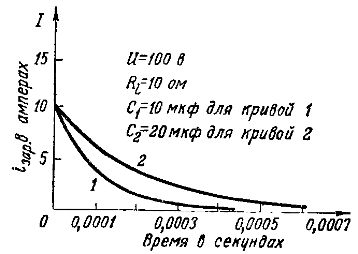
Рисунок 3: Диаграммы зарядных токов при различных емкостях
Отключим заряженный конденсатор от генератора и подключим к его клеммам резистор.
На катушках конденсатора имеется напряжение U c, поэтому в замкнутой цепи течет ток, называемый током емкостного разряда i dp.
Ток течет от положительной стороны конденсатора через резистор к отрицательной стороне. Это соответствует переносу избыточных электронов с отрицательной обкладки на положительную, где их не хватает. Этот процесс продолжается до тех пор, пока потенциалы обеих обкладок не сравняются, т.е. разность потенциалов между ними не станет равной нулю: Uc=0 .
Рис. 4, a показан график падения напряжения на конденсаторе при разряде от Uc o = 100 В до нуля, причем сначала напряжение быстро уменьшается, а затем все медленнее и медленнее.
На рисунке 4b показан график изменения тока разряда. Сила тока разряда зависит от величины сопротивления R и согласно закону Ома и разряда = Uc / R
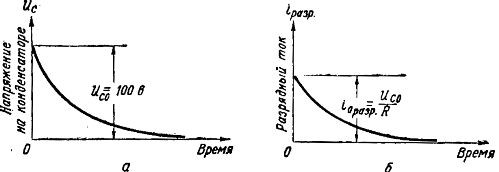
Рис. 4. Кривые напряжения и тока во время разрядки конденсатора
В начальный момент, когда напряжение на катушках конденсатора наибольшее, ток разряда также наибольший, и по мере уменьшения Uc в процессе разряда ток разряда также уменьшается. При Uc=0 ток разряда прекращается.
Продолжительность разряда зависит от:
1) емкость конденсатора C
2) величина сопротивления R, на которое разряжается конденсатор.
Чем больше сопротивление R , тем медленнее будет происходить разряд. Это связано с тем, что при высоком сопротивлении ток разряда мал и величина заряда на катушках конденсатора уменьшается медленно.
Это можно показать на графиках тока разряда одного и того же конденсатора емкостью 10 мкф и заряженного до 100 В, при двух различных значениях сопротивления (рис. 5): кривая 1 – при R = 40 Ом, и orp = Uc o/ R = 100/40 = 2,5 А и кривая 2 – при 20 Ом и orp = 100/20 = 5 А.
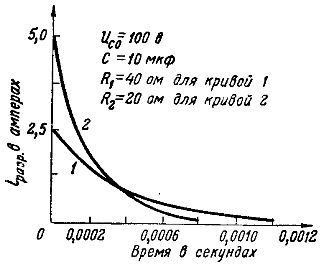
Рисунок 5: Графики токов разряда при различных сопротивлениях
Разряд также происходит медленнее, если емкость конденсатора велика. Это происходит потому, что при большей емкости в катушках конденсатора находится больше электричества (больший заряд) и требуется больше времени, чтобы заряд стекал вниз. Это хорошо видно на примере разрядных токов для двух конденсаторов разной емкости, заряженных до одинакового напряжения 100 В и разряженных до сопротивления R =40 Ом (рис. 6: кривая 1 для конденсатора 10 мкФ и кривая 2 для конденсатора 20 мкФ).
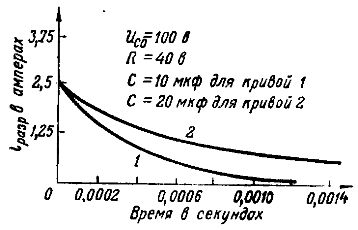
Рисунок 6: Токи разряда при различных емкостях
Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток течет только в моменты зарядки и разрядки, когда изменяется напряжение на катушках.
Это связано с тем, что при изменении напряжения меняется количество заряда на катушках, а это требует перемещения зарядов по цепи, т.е. по цепи должен протекать электрический ток. Заряженный конденсатор не пропускает постоянный ток, потому что диэлектрик между его витками размыкает цепь.
В процессе зарядки конденсатор накапливает энергию, получая ее от генератора. Когда конденсатор разряжается, вся энергия электрического поля преобразуется в тепловую энергию, т.е. используется для нагрева сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его катушках, тем больше будет энергия электрического поля конденсатора. Количество энергии, которой обладает конденсатор емкостью C, заряженный до напряжения U, равно: W = W c = C U 2 /2
Пример. Конденсатор C=10 мкф заряжен до напряжения U в = 500 В. Определите энергию, которая выделится в виде тепла в резисторе, через который был разряжен конденсатор.
Решение. При разряде вся энергия, накопленная в конденсаторе, преобразуется в тепловую энергию. Поэтому W = W c = C U 2 /2 = (10 x 10 -6 x 500)/2 = 1,25 Дж.
Если вам понравилась эта статья, пожалуйста, поделитесь ею в своих социальных сетях. Это очень поможет в развитии нашего сайта!
1 фарад – это очень большая величина, поэтому конденсаторы, используемые в технике, имеют свои значения: – пикофарады – 10-12; нанофарады – 10-9; микрофарады – 10-6.
Процессы, происходящие в конденсаторе на временной диаграмме при подключении конденсатора к источнику однополярного прямоугольного сигнала, показаны на рисунке.
Из рисунка видно, что при подаче прямоугольного импульса источника тока (красный) напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и со временем экспоненциально увеличивается – конденсатор заряжается, а ток конденсатора (зеленый) наоборот – сначала максимален, но затем экспоненциально уменьшается по мере заряда. После исчезновения импульса напряжение на выводах конденсатора уменьшается экспоненциально – конденсатор разряжается, и ток, меняющий полярность, сначала максимален, а затем по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от величины емкости. Чем выше емкость, тем медленнее они изменяются (экспонента более растянута во времени). Напряжение и ток через резистор нагрузки ведут себя одинаково и выделены оранжевым цветом на временной диаграмме. Их взаимосвязь описывается законом Ома.
Фактически, мы рассмотрели “четырехполюсник”, состоящий из конденсатора и резистора, который называется дифференциальной схемой.
QoL. Лекция 2 Конденсатор.
Конденсатор (емкость)
Конденсатор (емкость) -компонент, способный накапливать электромагнитную энергию в собственном электрическом поле, создаваемом клеммами конденсатора. Назначен как – С. Напряжение и ток на его клеммах связаны корреляцией:
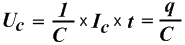
Величина емкости измеряется в фарадах (F). 1 фарад – это значение емкости, на которой возникает падение напряжения в 1 В при заряде емкости в 1 кулон.
1 фарад – это очень большая величина, поэтому конденсаторы, используемые в технике, имеют свои значения: – пикофарады – 10-12; нанофарады – 10-9; микрофарады – 10-6.
Процессы, происходящие в конденсаторе на временной диаграмме при подключении конденсатора к источнику однополярного прямоугольного сигнала, показаны на рисунке.
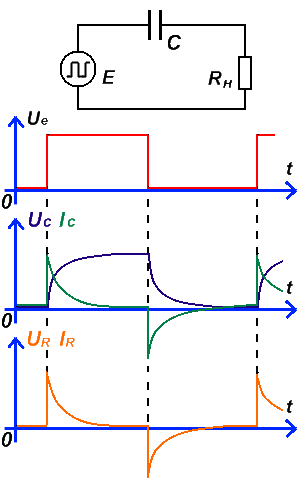
Из рисунка видно, что при подаче прямоугольного импульса источника тока (красный) напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и со временем экспоненциально увеличивается – конденсатор заряжается, а ток конденсатора (зеленый) наоборот – сначала максимален, но затем экспоненциально уменьшается по мере заряда. После исчезновения импульса напряжение на выводах конденсатора уменьшается экспоненциально – конденсатор разряжается, и ток, меняющий полярность, сначала максимален, а затем по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от величины емкости. Чем выше емкость, тем медленнее они изменяются (экспонента более растянута во времени). Напряжение и ток через резистор нагрузки ведут себя одинаково и выделены оранжевым цветом на временной диаграмме. Их взаимосвязь описывается законом Ома.
Фактически, мы рассмотрели “четырехполюсник”, состоящий из конденсатора и резистора, который называется дифференциальной схемой.
Дифференцирующая цепь используется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Для облегчения понимания дифференцирующая схема и преобразование импульсов показаны на рисунке ниже.
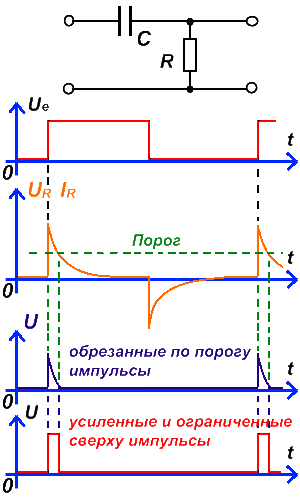
За дифференцирующей схемой установлена пороговая схема, которая не пропускает ничего ниже амплитуды установленного порога, с выхода пороговой схемы отсекающие импульсы поступают на ограничивающий усилитель, который усиливает “кривой” импульс и, ограничивая его амплитуду “сверху”, пропускает его на выход.
В дополнение к функции преобразования квадратной волны, дифференцирующая схема также может быть использована как Фильтр высоких частот (HPF). Конденсатор – это инертный элемент. Если на конденсатор большой емкости подать низкочастотное переменное напряжение, он не сможет проводить ток из-за своей инертности, поскольку конденсатор должен сначала зарядиться, а затем зарядить. Свойство конденсатора сопротивляться переменному электрическому току называется реактивное сопротивление конденсаторакоторый используется при построении частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается как Xc или Zc и измеряется в омах. Реактивное сопротивление конденсатора связано с емкостью и частотой тока выражением:
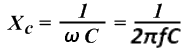
Формула показывает, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.
Теперь представьте, что дифференциальная цепь – это делитель напряжения, где вместо первого резистора стоит конденсатор. И теперь мы знаем из формулы, что конденсатор легко пропускает высокие частоты – его сопротивление минимально, и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике при расчете частотных фильтров характеристикой фильтра является частота среза, которая определяется как частота сигнала, при которой амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы сделать это более понятным, я проиллюстрирую это на рисунке.
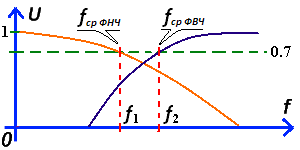
То, что показано, называется амплитудно-частотная характеристикаили сокращенно амплитудно-частотная характеристика. АФК. Для фильтра высоких частот АЧХ имеет фиолетовый цвет, а частота среза равна f2.
Зная, как рассчитать реактивное сопротивление делителя напряжения и конденсатора на заданной частоте, легко рассчитать простейший g-фильтр фильтр высокой частоты с конденсатором и резистором.
Если поменять местами конденсатор и резистор в дифференциальной цепи, то получим -. интегрирующая цепочка. Все процессы в интегрирующей цепи происходят точно так же, как и в дифференцирующей. Временные диаграммы, показанные на первом рисунке, точно такие же для интегрирующей цепи. Разница в том, что выходным элементом является не резистор, а конденсатор. Поэтому на выходе интегрирующей цепи будет не указанный дифференциальный импульс (зеленый), а импульс напряжения, присутствующий на выводах конденсатора (фиолетовый). И если дифференцирующая схема представляет собой фильтр высоких частот, а интегрирующая схема представляет собой фильтр низких частот (ФНЧ). И рассчитывается он точно так же, через делитель напряжения. Для фильтра низких частот АЧХ на диаграмме оранжевого цвета, а частота среза составляет f1.
Следует добавить, что частотные фильтры из конденсаторов и резисторов имеют плоские амплитудно-частотные характеристики. Другими словами, эти фильтры имеют плохо определенную частоту среза. Фильтры, состоящие из конденсаторов и индукторов (дросселей), имеют лучшую отсечку, но подробнее об этом позже, при обсуждении индукторов.
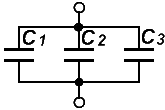
Параллельное соединение конденсаторов
Общая емкость конденсаторов при параллельном соединении равна их сумме.
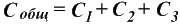
Последовательное подключение конденсаторов
В последовательно соединенных конденсаторах обратная величина их общей емкости равна сумме величин емкостей, обратно пропорциональных их общей емкости.
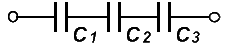
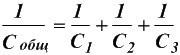
Для двух конденсаторов, соединенных последовательно, их общая емкость равна:
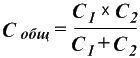
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
- Электричество и магнетизм.
- Конденсаторы.
- Расчет цепи постоянного тока с конденсаторами.
- Как и откуда берутся молнии: типы, физическая природа, причины. Физика атмосферы.
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.