Между домами Андрея и Дмитрия находится один дом, поэтому дом Андрея не может быть предпоследним, следовательно, его номер – 4, что автоматически исключает, что там живут Дмитрий и Владимир.
Таблицы истинности
Многие проблемы можно решить с помощью инструментов булевой алгебры. Чтобы получить результат, вы можете пойти тремя путями:
- рассуждая об условиях;
- путем решения логических операций;
- с помощью таблиц истинности.
Логический подход заключается в переводе условия с естественного языка на язык символов, диаграмм и формул. Чтобы формализовать утверждения таким образом, необходимо выполнить несколько шагов.
Шаги в решении логических задач:
- Организовать условие на естественном языке, извлекая простые утверждения и придавая им символические обозначения (латиница).
- Запишите утверждение в виде формулы. Решите ее шаг за шагом, упрощая с учетом приоритетов (( ), ¬, &, V).
- Вычислите формулы построчно или с помощью таблиц истинности, учитывая законы алгебры логики.
- Убедитесь, что результат соответствует состоянию проблемы.
(A V B) V C = A V (B V C).
Чтобы получить доступ к этому и другим видеоурокам комплекта, вы должны добавить его в свой личный кабинет, купив в каталоге.
Получите удивительные возможности



Конспект урока “Построение таблиц истинности для логических выражений. Свойства логических операций”.
Сегодня мы изучим правила построения таблиц истинности для логических выражений с более чем одной логической операцией. Мы также узнаем о свойствах логических операций.
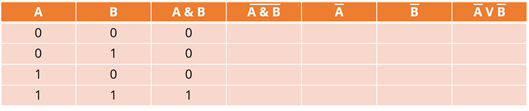
Сначала вспомним логические операции, которые мы изучали в прошлом уроке. К ним относятся инверсия, связь и дизъюнкция. Внимательно посмотрите на таблицу с обозначениями логических операций, которые мы будем использовать через некоторое время.
Конъюнктура – это логическая операция, объединяющая два высказывания в одно новое высказывание, которое будет истинным тогда и только тогда, когда оба исходных высказывания истинны.
Дисъюнкция – это логическая операция, объединяющая два высказывания в одно новое высказывание, которое будет ложным тогда и только тогда, когда оба исходных высказывания ложны.
Инверсия – это логическая операция, которая преобразует исходное выражение в новое, значение которого противоположно исходному.
Логические выражения могут состоять более чем из двух логических операций. В то же время для любого логического выражения можно построить таблицу истинности, чтобы увидеть, какие значения принимает это выражение. Логические операции выполняются в следующем порядкеИнверсия, конъюнкция и дизъюнкция.
Итак, прежде всего, давайте посмотрим, что …мы должны продемонстрировать… для построить таблицы таблица истинности:
1. рассчитать n – количество переменных в выражении.
Мы с вами знаем, что переменные обозначаются буквами латинского алфавита.
2 Подсчитайте общее количество логических операций в выражении.
Количество логических операций: 2
То есть нам нужно подсчитать, сколько инверсий, конъюнкций и дизъюнкций содержится в нашем выражении.
3 Определите порядок логических операций, принимая во внимание скобки и приоритеты. Как известно, сначала выполняются операции со скобками, затем инверсия, конъюнкция и дизъюнкция.
Определите количество столбцов в таблице: количество переменных плюс количество операций. То есть, нам нужно сложить количество переменных и логических операций. Мы получим количество столбцов в таблице.
Количество столбцов: 5.
5. заполните шапку таблицы, записывая переменные и операции в порядке, установленном в третьем шаге. То есть, сначала запишите все наши переменные в шапке таблицы. Затем операции в том порядке, в котором они перечислены.

6. Укажите количество строк в таблице (не считая заголовка таблицы):
m – количество строк. n – количество переменных в выражении. То есть, если наше булево выражение содержит, например, три переменные, то количество строк m = 2 3 = 8. Заголовок не включается в число этих строк.
7. перечислите наборы входных переменных, если они представляют собой последовательность n-разрядных двоичных чисел от 0 до 2 n – 1. Здесь мы должны перечислить все возможные входные переменные, как мы это делали при построении таблиц истинности.
(8) Заполните таблицу столбцами, выполняя логические операции в соответствии с установленным порядком. То есть, выполнять логические операции над входными данными в зависимости от логической операции.
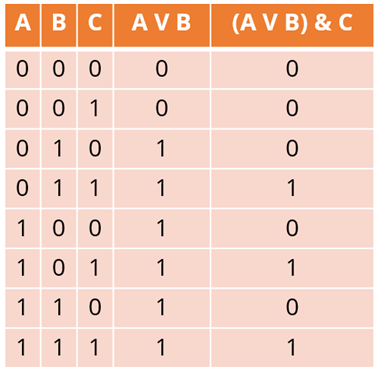
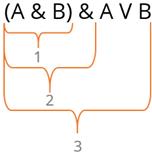
Давайте теперь разберемся с примером. Вам необходимо построить таблицу истинности для следующего логического выражения: (A & B) & A V B.
Исходя из первого элемента плана таблицы истинности, нам необходимо подсчитать количество переменных в выражении. У нас есть две переменные: n = 2. A и B.
Общее количество логических операций равно 3.
Давайте теперь определим порядок логических операций. Логическая операция в круглых скобках – конъюнкция – будет выполнена первой. То есть A и B будут выполнены первыми.
Второй логической операцией снова является конъюнкция. И третья логическая операция – дизъюнкция.
Поскольку у нас есть 2 переменные и 3 логические операции, у нас будет 5 столбцов. Потому что четвертый пункт определяет, как именно следует подсчитывать столбцы.

Теперь заполним заголовок таблицы. Переменные A и B будут идти первыми. Затем логические операции в порядке их выполнения.

Определим количество рядов. Приведена формула для расчета рядов:
m = 2 n .
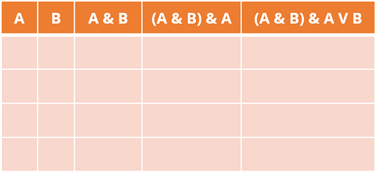
Теперь нам нужно вывести входные наборы данных. То есть, заполните первые две колонки.
Нам нужно заполнить столбцы числами от 0 до 3. Поскольку все операции выполняются в двоичной системе счисления, мы будем представлять числа от 0 до 3 в двоичном коде. Мы получаем следующие цифры:
Теперь запишите эти числа в первый и второй столбцы. Один номер на ячейку.
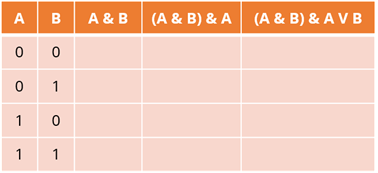
Теперь заполним все оставшиеся колонки. Первая операция – это конъюнкция. Данные будут записаны в третьем столбце. Прежде чем мы начнем заполнять таблицу истинности, давайте вспомним, что правило о союзеНовое высказывание будет истинным тогда и только тогда, когда истинны исходные высказывания. Таким образом, четвертая строка этого столбца будет содержать 1, потому что это единственный случай, когда оба исходных утверждения истинны, поэтому новое утверждение также будет истинным. Первые три строки одного и того же столбца будут содержать нули, потому что оба утверждения ложны в первой строке, утверждение A – во второй, а утверждение B – в третьей.
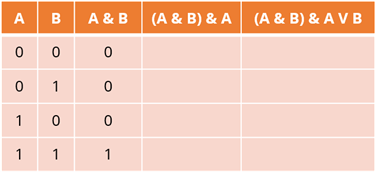
Перейдите к четвертой колонке. Опять же, логической операцией здесь является конъюнкция. И мы возьмем данные из первого и третьего столбцов. Опять же, 1 будет в четвертой строке только для этого столбца, так как оба наших утверждения верны. Остальные будут содержать нули.
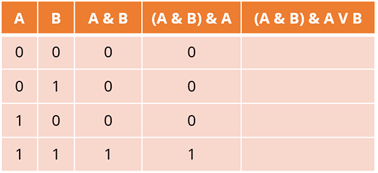
Нам остается заполнить последнюю, пятую колонку. Логической операцией является дизъюнкция. Правило такова: новое утверждение будет ложным тогда и только тогда, когда ложны исходные утверждения. Рассмотрим второй и четвертый столбцы. Это означает, что первая и третья строки для данного столбца будут содержать нули, поскольку оба утверждения в данной ситуации ложны. Остальные строки в том же столбце будут содержать единицы.
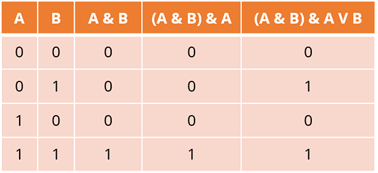
Мы построили таблицу истинности для нашего логического выражения. Обратите внимание, что данные в последнем столбце совпадают с данными в столбце B. В этой ситуации мы говорим, что логическое выражение (A & B) & A V B равно логической переменной B.
Давайте теперь рассмотрим основные свойства логических операций. Они называются законы алгебры логики.
1. Положительный (коммутативный) закон: Когда переменные в конъюнкции и дизъюнкции меняются местами, значение выражения не меняется.
Как мы знаем, конъюнкция называется логическим умножением, а дизъюнкция – логическим сложением. Если мы заменим наши логические операции на соответствующие им арифметические знаки, то увидим, что если поменять местами переменные в умножении и сложении, то значение выражения не изменится.
2. Закон об ассоциацииЗакон ассоциации: если все операции в выражении одинаковы, например, две конъюнкции, мы можем свободно ставить скобки или вообще их опускать.
(A V B) V C = A V (B V C).
Опять же, если мы заменим логические операции соответствующими арифметическими знаками, то увидим, что где бы мы ни поставили скобки, смысл не меняется, даже если скобок нет вообще.
(A – B) – C = A – (B – C); (A – B) – C = A – B – C.
(A + B) + C = A + (B + C); (A + B) + C = A + B + C.
3. Распределительный закон.
A & (B V C) = (A & B) V (A & C)
A V (B & C) = (A V B) & (A V C)
Опять же, давайте заменим логические операции арифметическими знаками. Давайте сначала рассмотрим логическое умножение. Получаем:
A – (B + C) = (A – B) + (A – C).
A + (B – C) = (A + B) – (A + C).
Это то же самое, что и в алгебре.
4. Закон двойного отрицанияДвойное отрицание исключает отрицание.
С математической точки зрения можно сказать, что минус на минус – это плюс.
5. Закон исключенных третей.
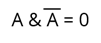
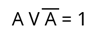
Рассмотрим логическое умножение.
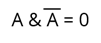
То есть, если A = 0, то Ā = 1.
И наоборот, если A = 1, то Ā = 0.
Перейдем к логическому сложению.
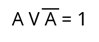
Если A = 0, то Ā = 1.
И наоборот, если A = 1, то Ā = 0.
Из этого мы можем сделать вывод, что заключение: Из двух противоречивых утверждений об одном и том же предмете одно всегда истинно, а другое всегда ложно; третьего не дано.
6. Закон повторения: Соединение или дизъюнкция одного и того же высказывания дает одно и то же высказывание.
Рассмотрим логическое умножение. Например, если A = 0, то:
В логическом завершении, если A = 0, то:
Если A = 1, то:
Булева алгебра оперирует только двумя значениями: false (логический ноль) и true (логическая единица). Истину нельзя удвоить, утроить или возвести в квадрат, поэтому, когда мы складываем две истины, результатом будет просто истина, то есть число 1.

7. Законы операций над числами 0 и 1.
Здесь дело обстоит просто. Давайте рассмотрим связь.
При умножении любого выражения на 0 мы всегда получаем 0, а при умножении любого выражения на 1 мы всегда получаем одно и то же выражение.
A & 0 = 0; A – 0 = 0.
A & 1 = A; A – 1 = A.
А если мы рассмотрим дизъюнкцию, то если мы добавим 0 к выражению, то получим то же самое выражение. Но если мы прибавим к выражению 1, то в итоге получим 1. Мы уже видели, почему мы получаем 1, используя последний закон.
A V 0 = A; A + 0 = A.
A V 1 = 1; A + 1 = 1.
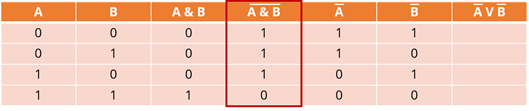
8. Закон общей инверсии. Чтобы найти инверсию конъюнкции, мы должны найти дизъюнкцию инверсии каждого логического выражения. Чтобы найти инверсию дизъюнкции, необходимо найти инверсию конъюнкции для каждого логического выражения.
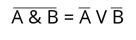
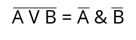
Все законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем закон общей инверсии для логического умножения.
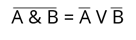
Давайте построим таблицу. В выражении у нас есть 2 переменные. Количество логических операций равно 5. Таким образом, количество столбцов будет равно 7.

Давайте теперь определим порядок логических операций. Сначала разберемся с выражением в левой части равенства. Поэтому сначала будет выполнена конъюнкция, а затем инверсия.
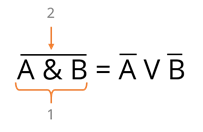
Справа от равенства сначала выполняется инверсия A, затем инверсия B, а затем дизъюнкция полученных выражений.
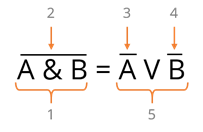
Давайте назовем наши столбцы в соответствии с порядком операций.

Количество строк будет равно 4 (заголовок таблицы здесь не учитывается), потому что:
Теперь перечислим наборы входных переменных. Это будут числа от 0 до 3. Представим их в двухзначном коде и получим следующие числа:
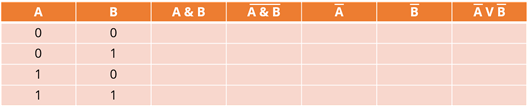
Теперь перейдем непосредственно к логическим операциям. Первый – это соединение A и B. Новое утверждение будет истинным тогда и только тогда, когда истинны исходные утверждения. Это означает, что единица будет находиться в последней строке данного столбца, а нули – во всех остальных строках.
Следующая операция – инверсия. Если исходное утверждение было истинным, то после инверсии оно становится ложным, а если исходное утверждение было ложным, то после операции инверсии оно становится истинным. Поэтому если у нас есть единица, она будет заменена на ноль, а если ноль, то на единицу. Заполним четвертый столбец на основе данных третьего столбца.
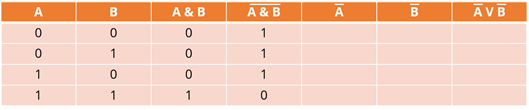
Мы имеем результат выражения, стоящего слева от равенства. Давайте обведем нашу колонну. Это понадобится нам позже.
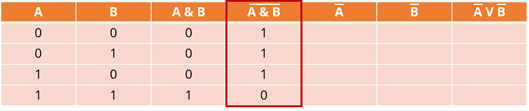
Давайте двигаться дальше. Пятый столбец – обратный столбец A. Опять же, если исходное выражение равно единице, то оно станет равным нулю, и наоборот. Используя данные в первом столбце, заполним его числами.
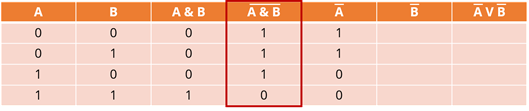
Аналогично заполним шестую колонку. Опираться можно только на второе.
Последняя операция – дизъюнкция. Новое утверждение будет ложным тогда и только тогда, когда ложны исходные утверждения. Таким образом, 0 будет в последней строке этого столбца, а во всех остальных строках будут единицы.
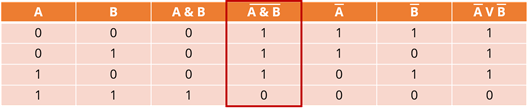
Мы имеем результат выражения в правой части равенства. Давайте и его обведем кружком.
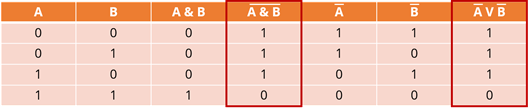
Давайте посмотрим на выделенные столбцы. Их ценности совпадают. Это доказывает справедливость закона общей инверсии.
Найдем значение логического выражения: (D > 1) V (D < 2). Число D = 1.
Переходим к решению. D = 1 мы получаем следующее соотношение:
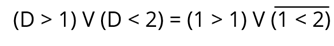
Логическое выражение “1 > 1” не является истинным. Преобразуйте его в 0. Выражение “1 < 2" истинно, поэтому преобразуйте его в 1. Мы это понимаем:
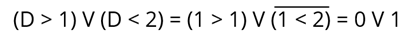
И это будет равнозначно:
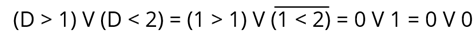
Мы возвращаемся к закону повторения. Согласно этому закону, значение этого логического выражения равно нулю. Поэтому значение нашего логического выражения, при D = 1, равно 0.
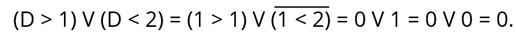
Давайте теперь подведем итоги нашего урока. Сегодня мы научились строить таблицы истинности для логических выражений. На примере мы узнали, как построить таблицу истинности для логического выражения. Мы также узнали, что такое законы булевой алгебры, и использовали таблицу истинности для доказательства истинности одного из них.
✍ Решение:
Решение задач по информатике 2. ЕГЭ
Видеоплейлист YouTube с заданиями: 
Булева функция F определяется выражением
Ниже приводится выдержка из таблицы истинности Fсодержащий все наборы аргументовпри котором функция F является ложной.
Определите, в каком столбце таблицы истинности функции F соответствует каждой из переменных x, y, z, w.
| Переменная 1 | Переключатель 2 | Трубы 3 | Ток перегрузки 4 | F |
| . | . | . | . | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В своем ответе напишите буквы в порядке их расположения в соответствующих колонках.
✍ Решение:
- Отображает перечисление всех значений переменных, используемых в выражении (вся таблица истинности). Поскольку в выражении использовалось 4 переменных, длина строк таблицы будет 2 4 =16:



- ✎ Метод 2 программирования:
Язык Python:
print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
Язык pascalAbc.net:
begin writeeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeeln(x:7, y:7, z:7,w:7); end.
Ответ:
- ✎ Метод 3 Логическое рассуждение:
- Внешней операцией выражения является конъюнкция (∧). Во всех заданных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна в целых трех случаях, поэтому проверить ее ложность очень сложно. Конъюнкция истинна (= 1) истинно только в одном случае: все операнды истинны. То есть в нашем случае:
- Общая идея дальнейшего решения заключается в следующем: поскольку внешняя операция является конъюнкцией, и ее результат истинен, когда оба родительских фактора истинны (=1), мы должны сначала составить все наборы таблиц истинности для обоих родительских факторов. Тогда, поскольку конъюнкция подразумевает пересечение, мы должны сопоставить обе таблицы истинности и выбрать для каждого совпадающего множества первого фактора совпадающее множество (множества) второго фактора. НО! Поскольку в нашей задаче мы знаем только множества для F = 0то мы сопоставляем наборы, которые возвращают false. Теперь о деталях.
- Давайте разделим исходное выражение на две части и составим таблицу истинности для двух частей по отдельности.
- Для фактора (¬x ∨ y ∨ z):
x y z результат 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 - Мы получаем ложность в одном множестве, так как дизъюнкция (∨) ложен только в том случае, если все операнды ложны.
- Для фактора (x ∨ ¬z ∨ ¬w):
x z w результат 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 - Таким образом, мы снова имеем false в одном наборе, когда все операнды ложны.
- Рассмотрим, что нам нужно выбрать и “отрезать” (поскольку внешний операнд ∧) из всех множеств только те, которые возвращают false (поскольку из задачи нам известны только те строки, в которых F = 0):

Результат: xwzy
? Видео решения задачи 169 К.Полякова (вариант без компьютера):
Миша заполнил таблицу истинности этой функции:
но сумел заполнить лишь фрагмент из трех разные Миша сумел заполнить только часть трех разных строк, не указав, какому столбцу таблицы соответствует каждая переменная. w, x, y, z:
| Волна 1 | Перерыв 2 | Rel. 3 | Rel. 4 | F |
| . | . | . | . | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какой столбец в таблице соответствует каждой из переменных x, y, z, w.
Ответьте на вопрос, введя буквы w, x, y, z в порядке соответствующих столбцов.
- Решите задачу, построив полную таблицу истинности.
- Подсчитайте общее количество строк в таблице истинности и постройте ее:

Результат: jwxz
✎ Метод 2 программирования:
begin writeeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do if not((not z and (xor y) <= not(y or w)) then writeeln(x:7, y:7, z:7,w:7); end.
Сравнивая ее с исходной таблицей, мы получаем результат: jwxz
print (‘x y z w’) for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
Результат: jwxz
? Доступно видео с решением этой задачи (версия без компьютера):
? Видео (решение ЕГЭ по Excel 2):
Булева функция F определяется выражением
Ниже приведена выдержка из таблицы истинности функции Fсодержащий все наборы аргументов, для которых функция F это правда.
Определите, какой столбец таблицы истинности F соответствует каждой из переменных a, b, c, d.
| Директива 1 | Изменение.2 | Трубы 3 | Более 4 | F |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В своем ответе напишите буквы в порядке их расположения в соответствующих колонках.
✍ Решение:
Результат: cbad
? (некомпьютерный вариант) Предлагаем вам посмотреть подробную разборку в видео:
Логическая функция F определяется выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке показан участок таблицы истории функции F, содержащий все наборы аргументов, для которых функция F ложна.
Определите, в каком столбце таблицы истинности функции F соответствует каждой из переменных w, x, y, z.
| Разновидность. 1 | Изменения. 2 | Rev. 3 | Прием. 4 | F |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В своем ответе напишите буквы w, x, y, z в порядке их колонок (сначала буква, соответствующая первой колонке; затем буква, соответствующая второй колонке, и т.д.) Запишите буквы в ряд, не ставя между ними разделителей.
✍ Решение:
- ✎ Логическое мышление (некомпьютерная версия):
Результат: xzwy
✎ Метод 2 программирования:
Язык PascalABC.NET:
begin writeeln(‘x ‘,’y ‘,’z ‘,’w ‘); for var x:=false to true do for var y:=false to true do for var z:=false to true do if not(not x or y or(not z and w)) then writeeln(x:7,y:7,z:7,w:7); end.
? (некомпьютерный вариант) Подробное решение этого 2 задания из демоверсии ЕГЭ 2018 смотрите в видео:
Булева функция. F определяется выражением
Определите, в каком столбце таблицы истинности функции F соответствует каждой из переменных x, y, z, w.
Ответьте на вопрос, написав буквы x, y, z, w в порядке соответствующих столбцов.
| Антракт 1 | Перерыв 2 | Ход 3 | Rel. 4 | F |
| . | . | . | . | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
Результат: xwzy
? Видеорешение (версия без компьютера):
Практические задания.
Каждое из логических выражений F и G содержать 5 переменные. Таблица истинности для F и G содержит ровно 5 одинаковых рядов, где именно в 4 из них в колонке значений является 1.
Сколько строк в таблице истинности для F ∨ G содержит 1 в колонке значений?
✍ Решение:
- Поскольку в каждом выражении есть 5 переменных, эти 5 переменных создают таблицу истинности в виде 32 линия: Поскольку каждая переменная может принимать одно из двух значений (0 или 1), различные варианты пяти переменных будут иметь 2 5 =32т.е. 32 строки.
- Из этих 32 струн для F и G мы точно знаем только 5 струн: 4 из них истинны (=1) и один ложный (=0).
- Вопрос в том. количество строк = 1 для таблицы истинности F ∨ G. Эта операция является дизъюнкцией, т.е. является ложным только в одном случае – если F = 0 и в то же время G = 0
- В исходных таблицах для F и G мы знаем только о существовании одного 0т.е. другие ряды могут быть 1. Таким образом, для F и G в 31 линия может иметь такие (32-1=31), и только один из них может быть нулевым.
- Затем для F ∨ G будет равен 0 только в одном случае, когда и F = 0, и G = 0:
№ F G F ∨ G 1 0 0 0 2 0 1 1 … … … 1 32 … … 1 - Соответственно, все остальные строки будут истинными:
Результат: 31
Подробное объяснение этой задачи смотрите в видеоролике:
Каждое логическое выражение A и B зависит от одного и того же набора 7 переменные. В таблицах истинности каждого из этих выражений столбец значений содержит ровно 4 штуки.
Каково максимально возможное количество единиц в столбце значений таблицы истинности A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 2 7 = 128 ряды.
- В четырех из них результат равен единице, а в остальных – единице. 0.
- A ∨ B истинно, если либо A = 1, либо B = 1или и A и B = 1.
- С сайта А = 1 только в 4 случаях, то для получения максимального количества единиц в результирующей таблице истинности (для A ∨ B), присвоим всем единицам t.i. выражение A так, чтобы они располагались на линиях, где B = 0и наоборот, все ряды, в которых B = 1место в рядах, где A = 0:
A B 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 … … - В общей сложности мы получаем 8 ряды.
- Если бы в задании требовалось найти минимальное количество единиц, мы бы объединили строки со значением = 1, и получили бы значение 4.
Результат: 8
Каждое логическое выражение A и B зависит от одного и того же набора 8 переменных. В таблицах истинности каждого из этих выражений столбцы значений содержат ровно 6 штук.
Каково максимально возможное количество нулей в столбце значений таблицы истинности A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 2 8 = 256 ряды.
- В шести из них счет равен единице, а в остальных – 0.
- A ∧ B ложно в том случае, если:
- Во всех случаях, в которых А=1 может быть B=0и тогда результат будет F = 0. Поскольку нам нужно найти максимально возможное количество нулей, только для всех шести А=1 мы сравниваем B=0и наоборот, для всех шести возможных B=1 Сравнить A=0
A B F 1 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0 … … … - Поскольку существуют только ряды 256возможно, что все 256 из них вернутся в результат 0
Результат: 256
Вот фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Какое из следующих выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом случае внешняя операция (выполняемая последней) является конъюнкцией. Давайте начнем с этого. Соответственно, проверяем во второй строке статистической таблицы, где F = 1потому что в этом случае все аргументы должны быть истинными (см. таблицу истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, функция вернет true. То есть, первый пункт совпадает:




Результат: 1
Решение задачи по информатике GVE 2 смотрите на видео:
Дано логическое выражение, которое зависит от 5 логические переменные:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение правда?
✍ Решение:
- Поскольку выражение включает в себя 5 переменных, таблица достоверности состоит из 2 5 = 32 ряды.
- Внешняя (последняя) операция – это конъюнкция (логическое умножение), а внутри скобок – дизъюнкция (логическое сложение).
- Отметьте первую скобку следующим образом Аа вторая скобка B. Получаем A ∧ B.
- Найти сколько нулей существуют для таблицы истинности:
Давайте теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
Результат: 2
Подробное решение проблемы смотрите в обучающем видео:
Вот выдержка из таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное количество количество различных строк полной таблицы истинности этого выражения, в которых значение x3 не равно F.
✍ Решение:
- Полная таблица истинности будет иметь 2 6 = 64 строк (поскольку имеется 6 переменных).
- Мы знаем 4 из них: в них x3 не совпадает дважды с F.
- Неизвестные струны:
- В неизвестности x3 может не совпадать с FБолее того, в двух известных x3 это не то же самое, что F. Таким образом, максимально возможное количество строк с несовпадением x3 и Fбудет:
Результат: 62
Приведен фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким типом выражения может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрите каждый элемент в отдельности и найдите последнюю операцию, которую необходимо выполнить (внешнюю).

2 pts:

3 pts:

Зачет: 4
В учебном видеоролике показано подробное решение задачи 2:
Булева функция F определяется выражением
(y → x) ∧ (y → z) ∧ z.
Определите, в каком столбце таблицы истинности функции F соответствует каждой из переменных x, y, z.
| № | Разновидность. 1 | Переменная 2 | Переменная 3 | F |
|---|---|---|---|---|
| . | . | . | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В своем ответе напишите буквы x, y, z в порядке их соответствующих столбцов.
✍ Решение:
- Сначала нам нужно рассмотреть логическую операцию, которую мы будем выполнять последней, т.е. логическую И (соединение) или ∧. то есть внешний эксплуатация:
- Связку удобнее рассматривать по тем строкам таблицы чисел, в которых F = 1т.е. №3, №4 и №8.
- Поскольку для функции конъюнкции она истинна только в том случае, если истинны все переменные, необходимо, чтобы каждая скобка в отдельности была истинной ((y → x) = 1 и (y → z)=1), а переменная z также является истинным (=1).
- Поскольку работа с выражениями в круглых скобках сложнее, мы сначала определяем, какой столбец соответствует выражению z. Для этого выбираем ряд (#3), в котором F = 1а в остальных клетках только одна единица, остальные – нули.
№ Альтернатива. 1 Альтернатива. 2 Тогл. 3 F 3 0 1 0 1 - Поэтому мы пришли к выводу, что z находится во второй колонке (считая слева):
№ Разновидность. 1 Разновидность. 2 Разновидность. 3 F _ . z . F - Далее нам нужно рассмотреть две скобки, которые содержат операцию импликации: (y → x) и (y → z). Обе эти скобки должны возвращать true (=1). В таблице истинности для импликации функция возвращает 1 в качестве результата, когда:
- вторая переменная (вывод) равна 1 (первое может быть произвольным),
- вторая переменная (вывод) равна 0, а первая в обязательном порядке должна быть равна 0.
- Рассмотрим скобку (y → x) и строку 4 таблицы:
№ Rev. 1 z Rev. 3 F 4 0 1 1 1 - Только для этой линии y может быть равен 0, так как если x = 0тогда y=1и результирующая скобка возвращает значение false (1 → 0 = 0). Соответственно, y находится в первой колонке. А x должны быть в третьем столбце:
y z x F
Результат: yzx
Подробно Предлагаем вам посмотреть видео, чтобы узнать, как решить этот вопрос 2 из ЕГЭ:
введите bc следующим образом: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической диаграммы используйте этот сервис.
Таблица истинности
bc должен быть введен как: a*b*c+a*b=c+a=b*c
Для ввода данных в булевом виде используйте этот сервис.
Правила ввода булевой функции
- Используйте + вместо v (дизъюнкция, OR).
- Не ставьте имя функции перед булевой функцией. Например, вместо F(x,y)=(x|y)=(x^y) напишите (x|y)=(x^y).
- Максимальное количество переменных – 10.
- Вербальное описание – это форма, которая используется на начальном этапе проектирования, она имеет характер условного представления.
- Описание функции булевой алгебры в виде таблицы истинности.
- Описание функции булевой алгебры в виде алгебраического выражения: используются две алгебраические формы FAL:
а) ДНФ – дизъюнктивная нормальная форма – является логической суммой элементарных логических произведений. ДНФ получается из таблицы истинности с помощью следующего алгоритма или правила:
1) в таблице выбираются те строки переменных, для которых функция выхода =1 .
2) Для каждого ряда переменных записываем логическое произведение; переменные =0 записываются с инверсией.
3) Полученный продукт логически суммируется.
Fdnf= X 1*Х2*Х3 ∨ Х1 x 2Х3 ∨ Х1Х2 x 3 ∨ Х1Х2Х3
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. любое произведение обязательно должно содержать все переменные в прямой или обратной форме.
б) QNF – условная нормальная форма – является логическим произведением элементарных логических сумм.
КНФ можно получить из таблицы истинности с помощью следующего алгоритма:
1) Выберите наборы переменных, для которых функция выхода =0
2) Напишите элементарную логическую сумму для каждого набора переменных, при этом переменные =1 запишите с инверсией.
3) Логически перемножьте полученные суммы.
Fsknf=(X1 V X2 V X3) ∧ (X1 V X2 V X 3) ∧ (X1 V X 2 V X3) ∧ ( X 1 V X2 V X3)
Считается, что КНФ является совершеннойесли все переменные имеют одинаковый ранг.
Все операции в булевой алгебре определяются через таблицы истинности значения. Таблица истинности определяет результат операции для все возможныеКоличество вариантов, отражающих результат операции, будет зависеть от количества предложений в логическом выражении. Количество вариантов, отражающих результат операции, будет зависеть от количества утверждений в логическом выражении. Если число высказываний в логическом выражении равно N, то таблица истинности будет содержать 2 N строк, поскольку существует 2 N различных комбинаций возможных значений аргументов.
Логические операции включают конъюнкцию, дизъюнкцию, импликацию, дизъюнкцию, эквивалентность, антиконъюнкцию, антидисъюнкцию.
Примеры построения таблиц истинности
Задание
Давайте построим таблицу истинности и решим выражение ¯ F = (A ¯ B) ¯ (¬A ¯ B)¯ . Мы будем использовать приведенный выше алгоритм.
- Количество переменных в выражении n = 2.
- Общее количество логических операций в этом выражении равно 5.
- Порядок логических операций – 1, 5, 2, 4, 3.
- Количество столбцов равно 7. Булевы переменные (A и B) + булевы операции ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ = 2 +5 = 7.
- Число строк равно 5, исходя из m =2 n , поэтому 2 2 = 4, 4+1 (столбец возглавляет строку) = 5.
- Давайте заполним таблицу.
Решение
| А | В | (A B) | ¬А | ¬В | ¬(A ¬B) | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы ответ будет следующим:
F = 0 при A = B = 0 и A = B = 1
Проблема
Нарисуйте другую таблицу истинности и решите выражение ¬(F = X ¬vee Y ¬wedge ¬).
Примеры: конъюнкция – 1&0=0, импликация – 1→0=0.
- Наборы или выражения с заглавными латинскими буквами: A, B, C, D.
- A” – тире – дополнения множеств
- && – соединение (“и”)
- || – дизъюнкция (“или”)
- ! – отрицание (например, !A)
- кап – пересечение множеств
- cup – объединение множеств (дополнение) cup
- A&!B – разность множеств A∖B=A-B
- A=>B – импликация “Если . то”
- A B – эквивалентность
Все для учебы ” Математика в школе ” Онлайн таблица истинности с примерами – логика
Читайте далее: