Урок 8. 3 – Логические элементы

Элемент AND (Элемент AND), также называемый конъюнкцией, выполняет операцию логического умножения:

Урок 8.3 – Логические элементы

Все или почти все электронные компоненты для обработки цифровых сигналов состоят из небольшого числа одинаковых “строительных блоков”. В чипах с низкой степенью интеграции может быть всего один или несколько десятков таких элементов. Они известны как логические элементы. Логический элемент – это электрическая схема, предназначенная для выполнения логических операций над входными данными. Логический элемент – это компонент, который реализует определенные логические отношения между входами и выходами. Здесь входные данные представлены в виде напряжения с различными уровнями, а результат логической операции на выходе также получается в виде напряжения с определенным уровнем. Логические элементы обычно используются для построения логических схем для вычислительных машин, дискретных схем для автоматического управления и контроля.

Однако принцип цифровой логики остается прежним – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.

Конечно, логические элементы последовательно строятся из резисторов, транзисторов и других электронных элементов, уже рассмотренных в предыдущих уроках, но с точки зрения проектирования цифровой схемы именно логический элемент является ее “элементарной” частью.

Для анализа работы логических элементов используется так называемая булева алгебра. Начало этой отрасли математики было положено в работах Джорджа Буля, английского математика и логика XIX века, одного из основателей математической логики. Основами булевой алгебры являются теоремы, логические операции, а также функции и законы. Нет необходимости изучать все тонкости булевой алгебры, чтобы понять принципы работы логических элементов; мы изучим основы по ходу работы над таблицами истинности.

Еще несколько комментариев. Логические элементы (как и другие элементы электронных схем) обычно маркируются так, чтобы входы располагались слева, а выходы – справа. Количество входов, в общем случае, может быть любым, отличным от нуля. Цифровые схемы в реальном мире могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Символы приведены в соответствии с национальным ГОСТом, в других стандартах они могут отличаться.

Каковы различные типы логических элементов?

Логические элементы имеют один или несколько входов и один или два выхода (обычно расположенных друг за другом). Значения “нулей” и “единиц” выходных сигналов логических элементов определяются логической функцией, которую реализует элемент, и значениями “нулей” и “единиц” входных сигналов, которые выступают в качестве независимых переменных. Существуют элементарные логические функции, которые можно использовать для написания любой сложной логической функции.

Элемент AND (AND), также называемый конъюнкцией, выполняет операцию логического умножения:

Условные обозначения – таблица истинности

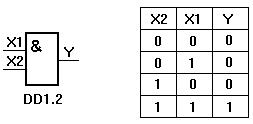
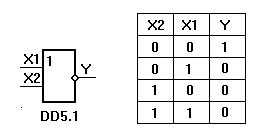
На следующем рисунке показан логический элемент “2И (Число перед “И” указывает на количество входов). Знак & (амперсанд) в левом верхнем углу прямоугольника указывает на то, что это логический элемент “И”. Первые две буквы обозначения DD1.2 указывают на то, что это цифровая схема, цифра слева от точки указывает на номер схемы в схеме, а цифра справа от точки – на номер логического элемента в схеме. Одна интегральная схема может содержать несколько логических элементов.

Состояние входов в таблице обозначено как ‘0’ и ‘1’ (‘false’ и ‘true’). Из таблицы видно, что выход “Y” будет иметь состояние “1”, только если оба входа “X1” и “X2” имеют состояние “1”. Это легко запомнить: умножение на “0” всегда дает “0”.

Элемент ИЛИ (OR), также являющийся дизъюнктором, выполняет логическое сложение:

Условные обозначения – таблица истинности

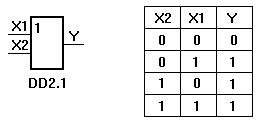
На выходе всегда будет “1”, пока на входах есть хотя бы одна “1”.

Элемент “НЕ” (Элемент NOT, также называемый инвертирующим, выполняет логическое отрицание:

Условные обозначения – таблица истинности

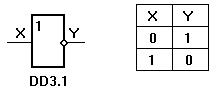
Состояние на входе является обратным состоянию на входе.

Это три элемента, из которых состоят все цифровые устройства!

Рассмотрим еще три логических элемента, которые можно получить, объединив три уже рассмотренных. Из-за исторически сложившейся схемы эти комбинированные схемы также считаются логическими элементами.

Элемент AND-NE (NAND), соединение с отрицанием:

Условные обозначения – таблица истинности

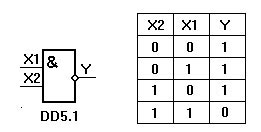
Элемент AND-NE работает так же, как и элемент AND, только выход обратный. Там, где элемент AND должен давать 0, элемент AND-NE дает 1. Все происходит наоборот.

Элемент OR-NE (NOR), дизъюнктор с отрицанием:

Условные обозначения – таблица истинности

Элемент работает так же, как и ИЛИ, но вывод обратный.

Элемент минус ИЛИ (XOR), сумматор по модулю 2:

Условные обозначения – таблица истинности

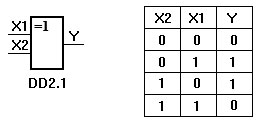
В этом элементе выход будет равен ‘1’ только в том случае, если входы имеют различные условия.

Двоичные многоразрядные сумматоры основаны на этих элементах. Для этого используется дополнительный выход, на входах которого при появлении двух “1” появляется сигнал переноса цифр.

Мы рассмотрели логические элементы, которые используются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут выполнять одну очень важную работу – они не могут хранить информацию. Для хранения данных используется более сложный класс устройств, называемых элементами памяти или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, кодеры (декодеры), мультиплексоры (демультиплексоры) и сумматоры. Некоторые из этих устройств мы рассмотрим в следующем уроке.

Поскольку вы будете иметь дело как с русской, так и с французской технической документацией, я приведу условные графические обозначения элементов в соответствии с нашими и неамериканскими стандартами.

Логические элементы и таблицы истинности

Абсолютно все цифровые схемы состоят из одних и тех же логических элементов – “строительных блоков” каждой цифровой схемы. Это строительные блоки каждой цифровой схемы.

Логический элемент – это схема, которая имеет несколько входов и один выход. Каждому состоянию сигналов на входах соответствует определенный сигнал на выходе.

Что же это за элементы?

Элемент AND (И).

Его также называют “равновесием”.

Чтобы понять, как это работает, необходимо нарисовать таблицу, в которой перечислены состояния выхода для любой комбинации входных сигналов. Такая таблица называется “таблица истинности“. Таблицы истинности широко используются в цифровой технике для описания работы логических схем.

Вот как выглядит элемент AND и его таблица истинности:

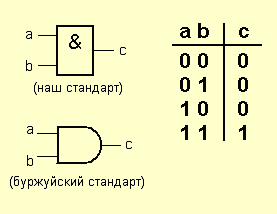
Поскольку вам придется общаться как с русской, так и с буржуйской технической документацией, я приведу условные графические обозначения (УГО) элементов как по нашим, так и не по нашим стандартам.

Давайте посмотрим на таблицу истины и объясним принцип работы мозга. Это нетрудно понять: единица на выходе элемента “I” возникает только в том случае, если на оба входа подаются единицы. Это объясняет название элемента: на одном входе должны быть единицы, а на другом – единицы.

Если посмотреть на это несколько иначе, то можно сказать, что выход элемента И будет равен нулю, если хотя бы один из его входов равен нулю. Теперь вспомните. Давайте двигаться дальше.

ИЛИ элемент.

Другое название для него – дизъюнктор.

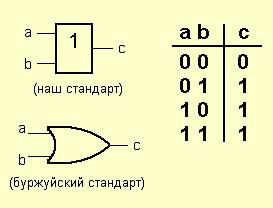
Опять же, название говорит само за себя.

Он производит единицу на выходе, когда один вход ИЛИ подается на другой вход ИЛИ на оба входа одновременно. Этот элемент также можно назвать элементом И для отрицательной логики: его выход равен нулю только тогда, когда на обоих входах нули.

Давайте двигаться дальше. Это очень простой, но очень необходимый элемент.

Элемент “НЕ”.

Его часто называют “инвертором”.

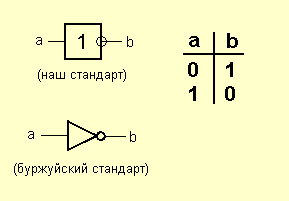
Нужно ли говорить о том, как это работает?

Что ж, давайте двигаться дальше. Следующие два элемента получаются путем размещения инвертора на выходе элементов И и ИЛИ.

Элемент AND-NE (NAND)

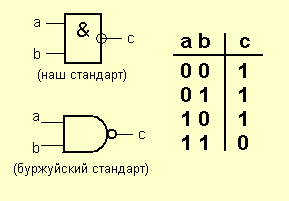
Элемент И-НЕ работает точно так же, как и элемент И, за исключением того, что выходной сигнал является прямо противоположным. Там, где элемент AND должен давать 0, элемент AND-NE дает 1. И наоборот. Это можно легко увидеть в схеме замещения элемента:

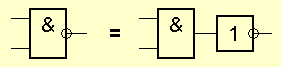
Элемент OR-NE (NOR).

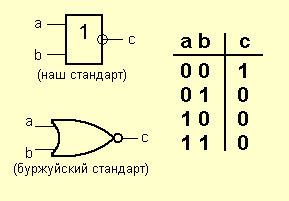
Это та же история – элемент ИЛИ с инвертором на выходе.

Следующий случай немного сложнее:
Элемент XOR (исключающее ИЛИ).

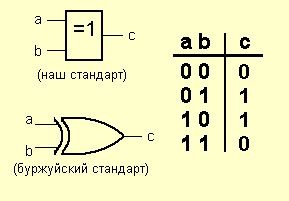
Операцию, которую он выполняет, часто называют “сложение по модулю 2”. Фактически, цифровые сумматоры построены на этих элементах.

Посмотрите на таблицу истинности. Когда происходит сингулярность выходов? Правильно: когда на входы подаются разные сигналы. Одна из них равна 1, а другая – 0. Вот как хитро все устроено.

Схема замещения выглядит примерно так:

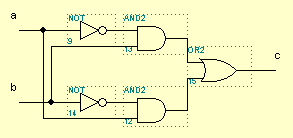
Вам не нужно об этом помнить.

Фактически, это основные логические элементы. Он является основой всех цифровых схем. Даже ваш любимый Pentium 4.

Далее мы рассмотрим, как синтезировать цифровую схему с помощью таблицы истинности. Это совсем не сложно, но это важно знать, потому что это пригодится позже (и пригодится).

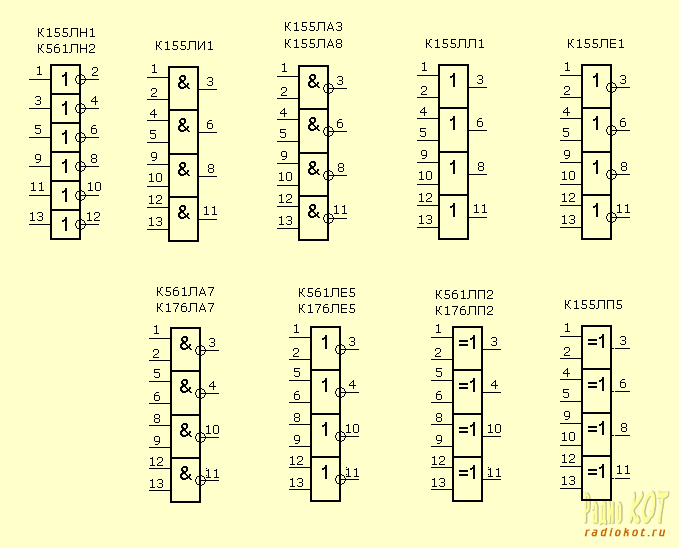
И, наконец, некоторые микрочипы с цифровыми элементами внутри. Номера соответствующих выводов микросхемы нанесены рядом с выводами. Все перечисленные здесь микросхемы имеют 14 выводов. Питание подается на контакты 7 (-) и 14 (+). Напряжение питания указано в таблице в предыдущем параграфе.

нет Опубликовано: 2005. 0 1 Награда I собрана 0 0Выражение A ∨ B истинно для тех сайтов, где A истинно (4800) и для тех сайтов, где B истинно (4500). Если бы все сайты были разными, то A ∨ B было бы верно для 9300 (4800 + 4500) сайтов. Но, по данным государства, существует всего 7000 сайтов. Это означает, что на 2300 (9300 – 7000) веб-страницах оба слова встречаются одновременно. Таким образом, выражение A и B верно для 2300 веб-страниц.

Преподаватель информатики

Компьютерные науки. 8 класс Босова Л.Л. Оглавление

Ключевые слова:

• алгебра логики
• заявление
• логическая операция
• связь
• дизъюнкция
• отрицание
• логическое выражение
• таблица истинности
• законы логики

1.3.1 Заявления

Алгебра в широком смысле – это наука об общих операциях, подобных сложению и умножению, которые можно выполнять над различными математическими объектами. Многие математические объекты (целые числа, измеримые числа, многочлены, векторы, множества) изучаются в школьном курсе алгебры, где нас знакомят с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т.д.

Для компьютерных наук существует ветвь математики, называемая алгебра логикиОбъектами алгебры логики являются теоремы.

Заявление – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Например, в отношении предложений “Великий русский ученый М.В. Ломоносов родился в 1711 году” и “Два плюс шесть – восемь” можно однозначно утверждать как истину. Предложение “Воробьи впадают в зимнюю спячку” является ложной. Таким образом, эти предложения являются утверждениями.

В русском языке высказывания выражаются повествовательными предложениями. Но не каждое повествовательное предложение является утверждением.

Например, предложение “Это предложение ложное” не является высказыванием, поскольку мы не можем сказать, истинно оно или ложно, не получив противоречия. Действительно, если мы предполагаем, что тезисное высказывание истинно, то оно является противоречием высказывания. Если предположить, что предложение ложно, то из этого следует, что предложение истинно.

Что касается предложения “Компьютерная графика – самый интересный предмет в школьном курсе информатики”. Также невозможно с уверенностью сказать, правда это или ложь. Подумайте, почему.

Мотивировочные и вопросительные предложения не являются указательными предложениями.

Например, такие предложения, как: “Запиши домашнее задание”, “Как пройти в библиотеку?”, “Кто здесь?”..

Высказывания могут быть построены с использованием знаков различных формальных языков – математики, физики, химии и т.д.

Примерами таких заявлений являются:

• 1) “Na – это металл” (истинное утверждение);
• 2) “Второй закон Ньютона выражается формулой F = m – a”. (истинное утверждение);
• 3) “Периметр прямоугольника со сторонами длиной a и b равен a – b”. (ложное заявление).

Числовые выражения не являются высказываниями, но вы можете составить высказывание из двух числовых выражений, объединив их знаками равенства или неравенства. Например:

• 1) “3 + 5 = 2 4” (истинное утверждение);
• 2) “II + VI > VIII” (ложное заявление).

Уравнения или неравенства, содержащие переменные, также не являются утверждениями. Например, утверждение “X < 12" становится утверждением только в том случае, если переменная заменяется на какое-то конкретное значение: "5 < 12" - истинное высказывание; "12 < 12" - ложное высказывание.

Обоснование истинности или ложности утверждений решается теми науками, к сфере которых они относятся. Алгебра логики воспринимает семантическое содержание высказываний. Его интересуют только истинные или ложные утверждения. В алгебре логики утверждения обозначаются буквами и называются логические переменные.. Если высказывание истинно, мы обозначаем значение соответствующей логической переменной единицей (A = 1), а если ложно – нулем (B = 0). 0 и 1, обозначающие значения логических переменных, называются логические значения.

Булева алгебра определяет правила написания, вычисления значений, упрощения и преобразования утверждений.

1.3.2 Логические операции

Заявления могут быть простыми и сложными. Заявление называется простойесли ни одна его часть сама по себе не является утверждением. Комплекс (Сложные) утверждения формируются из простых с помощью логические операции.

Рассмотрим основные логические операции, определяемые на высказываниях. Все они соответствуют связкам, используемым в естественном языке.

Конъюнктура

Рассмотрите два утверждения: A = “Создателем алгебры логики является Джордж Буль”, B = “Исследования Клода Шеннона позволили применить алгебру логики в информатике”.. Конечно, новое заявление “Создателем алгебры логики является Джордж Буль, а исследования Клода Шеннона позволили применить алгебру логики в информатике”. истинно только в том случае, если оба исходных утверждения истинны одновременно.

Определите для себя, являются ли три утверждения, рассмотренные выше, истинными или ложными.

Конъюнктура – это логическая операция, которая сопоставляет любые два высказывания с новым высказыванием, которое истинно тогда и только тогда, когда оба исходных высказывания истинны.

Для записи конъюнкции используются следующие символы: AND, ∧, -, &.
Например: A И B, A ∧ B, A – B, A&B.

Конъюнкция может быть описана в виде таблицы, которую мы называем таблица истинности:

Таблица истинности содержит все возможные значения исходных утверждений (столбцы A и B), а соответствующие двоичные числа обычно располагаются в порядке возрастания: 00, 01, 10, 11. Последний столбец содержит результат логической операции для соответствующих операндов.

Конъюнкцию также называют логическим умножением.

Дисфункция. Инверсия

Рассмотрите два утверждения: A = “Идея использования математических символов в логике принадлежит Готфриду Вильгельму Лейбницу”, B = “Лейбниц является основателем двоичной арифметики”. Очевидно, что новое утверждение “Идея использования математических символов в логике принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основателем двоичной арифметики” ложно только в том случае, если оба исходных утверждения ложны одновременно.

Определите для себя, являются ли три вышеприведенных утверждения истинными или ложными.

Дисъюнкция – это логическая операция, которая для каждых двух высказываний соответствует новому высказыванию, которое ложно тогда и только тогда, когда оба исходных высказывания ложны.

Для записи дизъюнкции используются следующие символы: OR, ∨, |, +. Например: A ИЛИ B, A∨B, A|B, A+B.

Дисъюнкция определяется следующей таблицей истинности:

Дисъюнкцию также называют логическим сложением. Подумайте, почему.

Инверсия

Инверсия – это логическая операция, в которой каждому выражению ставится в соответствие новое выражение, значение которого противоположно значению исходного выражения.

Для записи инверсий используются следующие символы: NOT, ¬, – . Например: НЕ А, ¬ А,

Инверсия определяется следующей таблицей истинности:

Инверсию также называют логическим отрицанием.

Отрицание утверждения “У меня дома есть компьютер” это утверждение “Это неправда, что у меня дома есть компьютер”. Или, что то же самое в русском языке, “У меня дома нет компьютера”.. Отказ от заявления “Я не знаю китайского языка”. это утверждение “Это неправда, что я не знаю китайского”. или, что по-русски означает то же самое, “Я знаю китайский”.. Отказ от заявления “У всех восьмиклассников одни пятерки”. это утверждение “Это неправда, что все восьмиклассники получают одни пятерки”, – …Другими словами, “Не все восьмиклассники получают одни пятерки”..

Так, при построении отрицания к простому высказыванию используется либо фраза “it is not true that…”, либо строится отрицание к предикату, после чего к соответствующему глаголу добавляется частица “not”.

Составное высказывание может быть записано в виде логическое выражение – с логическими переменными, знаками логических операций и круглыми скобками. Логические операции в логическом выражении выполняются в следующем порядке: инверсия, конъюнкция, дизъюнкция. Вы можете изменить порядок операций, заключив их в круглые скобки.

Булевы операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.

1.3.2 Булевы операции

Пример 1. Пусть A “Страница содержит слово “крейсер””, B = “Страница содержит слово “линкор””.. Рассмотрим сегмент Интернета, содержащий 5 000 000 веб-страниц. Утверждение A верно для 4 800 страниц, утверждение B верно для 4 500 страниц, а утверждение A ∨ B верно для 7 000 страниц. Для какого количества веб-страниц в данном случае будут верны следующие выражения и утверждения?

• (a) НЕ (A ИЛИ B);
• (b )A&B;
• в) Эта страница содержит слово “крейсер” И не содержит слова “линкор”.

Решение. Представим множество всех WWW-сайтов в рассматриваемом секторе Интернета окружностью и сделаем в ней две окружности: первая окружность – это множество WWW-сайтов, где верно утверждение А, а вторая – те, где верно утверждение В (рис.1.3).

Представим графически наборы веб-страниц, для которых истинны выражения и утверждения a) – c) (рис. 1.4).

Диаграммы помогут нам ответить на вопросы задачи.

Выражение A OR B верно для 7000 веб-страниц, то есть для общего числа 5 000 000 страниц. Следовательно, выражение A OR B является ложным для 4 993 000 веб-страниц. Другими словами, для 4 993 000 веб-сайтов выражение NOT (A OR B) является истинным.

Выражение A ∨ B истинно для тех сайтов, где A истинно (4 800), а также для тех сайтов, где B истинно (4 500). Если бы все сайты были разными, то A ∨ B было бы верно для 9300 (4800 + 4500) сайтов. Но, по данным государства, существует всего 7000 веб-страниц. Это означает, что на 2300 (9300 – 7000) веб-страницах оба слова встречаются одновременно. Следовательно, выражение A и B верно для 2300 веб-страниц.

Чтобы узнать, сколько страниц из A одновременно истинны и сколько ложны, вычтем 2300 из 4800. Таким образом, утверждение “Слово “крейсер” появляется на сайте, а слово “линкор” не появляется”. верно на 2500 веб-страницах.

Самостоятельно запишите логическое выражение, соответствующее приведенному выше утверждению.

На сайте Федерального центра информационно-образовательных ресурсов (http://fcoir.edu.ru/) размещен информационный модуль “Экспрессия. Простые и сложные утверждения. Основные логические операции”. Знакомство с этими ресурсами позволит вам расширить свои знания по изучаемой теме.

1.3.3 Создание таблиц истинности для логических выражений

Вы можете построить таблицу истинности для логического выражения, которая показывает, какие значения принимает выражение для всех наборов значений переменных, которые оно содержит. Чтобы построить таблицу истинности

• 1) подсчет n – количество переменных в выражении;
• 2) подсчитать общее количество логических операций в выражении;
• 3) определять порядок логических операций с учетом скобок и приоритетов;
• 4) определить количество столбцов в таблице: количество переменных + количество операций;
• 5) Заполните шапку таблицы, записав переменные и операции в порядке, установленном в шаге 3;
• 6) Определите количество строк в таблице (без учета заголовка таблицы): m = 2 n ;
• 7) записать наборы входных переменных, если они являются n-разрядными двоичными числами от 0 до 2 n – 1
• заполнить таблицу столбцами, выполняя логические операции в соответствии с установленным порядком.

Постройте таблицу истинности для логического выражения A ∨ A & B. Он содержит две переменные, две операции, сначала конъюнкцию, а затем дизъюнкцию. Всего в таблице будет четыре столбца:

Наборы входных переменных – это целые числа от 0 до 3, представленные в двоичном коде: 00, 01, 10, 11.

Завершенная таблица истинности выглядит следующим образом:

Обратите внимание, что последний столбец (результат) такой же, как и столбец А. В этом случае говорят, что логическое выражение A ∨ A & B равно логической переменной A.

1.3.4 Свойства логических операций

Рассмотрим основные свойства логических операций, также называемых Законы булевой алгебры.

1. Закон коммутации:

• Для логического умножения:

• Для логического дополнения:

2. Закон комбинаторики (ассоциация):

• Для логического умножения:

• Для логического дополнения:

(A ∨ B) ∨ C = A ∨ (B ∨ C).

Если символы операций одинаковы, круглые скобки могут быть расставлены свободно или вовсе опущены.

3. Закон о раздельном проживании:

• Для логического умножения:

• Для логического дополнения:

A ∨ (B & C) = (A ∨ B) & (A v C).

4 Закон двойного отрицания:

Двойное отрицание исключает отрицание.

5. Право исключенного третьего лица:

• Для логического умножения:

• Для логического сложения

Из двух противоречивых высказываний на одну и ту же тему одно всегда истинно, а другое всегда ложно, третье не дано.

6. Закон повторения:

• Для логического умножения:

• Для логического дополнения:

7. Законы операций над числами 0 и 1:

• Для логического умножения:

• Для логического дополнения:

8. Законы общей инверсии:

• Для логического умножения:

• Для логического дополнения:

Законы булевой алгебры можно доказать с помощью таблиц истинности.

Докажем закон делимости для логического сложения:

• A ∨ (B & C) = (A ∨ B) & (A ∨ C).

Сходимость значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает закон делимости для логического сложения.

Пример 2. Найти значение логического выражения

Решение. При X = 0 мы получаем следующее логическое выражение:

Поскольку логические выражения 0 < 3, 0 < 2 истинны, подставив их значения в логическое выражение, получим

Элементы алгебры логики. Решение логических задач

Рассмотрим несколько способов решения логических задач.

Проблема 1. Коля, Вася и Сережа летом гостили у бабушки. Однажды один из мальчиков случайно разбил любимую вазу своей бабушки. На вопрос, кто разбил вазу, они дали следующие ответы:

• Сергей: 1) Я не делал этого. 2) Вася – нет.
• Вася: 3) Сергей не сломал. 4) Это Коля сломал его.
• Коля: 5) Я не сломал его. 6) Сергей разбил вазу.

Бабушка знала, что один из ее внуков, назовем его правдивым, сказал правду оба раза; другой, назовем его шутником, сказал неправду оба раза; третий, назовем его хитрым, сказал правду один раз и неправду другой раз. Назовите имена: правдивый, шутник и хитрец. Кто из внуков разбил вазу?

Решение. Пусть K =. “Коля разбил вазу”., В = “Вася разбил вазу”, С – “Сергей разбил вазу”.. Чтобы решить эту задачу, можно создать таблицу истинности, в которой будут представлены высказывания каждого мальчика. Поскольку ваза была разбита одним из внуков, для определения того, кто это сделал, вам понадобится только участок таблицы истинности, содержащий наборы значений входных переменных: 001, 010, 100.

Исходя из того, что бабушка знает о своих внуках, найдите в таблице строку, содержащую три комбинации значений, расположенных в определенном порядке: 00 (слова джокера), 11 (слова правдивого внука), 01 или 10 (слова хитрого внука). Такая линия отмечается галочкой. Согласно этой версии, ваза была разбита Сергием, который оказался плутом. Проказником оказался Вася. Имя правдивого внука – Кола.

Задача 2. Алла, Валя, Сима и Даша участвуют в соревнованиях по гимнастике. Поклонники высказывали предположения о возможных победителях:

• 1) Сима будет первой, Валя – второй;
• 2) Сима будет второй, Даша – третьей;
• 3) Алла будет второй, Даша – четвертой.

В конце конкурса выяснилось, что в каждом предположении только одно из утверждений истинно, а другое – ложно. Какое место заняла каждая девушка в конкурсе, если все они заняли разные места? Решение. Рассмотрим простое утверждение:

• C₁ = “Сима заняла первое место”;
• В₂ = “Валя заняла второе место”;
• С₂ = “Сима заняла второе место”;
• Д₃ D = “Даша заняла третье место”;
• А₂ A = “Ала заняла второе место”;
• Д₄ A = “Даша заняла четвертое место”.

Поскольку в каждом из трех предположений одно из утверждений истинно, а другое ложно, мы можем заключить следующее

• 1) C₁ + В₂ = 1, C₁ – В₂ = 0;
• 2) С₂ + Д₃ = 1, С₂ – Д₃ = 0;
• 3) А₂ + Д₄ = 1, А₂ – Д₄ = 0.

Логическое произведение истинных высказываний будет истинным:

• (C₁ + В₂) – (С₂ + Д₃) – (А₃ + Д₄) = 1.

Исходя из закона делимости, преобразуйте левую часть этого выражения:

• (C₁ – С₂ + C₁ – Д₃ + В₂ – С₂ + В₂ – Д₃) – (А₂ + Д₄) = 1.

Заявление C₁ – С₂ означает, что Сима заняла и первое, и второе место. Согласно описанию проблемы, это утверждение неверно. Утверждение B также является ложным₂ – С₂. Учитывая закон действия с постоянной 0, напишите

• (C₁ – С₂ + C₁ – Д₃ + В₂ – С₂ + В₂ – Д₃) – (А₂ + Д₄) = 1.

Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных утверждений дает

• С₁ – Д₃ – А₂ + С₁ – Д₃ – Д₄ + В₂ – Д₃ – А₂ + В₂ – Д₃ – Д₄ = 1.
• C₁ – Д₃ – А₂ = 1

Из последнего уравнения следует, что C₁ = 1, Д₃ = 1, А₂ = Это значит, что Сима заняла первое место, Алла – второе, а Даша – третье. В результате Валя заняла четвертое место.

Другие способы решения логических задач, участие в онлайн-олимпиадах и конкурсах по их решению можно найти на российском сайте Международного математического конкурса “Кенгуру” (http://mathkang.ru/).

На сайте http://www.kaser.com/ вы можете скачать демо-версию очень полезной логической головоломки Sherlock, развивающей навыки логики и мышления.

Логические элементы

Булева алгебра – это раздел математики, который играет важную роль в проектировании автоматических устройств и разработке аппаратного и программного обеспечения информационно-коммуникационных технологий.

Вы уже знаете, что любую информацию можно представить в дискретной форме – как фиксированный набор отдельных значений. Устройства, обрабатывающие такие значения (сигналы), называются дискретными устройствами. Дискретный преобразователь, который после обработки двоичных сигналов выдает значение одной из логических операций, называется логический элемент.

На рисунке 1.5 показаны символы (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.

Логический элемент И (связь) реализует операцию логического умножения (рисунок 1.5, а). Единица на выходе этого элемента появляется только в том случае, если все входы имеют единицы.

Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рисунок 1.5, б). Если хотя бы один из входов равен единице, то выход элемента также будет равен единице.

Логический элемент НЕ (инвертор) реализует операцию отрицания (рисунок 1.5, c). Если на входе элемента 0, то на выходе 1 и наоборот.

Компьютерные устройства, выполняющие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти темы будут рассмотрены в курсе “Информатика” для 10-11 классов.

Пример 3. Давайте проанализируем электронную схему, то есть выясним, какой сигнал должен быть на выходе F при любом возможном наборе сигналов A и B на входах.

Решение. Запишем в таблицу истинности все возможные комбинации сигналов A и B на входах. Проследите преобразование каждой пары сигналов при прохождении их через логические элементы и запишите результат в таблицу. Заполненная таблица истинности полностью описывает электронную схему из вопроса 4.

Таблица истинности также может быть построена из логического выражения, соответствующего электронной схеме. Последним логическим элементом в рассматриваемой схеме является конъюнкция. Он получает сигналы от входа A и от преобразователя. Инвертор, в свою очередь, получает сигнал со входа B. Таким образом,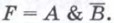

Чтобы лучше понять логические элементы и электронные схемы, используйте симулятор логики (http://kpolyakov.narod.ru/prog/logic.htm).

Элементы алгебры логики. Основы

Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Основные логические операции, определяемые на высказываниях: инверсия, конъюнкция, дизъюнкция.

Таблицы истинности для основных логических операций:

При вычислении логических выражений сначала выполняются операции, заключенные в круглые скобки. Приоритет выполнения логических операций:

В зависимости от конструкции схемы элемента, от его электрических параметров, логические уровни (уровни высокого и низкого напряжения) входов и выходов имеют одинаковые значения для высокого и низкого состояний (истина и ложь).

Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности.

Схема, выполняющая логическую операцию над входными данными, называется логическим затвором. Входные данные представляются в виде напряжения с различными уровнями, а результат логической операции на выходе также получается в виде напряжения с определенным уровнем.

Операнды в этом случае задаются в двоичной нотации – на вход логической схемы подается напряжение высокого или низкого уровня, которое де-факто служит входными данными. Например, высокое напряжение – это булева 1 – указывает на истинное значение операнда, а низкое напряжение 0 – на ложное значение. 1 – ИСТИННО, 0 – ЛОЖНО.

Логический элемент – это компонент, который реализует определенные логические отношения между входными и выходными сигналами. Логические элементы чаще всего используются для построения логических схем вычислительных машин, дискретных схем автоматического управления и контроля. Все типы логических элементов характеризуются дискретными входными и выходными сигналами, независимо от их физической природы.

Логические элементы имеют один или несколько входов и один или два (обычно инверсных) выхода. Нули” и “единицы” выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и “нулями” и “единицами” входных сигналов, которые выступают в качестве независимых переменных. Существуют элементарные логические функции, из которых можно собрать любую сложную логическую функцию.

В зависимости от схемотехнического исполнения элемента и его электрических параметров, логические уровни (уровни высокого и низкого напряжения) входа и выхода имеют одинаковые значения для высокого и низкого состояний (истина и ложь).

Традиционно логические элементы изготавливались в виде специальных радиочастотных элементов – интегральных схем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (AND, OR, NOT, Exclusive OR), являются основными операциями, выполняемыми над основными типами логических элементов. Давайте теперь подробнее рассмотрим каждый из этих типов логических элементов.

Логический элемент И – конъюнкция, логическое умножение, AND

“И” – это логический элемент, который выполняет операцию конъюнкции или логического умножения над входными данными. Этот элемент может иметь от 2 до 8 (наиболее распространенными являются элементы “И” с 2, 3, 4 и 8 входами) входов и один выход.

Символ логических элементов “И” с различным количеством входов показан на рисунке ниже. В тексте логическое устройство “И” с определенным количеством входов обозначается как “2И”, “4И” и т.д. – Элемент AND с двумя входами, с четырьмя входами и т.д.

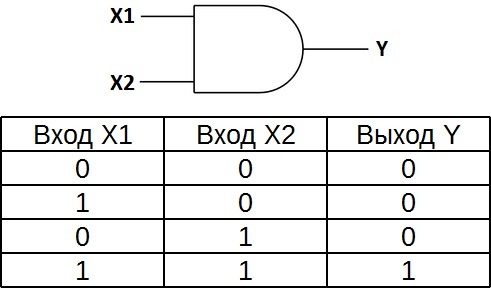
Таблица истинности для элемента 2I показывает, что на выходе этого элемента будет логическая единица, только если на первом входе и на втором входе есть обе логические единицы. В остальных трех возможных случаях выход будет равен нулю.

В западных диаграммах символ элемента “И” имеет прямую линию на входе и закругленную линию на выходе. На отечественных диаграммах это прямоугольник с символом “&”.

Логический элемент ИЛИ – дизъюнкция, логическое сложение, ИЛИ

“ИЛИ” – это логический элемент, выполняющий дизъюнкцию или логическое сложение входных данных. Он может быть с двумя, тремя, четырьмя и т.д. входами и одним выходом, как и элемент AND. Символы логических элементов ИЛИ с различным количеством входов показаны на рисунке ниже. Эти элементы обозначаются как: 2 OR, 3 OR, 4 OR и т.д.

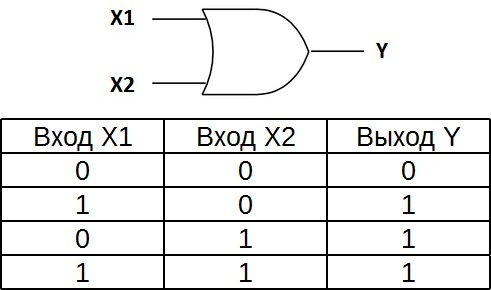
Таблица истинности для элемента 2-LI показывает, что для того, чтобы на выходе появилась логическая 1, достаточно, чтобы на первом входе ИЛИ на втором входе была логическая 1. Если на обоих входах одновременно присутствуют логические 1, то на выходе также будет 1.

На западных схемах значок элемента ИЛИ закруглен на входе и закруглен точкой на выходе. На домашних схемах это прямоугольник с символом “1”.

Логический элемент “NOT” является отрицанием, инверсией NOT

“NOT” – это логический элемент, который выполняет операцию логического отрицания над входными данными. Этот элемент, имеющий один выход и только один вход, также называется инвертором, поскольку он фактически инвертирует входной сигнал. На рисунке показан символ логического элемента “НЕ”.

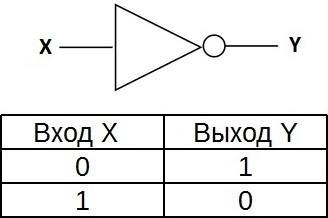
Таблица истинности для инвертора показывает, что высокий потенциал на входе дает низкий потенциал на выходе и наоборот.

На западных диаграммах символ элемента “NOT” представляет собой треугольник с кругом на выходе. На отечественных диаграммах это прямоугольник с символом “1”, с кружком на выходе.

Булевский элемент “И-НЕ” – конъюнкция (логическое умножение) с отрицанием, NAND

“И-НЕ” – это логический элемент, который выполняет операцию логического сложения входных данных, за которой следует операция логического отрицания, с выдачей результата на выход. Другими словами, по сути, это элемент “И”, дополненный элементом “НЕ”. На рисунке показан символ логического элемента 2I-NE.

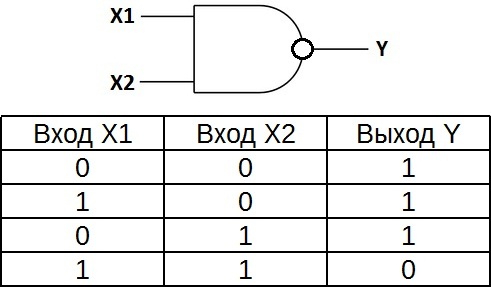
Таблица истинности для элемента И-НЕ противоположна таблице для элемента И. Вместо трех нулей и единицы – три единицы и ноль. Элемент I-NE также называют элементом Шеффера, в честь математика Генри Мориса Шеффера, который впервые обратил внимание на важность этой логической операции в 1913 году. Он имеет маркировку “AND”, только с кружком на выходе.

Логический элемент “ИЛИ-НЕ” – дизъюнкция (логическое дополнение) с отрицанием, NOR

“ИЛИ-НЕ” – это логический элемент, который выполняет операцию логического сложения входных данных, а затем операцию логического отрицания, результат выдается на выход. Другими словами, это элемент ИЛИ, дополненный элементом НЕ, т.е. инвертор. На рисунке показан символ для логического элемента 2 ИЛИ-НЕ.

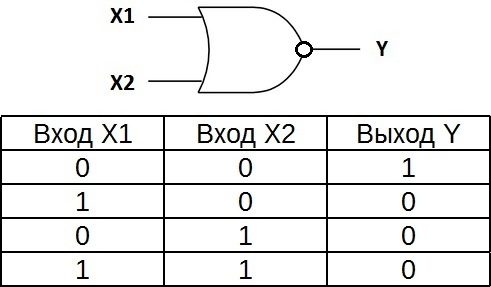
Таблица истинности для элемента ИЛИ-НЕ противоположна таблице для элемента ИЛИ. Высокий потенциал на выходе получается только тогда, когда на оба входа одновременно подаются низкие потенциалы. Обозначается как ИЛИ, только с кружком на выходе для обозначения инверсии.

Исключая логический элемент OR – сложение по модулю 2, XOR

“Логический элемент исключающее ИЛИ, который выполняет сложение по модулю 2 на входных данных, имеет два входа и один выход. Эти элементы часто используются в схемах управления. На рисунке показан символ этого элемента.

В западных схемах он выглядит как “OR” с дополнительной изогнутой полосой на стороне входа, а в отечественных схемах он выглядит как “OR”, только вместо “1” будет написано “=1”.

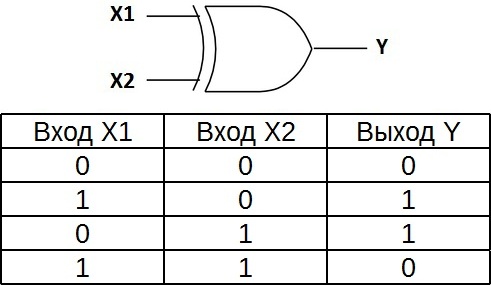
Этот логический элемент также называют “несбалансированным”. На выходе будет высокое напряжение, только если сигналы на входе не равны (один – один и один – ноль, или один – ноль и один – один), даже если на входе одновременно две единицы, на выходе будет ноль – в этом отличие от “ИЛИ”. Эти логические элементы широко используются в сумматорах.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Любое самое сложное логическое утверждение, в частности, функциональное устройство, электрическая цепь и т.д., может быть описано тремя логическими операциями: сложением (дизъюнкция), умножением (конъюнкция) и отрицанием (инверсия), – с помощью которых можно объединять простые утверждения. В этом смысле такое множество логических функций называется функционально полным множеством или базой.
Логическое сложение (дизъюнкция) переменных X 1 , X 2 . X n записывается в виде y=X 1 +X 2 +. +X n
Значение y = 0 имеет место только в том случае, если X 1 +X 2 +. +X n =0. E
Если хотя бы одно слагаемое равно единице (X i = 1 событие произошло), то y = 1. Сумма вхождений (X 1 + X 2 + . где X 1 = 1, X 2 = 1, . . . ) указывает на наступление события, т.е. если любая сумма равна единице, то сумма равна единице: y = 1, если X 1 = 1 или X 2 = 1 или X i = 1, или все переменные X равны единице. Отсюда и другое название этой операции, а именно ИЛИ.
Таблица истинности для операции ИЛИ ИЛИ двух переменных приведен ниже:

Сложные логические элементы

Помимо простых логических элементов, рассмотренных ранее, стандартная серия содержит более сложные элементы, которые представляют собой комбинации простейших, объединенных в один корпус:

Ситуационный анализ показывает, что левым операндом импликации должна быть переменная `p’. Таким образом, в формализованном виде исходное утверждение выглядит как `bb(p -> q)`. .

Дисъюнктор

• 

§2 Логические операции. Формализация утверждений

Теперь мы познакомимся с шестью основными логическими операциями. Каждый из них имеет несколько названий и обозначений.

Названия операций

Возможные обозначения

Конъюнкция, логическое умножение, операция AND.

`&, ^^, *,` по аналогии с алгебраическим умножением не могут быть обозначены никаким образом

Дисъюнкция, нестрогая дизъюнкция, логическое сложение, ИЛИ, операция ИЛИ.

Строгая дизъюнкция, дизъюнктивная дизъюнкция, исключающее ИЛИ, сложение по модулю `2′.

Эквивалентность, эквивалентность, равенство, эквивалентность.

Импликация, следствие, преемственность.

Теперь, чтобы строго определить эти логические операции, нам нужно перечислить таблицу истинности для каждой из них. Все упомянутые операции, кроме отрицания, имеют два операнда. Знак операции в выражениях записывается между операндами (как в числовой алгебре). Операция отрицания имеет один операнд и в выражениях записывается либо в виде строки над операндом, либо в виде префиксного символа слева от операнда.

Чтобы избежать путаницы и гарантировать все возможные комбинации значений операндов, принято записывать их в лексикографическом порядке (по условию, предполагается “false” “<`true'').

Таблица истинности для конъюнкции

Первый операнд

Второй операнд

Значение операции

Таблица истинности для дизъюнкции

Первый операнд

Второй операнд

Операционная ценность

Таблица истинности для строгой дизъюнкции

Первый операнд

Второй операнд

Значение операнда

Таблица истинности для эквивалентности

Первый операнд

Второй операнд

Операционная ценность

Таблица истинности для импликации

Первый операнд

Второй операнд

Операционная ценность

Таблица истинности для отрицания

Значение операнда

Значение операнда

Теперь осталось установить соответствие между логическими операциями и логическими союзами в русском языке.

Логическая операция

Логические союзы в русском языке

и, а, но, а также, включая,

в одно и то же время, хотя

Тогда и только тогда,

необходимо и достаточно, чтобы

Поэтому, если необходимо, чтобы, то достаточно, чтобы

Обратите внимание, что конъюнкция OR может обозначать как строгую, так и нестрогую дизъюнкцию. Его интерпретация зависит от содержания (. ) высказывания.

Подумайте над утверждением: “Мы собираемся пойти в кино в субботу или воскресенье”. Есть два простых утверждения: ‘Мы идем в кино в субботу’ и ‘Мы идем в кино в воскресенье’. Между ними находится связка OR, которую можно интерпретировать двумя способами. В этом случае очевидно, что мы можем пойти в кино и в субботу, и в воскресенье, поэтому дизъюнкция будет несжимаемой. Возьмем две логические переменные, `p` и `q`, и присвоим им простые утверждения. Тогда исходное утверждение в формализованном виде будет выглядеть как `bb(pvvq)`.

Рассмотрим высказывание `Я сейчас нахожусь на севере Москвы или на юго-западе Москвы`. Здесь мы снова имеем дело с двумя простыми утверждениями, которые связаны связкой OR. Но в данном случае связка OR интерпретируется как строгая дизъюнкция, потому что вы не можете находиться в двух местах одновременно. Таким образом, если мы снова возьмем логические переменные `p` и `q`, то получим следующую логическую формулу: `bb(p “o+q)`.

Подумайте над утверждением: “Чтобы четырехугольник был квадратом, все его стороны должны быть равны”. Есть два простых утверждения: Четырехугольник – это квадрат” и “Все стороны четырехугольника равны”. Присвойте их логическим переменным `p` и `q` соответственно. Логическая связка “необходимо, чтобы” является импликацией. Весь вопрос в том, что из чего следует. (Какая запись верна: `bbp -> bbq` или `bbq ->bbp`?) Импликация ложна только в одном случае: когда левый операнд истинен, а правый – ложен. Рассмотрите все возможные значения операндов и проанализируйте, какая из ситуаций невозможна.

1) `p’ и `q’ ложны. Это означает, что данный четырехугольник не является квадратом и его стороны не равны. Это возможная ситуация.

2) `p’ ложно, `q’ истинно. Это означает, что данный четырехугольник не является квадратом, но его стороны равны. Это возможная ситуация (ромб).

3) `p` истинно, `q` истинно. Это означает, что данный четырехугольник является квадратом и его стороны равны. Это возможная ситуация.

4) `p` – истинно, `q` – ложно. Это означает, что четырехугольник является квадратом, но его стороны не равны. Это невозможная ситуация.

Анализ ситуации показывает, что левым операндом импликации должна быть переменная `p`. Таким образом, в формализованном виде исходное утверждение выглядит как `bb(p -> q)`. .

Очень часто вместо “назначить эти утверждения логическим переменным” мы говорим “обозначить эти утверждения как следующие”. В дальнейшем мы также будем использовать эту фразу.

Читайте далее:

• Что это такое: Алгебра логики.
• Логика в компьютерных науках.
• Логическое мышление – развитие логики.
• Таблицы истинности и булевы графы.
• Урок 3: Таблицы истинности.
• Цепь. Минимизация логических функций /.
• Логическое ИЛИ – это. Что такое логическое ИЛИ?.