V. Точность измерительных приборов - услуги электромонтажа, строительства и ремонта

Этот пример показывает, что в третьем случае относительная погрешность наименьшая, т.е. чем выше показания прибора, тем меньше относительная погрешность измерения. Для оптимального использования измерительных приборов рекомендуется выбирать их таким образом, чтобы значение измеряемой величины находилось в конце шкалы прибора. В этом случае относительная погрешность близка к классу точности прибора. Если точность прибора неизвестна, абсолютная погрешность принимается равной половине значения наименьшего деления (линейка, термометр, секундомер). Для штангенциркулей и микрометров – точность их нониуса (0,1 мм, 0,01 мм).

Содержание

V. Точность измерительных приборов.

Точность измерительного прибора – это свойство, которое описывает близость показаний данного измерительного прибора к истинным значениям измеряемой величины и определяется как наименьшая величина, которая может быть надежно определена с помощью данного прибора.

Точность прибора зависит от наименьшего деления его шкалы и указывается либо на самом приборе, либо в инструкции по эксплуатации (datasheet) производителя. Следует отметить, что точность 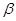обратно пропорциональна относительной погрешности измерения E: = .

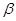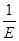Погрешность электроизмерительных приборов определяется классом точности (или приведенной погрешностью E_pr), который обозначается на передней панели прибора цифрой в круге. Класс точности прибора – это процентное отношение абсолютной погрешности 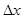до предельного (номинального) значения x_pr измеряемой величины, т.е. до наибольшего значения, которое может быть измерено на шкале прибора (предел измерения):

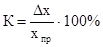Если вы знаете класс точности и предел прибора, вы можете рассчитать его абсолютную неопределенность:

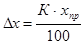Эта неопределенность одинакова для каждого измерения, выполненного с помощью прибора. Существует семь классов точности: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Приборы первых трех классов точности (0,1, 0,2, 0,5) обозначаются как точные приборы и используются для точных научных измерений, приборы других классов точности называются технические инструменты .. Приборы, не имеющие класса точности, считаются вне класса.

Пример. Сила тока измеряется в цепи с помощью амперметра, класс точности которого K=0,5 и шкала которого имеет предел измерения I_pr=10 A. Найдите абсолютную погрешность амперметра:

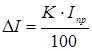
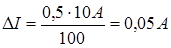
Из этого следует, что амперметр может измерять силу тока с точностью 0,05 А или менее, и поэтому снимать показания на шкале прибора с большей точностью нецелесообразно.

Предположим, что с помощью данного амперметра измеряются три тока: I₁=2 A; I₂=5 A; I₃=8 A. Найдите относительную ошибку для каждого случая: ; .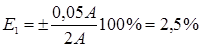

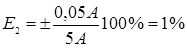
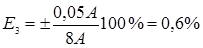Этот пример показывает, что третий случай имеет наименьшую относительную погрешность, т.е. чем больше показания прибора, тем меньше относительная погрешность измерения. Для оптимального использования измерительных приборов рекомендуется выбирать их таким образом, чтобы значение измеряемой величины находилось в конце шкалы прибора. В этом случае относительная погрешность близка к классу точности прибора. Если точность прибора неизвестна, абсолютная погрешность принимается равной половине значения наименьшего деления (линейка, термометр, секундомер). Для штангенциркулей и микрометров – верньерная точность (0,1 мм, 0,01 мм).

Примечания: 1) При снятии показаний убедитесь, что линия взгляда перпендикулярна шкале. Для того чтобы устранить так называемую. Для устранения ошибки параллакса многие приборы оснащены зеркалом (“зеркальные приборы”). Глаз экспериментатора расположен правильно, если рука с инструментом загораживает его изображение в зеркале.

2) При косвенных измерениях (например, определение объема цилиндра по его диаметру и высоте) все измеренные вершины должны быть определены с примерно одинаковой относительной точностью.

3) При обработке результатов измерений следует помнить, что точность расчетов должна соответствовать точности самих измерений. Вычисления, выполняемые с большим количеством знаков после запятой, чем необходимо, приводят к большому количеству ненужной работы. Например, если хотя бы одна из величин в выражении задана с точностью до двух значащих цифр, нет смысла вычислять результат с точностью более двух значащих цифр. При этом рекомендуется оставлять одну дополнительную цифру в промежуточных расчетах, чтобы отбросить ее позже – при записи окончательного результата. В теории неопределенности существует исключение из существующих правил округления: при ошибках округления последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра равна 3 или больше.

Класс точности определяет гарантированные пределы, в которых ограничена погрешность прибора в заданном диапазоне измерений.

Классы точности приборов

Приборы делятся на восемь классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы с классами точности 0,05, 0,1, 0,2 и 0,5 используются для прецизионных лабораторных измерений и называются точные приборы (Приборы класса точности используются для точных лабораторных измерений и называются прецизионными приборами). Инструменты классов 1.0, 1.5: 2.5 и 4.0 (технические) используются в машиностроении.

Класс точности прибора указывается на шкале прибора. Если он не отмечен на шкале, то прибор находится вне класса, т.е. его приведенная погрешность превышает 4%. Изготовитель прибора гарантирует относительную точность прибора, которая равна классу точности (уменьшенной погрешности) прибора при измерении величины, дающей падение указателя по шкале. Определив класс точности и предельное значение по шкале прибора, его абсолютную погрешность ΔX = ± rX_pr / 100 %, которая принимается одинаковой по всей шкале прибора. Знаки “+” и “-” указывают на то, что ошибка может быть больше или меньше истинного значения измеряемой величины.

Когда приборы используются для конкретных измерений, редко бывает так, что измеряемая величина заставляет стрелку прибора колебаться по всей длине шкалы. Как правило, измеренное значение меньше. Это увеличивает относительную погрешность измерения. Для оптимального использования приборов их выбирают так, чтобы значения измеряемой величины находились в конце шкалы прибора, что позволит уменьшить относительную погрешность измерения и приблизить ее к классу точности прибора. Если класс точности не указан на приборе, абсолютная погрешность принимается равной половине цены наименьшего деления.

Погрешность электроизмерительных приборов определяется классом точности (или приведенной погрешностью E_pr), который обозначен на передней панели прибора соответствующей цифрой в круге. Класс точности K – это процентное отношение абсолютной погрешности к предельному (номинальному) значению x_pr измеряемого вещества, т.е. до его максимального значения, которое может быть измерено с помощью шкалы прибора (предел измерения):

Чтобы использовать качественное измерительное оборудование, необходимо знать погрешность, с которой прибор производит измерения. Технические характеристики каждого измерительного прибора включают следующие значения, которые обычно указываются на шкале:

единица измерения величины, измеряемой прибором;
принцип работы (магнитный, электромагнитный, индуктивный и т.д.)
класс точности устройства
положение равновесия прибора (горизонтальное, вертикальное или наклонное)
напряжение, при котором проводилось испытание изоляции корпуса;
серийный номер и год выпуска
тип тока, при котором должны проводиться измерения (постоянный ток, переменный ток).

Одной из характеристик технического средства измерения является его класс точности – величина, определяемая несколькими погрешностями, а именно их пределами. Формула для определения этой характеристики прибора выглядит следующим образом:

γ = ΔXnaib / Xpr⋅× 100%, где

ΔXнаиб – максимальная абсолютная погрешность измерения;

Xpc – максимальное значение на шкале прибора.

Класс точности устройства также называется приведенной погрешностью. В соответствии с этим обозначением все измерительные приборы делятся на восемь классов:

Приборы с такими классами погрешности называются прецизионными, от английского слова “precision”, что в переводе на русский означает точность. Это самые точные приборы, используемые в лабораторных исследованиях.

Следующие четыре класса точности

используются в технической промышленности и называются техническими измерительными приборами.

Производители технических манометров отмечают на шкале их класс точности; отсутствие маркировки означает, что прибор не соответствует классу и погрешность его измерений превышает 4%.

Класс точности прибора является показателем точности самих приборов, но он не определяет точность проводимых измерений. Например, класс точности амперметров характеризуется абсолютными пределами погрешности и не гарантирует, что на показания не будут влиять магнитные поля, частоты переменного тока, колебания температуры или другие внешние факторы.

Классы точности приборов могут обозначаться латинскими буквами, арабскими цифрами или римскими цифрами. Арабские цифры указывают на то, что основной точностью является уменьшенная погрешность и что следует учитывать наибольшее и наименьшее значения из серии измерений. Римская цифра, обозначающая класс точности, указывает на то, что точность прибора была определена по значению относительной погрешности.

Если класс точности прибора обозначен дробным числом на шкале (например, “0,01/0,02”), это означает, что приведенная погрешность на максимуме шкалы составляет ±0,01%, а в начале ±0,01%. Это относится к высокочастотным электроизмерительным приборам.

Все значения точности для любого измерительного прибора стандартизированы и приняты в качестве стандартов, и они не должны превышать эти значения. Они могут иметь различные значения в зависимости от условий, в которых используется измерительный прибор, но в целом они должны находиться в стандартизированных пределах. Методы определения показателей допусков и обозначения классов точности приборов указаны в ГОСТе.

Плюсы и минусы установки интеллектуальных счетчиков в жилом доме
213115

РО считают, что различия в классах точности UUT и MUT являются причиной увеличения объема работ по техническому обслуживанию и ремонту в ИСУ

Группа управляющих организаций не согласилась с требованием об установке на МФБ приборов учета с разными классами точности, т.е. с точки зрения погрешности измерений. Они подали административный иск в Верховный суд Российской Федерации, требуя отменить п. № 442 ОТ С. 138.

Управляющие компании указали, что этот пункт противоречит части 1 статьи 1 Гражданского кодекса и части 1 статьи 1 Жилищно-коммунального кодекса. Это также ставит в неравное положение стороны отношений по покупке и оплате фактически потребленной электроэнергии. Следовательно, нормы, содержащиеся в п. 138 ПП РФ № 442, нарушают принципы равенства участников гражданско-правовых отношений и равенства участников отношений, регулируемых жилищным законодательством в сфере владения, пользования и распоряжения жилыми помещениями.

Различный механизм работы УУТ и ОДПУ увеличивает разницу между показаниями квартирных и индивидуальных счетчиков. Объем средств, расходуемых зданием на содержание общего имущества, значительно превышает норму, и расходы на их оплату ложатся на ЖЭК.

Из-за разной погрешности приборов учета, показания которых учитываются при расчете платы за электроэнергию для граждан и для плательщиков РН в ИСО, возникает ситуация, когда за один и тот же объем ресурса плательщикам начисляются разные суммы. Все ошибки приборов учета трактуются в пользу жильцов дома, что нарушает принципы справедливости, честности и равенства.

В результате, как говорится в иске, управляющие организации вынуждены платить завышенные суммы за электроэнергию, используемую для содержания общего имущества собственников в жилых домах, что ухудшает их финансовое положение и увеличивает задолженность перед РСО.

Плюсы и минусы установки интеллектуальных счетчиков в жилом доме
21311

Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от величины измеряемого напряжения, становясь неприемлемо высокой для низких напряжений. При измерении напряжения 0,5 В погрешность составляет 60 %. Поэтому такое устройство не подходит для тестирования процессов, в которых напряжение изменяется на 0,1-0,5 В.

Класс точности

Класс точности – это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других характеристик, влияющих на точность выполняемых с их помощью измерений.

Точность может быть стандартизирована, в частности, в отношении:

В этом случае, согласно ГОСТ 8.401-80 (заменяет ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) обводится кружком. Это число дает максимально допустимую погрешность прибора, выраженную в процентах от наибольшего значения измеряемой величины в рабочем диапазоне прибора. Например, для вольтметра, работающего в диапазоне измерений 0-30 В, класс точности 1,0 определяет, что погрешность показаний при установке указателя в любом месте шкалы не превышает 0,3 В.

Относительная погрешность результата, полученного с помощью конкретного вольтметра, зависит от величины измеряемого напряжения и становится неприемлемо большой для малых напряжений. При измерении напряжения 0,5 В погрешность составляет 60 %. Поэтому он не подходит для процессов тестирования, в которых напряжение изменяется на 0,1-0,5 В.

Обычно наименьшее значение на шкале аналогового прибора связано с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, то погрешность s прибора всегда равна половине его наименьшего деления. Очевидно, что при считывании показаний со шкалы не стоит пытаться определить доли деления, так как результат измерения не становится более точным.

Следует отметить, что понятие класса точности встречается в различных областях техники. Например, в станкостроении существует понятие класса точности для металлорежущих станков, класса точности для электроискровых станков (по ГОСТ 20551).

Обозначения классов точности могут быть в виде прописных латинских букв, римских цифр и арабских цифр с добавлением символов. Если класс точности указан латинскими буквами, то класс точности определяется абсолютными пределами погрешности. Если класс точности обозначен арабскими цифрами без символов, то класс точности определяется пределами соответствующей погрешности, а в качестве стандартного значения используется наибольшее по модулю из пределов измерения. Если класс точности обозначен арабскими цифрами с символами, то класс точности определяется пределами рассматриваемой погрешности, но в качестве стандартного значения используется длина шкалы. Если класс точности обозначен римскими цифрами, то класс точности определяется пределами относительной погрешности.

В зависимости от работы оборудования:

Точность. Классы точности измерительных приборов.

В самом начале можно позволить себе небольшое отступление. Такие понятия, как погрешность, класс точности подробно описаны в нормативной документации ГОСТ 8.009-84 “Нормативные метрологические свойства средств измерений”, ГОСТ 8.401-80 “Классы точности средств измерений. Общие требования” и другие подобные. Но, открывая эти документы, мы сразу чувствуем скуку … Эти понятия объясняются так просто и непонятно для начинающего “кита”. Давайте отбросим такие претенциозные и непонятные определения, как “стандартное отклонение случайной составляющей ошибки” или ““стандартизированная автокорреляционная функция” илигистерезисные характеристики случайной составляющей погрешности – H изменение выходного сигнала (показаний) средства измерений“и т.д. Давайте попробуем понять, а затем свести в одну небольшую, но понятную таблицу, что такое “неопределенность” и из чего она состоит.

Погрешности измерения – Отклонение результата измерения от истинного значения измеряемой величины. Ошибки неизбежны, и истинное значение определить невозможно.

Они делятся в соответствии с числовой формой представления:

Абсолютная погрешность: Δ = X_д – X_{измерять и}выражается в единице измерения, например, в килограммах (кг) для измерения массы.
где X_д – истинное значение измеряемой величины, обычно принимаемое за показания эталона, т.е. стандартного средства измерения;
X_{измерять и} – измеренное значение.
относительная погрешность: δ = (Δ ⁄ X_д) – 100, выраженное в % от реального значения измеряемой величины.
Ограниченная ошибка: γ = (Δ ⁄ X_н) – 100, выраженное в % от стандартного значения.
где X_н – является нормирующей величиной, выраженной в тех же единицах, что и Δ, обычно берется диапазон измерения (шкала).

В соответствии с природой проявления:

Систематические (могут быть исключены из результатов);
Случайно;
Грубые или пропущенные (обычно не включаются в результаты измерений).

В соответствии с работой оборудования:

основной – погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
дополнительная ошибка – это составляющая погрешности средства измерений, дополнительно возникающая в результате отклонения любой из влияющих величин от стандартного значения или выхода за пределы диапазона стандартного значения. Например: измерение избыточного давления в рабочих условиях в цехе, при температуре окружающей среды 40ºC, относительной влажности 18% и атмосферном давлении 735 мм рт.ст., что не соответствует номинальным значениям влияющих величин при поверке.

Как определить неопределенность набора приборов, включающего первичный преобразователь, вторичный преобразователь (усилитель) и вторичный прибор. Каждый из элементов этого набора имеет свою абсолютную, относительную или уменьшенную неопределенность. Для оценки общей погрешности измерений все погрешности должны быть приведены к единой форме, а затем рассчитаны по формуле:

Следующая информация, вероятно, будет интересна только метрологам и только начинающим. Теперь небольшое напоминание о среднеквадратичных отклонениях (СКО). Для чего они используются? Поскольку истинное значение определить невозможно, необходимо подойти к нему как можно ближе или определить доверительный интервал, в котором с высокой вероятностью находится истинное значение. Для этого используются различные статистические методы, наиболее распространенными из которых являются формулы. Например, вы провели n измерений какого-либо предмета и вам нужно определить доверительный интервал:

Определите среднее арифметическое отклонений:

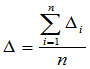
где n – количество отклонений
Определите стандартное отклонение (СКО) среднего арифметического:

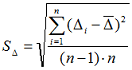
Вычислите случайную составляющую ошибки:

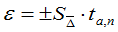
где t – коэффициент Стьюдента, который зависит от числа степеней свободы
Таблица 1.

α =0,68		α =0,95		α =0,99
n	t_α,n	n	t_α,n	n	t_α,n
2	2,0	2	12,7	2	63,7
3	1,3	3	4,3	3	9,9
4	1,3	4	3,2	4	5,8
5	1,2	5	2,8	5	4,6
6	1,2	6	2,6	6	4,0
7	1,1	7	2,4	7	3,7
8	1,1	8	2,4	8	3,5
9	1,1	9	2,3	9	3,4
10	1,1	10	2,3	10	3,3
15	1,1	15	2,1	15	3,0
20	1,1	20	2,1	20	2,9
30	1,1	30	2,0	30	2,8
100	1,0	100	2,0	100	2,6

Вычислите среднеквадратичное значение систематической составляющей ошибки:
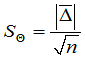
Рассчитайте общее среднеквадратичное значение:
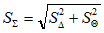
Определите коэффициент, зависящий от соотношения случайной и систематической составляющих ошибки:
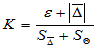
Оцените доверительные границы ошибки:

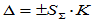
В последнее время все чаще используется термин “неопределенность”. Медленно, но верно и настойчиво она внедряется в национальную метрологию. Это связано с интеграцией нашей экономики в мировое хозяйство и, конечно, необходимо привести нормативную документацию в соответствие с международными стандартами. Я не собираюсь здесь преувеличивать, это хорошо сделано в различных нормативных документах. По моему чистому мнению, “расширенная неопределенность измерения” = базовая неопределенность + дополнительная неопределенность, которая учитывает все факторы, влияющие на результат измерения.

Читайте далее: