Вебер (единица) - Вебер (единица) - услуги электромонтажа, строительства и ремонта

Было решено расширить существующую серию практических единиц в полную комплексную систему физических единиц. В 1935 году была принята рекомендация “принять систему с четырьмя базовыми единицами, предложенную профессором Джорджем, при условии, что в конечном итоге будет выбрана четвертая базовая единица”. Эта система получила название “Система Джорджа”.

SI кратное Веберу (Wb)

Подмножества			Множество
Значение	Символ СИ	Имя	Значение	SI-символ	Имя
10 -1 W	dWb	коллектор	10 1 W	daWb	коллектор
10 -2 W	cWb	santifaber	10 2W	hWb	Гектовебер
10 -3 W	мВт	Милливебер	10 3 W	кВтб	kiloveber
10 -6 W	мкВб	микровебер	10 6 W	MWb	megaveber
10 -9 W	nWb	nanoweber	10 9 W	GWb	gigaweber
10 -12 W	pWb	Пиковебер	10 12 W	TWb	Теравебер
10 -15W	fWb	фемтовебер	10 15 W	PWb	Петавебер
10 -18 W	aWb	Аттовебер	10 18 W	EWb	эксавебер
10 -21 W	zWb	zeptoweber	10 21 W	ZWb	Zettaweber
10 -24 W	yWb	Joktweber	10 24 W	YWb	Yottaweber
Общие кратные числа выделены жирным шрифтом.

Вебера можно определить в терминах закона Фарадея, который связывает изменяющийся магнитный поток, проходящий через контур, с электрическим полем вокруг контура. Изменение потока в один Вебер в секунду создаст электродвижущую силу в один вольт (создаст разность электрических потенциалов в один вольт между двумя открытыми клеммами).

Вебер (единица измерения магнитного потока). Вебер – это магнитный поток, который, будучи подключенным к цепи с одной катушкой, создаст в цепи электродвижущую силу в 1 вольт, если он будет уменьшаться до нуля с постоянной скоростью в течение 1 секунды.

Вебер обычно выражается во многих других единицах:

Вебер назван в честь Вильгельма Эдварда Вебера. Как и любая единица СИ, ее символ начинается с заглавной буквы (Wb), но при полном написании применяются правила написания существительных с заглавной буквы, т.е. вебер » написано с с прописной буквы в начале предложений и в заголовках, в остальных случаях – со строчной буквы.

тесламетры – это приборы для измерения напряженности магнитного поля H или индукции магнитного поля B;

Содержание

Принципы измерения магнитного поля, приборы для измерения параметров магнитного поля

Первые магнитные компасы, указывающие направления на магнитные полюса Земли, появились еще в III веке до нашей эры в Китае. Это были устройства в виде круглых ложек с короткими ручками из магнитного железняка.

Ложку клали выпуклой стороной на гладкую медную или деревянную поверхность, вокруг которой были нанесены деления с изображениями знаков зодиака, указывающих направления сторон света. Чтобы активировать компас, слегка надавите на ложку и поверните ее. Наконец, когда ложка остановится, ее ручка будет направлена точно на южный магнитный полюс Земли.

С XII века компасы стали активно использоваться путешественниками в Европе. Они устанавливались как на сухопутных, так и на морских судах для определения магнитного склонения.

С конца 18 века магнитные явления стали предметом интенсивных наблюдений и исследований ученых того времени. Кулон в 1785 году предложил метод количественной оценки силы магнитного поля Земли. В 1832 году Гаусс продемонстрировал возможность определения абсолютного значения напряженности магнитного поля путем более точных измерений.

Связь между магнитными явлениями и силовыми эффектами, наблюдаемыми при движении электрических зарядов, была впервые установлена Эрстедом в 1820 году. Позже Максвелл записал эту взаимосвязь в рациональной форме – в виде математических уравнений (1873):

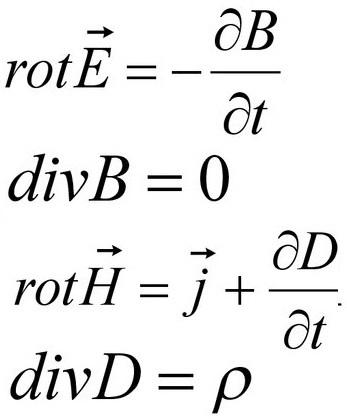
В настоящее время для измерения параметров магнитного поля используются следующие методы:

тесламетры: приборы для измерения величины напряженности магнитного поля H или индукции магнитного поля B;

Веберметры: приборы для измерения магнитного потока Ф;

градиометры: приборы для измерения неоднородности магнитного поля

Приборы для измерения магнитного момента M;

Приборы для измерения направления вектора B;

приборы для измерения магнитных констант различных материалов.

Вектор магнитной индукции B характеризует интенсивность силы, исходящей от магнитного поля (на полюс или на ток), и поэтому является его основной характеристикой в данной точке пространства.

Таким образом, тестируемое магнитное поле может действовать с силой как на магнит, так и на элемент тока, а также способно индуцировать ЭДС в контуре, если магнитное поле, проникающее в контур, изменяется со временем или если контур изменяет свое положение относительно магнитного поля.

На элемент проводника с током длиной dl в магнитном поле индукции B будет действовать сила F, значение которой можно найти по следующей формуле:

Таким образом, индукция B изучаемого магнитного поля может быть найдена по силе F, действующей на проводник заданной длины l с постоянным током известного значения I, помещенный в это магнитное поле.

На практике удобно проводить магнитные измерения, используя величину, называемую магнитным моментом. Магнитный момент Pm характеризует контур площадью S с током I, а величина магнитного момента определяется следующим образом:

Если мы используем катушку с N витками, то ее магнитный момент будет равен:

Механический момент M магнитной силы может быть найден из значений магнитного момента Pm и индукции магнитного поля B следующим образом:

Однако для измерения магнитного поля не всегда удобно использовать его механические силовые проявления. К счастью, есть еще одно явление, на которое мы можем положиться. Это явление электромагнитной индукции. Закон электромагнитной индукции в математической форме записывается следующим образом:

Таким образом, магнитное поле проявляется как сила или индуцированная ЭДС. Известно, что источником самого магнитного поля является электрический ток.

Если известен ток, создающий магнитное поле в данной точке пространства, то напряженность магнитного поля в этой точке (на расстоянии r от элемента, создающего ток) может быть найдена с помощью закона Био-Савари-Лапласа:

Следует отметить, что магнитная индукция B в вакууме связана с напряженностью магнитного поля H (создаваемого соответствующим током) следующим соотношением:

Магнитная постоянная вакуума в СИ определяется в амперах. Для любой среды эта постоянная представляет собой отношение магнитной индукции в среде к магнитной индукции в вакууме и называется магнитной проницаемостью среды:

Магнитная проницаемость воздуха почти идентична магнитной проницаемости вакуума, поэтому для воздуха магнитная индукция B почти идентична напряженности магнитного поля H.

Единицей магнитной индукции в СИ является тесла [Тесла], а единицей СГС – гаусс [Гс], где 1 Тесла = 10000 Гс. Приборы для определения индукции магнитного поля называются тесламетрами.

Напряженность магнитного поля H измеряется в амперах на метр (А/м), 1 ампер/м определяется как напряженность магнитного поля бесконечно длинного соленоида с единичной плотностью витков при токе в 1 ампер, протекающем через соленоид. Один ампер на метр можно также определить как напряженность магнитного поля в центре круговой катушки с током 1 ампер и диаметром катушки 1 метр.

Стоит также отметить магнитный поток индукции, Ф. Это скалярная величина, измеряемая по Веберу в СИ и по Максвеллу в СГС, причем 1 мкс = 0,00000001 Вб. 1 Вебер – это магнитный поток такой величины, что при его уменьшении до нуля через связанную проводящую цепь с сопротивлением 1 Ом пройдет заряд в 1 кулон.

Если принять магнитный поток Ф за начальное значение, то индукция магнитного поля В есть не что иное, как плотность магнитного потока. Приборы для измерения магнитного потока называются веберметрами.

Выше мы отметили, что магнитную индукцию можно определить либо по силе (или механическому моменту), либо по ЭДС, индуцированной в цепи. Это так называемые прямые преобразования измерений, когда магнитный поток или магнитная индукция выражаются в терминах другой физической величины (силы, заряда, момента, разности потенциалов), которая однозначно связана с магнитной величиной фундаментальным физическим законом.

Преобразования, в которых магнитная индукция B или магнитный поток F расположены через ток I или через длину l или радиус r, называются обратными преобразованиями. Такие преобразования выполняются на основе закона Био-Савара-Лапласа, используя известное соотношение между магнитной индукцией B и напряженностью магнитного поля H.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это поможет нашему сайту сильно вырасти!

Магнитное поле – это поле сил вокруг постоянного магнита или тока заряженных частиц, действующих на ферромагнитные материалы или движущиеся электрические заряды. Магнитное поле – это векторное поле, поскольку оно характеризуется величиной и направлением. Магнитные силовые линии используются для визуализации магнитных полей. Количество линий на единицу площади показывает, насколько сильным является магнитное поле. Узоры линий магнитного поля можно наблюдать с помощью стальных или железных опилок, магнитной фольги или других средств.

История

Основные открытия, связанные с электромагнетизмом, произошли в первой половине 19 века. Понимание взаимосвязи между электричеством и магнетизмом связано с работой датского физика Ханс Кристиан Эрстедкоторый обнаружил, что электрический ток вызывает магнитное поле. Во время лекции в Копенгагенском университете в 1819 году он обнаружил, что игла компаса реагирует на включение и выключение электрического тока, проходящего по проводу рядом с компасом.

Позже, в 1820 году, французский физик Андре-Мари Ампер обнаружил, что два параллельных проводника, по которым течет постоянный электрический ток, отталкиваются или притягиваются друг к другу в зависимости от направления тока. Чтобы лучше понять это явление, он использовал математику. Результат этой работы теперь называется законом Ампера. В самом известном примере, иллюстрирующем закон Ампера, параллельные проводники с электрическим током притягиваются или отталкиваются с силой, пропорциональной их длине и силе протекающего в них тока.

Примерно в то же время, в 1820 году. Жан-Батист Био и Феликс Савард открыл то, что сейчас известно как закон Био-Саварда (или закон Био-Саварда-Лапласа). Она описывает взаимосвязь между магнитной индукцией, направлением тока в проводнике, расстоянием до этого проводника и его длиной.

Важный вклад в изучение электромагнетизма внес английский ученый Майкл Фарадей.. В 1821 году он изобрел униполярный электродвигатель – первое устройство, преобразующее электрическую энергию в круговое движение. Позже он открыл взаимную индукцию, используя для своих экспериментов две катушки изолированного провода, намотанные на железное кольцо. Это устройство было очень похоже на современный тороидальный трансформатор. При включении тока в одной катушке наблюдался кратковременный всплеск тока в другой катушке. Позже Фарадей обнаружил, что если поместить магнит в катушку или рядом с ней, то в катушке возникнет электрический ток. Таким образом, было обнаружено, что изменяющееся магнитное поле порождает электрическое поле.

Когда проводились эксперименты в 1831 году. Фарадей изобрел униполярный генератор, который, несмотря на низкий КПД, стал прототипом современных генераторов и первым устройством для преобразования механической энергии в электрическую. Униполярный генератор продемонстрировал возможность выработки электроэнергии с помощью явления магнетизма.

В 1831 году Майкл Фарадей сформулировал фундаментальный закон электродинамики, который описывает возникновение электродвижущей силы в проводнике в изменяющемся магнитном поле. Этот закон гласит, что для любого контура в изменяющемся магнитном поле индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.

В 1835 году немецкий математик Карл Фридрих Гаусс сформулировать теорему Гаусса (также называемую законом Гаусса), которая описывает зависимость напряженности электрического поля от величины электрического заряда. Этот закон был опубликован в 1867 году. после смерти математика.

В середине 1960-х годов шотландский математический физик Джеймс Клерк Максвелл изучал взаимосвязь между электричеством и магнетизмом. Работая в Королевском колледже Лондона, он разработал теорию электромагнитного поля, представленную математически в виде 20 дифференциальных уравнений. Первая публикация этой теории появилась в книге “О физических полях” в марте 1861 г. Уравнения Максвелла описывают поведение электрических и магнитных полей и их взаимодействие со средой, в которой действуют эти поля. Позже Максвелл рассчитал скорость распространения электромагнитного поля и понял, что свет и магнетизм имеют одну природу и что свет – это электромагнитное поле.

Сейчас, в 21 веке, теория электромагнетизма продолжает развиваться. За последние несколько десятилетий была разработана Стандартная модель для описания взаимодействий всех элементарных частиц. Это основано на теории полей особенностей, впервые разработанной в классической электродинамике, которая описывает взаимодействие электромагнитных полей с заряженными телами. За ней последовала теория электрически слабого поля, описывающая слабое и электромагнитное взаимодействие между частицами. Наконец, во второй половине 20-го века была разработана Стандартная модель физики частиц. Эта теория описывает электромагнитные взаимодействия, сильные и слабые ядерные взаимодействия и дает полную классификацию всех элементарных частиц, то есть субъядерных микрообъектов, которые нельзя разложить на составные части в соответствии с современными представлениями. Открытие, сделанное учеными ЦЕРН в 2012 году. Бозон Хиггса, постулированный британским физиком Питером Хиггсом почти полвека назад, в 1964 году, завершил экспериментальное открытие всех элементарных частиц, предсказанных Стандартной моделью. Как мы видим, электромагнетизм занимает важное место во всех этих теориях.

С помощью этого калькулятора вы можете ввести значение, которое необходимо перевести, вместе с исходной единицей измерения, например, “556 милливебер”. Вы можете использовать либо полное название единицы измерения, либо ее сокращение, например, “милливольтметр” или “мВб”. После ввода единицы измерения, которую вы хотите преобразовать, калькулятор определяет ее категорию, в данном случае “Магнитный поток”. Затем он преобразует введенное значение во все известные ему единицы измерения. В списке результатов вы, несомненно, найдете нужное вам значение конверсии. В качестве альтернативы можно ввести преобразованное значение следующим образом: ’46 мВб – Вб‘ или ’58 мВб – Вб‘ или ‘5 милливебер -> вебер‘ или ’59 mVb = ‘Vb‘ или ’33 милливебер – ‘Vb‘ или ’12 мВб – Вебер‘ или ’16 Милливебер – Вебер‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения следует перевести исходное значение. Какой бы вариант ни использовался, он устраняет необходимость сложного поиска в длинных списках выбора с бесчисленными категориями и поддерживаемыми единицами измерения. Все это за нас делает калькулятор, который выполняет свою работу за доли секунды.

Преобразование милливольт в вебер (мВб в Вб):

С помощью этого калькулятора вы можете ввести значение, которое нужно перевести, вместе с исходной единицей измерения, например, “556 милливебер”. Вы можете использовать либо полное название единицы измерения, либо ее сокращение, например, “millivolume” или “mVb”. После ввода единицы измерения, подлежащей преобразованию, калькулятор определяет ее категорию, в данном случае “Магнитный поток”. Затем он преобразует введенное значение во все известные ему единицы измерения. В списке результатов вы, несомненно, найдете нужное вам значение конверсии. В качестве альтернативы можно ввести преобразованное значение следующим образом: ’46 мВб – Вб‘ или ’58 мВб – Вб‘ или ‘5 милливебер -> вебер‘ или ’59 mVb = ‘Vb‘ или ’33 милливебер – Vb‘ или ’12 мВб – Вебер‘ или ’16 Милливебер – Вебер‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения следует перевести исходное значение. Какой бы из этих вариантов не использовался, он устраняет необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Калькулятор делает все это за нас, причем за доли секунды.

Калькулятор также позволяет применять математические формулы. В результате учитываются не только такие числа, как “(39 * 24) мВб”. Можно даже использовать несколько единиц измерения непосредственно в поле преобразования. Например, такая комбинация может выглядеть следующим образом: ‘556 милливебер + 1668 вебер’ или ’71 мм х 4 см х 29 дм = ? см^3′. Единицы, объединенные таким образом, конечно же, должны подходить друг другу и иметь смысл в комбинации.

Если поставить галочку напротив “Числа в научной записи”, ответ будет представлен в виде экспоненциальной функции. Например, 1 944 809 982 302 2 × 10 31 . В этой форме представление числа делится на экспоненту, здесь 31, и вещественное число, здесь 1,944 809 982 302 2. Устройства, имеющие ограниченные возможности отображения чисел (например, карманные калькуляторы), также используют способ записи чисел 1,944 809 982 302 2E+31. В частности, это облегчает наблюдение очень больших и очень маленьких чисел. Если эта ячейка не выбрана, результат отображается обычным методом ввода чисел. В приведенном выше примере это будет выглядеть следующим образом: 19,448,099,823,022,000,000,000,000,000,000,000.Независимо от того, как представлен результат, максимальная точность этого калькулятора составляет 14 знаков после запятой. Этой точности должно быть достаточно для большинства целей.

Рисунок 7 – Иллюстрация применения правила большого пальца

Магнитный поток

Плоский контур. Явление электромагнитной индукции

Как уже неоднократно упоминалось, магнитное поле генерируется электрическим током. Так возможно ли, что, наоборот, магнитное поле порождает электрический ток?

На основе экспериментов было установлено, что магнитное поле действительно может генерировать ток. Один из самых простых экспериментов, доказывающих это, заключается в следующем: замкнутый плоский контур (все точки которого лежат в одной плоскости) из проводящего материала подключается к амперметру (для определения силы тока), а затем вводится в область U-образного магнита (см. рис. 11).

Рисунок 11 – Проводящая цепь в магнитном поле (K – цепь, A – амперметр)

В ходе этого эксперимента выяснилось, что:

цепь включается в работу (в движение) – амперметр регистрирует ток;
контур находится в состоянии покоя внутри магнита – игла амперметра находится на нуле;
цепь удалена из области магнита – ток присутствует;
изменение положения цепи (вращение вокруг диаметра) – ток присутствует.

Что изменилось в ходе эксперимента? Если судить по рисунку, то видно, что количество магнитных линий, пересекающих контур, изменилось (они показаны нисходящими стрелками). На языке физики говорят, что магнитный поток (F) через замкнутый контур изменился.

Магнитный поток обозначается буквой F и измеряется в единицах Вебера.

Она прямо пропорциональна количеству линий магнитного поля, пересекающих плоскость, ограниченную контуром.

Если бы в эксперименте использовалось кольцо с большим радиусом, оно имело бы больший поток (большая площадь петли могла бы захватить больше магнитных линий). Предполагается, что поле между ветвями U-образного магнита является однородным.

Если оставить схему без изменений, но взять более сильный магнит, поток Ф также станет больше (при более сильном поле магнитные линии толще).

Если мы повернем контур вдоль диаметра, то площадь, через которую он “захватывает” магнитные линии, уменьшится, а значит, уменьшится и магнитный поток.

Получается, что чем больше магнитная индукция (B) и чем больше площадь контура, тем больше поток F. Это также зависит от того, как контур расположен на местности.

Возникновение тока в замкнутом контуре (из проводящего материала) при изменении магнитного потока Ф, протекающего через область, ограниченную контуром, называется явлением электромагнитной индукции. Результирующий ток называется индукционным.

Это явление было подробно изучено английским ученым Фарадеем.

Свойства индуктивного элемента определяются его способностью создавать магнитный поток при протекании через него тока. Если индуктивный элемент состоит из нескольких катушек, его поток-ток (общий магнитный поток) представляет собой алгебраическую сумму потоков, проходящих через отдельные катушки индуктора:

Индуктивный элемент

Индуктивный элемент (катушка) – это идеализированный элемент цепи, в котором напряжение и ток связаны по дифференциальному закону для напряжения и интегральному закону для тока:

Это означает, что величина напряжения на катушке определяется скоростью изменения тока. Поскольку ток, протекающий через катушку, имеет целочисленный (т.е. суммирующий) вид, индуктивный элемент, как и емкостной, можно отнести к накопительным элементам. Можно предположить, что индуктивный элемент преобразует электрическую энергию в энергию магнитного поля и наоборот. Идеальный индуктивный элемент не теряет энергию.

Обычное представление индуктивного элемента показано на рисунке 1.6.

Рисунок 1.6. Индуктивный элемент

Индуктивный элемент характеризуется способностью создавать внутри себя магнитный поток при протекании через него тока. Если индуктивный элемент состоит из нескольких катушек, то его коэффициент контура тока (полный магнитный поток) равен алгебраической сумме потоков, проходящих через отдельные катушки индуктивности:

где |/ – емкость потока; Ф – величина магнитного потока. Если все катушки индуктивности нагружены одинаковым потоком, то емкость потока равна j/ = EF, где W – число витков катушки. Параметром для индуктивного элемента является индуктивность

L = – измеряется в henri [Hn]. Магнитный поток и поток

измеряется в единицах Вебера [Вб]. Магнитный поток и ток всегда имеют один и тот же знак (их направления связаны правилом винта по часовой стрелке), поэтому L > 0.

Веберовская характеристика индуктивности, т.е. зависимость потока от тока, может быть линейной (рис. 1.7, прямая линия а) или нелинейной (рис. 1.7, кривая б).

Изменение тока в индукционной катушке во времени приводит к изменению во времени магнитного потока (контура потока) в ней, что в свою очередь приводит к индукции ЭДС в катушке в соответствии с законом Фарадея-Максвелла, eq.

е, = Для линейной индуктивности (L = const) выражение для dt

ЭДС становится

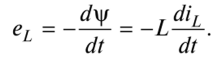
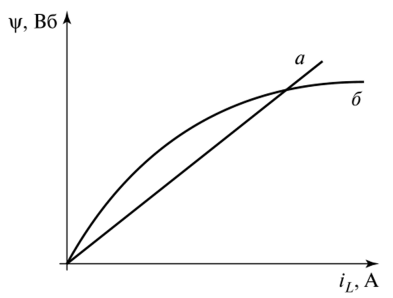
Рис. 1.7. Форма волны в индуктивном элементе

Направления ЭДС и тока одинаковы. Знак минус учитывает тот факт, что ЭДС согласно закону Ленца не позволяет изменяться коэрцитивной силе тока. При анализе цепей обычно рассматривается не ЭДС, а напряжение на элементе, положительное направление которого выбирается так, чтобы совпадать с положительным направлением _т ди,

направление тока: и, = -е, – – 1L = L——.

L L dt dt

Мгновенная мощность на индукционной катушке может быть рассчитана по формуле

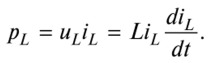
Мощностьp_L является положительным, если знаки напряжений u_L и текущий i_L и является отрицательным, если знаки не совпадают u_L и i_L.

Энергия магнитного поля индуктивного элемента в любой выбранный момент времени равна

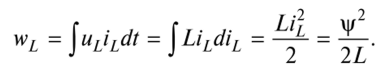
Все описанные выше свойства элементов следует рассматривать как идеализированные модели реальных резисторов, конденсаторов, индукторов. Модель – это упрощенное представление реальной системы, для которой законы ее поведения и свойства могут быть описаны достаточно подробно. Идеальные модели используются для построения систем, поведение которых максимально приближено к реальному. Например, реальная катушка обладает как индуктивными, так и резистивными и емкостными свойствами. Это следует учитывать при составлении электрических схем.

Читайте далее: