Уравнения трансформатора (16) могут быть решены аналитически или графически. Графический метод основан на построении векторных диаграмм. Он носит скорее иллюстративный характер и часто используется для качественного анализа различных режимов работы трансформатора.
В отсутствие нагрузки первичная обмотка трансформатора находится под напряжением, а его вторичная обмотка – в разомкнутом состоянии. В этом случае можно использовать следующие уравнения
(17)
Первичный ток представляет собой ток намагничивания трансформатора. Векторная диаграмма (рис.10) начинается с вектора потока . ЭДС и поток отстают на угол 90°. Реактивная составляющая тока намагничивания находится в фазе с потоком, а его активная составляющая обгоняет поток на 90°. Ток намагничивания немного обгоняет поток. Чтобы получить вектор первичного напряжения, постройте вектор и добавьте к нему падения напряжения на активном и индуктивном резисторах. Векторная диаграмма показывает, что она очень мала. Как правило Трансформатор потребляет реактивную мощность из сети для создания магнитного поля в трансформаторе.
Работа трансформатора зависит от типа нагрузки на вторичной стороне трансформатора. Нагрузка может быть двух типов: активно-индуктивная и активно-отрицательная. Теоретически, он может быть чисто активным. В зависимости от нагрузки, вектор тока I2‘ может отставать от ЭМП E2‘ на угол f2который называется углом вторичной нагрузки.
Работа трансформатора под нагрузкой и векторные диаграммы

Работа трансформатора зависит от типа нагрузки на вторичной обмотке трансформатора. Нагрузка может быть двух типов: активно-индуктивная и активно-отрицательная. Теоретически, он может быть чисто активным. В зависимости от нагрузки, вектор тока I2‘ может отставать от ЭМП E2‘ на угол f2который называется углом вторичной нагрузки.
Если нагрузка активно-отрицательная, I2‘ впереди ЭМП E2перед ЭДС E ‘ на угол нагрузки f2.
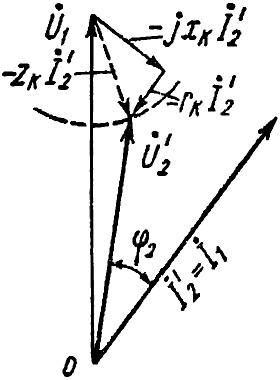
Чтобы найти ток, проведем вектор, параллельный I2‘ и равным ему. Соедините конец вектора I2‘ к истокам. Поскольку ток протекает через первичную и вторичную обмотки трансформатора в режиме нагрузки, напряжение будет изменяться в зависимости от ЭДС.
Построим векторы напряжения. Во-первых, U1. Для этого из конца вектора E1 проведем вектор, параллельный вектору тока I1 и равна r1I1. С конца этого вектора r1I1 проведите перпендикуляр jx1I1.
Векторная диаграмма трансформатора со смешанной активно-индуктивной нагрузкой.
Векторная диаграмма трансформатора со смешанной активно-индуктивной нагрузкой.
Из векторной диаграммы следует, что напряжение U1 не зависит от типа нагрузки и всегда проводит ЭДС E1.
Напряжение U2 всегда запаздывает по отношению к ЭДС E2‘ и не зависит от типа нагрузки, но угол опережения напряжения U1 и угол замедления U2.
Угол между током I1 и ЭДС E1 обозначается через f1 и называется углом первичной нагрузки.
Ток I2‘ – ток нагрузки – зависит от величины активной и реактивной составляющих.
Если активная составляющая тока нагрузки I2‘, как длина, так и амплитуда ф1. Если мы изменим реактивную составляющую тока I2‘ угол f2а длина вектора остается неизменной.
Упрощенная векторная диаграмма трансформатора со смешанной активно-индуктивной нагрузкой.
Рис. 1.10 Векторная диаграмма трансформатора с активной индуктивной (a) и активной емкостной (b) нагрузками
Векторная диаграмма трансформатора с активной индуктивной нагрузкой
Одним из приемов, облегчающих изучение электромагнитных процессов и расчет трансформаторов, является замена реального трансформатора с магнитными связями между обмотками эквивалентной электрической схемой (рис. 4.6.1).
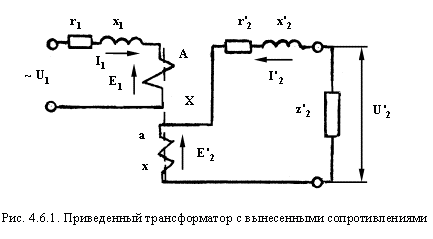
На этом рисунке показана эквивалентная схема данного трансформатора, в которой сопротивления d и x условно выведены из соответствующих обмоток и соединены с ними последовательно. Поскольку k = 1, E1 = E2. Поэтому точки A и A и X и X имеют одинаковые потенциалы, поэтому мы можем соединить эти точки электрически, получив Т-образную эквивалентную схему (рис. 4.6.2).
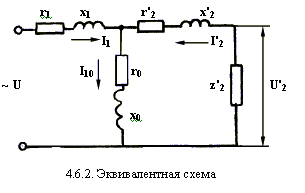
Описывая эту схему математически, используя методы Кирхгофа, можно обнаружить, что она полностью соответствует уравнениям ЭДС и тока реального трансформатора (см. раздел 4.5). Следовательно, можно электрически смоделировать трансформатор на компьютере. Проведение испытаний с учетом нагрузки z2‘ (единственная переменная характеристика схемы) можно предсказать фактические характеристики трансформатора от холостого хода (z2= ) до короткого замыкания (z2‘ = 0).
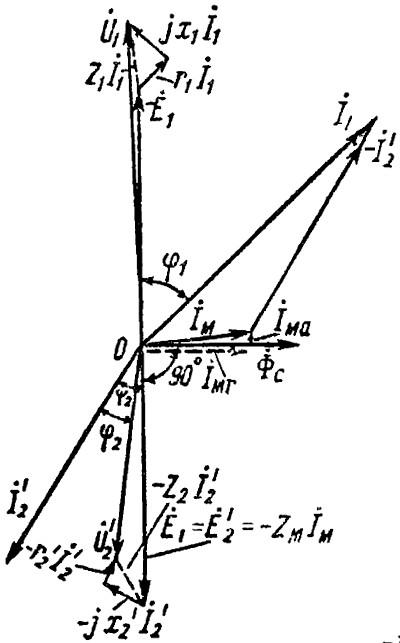
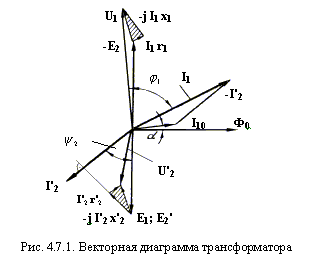
Построение векторной диаграммы удобно начать с главного вектора потока Ф. Построим его на оси абсцисс. Вектор I10 обгоняет его на угол a . Тогда векторы ЭДС E1 и Е2‘ векторы, которые отброшены относительно потока Ф на 90°. Для определения фазового угла между E2‘ и я2Мы должны знать характер нагрузки. Предположим, что это активно-индуктивная нагрузка. Тогда я2‘ отстает от E2’ на угол f2.
Мы получили так называемый шаблон векторной диаграммы (рис. 4.7.1). Чтобы завершить его, нам нужно использовать три основных уравнения данного трансформатора.
Воспользуемся вторым фундаментальным уравнением:
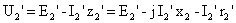
E и выполнить векторное сложение.
Для этого к концу вектора E2‘ мы добавляем вектор – j I2‘ x2‘ и на его конце вектор – I2‘ r2‘. Результирующий вектор U2‘ будет вектор, соединяющий начало координат с концом последнего вектора.
Теперь используйте третье фундаментальное уравнение
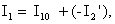
из чего следует, что вектор тока I1 состоит из геометрической суммы векторов I10 i – I2‘. Выполним это суммирование и завершим векторную диаграмму.
Теперь вернемся к первому основному уравнению:
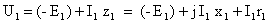
Для построения вектора – E1 мы должны взять вектор +E1 и направьте его в противоположную сторону.
Теперь к нему можно добавить другие векторы: + j I1 x1 и я1 r1 . Первый будет идти перпендикулярно току, а второй – параллельно ему. Результатом является целочисленный вектор u1.
Построенная векторная диаграмма носит общий характер. Используя ту же методику, можно определить его для различных режимов работы и для различных типов нагрузки.
Не нашли то, что искали? Используйте поиск:
Лучшие высказывания: Однажды на занятии один из преподавателей сказал, когда лекция заканчивалась – это конец занятия: “Что-то мне кажется, что это конец”. 8406 – | 8023 – или читать все.
78.85.5.224 © studopedia.ru Я не являюсь автором размещенного материала. Но я обеспечиваю его бесплатное использование. Было ли нарушено авторское право? Свяжитесь с нами | Обратная связь.
Снова активируйте AdBlock!
и обновите страницу (F5)
Вы действительно этого хотите
Читайте также:
- (C) Диаграмма чешуек
- H,d – диаграмма влажного воздуха
- I,d – диаграмма влажного воздуха и способ его всасывания
- Активная мощность на нагрузке
- Бифуркационная диаграмма
- Вектор
- Размер вектора
- Векторная диаграмма
- Векторная диаграмма
- Векторная диаграмма
- Векторная графика
- Векторная диаграмма
После намотки вторичной обмотки трансформатора на первичную можно приступать к построению векторной диаграммы. На рисунке показан векторный график для активно-индуктивной (рис. 1.10, a) и для активно-емкостной нагрузки (рис. 1.10, b).
Для построения векторных диаграмм напишем основные уравнения для ЭДС и токов.
Уравнение для первичной обмотки:
Из уравнения ЭДС трансформатора (1.28), разделив обе части на , получим уравнение для токов:
В ведущем направлении, по отношению к вектору потока основного трансформатора Фmaxпод углом α, вектор тока I и в направлении замедления на угол π/2 – векторы ЭДС первичной и уменьшенной вторичной обмоток . На запаздывающей стороне с индуктивным характером нагрузки (рис. 1.10, а) и на опережающей стороне с емкостным характером нагрузки (рис. 1.10, б) на угол ψ2 вектор уменьшенного вторичного тока.
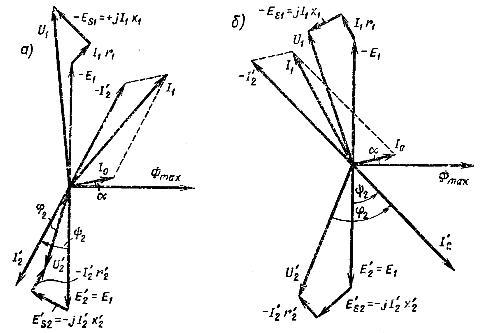
Векторная диаграмма трансформатора с активной индуктивной нагрузкой (a) и активной емкостной нагрузкой (b)
Напряжение на зажимах вторичной обмотки трансформатора под нагрузкой равно сумме ЭДС вторичной обмотки минус падение напряжения на сопротивлении вторичной обмотки, т.е. уравнение напряжения для вторичной обмотки трансформатора имеет следующий вид:
где – ЭДС, наведенная во вторичной обмотке основным магнитным потоком трансформатора; – ЭДС от потока утечки вторичной обмотки – индуктивное сопротивление этой обмотки.
Когда трансформатор нагружен вторичным током, возникает блуждающий поток, магнитные линии которого закорочены воздухом и проникают только во вторичные обмотки. После приведения вторичной обмотки к первичной мы запишем это уравнение в следующем виде:
Поэтому, чтобы определить вектор напряжения на вторичных зажимах трансформатора под нагрузкой, нужно построить из конца вектора ЭДС вектор , который на π/2 отстает от вектора тока, а затем вектор , который параллелен и противоположен вектору тока. Геометрическая сумма этих трех векторов дает уменьшенное вторичное напряжение трансформатора.
Для определения первичного тока, согласно уравнению тока (1.30), построим геометрическую сумму векторов тока и приведенного вторичного тока противоположного знака.
Для определения первичного напряжения воспользуемся уравнением баланса первичного напряжения (1.29). Постройте вектор, равный вектору противоположного направления. Из конца вектора строим вектор, повернутый относительно текущего вектора на π/2, а затем вектор, параллельный текущему вектору. . Геометрическая сумма трех векторов, которые мы построили, является вектором приложенного напряжения .
Из векторных диаграмм следует, что вторичное напряжение зависит от величины тока нагрузки трансформатора и характера нагрузки, т.е. от угла φ2. Если нагрузка индуктивная, вторичное напряжение по абсолютной величине меньше ЭДС (); если нагрузка емкостная, вторичное напряжение по абсолютной величине больше ЭДС ().
Дата добавления: 2014-01-20 ; Просмотров: 6050 ; Нарушение авторских прав? ;
Нам важны ваши отзывы! Был ли опубликованный материал полезен? Да | Нет
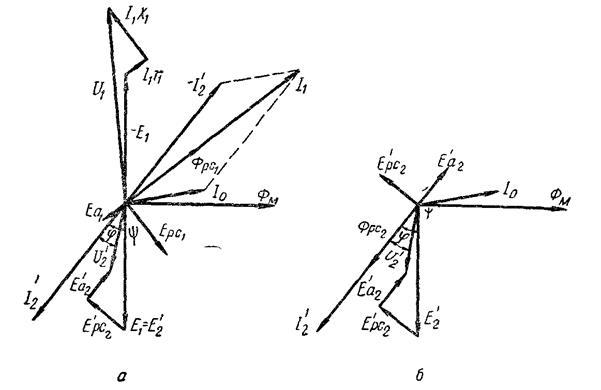
Рисунок 93: Векторная диаграмма трансформатора с активно-индуктивной нагрузкой:
а – полный, б – для вторичной обмотки
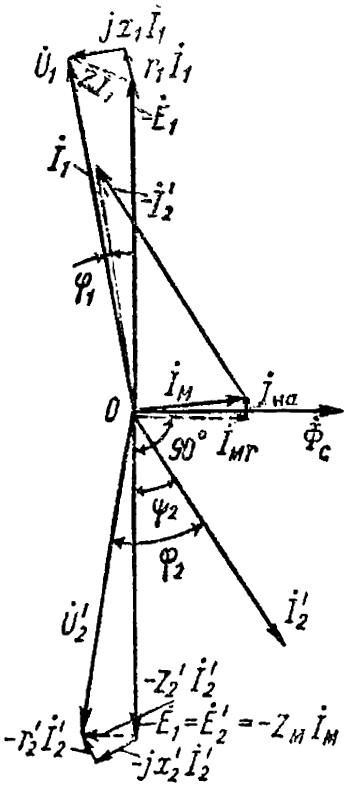
Рассмотрим векторную диаграмму данного трансформатора с активно-индуктивной нагрузкой (рис. 93).
Сначала рассмотрим векторную диаграмму для вторичной обмотки отдельно (рис. 93, б). Нарисуем вектор основного магнитного потока Фм. Этот магнитный поток индуктируется в первичной и вторичной обмотках трансформаторов, например, с. Е1 и Е’2 , векторы которых заторможены по отношению к вектору магнитного потока Fм o 90°. Поскольку нагрузка трансформатора является активно-индуктивной, ток I’2 заторможена по отношению к вектору ЭДС. Е’2 под углом ψ.
Согласно уравнению э.д.с. вторичной обмотки, напряжение на зажимах вторичной обмотки составляет U’2 можно рассматривать как геометрическую сумму э.д.с., индуцированных в этой обмотке. Во вторичной обмотке индуцируются следующие энергии:
1) э.д.с. Е’2, создаваемый основным магнитным потоком Фм;
2) рассеивание мощности Еrs2, создаваемый рассеянным магнитным потоком Фrs2который находится в фазе с током I’2, и вектор напряженности электромагнитного поля. Е’pc2 тормозится относительно вектора диффузии магнитного потока Frs2 o 90°;
3) активное сопротивление e.f. Е’а созданный текущим I’2 в активном сопротивлении вторичной обмотки r’2 и направлена против течения.
Уравнение для вывода вторичной обмотки выглядит следующим образом
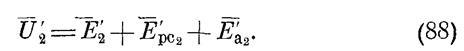
Путем геометрического суммирования всех трех векторов ЭДС получаем вектор напряжения на зажимах обмотки U’2. Угол между векторами тока и напряжения обозначается φ2. При чисто активной нагрузке φ2 = 0.
Для построения полной векторной диаграммы найдем вектор тока I1. Для этого мы поворачиваем вектор тока I’2 на 180° и, добавив его геометрически к вектору тока / , найти ток I1 (рис. 93, а).
Согласно уравнению первичного напряжения, напряжение, приложенное к первичной обмотке трансформатора, уравновешивается суммой токов, индуцированных в первичной обмотке.
В первичной обмотке, как и в случае работы в режиме холостого хода, индуцируются следующие явления
1) например. Е1 – основным магнитным потоком Фм;
2) например, Eärc1 магнитным потоком дисперсии Фppc1который создается током I1;
3) э.д.с. Еа1 – током I1 в активном сопротивлении обмотки r1 , направленный против тока, т.е. в соответствии с формулой (75)
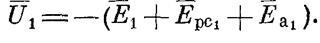
Вектор напряжения, как и в режиме холостого хода, представлен в виде геометрической суммы трех компонентов, каждый из которых равен соответствующей обратной величине э.д.с.
Обратите внимание, что э.м.с. векторов Eа и Ерк на самом деле очень малы по сравнению с э.м.с. главных, поэтому векторные диаграммы показывают их в гораздо большем масштабе, чем э.м.с. векторов главных.
Когда трансформатор напряжения работает без ошибок, его первичное и вторичное напряжения находятся в фазе друг с другом, а отношение этих напряжений равно K n. При коэффициенте трансформации K n = 1, напряжение U 2 = U 1 (рис. 1c).
Измерительные трансформаторы напряжения
Трансформатор напряжения используется для понижения высокого напряжения, которое подается на измерительные приборы, реле защиты и автоматику в системах переменного тока.
Прямое подключение к высокому напряжению потребовало бы очень громоздких устройств и реле из-за необходимости изоляции высокого напряжения. Производство и использование таких устройств нецелесообразно, особенно при напряжении 35 кВ и выше.
Использование трансформаторов напряжения позволяет использовать стандартные измерительные приборы для высоковольтных измерений, расширяя их диапазон измерений; обмотки реле, подключенных через трансформаторы напряжения, также могут быть стандартной конструкции.
Кроме того, трансформатор напряжения изолирует (отделяет) измерительные приборы и реле от высокого напряжения, обеспечивая тем самым безопасность их работы.
Трансформаторы напряжения широко используются в высоковольтных электроустановках, и от их характеристик зависит точность электрических измерений и учета электроэнергии, а также надежность релейной защиты и систем противоаварийной автоматики.
Трансформатор измерительного напряжения принципиально не отличается от понижающего трансформатора мощности. Он состоит из стального сердечника, изготовленного из пластин электротехнической стали, первичной обмотки и одной или двух вторичных обмоток.
На рисунке 1a показан трансформатор напряжения с одной вторичной обмоткой. На первичную обмотку подается высокое напряжение U1, а к напряжению вторичной обмотки U2 подключается измерительный прибор. Первичная и вторичная обмотки обозначаются буквами A и a, а концы – буквами X и x. Обычно они обозначены на корпусе трансформатора напряжения рядом с выводами обмоток.
Отношение номинального напряжения первичной обмотки к номинальному напряжению вторичной обмотки называется номинальным коэффициентом трансформации трансформатора напряжения Kn = U1 ном / U2 ном
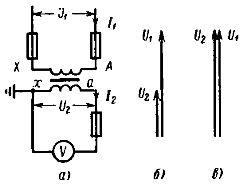
Рис. 1 Принципиальная схема и векторная диаграмма напряжения трансформатора напряжения: a – принципиальная схема, b – векторная диаграмма напряжения, c – векторная диаграмма напряжения
Если трансформатор напряжения работает правильно, то первичное и вторичное напряжения будут согласованы по фазе, а коэффициент трансформации между ними будет равен K n. Если коэффициент трансформации K n = 1, то напряжение U 2 = U 1 (рис. 1, в).
Обозначение: E – один вывод заземлен; O – однофазный; T – трехфазный; C – каскадный или с компенсационной обмоткой; F – с фарфоровой внешней изоляцией; M – масляный; S – сухой (с воздушной изоляцией); E – емкостной; D – делитель.
Клеммы первичной обмотки (ВН) имеют маркировку A, X для однофазных трансформаторов и A, B, C, N для трехфазных трансформаторов. Основные вторичные проводники (NN) обозначены a, x и a, b, c, N соответственно, вторичные проводники – aд и хд.
Начала первичной и вторичной обмоток подключены к проводникам A, B, C и a, b, c соответственно. Первичные вторичные обмотки обычно соединяются в звезду (группа соединения 0), а вторичные – в разомкнутый треугольник. Как известно, напряжение на зажимах вторичной обмотки при нормальной работе близко к нулю (неравновесное напряжение Unb = от 1 до 3 В), а в случае короткого замыкания на землю равно утроенному значению 3UО Напряжение в нейтральном проводнике UО фаза.
В сети с заземленным нейтральным проводником максимальное значение 3U0 равно фазному напряжению, а в случае изолированной сети – в три раза больше фазного напряжения. Соответственно, вспомогательные обмотки рассчитаны на номинальные напряжения Vnom = 100 В и 100/3 В.
Номинальное напряжение телевизора – это номинальное напряжение его первичной обмотки; это значение может меняться в зависимости от класса изоляции. Предполагается, что номинальное вторичное напряжение составляет 100, 100/3 и 100/3 В. Трансформаторы напряжения обычно работают в режиме холостого хода.
Трансформаторы напряжения с двумя вторичными обмотками
 Трансформаторы напряжения с двумя вторичными обмотками, помимо питания аппаратуры и реле, служат для сигнализации о замыканиях на землю в сетях с изолированной нейтралью или для защиты от замыканий на землю в сетях с заземленной нейтралью.
Трансформаторы напряжения с двумя вторичными обмотками, помимо питания аппаратуры и реле, служат для сигнализации о замыканиях на землю в сетях с изолированной нейтралью или для защиты от замыканий на землю в сетях с заземленной нейтралью.
Принципиальная схема трансформатора напряжения с двумя вторичными обмотками показана на рисунке 2a. Выводы второй (вспомогательной) обмотки, используемой для сигнализации или защиты от замыкания на землю, обозначены ad и xd.
На рисунке 2.6 показана схема трех таких трансформаторов напряжения в трехфазной системе. Первичная обмотка и основная вторичная обмотка соединены звездой. Нейтраль первичной обмотки заземлена. Три фазы и ноль могут подаваться от основной вторичной обмотки на измерительные приборы и реле. Вспомогательные вторичные обмотки соединены в разомкнутый треугольник. Из них сумма фазных напряжений всех трех фаз подается на устройства сигнализации или защиты.
При нормальной работе сети, к которой подключен трансформатор напряжения, векторная сумма равна нулю. Это можно увидеть на векторных диаграммах на рис. 2c, где Ua, Vc и Uc – векторы фазных напряжений, приложенных к первичным обмоткам, а Uad, Ub e и Ucd – векторы дополнительных первичных и вторичных напряжений, имеющих то же направление, что и векторы на соответствующих первичных обмотках (как на рис. 1c).
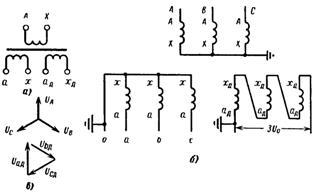
Рис. 2. Трансформатор напряжения с двумя вторичными обмотками. a – принципиальная схема; b – подключение в трехфазной цепи; c – векторная диаграмма
Сумма векторов UaD, Ubd и Ucd была получена путем их наложения в соответствии со схемой соединения вторичных обмоток, предполагая, что стрелки первичного и вторичного напряжений соответствуют началам обмоток трансформатора.
Результирующее напряжение 3U0 между концом обмотки фазы С и началом обмотки фазы А равно нулю.
В реальных условиях на выходе разомкнутой треугольной цепи обычно имеется небольшой дисбаланс напряжения, не превышающий 2-3% от номинального напряжения. Этот дисбаланс создается постоянно присутствующим небольшим дисбалансом вторичных фазных напряжений и небольшим отклонением их формы волны от синусоиды.
Напряжение, обеспечивающее надежную работу реле открытого треугольника, может возникнуть только в случае замыкания на землю на первичной стороне трансформатора напряжения. Поскольку при замыканиях на землю ток протекает через нейтральный проводник, результирующее напряжение на выходе разомкнутой треугольной цепи называется напряжением нулевой последовательности в соответствии с методом симметричных составляющих и обозначается 3U0. Цифра 3 в этом обозначении указывает на то, что напряжение в цепи является суммой напряжения трех фаз. Обозначение 3U0 также применяется к разомкнутой выходной цепи в треугольнике к реле сигнализации или защиты (рис. 2, 6).
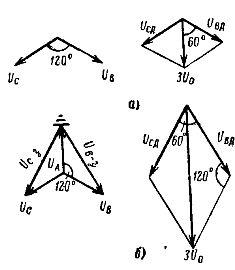
Рисунок 3. Векторные диаграммы первичных и вторичных вспомогательных напряжений при однофазном замыкании на землю: a – в сети с заземленным нейтральным проводником, b – в сети с изолированным нейтральным проводником.
Напряжение 3U0 имеет наибольшее значение в случае однофазного замыкания на землю. Обратите внимание, что максимальное напряжение 3U0 в сети с изолированной нейтралью значительно выше, чем в заземленной сети.
Общие электрические схемы трансформаторов напряжения
Простейшая система с использованием однофазного трансформатора напряжения, показанная на рис. 1,а, применяется в шкафах запуска двигателей и в распределительных пунктах 6-10 кВ для питания вольтметра и реле напряжения устройства АВР.
На рисунке 4 показаны электрические схемы однофазных трансформаторов напряжения с одной обмоткой для питания трехфазных вторичных цепей. Группа из трех однофазных трансформаторов, соединенных звездой, показана на рис. 4а должны использоваться для питания счетчиков контроля изоляции, счетчиков и вольтметров в установках 0,5-10 кВ с изолированными нейтралями и неразветвленными сетями, где нет необходимости сигнализировать о возникновении однофазных замыканий на землю.
Эти вольтметры должны показывать первичные напряжения между фазами и землей для определения “земли” (см. “Первичные напряжения между фазами и землей”, см.) векторная диаграмма на рис. 3.6). Для этого нейтральная точка обмотки ВН заземляется, а вольтметры подключаются к вторичным фазным напряжениям.
Поскольку в случае однофазных замыканий на землю трансформаторы напряжения могут находиться под сетевым напряжением в течение длительного времени, их номинальное напряжение должно соответствовать напряжению первичной сети между фазами. Как следствие, при нормальной работе под напряжением фаза-фаза мощность каждого трансформатора, а значит и всей группы, снижается в √ 3 раза. Поскольку нейтральная точка заземлена в цепи вторичной обмотки, во вторичной цепи всех трех фаз установлены предохранители.
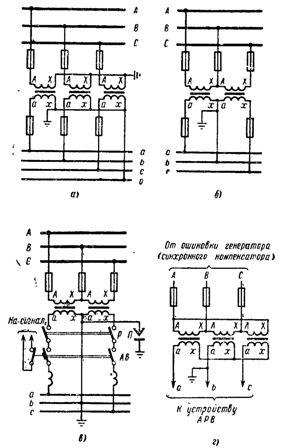
Рисунок 4. Схемы подключения однофазных измерительных трансформаторов напряжения с одной вторичной обмоткой: а – схема звезда – звезда для электроустановок 0,5 – 10 кВ с изолированным нейтральным проводником, б – схема разомкнутый треугольник для электроустановок 0,38 – 10 кВ, в – то же для электроустановок 6 – 35 кВ, г – включение трансформаторов напряжения 6 – 18 кВ в схему треугольник – звезда для питания синхронных машин оборудования АРВ.
На рис. 4, 6 и в, трансформаторы напряжения для питания приборов учета, счетчиков и реле, включенных на фазные напряжения, соединены по схеме разомкнутого треугольника. Такое расположение обеспечивает симметричные междуфазные напряжения Uab , Ubc, U c a при работе трансформаторов напряжения любого класса точности.
Особенностью системы разомкнутого треугольника является то, что мощность трансформаторов не используется, так как мощность такой группы из двух трансформаторов меньше мощности группы из трех трансформаторов, соединенных в полный треугольник не в 1,5 раза, а в √ 3 раза.
Схема рис.4, б используется для питания неразветвленных цепей напряжения электроустановок 0,38 -10 к В, что позволяет заземлять вторичные цепи непосредственно у трансформатора напряжения.
Во вторичных цепях схемы, показанной на рис. 4, в, вместо предохранителей установлен двухполюсный автоматический выключатель, который при срабатывании замыкает цепь сигнализации “разомкнутого напряжения”. Вторичная обмотка заземлена в распределительном устройстве фазы B, которое дополнительно заземлено непосредственно на трансформаторе напряжения через предохранитель. Автоматический выключатель обеспечивает видимое отключение вторичных цепей от трансформатора напряжения. Эта схема используется в установках 6 – 35 кВ при питании разветвленных вторичных цепей от двух или более трансформаторов напряжения.
На рис. 4d трансформаторы напряжения соединены по схеме “треугольник-звезда”, обеспечивая вторичное сетевое напряжение U = 173 В, необходимое для питания устройств автоматического регулирования возбуждения (АРВ) синхронных генераторов и компенсаторов. Для повышения надежности работы AVR во вторичных цепях не устанавливаются предохранители, что допускается ПУЭ для неразветвленных цепей.
Если вам понравилась эта статья, пожалуйста, поделитесь ссылкой в социальных сетях. Это очень поможет в развитии нашего сайта!
Мощность, отдаваемая в нагрузку (мощность на вторичной обмотке),
Векторная диаграмма трансформатора
Для трансформаторных уравнений можно предложить векторную диаграмму, которая представляет собой геометрическую интерпретацию трансформаторных уравнений в комплексной плоскости.
Поскольку коэффициент трансформации может быть в несколько десятков раз больше, неудобно рисовать схему, в которой векторы первичной и вторичной обмоток отличаются в несколько десятков раз. По этой причине принято рассматривать векторную диаграмму и эквивалентную диаграмму для данного трансформатора.
В данном трансформаторе число витков первичной и вторичной обмоток одинаково (Wi = w2). Все электромагнитные процессы в реальных и деформированных трансформаторах одинаковы. Потери, МП, магнитные потоки, активная и реактивная мощности остаются одинаковыми в реальном и пониженном трансформаторах. Если определить коэффициент трансформации как отношение числа витков первичной обмотки к числу витков вторичной (2.6), то для реального и истинного трансформатора можно получить следующие коэффициенты:
U 2 = W 12
Эквивалентность напряжений и токов вытекает из равенства мощностей реальной и пониженной обмоток трансформатора:

Магнитодвижущие силы уменьшенной и реальной обмоток одинаковы

Чтобы магнитные поля в реальном и вещественном трансформаторе оставались неизменными, уравнение (2.24) должно быть выполнено, а конфигурация обмоток сохранена. Сечения реальной и уменьшенной обмоток должны быть одинаковыми, поэтому витки уменьшенной обмотки различаются на пу> времена.
Активное сопротивление уменьшенной обмотки “в 12 раз больше, чем активное сопротивление реальной обмотки, из-за изменения п12 в раз больше числа витков и сечения обмотки:

Поскольку при неизменных геометрических размерах индуктивные сопротивления зависят от квадрата числа катушек


Эти коэффициенты также могут быть получены из равенства активных и реактивных мощностей трансформаторов.
Для трансформатора с заданными обмотками уравнения выглядят следующим образом: 
Геометрической интерпретацией уравнений (2.28)-(2.30) является векторная диаграмма редуцированного трансформатора (рис,) а).
Лучше начать построение диаграммы с уравнения (2.30), отбросив поток в фазе F”, а затем построить уравнения (2.28) и (2.29).
Входная мощность на первичной обмотке трансформатора (см. рис, а),

Мощность, отдаваемая в нагрузку (мощность на вторичной обмотке),

включая P> 2 G2 обмотки. Помимо потерь в меди, существуют потери в стали, которые могут быть определены следующим образом Е и активная составляющая тока холостого хода /oа– Обмотки трансформатора изготавливаются из меди и алюминия. Поэтому правильнее говорить о потерях в металле обмотки, а принято называть их потерями в меди, и пока нет необходимости заменять устоявшуюся терминологию. Потери в меди иногда называют электрическими потерями.
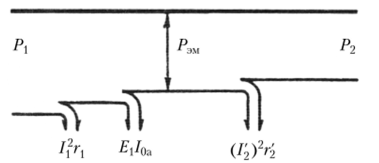
Рисунок 23. Энергетическая диаграмма активной мощности трансформатора
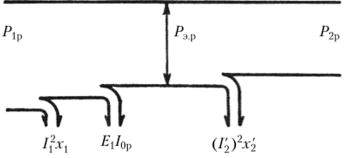
Рисунок 2.4. Энергетическая диаграмма реактивной мощности трансформатора
Электромагнитная мощность трансформатора – это мощность, передаваемая магнитным полем от первичной обмотки к вторичной или наоборот. Трансформаторы обратимы: как активная, так и реактивная мощность может передаваться от первичной к вторичной или от вторичной к первичной.
Для создания поля в трансформаторе необходима реактивная мощность, которая идет на создание первичного поля – поля взаимной индукции – и полей рассеяния первичной и вторичной обмоток.
На рисунке 2.4 показана диаграмма реактивной мощности в трансформаторе. Согласно векторной диаграмме, реактивная мощность, поступающая в первичную обмотку, равна

Мощность, поглощаемая для создания паразитного поля, равна Ifxv и реактивная мощность
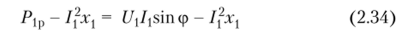
сосредоточена в поле взаимной индукции. Реактивная мощность вторичной обмотки используется для создания вторичного паразитного поля (Г2) 2 Х2. Реактивная составляющая электромагнитной мощности Рэ p – мощность, передаваемая от первичной обмотки ко вторичной (см. рис. 2.4).
Если нагрузка трансформатора индуктивная, то реактивная мощность от трансформатора подается на нагрузку. Если нагрузка трансформатора емкостная и активная, то при высокой емкости реактивная мощность течет в трансформатор и в сеть. В этом случае Р2Р > LR- Направления активной и реактивной мощности могут быть одинаковыми или противоположными.
Как видно из векторной диаграммы трансформатора, при смешанной емкостной нагрузке Щ > U (См. рис. 2.2, б). В случае чисто емкостной нагрузки рост напряжения во вторичной обмотке может быть настолько велик, что подвергает опасности изоляцию. Увеличение напряжения трансформатора при емкостной нагрузке называется трансформаторной стойкостью.
Отсюда следует, что вектор тока I1 состоит из геометрической суммы векторов I10 i – I2‘. Выполним это суммирование и завершим векторную диаграмму.
Теперь вернемся к первому основному уравнению:
ВЕКТОРНАЯ ДИАГРАММА ТРАНСФОРМАТОРОВ
Одним из приемов, облегчающих изучение электромагнитных процессов и расчет трансформаторов, является замена реального трансформатора с магнитными муфтами между обмотками эквивалентной электрической схемой (рис. 4.6.1).

На этом рисунке показана эквивалентная электрическая схема данного трансформатора, в которой сопротивления d и x условно получены из соответствующих обмоток и соединены с ними последовательно. Поскольку k = 1, E1 = E2. Таким образом, точки A и A и X и X на этом трансформаторе имеют одинаковые потенциалы, что позволит электрически соединить эти точки, в результате чего получится Т-образная эквивалентная схема (рис. 4.6.2).

Описывая эту цепь математически, используя методы Кирхгофа, можно обнаружить, что она полностью соответствует уравнениям ЭДС и тока реального трансформатора (см. раздел 4.5). Следовательно, можно электрически смоделировать трансформатор на компьютере. Проведение испытаний с учетом нагрузки z2‘ (единственный переменный элемент в цепи), можно предсказать реальное поведение трансформатора от холостого хода (z2= ) до короткого замыкания (z2‘ = 0).
Построение векторной диаграммы удобно начать с главного вектора потока Ф. Построим его на оси абсцисс. Вектор I10 опережает его на угол a . Затем, векторы ЭДС E1 и Е2‘ векторы, которые отброшены относительно потока Ф на 90°. Для определения фазового угла между E2‘ и я2Мы должны знать характер нагрузки. Предположим, что это активно-индуктивная нагрузка. Тогда я2‘ отстает от E2’ на угол f2.
Получается так называемый шаблон векторной диаграммы (рис. 4.7.1.). Для его завершения нам необходимо использовать три основных уравнения приведенного трансформатора.

Воспользуемся вторым основным уравнением:
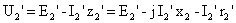
1 и выполнить векторное сложение.
Для этого в конце вектора E2‘ мы добавляем вектор – j I2‘ x2‘, а на его конце вектор – I2‘ r2‘. Результирующий вектор U2‘ будет вектор, соединяющий начало и конец последнего вектора.
Теперь используйте третье фундаментальное уравнение
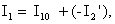
из чего следует, что вектор тока I1 состоит из геометрической суммы векторов I10 i – I2‘. Выполним это суммирование и завершим векторную диаграмму.
Теперь вернемся к первому основному уравнению:
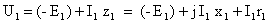
Для построения вектора – E1 мы должны взять вектор +E1 и направьте его в противоположную сторону.
Теперь к нему можно добавить другие векторы: + j I1 x1 и я1 r1 . Первый будет идти перпендикулярно току, а второй – параллельно ему. Результатом является целочисленный вектор u1.
Векторная диаграмма имеет общий характер. Один и тот же метод может быть использован для построения его для различных режимов, а также для различных типов нагрузки.
- Полное сопротивление цепи переменного тока – Основы электроники.
- Шаговые двигатели: свойства и практические схемы управления. Часть 2.
- Трехфазные электрические цепи; Студопедия.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Как проверить правильность подключения счетчика к проводу под напряжением.
- Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля; Школа для электриков: электротехника и электроника.
- Лекции по ТЭ – #27 Явление резонанса в электрических цепях.