Векторное поле

– Интеграл по замкнутому контуру:

Содержание

Определение и вариации

Евклидово пространство

Векторное поле на евклидовом (или псевдоевклидовом) пространстве [1] определяется как векторная функция точки пространства, которая отображает пространство в (на) себя [2] :

То есть, каждая точка пространства отображается на некоторый вектор (значение векторного поля в этой точке пространства). В общем случае этот вектор различен для разных точек пространства, то есть в общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенное значение и определенное (за исключением случая, когда поле обращается в ноль) направление в этом пространстве [3] .

В литературе (особенно в старой литературе, но также и в физике) предлог в (т.е. они утверждают, что также поле в пространство, и поле в пространство).

Разнообразие

В более общем случае, когда пространство источников является многообразием, векторное поле определяется как сечение отрезка, касательного к многообразию, т.е. отображение, которое каждая точка соответствует вектору соответствует вектору пространства, касательного к .

В физике

В физике термин векторное полев дополнение к общему значению, описанному выше, имеет специальное значение, в основном касающееся фундаментальных полей (см. ниже). Смысл этого использования заключается в том, что фундаментальные физические поля классифицируются по природе их потенциала, и одним из таких типов являются векторные поля (такие как электромагнитные или глюонные поля).

Циркуляция векторного поля

Определение векторного поля, характеристики, понятия, формулы и примеры (Таблица)

B) Предположим, что направление нормали к плоскости совпадает с направлением оси OZ.

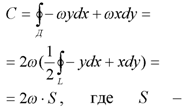
Площадь, заключенная в кривой L.

Обратите внимание, что если нормаль к поверхности S составляет угол γ с осью OZтогда циркуляция

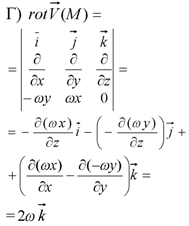
Ротор поля параллелен оси вращения, а его модуль равен удвоенной угловой скорости. С точностью до числового множителя ротор поля скоростей представляет собой угловую скорость вращения твердого тела

Векторные линии – это кривые, в которых каждая точка направлена по касательной к вектору поля:

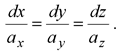
Векторная труба – это поверхность, образованная векторными линиями

Поток вектора через поверхность σ

Поток вектора α через поверхность σ является поверхностным интегралом скалярного произведения вектора поля на единичный вектор нормали к поверхности:

Дивергенция векторного поля

Дивергенция вектора α является скалярным интегралом плотности потока в данной точке поля:

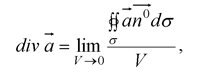
где σ – замкнутая граничная поверхность объема Vзамкнутая граничная поверхность объема V; n° – ортодромия ее внешней нормали; объем V->0 проводится в заданную точку.

Взаимосвязь между характеристиками

Векторная формулировка теоремы Гаусса-Остроградского:

Циркуляция векторного поля

– вектор радиуса точки М по контуру L.

Вектор циркуляции α вдоль L -это криволинейный интеграл замкнутого контура L от скалярного произведения вектора α на вектор касательная к контуру L.

– силовая работа F(M) поля при перемещении материальной точки по замкнутому контуру L

Ротор векторного поля

Полевой ротор гниение α – вектор, проекция которого на любое направление n равна поверхностной плотности циркуляции вдоль контура области, перпендикулярного этому направлению.

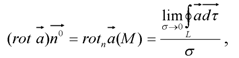
где σ – поверхностное натяжение на замкнутом контуре L; n° – ортодромия нормали к поверхности, направленной в сторону поверхности, от которой проходит контур L как видно, движется против часовой стрелки.

Это система дифференциальных уравнений для определения уравнений векторных линий.

Примеры векторных полей: 1) поле скоростей текущей жидкости;
2) силовые поля: электрическое, магнитное, гравитационное.

Векторное поле считается заданным, если в каждой его точке М является векторной функцией . Если соотнести векторное поле с декартовой системой координат, то векторную функцию можно записать в виде:

Простейший геометрические характеристики векторного поля являются векторные линии.

Векторные линии – это прямые, в каждой точке которых касательная имеет направление соответствующего вектора.

Примеры векторных линий: 1) если мы рассматриваем поле скоростей текущей жидкости, то векторные линии являются строки текущего этой жидкости, т.е. (2) для геометрического представления магнитного поля используются линии магнитного поля (для экспериментального представления линий магнитного поля – металлические опилки, помещенные на лист бумаги, которые в магнитном поле лежат вдоль линий поля).

Примечание. В дополнение к термину векторная линия часто используется термин векторная труба. Векторная труба это поверхность, образованная векторными линиями, проходящими через некоторую замкнутую кривую, лежащую в поле и не совпадающую (даже частично) с векторной линией.

Проблема нахождения векторной линии поля, проходящей через заданную точку, играет важную роль в полевых исследованиях. M. Пусть уравнение векторной линии имеет вид

или в векторной форме

По условию, в каждой точке этой линии вектор поля направлен по касательной к ней. Из геометрического смысла производной известно, что производная любой функции определяет направление касательной к этой функции. Поэтому производная направлена вдоль касательной к векторной линии. Следовательно, векторы и – коллинеарны. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. В результате получаем

Это система дифференциальных уравнений для определения уравнений векторных линий.

Пример 1.2. Найдите уравнение линий векторного поля

Решите. Для двумерных полей система дифференциальных уравнений векторных линий принимает вид

В этом случае ; . Поэтому

Разделив переменные и проинтегрировав, получаем

Таким образом, векторные линии представляют собой набор окружностей (см. рис. 1.2).

Решение:

Скалярное поле

Поверхности и линии уровня:

Рассмотрим скалярное поле, определяемое функцией U = U(x,y,z). Поверхности и линии уровня используются для визуализации скалярного поля.

Ровная поверхность скалярного поля – это геометрическое расположение точек, в которых функция U(M) принимает постоянное значение, т.е.

Придавая c различные значения в уравнении (70.1), мы получаем различные поверхности уровня, которые вместе кажутся стратифицированными. Через каждую точку поля проходит только одна ровная поверхность. Его уравнение можно найти, подставив координаты точки в уравнение (70.1).

Для скалярного поля, образованного функцией

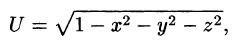
поверхности уровня представляют собой набор концентрических сфер с центром в начале координат: 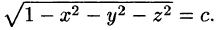В частности, если с = 1 получаем 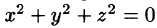То есть сфера сжимается в точку.

Для равномерно нагретой нити ровные поверхности температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых является нить.

В случае плоского поля U – U(x; y) уравнение U(x; y) = c уравнение линия уровня поле, т.е. линия уровня – это линия в плоскости Охув точках, функция которых U(x; y) в этой точке функция U (x; y) остается постоянной.

В метеорологии, например, сети изобар и изотерм (линии равных средних давлений и равных средних температур) представляют собой горизонтальные линии и являются функциями координат точек поля.

Линии уровня используются в математике для изучения поверхностей методом сечений (см. раздел 12.9).

Направленная производная

Для характеристики скорости изменения поля U =U(M) в заданном направлении, введем понятие “направленная производная”.

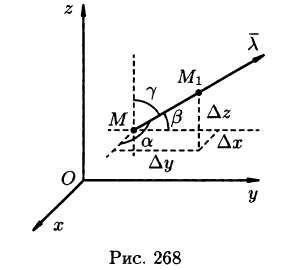
Возьмем пространство, в котором задано поле U = U(x;y;z)в определённый момент М и найти скорость изменения функции U во время движения точки М в любом направлении 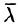. Пусть вектор 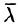имеют начало в точке М и косинус направления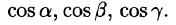

Приращение функции Uобразуется при переходе из точки М до определенного момента 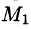в направлении вектора 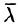определяется как

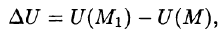
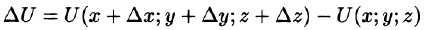
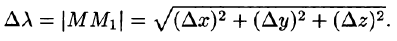
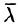
Производная функции U = U(M) в точке М в направлении предел

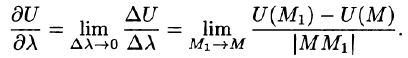
Производная с направлением 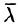и характеризует скорость изменения функции (поля) в точке М вдоль этого направления. Если 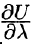> 0, тогда функция U увеличивается в направлени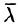и если 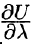< 0, то функция U в направлении 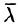уменьшается. Кроме того, количество 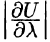представляет собой
мгновенная скорость изменения функции U в направлении 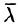в точке Мбольше 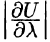тем быстрее функция U. В этом заключается физический смысл производной направленности.

Выведем формулу для вычисления направленной производной, предполагая, что функция U(x;y;z) дифференцируема в точке М. Тогда его общий прирост в этот момент М можно записать следующим образом:

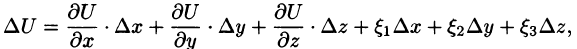
где 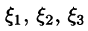– является бесконечно малой функцией в 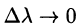(см. (44.3)). С сайта

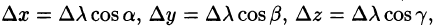
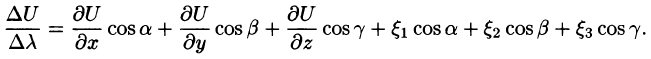
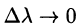
Переходя к пределу на , получаем формулу для вычисления направленной производной:

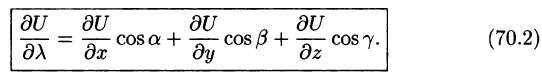
Для плоского поля U = U(x;y) у нас есть:

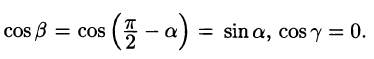
Формула (70.2) имеет вид:

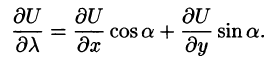
Примечание:

Понятие направленных производных является обобщением понятия частичных производных 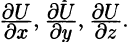Их можно рассматривать как производные от функций, также расположенных в направлении координатной оси О, О и Oz. Таким образом, если направление 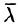совпадает с положительным направлением оси Ото если в (70.2) мы напишем 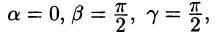получаем

Пример:

Найдите производную функции 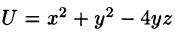в точке М(0; 1; 2) в направлении от этой точки к точке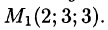
Решение:

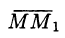
Найдите вектор и его направленные косинусы:

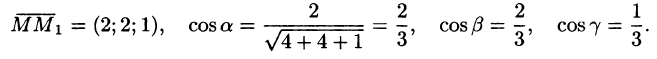
Найдите частные производные функции и вычислите их значения в точке М:

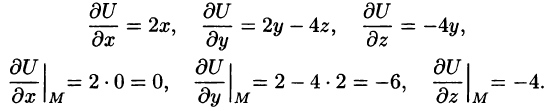
Отсюда, в силу уравнения (70.2), имеем:

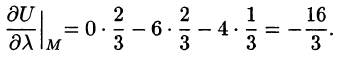
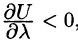
Поскольку jj^- < 0, функция убывает в этом направлении.

Градиент скалярного поля и его свойства

В каком направлении 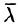производная 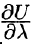имеет наибольшее значение? Это направление обозначается вектором, называемым градиентом скалярного поля.

Вы видите, что правая часть уравнения (70.2) является скалярным произведением единичного вектора

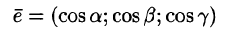
и вектор

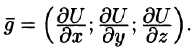
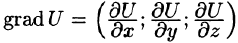
вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x;y,z)называется градиентом функции и обозначается через выпускU, т.е.

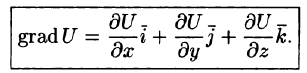
Следует отметить, что градация U является векторной величиной. Говорят, что скалярное поле U порождает векторное поле градиента U. Теперь уравнение (70.2) можно записать в виде

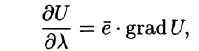
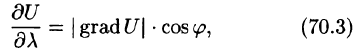
где 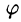угол между вектором градация U и направление 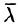(см. рис. 269).

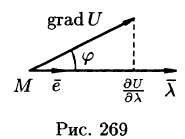
Из уравнения (70.3) сразу следует, что направленная производная достигает своего наибольшего значения, когда, следовательно, направление градиента совпадает с направлением A, вдоль которого функция (поле) изменяется наиболее быстро, т.е. градиент функции указывает в направлении наиболее быстрого роста функции. Самая быстрая скорость изменения функции U в точке М равен

В этом заключается физический смысл градиента. Это свойство градиента является основой его широкого использования в математике и других дисциплинах.

Вот некоторые важные свойства градиента функции.

1. градиент направлен вдоль нормали к горизонтальной поверхности, проходящей через данную точку.

Действительно, в любом направлении вдоль горизонтальной поверхности 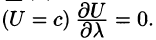Но тогда из (70.3) следует, что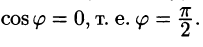

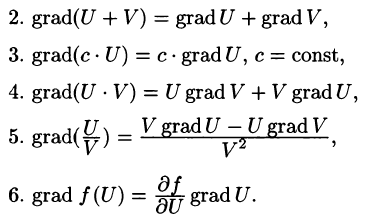
Докажите эти свойства из определения градиента. Докажем, например, последнее свойство. Тогда мы имеем:

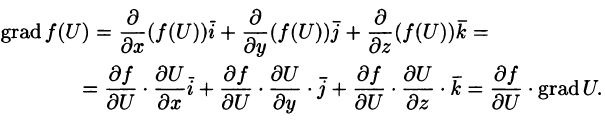
Примечание. Приведенные выше свойства функции градиента остаются справедливыми для плоского поля.

Пример:

Найдите максимальную скорость роста функции

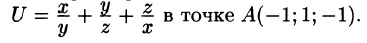
Решение:

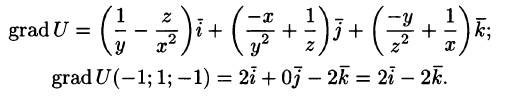
Максимальная скорость роста функции составляет

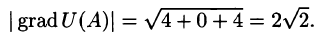
Обратите внимание, что функция U будет уменьшаться с наибольшей скоростью если точка А движется в направлении 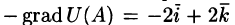(антиградиентное направление).

Уравнение линии уровня скалярного поля u(x,y) :

Скалярное поле: определение, равные площади и равные линии

Пусть D – конечная область на плоскости или в пространстве.

Определение скалярного поля. Если в области D каждая точка M(x,y,z) пространство или точка M(x,y,z) самолета в каждый момент времени t значение скалярной величины u это функция u(x,y,z,t) для пробела или u(x,y,z,t) в случае плоскости называется скалярным полем.

Понятия скалярного поля и функции, определенные в D одинаковы.

Примером скалярного поля является поле температуры воздуха в некоторой комнате, если эта температура рассматривается как функция точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, удаленных от источника тепла. Можно также привести примеры, такие как поле освещенности, поле плотности массы и тому подобное.

Для получения более полного представления о скалярном поле используются графические представления – равные области в пространстве и равные линии на плоскости.

Линии уровня широко используются на топографических и метеорологических картах. На топографических картах линия уровня – это линия с точками, где отмечена одинаковая высота. На метеорологических картах существует два типа линий уровня: изотермы (линии равной температуры) и изобары (линии равного давления).

Определение. Горизонтальная поверхность скалярного поля это множество всех точек пространства, в которых скалярное поле постоянно.

Уравнение горизонтальной плоскости скалярного поля u(x,y,z) :

Если происходит непрерывное изменение C поверхности уровня заполняют всю область пространства. Если плоские поверхности плотно распределены, скалярное поле быстро меняется. Однако, если плоские поверхности разрежены, скалярное поле изменяется медленно.

Определение. Линия уровня скалярного поля это множество всех тех точек плоскости, в которых скалярное поле постоянно.

Уравнение линии уровня скалярного поля u(x,y) :

Пример 1. Определите линии уровня скалярного поля и их форму.

Решение. Уравнение поверхностей уровня скалярного поля имеет вид

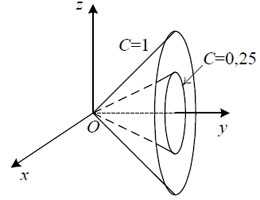
Конусы с вершиной в начале координат и осью вращения Oy . Поскольку, по определению, не может существовать одновременно x = 0 и z = 0 . Поэтому вершина конуса должна быть исключена.

Пример 2. Определите линии уровня скалярного поля и их форму.

Решение. Уравнение линий уровня данного скалярного поля имеет вид

Выразим “arcsin” из этого уравнения:

Поскольку arcsinC – также является константой, обозначим через C 1 . Затем

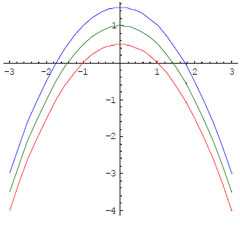
Графики этих линий представляют собой параболы с вершинами в точках и ветвями вниз. На рисунке показаны линии уровня в трех случаях: C 1 = 1 – красная линия, C 1 = 2 – зеленая линия, C 1 = 3 – синяя линия.

Вы можете найти эти страницы полезными:

Векторные поля. Векторные линии и их дифференциальные уравнения

Определение. Если в каждой точке M(x,y,z) пространства или его части определена векторная величина, то говорят, что там определено векторное поле. Определение векторного поля эквивалентно заданию вершин скалярных функций трех переменных. Примерами векторных полей являются: поле сил – поле силы F, поле скоростей v потока жидкости и т.д.

Векторные линии используются для геометрической характеристики векторного поля. Векторная линия поля вектора a – это кривая, касательная к которой в любой точке M имеет то же направление, что и вектор поля a в этой точке (рис. 7). В поле сил векторные линии называются линиями сил’, в поле скоростей жидкости векторные линии называются линиями тока. Рис. 7 3.1.

Пусть векторное поле определяется векторными функциями ) – непрерывные функции переменных x, y, z, имеющие ограниченные частные производные первого порядка. Пусть – – радиус-вектор текущей прямой точки векторного поля a (t – параметр). Из определения векторной линии следует, что вектор и вектор, касательный к этой кривой, должны быть коллинеарны в каждой точке векторной линии. Условием коллинеарности векторов является пропорциональность их координат:

Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток векторной линии через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности Итак, мы получили для векторных линий систему дифференциальных уравнений в симметричной форме. Предположим, что мы нашли два независимых интеграла системы (2): . Система уравнений (3) определяет векторную линию как линию пересечения двух поверхностей. Произвольно изменяя параметры c, и Cr, мы получаем семейство векторных линий как семейство с двумя степенями свободы.

Пример 1. Найдем векторные линии векторного поля 4 Запишем дифференциальные уравнения векторных линий, т.е. интегралы этой системы, получим два уравнения – произвольные постоянные. Пересечение плоскостей y – C с параболическими цилиндрами дает два параметрических семейства линий векторного поля (рис.8). Olredrm*t . Векторное поле называется плоским, если все векторы a параллельны одной плоскости и в каждой плоскости, параллельной определенной, векторное поле одно и то же.

Давайте посмотрим, как плоское векторное поле описывается координатами.

Если принять плоскость, указанную в определении (или любую параллельную ей плоскость), за плоскость xOu, то векторы поля плоскости не имеют компонент на оси Oz и их координаты не зависят от z: Дифференциальные уравнения векторных линий плоского поля могут быть записаны в следующем виде. Видно, что векторные линии плоского поля являются плоскими кривыми, лежащими в плоскостях, параллельных плоскости xOu.

Вы можете найти эти страницы полезными:

Пример 2 Найдите линии вектора магнитного поля бесконечно длинного прямого провода. ^ Предположим, что проводник направлен вдоль оси Oz и по нему течет ток силой J, т.е. H. Тогда вектор напряженности H магнитного поля задается формулой – радиус-вектор точки M, p – расстояние от оси проводника до точки M. Разложив векторное произведение (6), получим дифференциальные уравнения векторных линий: Отсюда x = const, = или . В итоге мы имеем, что линии вектора являются абсциссами с центрами на оси O (рис.9). Пример 3.

Найдите векторные линии гравитационного силового поля, создаваемого веществом, притягивающим к*h массу, находящуюся в начальной точке. Чтобы получить уравнения векторных линий в параметрической форме, приравняем каждую дробь к y. Это лучи, выходящие из источника. Чтобы выбрать векторную линию из семейства векторных линий, укажите точку ), через которую должна пройти эта векторная линия, и используйте координаты указанной точки для определения значения.

Например, предположим, что точка A/o имеет координаты . Уравнение векторной линии, проходящей через точку, можно записать следующим образом: . Сама точка L/o получается при значении параметра § 4. Векторное течение через поверхность и его свойства Рассмотрим сначала частный случай поля скорости v потока жидкости. Определим некоторую поверхность в поле Поток жидкости через поверхность E – это количество жидкости, которое протекает через поверхность E в единицу времени.

Этот поток можно легко рассчитать

если скорость потока постоянна (v = const) и поверхность Ł плоская. В этом случае поток жидкости равен объему цилиндрического тела с параллельными основаниями и длинами |v|, поскольку в единицу времени каждая частица перемещается на величину v (рис. 1). 10), где S – площадь основания, S – высота цилиндра, а n – нормаль к его основанию, Таким образом, для постоянной скорости v поток жидкости через плоскую поверхность E равен Если скорость v меняется непрерывно, а поверхность E гладкая, мы можем разделить поверхность E на такие маленькие части, что каждая E* может быть аппроксимирована как плоская и вектор v на ней постоянен.

Поскольку поток жидкости через поверхность E равен сумме потоков жидкости через все ее части E*, то для расчета потока получаем приближенную формулу Векторные линии Векторные линии и их дифференциальные уравнения Векторные линии Поток через поверхность и его свойства Векторный поток через поверхность Понятие ориентации поверхности где n – общее число частей Efc, на которые делится поверхность E, Pk – точка, лежащая на fc-й части, Aak – площадь поверхности части E*, обозначает скалярное произведение векторов 11).

Назовем поток жидкости через поверхность E пределом суммы (2), когда наибольший из . диаметров E*, где d – наибольший диаметр . Интеграл (3), определяющий поток жидкости, берется от скалярной функции (v, p°) вдоль поверхности E. Мы вводим понятие потока любого вектора a над поверхностью E по аналогии с понятием потока жидкости над поверхностью, введенным выше. Определение.

Тогда вектор напряженности поля в любой точке P будет равен где ch – величина заряда (массы), r OR – вектор радиуса точки P. Нам нужно найти поток вектора напряженности поля E через Sn – сферу радиуса R с центром в начале координат. Поскольку направление нормали к сфере совпадает с направлением радиус-вектора r, то на 5d сфере радиуса R имеем . Таким образом, поток вектора через Sn равен 4.1. Свойства потока вектора через поверхность 1. Линейность. где A и ц – постоянные числа. 2. аддитивность. Если поверхность E разделена гладкой кривой на две части , то поток через поверхность E равен сумме потоков через поверхности Ei и E2, Это свойство позволяет распространить понятие потока на гладкие поверхности E.

На примере цилиндрической поверхности мы увидим, что если выбрать определенный (один из двух) единичный вектор нормали в некоторой точке M поверхности, а затем непрерывно двигаться вдоль поверхности с соответствующей нормалью по любому пути, не проходящему через край поверхности, то единичный вектор нормали совпадет с исходным, когда мы вернемся в точку M (рис. 12). Однако есть поверхности, для которых это не так.

Примером такой поверхности является лист Мёбиуса (рис. 13). Существует путь (отмечен пунктирной линией в середине листа на рисунке), перемещение по которому вернет в исходную точку единичный вектор нормали, противоположный исходному. Описанное свойство делит все поверхности на два класса – двусторонние, т.е. ориентируемые (плоскость, сфера, поверхность куба и т.д.) и односторонние, т.е. неориентируемые (лист Мёбиуса). 3. Зависимость потока от ориентации поверхности (от ориентации вектора нормали к поверхности). Понятие потока вводится только для двусторонних поверхностей.

Предположим, что если в одной точке такой поверхности направление нормального вектора уже выбрано, то в каждой другой точке этой поверхности берется нормальный вектор, который получается из выбранного вектора при непрерывном движении точки вдоль поверхности (без пересечения границы). В частности, на замкнутой поверхности во всех точках берется либо внешняя нормаль, либо внутренняя нормаль (внутренняя нормаль направлена внутрь, ограничена замкнутой поверхностью).

Обозначим через это сторону поверхности Ł, на которой выбран вектор нормали n+ = n, а через E

– сторона поверхности E, на которой мы берем нормальный вектор (n_ = -n). Тогда получаем (7), где . Таким образом, при изменении ориентации поверхности (при изменении направления вектора нормали n° к поверхности E) поток вектора меняет знак на противоположный.

Пример 2 Вычислите поток лучевого вектора через поверхность простого кругового цилиндра высоты H с радиусом основания R и осью O. Эта поверхность состоит из трех частей: боковой поверхности Łj, верхнего основания Ł2 и нижнего основания Ł3 цилиндра. Поток P в силу свойства аддитивности равен – потокам данного поля на и , соответственно. На боковой поверхности цилиндра вектор внешней нормали p? параллелен плоскости xOu, и поэтому (см. рис. 14).

Отсюда векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток векторной линии через поверхность и его свойства Поток векторной линии через поверхность Понятие ориентации поверхности У верхнего основания £2 вектор нормали параллелен оси Oz и поэтому мы можем положить p§ = k – тогда имеем так У нижнего основания вектор g перпендикулярен вектору нормали p” = -k. Таким образом, этот символ обозначает двойной интеграл по замкнутой поверхности,

Отправляйте задания в любое время дня и ночи на ➔.

Официальный сайт Брилёнова Наталья Валерьевна преподаватель кафедры информатики и электроники, Екатеринбургский государственный институт.

Все авторские права на размещенные материалы принадлежат их владельцам. Любое коммерческое и/или иное использование, кроме первичного просмотра материалов natalibrilenova.ru, запрещено. Публикация и распространение размещенных материалов не преследует коммерческой и/или любой другой выгоды.

Цель сайта – облегчить студентам очной и заочной форм обучения путь в вопросах, связанных с учебой. Наталья Брилёнова не предлагает и не предоставляет услуги или товары.

Читайте далее: