Вязкое трение и устойчивость к воздействию среды - услуги электромонтажа, строительства и ремонта

Прыгун с парашютом летит со скоростью 35 м/с до раскрытия парашюта, а затем со скоростью 8 м/с. Определите предел прочности линий на разрыв в момент раскрытия парашюта. Масса парашютиста равна 65 г, а ускорение свободного падения – 10 м/с 2 . Определите пропорциональность F t r относительно υ .

Помимо сил трения, при движении в жидкой и газообразной среде возникают силы сопротивления среды, которые гораздо более значительны, чем силы трения.

Поведение жидкостей и газов в отношении сил трения не отличается. Поэтому характеристика, представленная ниже, применима к обоим состояниям.

Действие силы сопротивления, возникающей при движении тела в вязкой среде, обусловлено свойствами среды:

Отсутствие трения покоя, т.е. перемещение плавающего многотонного судна с помощью каната;
Зависимость силы сопротивления от формы движущегося тела, другими словами, от его обтекаемости для уменьшения силы сопротивления;
Зависимость абсолютного значения силы сопротивления от скорости.

Олово

Алюминий

Вольфрам

Железо

Золото

Константан (сплав Ni-Cu + Mn)

Латунь

Магний

Марганец (сплав меди, марганца и никеля)

Марганец

Медь

Neusilber

Никелин (сплав меди и никеля)

Никель

Нихром (Никель-хром-марганцевый сплав)

Олово

Платина

Ртуть

Вести

Серебро

Сталь

Фехраль (Cr (12-15 %); Al (3,5-5,5 %); Si (1 %); Mn (0,7 %); + Fe)

где – плотность среды (для воздуха = 1,29 кг/м 3 ), а – средняя плотность тела.

Содержание

9.4 Движение тел в сопротивляющейся среде

Со времен экспериментов Галилея на Пизанской башне известно, что все тела падают в гравитационном поле с одинаковым ускорением. g.

Однако повседневная практика показывает обратное: легкое перо падает медленнее, чем тяжелый металлический шар. Причина этого также ясна – сопротивление воздуха.

Уравнения движения. Если мы ограничимся случаем поступательного движения невращающихся тел в неподвижной среде с сопротивлением, то сила сопротивления будет противоположна скорости. В векторной форме это можно записать как

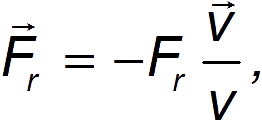
где 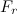– абсолютное значение силы сопротивления и – модуль скорости тела. Учет сопротивления среды изменяет форму уравнений движения тела, брошенного под углом к горизонту:

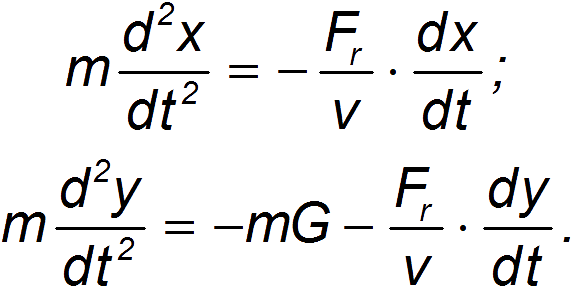
Эти уравнения также учитывают архимедову выталкивающую силу, действующую на тело: ускорение g заменяется меньшим значением

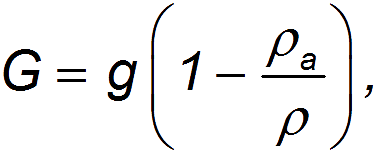
где 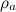– плотность среды (для воздуха 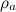= 1,29 кг/м 3 ), и 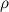– средняя плотность тела.

Действительно, вес 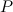тела в среде уменьшается на величину выталкивающей силы Архимеда

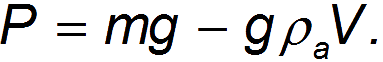
Выражение объема 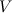тела по его средней плотности

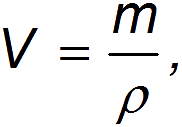
мы получаем выражение

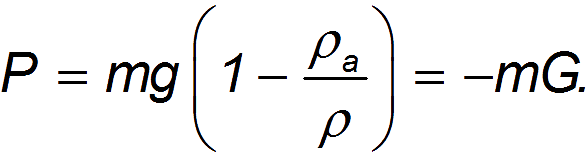
При наличии сопротивления воздуха скорость падающего тела не может увеличиваться бесконечно. В предельном состоянии она стремится к определенному установившемуся значению, которое зависит от свойств тела. Если тело достигло скорости падения в установившемся состоянии 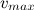Из уравнений движения следует, что сила сопротивления равна весу тела (включая силу Архимеда):

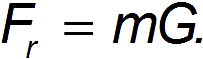
Сила сопротивления 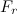как мы скоро увидим, является функцией скорости падения. Полученное выражение для силы сопротивления является уравнением, используемым для определения установившейся скорости падения 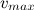. Понятно, что в присутствии среды энергия тела частично расходуется на преодоление ее сопротивления.

Число Рейнольдса. Конечно, уравнения движения тела в жидкости невозможно даже начать решать, пока мы ничего не знаем о модуле упругости. 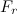силы сопротивления. Величина этой силы существенно зависит от характера обтекания тела противоположным потоком газа (или жидкости). При низких скоростях этот поток ламинар (т.е. многослойные). Его можно представить как относительное движение слоев жидкости, которые не смешиваются друг с другом.

Ламинарное течение жидкости иллюстрируется экспериментом, показанным на рисунке 13.

Как уже упоминалось в разделе 9.3, относительное движение слоев жидкости или газа между этими слоями создает силы сопротивления, которые называются силы внутреннего трения. Эти силы возникают в результате особого свойства жидких тел – вязкостькоторый численно описывается коэффициент вязкости 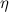. Приведем характерные значения 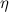для различных веществ: воздух ( 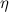= 1,8-10 -5 Па-с), вода ( 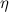= 10 -3 Па-с), глицерин 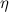= 0,85 Па-с). Эквивалентное обозначение единиц, в которых измеряется коэффициент вязкости: Па-с = кг-м -1 -с -1 .

Между движущимся телом и средой всегда существуют силы сцепления, так что непосредственно у поверхности тела слой газа (жидкости) полностью задерживается, как бы “прилипая” к ней. Он трется о другой слой, который находится немного позади тела. Этот слой, в свою очередь, испытывает силу трения еще более удаленного слоя, и так далее. Слои, более удаленные от тела, можно считать находящимися в состоянии покоя. Теоретический расчет внутреннего трения для движения шара диаметром D результаты Формула Стокса:

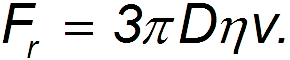
Подставив формулу Стокса в выражение для силы сопротивления при установившемся движении, мы получим выражение для установившейся скорости падающего шарика в среде:

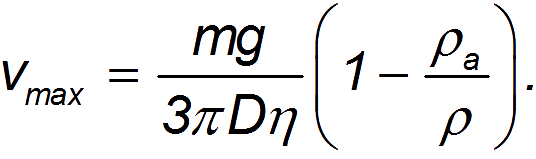
Видно, что чем легче тело, тем меньше скорость его падения в атмосфере. Это уравнение объясняет, почему пух падает медленнее, чем стальной шар.

При решении реальных задач, например, при расчете постоянной скорости падения парашютиста во время затяжного прыжка, нельзя забывать, что сила трения пропорциональна скорости тела только для относительно медленного ламинарного движения. ламинар противоположный воздушный поток. По мере увеличения скорости тела вокруг него образуются воздушные вихри, слои перемешиваются, и движение в некоторой точке становится турбулентныйи сила сопротивления быстро возрастает. Внутреннее трение (вязкость) перестает играть сколько-нибудь заметную роль.

Рисунок 9.15: Изображение потока жидкости при переходе от ламинарного к турбулентному течению (число Рейнольдса Re=250)

Возникновение силы сопротивления можно представить следующим образом. Пусть тело проходит расстояние в среде длины 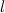. Если сила сопротивления 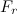тогда для этого нужно работать

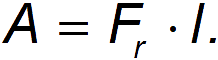
Если площадь поперечного сечения тела составляет 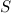тогда тело “сталкивается” с частицами, занимающими объем 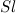. Общая масса частиц в этом объеме равна 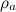· 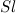Представим, что эти частицы полностью увлекаются телом и приобретают скорость . Тогда их кинетическая энергия становится равной .

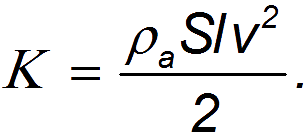
Эта энергия не появляется из ниоткуда: она возникает за счет работы внешних сил по преодолению силы сопротивления. Поэтому, A=Kследовательно

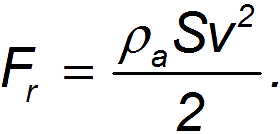
Мы видим, что сила сопротивления теперь более сильно зависит от скорости движения, становясь пропорциональной ее второй мощности (ср. формулу Стокса). В отличие от силы внутреннего трения, ее часто называют динамическая сила сопротивления.

Однако предположение о полном увлечении частиц среды движущимся телом является слишком сильным. В действительности каждое тело так или иначе увлекается потоком, что уменьшает силу сопротивления. Принято использовать так называемый коэффициент сопротивления Cиспользуется, записывая силу сопротивления в виде:

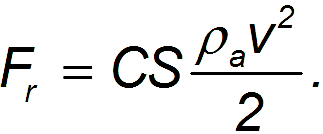
Для турбулентного потока в определенном диапазоне скоростей C не зависит от скорости тела, но зависит от его формы: скажем, для диска она равна единице, а для сферы около 0,5.

Подставляя формулу силы сопротивления в выражение для установившейся силы сопротивления, мы получаем другое выражение для установившейся скорости шарика (при C = 0,5):

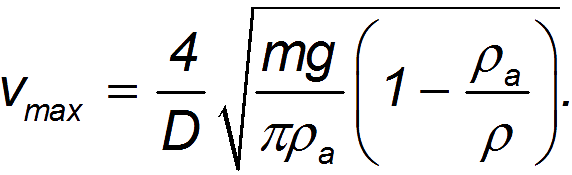
Применяя эту формулу к движению парашютиста с массой 100 кг и размером парашюта 10 м, получаем

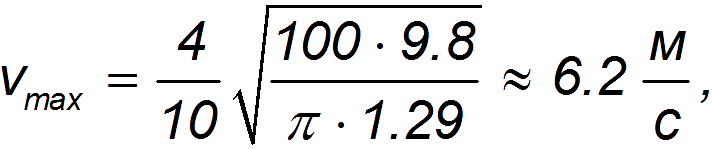
что соответствует скорости приземления при прыжке без парашюта с высоты 2 м. Видно, что для описания движения парашютиста больше подходит формула, соответствующая турбулентному потоку воздуха.

Выражение для силы сопротивления с коэффициентом сопротивления может быть удобно применено во всем диапазоне скоростей. Поскольку режим сопротивления меняется при малых скоростях, коэффициент сопротивления в области ламинарного потока и в области перехода к турбулентному потоку будет зависеть от скорости тела. Однако прямая взаимосвязь C на невозможно, поскольку коэффициент сопротивления безразмерен. Поэтому она может быть только функцией некоторой безразмерной комбинации, связанной со скоростью. Такая комбинация, играющая важную роль в гидродинамике и аэродинамике, называется число Рейнольдса (см. тему 1.3).

Число Рейнольдса – это параметр, который описывает изменение режима от ламинарного к турбулентному потоку. Это может быть отношение силы сопротивления к силе внутреннего трения. Подставив выражение для площади поперечного сечения сферы в формулу силы сопротивления 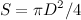мы видим, что величина силы сопротивления, с точностью до несущественных в настоящее время численных коэффициентов, определяется выражением

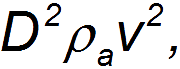
в то время как значение силы внутреннего трения задается величиной

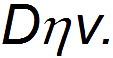
Отношение этих двух выражений и есть число Рейнольдса:

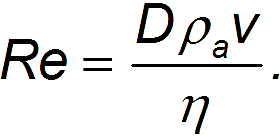
Если мы не говорим о движении сферы, то под D это характерная величина системы (например, диаметр трубы в задаче о потоке жидкости). Из важности самого числа Рейнольдса следует, что при низких числах Рейнольдса доминируют силы внутреннего трения: вязкость высока, и мы имеем дело с ламинарным потоком. При высоких числах Рейнольдса, наоборот, преобладают динамические силы сопротивления, и поток становится турбулентным.

Числа Рейнольдса имеют большое значение для моделирования реальных процессов в небольших (лабораторных) масштабах. Если числа Рейнольдса одинаковы для двух течений разного размера, то течения похожи, и явления можно вывести, просто изменив масштаб измерения координат и скорости. Таким образом, например, на модели самолета или автомобиля в аэродинамической трубе можно предсказать и изучить процессы, которые будут происходить в реальной эксплуатации.

коэффициент сопротивления. Таким образом, коэффициент сопротивления в формуле силы сопротивления зависит от числа Рейнольдса:

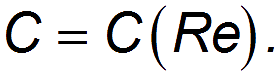
Это сложная зависимость, показанная (для сферы) на рис. 9.16. Теоретически получить такую кривую трудно, поэтому обычно используются экспериментально измеренные зависимости для данного тела. Однако возможна и качественная интерпретация.

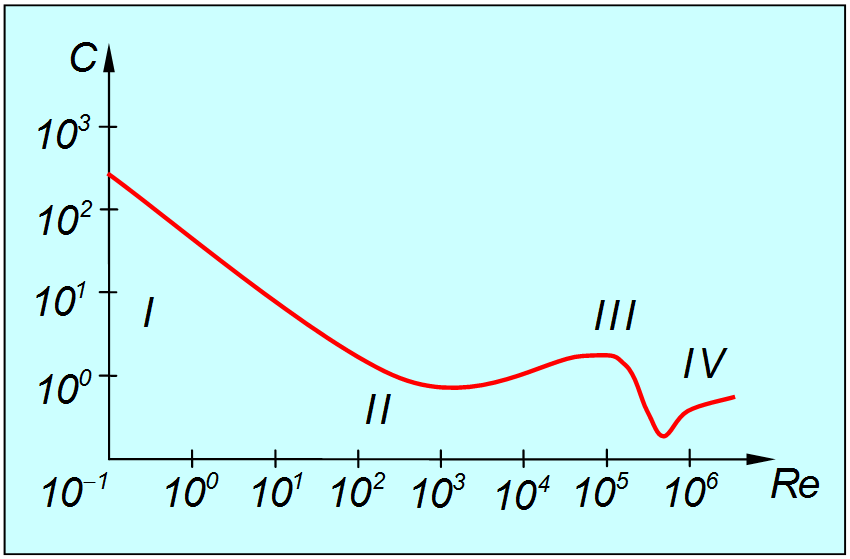
Рис. 9.16. Зависимость коэффициента сопротивления от числа Рейнольдса (римскими цифрами обозначены области значений Re, которые соответствуют различным типам воздушного потока).

Область I. В этом случае число Рейнольдса очень мало ( < 1) и является ламинарным. В этой области экспериментальная кривая описывается функцией

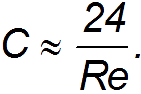
Подставив это значение в формулу силы сопротивления, найденную ранее, и используя 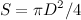и выражение для числа Рейнольдса получаем формулу Стокса. В этой области, как уже обсуждалось, сопротивление обусловлено вязкостью среды.

Регион II. Здесь число Рейнольдса лежит в диапазоне 1 < < 2-10 4 . Эта область соответствует переходу от ламинарного к турбулентному потоку. Экспериментальные данные показывают, что с увеличением числа Рейнольдса достигается критическое значение, после которого стационарное ламинарное течение становится неустойчивым. Конечно, это критическое значение не является универсальным и варьируется для различных типов токов. Однако его характерная величина составляет порядка нескольких десятков.

На немного больше критического значения, возникает нестационарный периодический поток, характеризующийся определенной частотой. При дальнейшем увеличении критического значения периодическое движение становится более сложным и в нем появляются новые частоты. Эти частоты соответствуют периодическим движениям (вихрям), пространственные масштабы которых становятся все мельче и мельче. Движение становится более сложным и запутанным – создается турбулентность. В этой области коэффициент сопротивления продолжает уменьшаться с увеличением но более медленными темпами. Минимум достигается при = (4-5)-10 3 , после чего С слегка поднимается.

Регион III. Эта область соответствует развитому турбулентному потоку вокруг сферы, который мы уже рассматривали выше. Характерные значения числа Рейнольдса здесь находятся в диапазоне 2-10 4 < 0. < 2·10 5 .

При движении тело оставляет турбулентную полосу, за которой поток становится ламинарным. След вихревой турбулентности можно легко наблюдать, например, за кормой судна. Часть поверхности тела прилипает непосредственно к турбулентному шлейфу, в то время как передняя часть тела прилипает к ламинарному потоку. Граница между ними на поверхности тела называется линией разделения. Физической причиной силы сопротивления является разность давлений на передней и задней поверхностях тела. Оказывается, что положение линии разделения определяется свойствами пограничного слоя и не зависит от числа Рейнольдса. Поэтому коэффициент сопротивления приблизительно постоянен в этом режиме.

Регион IV. Однако такой режим течения не может поддерживаться до произвольно больших значений />. В какой-то момент ламинарный пограничный слой становится турбулентным, отталкиваясь от линии отрыва. Турбулентный путь за телом сужается, что приводит к быстрому (в 4-5 раз) уменьшению сопротивления среды. Это явление называется драматический кризиспроисходит в узком диапазоне значений />= (2-2.5)-10 5 . Строго говоря, вышеприведенные теоретические соображения могут измениться, если принять во внимание сжимаемость среды (в нашем случае воздуха). Однако это проявится, как мы уже говорили, при скоростях объекта, сравнимых со скоростью звука.

Значение y пропорционально диаметру цилиндра, поэтому уравнение эквивалентности имеет вид (8.10)）. На практике, однако, процентная потеря импульса жидкости в препятствии изменяется в зависимости от числа Рейнольдса. Поэтому мы пишем Or (8. H）. (8.12） Где Co – функция числа Рейполлена, называемая коэффициентом сопротивления. Коэффициент сопротивления определяется немного по-другому в случае с мячами и другими препятствиями. Коэффициент здесь – это общая сила сопротивления. A – фронтальный поперечный разрез. 8 На рисунке 9 показано, как изменение числа Рейнольдса влияет на коэффициент сопротивления при обтекании цилиндра.

Коэффициент сопротивления

Значение y пропорционально диаметру цилиндра, поэтому уравнение эквивалентности имеет вид (8.10)）. На практике, однако, процентная потеря импульса жидкости в препятствии меняется в зависимости от числа Рейнольдса. Поэтому мы пишем Or (8. Н） (8.12） Где Co – функция числа Рейполлена, называемая коэффициентом сопротивления. Коэффициент сопротивления определяется немного по-другому в случае с мячами и другими препятствиями. Коэффициент здесь – это общая сила сопротивления. A – фронтальный поперечный разрез. 8. На рисунке 9 показано, как изменение числа Рейнольдса влияет на коэффициент сопротивления при обтекании цилиндра.

Коэффициент сопротивления потока вокруг бесконечного цилиндра [144].. Было установлено, что перепад давления при ламинарном движении в трубе пропорционален средней скорости u. То же самое справедливо и для потока вокруг цилиндров с низким числом Рейнольдса. Из уравнения (8.12) следует, что коэффициент сопротивления Co должен быть обратно пропорционален U0 и числу Рейнольдса. Область числа Рейнольдса, для которой это происходит, соответствует части кривой с углом наклона около 45°. С увеличением числа Рейнольдса эффект вязкости уменьшается.

Резкое падение коэффициента сопротивления при Be = 500 000 соответствует переходу от ламинарного пограничного слоя к турбулентному.

Образовательная страница для студентов и школьников

Эта страница не может быть воспроизведена без использования активной ссылки “www.lfirmal.com” в качестве источника.

Для определенных форм тела коэффициент сопротивления зависит только от числа Рейнольдса, числа Маха и направления потока. При низком числе Маха коэффициент сопротивления не зависит от числа Маха. Кроме того, изменение числа Рейнольдса в интересующем нас практическом диапазоне обычно невелико, а для автомобилей, движущихся со скоростью автострады, и самолетов, движущихся с крейсерской скоростью, направление входящего потока также более или менее одинаково. Поэтому коэффициент сопротивления часто можно считать постоянным. c d < displaystyle c _ < mathrm >> p e < displaystyle ■ mathrm > M a < displaystyle mathrm > M a < displaystyle mathrm > p e < displaystyle ™ mathrm > c d < displaystyle c _ < mathrm >>

Тупые и обтекаемые формы тела

Концепция

Сила между жидкостью и телом, находящимся в относительном движении, может передаваться только нормальным давлением и касательным напряжением трения. Таким образом, для целого тела сила сопротивления, соответствующая движению приближающейся жидкости, состоит из сопротивления трения (вязкого сопротивления) и сопротивления давления (сопротивления формы). Полное сопротивление и компоненты силы сопротивления могут быть связаны следующим образом:

Следовательно, когда в сопротивлении преобладает компонент трения, тело называется обтекаемая форма тела в то время как, когда в сопротивлении преобладает давление, тело называется тупой или обтекаемая форма тела . Таким образом, форма тела и угол атаки определяют тип сопротивления. Например, аэродинамическая спираль рассматривается как тело с малым углом атаки протекающей через него жидкости. Это означает, что к нему прикреплены пограничные слои, которые оказывают гораздо меньшее сопротивление давлению.

Возбуждение очень мало, и в сопротивлении преобладают компоненты трения. Поэтому такое тело (здесь аэродинамическое) называется обтекаемым, тогда как для тел, обтекаемых жидкостью под большими углами атаки, происходит отделение пограничного слоя. Это происходит в основном из-за неблагоприятных градиентов давления в верхней и задней частях аэродинамического профиля.

Это приводит к образованию следов, с последующими вихрями и потерей давления из-за сопротивления давления. В таких ситуациях аэродинамический профиль останавливается и оказывает большее сопротивление давлению, чем сопротивление трению. В этом случае тело описывается как тупое тело.

Обтекаемое тело похоже на рыбу (тунец), оропу и т.д. Обтекаемое тело похоже на кирпич, цилиндр или планер с большим углом атаки, в то время как тупое тело похоже на кирпич, цилиндр или планер с большим углом атаки. Для данной площади и скорости обтекаемое тело будет иметь меньшее сопротивление, чем тупое тело. Цилиндры и сферы считаются тупыми телами, так как при высоких числах Рейнольдса сопротивление доминируется компонентом давления в области следа.

Чтобы уменьшить это сопротивление, можно уменьшить отрыв потока или уменьшить площадь, контактирующую с жидкостью (для уменьшения сопротивления трения). Это снижение необходимо в таком оборудовании, как автомобили, велосипеды и т.д. и т.п., чтобы избежать вибрации и шума.

Практический пример

Аэродинамический дизайн автомобилей развивался с 1920-х годов до конца 20-го века. Это изменение конструкции от тупых корпусов к более обтекаемым позволило снизить коэффициент сопротивления с 0,95 до 0,30.

Простейшая аэродинамическая труба показана на рис. 25. Воздух втягивается в трубу вентилятором, который приводится в действие электродвигателем. Во входной части трубы имеется спрямляющая решетка. Он создает равномерный поток в рабочей части. За рабочей частью, где установлена тестовая модель, труба плавно расширяется. Если выход трубы соединен каналом с входом, получается труба с закрытым потоком. При одинаковых размерах рабочей части и одинаковой мощности двигателя скорость в рабочей части трубы этого типа будет выше, чем в трубе с открытым потоком.

Как найти коэффициент сопротивления

Когда модель ракеты поднимается, у нее есть друзья и враги. Ракета разгоняется за счет тяги, а ускорению препятствуют две силы: сила земного притяжения и сила аэродинамического сопротивления (буквально: воздушная сила). Велики ли силы, тормозящие ракету? Силен ли враг?

Теперь обратимся к космическим технологиям. Было установлено, что при выводе космического аппарата на круговую орбиту высотой 500 км потеря скорости из-за аэродинамического торможения составляет 0,4 км/с, а гравитационная потеря (потеря из-за действия силы тяжести Земли) – 1,1 км/с. Как мы видим, потери значительны.

Еще большие потери сопровождают полет модели, особенно аэродинамические потери: полет космической ракеты происходит лишь частично в плотных слоях атмосферы (напомним, что 75% общей массы атмосферы содержится в ее 10-км нижнем слое), тогда как полет модели происходит полностью в плотной среде.

Расчеты показывают, что потеря высоты модельной ракеты из-за аэродинамического сопротивления может быть равна, а иногда и больше, чем гравитационная потеря. Поэтому для моделиста особенно важно изучить “воздушного” противника, чтобы иметь возможность эффективно бороться с ним.

Какова природа аэродинамического сопротивления?

Сопротивление, которое создают модели ракет и сами ракеты, самолеты, автомобили, корабли – в общем, все, что движется в жидкой или газообразной среде, – создается двумя силами: трением и давлением.

Сопротивление трению обусловлено “вязкостью” среды, в которой происходит движение. Двигаясь через атмосферу, тело “перемещает” слои воздуха, находящиеся очень близко к его поверхности. Напряжения сдвига возникают потому, что молекулы воздуха у самой поверхности движутся вместе с телом, в то время как на относительно небольшом расстоянии от тела воздух неподвижен. В этом отношении сопротивление трения похоже на силы, возникающие, например, при скольжении предмета по столу.

Сопротивление давлению возникает потому, что воздушная среда обладает инерцией, мерой которой является ее масса или плотность массы. Когда тело движется через атмосферу, молекулы воздуха должны расходиться, освобождая место для тела. Таким образом, они ускоряются и, согласно физическим законам движения Ньютона, оказывают сопротивление движущемуся телу. Результатом этого сопротивления является сопротивление давлению.

Велики ли силы сопротивления и давления, когда модель находится в полете? Какова их относительная роль в создании общего сопротивления?

Расчеты показывают, что для модели длиной около четверти метра и диаметром 25 мм сила сопротивления может достигать 4 G, а сила тяги – 60 G. Как видите, силы тяги играют большую роль в создании аэродинамического сопротивления. Однако при определенных условиях, которые мы обсудим ниже, силы трения могут быть гораздо выше.

Аэродинамическое сопротивление ракет и моделей рассчитывается по формуле:

Q = c x	r V 2	S ,
	2

где Q – полное аэродинамическое сопротивление;

r – массовая плотность воздуха;

V – скорость полета;

S – площадь наибольшего поперечного сечения (центра) снаряда.

Буквы c x (читается: c-e-x) в формуле обозначают безразмерный поправочный коэффициент, называемый коэффициентом сопротивления. Таким образом, сопротивление модели или ракеты будет тем больше, чем плотнее среда, в которой происходит полет (чем больше плотность массы воздуха r ). Кроме того, сопротивление очень сильно зависит от скорости полета: если, например, скорость удваивается, то сопротивление увеличивается в четыре раза, при трехкратном увеличении скорости сопротивление увеличивается в девять раз!

Особое внимание следует уделить коэффициенту сопротивления – именно он может оказать огромное влияние на величину аэродинамического сопротивления, а значит, и на летные характеристики модели.

Для одноступенчатой модели коэффициент сопротивления будет где-то около 0,4 – 0,5. Обычно он определяется экспериментально путем надувания моделей в аэродинамических трубах.

Рисунок 25: Конструкция аэродинамической трубы.

Простейшая аэродинамическая труба показана на рисунке 25. Воздух всасывается в трубу вентилятором, который приводится в действие электродвигателем. Во входной части трубы находится спрямляющая решетка. Он создает равномерный поток в рабочей части. За рабочей секцией, где установлена тестовая модель, труба плавно расширяется. Если выход трубы соединен с входом каналом, получается труба с закрытым потоком. Этот тип трубы при одинаковых размерах рабочей части и одинаковой мощности двигателя будет иметь большую скорость в рабочей части, чем труба с открытым потоком.

Коэффициент сопротивления характеризует важную особенность летающего тела – его обтекаемость. Посмотрите на рисунок 26, на нем показаны различные формы тел: простые, такие как тарелка, цилиндр, шар, и более сложные, такие как комбинация полусферы и конуса, каплевидное тело. Все они имеют разные коэффициенты сопротивления, причем у последнего он самый низкий, поскольку он обтекаемый. Обтекаемое тело, как следует из названия, имеет контуры, которые точно отображают путь молекул воздуха на его поверхности, причем движение молекул происходит плавно, без резких изменений их траектории. Природа дает нам множество примеров обтекаемых тел. Обратите внимание, как быстро рыба или головастик пересекает воду, как быстр полет птиц – все это возможно только потому, что природа позаботилась об обтекаемой форме их тел.

Рис. 26: Коэффициенты сопротивления для различных тел.

Таким образом, идеальное обтекаемое тело имеет округлую головную часть, удлиненную “грудную клетку”, плавно переходящую в удлиненную, сильно сужающуюся хвостовую часть.

Для ракетной модели также лучше всего подходит обтекаемая форма. К сожалению, мы не можем точно следовать мудрым указаниям природы: округлую голову и вытянутое тело еще можно сделать, но для кормовой части ракеты сужающаяся, коническая форма не подойдет: если хвост ракеты сделать в такой форме, то некуда будет поставить двигатель, который будет двигать ракету вперед.

В аэродинамике скорость движущегося тела обычно сравнивают со скоростью распространения звука в воздухе. Когда скорость полета приближается к скорости звука, структура потока вокруг тела резко меняется. Доступны ли такие скорости для моделей? Конечно, они имеются, особенно для многоступенчатых моделей. Но природа не способна развивать такие скорости, и поэтому мы не можем найти хороший живой пример, который подсказал бы нам, какой должна быть форма тела при трансзвуковых или сверхзвуковых скоростях. Что же происходит на скоростях, близких к скорости звука?

Напомним, что звук – это процесс распространения слабых возмущений давления и плотности в воздухе. Каждая точка на поверхности летящего снаряда является генератором звуковых возмущений. Если скорость снаряда меньше скорости звука, эти возмущения обгоняют снаряд и “предупреждают” молекулы воздуха перед ним о приближении летящего тела. Молекулы воздуха выстраиваются заранее и плавно обтекают ракету. Точно так же толпа на переполненной привокзальной площади расступается, когда носильщик предупреждает их криком “Внимание!”.

Рисунок 27: Тюлень запрыгивает на модель самолета.

Теперь представьте, что ракета летит со скоростью звука или быстрее (для воздуха скорость звука при нормальных атмосферных условиях составляет 340 мМолекулы воздуха не получают предупреждающего сигнала (снаряд догоняет звуковая помеха) и как бы “натыкаются” на препятствие, создавая гораздо большее сопротивление движению снаряда. Это приводит к образованию в воздушном потоке скачков уплотнения – тонких слоев сильно сжатого воздуха, в которых происходят резкие изменения температуры, давления и плотности. Используя специальные методы визуализации, шипы можно даже сфотографировать: На рисунке 27 показана фотография скачков уплотнения, полученных во время испытаний модели сверхзвукового самолета. Эти шипы по внешнему виду очень похожи на клиновидные волны, которые образуются, когда лодка движется по поверхности воды.

В аэродинамике для сравнения скорости потока со скоростью звука используется специальная величина, число М, отношение скорости воздуха к скорости звука. Чем ближе скорость воздуха к скорости звука, тем ближе число M к единице. На сверхзвуковых скоростях он, естественно, больше единицы. При трансзвуковых и сверхзвуковых скоростях формула для расчета сопротивления не меняется, но коэффициент c x в формуле сильно меняется. На рисунке 28 показана его зависимость от числа М для одной из баллистических ракет. На этом же рисунке сбоку показано, как возникают и усиливаются скачки уплотнения на теле пули по мере увеличения числа М. Условно весь график можно разделить на три зоны. В первой зоне c x постоянна и не зависит от числа M . На нашей схеме первая зона заканчивается при числе М = 0,6. Режим течения в этой зоне называется чисто дозвуковым.

Рисунок 28: Зависимость коэффициента сопротивления от числа M .

Во второй зоне c x увеличивается. Чем объясняется увеличение коэффициента сопротивления, когда число M меньше единицы? Идея заключается в том, что потоки воздуха, обтекающие тело, прижимаются к нему, и воздух у поверхности ракеты ускоряется. В этом случае локальная скорость воздуха может стать равной или даже превышать скорость звука, что приводит к скачкообразному уплотнению даже при дозвуковых скоростях полета!

По мере увеличения числа М полета интенсивность толчков возрастает, и при скоростях, немного превышающих скорость звука, коэффициент сопротивления становится наибольшим.

В третьей зоне c x постепенно уменьшается – в этой зоне прыжки все больше наклоняются к поверхности тела, а интенсивность наклонных прыжков, как доказано аэродинамикой, уменьшается.

Посмотрите еще раз на график. Разве он не выглядит как препятствие, барьер, который нужно преодолеть, чтобы достичь высокой сверхзвуковой скорости? Возможно, именно поэтому в технике был введен термин “звуковой барьер”. Что ж, теперь мы можем пожелать маленьким моделям успеха в преодолении этого барьера!

Аэронавтика и ракетостроение научились выбирать наиболее выгодные формы самолетов. Так какие же формы имеют современные ракеты?

Ракета или модель обычно состоит из двух основных частей: корпуса и оперения (не будем забывать, что такое разделение происходит из-за формы ракеты).

Типичный корпус ракеты (рис. 29) состоит из носовой головной части, центральной цилиндрической части и задней кормовой части (или хвоста).

Рисунок 29: Форма корпуса ракеты.

Наиболее распространенные формы головной части – коническая, хвостовая и параболическая. Коническая форма головки представляет собой прямую линию, оживальная – круговую дугу, а параболическая – параболическую дугу. Касательная к сечению головной части в точке пересечения сечения с осью снаряда образует с осью угол, называемый углом конусности. На рисунке 29 этот угол обозначен b 0 . В некоторых случаях носовая часть носового конуса закруглена (как показано пунктирной линией на рисунке).

Что необходимо для изготовления носа ракеты?

Большинство моделей “головы” изготавливаются из дерева – сосны, березы, бука, липы. Обратите внимание, что не всегда выгодно делать головку из легкого дерева: более тяжелая головка способствует стабильному полету. Если у вас есть трудности с токарным станком, вы можете склеить носовой обтекатель из бумаги. Как это сделать, показано на рисунке 30.

Рисунок 30: Основную часть модели ракеты можно сделать из бумаги.

Форма кормовой части корпуса судна оказывает большое влияние на величину так называемого донного сопротивления. Это является частью сопротивления давления и вызвано разрежением за кормой, поскольку кольцевой поток воздуха в кормовой части стремится всасываться из-за кормы, аналогичный эффект всасывания (выталкивания) воздушного потока можно наблюдать в обычном распылителе или струйном насосе. Чтобы уменьшить сопротивление днища, кормовую часть делают сужающейся, но существуют цилиндрические и даже расширяющиеся конические кормовые части.

Геометрия тела снаряда в целом характеризуется двумя основными данными: диаметром центральной части d и удлинением l (отношение длины тела l к диаметру центральной части).

l =	l	.
	d половина

Корпус большинства моделей ракет выполнен по схеме, показанной на рисунке 29, а иногда и проще – без конической кормы. Формы “больших” ракет очень разнообразны и могут быть гораздо сложнее, чем у обычной ракеты. На рисунке 31 несколько схематично показаны вторая и третья ступени космической ракеты “Восток”. Ведущая часть ракеты, с закругленным носом, состоит из двух конусов с разными углами наклона. Средняя и кормовая часть третьей ступени представляет собой цилиндр, а вторая ступень состоит из трех вращающихся твердых тел: расширяющегося конуса, сужающегося конуса и цилиндра.

Рисунок 31: Формы второй и третьей ступеней ракеты-носителя “Восток”.

Большая часть аэродинамического сопротивления вызвана плавниками. Более половины сопротивления всей ракеты может быть вызвано плавником. Как и формы крыльев самолетов, геометрические формы плавников обычно классифицируются по типу профиля и типу плана.

Форма профиля хвоста может быть дозвуковой или сверхзвуковой. В обоих случаях используются симметричные профили, осью симметрии которых является центральная линия профиля. Прямая линия, соединяющая две наиболее удаленные точки контура профиля, называется хордой (обозначена буквой b на рисунке 32).

Очень важной геометрической характеристикой профиля является его относительная толщина ( c ), которая определяется путем деления максимальной толщины профиля c (см. рисунок) на длину хорды

c	=	c	.
		b

Дозвуковой профиль напоминает каплевидное вращающееся твердое тело. Она имеет высокую относительную толщину 10 – 12%, закругленный носок и плавный контур. Сверхзвуковой профиль характеризуется острым носком и малой относительной толщиной (c = 3 – 5%). Его контур формируется либо дугами кривых линий с малой кривизной, либо отрезками прямых линий. На рисунке показаны два наиболее распространенных профиля: линзовидный (образованный дугами окружности или параболы) и ромбический.

Для характеристики формы хвоста в плане необходимо задать размеры концевой хорды (b end) и основной хорды (b root), размах наконечника (на рисунке 32 показана полуширина l /2) и угол атаки c (угол между передней кромкой и поперечной осью снаряда). В зависимости от выбора линейных и угловых размеров меняется и форма ламелей. Наиболее распространенные формы – прямоугольная, трапециевидная, сагиттальная и треугольная. Как и корпус ракеты, плавники настоящей ракеты или модели могут быть гораздо сложнее, чем те, которые мы описали. Есть ракеты, у которых вообще нет плавников – все зависит от того, как вы решите стабилизировать ракету в полете. Если вы решили использовать плавники в своей модели ракеты, не забудьте придать ей обтекаемую форму. Не пропустите интересный факт: круглая проволока толщиной в миллиметр создает такое же сопротивление, как обтекаемый профиль толщиной в сантиметр. И подъемные свойства такого профиля (этот термин относится к способности профиля создавать подъемную силу – очень важно для устойчивости ракеты!) намного лучше, чем у непрофилированного профиля.

ФИНАНСОВЫЕ ПРОФИЛИ

ФОРМА ПЛАВНИКА В ПЛАНЕ

Рис. 32: Геометрические характеристики ребер.

Теперь необходимо подытожить все, что мы узнали о “враге номер два” ракеты, аэродинамическом сопротивлении, и дать несколько советов по выбору форм с наименьшим сопротивлением для моделей.

Внешняя поверхность модели должна быть гладкой. Шероховатость вносит свой вклад в сопротивление трения, и в этом случае (если модель шероховатая) общее сопротивление может увеличиться почти на 20%! Было установлено, что выступы на модели не должны превышать 0,1 мм, что составляет толщину листа обычной писчей бумаги.

Отрыв пограничного слоя и образование вихрей увеличивает сопротивление – форма должна обтекать модель без засорения, т.е. она должна быть хорошо обтекаемой.

Прежде чем выбирать форму любой части модели, необходимо знать, с какой скоростью, а точнее при каком числе М, она будет летать. Современные ракеты достигают огромных чисел М и разгоняются до космических скоростей. Количество полетов “М” среди моделей ракет все еще меньше одного. Но скорость звука – это далеко не предельная скорость модели, особенно многоступенчатой. Расчет скорости полета спроектированной модели или ее оценка с помощью экспериментальной ракеты – это способ найти наиболее подходящую форму модели.

На дозвуковых скоростях предпочтительнее закругленный нос, а на сверхзвуковых – заостренный. Угол конуса головной части следует выбирать в диапазоне от 10° до 45°. Следует помнить, что очень удлиненная и заостренная головная часть способствует увеличению сопротивления трения, а на дозвуковых скоростях – срыву и нарушению потока.

Иногда при выборе формы головы руководствуются не только соображениями снижения сопротивления. Например, при полете на скорости М = 5-10 и выше ракета подвергается интенсивному аэродинамическому нагреву. Ракетчики в этом случае выполняют своего рода “жертвоприношение фигуры”: они используют затупленную часть головы, которая создает мощный уплотняющий удар. Это увеличивает сопротивление, но большая часть тепловой энергии рассеивается в атмосферу, и нагрев ракеты уменьшается.

Подумайте, готовы ли вы пожертвовать пешкой или даже ферзем для достижения успеха конструкции: требование наименьшего сопротивления не всегда будет иметь первостепенное значение для успеха модели в соревнованиях.

Форма модели кормы должна способствовать снижению сопротивления днища. Как мы уже знаем, сопротивление днища меньше, когда корма сужается. Было замечено, что увеличение удлинения корпуса ракеты уменьшает донное сопротивление. Однако большое удлинение корпуса невыгодно с точки зрения сопротивления трению. Оптимальным значением удлинения для пернатой ракеты считается l = 8 – 15. Донное сопротивление значительно меньше при работе двигателя: поток газа заполняет застойную зону и уменьшает донное сопротивление. Например, испытание немецкой ракеты V-2 показало, что работающий двигатель снижает донное сопротивление на 50%.

Центр модели должен быть минимальным – необходимо приложить все усилия для уменьшения боковых размеров модели.

Форма хвостового профиля также должна быть выбрана соответствующим образом в соответствии с ожидаемой скоростью модели. Обратите внимание, однако, что на сверхзвуковых скоростях профиль плавника может быть дозвуковым, в зависимости от формы плавника. Таким образом, при угле наклона 60° дозвуковой характер профиля плавника сохраняется вплоть до летного числа М, равного примерно двум. Это также является причиной широкого распространения винтовых крыльев в современной авиации: дозвуковой профиль крыла обеспечивает прямой поток при низких скоростях воздуха, а вихревой профиль обеспечивает низкое сопротивление при высоких числах М.

Аэродинамики давно столкнулись с тем фактом, что сумма сопротивления, создаваемого каждой отдельной частью самолета, не равна сопротивлению всего самолета. Этот факт объясняется интерференцией или взаимодействием частей самолета. Интерференция бывает полезной, в этом случае сумма сопротивлений частей ракеты, измеренная при изолированном испытании каждой части, больше, чем сопротивление всей ракеты, и вредной, приводящей к увеличению сопротивления ракеты.

Поэтому недостаточно подобрать компоненты ракеты так, чтобы их сопротивления были минимальными, их нужно правильно скомбинировать, собрать вместе. Следует отметить, что аэродинамическая система снаряда определяется не только требованием минимального сопротивления всего снаряда, но и другими требованиями, в частности требованием аэродинамической устойчивости полета.

Читайте далее: