Свет, заключенный в полость, многократно воспроизводит стоячие волны для определенных резонансных частот. Результирующие модели стоячих волн называются “модами”. Продольные моды изменяются только по частоте, в то время как поперечные моды изменяются для различных частот и имеют различные картины интенсивности в поперечном сечении луча. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов, которые не создают стоячих волн.
Феномен резонанса: примеры, польза и вред резонанса в жизни, методы работы с резонансом
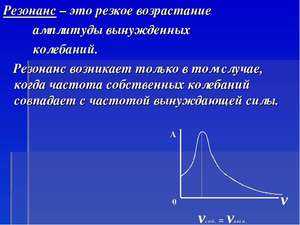
 Определение понятия резонанса (отклика) в физике оставлено специальным техникам, у которых есть статистические диаграммы, на которых они часто сталкиваются с этим явлением. В настоящее время резонанс – это частотно-избирательная реакция, при которой колебательная система или внезапное увеличение внешней силы заставляет другую систему колебаться с большей амплитудой на определенных частотах.
Определение понятия резонанса (отклика) в физике оставлено специальным техникам, у которых есть статистические диаграммы, на которых они часто сталкиваются с этим явлением. В настоящее время резонанс – это частотно-избирательная реакция, при которой колебательная система или внезапное увеличение внешней силы заставляет другую систему колебаться с большей амплитудой на определенных частотах.
Сайт написан, поддерживается и управляется командой преподавателей
Что вызывает резонанс
Вы будете раскачивать качели взад и вперед на произвольно выбранной частоте, хотя бы ради физического эксперимента, поскольку ваш жизненный опыт подсказывает вам действовать в такт с собственной вибрацией качелей. Амплитуда колебаний резко возрастет, если частота переменной внешней силы совпадет с частотой собственных колебаний качелей. Явление быстрого увеличения амплитуды вынужденной вибрации, когда частота периодически изменяющейся внешней силы совпадает с собственной частотой системы, называется резонанс.
Для наблюдения явления резонанса проведите эксперимент с маятниками (рис. 21.1). Выведите тяжелый шар 3 из состояния равновесия – он начнет колебаться. Колебания тяжелого маятника будут передаваться на стержень, который начнет совершать вынужденные колебания той же частоты и оказывать периодически меняющуюся силу на другие маятники. В результате маятники начнут вибрировать. Маятник 5, длина которого (и, следовательно, собственная частота) равна длине тяжелого маятника 3, будет раскачиваться сильнее всего.
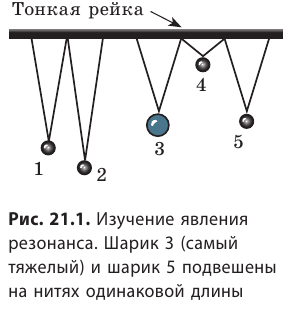
Давайте исследуем причины такого поведения маятников. Дело в том, что когда частота внешней переменной силы не совпадает с собственной частотой маятника ( 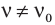
Если частота внешней переменной силы совпадает с собственной частотой маятника (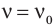 ) работа внешней переменной силы положительна на протяжении всего колебания. Энергия системы быстро увеличивается – так же, как и амплитуда колебаний. Из-за трения колебания со временем становятся фиксированными, и их энергия перестает увеличиваться.
) работа внешней переменной силы положительна на протяжении всего колебания. Энергия системы быстро увеличивается – так же, как и амплитуда колебаний. Из-за трения колебания со временем становятся фиксированными, и их энергия перестает увеличиваться.
График зависимости амплитуды вынужденного колебания от частоты изменения внешней силы называется Резонансная кривая.
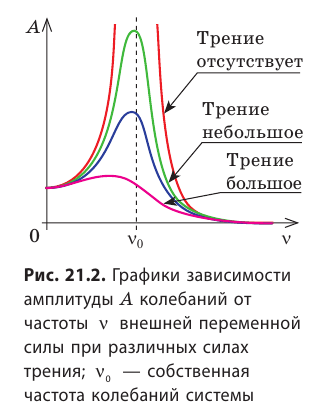
На рисунке 21.2 показаны резонансные кривые для различных сил трения. Проанализировав графики, можно сделать выводы: 1) наибольшая амплитуда колебаний получается, когда частота переменной внешней силы совпадает с собственной частотой системы (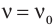 ); 2) чем больше сила трения в системе, тем меньше пик резонансной кривой, т.е. тем менее выражен резонанс.
); 2) чем больше сила трения в системе, тем меньше пик резонансной кривой, т.е. тем менее выражен резонанс.
Амплитудно-частотная характеристика (АЧХ) и полоса пропускания
собственная частота резонансного контура
Емкость конденсатора (C) и индуктивность катушки (L) определяют собственную частоту (Wc) цепи. Для приблизительных расчетов используется формула Wc=1/√L*C. В данном случае речь идет об идеальных условиях, когда потерями пренебрегают из-за минимальных значений.
Для повышения точности используется коэффициент демпфирования (Kz). Учитывая этот фактор, можно привести следующую зависимость между собственной частотой и резонансной частотой:
Легко видеть, что при колебаниях шарика энергия, передаваемая системе, все время меняется от энергии деформации (сжатия и растяжения) пружины к энергии движения шарика и обратно. В механике первый вид энергии называется потенциальной энергией, а второй – кинетической.
Явление резонанса
Резонансные явления связаны с периодическим колебательным движением электронов в контуре и основаны на том, что электроны в данном колебательном контуре легче всего “раскачиваются” на определенной частоте, которую мы называем резонансом. Мы повсюду сталкиваемся с периодическим колебательным движением. Колебания маятника, колебания струны, движение качелей – все это примеры колебательного движения.
Рассмотрим, например, колебательную систему, показанную на рис. 1. Эта система, как мы увидим позже, имеет много общего с электрическим колебательным контуром. Он состоит из пружины и массивного шара, прикрепленного к стержню.
Рисунок 1. Механическая модель колебательного контура. Масса-индуктивность, упругость-емкость, трение-сопротивление.
Если потянуть шарик вниз из положения равновесия, то под действием пружины он немедленно устремится обратно; но, набрав определенную скорость, шарик не остановится в точке равновесия, а по инерции устремится дальше, вызывая тем самым новую деформацию (сжатие) пружины. Затем этот процесс будет повторяться в обратном направлении и так далее. Шарик будет продолжать колебаться в обоих направлениях до тех пор, пока вся энергия, переданная пружине при отклонении шарика, не будет израсходована на трение.
Легко видеть, что при колебаниях шарика энергия, отдаваемая системе, все время меняется от энергии деформации (сжатия и растяжения) пружины к энергии движения шарика и обратно. В механике первый вид энергии называется потенциальной энергией, а второй – кинетической.
Когда шар находится в одном из крайних положений, он на мгновение останавливается. В этот момент энергия его движения равна нулю. С другой стороны, пружина в этот момент очень сильно деформирована: она либо сжата, либо растянута; поэтому она содержит наибольшее количество энергии. В момент, когда мяч проходит через положение равновесия с наибольшей скоростью, он обладает наибольшей энергией, но энергия пружины равна нулю, потому что она не сжимается и не растягивается.
Подбрасывая мяч на разные расстояния и наблюдая каждый раз за частотой последовательных свободных колебаний системы, мы замечаем, что частота системы всегда остается одной и той же. Другими словами, он не зависит от величины начального прогиба. Мы будем называть эту частоту собственная частота системы система.
Если взять не одну, а несколько таких систем, то можно заметить, что собственная частота системы уменьшается при увеличении массы шарика и увеличивается при увеличении упругости, т.е. при уменьшении упругости пружины. Эту зависимость можно обнаружить и на более простом примере с колеблющимися струнами разной толщины и разной степени натяжения.
Если мы хотим качать мяч с минимально возможным усилием, то, конечно, постараемся, во-первых, установить строгую периодичность наших ударов, т.е. постараемся, чтобы удары следовали один за другим через определенное время, а во-вторых, постараемся, чтобы интервал между ударами был равен периоду собственных колебаний системы (рис. 2).
Рис. 2. Механическая модель колебательного контура с незатухающими колебаниями. Частота действующей силы равна собственной частоте системы (резонанс).
Для того чтобы колебания колебательной системы происходили с минимально возможным усилием, необходимо, чтобы частота силы, действующей на систему, была равна собственной частоте системы. Каждый из нас знает этот принцип с детства, когда мы применяли его, качаясь на качелях.
Фото 3. Явление резонанса на примере качелей.
Таким образом, когда частота вынуждающей силы совпадает с собственной частотой системы, амплитуда колебаний становится наибольшей.
Поэтому следует заключить, что совпадение частоты вынуждающей силы с собственной частотой системы составляет резонанс.
Не нужно далеко ходить, чтобы найти примеры резонанса. Оконное стекло дрожит с определенной частотой каждый раз, когда мимо проезжает трамвай или грузовик; струна музыкального инструмента дрожит после прикосновения к соседней струне в согласии с первой и т.д. – Все это явления резонанса.
Зарядите конденсатор током (рис.4, a), а затем подключите его к индуктору (рис.4, b). Конденсатор немедленно начнет разряжаться. Разрядный ток будет протекать через индукционную катушку, и появление тока в катушке создаст вокруг нее магнитное поле. Это создаст ЭДС самоиндукции в катушке, которая задержит разряд конденсатора. Когда конденсатор разрядится, ток в катушке не прекратится, потому что теперь он будет поддерживаться ЭДС самоиндукции от энергии, накопленной в магнитном поле катушки при разряде конденсатора. Этот непрерывный ток будет заряжать конденсатор в обратном направлении, т.е. пластина, которая ранее была положительной, станет отрицательной и наоборот (рис. 4, в).
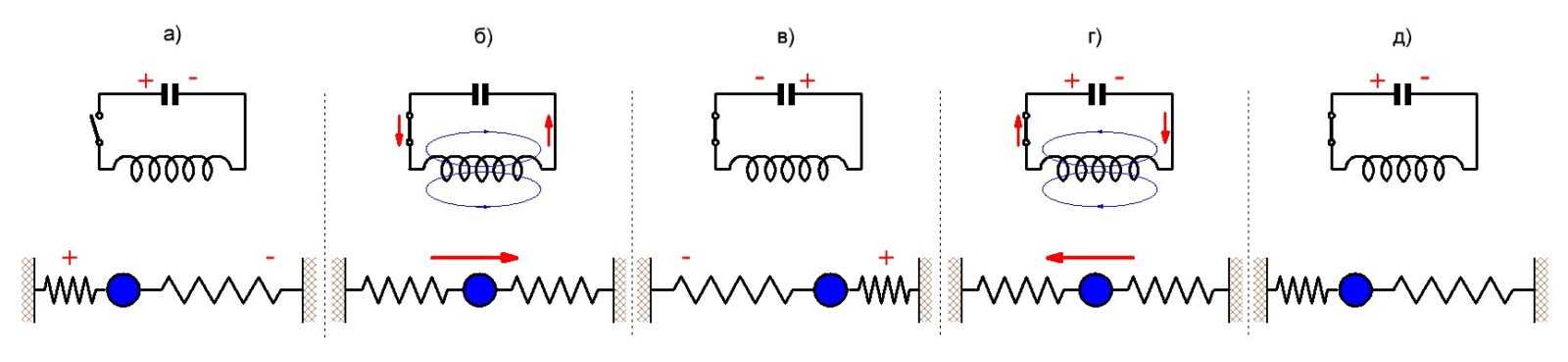
Рисунок 4. Свободная вибрация. В верхней части находятся электрические колебания, а в нижней – механические.
Затем конденсатор снова начнет разряжаться, снова заряжаться (рис.4, г, д) и т.д. Колебания тока в цепи будут продолжаться до тех пор, пока вся электрическая энергия, переданная цепи при зарядке конденсатора, не превратится в тепловую энергию. Это произойдет тем быстрее, чем выше активное сопротивление цепи.
Таким образом, разряд конденсатора через индуктор является колебательным процессом. Во время этого процесса конденсатор заряжается и разряжается несколько раз, энергия попеременно передается от электрического поля конденсатора к магнитному полю катушки и обратно.
Рисунок 5. Колебания в колебательном контуре.
Колебательный ток, возникающий во время этого разряда, имеет затухающий характер (рис. 6).
Рисунок 6. Колебания в цепи.
Частота колебаний при выбранных значениях емкости и индуктивности является вполне определенным значением и называется собственной частотой контура. Чем меньше значение емкости и индуктивности цепи, тем выше собственная частота цепи.
Если в колебательный контур ввести источник переменного тока, частота которого совпадает с собственной частотой контура, то колебания в контуре достигают своего максимального значения, т.е. возникает явление резонанса.
Между электрическими и механическими колебаниями можно провести далеко идущее сходство.
В таблице 1 электрические величины и явления показаны слева, а аналогичные величины и явления из механики показаны справа применительно к нашей модели механического колебательного контура.
| Электрические величины | Механические величины |
| Индуктивность колебательного контура | Масса сферы; |
| Емкость колебательного контура | Упругость пружин |
| Активное сопротивление цепи | Механическое трение |
| Пластины конденсатора | Пружины |
| Зарядка конденсатора | Деформация (сжатие и растяжение) пружин |
| Положительная нагрузка на пластину | Сжатие пружины |
| Отрицательная нагрузка на пластину | Натяжение пружины |
| Текущая страница | Скорость мяча |
| Направление тока | Направление движения мяча |
| Самоиндуцированная электродвижущая сила | Сила инерции шарика |
| Амплитуда (наибольшее мгновенное значение тока) | Амплитуда (наибольшее отклонение шарика от положения равновесия) |
| Частота (количество циклов в секунду) | Частота (количество колебаний в секунду) |
| Резонанс (совпадение частоты внешнего ЭМП с собственной частотой диффузора) | Резонанс (совпадение частоты воздействия вынуждающей силы с собственной частотой сферы) |
Отдельные моменты электрических колебаний и соответствующие моменты колебаний нашей механической модели колебательного контура показаны на рисунке 4.
ПОНРАВИЛАСЬ ЛИ ВАМ ЭТА СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Коэффициент качества определяет отношение энергии, запасенной в КС, к потерям за фазовый интервал на 1 радиан. Он информирует о ширине резонансной полосы.
Коэффициент качества колебательной системы
Другой характеристикой колебательной системы (DS) является ее коэффициент качества. На это указывает буква Q и рассчитывается по общей формуле:
Q = ω0*W/Pd = 2πf0W/Pd ,
где:
- ω0 – круговая резонансная частота;
- f0 – резонансная частота;
- W – запас энергии в КВт;
- Pd – мощность рассеяния.
Коэффициент Q определяет отношение энергии, запасенной в КС, к потерям за интервал изменения фазы в 1 радиан. Он указывает на ширину резонансной полосы.
Внимание! Формула для расчета Q-фактора гласит, что в каждый период скорость затухания колебаний и количество теряемой энергии тем меньше, чем выше значение Q-фактора VSD.
Период колебаний определяется по формуле Томпсона:
Заключение
Резонанс напряжений и токов – интересное явление, о котором необходимо знать. Он может наблюдаться только в индуктивно-емкостных цепях. Он не может возникнуть в цепях с высоким активным сопротивлением. Давайте подведем итог, кратко ответив на основные вопросы по этой теме:
- Где и в каких цепях возникает резонанс?
В индуктивно-емкостных цепях.
- Каковы условия резонанса токов и напряжений?
Это происходит, когда пассивные сопротивления равны. Цепь должна иметь минимальное активное сопротивление, а частота питания должна совпадать с резонансной частотой цепи.
- Как найти резонансную частоту?
В обоих случаях с помощью формулы: w=(1/LC)^(1/2)
- Как можно устранить это явление?
Путем увеличения активного сопротивления в цепи или изменения частоты.
Теперь вы знаете, что такое резонанс тока и напряжения, при каких условиях он возникает и его практическое применение. Чтобы закрепить эти знания, рекомендуем посмотреть полезное видео на эту тему:
Читайте далее:- Механические колебания и волны; FIZI4KA.
- Значение слова "амплитуда" в 11 словарях.
- Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
- Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
- Затухающие колебания – это. Что такое затухающие колебания?.
- Шаговые двигатели: свойства и практические схемы управления. Часть 2.
- 56 Резонанс напряжения и резонанс тока.