Пререквизиты
Задача об энергии магнитного поля с решением
Мы продолжаем серию статей о решении задач по физике. Сегодня мы решим несколько примеров об энергии магнитного поля.
Надоело решать проблемы? Загляните в наш Telegram-канал, там вы найдете много интересной и полезной информации для всех студентов. А если вы хотите получить скидку на наши услуги, подпишитесь на другой канал с приятными бонусами и акциями!
Из закона Ома следует, что энергия магнитного поля равна
Чтобы получить доступ к этому и другим видеоурокам из набора, вам необходимо добавить его в личный кабинет, купив в каталоге.
Получите удивительные возможности



Конспект урока “Энергия магнитного поля электричества”.
“Искусство экспериментатора – это
“это иметь возможность спросить у природы
и понять его ответы”.
Майкл Фарадей
Проблема 1. Каким должен быть ток в катушке индуктивностью 20 мГн, чтобы энергия магнитного поля составляла 5 Дж?
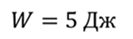

Энергия магнитного поля задается формулой
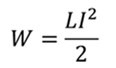
Исходя из этой формулы, выразим требуемую силу тока
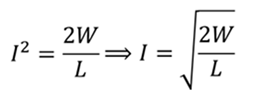
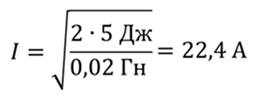
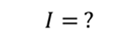
Ответ: 22,4 А.
Проблема 2. На катушке индуктивностью 80 мГн поддерживается постоянное напряжение 12 В. Известно, что сопротивление катушки составляет 3 Ом. Найдите энергию, которая выделяется при размыкании цепи. Также найдите ЭДС самоиндукции в катушке, предполагая, что открытие длилось 10 мс.

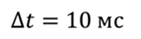
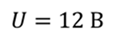
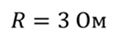

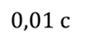
Энергия магнитного поля задается выражением
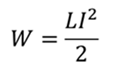
Запишите закон Ома для цепи
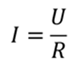
Тогда, используя закон Ома, энергия магнитного поля равна
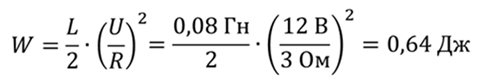
Запишите закон самоиндукции
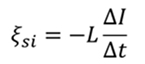
Когда цепь разомкнута, изменение тока будет равно току, протекающему в цепи. Знак минус означает, что ток уменьшился
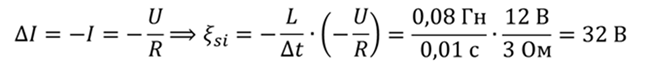
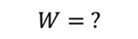

ОтветЭнергия магнитного поля = 0,64 Дж; ЭДС самоиндукции = 32 В.
Проблема 3. Катушка длиной 40 см содержит 5 витков на каждый сантиметр. Найдите энергию магнитного поля при силе тока 5 А, если магнитный поток через соленоид равен 10 мВб.

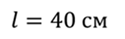

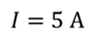
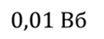
Энергия магнитного поля задается формулой
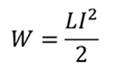
Индуктивность соленоида равна отношению магнитного потока к силе тока. В данном случае это отношение умножается на количество витков, так как каждый виток катушки имеет такую индуктивность
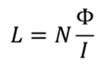
Тогда, исходя из последней формулы, имеем
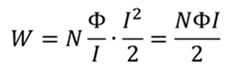
Количество витков можно рассчитать по формуле
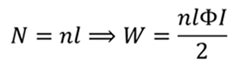
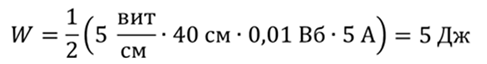
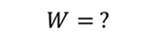
Ответэто: 5 J.
Проблема 4. Когда ток в катушке увеличился с 3 А до 8 А, энергия магнитного поля увеличилась на 20 Дж. Найдите индуктивность этой катушки.
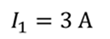
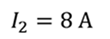
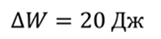
Энергия магнитного поля задается формулой
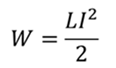
Примените эту формулу к начальной и конечной силе тока
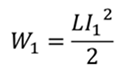
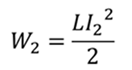
Изменение энергии магнитного поля можно рассчитать по формуле
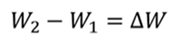
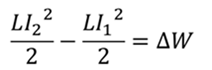
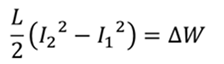
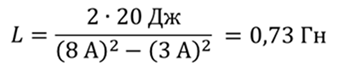
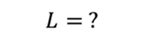
Ответ: 0.73 Гн.
Проблема 5. В цепь включена катушка индуктивностью 0,5 Гн. Всплеск напряжения в цепи показан на рисунке. Известно, что этот скачок вызвал в катушке самоиндуцированную ЭДС в 10 В. Как изменилась энергия магнитного поля?
Если теперь резко разомкнуть выключатель между источником питания и цепью нагрузки, лампочка будет мигать коротко, но вполне отчетливо. Это означает, что когда мы выключили источник питания, ток из катушки потек в лампочку, поэтому этот ток в катушке был там, у него было магнитное поле вокруг него, и когда магнитное поле в катушке исчезло, возникла ЭДС.
Энергия индукционной катушки
Энергия индукционной катушки (W) – это энергия магнитного поля, создаваемого электрическим током I, протекающим по проводу данной катушки. Основной характеристикой катушки является ее индуктивность L, т.е. способность создавать магнитное поле, когда по проводу катушки течет электрический ток. Каждая катушка имеет разную индуктивность и форму, поэтому магнитное поле для каждой катушки будет отличаться по величине и направлению, хотя ток может быть совершенно одинаковым.

В зависимости от геометрии данной катушки, от магнитных свойств среды внутри и вокруг нее – магнитное поле, создаваемое протекающим током, будет иметь конкретную индукцию B в каждой рассматриваемой точке, так же как и магнитный поток F – также будет иметь конкретное значение в каждой рассматриваемой области S.

Чтобы попытаться объяснить это простыми словами, индукция указывает на интенсивность магнитного воздействия (связанного с силой Ампера), которое данное магнитное поле способно оказывать на проводник с током, помещенный в это поле, а магнитный поток указывает на то, как магнитная индукция распределяется по заданной площади. Таким образом, энергия магнитного поля катушки с током находится не непосредственно в витках катушки, а в объеме пространства, в котором существует магнитное поле, связанное с током катушки.
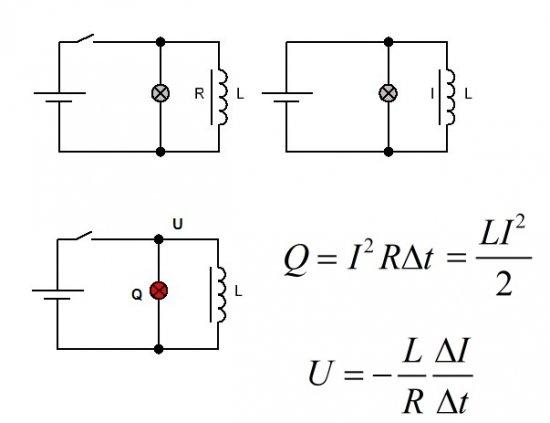
То, что магнитное поле катушки с током обладает реальной энергией, можно установить экспериментально. Давайте составим схему, в которой подключим лампочку параллельно катушке с железным сердечником. Подадим на катушку с лампочкой постоянное напряжение от источника питания. В цепи нагрузки ток, проходящий через лампочку и катушку, сразу же нарастает. Ток через лампочку будет обратно пропорционален сопротивлению ее нити, а ток через катушку будет обратно пропорционален сопротивлению провода, на который она намотана.
Если теперь резко разомкнуть переключатель между источником питания и цепью нагрузки, лампочка будет мигать коротко, но вполне отчетливо. Это означает, что когда мы выключили источник питания, ток из катушки потек в лампу, то есть этот ток в катушке был, вокруг него было магнитное поле, и когда магнитное поле исчезло, в катушке возникла ЭДС.
Эта наведенная ЭДС называется ЭДС самоиндукции, поскольку она была наведена собственным магнитным полем катушки на саму катушку. Тепловой эффект Q тока в этом случае можно выразить произведением величины тока, который был в катушке в момент открытия барабана, сопротивления R цепи (провод катушки и лампа) и длительности времени t для исчезновения тока. Напряжение, возникшее на сопротивлении цепи, можно выразить через индуктивность L, сопротивление цепи R и время dt затухания тока.
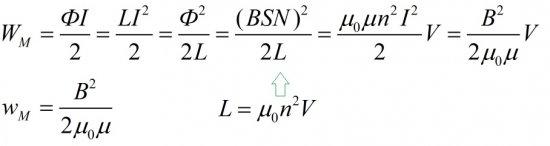
Теперь применим выражение для энергии катушки W к специальному случаю соленоида с сердечником определенной магнитной проницаемости, отличной от магнитной проницаемости вакуума.
Сначала выразим магнитный поток Ф через площадь поперечного сечения S катушки, число витков N и магнитную индукцию B на длине l. Сначала запишем индукцию B через ток в катушке I, число витков на единицу длины n и магнитную проницаемость вакуума.
Обозначим объем катушки V. Мы нашли формулу для магнитной энергии W и можем вывести из нее значение w – объемной плотности магнитной энергии внутри соленоида.
Джеймс Клерк Максвелл в свое время показал, что выражение для объемной плотности магнитной энергии справедливо не только для соленоидов, но и для магнитных полей в целом.
Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это очень поможет в развитии нашего сайта!
Магнитная индукция в соленоиде определяется из уравнения (7.18)
8.4 Энергия магнитного поля
Левая часть уравнения (8.29) представляет собой работу, совершенную источником тока в момент времени . Справа первый член – это количество джоулей тепла, выделившегося в проводнике. Понятно, что мы рассматриваем уравнение закона сохранения энергии в обсуждаемой цепи. Каково значение второго термина? Он связан с катушкой, о чем свидетельствует коэффициент умножения Lи представляет собой работу, затрачиваемую на преодоление противодействующей ЭДС самоиндукции. Куда уходит эта работа? В процессе замыкания цепи в Катушка генерирует магнитное поле. Поэтому именно в катушке эта работа сохраняется в виде энергии ее магнитного поля. Ток увеличивается от нуля до фиксированного значения I. Поэтому полная энергия поля катушки равна
Тот же результат можно записать в виде
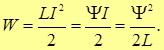
Эти формулы очень похожи на выражения для энергии конденсатора как функции его заряда или разности потенциалов на его выводах. Мы помним, что его можно свести к форме, в которой четко указан объем конденсатора. Это позволило нам связать плотность энергии электрического поля с его напряженностью. Проведем аналогичную схему для магнитного поля, используя в качестве “катушки” соленоид соответствующей длины.
Индуктивность соленоида задается (8.21)
Магнитная индукция в соленоиде задается (7.18)
Выразите плотность потока в соленоиде через магнитное поле, присутствующее в нем
и подставьте его в выражение для индуктивности катушки. Получаем
Наконец, подставим это выражение в (17.28) для энергии поля в катушке
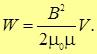
Мы достигли своей цели: параметры катушки, с которой мы начали, не фигурируют в этой формуле. Мы выразили все через магнитную индукцию поля, и энергия в катушке оказывается пропорциональной ее объему. Отсюда следует выражение для плотности энергии магнитного поля (независимо от того, что и как в нем производится)
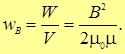
Напоминание о зависимости напряженности магнитного поля от плотности магнитного потока
мы находим эквивалентные представления для плотность энергии магнитного поля:
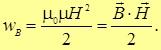
Для магнитного поля в вакууме все эти формулы должны быть подставлены. Легко заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).

Рис. 8.36: Сильное магнитное поле Солнца вызывает выбросы плазмы.

Рис. 8.37. Сильное магнитное поле нейтронной звезды
Пример. Сравните энергии, содержащиеся в объеме 1 л, если он пронизан: 1) однородное электрическое поле напряженностью Е = 100 кВ/м; 2) однородное магнитное поле с индукцией В = 1 Тесла.
Решение. Энергия электрического поля равна
Энергия магнитного поля равна
Оба эти поля считаются достаточно сильными, но могут быть созданы без особых проблем. Эта проблема показывает, что на практике выгоднее хранить энергию в магнитном поле: В этом примере соотношение энергии составляет
Какова индуктивность проволочной катушки, если ток 6 А создает магнитный поток 12 мВб?
Как найти энергию магнитного поля катушки?
Подробности Просмотров: 1126 
Задачи по физике – это просто!
Не забывайте.Всегда используйте систему СИ для решения!
А теперь о проблемах!
Элементарные задачи из школьного курса физики по расчету индуктивности, самоиндукции и энергии магнитного поля.
Проблема 1.
Какова индуктивность катушки провода, если ток 6 А создает магнитный поток 12 мВб?
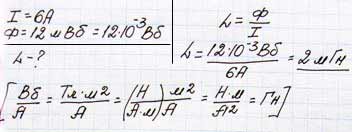
Проблема 2
В катушке из 150 витков течет ток 7,5 А, который создает магнитный поток 20 мВб.
Какова индуктивность этой катушки?
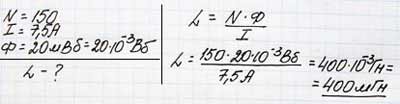
Проблема 3.
Через соленоид с индуктивностью 0,4 мГн и площадью поперечного сечения 10 см2 протекает ток 0,5 А.
Какова индукция поля внутри соленоида, если он содержит 100 витков?
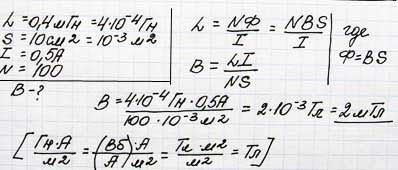
Проблема 4
Определите индуктивность контура с током 1,2 А, если площадь контура 20 см2 , поле магнитной индукции 0,8 Тесла, а вектор магнитной индукции направлен под углом 30 o к плоскости контура.

Проблема 5
Какая ЭДС самоиндукции наводится в катушке электромагнита с индуктивностью 0,4 Гн при изменении тока на 5 А в течение 0,02 с?
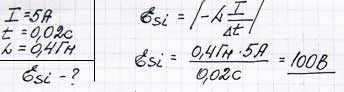
Проблема 6
Определите энергию магнитного поля катушки, если ее индуктивность равна 0,2 Гн, а ток в катушке 12 А.
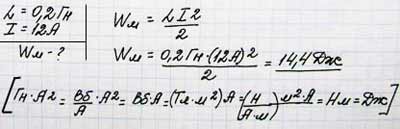
Проблема 7
Каким должен быть ток в катушке с индуктивностью 0,5 Гн, чтобы энергия магнитного поля была равна 1 Дж?
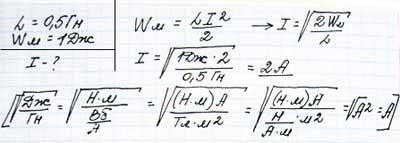
Проблема 8
Найти энергию магнитного поля соленоида с индуктивностью 0,02 Гн и магнитным потоком через него 0,4 Вб.
Приведенные выше условия справедливы только в вакууме, т.е. когда ∗ = 1. Если цепь с током помещена в вещество, рассмотрим следующие параметры:
Что такое энергия, как ее найти, формула
Согласно закону сохранения энергии, вся энергия магнитного поля преобразуется в джоулево тепло на сопротивлении R. Величина уменьшения энергии магнитного поля определяется как работа индукционного тока:
Результирующее значение тока, индукции магнитного поля и энергии равно нулю. Мы можем принять значение начальной энергии как (E_
Элементарная работа, которую совершает ток, рассчитывается таким образом:
(dA_= =varepsilon _Idt=-LIfrac
Здесь dt – время, в течение которого действует индукционный ток; (=varepsilon _).= Лифрак
В связи с изменением тока от I до 0, получаем:
Записанная формула действительна для любой цепи и определяет, как связаны между собой энергия магнитного поля, сила тока и индуктивность цепи. Это выражение можно сравнить с уравнением для кинетической энергии поступательного движения:
Это соотношение показывает связь между индуктивностью цепи и ее инерцией. Если тело находится в движении, его нельзя остановить без преобразования энергии. Точно так же невозможно остановить электрический ток без преобразования энергии.
- Самоиндукция. Энергия самоиндукции, индуктивность – материал по физике PSE.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Соленоид – это электромагнитная катушка. Что такое соленоид?.
- Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
- Значение слова ИНДУКЦИЯ. Что такое индукция?.
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
- Как работает индукционный нагреватель и как он устроен; Школа электротехники: электротехника и электроника.