В формуле r – расстояние данного участка Δ l от точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ 0 – магнитная постоянная.
Закон Био-Савара. Теорема о циркуляции
Французские физики Ж. Био и Ф. Савар в 1820 году проводил эксперименты по изучению магнитного поля постоянных токов. Физики доказали, что индукция магнитного поля токов, протекающих в проводнике, зависит от совместного действия всех участков этого проводника. Действие магнитного поля основано на принципе суперпозиции.
Принцип суперпозицииЕсли магнитное поле создается несколькими проводниками с током, то индукция магнитного поля равна сумме индукций поля, создаваемых каждым проводником в отдельности.
Индукция B → проводника с током представляется как векторная сумма элементарных индукций ∆ B →, создаваемых отдельными участками проводника. На практике невозможно изолировать отдельный участок проводника с током, поскольку прямые токи всегда замкнуты. Можно измерить только общую индукцию магнитного поля, создаваемую всеми элементами тока. Как найти индукцию магнитного поля?
Что такое циркуляция, закон Био-Савара
Вектор циркуляции ∗ прямолинейного вектора тока по замкнутому контуру, который не замыкает данный проводник, равен нулю. Когда в цепи несколько токов, вектор циркуляции ∗ равен их алгебраической сумме:
∗; (∗ ∗ ∗ ∗ ∗ ∗).
Закон Био-Савари определяет вклад ∗ в магнитную индукцию ∗ результирующего магнитного поля, создаваемого небольшим участком ∗ треугольника l проводника с током I.
В этом случае r – это расстояние от данного сегмента треугольника l до точки наблюдения, ∗ – угол между направлением на точку наблюдения и направлением тока в данном сегменте, а ∗ – магнитная постоянная.
Используя закон Био-Савара, можно определить магнитные поля токов различной конфигурации и рассчитать магнитное поле в центре круговой катушки с током.
где $overrightarrow
Дифференциальная форма теоремы о циркуляции
Пусть S – это площадь поверхности, которую охватывает путь L. Положительная нормаль к поверхности связана с направлением контура L правилом правого винта. Общий ток, протекающий через поверхность S, можно записать как
где $overrightarrow
На основании теоремы Стокса мы можем написать, что:
Равенство (11) справедливо для любой поверхности, следовательно, интеграл также равен нулю:
u2007————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————>Przedstawiciele władz lokalnych i regionalnych
Уравнение (12) представляет собой дифференциальную форму теоремы о циркуляции. Он действителен для любого поля в любой момент.
Напомним, что теорема о циркуляции в форме (7) и (12) записана для поля в вакууме и стационарных токов.
Задача: Тороид имеет каркас в форме тора, на него намотан проводник, по которому течет ток. Магнитное поле такой конфигурации тока в основном сосредоточено внутри тороида. Поле обладает осевой симметрией. Линии магнитного поля тороида представляют собой окружности, центрированные на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис. 2) (B(r)). Если ток в тороиде равен I. N – количество витков тороида.
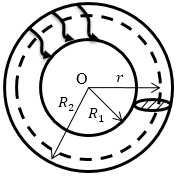
В качестве контура циркуляции выберем линию силы в виде окружности радиуса r (рис. 2). Напишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:
∆u2009.стрелка
Тогда теорема о циркуляции будет иметь вид:
$N$, где $N$ – число катушек с током. Выражая модуль вектора индукции, получаем:
Задача: Какова циркуляция вектора индукции по цепи, в которой текут токи $I_1=5 A$, I_2=6 A$, $I_3=10 A$, если первые два тока текут в одном направлении, а третий – в противоположном.
Из теоремы о циркуляции:
В нашем случае мы имеем:
Проведем расчеты и получим:
∆u2009.стрелка
∗Дельта ∗Гамма_.
Слободянюк А.И. Физика 10/12.12
Линии магнитного поля представляют собой замкнутые кривые, поэтому картины линий магнитного поля похожи на линии тока жидкости, движущейся с турбулентностью. Посмотрите еще раз на показанные ранее фотографии линий магнитного поля – массивные вихри. На рис. 49 показаны еще два примера линий магнитного поля, образованных длинными параллельными проводниками (три на рис. 49.a и три на рис. 49.b пять), через которые протекают равные токи.
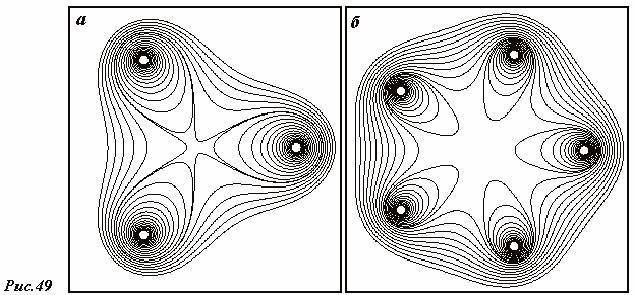
Для математического описания таких полей удобно использовать понятие векторной циркуляции.
Более точно, следует сказать, что знание циркуляции необходимо для описания любого векторного поля: напомним, что любое векторное поле однозначно определяется, если известны теоремы о потоке и циркуляции для векторов этого поля. Другое дело, что в электростатическом поле циркуляция вектора по любому контуру равна нулю, поэтому электростатическое поле – это потенциальное поле и для него можно ввести такое важное физическое свойство, как потенциал поля. Для магнитных полей циркуляция не имеет четкого физического смысла, но является скорее полезной вспомогательной математической величиной.
Определение циркуляции вектора магнитной индукции аналогично определению любой циркуляции векторного поля.
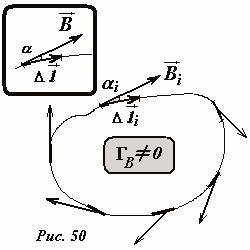
Рассмотрим любую замкнутую линию (это не обязательно должна быть линия многоугольника). Определим на этой прямой небольшой отрезок, определяемый вектором (
∆Дельта (рис. 50). Пусть вектор индукции магнитного поля на этом участке равен (
Вычисляем скалярное произведение этих векторов
∆Delta ∆Gamma_B = ∆dot ∆Delta ∆ = B ∆Delta l ∆cos ∆alpha ∆) ,
где α – угол между вектором индукции и вектором, касательным к выбранной линии (он совпадает с изолированной небольшой областью (
∆elpha ∆). Далее разделим всю замкнутую линию (рис. 50) на небольшие участки (
™vec l_i ™), на каждом из них вычисляем скалярное произведение ™(
∆Дельта ∆Гамма_.
∗Gamma_B = B_1 ∗delta l_1 ∗cos ∗alpha_1 + B_2 ∗delta l_2 ∗cos ∗alpha_2 + B_3 ∗delta l_3 ∗cos ∗alpha_3 + ∗ldots = ∗sum_i B_i ∗delta l_i ∗cos ∗alpha_i . (1)
Математическая конструкция, построенная таким образом, называется циркуляция вектора магнитной индукции по заданному контуру L. Его величина может быть положительной или отрицательной, знак определяется произвольным выбором направления, в котором проходит цепь, но, как обычно, предполагается, что направление против часовой стрелки является положительным.
Понятно, что циркуляция магнитного поля может быть отличной от нуля. Например, если в качестве произвольного контура выбрать замкнутую линию поля, то вектор индукции будет совпадать с направлением касательной, как уже говорилось, “мы все время будем обтекаться током”, когда она будет пройдена во всех сечениях.
Теперь нам нужно установить теорему для установления циркуляции вектора индукции. Отметим, что эта теорема является прямым следствием закона Био-Савара-Лапласа, можно сказать, что это еще одна математическая формулировка этого физического закона. Мы не будем заниматься строгим доказательством этой теоремы, а проиллюстрируем ее на простом примере.
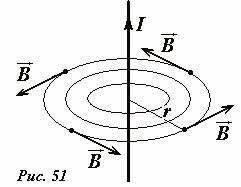
Пусть магнитное поле создается длинным прямым проводником, по которому течет электрический ток величиной I. Мы рассчитали индукцию такого поля: силовые линии представляют собой концентрические окружности с центрами на проводнике (рис. 51). Легко вычислить циркуляцию вектора индукции (1) по контуру, совпадающему с одной из линий силы (например, радиуса r). Действительно, на каждом участке этого контура вектор индукции направлен по касательной (поэтому все αi = 0), а модуль вектора индукции постоянен и равен (
B_i = frac< frac< frac< frac< I><2 frac r>), поэтому суммирование в формуле (1) сводится к вычислению длин отрезков малой окружности (после беглого рассмотрения можно сделать вывод, что она равна окружности), поэтому для данного контура
Gamma_B = ∆sum_i B_i ∆Delta l_i ∆cos ∆alpha_i = ∆frac
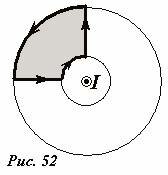
Таким образом, циркуляция по выбранному контуру равна произведению силы тока и магнитной постоянной, независимо от радиуса выбранной окружности. Такой прекрасный результат не может быть случайным – доказано [2], что такое же значение циркуляции будет получено для любого контура, окружающего токопровод, не обязательно прямой линии. Но что происходит в случае, когда петля не окружает проводник током? В этом случае вход будет равен нулю. Это можно очень легко доказать для схемы, показанной на рисунке 52 (сделай сам).
Для вектора магнитной индукции принцип суперпозиции верен, а циркуляция линейно выражается индукцией поля, поэтому принцип суперпозиции верен и для циркуляции магнитного поля.
Суммируя все эти утверждения, мы получаем окончательную формулировку Теорема о циркуляции: циркуляция вектора магнитной индукции в любом контуре равна сумме токов, проходящих через контур, умноженной на магнитную постоянную
∆Gamma_B = ∆Mu_0 I . (3)
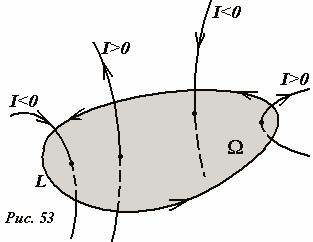
Сумма токов, протекающих через цепь (
I = sum_k I_k) понимается в алгебраическом смысле, т.е. токи могут быть положительными или отрицательными. Ток считается положительным, если его направление и направление циркуляции образуют правосторонний винт (рис. 53). Как и поток, циркуляция является интегральной (не точечной) характеристикой магнитного поля – из того, что циркуляция вдоль некоторого контура равна нулю, не следует, что магнитного поля нет – возможно, этот контур не охвачен никаким током, или их сумма равна нулю. Токи, не пересекающие контур, также создают магнитное поле, но циркуляция этого поля вдоль такого контура равна нулю.
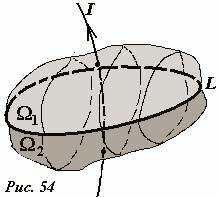
Наконец, давайте уточним, что имеется в виду под “течениями, пересекающими контур”, особенно если контур не плоский. Контур является замкнутой линией, поэтому вышеприведенное выражение следует понимать как то, что ток пересекает каждую поверхность (рис. 54), опирающуюся на контур (или можно также сказать “поверхность, натянутая на контур”). Легко доказать, что эта сумма токов не зависит от выбора поверхности, натянутой на данный контур: из закона сохранения электрического заряда следует, что в статическом случае (когда все токи и все заряды не меняются во времени) сумма токов, проходящих через любую замкнутую поверхность, равна нулю (“сколько входов, столько и выходов”).
Слово “электричество” происходит от греческого слова electron – янтарь, который электризуется при трении о шерстяную ткань. В природе известны два типа электрического заряда, которые условно называются положительным и отрицательным зарядами. Их взаимодействие также известно: заряды с одинаковыми именами отталкиваются друг от друга, заряды с разными именами притягиваются друг к другу.
Физика B1.B8.
Электростатика 1. Электрические заряды
Слово “электричество” происходит от греческого слова “электрон”. янтарь, который электризуется при трении о шерстяную ткань. В природе существует два типа электрических зарядов, которые условно называются положительным и отрицательным зарядами. Их взаимодействие также известно: заряды с одинаковыми именами отталкиваются друг от друга, заряды с разными именами притягиваются друг к другу.
Электрический заряд любого тела состоит из числа элементарных зарядов, равных приблизительно Этот заряд – заряд отрицательно заряженной частицы, называемой электроном. Электрон имеет массу покоя приблизительно. . Кроме отрицательно заряженного электрона существуют частицы с положительным элементарным зарядом. Стабильной частицей с положительным элементарным зарядом является протон. Протон является ядром атома водорода, самого легкого элемента таблицы Менделеева. Масса протона в 1836 раз больше массы электрона . Протон – это частица, образующая ядра всех элементов и определяющая заряд ядра. Электроны в атомах образуют электронную оболочку атома. Они могут покидать электронную оболочку атома или молекулы, превращая ее в положительный ион; они также могут присоединяться к другому атому или молекуле, превращая эти молекулы в отрицательный ион. Перенос электронов может происходить не только между атомами или молекулами, но и между телами, например, при их контакте друг с другом. Это явление называется электризацией тел при контакте. В результате электризации одни тела имеют избыток электронов, и эти тела заряжены отрицательно, а в других телах электронов не хватает, и эти тела заряжены положительно. Однако во всех случаях выполняется один из основных законов физики – закон сохранения электрического заряда: алгебраическая сумма зарядов частиц или тел, образующих электрически изолированную (замкнутую) систему, не меняется ни для каких процессов, происходящих в этой системе. Электрически изолированная система – это система тел (частиц), которые не обмениваются зарядами с телами, не входящими в эту систему.
B ∙ 2πr = μ0IN, где N – общее число витков, а I – ток, протекающий через витки катушки. Следовательно,
B=μ0IN/2πr
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, т.е. r2 – r1 << r, магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае
B=μ0W
Это выражение не учитывает радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Однако, в ограничении, любая часть тороидальной катушки может рассматриваться как длинная прямолинейная катушка. Такие катушки называются соленоидами. Вдали от концов соленоида модуль магнитной индукции выражается тем же соотношением, что и для тороидальной катушки.
хабарова
Для расчета магнитного поля удобно использовать законы и теоремы, аналогичные тем, которые используются для расчета электрического поля. Однако есть и различия.
Теорема Гаусса для вектора магнитной индукции.
Поскольку магнитных зарядов нет, линии индукции магнитного поля всегда замкнуты, а это значит, что поток вектора магнитной индукции через любую замкнутую поверхность всегда равен нулю.
В дифференциальной форме это означает, что divB=0.
2 Теорема о циркуляции вектора магнитной индукции.
Электростатическое поле – это потенциальное поле. Это означает, что работа электрических сил по перемещению заряда по замкнутому контуру равна нулю. Однако магнитное поле не является потенциальным полем. Циркуляция вектора магнитной индукции по замкнутому контуру может быть отлична от нуля, то есть равна произведению магнитной постоянной на сумму токов, протекающих по контуру. Теорема о циркуляции (также называемая законом полного тока) является прямым следствием закона Био-Савари-Лапласа и принципа суперпозиции.
В дифференциальной форме: rotB=μ0j
Существует множество практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является проблема расчета поля тороидальной катушки.
Предполагается, что катушка плотно намотана, т.е. виток к витку, на немагнитном тороидальном сердечнике. В такой катушке линии магнитной индукции замкнуты внутри катушки и представляют собой концентрические окружности. Они направлены таким образом, что если посмотреть вдоль них, то можно увидеть, что ток в катушках циркулирует по часовой стрелке. Одна из линий индукции с определенным радиусом r1 ≤ r < r2 показано на рисунке.
Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с линией индукции магнитного поля, показанной на рисунке. Из соображений симметрии следует, что модуль вектора одинаков вдоль всей линии. Исходя из теоремы о циркуляции, можно написать:
B ∙ 2πr = μ0IN, где N – общее число витков, а I – ток, протекающий в витках катушки. Следовательно,
B=μ0IN/2πr
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, т.е. r2 – r1 << r, магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае
B=μ0W
Это выражение не учитывает радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Однако в пределе любая часть тороидальной катушки может рассматриваться как длинная прямолинейная катушка. Такие катушки называются соленоидами. Вдали от концов соленоида модуль магнитной индукции выражается тем же соотношением, что и для тороидальной катушки.
Обратите внимание, что в центральной части катушки магнитное поле почти однородно и намного сильнее, чем за пределами катушки. На это указывает плотность линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью сосредоточено внутри соленоида.
План: 11.1, 11.2, 11.4, 11.7, 11.8, 11.9, 11.10, 11.11, 11.13, 11.14, 11.15 (например, все вопросы семинара)
Читайте далее:- Многоликий протон.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Электрический заряд и элементарные частицы. Закон сохранения заряда.
- Атомная структура.
- Определение количества нейтронов, протонов и электронов в атоме.
- Поток и циркуляция векторных полей; Школа для инженеров-электриков: Электротехника и электроника.
- Как работают атомы.